Experimental and Theoretical Investigations of Phonation Threshold Pressure as a Function of Vocal Fold Elongation

Summary

The relationship between the vocal fold elongation and the phonation threshold pressure (PTP) was experimentally and theoretically investigated. The PTP values of seventeen excised canine larynges with 0% to 15% bilateral vocal fold elongations in 5% elongation steps were measured using an excised larynx phonation system. It was found that twelve larynges exhibited a monotonic relationship between PTP and elongation; in these larynges, the 0% elongation condition had the lowest PTP. Five larynges exhibited a PTP minimum at 5% elongation. To provide a theoretical explanation of these phenomena, a two-mass model was modified to simulate vibration of the elongated vocal folds. Two pairs of longitudinal springs were used to represent the longitudinal elastin in the vocal folds. This model showed that when the vocal folds were elongated, the increased longitudinal tension would increase the PTP value and the increased vocal fold length would decrease the PTP value. The antagonistic effects contributed by these two factors were found to be able to cause either a monotonic or a non-monotonic relationship between PTP and elongation, which were consistent with experimental observations. Because PTP describes the ease of phonation, this study suggests that there may exist a nonzero optimal vocal fold elongation for the greatest ease for phonation in some larynges.

1. Introduction

Phonation threshold pressure (PTP) is defined as the minimum subglottal pressure required to initiate vocal fold oscillation [1], causing the transduction of aerodynamic energy into acoustic energy. PTP has received much attention for its potential value in developing laryngeal disease assessment methods [1, 2, 3, 4, 5, 6]. Titze predicted that PTP is directly related to vocal fold tissue properties and glottal configuration [1,2]. Specifically, he predicted

$$P_{th}=k_t{\mathit{Bcx}}_0/T,$$ (1)

where k_t is an empirical coefficient of pressure losses related to turbulent flow and glottal viscous resistance, B is the damping coefficient of tissue viscosity, c is the mucosal wave velocity, x₀ is the prephonatory glottal width, and T is the thickness of the vocal folds [1, 2]. Lucero analytically suggested the existence of an optimal glottal width to minimize PTP as a result of the loss of air pressure due to glottal viscous resistance [3, 4]. Using an in vitro setup, Ruty et al. studied the influence of the internal pressure of vocal folds on the phonation threshold pressure. They found that a vocal fold internal pressure of 5000 Pa corresponds to a minimum PTP in their model [5]. Tao and Jiang predicted the PTP value with a wide prephonatory glottal gap by inducing the pressure recovery effect at glottal exit [6]. Experimental measurements on physical models [7, 8] further confirmed the potential value of PTP as a parameter dependent upon biomechanical properties of the larynx. Because of this dependence, PTP may be considered a physiological indicator of the “ease” of phonation [7].

During phonation, elongation of the vocal folds or vocal fold strain is one important mechanism of controlling vocal fold configuration and voice production [9,10]. Studies of vocal fold elongation using finite-element modeling [9] and excised larynx experiments [10] have confirmed the importance of longitudinal elongation in controlling voice production. The vocal fold tissue contains an intricate extracellular matrix of longitudinal elastin parallel to the vocal fold surface. When the laryngeal muscles increase the vocal fold length, the tension of these longitudinal elastin fibers is increased [11, 12]. The increase in tension increases the PTP, because the mucosal wave velocity will be greater and the vocal fold thickness will be smaller (see equation 1). Therefore, it was believed that the elongation of the vocal folds monotonically increased PTP.

However, additional evidence for the relationship between PTP and vocal fold elongation comes from the relationship between PTP and fundamental frequency (F₀). While empirical data and theoretical models have attempted to determine the characteristics of PTP as a function of F₀, the monotonicity of the relationship is still largely uncertain. Vocal fold length is the primary configurational variable in the control of fundamental frequency, because it is responsible for changing the longitudinal tension and thus the longitudinal stress of the vocal fold cover [13]. Because the vocal fold thickness decreases and mucosal wave velocity increases as F₀ increases, PTP is expected to vary predictably with F₀ from Titze’s equation. Using PTP data from normal voice users and singers, Titze [14] found that a quadratic relationship empirically described PTP as a function of normalized F₀,

$$P_{th}=0.14+0.60{\left(\frac{F_0}{{\overline{F}}_0}\right)}^2,$$ (2)

where P_th is the PTP measured in kilopascals and F̄₀ was the mean F₀ for conversational speech of a given subject. However, he noticed that the behavior of PTP near the bottom of the frequency range was unclear, and he suggested that a minimum or optimal PTP for a “most comfortable pitch level” may exist [14]. Solomon et al. [15] expanded upon this hypothesis, and in a sample of eight subjects with untrained voices, the PTP was measured at ten different pitches across subjects’ 5% to 95% pitch range. One subject’s data could not be reliably fit to a regression (R² < 0.5), one subject’s data were best fit by a linear function, two subjects’ data were best fit by quadratic functions, and four subjects’ data were best fit by quartic functions. The overall function proposed to describe the sample population was quadratic without a linear term, like that of Titze’s,

$$P_{th}=0.34+0.028{\left(\frac{F_0}{{\overline{F}}_0}\right)}^2.$$ (3)

This relationship provided moderately good fit (R² = 0.548) [15]. Nevertheless, it was unclear from the data whether PTP was minimized at a pitch other than the lowest pitch in an individual’s range, because only three subjects showed a discernable trend of increasing PTP at the lower end of the pitch range.

While Titze’s equation (1) includes terms to show the impact of thickness and mucosal wave velocity on PTP, Lucero et al. [16] developed an equation for PTP based on a one-mass mucosal wave model which included the oscillation frequency explicitly,

$$P_{th}=\frac{k_t{x}_{0}B}{2\tau }\frac{\omega \tau }{sin(\omega \tau )},\forall \omega ,\tau :0<(\omega \tau )<\pi ,$$ (4)

where τ is the time delay for the mucosal wave to travel half the glottal thickness, and ω is the oscillation angular frequency, which can be converted to frequency by f = ω/(2π). This theoretical relationship suggests that PTP is proportional to F₀τ/sin(F₀τ).

In recent excised larynx experiments, we empirically noticed that although PTP generally increased with vocal fold elongation, the increase in PTP was not statistically significant when the vocal fold was elongated from 0% to 5%. Moreover, in some cases PTP non-monotonically varied as a function of elongation; a degree of elongation existed which minimized the PTP. Increased elongation beyond the optimal elongation or decreased elongation below the optimal elongation both increased the PTP. In most cases, the PTP monotonically increased as a function of elongation, and the optimal elongation for minimizing PTP appeared to be the minimum elongation. These observations are not surprising, given the variability in monotonicity of PTP as a function of F₀ and the strong relationship between F₀ and vocal fold elongation. However, this phenomenon regarding the relationship between PTP and elongation has not been explicitly reported or theoretically explained.

In this study, we experimentally and theoretically investigated the relationship between PTP and vocal fold elongation. Excised canine larynx experiments were conducted to examine the effect of elongation on PTP. Concurrently, to explain our experimental findings, a two-mass model of the vocal folds was modified to predict the relationship between PTP and vocal fold elongation. In most previous vocal fold models, the vocal folds were simplified to one or several spring oscillators, and the restoring force due to lateral deflection of vocal fold tissue was represented by equivalent lateral springs [1,3,4,17,18,19,20,21,22]. In this study, in order to simulate vibration of the elongated vocal folds, we modified the traditional two-mass model by adding two pairs of longitudinal springs to represent the longitudinal elastin in the vocal folds. A set of differential equations described its dynamic behavior, and the relationship between PTP and vocal fold elongation was investigated.

2. Investigation in an experimental model

2.1. Procedure

Seventeen excised canine larynges were obtained from canines not sacrificed for this study. Larynges with pathologies or trauma were excluded from the study. The larynges were stored frozen in 0.9% saline solution until experimentation. Before experimentation, the individual larynges were thawed slowly to 38 °C. Larynges were mounted on a bench apparatus as described by Jiang et al. [23,24,25], and were fixed to a pseudolung by a metal pull clamp (Figure 1). A pseudolung is a chamber that has the dampening characteristics of the respiratory system and is used to simulate the role of the lungs in phonation. The aforementioned bench apparatus was designed to simulate the role of the pulmonary system in phonation. Two three-pronged micromanipulators were inserted bilaterally into the arytenoids, allowing for the three-dimensional control of the arytenoids necessary for proper vocal fold adduction. An anterior micromanipulator was sutured to the laryngeal prominence of the thyroid cartilage, providing precise control of the elongation of the vocal folds. Calipers were used to record the resting, anatomically relaxed vocal fold length. Vocal fold length was defined as the membraneous length: from the anterior commissure to the vocal processes. The larynges were hydrated by frequent, liberal application of 0.9% saline solution.

Figure 1.

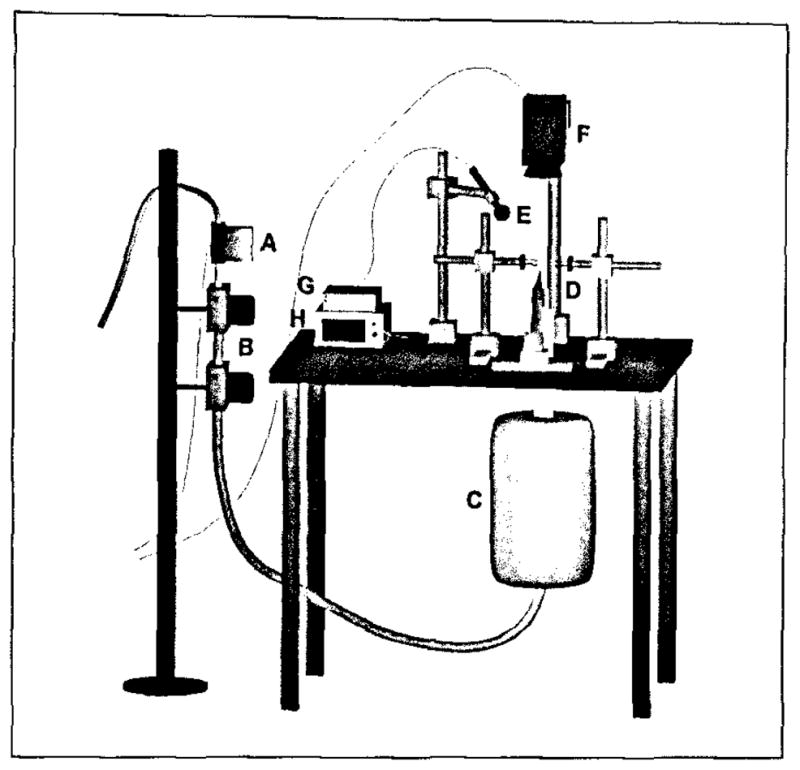
Schematic diagram of the experimental setup based on excised larynx. (A) Flow meter with pressurized air input from an internal building source, (B) Two heater-humidifiers in series, (C) pseudolung, (D) larynx mounting apparatus consisting of bilateral three-pronged micromanipulators inserted into the arytenoids and an anterior micromanipulator sutured to the laryngeal prominence of the thyroid cartilage, (E) microphone, (F) digital camera, (G) acoustic preamplifier, (H) manometer.

2.2. Experimentation

To minimize any confounding environmental noise in the acoustic measurements, all experimental investigations were conducted in a triple-walled sound-attenuated room. The larynx was mounted on a bench apparatus within the sound-proof room as shown in Figure 1. Acoustic measurements were obtained using a Symetrix preamplifier (Model 302; Symetrix, Inc., Mountlake terrace, WA) and a Sony microphone (model ECM-88; Sony Electronics, Inc., New York, NY) positioned approximately 10.0 cm from the glottal axis at a 45° angle. Subglottal pressure measurements were recorded with a Heise digital pressure meter (901 series; Ashcroft Inc., Stratford, CT). Custom LabVIEW 7.1 software (National Instruments Corp.) was designed to simultaneously measure acoustic and pressure signals, converting them from their raw voltages into their respective standard units in real time.

Each larynx was initially mounted at an anatomically relaxed vocal fold length; no additional tension from the anterior micrometer was applied. To measure PTP, subglottal pressure was controlled manually and increased slowly at a rate no greater than 1 cm H₂O/s from 0cm H₂O until phonation was both heard by the experimenter and observed in the acoustic signal trace on the LabVIEW 7.1 custom program. The phonation onset threshold was observed in the acoustic signal and spectrogram, and the subglottal pressure measurement at that time instant was recorded as the PTP. For each larynx, PTP was measured five times at four different vocal fold elongations: 0% (anatomically relaxed), 5%, 10%, and 15%. These elongations were calculated from the anatomically relaxed vocal fold length and achieved by adjusting the anterior micrometer slowly. The mean and standard deviation of PTP for each elongation for each larynx were calculated, and a one-way ANOVA on ranks test was performed on the PTP data.

2.3. Results

The mean PTP of the canine larynges under control conditions was 7.25 ± 2.91 cm H₂O. Because of inherent differences in biomechanical properties of different larynges, the PTP values for each elongation were normalized to a percentage change of the PTP at an anatomically relaxed vocal fold length (0% elongation). Thus, the normalized PTP at an elongation e for a given larynx is

$$\mathrm{\Delta }{P}_{th}(e)=\frac{P_{th}(e)-P_{th}(0)}{P_{th}(0)},$$ (5)

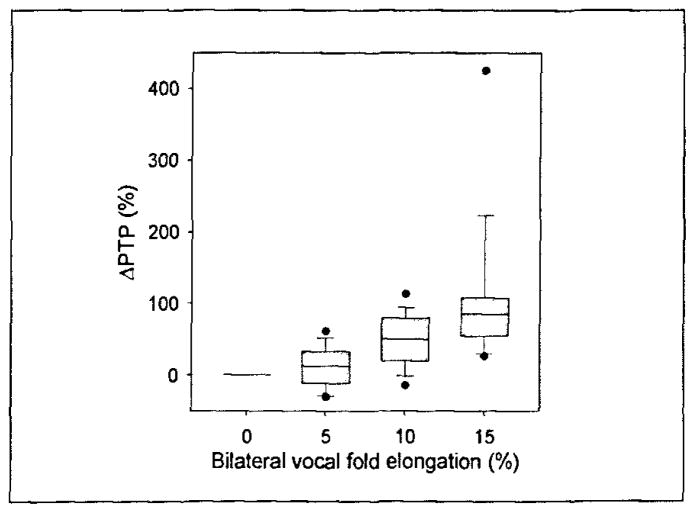
where ΔP_th(e) is the normalized PTP and P_th(e) is the absolute PTP. Figure 2 is a box plot of the normalized PTP in excised canine larynges with elongated vocal folds. It is important to note from Figure 2 that the 5% elongation group extends from a minimum of −29.8% to 61.7% PTP change from the anatomically relaxed vocal fold length group. The 0% elongation group exhibited the lowest PTP in ~ 70% (12 of 17) of all larynges (see Table I). The 5% elongation group exhibited the lowest PTP in ~ 30% (5 of 17) of all larynges. One-way ANOVA on ranks suggested that statistically significant differences existed among the median PTP from different elongation groups (p < 0.001). Post-hoc analyses further suggested that statistically significant differences existed between 0% and 10%, as well as 0% and 15% elongation groups. However, the difference between the 0% and 5% elongation groups was not significant. This indicates that the 0% and 5% elongation group PTP values of the sample population are distributed over similar domains, and that for a given larynx the minimum PTP may exist in one of these elongation groups.

Figure 2.

The percent change in PTP from the PTP at the anatomically relaxed vocal fold length. The upper and lower edges of the box represent the 75th and 25th, percentile, respectively, and a line within each box marks the median PTP for the given elongation level. Whiskers above and below each box represent the 90th and 10th percentiles, respectively. Statistical outliers are graphed as points.

Table I.

The change in PTP among different vocal fold elongation groups in a sample population of 17 excised canine larynges. Asterisks after the larynx number indicate that the 5% elongation group minimized PTP.

Larynx	Raw (cm H2O)				Normalized (%)
	0%	5%	10%	15%	0%	5%	10%	15%
1	4.77±1.01	4.80±0.05	5.91±1.08	7.04±1.45	0.00	0.67	23.81	47.49
2	6.48±0.91	8.34±0.74	11.56±0.79	14.56±1.21	0.00	28.72	78.48	124.90
3*	9.60±0.81	6.74±0.62	8.25±1.08	16.88±1.26	0.00	−29.83	− 14.05	75.86
4	4.09±0.73	5.76±0.91	7.54±1.21	11.17±1.81	0.00	40.74	84.21	172.98
5	4.46±1.00	5.95±1.05	7.12±1.33	9.72±1.11	0.00	33.28	59.51	117.77
6*	10.05±0.58	8.75±0.62	12.41±1.10	15.56±1.23	0.00	−12.98	23.40	54.76
7	4.74±0.52	7.14±0.31	5.88±0.82	8.28±0.58	0.00	50.43	24.03	74.47
8*	8.91±0.43	8.02±0.28	9.43±0.58	16.92±1.18	0.00	−10.01	5.89	89.89
9	8.65±0.61	10.75±1.03	13.02±0.36	16.04±1.06	0.00	24.34	50.53	85.52
10	4.29±0.22	5.76±0.25	8.17±0.42	8.33±0.49	0.00	34.07	90.24	94.07
11	7.31±1.01	7.34±0.93	8.47±1.21	11.23±0.89	0.00	0.46	15.83	53.64
12	3.90±0.33	4.45±0.52	7.04±1.52	5.09±0.59	0.00	14.24	80.49	30.69
13	8.50±0.72	9.58±1.19	8.68±0.77	15.84±2.28	0.00	12.67	2.08	86.31
14	5.77±1.73	6.49±0.73	7.16±0.81	7.29±0.59	0.00	12.52	24.02	26.35
15	6.58±0.73	10.64±0.87	14.02±0.60	13.05±1.35	0.00	61.74	113.09	98.46
16*	14.16±1.21	10.16±0.65	24.85±2.89	74.33±4.90	0.00	−28.25	75.48	424.86
17*	11.05±0.59	9.12±0.74	19.81±1.19	19.96±1.93	0.00	−17.51	79.29	80.64

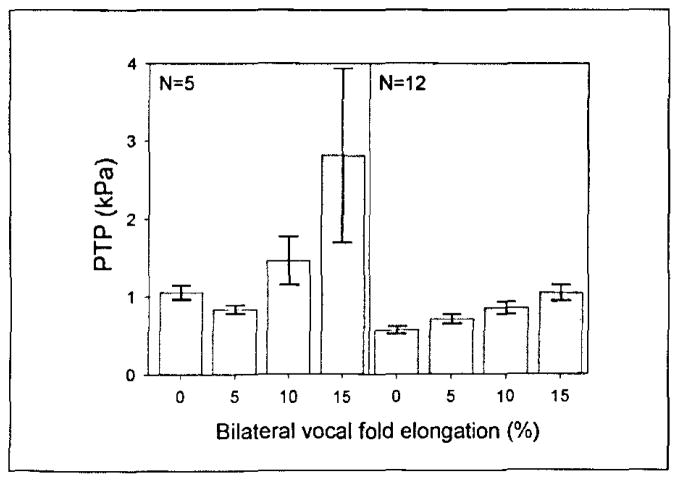
Figure 3 is a bar graph of the twelve larynges that increased monotonically with elongation and the five larynges that did not, illustrating the fact that the 5% elongation group was characteristically low in some larynges. The detailed experimental results are presented in Table I.

Figure 3.

The average PTP of the five larynges that did not increase monotonically with elongation and the twelve larynges that did. Whiskers above and below each bar represent the standard error.

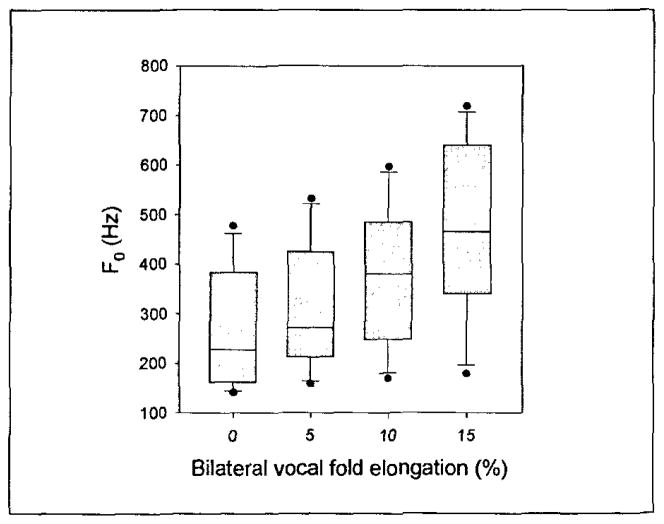
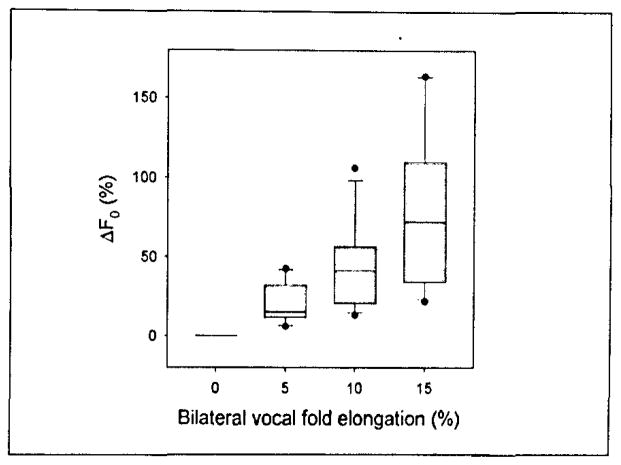
Figure 4 is a box plot of the phonation threshold frequency data. One-way ANOVA on ranks suggested that statistically significant differences existed between the median frequencies in each elongation group (p = 0.013). However, the relationship between phonation threshold frequency and vocal fold elongation was monotonic in all cases (Figure 5).

Figure 4.

Phonation threshold frequency of the samples. The upper and lower edges of the box represent the 75th and 25th, percentile, respectively, and a line within each box marks the median PTP for the given elongation level. Whiskers above and below each box represent the 90th and 10th percentiles, respectively. Statistical outliers are graphed as points.

Figure 5.

The percent change in phonation threshold frequency from the phonation threshold frequency at the anatomically relaxed vocal fold length. The upper and lower edges of the box represent the 75th and 25th, percentile, respectively, and a line within each box marks the median PTP for the given elongation level. Whiskers above and below each box represent the 90th and 10th percentiles, respectively. Statistical outliers are graphed as points.

3. Investigation in a theoretical model

Two main physiological effects can be attributed to vocal fold elongation. First, elongation alters the vocal fold geometry, specifically the vocal fold length and the area involved in the tissue-airflow interaction. Second, elongation changes the tension in the vocal fold tissue. In order to explain the experimental observations from a theoretical basis, a modified tensile two-mass vocal fold model developed from Ishizaka and Flanagan’s two-mass model [17] was used to simulate vocal fold elongation. This model provides a simplified description of the vocal fold elongation in comparison to multiple mass models, and has been demonstrated to be useful in modeling phonation [5].

3.1. The tensile two-mass vocal fold model

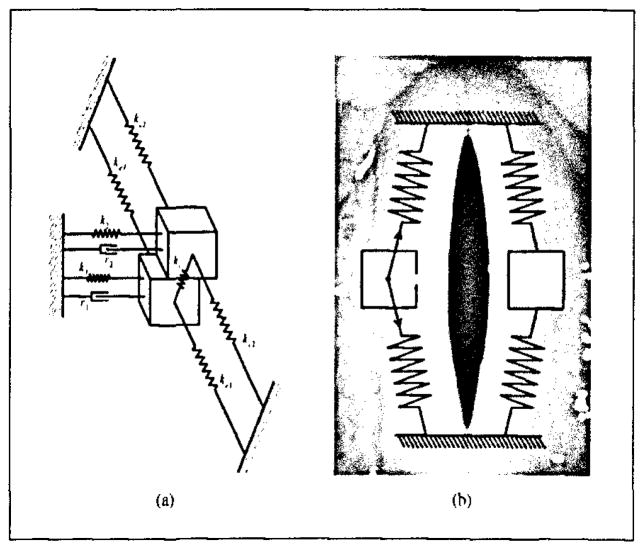
Figure 6a shows a schematic diagram of our model. The difference between the tensile two-mass model and the traditional two-mass model was that two pairs of longitudinal springs, k_e1 and k_e2, were used to model the longitudinal elastin in the vocal fold. Assuming that the neutral vocal fold length is L₀ and the prephonatory vocal fold elongation is e₀, the initial vocal fold length was represented as L = (1 + e₀)L₀. When the mass m_i departs from its balance position and moves a lateral distance x_i, as shown in Figure 6b, the total vocal fold elongation due to initial elongation and lateral displacement can be represented as

Figure 6.

The tensile two-mass model. (a) Schematic diagram of the tensile two-mass vocal fold model. (b) Restoring force due to the elongation spring.

$$e_i(e_0,x_i)=\sqrt{4{(x_i/L_0)}^2+{(1+e_0)}^2}-1.$$ (6)

For a small amplitude (x_i ≪ L₀) vibration characteristic at phonation threshold, equation (6) can be reduced to e_i(e₀, x_i) ≈ e₀. The longitudinal elastic force σ_i (i = 1, 2) due to the elongation ei of the i-th longitudinal springs can be estimated from σ_i = f_i(e), where the function fi describes the nonlinear force-deformation relationship of the vocal fold tissue in the anterior-posterior direction. According to the force composition law, the resultant force in the x-direction due to the longitudinal elongation is

$${\sigma }_{xi}=\frac{4x}{L}{f}_i\left[e_i(e_0,x_i)\right].$$ (7)

Therefore, modifying the dynamic equation of the traditional two-mass model [17, 18], the vibration dynamics of the tensile two-mass model can be described using the following equations:

$$m_1\frac{{\mathrm{d}}^2{x}_1}{\mathrm{d}{t}^2}+r_1\frac{\mathrm{d}{x}_1}{\mathrm{d}t}+k_1{x}_1+k_c(x_1-x_2)+\frac{4x_1}{L}{f}_1\left[e(e_0,x_1)\right]=P_1{A}_1+F_1,$$ (8)

$$m_2\frac{{\mathrm{d}}^2{x}_2}{\mathrm{d}{t}^2}+r_2\frac{\mathrm{d}{x}_2}{\mathrm{d}t}+k_2{x}_2+k_c(x_2-x_1)+\frac{4x_2}{L}{f}_2\left[e(e_0,x_2)\right]=F_2,$$ (9)

where r_i (i = 1, 2) is the damping constant, k_i is the spring constant of mass m_i, and k_c is stiffness of the coupling spring. Just as in the standard two-mass model [17, 18], we assume the air pressure P₁ is applied on the lower mass m₁. In this study, we focused mainly on the PTP; under low subglottal pressure levels, the small-amplitude oscillation condition of the vocal folds is satisfied. In this situation, the lateral displacement of the vocal fold is small and the nonlinear factor of the lateral springs can be ignored. Therefore, the linear force-displacement relationship (Hooke’s law) is used for the lateral springs. A₁ is the interaction area between vocal fold tissue and glottal airflow. According to the conversion of volume of an incompressible tissue, the cross-sectional area S₀ of the vocal fold is decreased to S₀/(1 + e₀) when the vocal fold is elongated to (1 + e₀)L₀. Additionally, because the vocal fold tissue is transversally symmetric [11], it can be assumed that the size changes in the medial-lateral direction are the same as those in the inferior-superior direction. Therefore, $A_1=L_0{d}_1\sqrt{1+e_0}$.

$$F_1=-\mathrm{\Theta }(-a_1)c_1{a}_1/2L,F_2=-\mathrm{\Theta }(-a_2)c_2{a}_2/2L$$ (10)

are the impact forces due to vocal fold collision [17, 18]. c_i = 3k_i is the additional spring constant during collision,

$$P_1=P_s\left[1-\mathrm{\Theta }(a_{min}){\left(a_{min}/a_1\right)}^2\right]\mathrm{\Theta }(a_1)$$ (11)

is the intraglottal pressure following the Bernoulli equation, and P_s is the subglottal pressure. a₁ and a₂ are approximations of the lower and upper glottal areas, respectively, such that

$$a_1=2(x_{01}+x_1)L,a_2=2(x_{02}+x_2)L,$$ (12)

where x₀₁ and x₀₂ are the prephonatory lower and upper glottal half-width. a_min is the minimum glottal area,

$$a_{min}=min\left(a_{2}1,a_2\right)=\{\begin{array}{ll}{a}_1,\hfill & x_1<x_2,\hfill \\ a_2,\hfill & x_2\le x_1.\hfill \end{array}$$ (13)

The function Θ(x) describing the collision is approximated by

$$\mathrm{\Theta }(x)=\{\begin{array}{ll}tanh(50x/x_0)\hfill & x>0,\hfill \\ 0\hfill & x\le 0.\hfill \end{array}$$ (14)

For a normal vocal fold, the following default model parameter values were used: m₁ = 0.125, m₂ = 0.025, r₁ = r₂ = 0.02, k₁ = 0.08, k₂ = 0.008, c₁ = 3k₁, c₂ = 3k₂, k_c = 0.025, d₁ = 0.25, d₂ = 0.05, x₀₁ = x₀₂ = 0.00893, L₀ = 1.4, and ρ = 0.00113 [17]. Alipour and Titze [11] obtained the stress-strain data of canine vocal fold tissue in the range of 0% to 40% vocal fold elongation by using a slow cyclic stretch and release technique. They proposed an exponential function to fit the experimentally measured force-elongation data. Therefore, assuming a cross-sectional area 1.0 cm2 of vocal folds, we considered a longitudinal force using the formulae by Ishizaka and Flanagan [17] and Alipour and Titze [11]:

$$f_1(e)=10f_2(e)=A\left[exp(Be)-1\right]·{10}^{-2},$$ (15)

where 0% ≤ e ≤ 40% is the longitudinal elongation and f_i(e) (i = 1.2) is the elastic force of the longitudinal spring. A subglottal pressure as low as PTP usually corresponds to a small-amplitude oscillation; in this situation, only the vocal fold cover is vibrating and the vocal fold body is nearly stationary [26]. Therefore, the parameters in equation (15) are set as those measured from the vocal fold cover, that is, A = 7.1 ± 2.6, B = 4.2 ± 0.73 [11].

For insufficient subglottal pressure, the vocal fold model produces the fixed points $x_i^{\ast }(i=1,2)$ (i = 1, 2) that can be determined by setting it and its time differentiation term in equations (8) and (9) equal to zero. In order to describe the stability of these fixed points in our tensile model, we followed the analysis method used by Steinecke and Herzel [18]. A critical subglottal pressure can be determined for the fixed points [18, 27],

$$P_{\text{crit}}\approx \frac{x_{01}}{2A_1}\frac{K_1{K}_2+k_c(K_1+K_2)}{K_2},$$ (16)

where

$$\begin{array}{l}{K}_1=k_1+(4/L)f_1\left[e(e_0,x_1)\right],\\ K_2=k_2+(4/L)f_2\left[e(e_0,x_2)\right].\end{array}$$ (17)

Below P_crit, only one stable solution exists where $x_i^{\ast }=0$. From equation (16), we found that P_crit increases with K₁ and K₂, but decreases with the cross-sectional area A₁. Substituting $A_1=L_0{d}_1\sqrt{1+e_0}$ and equation (15) into equation (16), the derivative of with respect to the elongation e₀ can be determined,

$$\frac{\mathrm{d}{P}_{\text{crit}}}{\mathrm{d}{e}_0}=C_1\frac{(AB-C_2)+\left(B-1.5/(1+e_0)\right)f_2}{\sqrt{{(1+e_0)}^3}}·{10}^3,$$ (18)

where C₁ is a positive constant related to the prephonatory glottal configuration and C₂ is a constant related to k₁, k₂ and k_c. If AB is large enough to make (AB − C₂) > 0, dP_crit/de₀ is always positive and P_crit monotonically increases with the elongation. However, if AB is small enough to make (AB − C₂) < 0, it follows that f₂ approaches 0 and dP_crit/de₀ < 0 when e₀ ≪ 1. This indicates that P_crit decreases with the elongation. With sufficient elongation, f₂ exponentially increases with e₀ and dP_crit/de₀ > 0 is satisfied, causing P_crit to increase with elongation. This analysis indicates that a non-monotonic relationship between P_crit and e₀ could exist, depending upon the vocal fold stiffness and prephonatory glottal configuration.

The above analysis is based on the small amplitude simplification [18, 27] for a transcritical bifurcation, where stability is exchanged between an unstable and a stable fixed point. However, voice production is based on a Hopf bifurcation, where an unstable fixed point is replaced by a stable limit cycle. PTP is defined as the subglottal pressure at the Hopf bifurcation. To examine the above analysis, the tensile two-mass vocal fold model was solved numerically using a fourth-order Runge-Kutta method with a time step of 0.01 ms. Review of the model equations (3), (4) suggested that elongation of vocal fold could generate two physiological effects. One is that elongation changes the length and the medial surface area A1 of the vocal fold, and another is that the elongation increases the tension in the vocal fold. These two effects could simultaneously contribute different influences on PTP. We let f₁ = f₂ = 0 in equation (8) and (9) to simulate the influence of increases in length and area only on PTP. Line 7 in Figure 7 represents this result. It was seen that increased length and area monotonically decreased the PTP. Similarly, by using D₁L₀ and (x_i/L₀)f_i[e(e₀, x_i)] instead of the term A₁ and (x_i/L)f_i[e(e₀, x_i)] in equation (8) and (9), we simulated the contribution of increased tension on PTP. Dotted lines 1, 2, and 3 in Figure 7 illustrate the predicted results, where line 1 corresponds to the largest level of longitudinal stiffness (A = 7.1 + 2.6, B = 4.2 + 0.73), line 2 corresponds to a medium level of longitudinal stiffness (A = 7.1, B = 4.2), and line 3 corresponds to the smallest level of longitudinal stiffness (A = 7.1 – 2.6, B = 4.2 – 0.73). These values cover the variability in stiffness as reported by Alipour and Titze [11]. These results demonstrate the increase of PTP with tension. Because the longitudinal stress-strain relationship is nonlinear, it follows that the PTP-tension relationship is also nonlinear. When the strain (or elongation) is small, the PTP slowly increases with strain. When the strain is large, the PTP quickly increases with strain.

Figure 7.

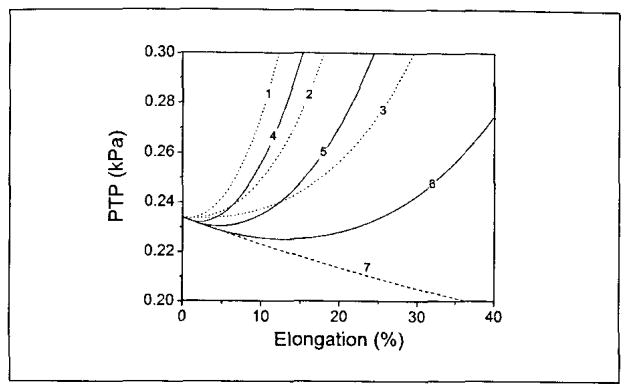
The PTP predicted by the tensile two-mass model as a function of elongation. Lines 1, 2, 3 illustrate the contribution of increased tension on the PTP value, where line 1 2, 3 correspond to the longitudinal stiffness parameters A = 7.1 + 2.6 and B = 4.2 + 0.73, A = 7.14 and B = 4.2, and A = 7.1 – 2.6 and B = 4.2 – 0.73, respectively. Line 7 represents the influence of increases in length and interaction area on the PTP. Lines 4, 5, 6 give the PTP change with the increases of elongation, where the stiffness parameters used to predict lines 4, 5, 6 correspond to those used to predict lines 1, 2, 3, respectively.

These two effects together determine the PTP of the vocal fold. The solid lines in Figure 7 give the PTP predicted by our model as a function of longitudinal elongation, where lines 4,5, and 6 correspond to large (A = 7.1 + 2.6, B = 4.2 + 0.73), medium (A = 7.1, B = 4.2), and small (A = 7.1 – 2.6, B = 4.2 – 0.73) levels of longitudinal stiffness, respectively. From these graphs, one case is that the relationship between the theoretically calculated PTP and longitudinal elongation is non-monotonic. In this numerical model, as vocal fold elongation increases from an anatomically relaxed length, PTP initially decreases. However, once elongation exceeds a certain threshold, PTP increases with elongation. For vocal folds with large longitudinal stiffness (A = 7.1 + 2.6, B = 4.2 + 0.73), the non-monotonic relationship between PTP and elongation is not prominent; the minimum PTP value corresponds to about 2% elongation (see solid line 4 in Figure 7). This is another case of this model, which is common experimentally: PTP increases monotonically due to large longitudinal stiffness. However, for vocal folds with relatively small longitudinal stiffness (A = 7.1 – 2.6, B = 4.2 – 0.73), the non-monotonic relationship between PTP and elongation was significant; the minimum PTP value existed at 13% elongation (see solid line 5 in Figure 7).

Figure 8 illustrates the influence of the stiffness parameters A and B on the predicted PTP value. It can be seen that the increase of either A or B will increase the PTP value. Moreover, it is found that the increase of these stiffness parameters will make the elongation corresponding to the minimum PTP value move toward zero.

Figure 8.

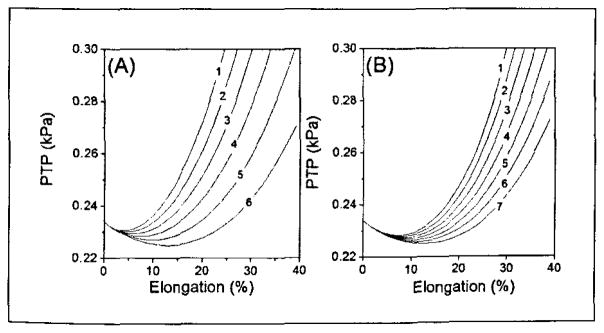
The influence of the longitudinal stiffness parameters A and B on the PTP value. (a) The influence of the stiffness parameter A on the PTP value, where the parameter B is fixed at 3.47 and lines 1 through 6 correspond to A = 9.5, 8.5, 7.5, 6.5, 5.5, and 4.5, respectively. (b) The influence of the stiffness parameter B on the PTP value, where the parameter A is fixed at 4.5 and lines 1 7 correspond to B = 4.9, 4.7, 4.5, 4.3, 4.1, 3.9, 3.7, and 3.5, respectively.

4. Discussion

The above investigations into the relationship between PTP and elongation suggest that when the vocal folds are elongated, two scenarios exist. We propose two possible cases to explain the phenomena observed in both the excised larynx experiments and theoretical models:

1. If the longitudinal stiffness is large, it predominantly dictates the change in PTP at all elongations and the optimal vocal fold length to minimize PTP is very close to the anatomically relaxed length. In this case, the difference between the optimal vocal fold length to minimize PTP and the anatomically relaxed length is not prominent, and thus it is difficult to detect. Therefore, a monotonic relationship between PTP and vocal fold elongation is observed in larynges with large longitudinal stiffness. If the stiffness of the vocal fold tissue is sufficiently high, the optimal elongation to minimize PTP is equal to the anatomically relaxed length. Although this is one case of the theoretical model, according to our experimental observations this is the more common situation (as seen in 12 larynges).

2. If the longitudinal stiffness is low, the airflow-tissue interaction area factor predominantly dictates the change in PTP at low levels of elongation, and thus PTP initially decreases with the elongation. The longitudinal stress exponentially increases with elongation, and will dominate the change in PTP when the elongation is large. PTP will increase with elongation again after it reaches its minimum value. Therefore, in this scenario there is an observable non- monotonic relationship between PTP and vocal fold elongation, as we observed in five excised larynges; the longitudinal stiffness may have been small in these samples. This is another case of the theoretical model, but is a less common case according to our experimental observations.

The present study intends to introduce a preliminary theoretical framework for empirical observations of these phenomena. Our model accounts for all of the experimental data. The case of our theoretical model in which a monotonic relationship exists was common experimentally, and is well understood. The other case of our model in which a non- monotonic relationship exists was less common experimentally.

One limitation of the present study is caused by the elongation interval size. The vocal folds of small canine larynges are on the order of 10 mm in length, which corresponds to a 0.5 mm change in tissue length if the elongation interval is 5%. The 5% elongation interval experimental design could miss the existence of a non- monotonic PTP-elongation relationship if the minimum PTP existed between 0% and 5% vocal fold elongation and the PTP at 5% vocal fold elongation was greater than the PTP at 0% vocal fold elongation. This limitation of the study causes the number of non-monotonic relationships observed in the sample population to be a potentially conservative estimate because it is possible that the experimental design obscured the existence of additional larynges that are non-monotonous in the course of PTP.

Changes in elongation or strain are dependent upon vocal fold posturing, including changes in intrinsic laryngeal muscle contraction. These tensile strain changes are caused primarily by antagonistic effects of cricothyroid and thyroarytenoid muscles and may be induced voluntarily, as in speech or singing, or involuntarily, as by pathology. Knowledge of the physical effect of elongation on PTP contributes to our understanding of this parameter as a measure of the biomechanical properties of the vocal folds and thus as an indicator of the ease of phonation. The results of this study suggest that in some larynges, a slightly elongated or strained vocal fold beyond the anatomically relaxed length may be optimal for the ease of phonation as quantified by PTP. Alternatively, in other larynges, no significant elongation beyond the anatomically relaxed length is best for minimizing PTP and thus the ease of phonation. This finding is clinically relevant, as some disorders such as vocal fold atrophy and paralysis alter the vocal fold tension. Surgical methods to approximate the vocal folds could benefit from basic science knowledge of the optimal degree of tension for phonation; however, more research is needed to clarify the complex relationships discussed here.

This preliminary report adds to the existing evidence in the literature describing the relationship between PTP and vocal fold elongation. Future studies should consider incorporating measurements of vocal fold stiffness into investigations of the optimal degree of elongation to minimize PTP. These relationships could be further investigated by measuring the PTP of excised larynges before and after a dehydration treatment; Chan et al. previously determined that dehydration significantly increases the vocal fold stiffness [28].

5. Conclusion

In this study, we investigated the relationship between vocal fold elongation and phonation threshold pressure in both ex vivo larynges and in a theoretical model. It was found that the 0% elongation state exhibited the lowest PTP for twelve larynges, and in these larynges the PTP-elongation relationship was monotonic. The other five larynges showed a non-monotonic relationship between PTP and elongation; the 5% elongation state exhibited the lowest PTP for these larynges. A tensile vocal fold model was proposed to simulate the vibration of the elongated vocal folds. Both the monotonic and non-monotonic cases of the theoretical model were observed theoretically. Numerical simulation showed that the non- monotonic relationship between PTP and elongation could be the result of competition between the increase in tissue tension and medial surface area. This case was less common experimentally. Because PTP describes the ease of phonation, this study suggests that there may exist an optimal elongation for the ease of phonation.