Motion Artifact Reduction in Pediatric Diffusion Tensor Imaging Using Fast Prospective Correction

Abstract

Purpose

To evaluate the patterns of head motion in scans of young children and to examine the influence of corrective techniques, both qualitatively and quantitatively. We investigate changes that both retrospective (with and without diffusion table reorientation) and prospective (implemented with a short navigator sequence) motion correction induce in the resulting diffusion tensor measures.

Materials and Methods

Eighteen pediatric subjects (aged 5–6 years) were scanned using 1) a twice-refocused, 2D diffusion pulse sequence, 2) a prospectively motion-corrected, navigated diffusion sequence with reacquisition of a maximum of five corrupted diffusion volumes, and 3) a T₁-weighted structural image. Mean fractional anisotropy (FA) values in white and gray matter regions, as well as tractography in the brainstem and projection fibers, were evaluated to assess differences arising from retrospective (via FLIRT in FSL) and prospective motion correction. In addition to human scans, a stationary phantom was also used for further evaluation.

Results

In several white and gray matter regions retrospective correction led to significantly (P < 0.05) reduced FA means and altered distributions compared to the navigated sequence. Spurious tractographic changes in the retrospectively corrected data were also observed in subject data, as well as in phantom and simulated data.

Conclusion

Due to the heterogeneity of brain structures and the comparatively low resolution (~2 mm) of diffusion data using 2D single shot sequencing, retrospective motion correction is susceptible to distortion from partial voluming. These changes often negatively bias diffusion tensor imaging parameters. Prospective motion correction was shown to produce smaller changes.

Diffusion weighted imaging (DWI) is a noninvasive technique that measures signal attenuation due to the random thermal motion of water in tissue. DTI allows quantification of microstructural changes in brain maturation (1–6) and in patients with white matter (WM) disorders (7–9).

Head motion causes misalignment of the diffusion volumes and, furthermore, individual voxels are exposed to a slightly different diffusion encoding direction/gradient than the desired one (10–12). Motion during diffusion sensitization gradients also causes signal dropouts in the images (13). Echo planar imaging (EPI) has been implemented in most diffusion pulse sequences to minimize the effect of subject motion by acquiring the whole image within a single shot (14).

Generally, some form of retrospective motion correction is applied computationally to estimate and correct any misalignment between diffusion volumes. These retrospective techniques rely on coregistration, which is limited even in conventional magnetic resonance imaging (MRI) by blurring artifacts and the influence of through-plane motion on the local history of magnetization. In DWI, the challenges are even greater due to low image contrast, low signal-to-noise ratio (SNR) with high b-values, and differing image contrasts per gradient. Several (often computationally expensive) algorithms have been developed for further outlier detection and rejection in DWI, such as RESTORE (15), PATCH (16), least median squares or least trimmed squares (LTS) (17), and local binary patterns (LBP) (18).

One improvement to retrospective, postscan motion estimation is to track and record the physical repositioning of the subject during data acquisition. This has the benefit of detecting effects leading to potential signal corruption, outliers, and dropouts in real time, with the additional ability to reacquire corrupted data immediately. This prospective motion correction may be performed using the diffusion sequence data itself, termed “self-navigation” (13,19), or by implementing short additional navigation pulses in a diffusion sequence (20–26). While the former “self-navigation” methods avoid the need for extra pulses, they are affected by the constantly changing DWI contrasts, and the online registration of an entire DW volume to a reference image can cause a significant increase in scan time (24). Despite the advanced strategies used in navigator design, nearly all navigated diffusion pulse sequences developed to date have been susceptible to effects of the diffusion weighting itself. This is due to the fact that most of the navigator pulses have been inserted before the readout gradients.

Recently, a fast navigator pulse sequence was introduced that obtains motion estimates that are unaffected by diffusion weighting (27). This diffusion navigation sequence can be implemented for different b values, on different types of scanners, for different head coils, and with or without parallel imaging (28). Moreover, the log file that is generated by the navigated diffusion sequence at the end of the scan can be analyzed, allowing improved positioning of subject populations by restraining the most common directions of motion using special foam pillows around the subject. Finally, it also has the ability to display each diffusion volume during the scan. In this manner, the scan can either be terminated at an early stage if there is severe motion, or the subject can be instructed to remain still. After navigated scanning, further processing steps (eg, outlier rejection, eddy current correction, etc.) may then be implemented as standard in existing pipelines.

The aim of the present study was to assess differences of DTI data acquired in children (aged 5–6 years) in the presence of incidental motion between the standard diffusion sequence, with different scenarios of retrospective motion correction, and the prospectively motion-corrected navigated diffusion sequence with reacquisition. In addition, we wanted to determine the patterns of head motion performed by children in this age range. To further assess whether retrospective motion correction itself may introduce artifacts in DTI measures, a stationary phantom was also used.

MATERIALS AND METHODS

Navigated Diffusion Pulse Sequence With 3D-EPI Navigator and Reacquisition

A twice-refocused 2D diffusion pulse sequence that minimizes the effects of eddy currents (29) was previously introduced to perform prospective motion correction by acquiring an additional 3D-EPI navigator (duration 526 msec) following the acquisition of each diffusion volume (27). The volumetric navigator contains 3D anatomical information for direct computation of motion parameters and is not diffusion weighted, rendering the accuracy of coregistration and motion estimates unaffected by the diffusion gradients, even for DWI studies at high b-values. The motion estimates are used to update in real time both the spatial encoding and the diffusion encoding gradients. In this way, a consistent anatomical location of the field-of-view (FOV) is ensured, as well as a consistent alignment of the diffusion gradient table with the anatomy being imaged. The influence of through-plane motion on the local history of magnetization, which is one of the disadvantages of retrospective motion correction, is thus recovered. The diffusion sequence was further modified to reacquire a fixed number of motion corrupted diffusion volumes for which motion exceeded a predefined non-variable threshold.

MRI Data Acquisition

Scans were performed on an Allegra 3 T (Siemens Healthcare, Erlangen, Germany) scanner at the Cape Universities Brain Imaging Centre according to protocols approved by the Faculty of Health Sciences Human Research Ethics Committees at the Universities of Cape Town and Stellenbosch. Eighteen young children, 5.1 ± 0.5 years (mean age ± standard deviation), were scanned. Parents/guardians provided written informed consent and children provided oral assent.

T₁-weighted structural images were acquired using the motion navigated (30) multiecho magnetization prepared rapid gradient echo (MEMPR) sequence (31) with TR 2530 msec, TEs (1.53, 3.19, 4.86, 6.53) msec, TI 1100 msec, flip angle 7°, resolution 1 × 1 × 1 mm³, acquisition matrix 224 × 224 × 144.

In all children, DWIs were acquired with both the standard diffusion pulse sequence (basic) (29) and the prospectively motion-corrected navigated diffusion sequence with five reacquisitions (vNav). The parameters for the diffusion sequences were: TR 9500 msec and TR 10,026 msec for the basic and vNav sequences, respectively; TE 86 msec; 72 slices; resolution 2 × 2 × 2 mm³; FOV 224 mm; single channel birdcage head coil; 30 noncollinear diffusion gradient directions with b = 1000s/mm²; four nondiffusion-weighted (B₀) acquisitions. The waiting period for feedback in the vNav sequence (including all navigator-related computations in the sequence and image construction environment) was 120 msec for each repetition time. The 3D-EPI navigator parameters were: TR 14 msec for each partition (slice of k-space) in the slab; 28 partitions; TE 6.6 msec; resolution 8 × 8 × 8 mm³; acquisition matrix size 32 × 32 × 28; bandwidth in the readout direction 3906 Hz/px; flip angle 2°; and total scan time 406 msec. The total scan time for the basic sequence was 5 minutes 33 seconds, and for vNav with five reacquisitions, 6 minutes 40 seconds.

Children were neither sedated nor anesthetized during scanning, but had been trained in a mock scanner to lie as still as possible in preparation for actual scanning. Foam padding was placed around the head to minimize head motion. We were interested to gauge the extent of movement typically made by children in this age range during scanning and to assess how such random motion would affect the DTI results in a group study.

In order to examine the effects of retrospective motion correction on a strictly motionless object, a structured stationary phantom was also scanned. A pineapple was selected for this purpose due to the presence of nontrivial microstructure and anisotropic diffusivity in a volume similar to that of a human head. The phantom was scanned using both the basic and navigated sequences using a protocol identical to that used in the children with the only difference being fewer slices (40 slices). The pineapple was further constrained using padding materials during the scan to limit the impact of table vibrations.

Processing of T₁-Weighted Structural Images

The T₁-weighted images of each subject were automatically segmented into cortical and subcortical regions using FreeSurfer (http://surfer.nmr.mgh.harvard.edu/) software. The outcome of the segmentation process is a labeled volume comprising 175 white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF) regions. FSL tools (FMRIB Software Library; http://www.fmrib.ox.ac.uk/fsl) and in-house scripts were implemented to extract, create, and map binary masks of volumes of interest (VOIs). VOIs used in the current study were whole brain WM, the cerebral cortex, left caudate (LC), right caudate (RC), left hippocampus (LH), right hippocampus (RH), left amygdala (LA), and right amygdala (RA).

Assessment of Diffusion Data for Presence of Motion

Since it was not possible in the current study to monitor the head pose inside the scanner when using the basic sequence, the resulting DWIs were inspected visually for the presence of motion. In contrast, the navigated acquisitions (vNav) were inspected for the presence of motion by reviewing the log files of the motion estimates that are generated by the sequence in addition to visual inspection of the DICOM volume images to detect any fast motion, which would lead to dropout slices in the images. For each child we computed the extent of translational motion in each direction and the amount of rotation around each axis as the difference between the maximum and minimum of the displacement or rotation estimates throughout the acquisition using FLIRT in FSL for basic acquisitions and PACE for vNav acquisitions, respectively.

Processing of Diffusion Data

DWIs were converted from DICOM format to NIfTI using FreeSurfer tools. Brain extraction (BET) was applied in FSL to diffusion images acquired using both sequences. Retrospective motion correction (retro) using FLIRT in FSL with 6 and 12 degrees of freedom (DOF) and a mutual information cost function was applied only to DWIs acquired using the basic sequence, both with rotation (R) and without rotation (N) of the diffusion table. For all combinations, diffusion tensors and parameters were estimated using dtifit in FSL.

The DICOM images of the pineapple were processed in the same way, with the exception that BET was not applied. Retrospective motion correction using FLIRT was performed for the pineapple data acquired with both the basic and vNav sequences (6DOF, with a mutual information cost function and with rotation of the diffusion table).

VOI Analyses

For each subject, the first B₀ DICOM volume image of each acquisition was registered to his/her T₁-weighted structural volume using FSL tools. FMRIB’s linear registration (FLIRT) was followed by nonlinear registration using FMRIB’s nonlinear image registration tool (FNIRT). This mapping was applied to the fractional anisotropy (FA) maps to transform these into the subject T₁ space. The binary masks that were created previously in T₁ space were applied to the FA maps to calculate the mean FA in different VOIs in order to compare these for different motion correction strategies.

Certain decisions need to be made when performing retrospective motion correction, such as the number of DOFs to use and whether or not to rotate the diffusion gradient table during correction. Here we examine four different scenarios: 6DOF both with and without rotating the diffusion table (Basic_6R and Basic_6N, respectively), and 12DOF both with and without rotating the diffusion table (Basic_12R and Basic_12N, respectively).

The mean FAs in each VOI for each retrospective motion correction strategy were compared to the mean FAs computed from the vNav data using paired Student’s t-tests. P < 0.05 was considered statistically significant. Additionally, for two subjects for whom the extent of motion was representative of the sample, maps were generated of the voxelwise differences in FA when performing retrospective motion correction with and without rotation of the gradient table, as well as for the voxelwise differences between retrospective motion-corrected FAs from the basic acquisition with prospectively motion-corrected FAs from the vNav acquisitions. These maps provide detailed information of the magnitude and location of the bias introduced across the entire brain when using different retrospective motion correction strategies.

Effects of Simulated Motion

DWIs differ from most other imaging modalities in that the contrast changes from volume to volume (as well as from the reference B₀ volume), which is likely to make retrospective motion correction particularly difficult. Even though the B₀s all have similar contrast, the fact that they comprise reference values for each DWI in the tensor fitting means that final results will be particularly sensitive to any errors or noise. In order to investigate the effect of motion correction alignment within each distinct class (ie, B₀s and DWIs), we performed a simulation with two different false transformation matrices (M1 and M2), whose values were derived from PACE estimates in the vNav acquisition of two children in order to ensure realistic movement profiles. Transformations were applied to the data acquired with the basic sequence for one subject (6-year-old, male) who was selected on the basis of having little (less than one voxel) motion as per both visual inspection and registration using 6DOF (Table 1, Child 1). The amount of motion applied using these matrices was still within the limits of Prospective Acquisition CorrEction (PACE, 20 mm translation and 8° rotation).

Table 1.

Amount of Translational and Rotational Motion in Each Direction During the Basic and vNav Acquisitions for Three Children in Whom Motion Did Not Lead to Dropout Slices

	Amount of Motion
	Child 16-year- old, male		Child 26-year- old, female		Child 35-year- old, male
Direction	Basic	vNav	Basic	vNav	Basic	vNav
T_X	0.1	0.4	1.4	0.7	2.3	1.8
T_Y	0.4	0.3	0.6	0.9	1.4	0.9
T_Z	0.5	0.7	3.5	2.2	1.7	5.2
R_X	0.2	0.3	0.7	1.2	0.2	2.5
R_Y	0.1	0.4	1.5	3.7	0.7	5.4
R_Z	0.0	0.2	0.3	0.7	0.5	0.7

Amounts of motion were computed as the difference between the maximum and minimum motion estimates. Motion estimates were determined using FLIRT in FSL with 6 degrees of freedom for the basic acquisitions, and using PACE during the vNav acquisitions. T, translation in mm; R, rotation in degrees.

Each transformation matrix was applied to the data in two different ways: 1) the first B₀ volume was unchanged, with the matrix applied to the other B₀s and to all DWIs (ie, with respect to the first B₀, all subsequent volumes have the same motion difference), and 2) the transformation was only applied to the second, third, and fourth B₀ images and not to any of the DWIs. Each case simulates a simple kind of motion observed in the pediatric subjects, respectively: case 1) the subject moves after the first B₀ volume and then remains stationary; and case 2) the subject moves after the first B₀ volume, pauses, and then returns to the original position. In both transformation cases, all B₀s after the initial one have “moved,” with the difference being whether the DWIs have also “moved” or not. Retrospective motion correction with 6DOF (with rotation of the gradient table) was applied to each dataset. The FA map of each transformed dataset (Basic_T6R) was subtracted from the FA map of the nontransformed data (Basic_6R), in order to quantify differences due to registering either case 1) B₀s and DWIs that are nonaligned by relative motion, or case 2) only nonaligned B₀s. It was hypothesized that if correction-induced errors were due predominantly to nonaligned DWIs (rather than B₀s), then the FA differences would be much larger when comparing changes in case 1 than in case 2.

Effects of Retrospective Motion Correction in Phantom Data

FA maps were computed for phantom data acquired using the basic sequence both without retrospective motion correction (Basic pineapple) and with retrospective motion correction and rotation of the diffusion table (Basic_6R pineapple). Maps were generated of the voxelwise FA differences between these. Additionally, the voxelwise differences in FA were calculated for the vNav acquisition with and without retrospective motion correction (vNav pineapple – vNav_6R pineapple).

Tractography Analysis

Changes to tensor fits due to processing strategies used affect not only local measures of diffusion properties, such as ellipsoid shape and spatial orientation, but also nonlocal tract reconstruction results. To compare the cumulative effects of motion correction strategies on tractographic algorithms, deterministic tractography was performed on two sets of scans from individuals with different motion characteristics: one basic (with varied processing: no motion correction, basic_6N, and basic_6R) and one vNav scan. Whole brain tractography was performed using the FACTID algorithm (32), implemented using the FATCAT tool-box in AFNI (33). A single target VOI was defined in the brainstem using Freesurfer. Tract results were compared for symmetry and location from known physiology and fiber atlases (34). Standard tractography criteria were used for tract propagation: FA > 0.2; maximum turning angle of 60°; minimum tract length 15 mm; 8 equally spaced seed points per voxel.

RESULTS

Motion Estimates

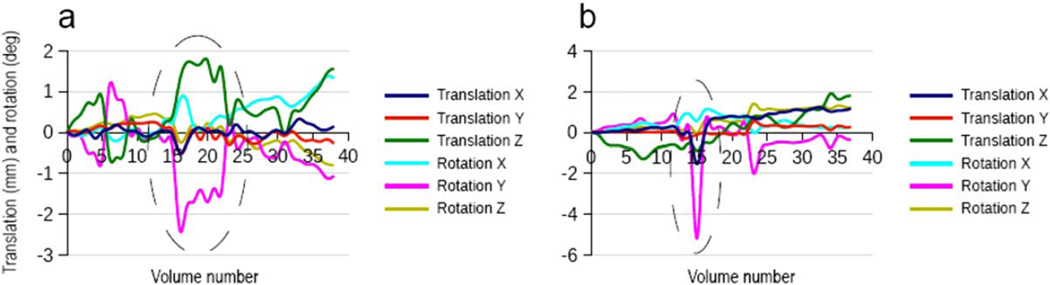
Figure 1 shows motion parameters that were estimated by the PACE algorithm in the vNav sequence for two children who moved during acquisition. Two distinct types of incidental motion were commonly observed in this study for children who moved during scans: continuous movement (Fig. 1a) and abrupt or fast movement (Fig. 1b).

Figure 1.

Representative displacements in x-, y-, and z-directions, and rotations around each axis for two children who moved during scanning, as estimated by PACE during the navigated sequence (vNav). a: An example of continuous movement over several volumes. b: Abrupt or fast movement "spikes." In the scanner coordinate system, these axes correspond to: x = anterior–posterior (AP), y = left–right (LR), and z = superior–inferior (SI) directions.

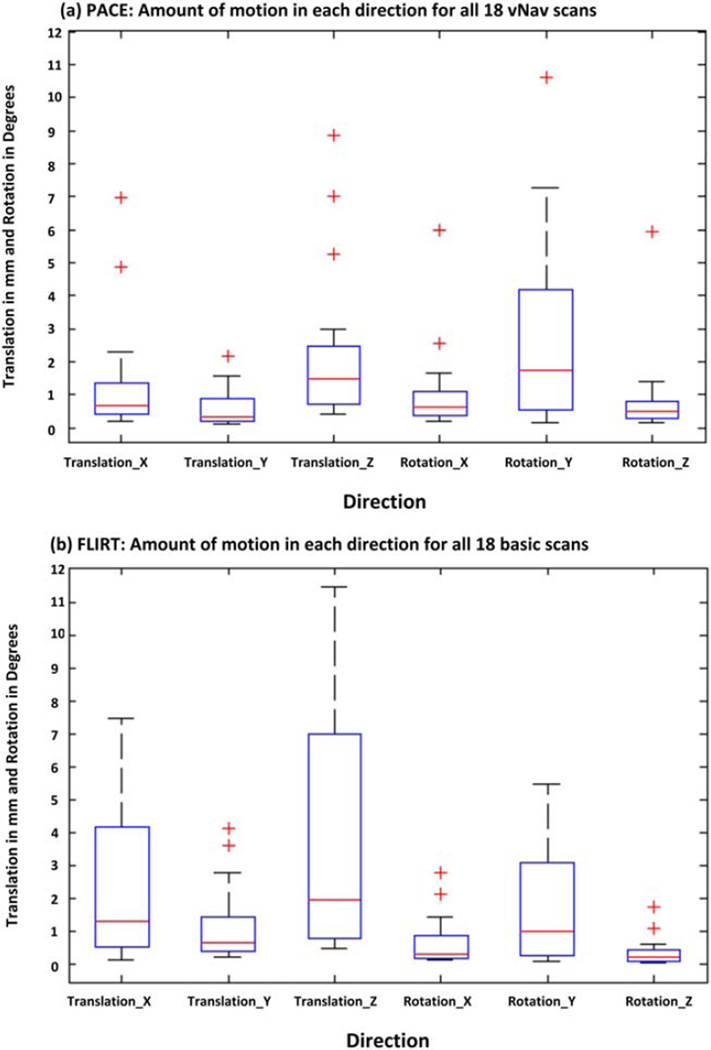
Figure 2a,b shows box-and-whisker plots of the extent of translational and rotational motion in each direction for all 18 vNav acquisitions as estimated by PACE and for the 18 basic acquisitions as estimated using retrospective motion correction, respectively. The extent of motion in each direction was computed as the difference between the maximum and minimum displacement along or rotation around the relevant axis. Motion characteristics of both datasets are qualitatively and quantitatively similar. In both cases, the two largest movements are translations along the bore of the magnet (superior–inferior axis) and rotations around the y-axis (left–right axis), which correspond to nodding of the head.

Figure 2.

Boxplots showing the amount of motion in each direction (translation and rotation in image space; outliers shown denoted by red "+") for all 18 children as estimated using PACE during the vNav acquisitions in (a) and using FSL-FLIRT for the basic acquisitions in (b). The amount of motion was computed as the difference between the maximum and minimum displacement and rotation for each child. In the scanner coordinate system, axes correspond to: x = AP, y = LR, and z = SI. Children in this study predominantly moved along the z-direction and rotated their heads around the y-axis, which corresponds to nodding motion. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Table 1 presents the extent of motion in each direction for three children in whom motion did not lead to dropout slices in any of the acquisitions. Motion estimates were determined using FLIRT for the basic acquisition and by PACE during the vNav acquisition. Table 2 shows the amount of motion in each direction for the stationary pineapple as estimated by FLIRT for the basic acquisition and by PACE during the vNav acquisition. It is evident from the pineapple data that FLIRT overestimates the amount of motion.

Table 2.

Extent of Translational and Rotational Motion for the Four Stationary Pineapple Acquisitions

	Amount of Motion
	Basic		vNav
Direction	Scan1	Scan2	Scan1	Scan2
T_X	1.39	1.66	0.13	0.14
T_Y	1.30	1.04	0.06	0.06
T_Z	2.73	2.56	0.18	0.16
R_X	0.21	0.19	0.11	0.20
R_Y	0.80	0.80	0.23	0.23
R_Z	0.57	0.39	0.28	0.25

Motion was estimated using FLIRT in FSL with 6 degrees of freedom for the two basic acquisitions, and using PACE during the two vNav acquisitions. T, translation in mm; R, rotation in degrees.

VOI Analyses

Table 3 presents the mean FA in the whole brain WM and cerebral cortex averaged for all 18 children as determined from the basic acquisition using four different retrospective motion correction strategies compared to the values obtained using the vNav acquisition. In both whole brain WM and cerebral cortex no significant differences were observed between retrospective motion correction with 6DOF and that with 12DOF (all P > 0.2), with or without rotation of the diffusion table. In contrast, mean FAs in whole brain white matter and cortex of the basic acquisition for each of the different retrospective motion correction strategies were significantly lower (P < 0.0001) than that of the vNav acquisition.

Table 3.

Mean FA in the Whole Brain WM and Cerebral Cortex Averaged Over All 18 Children for the Basic Acquisition With Different Retrospective Motion Correction Schemes Applied Compared to the vNav Acquisition

	Basic_6Na	Basic_6Ra	Basic_12Nb	Basic_12Rb	vNav
Mean FA in Whole Brain WM	0.380*(0.010)	0.380*(0.010)	0.378*(0.008)	0.378*(0.008)	0.399(0.011)
Mean FA in Cerebral Cortex	0.138*(0.006)	0.138*(0.006)	0.137*(0.006)	0.137*(0.006)	0.151(0.004)

Values are means (SD).

^aRetrospective motion correction with 6DOF without (N) and with (R) rotation of the diffusion table.

^bRetrospective motion correction with 12DOF without (N) and with (R) rotation of the diffusion table.

^*P < 0.05 (Student’s t-test compared to vNav).

Table 4 presents the mean FA, averaged over all 18 children, in the caudal, amygdala, and hippocampal subcortical gray matter VOIs for the basic acquisition with each different retrospective motion correction scheme applied compared to the mean FA for the vNav acquisition. Mean FA is significantly lower (P < 0.0001) in all the VOIs for the retrospectively motion-corrected data compared to the vNav data.

Table 4.

Mean FA in the Amygdala, Caudate, and Hippocampus, Averaged Over All 18 Children, for the Basic Acquisition With Different Retrospective Motion Correction Schemes Applied Compared to the vNav Acquisition

	Mean FA
VOI1	Basic_6Na	Basic_6Ra	Basic_12Nb	Basic_12Rb	vNav
LA	0.143*(0.012)	0.143*(0.012)	0.142*(0.012)	0.142*(0.012)	0.156(0.009)
LC	0.138*(0.008)	0.138*(0.008)	0.137*(0.008)	0.137*(0.008)	0.150(0.006)
LH	0.141*(0.006)	0.141*(0.006)	0.141*(0.006)	0.141*(0.006)	0.154(0.004)
RA	0.140*(0.007)	0.141*(0.007)	0.140*(0.007)	0.140*(0.007)	0.153(0.007)
RC	0.135*(0.008)	0.135*(0.008)	0.134*(0.007)	0.134*(0.007)	0.149(0.007)
RH	0.142*(0.004)	0.142*(0.004)	0.141*(0.005)	0.141*(0.005)	0.154(0.004)

¹Subcortical gray matter VOI’s: left amygdala (LA), left caudate (LC), left hippocampus (LH), right amygdala (RA), right caudate (RC), and right hippocampus (RH).

Values are means (SD).

^aRetrospective motion correction with 6DOF without (N) and with (R) rotation of the diffusion table.

^bRetrospective motion correction with 12DOF without (N) and with (R) rotation of the diffusion table.

^*P < 0.05 (Student’s t-test compared to vNav).

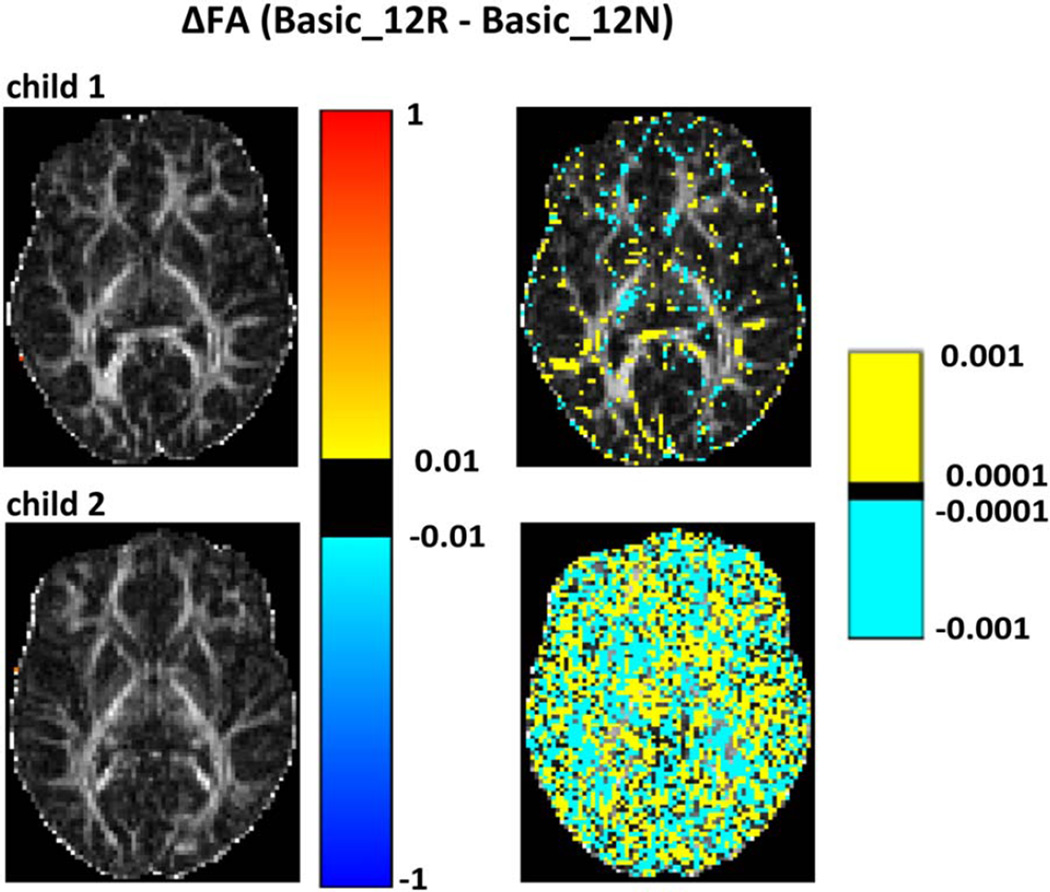
Figure 3 shows for two children (child 1 and child 2 in Table 1) voxelwise differences in FA between retrospective motion-corrected DTI data from the basic acquisition without (Basic_12N) and with (Basic_12R) rotation of the diffusion table superimposed on FA maps for a representative slice in DWI space. For both children, no differences are apparent on the images on the left that use a coarser scale, indicating that FA differences are less than 0.01. Even for the second child who moved more than the first child during the basic acquisition (Table 1), the magnitude of FA differences resulting from rotation of the diffusion table are on the order of 0.001 or less.

Figure 3.

Voxelwise differences for two children (child 1 and child 2 in Table 1) between FA maps generated for retrospectively motion-corrected data with (Basic_12R) and without (Basic_12N) rotation of the diffusion table superimposed on the basic_12R FA maps. FA differences are shown using two different scales: the left column shows differences on the scale 0.01 < |ΔFA| < 1, and the right on the scale 0.0001 < |ΔFA| < 0.001. Child 2 moved more than child 1.

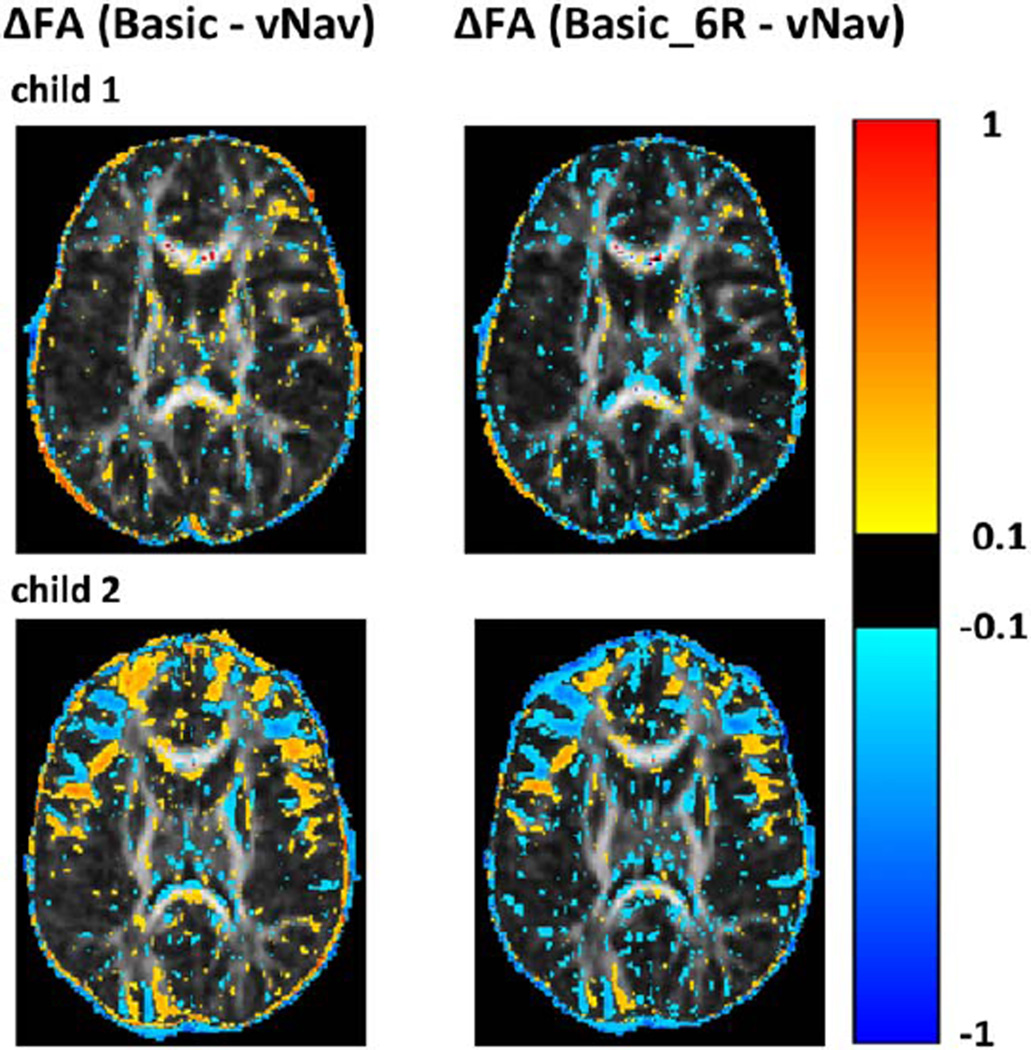
Figure 4 shows voxelwise FA differences between basic and vNav acquisitions for a representative axial slice for two children (child 1 and child 2 in Table 1) who moved different amounts during the scans. In the uncorrected basic scans, FA is generally higher in GM and lower in WM and near tissue boundaries compared to the vNav FAs (left column in Fig. 4). In contrast, FA is generally lower in both WM and GM in the basic acquisition after retrospective motion correction compared to the vNav FA (right column in Fig. 4).

Figure 4.

Voxelwise differences for two children (child 1 and child 2 in Table 1) between FA maps for the basic and vNav acquisitions on the left, and between the basic acquisition after retrospective motion correction with 6DOF and rotation of the gradient table (Basic_6R) and the vNav acquisition on the right. FA differences are overlaid on the vNav FA maps. All FA maps were coregistered to subject T₁ space prior to subtraction.

Effects of Simulated Motion

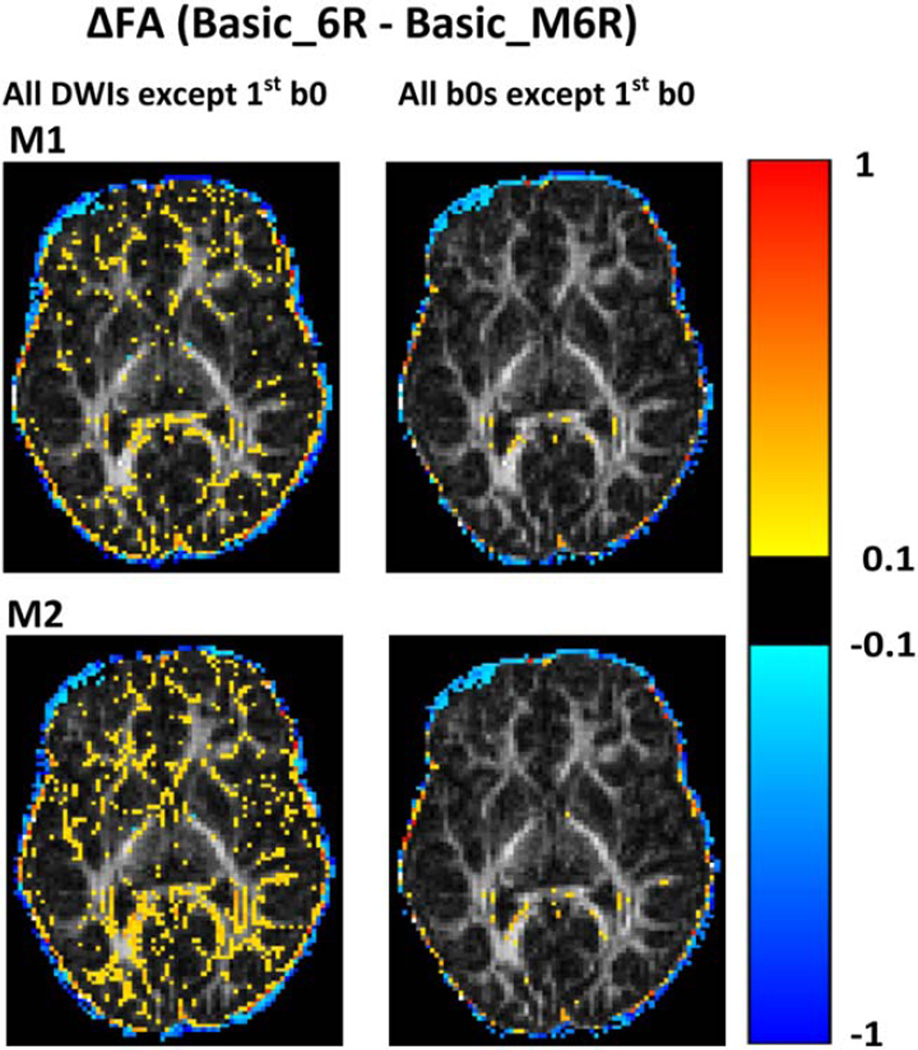
Table 5 shows the "false motion" transformation matrices (M1 and M2) that were used to simulate the effects of motion in the data. When both B₀s and DWIs were transformed, we observed reduced FA in WM (Fig. 5, left column). When only the 2nd, 3rd, and 4th B₀ images were transformed, the effects were negligible (Fig. 5, right column). Retrospective motion correction failed to recover the DWIs that were affected by the false motion and, furthermore, introduced bias into the results.

Table 5.

Translational and Rotational Motion in Each Direction for the False Transformation Matrices M1 and M2

False Transformation Matrix	T_X	T_Y	T_Z	R_X	R_Y	R_Z
M1	7.1	1.1	−11.4	0.26	4.1	−0.3
M2	5.0	2.3	−4.6	−1.1	1.2	−1.6

The values are representative of real subject motion as estimated by PACE in the vNav acquisitions. T, translation in mm; R, rotation in degrees.

Figure 5.

Map of voxelwise differences in FA between the basic acquisition of one child (Basic_6R) and the FA map generated after applying the false transformation matrices M1 (top) and M2 (bottom), respectively, to the same data (Basic_M6R). Preprocessing for all FA maps included retrospective motion correction using 6DOF and rotation of the diffusion table. For the images on the left, the transformations were applied to all the volumes except the first B₀ volume, while for the images on the right the transformation was applied only to the 2nd, 3rd, and 4th B₀ volume images. Differences are overlaid on the FA map of the retrospectively motion-corrected basic scan.

Effects of Retrospective Motion Correction in Phantom Data

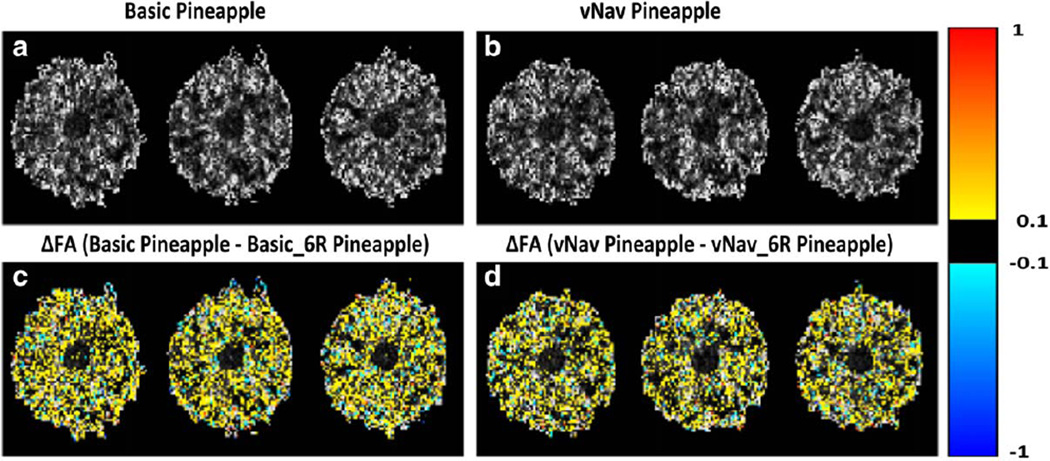
Figure 6 displays results from two scans of the stationary pineapple. Panel A shows the FA maps of three slices acquired using the basic sequence, and panel C shows the voxelwise differences in FA between the acquired data and data after performing motion correction with 6DOF and with rotation of the diffusion. Panels B and D show the same quantities for the same three slices for data acquired using the vNav sequence. Retrospective motion correction on a stationary phantom led to overestimated motion estimates, especially in the translation along the bore of the magnet and rotation around the y-axis (Table 2). It also significantly reduced FA (Fig. 6c,d), even though the phantom was stationary and supported by foam padding.

Figure 6.

a,b: FA maps for three slices of a pineapple acquired using the basic and vNav sequences, respectively. c: The voxelwise differences in FA (ΔFA) between FA values in ‘a’ before and after motion correction with 6DOF and rotation of the diffusion table (Basic Pineapple – Basic_6R Pineapple). d: The same for data acquired using the vNav sequence (vNav Pineapple – vNav_6R Pineapple). For both sequences retrospective motion correction significantly reduced the FA.

Tractography Analysis

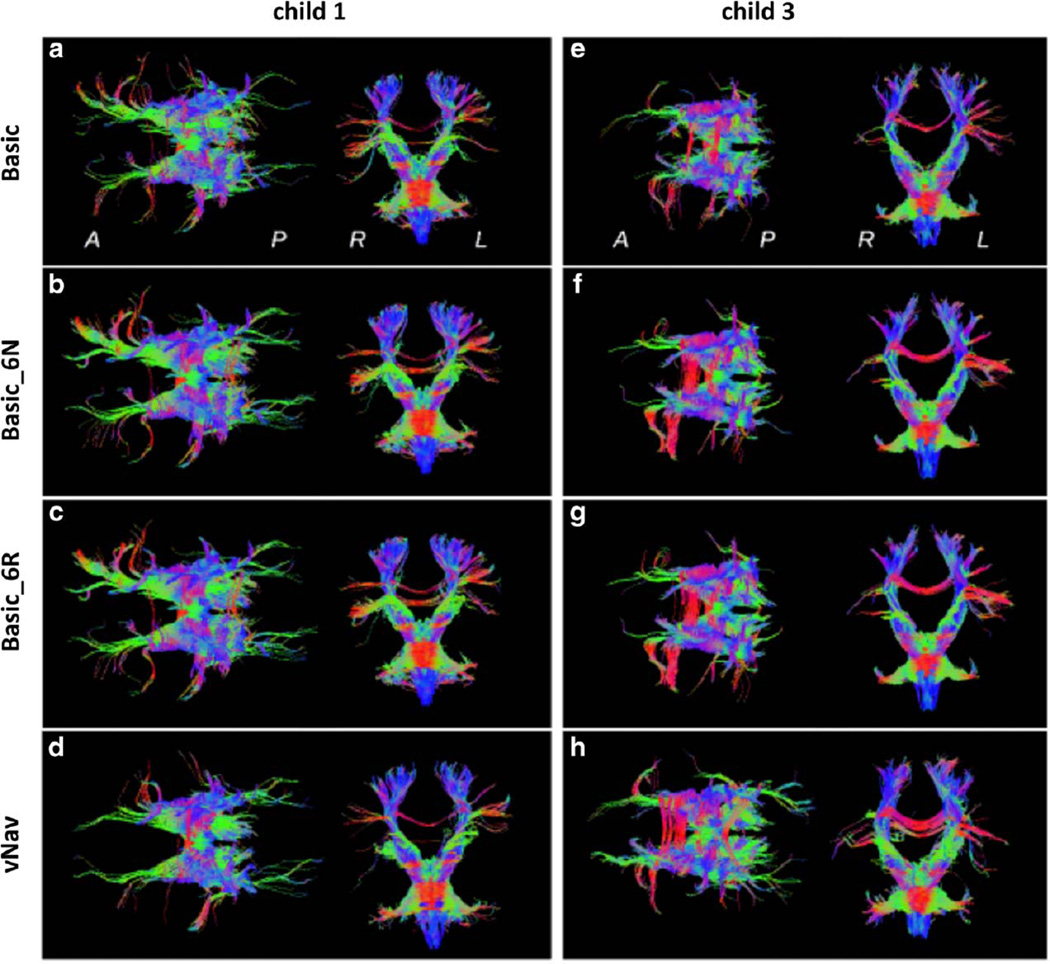
In Figure 7 the estimated tracts that pass through the brainstem VOI are shown for the first (left column) and third child (right column), for whom motion was summarized in Table 1. Axial and coronal projections are presented for four reconstructions: a basic scan with no retrospective correction; basic_6N; basic_6R; and vNav. All reconstructions typically show a high degree of left–right (L-R) symmetry as well as the presence of several of the main bundle locations to be expected from this VOI.

Figure 7.

Tractography reconstructions for fibers passing through the brainstem for two children. Axial projections (anterior is on the left) and coronal projections (anatomic left is on the right) are viewed from superior and anterior locations, respectively, for various reconstructions: (a,e) Basic scan, no retrospective correction; (b,f) Basic_6N; (c,g) Basic_6R; and (d,h) vNav. Coloration is by local spatial orientation: left–right (red); anterior–posterior (green); superior–inferior (blue).

For child 1, quite similar tract locations appear in the three basic scan panels, with fibers with retrospective correction generally showing higher density and cohesion. It can be observed that the results of retrospective correction, either without or with rotation of the diffusion table, are nearly identical. Differences in tract location are apparent in the vNav data (bottom panel), mainly in the anterior projection fibers identified with the anterior thalamic radiation (34), which provide cortico-brainstem connections.

In the three basic sets, anterior reconstructions connect both the anterior–posterior running projection fibers with the L-R running association fibers, while in vNav the projection fibers are cohesively reconstructed independently. Additionally, in the coronal projection, it can be noted that superior tracts are more narrow and L-R symmetric in vNav.

The tract reconstructions for child 3, who had larger motion events than child 1, are shown in the right column of Fig. 7. Qualitatively, traits of these fibers are similar to those for the first child. Results of the basic scans that were motion-corrected without and with rotation of the diffusion table (middle panels) are quite similar to each other; moreover, these reconstructions are similar to those of the uncorrected basic scan (top panel), with the latter generally showing lower track density. It can be noted in the three basic sets of child 3, however, that the anterior projection fibers have significantly less extent than those observable in child 1 (left column), and their posterior counterparts are largely absent. The vNav reconstruction in child 3, though, shows the presence of both the anterior and posterior fibers, particularly showing narrow bundles in the former case. In the coronal view, child 3 shows greater L-R symmetry and fiber bundle density.

DISCUSSION

This study presented results of an in-depth analysis of the effects of incidental motion and two classes of methods to correct these on DTI measures in 5–6-year-old children. In particular, both the degree and manner of changes in WM and GM measures were compared when using either retrospective motion correction (both with and without rotating the diffusion table) or prospective motion correction.

The patterns of motion observed in children in this study affect DWIs in different ways: continuous movement can corrupt many diffusion volumes, while abrupt or fast movement can occur within a single TR and can corrupt a single volume. While the navigator can readily detect and adjust orientations in real time for continuous motion, as well as abrupt motion that occurs on a time scale longer than one TR, motion occurring within a single TR (after which the subject returns to her/his initial position) will not be detectable directly by the vNav sequence and affected volumes will need to be detected by visual inspection and manually excluded prior to processing. One way to address this limitation would be to assess signal attenuation in each slice of a diffusion volume in real time, which can be compared to a reference signal of the same slice. This additional capacity is currently being designed and implemented.

Among different studies, observed patterns of motion will depend on several factors: the way children were placed in the MRI scanner, the orientation of the field of view, how the supporting foam pillows are placed around the child, etc. In the current study motion was evaluated in real time using the vNav sequence. In the majority of children, the predominant mode of motion was nodding.

This study is consistent with previous findings (27) in which retrospective motion correction led to an overestimation of motion parameters. These results were even obtained from the scanning of a strictly stationary pineapple phantom. The overestimation of motion in alignment is likely due to the influence of the diffusion contrast on retrospective motion correction. Both the extents and types of motion observed in the Basic and vNav scans were quite similar, with the larger values in the former likely due to this observed overestimation by retrospective methods.

Retrospective motion correction methods are generally similar, with small technical variations. Linear and affine transformations are commonly applied for image registration, with a choice of either 6 (rigid body motion) or 12 DOF (rigid body motion and warping). We compared retrospective motion correction of our basic acquisitions with either 6 or 12 DOF to prospectively motion-corrected acquisitions and detected significant reductions in mean FA in both WM and GM after retrospective motion correction. By contrast, no significant differences were detected between implementations of retrospective motion correction with either 6 or 12 DOF, indicating that most of the reduction in FA occurs due to rigid body motion correction, even in diffusion scanning where nonlinear effects such as eddy currents are known to occur.

Additionally, the recent literature emphasized the importance of rotating the gradient diffusion table after retrospective motion correction as a prerequisite for improvement of the final results. Although the logic of such a step is clear, the present study shows that rotating or not rotating the diffusion gradient table after retrospective motion correction did not significantly alter the results. The magnitudes of changes resulting from rotation of the gradient table found in the present study are on the same order as those presented in the original article that promoted gradient rotation (11). Here, however, we interpret these changes, which are at least an order of magnitude smaller than changes that can be reliably attributed to resulting from motion or pathology, as being insignificant. While the accurate estimation of a diffusion tensor must obviously depend on using the correct representations of the physical diffusion gradient directions, the present study demonstrates that only prospective correction of the B-matrix table and slice positions during the scan itself can significantly reduce the changes in FA that occur due to motion.

At boundaries between WM and GM, motion may increase FA in GM regions by introducing some orientational-dependence, while in WM regions FA may be decreased due to partial voluming with isotropic GM. Retrospective motion correction is susceptible to distortion from partial voluming. This was demonstrated by the global reduction in the mean FA values for data acquired using the basic sequence compared to the vNav sequence. The reductions in FA observed after retrospective motion correction (with either 6 or 12 DOF, and without or with rotation of the gradient table) can also likely be attributed to effective spatial smoothing of the data, which occurs during interpolation when aligning the images, even when no motion occurs. A dataset with more interpolation would produce more streamlines due to the smoothing effect.

The in vivo data were validated in two ways. First, we analyzed DWIs to which a false transformation had been applied. When the transformation was applied to B₀ volumes only, the results suggested that retrospective motion correction may still register well, due to the fact that these B₀ images all have a similar contrast. In contrast, when the false transformation was applied to DWIs, the interpolation process that occurs during retrospective motion correction was affected substantially by the induced partial volume effect. The latter effects are likely related to the fact that DWIs have different contrast to the B₀ images, as well as different contrasts for each applied gradient direction, creating inherently difficult challenges for retrospective motion correction.

Second, comparisons of methods for the stationary pineapple phantom revealed that standard rigid body (6DOF) retrospective motion correction introduced a bias in the DTI parameters. This occurred even in the absence of motion, and was equally present in data acquired using both the basic and vNav sequences. Interestingly, FA values at the center of the pineapple showed little change, as did other large, homogeneous regions. In contrast, large FA differences were seen in the most heterogeneous areas around the center, particularly at borders of high- and low-FA regions, again suggesting partial voluming effects.

These findings are in broad agreement with some previous examinations of motion in MRI. For example, Alhamud et al. (27) found that in general the relatively simple and standard retrospective transforms often used in DWI studies are unable to replace the information lost due to motion and susceptibility artifacts. In fact, in several cases postacquisition processing was shown to introduce bias into the data (35,36), particularly through increased partial voluming effects that tend to decrease FA and to reorient eigenvectors. When either examining individuals or comparing pathological groups that might be more susceptible to move during scanning than healthy controls, these biases are likely to have strong, unphysiological influences on the locations and strength of statistical differences observed.

Furthermore, these local changes alter global structural connectivity as estimated through tractography. In this study, several changes in tract location and presence were observed, including basic L-R symmetry alteration. Since most algorithms depend on FA threshold values as a proxy for WM in order to propagate tracts, GM- and CSF-partial voluming would have significant roles in altering tract locations and lengths (ie, likely decreasing these). While lowering FA propagation thresholds may counteract this effect, it would also increase the number of false-positive tracts propagating through non-WM locations and is therefore undesirable. Likewise, effective eigenvector rotation due to motion and processing before tensor fitting produces significant changes in connectivity, particularly in L-R symmetry.

While this study did not implement every possible method for retrospective motion correction, some of the more widely used methods were selected. In future studies we would like to process the vNav data using additional methods such as outlier detection/rejection, EPI distortion, and eddy current correction. In addition, the navigated sequence will be modified to reduce the interval between navigator scans in order to be able to detect motion on a shorter time-scale.

If prospective motion correction methods that are independent of diffusion images (27,37) are not available, further investigation is needed to develop more reliable retrospective motion correction methods. A particular challenge for all retrospective motion correction techniques will be the difficulty in accurately aligning images with inherently different contrasts, which is the case in DWI reconstruction. This situation becomes more difficult when the diffusion images are acquired with high b-values, as required in several important applications such as q-space imaging (38), Q-ball imaging (39), and diffusion spectrum imaging (40).

The current study is limited by the fact that the vNav sequence is unable to track very abrupt (sub-TR) motion, which is likely to still produce drop-out or other artifacts in the data. Additionally, the amount of motion that can be corrected is limited by the PACE algorithm. However, both fast and extreme motion would pose similar challenges using retrospective motion correction. Second, there are several software packages with tools for motion correction (as well as other pipeline processing steps), each with many options. It is not possible to test every possible retrospective motion correction algorithm in a single study. We have chosen to use one of the more popular, well-studied methods, FSL’s FLIRT, with a few different options. Subsequent studies may implement other tools and variations, although given the general nature of retrospective algorithms, it is likely that results will be similar to those observed here. Third, the vNav in this study is currently not able to correct for inherent B₀ distortions that arise from both motion and the use of a single-shot EPI acquisition. We are working on a method to correct for B₀ distortions in real time by using double volumetric navigators with different echo times (41).

In conclusion, retrospective motion correction using FLIRT with a mutual information cost function and either 6 or 12 DOF uniformly reduced the FA values across the brain. This can likely be attributed to partial voluming effects associated with the DWI resolution (2 × 2 × 2 mm³ voxel size), which is much larger than neuronal fiber bundles. Using multishot fast sequences increases DWI resolution, yet bulk motion between shots still presents significant challenges to analysis and tensor reconstruction. Using the current 3D-EPI navigator technique for real-time motion correction may enhance multishot fast imaging sequences by implementing the navigators between shots. The navigated diffusion sequence (27) both corrects motion prospectively (rotating the gradient table in real time during motion estimation) and reports motion parameters at the end of each scan. In addition, each diffusion volume image is displayed on the scanner during DTI acquisition, so that the radiographer can communicate with a subject who moves a lot, or terminate the scan, in order to prevent valuable scanner time being wasted. Importantly, the navigation requires only a very modest increase in acquisition time.