Abstract
Purpose
To design parallel transmit (pTx) simultaneous multi-slice (SMS) spokes pulses with explicit control for peak power, local and global specific absorption rate (SAR).
Methods
We designed SMS pTx least-squares and magnitude least squares spokes pulses while constraining local SAR using the virtual observation points (VOPs) compression of SAR matrices. We evaluated our approach in simulations of a head (7 T) and a body (3 T) coil with 8 channels arranged in two z-rows.
Results
For many of our simulations, control of average power by Tikhonov regularization of the SMS pTx spokes pulse design yielded pulses that violated hardware and SAR safety limits. On the other hand, control of peak power alone yielded pulses that violated local SAR limits. Pulses optimized with control of both local SAR and peak power satisfied all constraints and therefore had the best excitation performance under limiting power and SAR constraints. These results extend our previous results for single slice pTx excitations but are more pronounced because of the large power demands and SAR of SMS pulses.
Conclusions
Explicit control of local SAR and peak power is required to generate optimal SMS pTx excitations satisfying both the system's hardware limits and regulatory safety limits.
Keywords: Simultaneous multi-slice, multi-band, parallel transmission, specific absorption rate, pulse design, low flip-angle
Introduction
Simultaneous multi-slices (SMS) techniques accelerate the acquisition of volume MRI data by exciting several slices at once (1–5) and then un-alias the collapsed data using parallel imaging (PI) methods (6–8). SMS methods are compatible with fast echo-planar trajectories, which make them useful for a wide range of applications including functional and diffusion MRI (3,5). A drawback of multiplexed SMS pulses is their large SAR and peak power demands. To reduce peak power, Wong optimized the phases of the individual slice excitations so as to minimize the peak voltage of the total SMS pulse (9) and showed that this approach yields SMS pulses with peak power scaling with the number of multiband (MB) slices as opposed to MB2 as usual. Another strategy to reduce the SMS peak power consists in shifting the individual slice excitation by different time delays (10). While these techniques significantly reduce peak voltage of the total SMS pulse, they do not reduce total radio-frequency (RF) power or SAR. Indeed, at low flip-angles the Fourier relationship between transverse magnetization and the RF pulse (11) implies that total RF power is equal to the integral of the slice profile (squared) along the slice-direction (Parseval theorem). Therefore if the slices excited simultaneously are well separated spatially, the total RF power of the SMS pulse equals the sum of the total RF power of the individual slice excitations. SAR can be reduced, albeit at the cost of a degradation of off-isocenter slice profiles, by reducing the peak power of the individual slice excitations using the VERSE algorithm (12–15). This reduction may not be sufficient for high MB factors and spin-echo pulses at high field however. Power independent of number of slices (PINS) pulses have been proposed as another solution to this problem. PINS pulses approximate slice-selective RF profiles using trains of rectangular sub-pulses and excite many slices at once by under-sampling transmit (Tx) k-space in the slice direction (16). They provide significant peak power and SAR reduction at high MB factors and for demanding acquisition such as diffusion imaging (17) and turbo spin-echo (18) but are long and therefore, like VERSE pulses, sensitive to off-resonance effects.
Recently, SMS techniques have been combined with parallel transmission (pTx) in order to yield uniform excitations of multiple slices or slabs at ultra-high field, which was first demonstrated by Katscher et al. (19). In a study by Wu et al. (20), SMS RF-shimming pTx pulses were designed by optimization of RF-shimming coefficients for the different slices excitations while constraining the average power of the total SMS pulse (Tikhonov regularization). This led to excitations that were more uniform and with smaller average power than SMS excitations designed by using the same set of RF-shimming coefficients for all slices. In another study, Poser et al. used an 8 channels pTx coil with two rows in the z-direction (4 channels per row) and showed that such a coil is beneficial for SMS RF-shimming because it creates slice excitations that are largely contained in the two distinct rows, thus reducing total power and SAR (21). Finally, in a recent abstract, PINS and kT points pulses (22) were combined by adding small rectangular kx-ky excitations between the PINS rectangular sub-pulses to improve the homogeneity of the slice excitations (23). This approaches yields pulses that are even longer than traditional PINS pulses however.
These early combinations of pTx and SMS focused on flip-angle uniformization and reduction of peak power using RF-shimming strategies and did not consider SAR explicitly in the pulse design process. Control of RF power and SAR are not equivalent in pTx, and explicit control of both SAR (local and global) and RF power is required to yield pulses of the highest quality that are both safe and playable on the scanner (24). In this work, we extend the SMS pTx design strategies of Wu et al. and Poser et al. beyond RF-shimming to the design of magnitude least-squares pTx SMS pulses with multiple spokes. Like in “standard” pTx (i.e. without SMS), we show that local SAR can be constrained explicitly in the design of spokes SMS pTx pulses along with global SAR and peak power. This strategy allows generation of the best possible SMS pulses compatible with all safety and system limits, which is not possible using Tikhonov-regularized approaches that typically handle a single constraint.
Methods
Parallel transmission pulse design
We design low flip-angle multiplexed SMS pTx spokes pulses with explicit control for local SAR using a compression of the SAR matrices called the virtual observation points (VOPs) (24,25). Global SAR and peak power are also constrained:
| [1] |
In Eq. [1], n (varies from 1 to N), c and i are the time, channel and VOP indices, respectively. As explained in Ref. (20), the SMS system matrix A is the block-diagonal of the system matrices associated with the individual slices excitations (26) and b is the vertical concatenation of the target magnetization of all slices. x is the vertical concatenation of the spokes amplitudes of all simultaneously excited slices and xSMS (t) is the total SMS RF pulse, which is the sum of the individual excitations, at time t. To achieve the best possible flip-angle uniformity, we use a magnitude least-squares (MLS) objective in Eq. [1] which can be simply implemented as a series of least-squares constrained optimizations with phase adaptation (24,27). Constraints a), b) and c) constrain local SAR at all VOPs, global SAR and peak power, respectively. Z0 is the reference impedance (see Ref. (24) for an explanation of the factor of 8 in constraint c)), 〈Q〉 is the global SAR matrix and VOPi is the VOP matrix number i (all SAR matrices are C×C, where C is the number of channels). Note that these constraints depend on the total SMS pulse, not on the individual slice excitations. In regular spokes pTx pulses with no SMS acceleration, the maximum peak power occurs at the maximum of the sub-pulses. This is not necessarily the case in SMS pulses, therefore we apply the peak power constraint at all time points, which increases computation time. We solve the constrained optimization problem of Eq. [1] using the fmincon optimizer of Matlab 8 (28).
Specific absorption rate of simultaneous multi-slice pulses
It is instructive to expand a quadratic SAR constraint of Eq. [1] in the case of an SMS2 pulse (we note “SMSX” an SMS pulse exciting X slices simultaneously). In this case, we have xSMS (t) = x1 (t) + x2 (t) = A1su (t) + A2su(t)ejϕSMS(t), where A1s contains the complex amplitudes played on all channels for spoke s (we note S the total number of spokes) for the first slice excitation, u (t) is the slice-select sub-pulse shape and , where γ is the gyromagnetic ratio, z is the distance between the two slices, Gz is the slice-selection gradient and T is the pulse duration. Assuming that RF is played during constant gradient only, this formula reduces to φSMS (t) = ωSMS (T − t) with ωSMS = 2πγzGz. Using these notations, a generic SAR term in Eq. [1] becomes:
 |
[2] |
where Ns is the number of time samples in the sub-pulse shape u. A first observation is that the final SAR expression only involves sums of quadratic forms over the number of spokes instead of the number of time samples, which considerably reduces computation time of the constraints and their derivatives (24). The first and second terms of the last equality in Eq. [2] are the SAR associated the excitation of slices #1 and #2 if they were played independently (i.e., one after the other) and the last term contains the destructive and constructive SAR interferences between them. We note that this term is proportional to the discrete Fourier transform (DFT) of |u(t)|2 evaluated at the frequency ωSMS. By replacing the discrete DFT by a continuous Fourier integral and using the sinc sub-pulse u (t) = sinc(ωt) where ω = 2πγΔzGz (Δz is the slice thickness), this Fourier term becomes the triangle function Tri(ωSMS/ω) = Tri(z/Δz), which is zero for z ≥ Δz. In other words, for an idealized slice-selection, the SAR cross term in Eq. [2] is exactly zero if and only if the slices excited simultaneously are not overlapping. In practice, slice-selection and the low-flip angle approximation are not perfect and this SAR cross term is not exactly zero, however as long as the excited slices are well separated the SAR of the SMS pulse is, to an excellent approximation, the sum of the SAR of the individual slice excitations (Fig. 1e). This result generalizes to pTx the observation, mentioned in the Introduction section, that the RF power of a single channel SMS pulse is equal to the sum of the total RF power of the individual slice excitations (Parseval theorem).
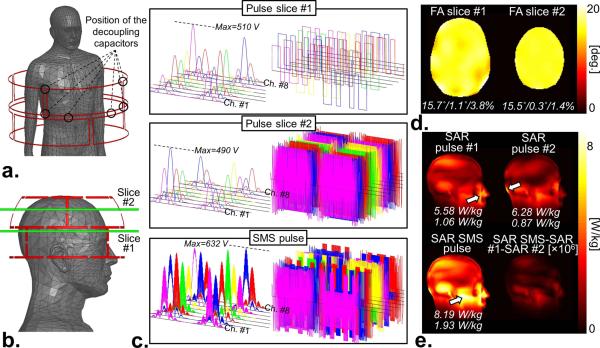
Fig. 1.
a: 3 T parallel transmission (pTx) body array simulated in this work (2 z-rows of 4 channels per row). b: 7 T pTx head array simulated in this work (also 2 z-rows). Panels c–e show detailed data for a magnitude least-squares SMS2 2-spoke pulse designed with constraints for local specific absorption rate (SAR), global SAR and peak radio-frequency (RF) power. Target Ernst flip-angle was 16°, TR was 30 ms, duty-cycle was 10% and inter-slice distance was 5.4 cm. Local SAR, global SAR and peak power were constrained to 10 W/kg, 3 W/kg and 1000 W/channel (equivalent to 632 V/channel), respectively, for the total SMS pulse. c: RF waveforms of the individual slice excitations and the total SMS pulse. d: Flip-angle maps created by the SMS2 pulse at the 2 slice locations (Bloch simulation). The 3 numbers at the bottom of each maps are the mean (in degrees), standard deviation (in degrees) and root mean square error of the flip-angle excitations (in percent of the target flip-angle). e: SAR maximum intensity projection maps of the SMS2 pulse and its individual slice excitations (1 gram average, the numbers below each SAR map are the local SAR/global SAR in W/kg). For these well separated slices, the SAR of the SMS pulse is equal (to an excellent approximation) to the sum of the SAR of the individual slice excitations (see Methods section). However, since the local SAR hotspots of slice excitations #1 and #2 (white arrows) do not occur at the same locations, the local SAR of the SMS pulse is smaller than the sum of the local SAR of the individual slice excitations
If only global SAR and/or average RF power were constrained in Eq. [1], the observation of the previous paragraph implies that it would be equivalent to design the slice excitations of the SMS pulse jointly (as in Eq. [1]) or separately. However, when constraining local SAR, these approaches are not equivalent because the maximum of the sum of two SAR maps is not necessarily equal to the sum of the maximum of these maps (this only occurs if the SAR hotspots of the individual slice excitations occur at the same location, see Fig. 1e). Therefore, the joint design strategy of Eq. [1] is expected to yield pulses achieving better tradeoffs between flip-angle uniformity and local SAR than an independent design strategy consisting in optimizing independently the individual slice excitations with respect to local SAR and flip-angle (from this point-of-view the joint design of Eq. [1] is similar to “SAR hopping” approaches, also referred to as “time-multiplexed” or “time-averaging” SAR methods, described in Ref. (29–32)).
Evaluation in electromagnetic simulations
We evaluated the SMS design strategy of Eq. [1] in electromagnetic (EM) simulations of an 8 channel 7 T head and an 8 channel 3 T body coil (Fig. 1). Both coils were composed of two staggered z-rows each containing 4 Tx channels, which is a design that has been shown to be beneficial for SMS (21). The coils were loaded with the male Ansys body model (33 tissue types). The fields generated by these coils were simulated using a co-simulation strategy based on the field simulator HFSS (Ansys, Canonsburg PA) and the circuit simulator ADS (Agilent, Santa-Clara CA) (24,33,34). Matching and decoupling between any two channels were better than −30 dB and −15 dB, respectively. SAR matrices obtained from the electric fields were averaged over 1 gram and 10 grams in the head and body simulations, respectively, and were compressed into a smaller set of virtual observation points (VOPs) (24,25). We designed SMS2 and SMS8 RF-shimming and 2-spoke pTx pulses based on a Hanning-filtered 7 lobes sinc sub-pulse profile. When using two spokes, the first spoke was placed at the center of Tx k-space and the second was placed at [2; 2; 0] and [3; 3; 0] in unit of m−1 for the body and head simulations, respectively. The second spoke position was chosen so that it laid at a distance approximately equal to 1/FOV, where FOV is the field-of-view of the flip-angle excitation and is equal to 30 cm for the torso (1/0.3=3.3 m−1) and 20 cm for the head (1/0.2=5 m−1). All pulses were designed to achieve a uniform flip-angle of 16°. The repetition time (TR) was fixed to 30 ms for all pulses, so that the duty-cycle varied depending on the pulse duration (indicated on Figs. 2–5). Peak power was limited to 1000 W and 5000 W in the head and torso simulations, respectively. In the head simulation, the interslice distance was 5.6 cm and 1 cm for SMS2 and SMS8, respectively. In the torso simulation, the inter-slice distance was 20 cm and 2.5 cm for SMS2 and SMS8, respectively. We compared our local SAR- and peak power-constrained pulse design strategy to the Tikhonov-regularized SMS pTx design approach of Wu et al.:
| [3] |
where γ is a free parameter (20).
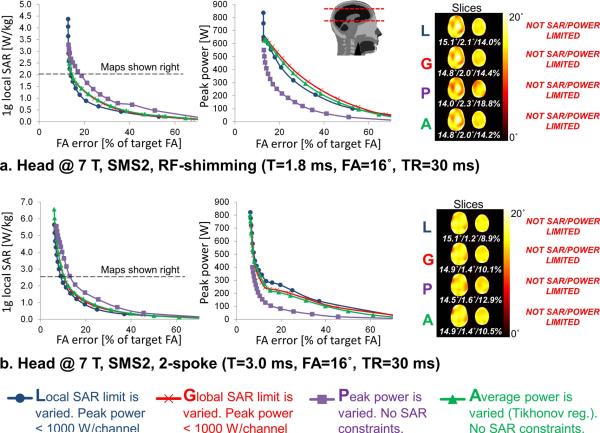
Fig. 2.
Tradeoffs between local specific absorption rate (SAR), peak power and excitation fidelity for SMS2 radio-frequency (RF)-shimming (a) and 2-spokes (b) pulses in the head at 7 T. The flip-angle maps on the right are the best excitations that could be obtained with each design method (L, G, P and A) while satisfying both the power and SAR limits. Pulses were designed using a least-squares objective with a uniform 16° Ernst flip-angle target profile and a target phase profile obtained from a magnitude least-squares design (the same target phase was used for all RF-shimming pulses, but the RF-shimming and 2-spoke target phases were different). The inter-slice distance was 5.6 cm. Blue and red L-curves were obtained by varying the local SAR land global SAR limits, respectively, while simultaneously constraining peak power to 1000 W/channel. The purple L-curves were obtained by varying the peak power limit (no SAR limits). The green L-curves were obtained by varying the total average power by variation of the Tikhonov regularization free parameter as in Ref. 18 (no SAR limits). The 3 numbers below flip-angle maps indicate the mean (in degrees), standard-deviation (in degrees) and root mean square error of the flip-angle excitation of all slices (in percent of the target flip-angle).
Fig. 5.
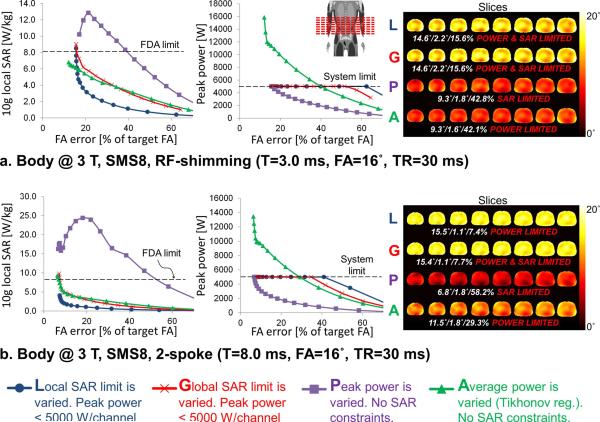
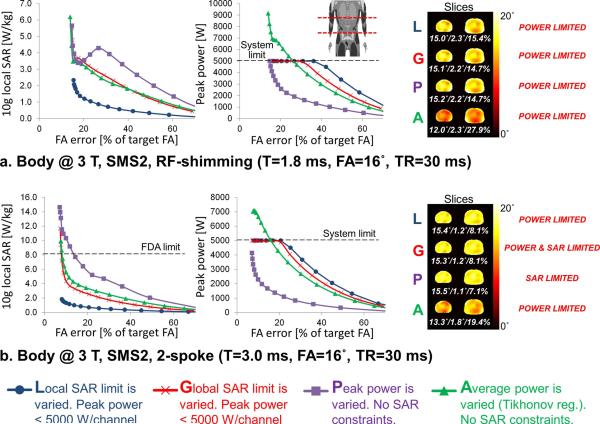
Tradeoffs between local specific absorption rate (SAR), peak power and excitation fidelity for SMS8 radio-frequency (RF)-shimming (a) and 2-spokes (b) pulses in the body at 3 T. The flip-angle maps on the right are the best excitations that could be obtained with each design method (L, G, P and A) while satisfying both the hardware and SAR limits. Pulses were designed using a least-squares objective with a uniform 16° Ernst flip-angle target profile and a target phase profile obtained from a magnitude least-squares design (the same target phase was used for all RF-shimming pulses, but the RF-shimming and 2-spoke target phases were different). The inter-slice distance was 2.5 cm. The 3 numbers below flip-angle maps indicate the mean (in degrees), standard-deviation (in degrees) and root mean square error of the flip-angle excitation of all slices (in percent of the target flip-angle).
Results
The VOP algorithm yielded 2209 and 304 VOPs in the head (5% SAR overestimation) and body simulations (1% SAR overestimation), respectively. These VOP compression parameters are typical and were chosen because they yielded a reasonable number of VOPs in both the head and the body and led to only minor overestimations of SAR (for a discussion on the relationship between the number of VOPs and the SAR overestimation factor, see Refs. (25,35)). Average computation times (Matlab 8 code parallelized on 8 Intel Xeon 2.27 GHz CPUs) for the peak power, local and global SAR constrained 2-spoke pulse design in the torso were 8.9 min. and 22.5 min. for SMS2 and SMS8, respectively. Average computation times in the head were 7.6 min. and 7.3 min for SMS2 and SMS8, respectively. Note that computation times depend on the number of channels, the number of pixels in the optimization mask, the number of VOPs and the convergence rate which can vary dramatically depending on the number of binding constraints. In previous work (24), we found that power- and SAR-constrained single slice pTx excitations could be designed in less than 10 sec. using a dedicated primal-dual algorithm implemented in C++, which is ~15 times faster than using the fmincon function of Matlab parallelized on 8 CPUs. Therefore, we expect that MLS SMS8 pulse design with 2 spokes can be performed in less than 2 min. using a C++ implementation similar to that described in Ref. (24).
Fig. 1c–e show detailed data for a 2-spoke MLS pTx pulse designed at 7 T and exciting 2 slices separated by 5.6 cm. The peak power (632 V), local SAR (8.19 W/kg) and global SAR (1.93 W/kg) of the total SMS pulse are all within their prescribed limits of 632 V, 10 W/kg and 3 W/kg, respectively. As expected for these well separated slices (Methods section), the SAR map of the SMS pulse of Fig. 1c is equal, to a very good approximation, to the sum of the SAR maps of the 2 slice excitations. Moreover, since the SAR hotspots of the 2 slice excitations occur at different locations, the local SAR of the SMS pulse is smaller than the sum of the local SAR of pulses #1 and #2 (“SAR hopping” between excitations #1 and #2).
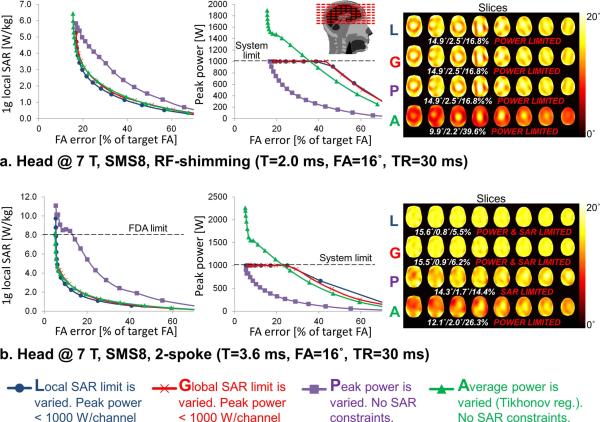
Figs. 2–5 show L-curves obtained by varying individual constraints of the pulse design of Eq. [1]. The SMS2 pulses of Fig. 2 are not significantly power- and/or SAR-limited, therefore there was no great difference between our SAR- and peak power-constrained approach and the Tikhonov-regularized pulse design strategy of Wu et al (20). For brain imaging at 7 T using the 2 z-rows 8 channels system shown in Fig. 1b, constraining both SAR and peak power was necessary to yield SMS8 pulses satisfying both the hardware limits and the FDA regulatory SAR limits (Fig. 3). For both SMS2 and SMS8 pulses, there seems to be little difference between control of local SAR and global SAR in the head at 7 T.
Fig. 3.
Tradeoffs between local specific absorption rate (SAR), peak power and excitation fidelity for SMS8 radio-frequency (RF)-shimming (a) and 2-spokes (b) pulses in the head at 7 T. The flip-angle maps on the right are the best excitations that could be obtained with each design method (L, G, P and A) while satisfying both the hardware and SAR limits. Pulses were designed using a least-squares objective with a uniform 16° Ernst flip-angle target profile and a target phase profile obtained from a magnitude least-squares design (the same target phase was used for all RF-shimming pulses, but the RF-shimming and 2-spoke target phases were different). The inter-slice distance was 1 cm. The 3 numbers below flip-angle maps indicate the mean (in degrees), standard-deviation (in degrees) and root mean square error of the flip-angle excitation of all slices (in percent of the target flip-angle).
In the body at 3 T, local SAR and global SAR are not as correlated as in the head, which is a phenomenon that we have described previously (24). Therefore, constraining global SAR did a poorer job at keeping local SAR under control than controlling local SAR explicitly (i.e., the blue and red L-curves of Figs. 4 and 5 are significantly different). In the body at 3 T, controlling peak power does not allow any control of local SAR: This strategy yields pulses within hardware capabilities but that can clearly violate the FDA local SAR limit of 8 W/kg (Fig. 4 and 5). This phenomenon is much more pronounced for SMS8 pulses (Fig. 5) than SMS2 pulses (Fig. 4). Therefore, both local SAR and peak power control are needed for high MB factors in the body at 3 T.
Fig. 4.
Tradeoffs between local specific absorption rate (SAR), peak power and excitation fidelity for SMS2 radio-frequency (RF)-shimming (a) and 2-spokes (b) pulses in the body at 3 T. The flip-angle maps on the right are the best excitations that could be obtained with each design method (L, G, P and A) while satisfying both the hardware and SAR limits. Pulses were designed using a least-squares objective with a uniform 16° Ernst flip-angle target profile and a target phase profile obtained from a magnitude least-squares design (the same target phase was used for all RF-shimming pulses, but the RF-shimming and 2-spoke target phases were different). The inter-slice distance was 20 cm. The 3 numbers below flip-angle maps indicate the mean (in degrees), standard-deviation (in degrees) and root mean square error of the flip-angle excitation of all slices (in percent of the target flip-angle).
Both in the head at 7 T and the body at 3 T, control of average power of the total SMS pulse using a Tikhonov regularization (Eq. [3]) did a poor job at controlling both SAR and peak power at high MB factors. For the pulses of Figs. 3–5, enforcing the peak power (and to a smaller extend the local SAR limit) with this approach required heavy over-regularization of the pulse design problem which, in turn, yielded poor flip-angle excitations compared to our joint pTx SMS design with local SAR and peak power constraints.
Discussion
We described an MLS pTx SMS spokes pulse design strategy with simultaneously control of local SAR, global SAR and peak power. We showed in electromagnetic simulation of a 3 T body coil and a 7 T head coil that, even for a relatively small flip-angle of 16°, SMS pulses are often SAR- and peak power-limited, especially at high MB factors and large duty-cycles (for the sinc sub-pulses and duty-cycles studied in this work, only the RF-shimming and 2-spoke SMS2 pulses in the head at 7 T were neither SAR- nor peak power-limited). This indicates that pTx SMS pulses should be designed not only using flip-angle uniformity metrics but also local SAR and peak power metrics. In this study, simply controlling average RF power (20) yielded pulses with peak power demands that exceeded the hardware capability. This strategy also created local SAR hotspots exceeding the local SAR limit, however this violation was less pronounced than the peak power violation. Because of the sub-optimality of the Tikhonov regularization design strategy with respect to the peak power metric, enforcing the peak power constraint using this strategy required over-regularization of the pulse design process thus yielding poor flip-angle excitation profiles that did not achieve the target flip-angle. In contrast, explicitly enforcing the peak power and local SAR limits in the pulse design process allowed getting the most out of the hardware system in a way that did not violate the FDA SAR limits. Thus this strategy yielded the best flip-angle maps under limited local SAR and peak power. These results are in accordance with our findings for non-SMS pTx pulses (24) and extend them to SMS. However, because of the large power demands and SAR of SMS pulses, the benefit of explicitly controlling these quantities in the pulse design process compared to the simpler Tikhonov power regularization approach is greater for SMS than single slice excitations.
Because of the quadratic dependence of SAR with RF voltage, one would intuitively expect the SAR of an SMS pulse to be greater than the sum of the SAR created by the individual slice excitations. We have shown that this is not the case however: When the slices excited simultaneously are well separated, the SAR cross terms between slice excitations are null (Fig. 1e). Therefore, a possible way of controlling SAR in pTx SMS could consist in designing individual slice excitations with some form of SAR control (i.e., without SMS). Such a technique would allow control of the local SAR of the SMS pulse by controlling the local SAR of the individual pulses. It would not be optimal however, because it would not take into account possible reductions of local SAR obtained by moving the SAR hotspots of the individual slice excitations to different locations (“SAR hopping”, see Fig. 1e). The joint pulse design strategy proposed in this work explicitly constrains the SAR of the total SMS pulse and therefore uses “SAR hopping” to reduce the total local SAR. In this sense, this design algorithm is similar to the “SAR hopping” local SAR reduction strategy that we proposed previously for rapid sequential multi-slice imaging (32).
To cope with the high peak power and SAR of multiplexed pTx SMS pulses, one can increase the duration of the RF excitation by applying VERSE to the sub-pulse sinc profile (12–15). This strategy can be combined with our proposed pulse design approach in order to yield pTx SMS pulse with even lower peak power demands and smaller local SAR hotspots. However, increasing the length of the excitation pulse usually degrades the slice profile quality for off-isocenter slices (36) so that this process should be limited.
Acknowledgement
NIH grant numbers: R01EB-0068547 and P41EB-015896.
References
- 1.Larkman DJ, Hajnal JV, Herlihy AH, Coutts GA, Young IR, Ehnholm G. Use of multicoil arrays for separation of signal from multiple slices simultaneously excited. Journal of Magnetic Resonance Imaging. 2001;13(2):313–317. doi: 10.1002/1522-2586(200102)13:2<313::aid-jmri1045>3.0.co;2-w. [DOI] [PubMed] [Google Scholar]
- 2.Breuer FA, Blaimer M, Heidemann RM, Mueller MF, Griswold MA, Jakob PM. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magnetic resonance in medicine. 2005;53(3):684–691. doi: 10.1002/mrm.20401. [DOI] [PubMed] [Google Scholar]
- 3.Feinberg DA, Moeller S, Smith SM, Auerbach E, Ramanna S, Glasser MF, Miller KL, Ugurbil K, Yacoub E. Multiplexed echo planar imaging for sub-second whole brain FMRI and fast diffusion imaging. PLoS One. 2010;5(12):e15710. doi: 10.1371/journal.pone.0015710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Moeller S, Yacoub E, Olman CA, Auerbach E, Strupp J, Harel N, Uğurbil K. Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fMRI. Magnetic Resonance in Medicine. 2010;63(5):1144–1153. doi: 10.1002/mrm.22361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magnetic Resonance in Medicine. 2012;67(5):1210–1224. doi: 10.1002/mrm.23097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magnetic Resonance in Medicine. 1999;42(5):952–962. [PubMed] [Google Scholar]
- 7.Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA) Magnetic Resonance in Medicine. 2002;47(6):1202–1210. doi: 10.1002/mrm.10171. [DOI] [PubMed] [Google Scholar]
- 8.Sodickson DK, Manning WJ. Simultaneous acquisition of spatial harmonics (SMASH): fast imaging with radiofrequency coil arrays. Magnetic Resonance in Medicine. 1997;38(4):591–603. doi: 10.1002/mrm.1910380414. [DOI] [PubMed] [Google Scholar]
- 9.Wong E. Optimized phase schedules for minimizing peak RF power in simultaneous multi-slice RF excitation pulses. 2012. p. 2209. [Google Scholar]
- 10.Auerbach EJ, Xu J, Yacoub E, Moeller S, Uğurbil K. Multiband accelerated spin-echo echo planar imaging with reduced peak RF power using time-shifted RF pulses. Magnetic Resonance in Medicine. 2013;69(5):1261–1267. doi: 10.1002/mrm.24719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pauly J, Nishimura D, Macovski A. A k-space analysis of small-tip-angle excitation. Journal of Magnetic Resonance (1969) 1989;81(1):43–56. doi: 10.1016/j.jmr.2011.09.023. [DOI] [PubMed] [Google Scholar]
- 12.Conolly S, Nishimura D, Macovski A, Glover G. Variable-rate selective excitation. Journal of Magnetic Resonance (1969) 1988;78(3):440–458. [Google Scholar]
- 13.Hargreaves BA, Cunningham CH, Nishimura DG, Conolly SM. Variable-rate selective excitation for rapid MRI sequences. Magnetic resonance in medicine. 2004;52(3):590–597. doi: 10.1002/mrm.20168. [DOI] [PubMed] [Google Scholar]
- 14.Xu D, King KF, Liang ZP. Variable slew rate spiral design: Theory and application to peak B1 amplitude reduction in 2D RF pulse design. Magnetic Resonance in Medicine. 2007;58(4):835–842. doi: 10.1002/mrm.21375. [DOI] [PubMed] [Google Scholar]
- 15.Lee D, Grissom WA, Lustig M, Kerr AB, Stang PP, Pauly JM. VERSE-guided numerical RF pulse design: A fast method for peak RF power control. Magnetic Resonance in Medicine. 2012;67(2):353–362. doi: 10.1002/mrm.23010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Norris DG, Koopmans PJ, Boyacioğlu R, Barth M. Power independent of number of slices (PINS) radiofrequency pulses for low-power simultaneous multislice excitation. Magnetic Resonance in Medicine. 2011;66(5):1234–1240. doi: 10.1002/mrm.23152. [DOI] [PubMed] [Google Scholar]
- 17.Eichner C, Setsompop K, Koopmans PJ, Lützkendorf R, Norris DG, Turner R, Wald LL, Heidemann RM. Slice accelerated diffusion-weighted imaging at ultra-high field strength. Magnetic Resonance in Medicine. 2013;71(4):1518–1525. doi: 10.1002/mrm.24809. [DOI] [PubMed] [Google Scholar]
- 18.Norris DG, Boyacioğlu R, Schulz J, Barth M, Koopmans PJ. Application of PINS radiofrequency pulses to reduce power deposition in RARE/turbo spin echo imaging of the human head. Magnetic Resonance in Medicine. 2014;71(1):44–49. doi: 10.1002/mrm.24991. [DOI] [PubMed] [Google Scholar]
- 19.Katscher U, Eggers H, Graesslin I, Mens G, Börnert P. Proc Intl Soc Mag Reson Med. Toronto: 2008. 3D RF shimming using multi-frequency excitation. [Google Scholar]
- 20.Wu X, Schmitter S, Auerbach EJ, Moeller S, Uğurbil K, de Moortele V. Simultaneous multislice multiband parallel radiofrequency excitation with independent slice-specific transmit B1 homogenization. Magnetic Resonance in Medicine. 2013;70(3):630–638. doi: 10.1002/mrm.24828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Poser BA, Anderson RJ, Guérin B, Setsompop K, Deng W, Mareyam A, Serano P, Wald LL, Stenger A. Simultaneous multi-slice excitation by parallel transmission Magnetic resonance imaging. 2013;71(4):1416–1427. doi: 10.1002/mrm.24791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Cloos M, Boulant N, Luong M, Ferrand G, Giacomini E, Le Bihan D, Amadon A. kT-points: Short three-dimensional tailored RF pulses for flip-angle homogenization over an extended volume. Magnetic Resonance in Medicine. 2011;67(1):72–80. doi: 10.1002/mrm.22978. [DOI] [PubMed] [Google Scholar]
- 23.Sharma A, Holdsworth S, O'Halloran R, Aboussouan E, Van AT, Maclaren J, Aksoy M, Stenger VA, Bammer R, Grissom WA. kT-PINS RF Pulses for Low-Power Field Inhomogeneity-Compensated Multislice Excitation. 2013:73. [Google Scholar]
- 24.Guérin B, Gebhardt M, Cauley S, Adalsteinsson E, Wald LL. Local specific absorption rate (SAR), global SAR, transmitter power, and excitation accuracy trade-offs in low flip-angle parallel transmit pulse design. Magnetic Resonance in Medicine. 2014;71(4):1446–1457. doi: 10.1002/mrm.24800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Eichfelder G, Gebhardt M. Local specific absorption rate control for parallel transmission by virtual observation points. Magnetic Resonance in Medicine. 2011;66(5):1468–1476. doi: 10.1002/mrm.22927. [DOI] [PubMed] [Google Scholar]
- 26.Grissom W, Yip C, Zhang Z, Stenger VA, Fessler JA, Noll DC. Spatial domain method for the design of RF pulses in multicoil parallel excitation. Magnetic Resonance in Medicine. 2006;56(3):620–629. doi: 10.1002/mrm.20978. [DOI] [PubMed] [Google Scholar]
- 27.Setsompop K, Wald L, Alagappan V, Gagoski B, Adalsteinsson E. Magnitude least squares optimization for parallel radio frequency excitation design demonstrated at 7 Tesla with eight channels. Magnetic Resonance in Medicine. 2008;59(4):908–915. doi: 10.1002/mrm.21513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Inc. TM . MATLAB 8. Natick, MA: 2012. [Google Scholar]
- 29.Zelinski A. Improvements in Magnetic Resonance Imaging Excitation Pulse Design. Massachusetts Institute of Technology; Cambridge MA: 2008. [Google Scholar]
- 30.Homann H, Graesslin I, Nehrke K, Findeklee C, Dössel O, Börnert P. Specific absorption rate reduction in parallel transmission by k-space adaptive radiofrequency pulse design. Magnetic Resonance in Medicine. 2010;65(2):350–357. doi: 10.1002/mrm.22663. [DOI] [PubMed] [Google Scholar]
- 31.Graesslin I, Steiding C, Annighoefer B, Weller J, Biederer S, Brunner D, Homann H, Schweser F, Katscher U, Pruessmann K. Proceedings of the International Society for Magnetic Resonance in Medicine. Stockholm, Sweden: 2010. Local SAR constrained hotspot reduction by temporal averaging; p. 4932. [Google Scholar]
- 32.Guerin B, Adalsteinsson E, Wald L. Local SAR reduction in multi-slice pTx via “SAR hopping” between excitations. Melbourne: 2012. p. 642. [Google Scholar]
- 33.Lemdiasov RA, Obi AA, Ludwig R. A numerical postprocessing procedure for analyzing radio frequency MRI coils. Concepts in Magnetic Resonance Part A. 2011;38(4):133–147. [Google Scholar]
- 34.Kozlov M, Turner R. Fast MRI coil analysis based on 3-D electromagnetic and RF circuit co-simulation. Journal of Magnetic Resonance. 2009;200(1):147–152. doi: 10.1016/j.jmr.2009.06.005. [DOI] [PubMed] [Google Scholar]
- 35.Lee J, Gebhardt M, Wald LL, Adalsteinsson E. Local SAR in parallel transmission pulse design. Magnetic Resonance in Medicine. 2012;67(6):1566–1578. doi: 10.1002/mrm.23140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Setsompop K, Cohen-Adad J, Gagoski B, Raij T, Yendiki A, Keil B, Wedeen VJ, Wald LL. Improving diffusion MRI using simultaneous multi-slice echo planar imaging. Neuroimage. 2012;63(1):569–580. doi: 10.1016/j.neuroimage.2012.06.033. [DOI] [PMC free article] [PubMed] [Google Scholar]