Stability of multifinger action in different state spaces

Abstract

We investigated stability of action by a multifinger system with three methods: analysis of intertrial variance, application of transient perturbations, and analysis of the system's motion in different state spaces. The “inverse piano” device was used to apply transient (lifting-and-lowering) perturbations to individual fingers during single- and two-finger accurate force production tasks. In each trial, the perturbation was applied either to a finger explicitly involved in the task or one that was not. We hypothesized that, in one-finger tasks, task-specific stability would be observed in the redundant space of finger forces but not in the nonredundant space of finger modes (commands to explicitly involved fingers). In two-finger tasks, we expected that perturbations applied to a nontask finger would not contribute to task-specific stability in mode space. In contrast to our expectations, analyses in both force and mode spaces showed lower stability in directions that did not change total force output compared with directions that did cause changes in total force. In addition, the transient perturbations led to a significant increase in the enslaving index. We consider these results within a theoretical scheme of control with referent body configurations organized hierarchically, using multiple few-to-many mappings organized in a synergic way. The observed volatility of enslaving, greater equifinality of total force compared with elemental variables, and large magnitude of motor equivalent motion in both force and mode spaces provide support for the concept of task-specific stability of performance and the existence of multiple neural loops, which ensure this stability.

one of the fundamental problems of motor control is that of redundancy (Bernstein 1967): at any level of description of the system involved in movement production, the number of elements (and of their output variables, elemental variables) is higher than the number of constraints associated with typical motor tasks. Recently, the problem of motor redundancy has been revisited in the context of the principle of motor abundance (Gelfand and Latash 1998; Latash 2012). This approach posits a way for the central nervous system (CNS) to take advantage of all of the elemental variables at its disposal to ensure stability of movement, rather than requiring the CNS to achieve a single, optimal solution by eliminating redundant degrees of freedom. Thus the principle of abundance avoids requiring computational, and physiologically unfeasible, control schemes, which involve explicit instruction to all body structures involved in a given action.

A theoretical scheme has been developed, which unites the principle of abundance with the idea of hierarchical control of motor actions (Latash 2010; described in more detail in the discussion). This scheme proposes that the CNS sets a relatively small number of neural variables related to task constraints and that a resultant sequence of few-to-many transformations leads to the involvement of redundant sets of elements at more peripheral levels. These few-to-many transformations are organized in a synergic way, meaning that they allow more variance in directions that do not affect task performance than in directions that do (cf. task-specific stability; Schöner 1995). These two components of variance can be quantified within the framework of the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999) as variance within the UCM (V_UCM, which does not affect performance) and variance orthogonal to the UCM (V_ORT, which affects performance). The two variance components, V_ORT and V_UCM, reflect different stability of the system in directions that affect important characteristics of performance (orthogonal to the UCM, high stability) and in directions that span the UCM (low stability). A few neurophysiological schemes have been suggested to account for the observed structure of variance in multieffector tasks (Latash et al. 2005; Martin et al. 2009). In particular, a scheme with central back-coupling loops resembling the classical systems of Renshaw cells was able to account for certain features of intertrial variance in multifinger tasks including stabilization of the total force and total moment of force (Latash et al. 2005).

Several recent studies have pointed to loops involving subcortical structures as crucial elements within the aforementioned hierarchical scheme of synergic control (Park et al. 2012, 2013). In those studies, patients with early state Parkinson's disease and olivo-ponto-cerebellar atrophy showed significantly reduced indexes of synergy (reflecting the relative amount of V_UCM in the total intertrial variance) in multifinger tasks with only minor changes in the indexes of performance such as speed and accuracy. These observations were in stark contrast to an earlier report on similar synergy indexes in the ipsilesional and contralesional extremities after a single cortical stroke (Reisman and Scholz 2003), even though movements in the contralesional extremities were significantly impaired.

This scheme predicts, in particular, that a transient perturbation applied during a motor action may be expected to lead to equifinality (return to the preperturbation state, cf. Bizzi et al. 1976; Kelso and Holt 1980; Schmidt and McGown 1980; Latash and Gottlieb 1990) of task-related variables but not of elemental variables, assuming that the subject is not reacting to the perturbation. Two recent experimental studies (Wilhelm et al. 2013; Zhou et al. 2014a) have confirmed this prediction. In the first of these studies, subjects were asked to produce a constant amount of force by pressing on force sensors with the four fingers of the right hand. A transient perturbation (lifting-and-lowering a finger with the “inverse piano” device; Martin et al. 2011) led to changes in all finger forces organized in such a way that intertrial variance in the space of finger forces was relatively high while variance of the total force was low. This was associated with V_UCM > V_ORT reflecting relatively low stability of the four-finger system in directions that span the UCM compared with the direction orthogonal to the UCM. The inequality V_UCM > V_ORT was also confirmed by the analysis of variance in the space of hypothetical commands to fingers, finger modes (Zatsiorsky et al. 1998; Latash et al. 2001; Danion et al. 2003). A finger mode is a hypothetical neural command to a finger that leads to force changes in all the fingers of the hand due to the phenomenon of enslaving (Kilbreath and Gandevia 1994; Schieber 2001; Zatsiorsky et al. 1998). In this article, we present results of experiments that allow distinction between stability properties of multifinger action in the spaces of finger forces and finger modes.

Consider a finger force production task in which subjects are instructed to use only some of their fingers, but the forces produced by all four fingers are analyzed. When a person is asked to press with one finger only, only one finger mode is expected to differ from zero, while all four fingers produce force. Therefore, the task is redundant in the space of finger forces but not in the space of finger modes. Our hypothesis 1 was that, both before and after a transient perturbation, total force would be stabilized (in a sense, V_UCM > V_ORT) in the redundant space of finger forces but not in the nonredundant space of finger modes (where all the variance is expected to be V_ORT because the dimensionality of the UCM is zero). Hypothesis 2 was that a transient perturbation applied to a finger in a one-finger task would lead to the mentioned variance inequality (V_UCM > V_ORT) computed for changes in finger forces but not for changes in finger modes (which are expected to be limited to one mode only). When more than one finger is explicitly involved in the production of the total force, then the task is redundant in both spaces. Therefore, in a two-finger task, the inequality V_UCM > V_ORT is expected in both force space and mode space for analyses of both steady states (before and after the perturbation), as well as those of changes between the two steady states. We tested these hypotheses by applying transient positional perturbations to an instructed finger and to a noninstructed finger. In the force space, perturbations applied to either finger were expected to lead to qualitatively similar results. In contrast (hypothesis 3), in mode space, perturbations to a noninstructed finger (which as a mode value, by definition, equal to zero) were expected to have no effect on the modes of other fingers and hence no special structure of variance was expected in either one-finger or two-finger tasks.

METHODS

Subjects.

Eight self-reported right-handed subjects (4 men and 4 women; ages 23–36 yr) participated in this study. All subjects were healthy, had no history of hand injury, and were not professional musicians, typists, or engaged in other activities likely to significantly alter their dexterity. All subjects provided written informed consent in accordance with the procedures approved by the Office of Research Protections at The Pennsylvania State University.

Equipment.

The entire experimental procedure was conducted using the inverse piano, a custom-built apparatus utilizing four force sensors placed on posts powered by Linmot PS01-23×80 linear actuators (Linmot, Spreitenbach, Switzerland), which can move the sensors along their vertical axes (for details, see Martin et al. 2011). This apparatus allows individual fingers to be lifted and lowered during multifinger pressing tasks. Force data were collected using PCB model 208C01 single-axis piezoelectric force transducers (PCB Piezotronics, Depew, NY). The signals from the transducers were sent to individual PCB 484B11 signal conditioners, one conditioner per sensor, and then digitized at 300 Hz using a 16-bit National Instruments PCI-6052E analog-to-digital card (National Instruments, Austin, TX). Sensor readings were zeroed with the subject's hand resting on the sensors just before data collection to ensure that the weight of the subjects' fingers was not included in the force recorded by the sensors. Each actuator could be moved independently of the others by means of a Linmot E400-AT four-channel servo drive. Data collection, visual feedback to the subject, and actuator control were all managed using a single program running in a National Instruments LabView environment. Visual feedback was provided by means of a 19-in. monitor placed 0.8 m from the subject. During the entire procedure, subjects were shown feedback on the total force they produced with all four fingers, regardless of the number of fingers they were instructed to use for the task.

Experimental procedure.

There were three main tasks involved in this procedure. First, each subject was asked to produce his or her four-finger maximal voluntary contraction (MVC) force. Collection of each subject's MVC allowed for the subsequent tasks to be adjusted to his or her force-production capabilities. During the MVC task, each subject was given a 6-s time window during which to produce maximal force in a smooth increasing manner. Trials in which subjects produced sharp force peak via countermovement were rejected. Each subject repeated the MVC task twice with a 30-s rest in between trials.

The second task in the procedure was the production of single-finger force ramps. Each subject was asked to produce force following a specific profile with one finger (the instructed finger). The target force profile corresponded to 5% of the instructed finger's contribution to the four-finger MVC for 2 s, a smooth increase from 5 to 45% of the finger's MVC contribution over 6 s, and then 2 s at 45% of MVC. The ramp task was repeated four times so that each finger was the instructed finger in one trial. The data from these trials were used to calculate enslaving matrices (Zatsiorsky et al. 2000; see later).

The third task was the main experimental task of the study. Each trial took 12 s and had basically the same form: during the first 6 s, the subject was asked to reach and maintain a target force with the assistance of visual feedback. After 6 s had elapsed, visual feedback on the force was removed, so the subject could only see a line corresponding to target force. There were four conditions corresponding to the fingers with which the subject was instructed to press: index (I); index and middle (IM); index, middle, and ring (IMR); and all fingers (IMRL). While data for IMR and IMRL were collected, they are not presented here. The task force was always set to 20% of the force produced by the instructed finger(s) during the MVC task. No subjects reported fatigue during the course of the procedure.

The first three trials in each condition were controls: although visual feedback was removed, no perturbation was applied. After the control trials, in each subsequent trial subjects experienced perturbations: Contemporaneously with the removal of feedback (after 6 s of steady-state force production), one of the sensors moved up and lifted the subject's finger (perturbed finger). The perturbed finger was raised 1.0 cm at a rate of 2.0 cm/s, held at the raised position for 1.5 s, and then lowered to the original position at a rate of −2.0 cm/s. In the I and IM conditions, the I finger and the R finger were perturbed in different trials. Note that the I finger was always an instructed (master) finger while the R finger was always a noninstructed (slave) finger. Each subject performed 24 consecutive trials in each of the four condition/perturbation combinations. Subjects were self-paced through each condition and given a 30-s rest after each condition. Conditions were block-randomized, while the R-perturbation trials always followed the I-perturbation trials.

Data processing.

In the MVC trials, individual finger forces were measured when the four-finger total force reached its peak.

Calculating finger modes and the enslaving matrix.

When one finger of a hand produces force intentionally, other fingers also produce force (enslaving, Li et al. 1998; Zatsiorsky et al. 2000). We quantified enslaving using the ramp trials when only one finger was instructed to produce force. Individual forces of all four fingers increased during the ramp task. The following linear regression equation was used:

$${\text{F}}_{i,j}={\text{F}}_i^0+{\text{k}}_{i,j}\times {\text{F}}_{\text{TOT},j},$$ (1)

where i,j = {I,M,R,L}, F_TOT,j is the total force produced by all fingers when j is the instructed finger, and F_i,j is the force produced by finger i when finger j is the instructed finger. The constants k_i,j were arranged into a 4 × 4 enslaving matrix [E]. Futhermore, [E] was used to calculate finger modes (hypothetical commands to fingers, Latash et al. 2001; Danion et al. 2003) from finger forces:

$$\mathbf{m}={\left[\mathbf{E}\right]}^{-1}\hspace{0.17em}\mathbf{F},$$ (2)

where m is a 4 × 1 mode vector and F is a 4 × 1 force vector.

Analysis of the main task.

During the main trials with accurate force production by the instructed finger(s), subjects showed consistent force changes during the finger lifting and lowering phases. Figure 1 illustrates typical force profiles during the I and IM tasks in control trials (no perturbation applied, thick dashed line) and when the perturbation was applied to the I finger (thick solid line) or R finger (thin solid line). The data were analyzed within three 250-ms phases. Phase 1 was from 3.00–3.75 s from the onset of the trial and represented a preperturbation steady state; phase 2 was from 7.23–7.48 s, which was the middle of the perturbation interval; phase 3 took place from 8.92–9.17 s and was considered a postperturbation steady state. Occasionally equipment malfunctions corrupted individual trials, so to balance the number of trials averaged to represent each subject, trials with the largest deviation from a subject's average performance were eliminated if necessary in order for all subjects to have 22 usable trials.

Fig. 1.

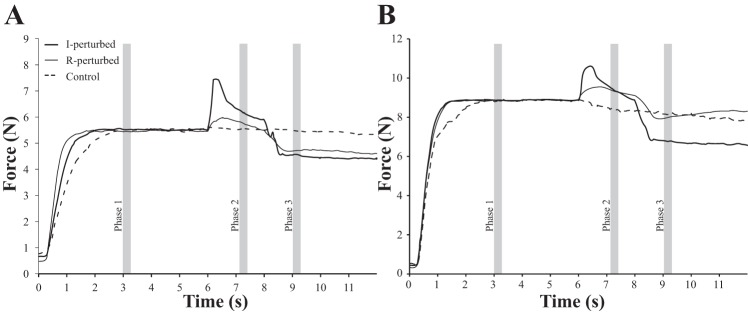
Average force profiles for a representative subject during the index (I; A) and index + middle (IM; B) pressing conditions. The perturbation onset at 6 s corresponded with removal of visual feedback in all conditions (including the no-perturbation conditions). The phase 1, phase 2, and phase 3 markings denote the time periods during which data were analyzed. R, ring finger.

Calculating an index of enslaving.

An index of enslaving (EN) was computed to quantify the amount of force produced by noninstructed fingers as the percentage of total force:

$$\text{EN}=\left[\left({\text{F}}_{\text{TOT}}-{\text{F}}_{\text{INS}}\right)/{\text{F}}_{\text{TOT}}\right]\times 100$$ (3)

where F_TOT is the total force produced by all fingers and F_INS is the force produced by all instructed fingers. EN was calculated for each phase of analysis; changes in EN (ΔEN) were also calculated as the difference between EN in phase 3 and in phase 1.

Analysis of force change.

For each subject, total force produced at phase 1 was compared with force produced at phase 3. Since the average magnitude of this difference was negative for all subjects and all conditions, this difference was termed decrease in total force (ΔF_TOT) and is calculated according to the equation:

$$\Delta {\text{F}}_{\text{TOT}}={\text{F}}_{\text{TOT,3}}-{\text{F}}_{\text{TOT,1}}$$ (4)

where F_TOT,1 is the total force a subject produced at phase 1 and F_TOT,3 is the total force that subject produced at phase 1. ΔF_TOT was calculated for each condition separately.

Analysis of the force variance.

We used the framework of the UCM hypothesis (Scholz and Schöner 1999) to quantify intertrial variance in two spaces, the UCM computed for the total force and the space orthogonal to the UCM (ORT). Note that variance in the UCM space has no effect on total force while variance in the ORT space does. The analysis was run using two sets of elemental variables, finger forces (F) and finger modes (m).

For each subject and each condition separately, all the accepted trials were aligned, and intertrial variance indexes were computed over 22 trials using force and mode values averaged over phase 1, phase 2, and phase 3 separately. The difference vectors representing the change in individual finger forces between phase 1 and phase 3 were computed for each trial. These difference vectors were demeaned and their intertrial variance was projected onto the UCM and ORT spaces. Detailed descriptions of variance computation within the two subspaces can be found in earlier publications (Latash et al. 2001; Scholz et al. 2002).

We will address the two variance components in the force space as V_UCM,F and V_ORT,F, while in the mode space the abbreviations will be V_UCM,m and V_ORT,m. Total variances in force and mode space are referred to as V_TOT,F and V_TOT,m, respectively. V_TOT,F and V_TOT,m were computed as the sums of the corresponding V_UCM and V_ORT values. The same nomenclature holds for the variance of difference vectors calculated for the change in force or mode between two time periods, except that their designations incorporate ΔF or Δm as in: V_UCM,ΔF.

In addition to the UCM and ORT variances, an index of multifinger synergy, ΔV, was computed after normalizing the variance indexes per degree of freedom in the corresponding spaces (resulting in V_UCM.N, V_ORT.N, and V_TOT.N), as the normalized difference between V_UCM.N and V_ORT.N:

$$\Delta \mathit{\text{V}}=\left({\mathit{\text{V}}}_{\text{UCM.N}}-{\mathit{\text{V}}}_{\text{ORT.N}}\right)/{\text{V}}_{\text{TOT.N}}$$ (5)

For statistical analyses, ΔV values were log transformed using Fisher's transformation adjusted for the actual computational limits of ΔV. This resulted in transformed synergy indexes (ΔV_ZF and ΔV_Zm) computed using finger forces and finger modes as elemental variables.

Analysis of motor equivalence.

We also quantified the average change of the four-finger force vector in the UCM and ORT spaces between phase 1 and phase 3. The system's movement within the UCM does not affect total force production and is therefore termed motor equivalent (ME) motion (Mattos et al. 2011), whereas movement in ORT does affect total force production and is called nonmotor equivalent (nME) motion. The ME and nME components of force changes were calculated for each trial performed by a given subject in each condition separately; these values were then normalized by the square root of the dimensionality of the corresponding spaces (cf. Mattos et al. 2011, 2013) and averaged over all the trials for each subject and each experimental condition separately. ME and nME components were calculated in both force and mode spaces and are designated with subscripts F and m, respectively.

Statistics.

Unless otherwise noted, data are presented as means ± SE. Two-way ANOVA with repeated measures were used to test the effects of condition (2 levels: I and IM) and finger perturbed (2 levels: I finger and R finger, or 3 levels including the control condition) on outcome variables such as finger forces and the enslaving index. To test the first and third specific hypotheses, three-way ANOVAs were run on variance indexes computed within the spaces of finger forces and finger modes with factors condition (2 levels, I and IM), finger perturbed (2 levels: I finger, R finger, or 3 levels including the control condition), and variance (2 levels: UCM and ORT). To test the second hypothesis, a similar analysis was run of the differences in finger forces and modes between phase 3 and phase 1. We also explored changes in the variance indexes and in the synergy index ΔV_Z across phases using a three-way ANOVA with factors condition (2 levels: I and IM), finger perturbed (2 levels: I and R), and phase (3 levels: 1, 2, and 3). Analysis of motor equivalence was run using a three-way ANOVA with factors condition (2 levels: I and IM), finger perturbed (2 levels: I finger, R finger), and component (2 levels: ME and nME). All statistical tests were run in SAS 9.3 (SAS Institute, Cary, NC). ANOVAs used a linear mixed model utilizing a compound symmetrical covariance structure. When necessary, data were log transformed for normality. Test degrees-of-freedom were adjusted with the Kenward-Roger method. Statistical significance was set at P < 0.05.

RESULTS

General patterns of force change.

Across both perturbation (I, R) and finger-pressing (I, IM) conditions, the perturbation resulted in the lifted finger increasing its force. This force decreased while the finger remained raised and then decreased further when the finger was lowered to its original position, often dropping below the level it had produced before the perturbation. The other fingers of the hand typically showed force changes in the opposite direction to those of the perturbed finger: a force drop when the perturbed finger was raised and an increase in force when the perturbed finger was lowered. Changes in total force were dominated by the changes in the perturbed finger force. Figure 1 shows total force profiles for a typical subject during both I perturbation (master finger perturbation) and R perturbation (enslaved finger perturbation) applied during the I condition (Fig. 1A) and the IM condition (Fig. 1B).

In the unperturbed (control) trials, the total force decreased (ΔF_TOT) modestly after the feedback removal between phase 1 and phase 3, on average by 0.2 ± 0.06 and 0.5 ± 0.1 N for the I and IM conditions, respectively. The magnitude of ΔF_TOT was larger in trials with perturbations. In the I condition, F_TOT decreased by 0.4 ± 0.26 N for I perturbation and 0.36 ± 0.15 N for R perturbation. In the IM condition, force decreased by 1.3 ± 0.36 N for I perturbation and 1.1 ± 0.15 N for R perturbation.

The two-way repeated measures ANOVA on ΔF with factors condition and finger perturbed showed significant main effects for condition (F_1,35 = 20.95; P < 0.001) and finger perturbed (F_2,35 = 4.36; P < 0.05). Tukey-Kramer adjusted post hoc analysis on finger perturbed showed that during control trials, ΔF was significantly smaller than in I-perturbed and R-perturbed trials but that I-perturbed and R-perturbed conditions were not significantly different from one another. This means that perturbations applied to the instructed and noninstructed fingers led to similar results in the single-finger and two-finger tasks. Figure 2 illustrates the ΔF data with associated significance indicated.

Fig. 2.

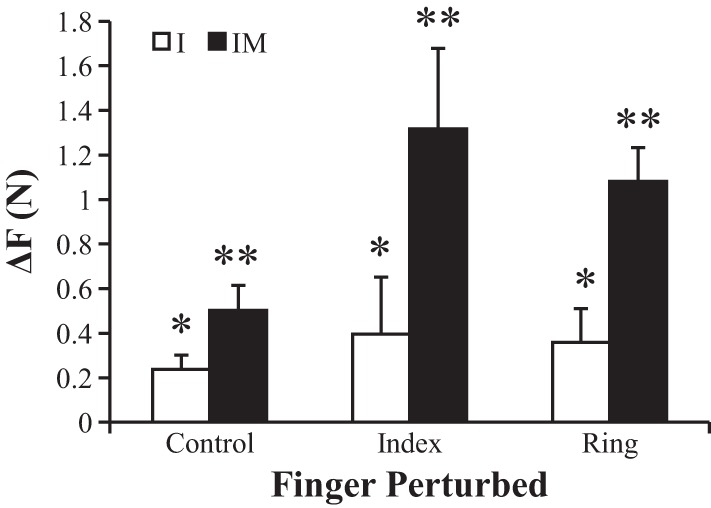
The decrease in total force from phase 1 to phase 3 for each perturbation and finger pressing condition. Positive values indicate that subjects produced less force in phase 3 than in phase 1. *Significant differences between conditions. **Significant differences between perturbations. Average across subjects data are shown with SE bars.

The amount of force produced by noninstructed fingers changed between phase 1 and phase 3. We quantified the phenomenon of enslaving with an index of EN calculated as the percentage of total force produced by fingers, which were not instructed to produce force (see methods). Typically, this index showed no changes during the control trials; the average change in EN, ΔEN was −0.3 ± 2.4 and 0.1 ± 0.96% for the I and IM conditions, respectively. In contrast, trials with perturbations resulted in an increase in EN from phase 1 to phase 3 (Fig. 3). In the I condition, ΔEN was 8.6 ± 2.0% for I perturbation and 7.4 ± 2.1% for R perturbation; in the IM condition, ΔEN was 1.9 ± 0.90% for I perturbation and 5.3 ± 1.7% for R perturbation. Single-group t-tests confirmed that ΔEN was not different from zero for the control trials and for the I perturbation during the IM condition. However, ΔEN was significantly different from zero in the other three conditions illustrated in Fig. 3. A two-way ANOVA confirmed significant effects of both factors, condition (F_1,35 = 4.14; p < 0.05) and finger perturbed (F_2,35 = 8.43; P < 0.001) without a significant interaction.

Fig. 3.

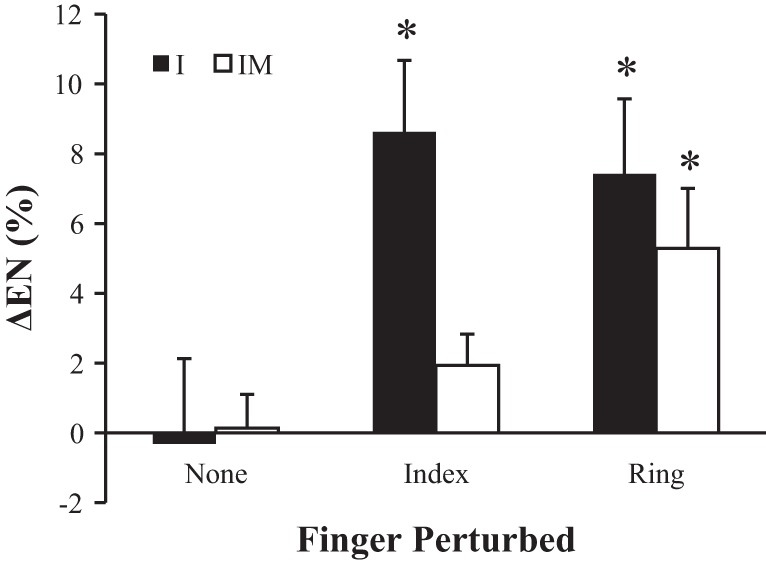
The change in enslaving from phase 1 to phase 3. Enslaving (EN) is presented as the percentage of total force produced by noninstructed fingers. Positive values indicate that noninstructed fingers produced a greater amount of total force during phase 3 than phase 1. *Values that are significantly different from zero. Average across subjects data are shown with standard error bars.

Mode profiles showed similar trends to force profiles. Some subjects showed mode values for noninstructed fingers that had negative magnitudes. Since modes are hypothetical variables, which reflect a subject's intention to press with a given finger, negative modes may be interpreted as subjects' efforts to unload a particular finger. Table 1 shows the number of subjects who produced a negative mode in each experimental condition with noninstructed modes in italics.

Table 1.

Incidence of negative mode values

Finger(s) Pressing × Finger Perturbed	Index			Index + Middle
	Control	Index	Ring	Control	Index	Ring
Phase 1
Index	0	0	0	0	0	0
Middle	3	1	1	0	0	0
Ring	2	2	1	2	2	1
Little	1	0	0	0	1	1
Phase 3
Index	0	0	0	0	0	0
Middle	2	0	2	0	0	0
Ring	2	1	2	1	1	3
Little	2	0	0	1	2	0

The number of subjects is shown who produced a negative mode value during a particular finger-pressing × finger-perturbed condition for the initial steady state (phase 1) and final steady state (phase 3). Noninstructed modes are in italics.

Analysis of the structure of variance.

To test our first and third hypotheses, the structure of intertrial variance was analyzed within the framework of the UCM hypothesis (see methods). These analyses were carried out in both force space and mode space. Overall, when intertrial variance was analyzed within each subject and each condition, ΔV was positive for all pressing and perturbation combinations in all three phases, reflecting V_UCM > V_ORT (both indexes normalized per dimension, see methods) in both force-based and mode-based analyses. Even in single-finger tasks, the inequality V_UCM > V_ORT was confirmed across all phases with the perturbation applied to the task finger (I) and to a nontask finger (R).

The index of synergy, ΔV, showed the highest values in phase 1 and dropped across the three phases in all conditions. Figure 4 illustrates these results over individual phases in mode space (Fig. 4A, ΔV_Z,m) and force space (Fig. 4B, ΔV_Z,F). Three-way ANOVAs with factors condition, finger perturbed, and phase (1, 2, and 3) on ΔV_Z confirmed a significant main effect of phase in both mode space (F_2,77 = 84.62; P < 0.001) and force space (F_2,77 = 77.31; P < 0.001), without other effects. Tukey-Kramer adjusted post hoc comparisons showed that each phase was significantly different from all other phases in both force space and mode space.

Fig. 4.

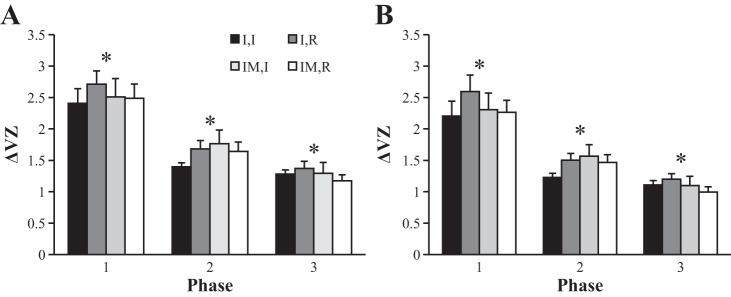
The z-transformed synergy index (ΔV_Z) for phase 1, phase 2, and phase 3 for both finger pressing conditions (I, IM) and for both perturbations (I, R). A: mode space (ΔV_Z,m). B: force space (ΔV_Z,F). *Significant differences between phases. Average across subjects data are shown with SE bars.

To test our second hypothesis, the changes in finger forces and modes between phase 3 and phase 1 were analyzed. This analysis showed that most of intertrial variance once again was confined to the UCM. This is illustrated in Fig. 5 for the analyses in both mode and force space. Again, even in one-finger tasks, transient perturbations resulted in changes in the finger force and finger mode spaces such that there was more variance in directions that did not affect total force; this occurred both for perturbations applied to the task finger (I) and those applied to a nontask finger (R).

Fig. 5.

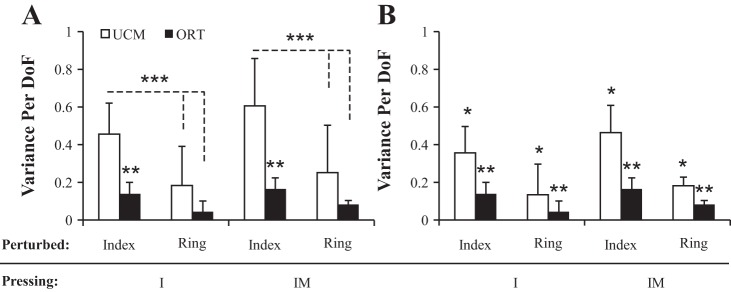
The structure of variance computed for the differences in force and mode vectors from phase 1 to phase 3 for each perturbation and finger pressing condition. A: mode space (V_UCM,Δm and V_ORT,Δm). B: force space (V_UCM,ΔF and V_ORT,ΔF). These data have been log transformed for normality. DoF, degrees-of-freedom. *Pressing/perturbed combinations that are significantly different from one another. **V_ORT that is significantly different from its associated V_UCM.

These results were confirmed by three-way ANOVAs with factors condition, finger perturbed, and variance performed in both force and mode spaces. Variance was log transformed for normality before statistical analysis. In both force and mode space, there were significant main effects for variance (F_1,49 = 18.13; P < 0.001) reflecting V_UCM > V_ORT and for finger perturbed (F_1,49 = 16.94; P < 0.001) reflecting larger variance in the I-perturbed trials, but the effect of condition (F_1,49 = 1.76; P = 0.19) was not significant. The finger perturbed × variance interaction was significant for the mode space analysis (F_1,49 = 4.99; P < 0.05) and was just under the significance level for the force-space analysis (F_1,49 = 3.89; P = 0.054). Tukey-Kramer analysis on the interaction showed that V_UCM was significantly greater than V_ORT in I-perturbed trials and that V_UCM in I-perturbed trials was significantly greater than V_UCM and V_ORT in R-perturbed trials.

Analysis of motor equivalence.

We explored the magnitude of the two components of changes in the force and mode vectors (ΔF and Δm) from phase 1 to phase 3, one component that did not lead to total force change (ME), and the other component that did (nME). For this purpose, in each trial ΔF and Δm vectors were projected onto the UCM and the subspace orthogonal to it (ORT). For quantitative comparison, the length of the projections was normalized by square root of the corresponding dimensionality (cf. Mattos et al. 2011).

Mean magnitudes of ME projections were larger than those for nME projections in both force space and mode space for all pressing and perturbation conditions. Figure 6 illustrates the relative magnitudes of ME (black bars) and nME (open bars) projections in mode space (Fig. 6A) and force space (Fig. 6B). Note that the ME projections were consistently larger than the nME ones.

Fig. 6.

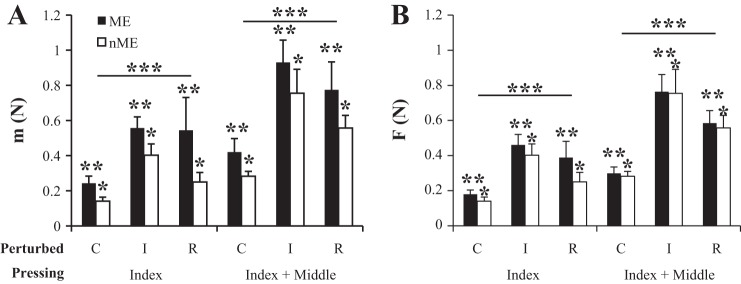
The magnitudes of motor equivalent (ME) and nonmotor equivalent (nME) components of the change in mode (A) and force vectors (B) between phase 1 and phase 3 for each perturbation type and in each pressing condition. *Significant effect of component. **Significant effect of finger perturbed. ***Significant effect of condition.

Three-way ANOVAs with factors condition, finger perturbed (control, I perturbed, and R perturbed), and component (ME and nME) were run in both mode space and force space. In both cases, ME and nME magnitudes were log transformed for normality (reflecting their lower bound at 0). In force space, condition, finger perturbed, and component all showed significant main effects without interactions (respectively: F_1,77 = 57.82; P < 0.001; F_2,77 = 45.69; P < 0.001; F_1,77 = 4.33; P < 0.05). Post hoc comparisons using the Tukey-Kramer method showed that all three levels (control, I perturbed, and R perturbed) were significantly different from one another. These results were consistent in the mode space analysis.

DISCUSSION

All three hypotheses formulated in the Introduction were falsified in conditions when subjects tried to press with only one finger. In the single-finger task (I condition), there was significantly more variance within the UCM (computed for the total force) than orthogonal to it (V_UCM > V_ORT). This was true for the analysis in each of the three phases: before the perturbation (phase 1), in-between the lifting and lowering phases of the perturbation (phase 2), and after the perturbation (phase 3). Hypothesis 1 predicted this result only in the space of finger forces. The experiment showed, however, that the inequality V_UCM > V_ORT was true for analysis in the space of finger modes (Fig. 4) as well, even though a single-finger task is supposed to be nonredundant in mode space, which would imply V_UCM must be zero (cf. Scholz and Schöner 1999; Hsu et al. 2007). This result suggests that the subjects were using more than one mode even though they were instructed to press with only one finger.

V_UCM was also greater than V_ORT when the differences in the finger forces (and modes) between phase 1 and phase 3 were the subjects of analysis (Fig. 5). Based on a previous study (Wilhelm et al. 2013), we expected V_UCM > V_ORT only when a redundant set of elemental variables was involved in the action. In contrast to this expectation, this inequality was observed in analyses of I condition in both finger force space and finger mode space. We therefore conclude that relative equifinality in the task variable (low V_ORT, reflecting low variance of total force) following a transient perturbation was accompanied by nonequifinality in both the redundant (force) and apparently nonredundant (mode) spaces of elemental variables (reflected in the high V_UCM). Therefore, there was no qualitative difference in all the variance characteristics between the one-finger and two-finger tasks despite the fact that the latter were redundant in the mode space while the former were not.

We also predicted (hypothesis 3) that a perturbation to a noninstructed finger would not lead to the V_UCM > V_ORT signature in the finger mode space, while the inequality was expected in the force space. This hypothesis was also rejected because both force and mode analysis showed similar results. Indeed, across conditions, in trials with perturbation applied to the ring finger (a nontask finger), total force was stabilized by covariation of finger forces and finger modes in all three analyzed phases of the movement. Futhermore, the changes in both finger forces and modes covaried in a way that resulted in relative equifinality of total force.

Taken together, these unexpected results force us to reconsider behavior of humans under the instructions to use only one finger of a hand. These results also suggest that the phenomenon of enslaving is not as stable as previously thought and that finger interactions may change within a few seconds under the action of an external perturbation, even if a person is trying not to change commands to the fingers.

Enslaving: are finger modes themselves synergies?

The two spaces of elemental variables used in our analyses, the finger force space and the finger mode space, are linked via the phenomenon of enslaving. This term reflects unintentional movement of (force production by) a finger when another finger of the hand moves (produces force) intentionally (Kilbreath and Gandevia; Li et al. 1998; Zatsiorsky et al. 2000; Kim et al. 2008). Enslaving results from a variety of factors including multidigit extrinsic hand muscles, connective tissue links between fingers, and overlapping cortical representations (reviewed in Schieber and Santello 2004; Zatsiorsky and Latash 2008). In all the mentioned studies, patterns of enslaving for a given person have been viewed as a stable characteristic of that person's hand. In particular, the assumption of stable enslaving allowed the introduction of the notion of finger modes (Zatsiorsky et al. 1998; Danion et al. 2003), which has been used in many studies of multifinger synergies within the framework of the UCM hypothesis (starting from Latash et al. 2001; reviewed in Latash et al. 2007; Latash 2008).

Changes in enslaving have been documented over years of specialized practice (Slobounov et al. 2002), with healthy aging (Shinohara et al. 2003, 2004), and with neurological disorder (Park et al. 2012). Several recent studies have provided evidence for changes in enslaving occurring relatively quickly, over a single 1-h session involving finger fatigue or specialized practice (Singh et al. 2010; Wu et al. 2013). The results presented here suggest that enslaving may be an even more volatile phenomenon than the previously cited articles suggest: we observed changes in enslaving within a single trial, over the time course of seconds (Fig. 3). Given the quickness of these changes, they likely reflect modifications in the control of fingers at a neural level. These observations force us to reconsider the notion of finger modes and its role in the analysis of multifinger synergies.

The word synergy has been used in literature to signify more than one phenomenon (reviewed in Latash 2008). In clinical literature, this word has been used with a negative connotation to mean a stereotypical pattern of muscle activation interfering with voluntary movements; this phenomenon is often observed in stroke survivors (Bobath 1978; DeWald et al. 1995). In the motor control literature, the most common meaning of synergy is a group of variables, which scale together across variations in task parameters or over task execution (d'Avela et al. 2003; Ivanenko et al. 2004; Ting and Mcpherson 2005; Tresch and Jarc 2009). This definition follows the tradition of Bernstein (1967) and implies that the role of synergies is to reduce the number of variables manipulated by the neural controller and thereby alleviate the problem of motor redundancy. Within the principle of motor abundance (Latash 2012), however, the problem of motor redundancy is only apparent. Hence, we use the term synergy to signify covariation within a high-dimensional state space of elemental variables that contributes to stabilization of a lower-dimensional task-specific performance variable.

Any study of a synergy must begin by selecting a level of analysis, a space of elemental variables within which synergies are quantified. This choice is frequently made to ensure that the central nervous system can change elemental variables one at a time such that covariation in the space of elemental variables may be interpreted as a reflection of a task-specific neural strategy. Our results suggest that finger modes may be viewed as elemental variables during analysis of multifinger actions but that their composition may reflect synergies in another state space of elemental variables (e.g., forces or muscle activations), which may stabilize aspects of performance that were not explicitly specified by the task. For example, the very first studies of multifinger synergies within the framework of the UCM hypothesis used an accurate total force production task in pressing (Latash et al. 2001; Scholz et al. 2002). Even though those subjects were only asked to stabilize total force, they showed strong synergies stabilizing the pronation-supination moment of force. This occurred despite the fact that neither feedback nor instruction regarding moment of force was supplied. Similarly, mode composition may change within the UCM to stabilize the moment of force, or another variable, reflecting a self-imposed constraint.

One outcome of this conceptualization of finger modes is that no task can truly be called a single-finger task. Even if a single finger mode is involved at the onset of a trial, natural variation in finger forces and muscle activations may lead to modifications of the mode vectors and unintentional deviations of other finger modes from zero values. These deviations may reflect low stability of finger modes in directions within the task-specific UCM. Indeed, Table 1 shows that some subjects produced negative values of finger modes for fingers that were not instructed to produce force. Since the enslaving matrices used to compute modes were based on subjects' performance in flexion tasks (“ramp” tasks; see methods), negative modes reflect a subject's apparent action into extension. Several recent studies explored the phenomenon of enslaving during both flexion and extension tasks and showed that enslaving is asymmetrical: higher enslaving indexes are typically seen during finger extension efforts (Shim et al. 2007; Oliveira et al. 2008). In our experiment, however, no explicit extension was observed. Therefore, in our case, a “negative mode” reflects an unloading of a finger counteracting the flexion action that would be expected of that finger as a result of enslaving from other fingers of the hand involved in a flexion action. Similar results were seen in an earlier study with the subjects performing an unusual task: pressing with a subset of fingers of a hand while avoiding pressing with the other fingers (Kang et al. 2004).

Neural control of movement based on a hierarchy of synergies.

We view the neural control of movement as based on a hierarchical scheme where control variables at each level may be associated with the specification of referent values for salient performance variables (Latash 2010). The referent configuration (RC) hypothesis (Feldman 2009) assumes that, at the task level, a few referent coordinates for task-specific variables are specified (RC_TASK). A sequence of few-to-many transformations then leads to RCs at lower levels, extending down to individual alpha-motoneuronal pools where the RC is equivalent to the threshold of the tonic stretch reflex as in the lambda-model (Feldman 1986).

Back-coupling loops, similar to those described in earlier models (Latash et al. 2005; Martin et al. 2009), ensure that variance in the RCs at each level is mostly within the UCM for the RC at the higher level. This sort of back-coupling loop operates in a manner similar to the function of Renshaw cells, small neurons excited by alpha-motoneurons and making short-latency inhibitory projections on all the motoneurons of the pool. In contrast to the classical Renshaw cell system, the hypothesized back-coupling loops may have adjustable gains that could even change sign (thereby changing role from inhibitory to excitatory) defined by hierarchically higher neurophysiological structures in a task-specific manner. In addition to these neural loops, a sensory-based loop on task-related variables further ensures that the movement ends at the RC_TASK or, if the movement is blocked, non-zero forces are generated. Variables recorded in typical experiments are only indirect reflections of corresponding RCs. For example, in our study a finger mode may reflect a shift in RC in another state space such as that of finger forces or muscle activations. On the other hand, RC for total force production is based on RCs in the finger-mode space, reflected in changes in the mode magnitudes. Interactions between the RC, the body, and the physical world lead to a given actual configuration of the body moving towards the RC, while the back-coupling loops ensure stability of this process.

Recent studies of patients with a variety of cortical and subcortical disorders suggest that overall motor performance relies more on cortical structures, whereas synergy indexes are more sensitive to dysfunction of subcortical pathways. In particular, Reisman and Scholz (2003) compared reaching movements by both arms after unilateral cortical stroke. Whereas overall performance on the contralesional side was impaired significantly, there were no significant differences between the indexes of kinematic multijoint synergies on the two sides (computed similarly to the multifinger synergy indexes in our study). In contrast, studies of multifinger actions by patients with disorders of subcortical structures and associated neural projections (Parkinson's disease and olivo-ponto-cerebellar atrophy) demonstrate relatively mild differences in overall performance accompanied by significant changes in the synergy index. Changes in synergy indexes were more pronounced in the patients with Parkinson's disease when they were not taking domapine-replacement drugs (Park et al. 2014), suggesting that loops through the basal ganglia sensitive to dopamine play an important role in the synergic control of the hand. These observations are compatible with a control scheme based on distributed processing modules involving subcortical loops suggested by Houk (2005).

Another sort of back-coupling has recently been suggested based on observations of unintentional movements in experiments when actual body configuration was kept away from the RC for long time intervals (Ambike et al. 2014; Zhou et al. 2014b). This process, addressed as RC-back-coupling, is thought to result in a relatively slow drift of RC toward the actual body configuration. In our experiment, during the perturbation that moved the finger away from its referent coordinate, finger force dropped and, as a result, total force was significantly lower at the end of the trial than early in the trial (Fig. 2). This force drop was significantly smaller in the absence of finger perturbation (similar to results of Wilhelm et al. 2013). The modest force drop in the control conditions (without perturbations) has been reported earlier after turning visual feedback off (Slifkin et al. 2000; Vaillancourt and Russell 2002).

Since RC control involves a hierarchy of synergies, and RCs are affected by actual body configuration, we may expect that the synergies which an RC actualizes will also change over time. Specifically, when looking at the development of a task over time, elemental variables on one time scale may turn out to be organized in a synergic fashion when analyzed on another time scale. This suggests that RC-back-coupling may occur on multiple time scales; indeed, RC-back-coupling has been observed with characteristic times varying from 1 s to 15 s (Zhou et al. 2014a,b; S. Ambike, V. M. Zatsiorsky, and M. L. Latash, unpublished observations) depending on, among other things, the magnitude of the perturbation and the dwell time during which the body is held away from the RC.

Equifinality and motor equivalence.

Within the equilibrium-point and RC hypotheses, transient perturbations during a movement are not expected to affect the end state of that movement as long as neural signals are not changed in response to the perturbation (Feldman and Latash 2005). This phenomenon is termed equifinality. While equifinality has been observed experimentally (Bizzi et al. 1976; Kelso and Holt 1980; Latash and Gottlieb 1990; Schmidt and McGown 1980), it can also be violated, in particular during movements performed in a centrifuge (DiZio and Lackner 1995; Lackner and DiZio 1994) and in an unusual velocity-dependent force field (with “negative damping”; Hinder and Milner 2003). Our experiment provides an example of a violation of equifinality due to the hypothesized RC-back-coupling: the drop in total force, particularly pronounced in trials with perturbations. Note that the drop in total force was stabilized by synergies in both finger force and finger mode state spaces (V_UCM > V_ORT, Fig. 4). These results are consistent with the basic idea of different stability of a multielement (abundant) system in directions that do (orthogonal to the UCM) and do not (within the UCM) affect performance, even if the performance changes unintentionally.

The stability properties of a system may be tested in multiple ways, by analysis of variance across repetitive trials (assuming that all trials start from somewhat different internal body states), by administering external perturbations and observing the response of the body, and by analysis of internally generated corrections. We used the first two methods in the experiments presented here. The first method showed higher variance (lower stability) in both finger force and mode spaces within the UCM than orthogonal to it. The second method showed that changes in finger forces and modes produced by transient perturbation also were characterized by the inequality V_UCM > V_ORT (as in Wilhelm et al. 2013). The third method was used in earlier studies of movement kinematics and muscle activation patterns during reaching when unexpected perturbations were introduced and the subjects were instructed to correct their movements (Mattos et al. 2011, 2013). Those studies projected the corrections onto the UCM and ORT spaces and showed strong ME components within the UCM: large components of the corrective action led to no correction at all. In fact, in those studies, ME components were significantly larger than nME ones, even though only nME components of motion actually corrected the action.

Figure 7 illustrates the concept of motor equivalence and how it is different from the UCM-based analysis of intertrial variance in a hypothetical two-element total force production task. Imagine that, on average, the total force produced by this person in phase 1 is 10 N. Intertrial variance is expected to be higher along the UCM (shown with the dashed line, UCM₁) compared with the ORT direction resulting in an ellipse of data points elongated along the UCM (cloud of points 1). Imagine now that an action leads to a change in the total force, for example, to 8 N. The corresponding UCM is shown as UCM₂. The finger forces may change in a way that leads to a deviation along only the ORT direction (the solid line, defined by points 1 and 2) or along both UCM and ORT directions (the dashed line, defined by points 1 and 3). In the former case, no ME motion is seen because all motion is nME. In the latter case, ME motion may be of any magnitude; in our experiments, it was larger than the nME motion. In contrast to the mentioned studies by Mattos et al. (2011, 2013), in our experiment, the inequality ME > nME was seen for the unintentional changes in both force and mode spaces (Fig. 6). Note that the shape of the data cloud and the direction of motion can change independently of each other. In our scheme, however, both reflect different stability properties of the four-finger system along the UCM (low stability, large variance, and large ME component) compared with the ORT direction (high stability, low variance, and small nME component).

Fig. 7.

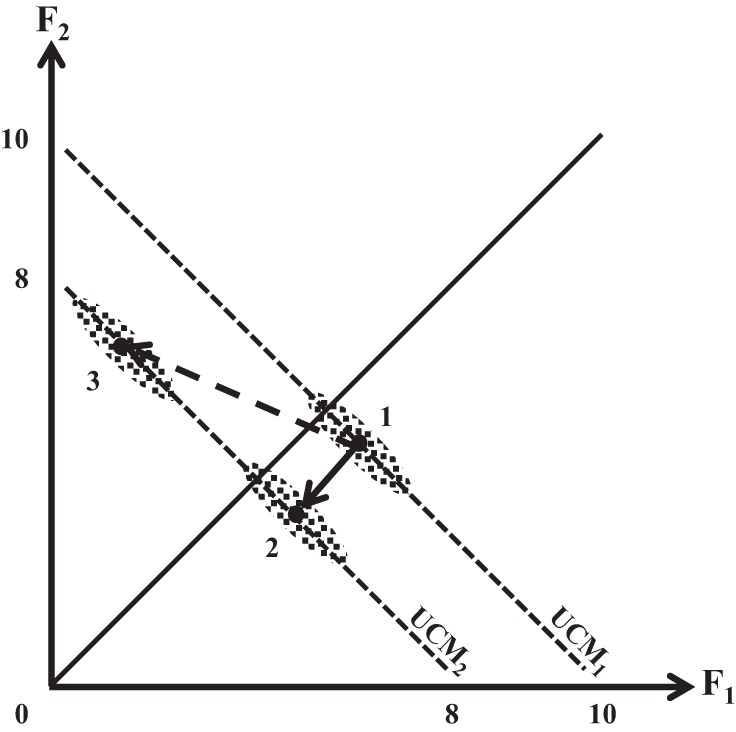
A schematic illustration of a 2-finger force production task from an initial value (on average, 10 N) to a lower value (on average, 8 N). Intertrial variance is illustrated with ellipses of data points; the ellipses are elongated along the corresponding uncontrolled manifolds (UMC₁ and UCM₂) leading to V_UCM > V_ORT. Two force trajectories are shown, with (dashed) and without (solid) a ME component.

The large amount of ME motion in the mentioned experiments with voluntary movement corrections (Mattos et al. 2011, 2013) and in the current study suggests that most motion of the system was wasteful, i.e., inefficient in moving the salient variable. These results seem at odds with the ideas of optimal control (including optimal feedback control) of abundant systems (Diedrichsen et al. 2010; Todorov and Jordan 2002). The fact that large “efforts” were spent on moving within the UCM suggests that no simple optimality principle can account for such data. This result is one of the many reasons (reviewed in Latash 2012) that motor control schemes requiring the CNS to solve computational problems posed by natural movement tasks should be replaced by a physical approach that views the observed motor and neural patterns as direct consequences of laws of nature.

Concluding comments.

The results of this study, while unexpected (all 3 main hypotheses have been falsified), generally support the notion of motor control by means of a hierarchical system with multiple few-to-many mappings organized in a synergic way. It is important to note, however, that there are certain factors that may confound the results. In particular, only the index finger was used for single-finger tasks, and only one nontask finger (ring) was perturbed. Each finger has different physical characteristics and it is known that the index finger is relatively independent, while the ring finger is relatively nonindependent (Li et al. 1998), so investigation of more single-finger tasks performed by other fingers may provide further insight. Additionally, the role of removal of feedback, while a necessary step to ensure subjects did not react to force changes, is difficult to disambiguate from the role of the physical perturbations. However, since every experimental condition removed feedback in the same way, these results are at least internally consistent.

In light of our findings and the mentioned potential confounding factors, we plan to continue research in this vein with more specific conditions and controls. In addition to investigating other finger pressing/finger perturbed pairs, we would like to expand our understanding of the hierarchical control of finger actions to other types of perturbations: downward with the inverse piano (the present study used upward perturbations only), as well as more ecological prehension-based ones using another device built in our laboratory, “the expanding handle” (Gao et al. 2005; Ambike et al. 2014), a handle that can change width (and thereby subjects' grip aperture) during trials. We also hope to investigate more thoroughly the role of visual feedback and the effects of its removal, as well as the effects of varying instructions (“do not interfere” vs. “try to maintain a constant force level”) on finger coordination in pressing tasks.

Even in light of the aforementioned drawbacks, the results presented here may be understood in the context of motor control in redundant systems by means of shifting RCs organized into a hierarchy, with potential insights into the contributions of the various cortical and subcortical structures responsible for stability of multifinger action. Futhermore, our observations regarding volatility of enslaving, greater equifinality of the performance variable compared with elemental variables, and large magnitude of ME motion all provide support for the concept of task-specific stability of performance and multiple neural loops that are potentially involved in ensuring this stability.

GRANTS

This study was supported in part by National Institutes of Health Grants NS-035032 and AR-048563.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: S.R. performed experiments; S.R. and M.L.L. analyzed data; S.R., V.M.Z., and M.L.L. interpreted results of experiments; S.R. prepared figures; S.R., V.M.Z., and M.L.L. drafted manuscript; S.R., V.M.Z., and M.L.L. edited and revised manuscript; S.R., V.M.Z., and M.L.L. approved final version of manuscript; V.M.Z. and M.L.L. conception and design of research.