Dynamics of Cell Area and Force during Spreading

Abstract

Experiments on human pulmonary artery endothelial cells are presented to show that cell area and the force exerted on a substrate increase simultaneously, but with different rates during spreading; rapid-force increase systematically occurred several minutes past initial spreading. We examine this theoretically and present three complementary mechanisms that may accompany the development of lamellar stress during spreading and underlie the observed behavior. These include: 1), the dynamics of cytoskeleton assembly at the cell basis; 2), the strengthening of acto-myosin forces in response to the generated lamellar stresses; and 3), the passive strain-stiffening of the cytoskeleton.

Main Text

When cells spread on a substrate, a thin lamella compartment develops at the cell basis and progressively extends the cell projected area (1). At the lamella front, lamellipodia protrusions are formed from a highly branched and dense actin network that polymerizes against the cell membrane and pushes the front of the cell forward (2). Supported by cell-substrate friction, these molecularly complex protrusions act as motor units that drive cell spreading and locomotion (2).

Experiments on endothelial cells are presented (Fig. 1) to demonstrate that the increase in cell projected area occurs concurrently with a rise in the exerted force on the substrate. Interestingly, we systematically find that the increase in cellular force is moderate at early times and that the rapid development of force occurs a few minutes past initial spreading; similar behavior has been reported for fibroblasts on a pillared surface (3). To explain these dynamics, we suggest an elastic picture whereby the motor activity of the cell front elastically stretches the lamellar cytoskeleton, and three mechanisms are examined that may underlie the observed delay in force generation. This elastic picture is motivated by previous studies that consistently show that cell area and force are both monotonically increasing functions of substrate rigidity (4, 5), and that the total steady-state force exerted onto the substrate increases with the projected cell area (Reinhart-King et al. (4), and see Fig. S3 in the Supporting Material).

Figure 1.

Evolution of mean (n = 47) cell radius (a) and force (b); (solid lines) theoretical fits to the three models; (insets) respective dynamics of individual cells. (c) Mean force, f(t), versus temporal cell radius R(t). See fitting parameters and additional information in the Supporting Material. To see this figure in color, go online.

Based on these evidences, we have recently developed an elastic theory of cell-spreading dynamics (5). The theory successfully accounts for a variety of spreading characteristics such as the concurrent increase in the actin retrograde flow with the slowing-down of spreading (1) and the dependence of cell-spreading dynamics on substrate rigidity and surface ligand density. We have also shown that the nonlinear elasticity of the cytoskeleton can explain the observed delay in force production. Here we present two alternative and complementary mechanisms that may underlie this behavior; for yet another mechanism, see Fouchard et al. (6).

Our starting point is the linear theory described in detail in Nisenholz et al. (5). Accordingly, the lamella is modeled as a homogeneous and isotropic elastic disk of thickness h and radius R, which is actively stretched by propulsion of the cell front-forward (see Fig. S1). The cell adheres to the substrate via multiple (transient) adhesion contacts that typically concentrate in a narrow rim at the cell front (2). The radial velocity of the cell front is dictated by two oppositely oriented motions:

$$\dot{R}\left(t\right)=v_{\text{pol}}-v_F\left(t\right).$$ (1)

Here, v_pol is the constant radial actin polymerization speed at the cell front (1, 5), and v_F(t) is the increasing retrograde flow of the lamellar network due to the rise in cellular tension (1, 2). Myosin activity is implicitly accounted for in its contribution to the effective elasticity of the lamella network. The forward motion of the lamellipodium stretches the cytoskeleton, and as a result a visco-elastic force is developed in the lamella:

$$f/h=2{\kappa }_c\left(R-R_0\right)/R_0+{\xi }_{c}d\left(R/R_0\right)/dt.$$ (2)

Here f = F/(2πR) is the radial force per unit length; F is the total cell force; κ_c is the effective, long-term, area-expansion modulus of the lamella; ξ_c is the effective viscosity coefficient; and R₀ is an associated rest length of this elastic continuum from which elastic forces are dictated.

Assuming linear (force-independent) cell-substrate friction coefficient, ξ_s (5), the retrograde flow, v_F(t), may be related to the force f(t) via v_F(t) = f(t)/ξ_s. Combining this with Eq. 1 results in the linear force-velocity relation

$$f=f_{\text{ss}}\left(1-\dot{R}/v_{\text{pol}}\right),$$ (3)

where f_ss = ξ_sv_pol is the steady-state force, which depends on substrate rigidity via ξ_s’s dependence on rigidity (5, 7). Equating 3 and 2 and assuming R₀ to be fixed, results in a linear differential equation for R(t) and f(t), with the simple solution $R\left(t\right)\sim f\left(t\right)\sim 1-\text{exp}\left(-t/\tau \right),$ where τ = [ξ_c + R₀ξ_s/h]/(2κ_c). We now describe three possible extensions of this basic model to explain the interesting (nonlinear) coupling in the behavior of R(t) and f(t); all three mechanisms are believed to contribute simultaneously (see Fig. S1), but for clarity, we treat them separately, as follows.

I: dynamics of lamellar network assembly

Our approach to this complex reorganization process of the cytoskeleton is based on a simple kinetic scheme in which suspended constituents of the cytoskeleton assemble the semi-two-dimensional lamellar network at the cell basis. This process, which gives rise to a gradual increase in the elastic rest length, R₀, occurs concurrently with cell spreading as observed in experiments (4); the driving force is assumed to be force-independent for simplicity and is reflected in the rate constants of the assembly process. We assume a constraint on the overall mass of cytoskeletal material that may eventually assemble at the cell basis and we denote this mass by M_tot. Furthermore, for simplicity, we consider only two forms of this material: either suspended in the cell volume, V, or incorporated in the two-dimensional network at the cell basis. Mass conservation is then given as

$$M_{\text{tot}}=c\left(t\right)V+\rho A_0\left(t\right),$$ (4)

where c(t) is the total concentration of suspended cytoskeleton material (primarily actin), A₀(t) = πR₀² is the total (elastically relaxed) area of the two-dimensional network, ρ is the surface density of this material, and ρ and V are assumed to be constant. Assuming that the rate of area growth is proportional to both c(t) and the assembled area, A₀(t), we write

$${\dot{A}}_0=\delta c\left(t\right)A_0\left(t\right),$$ (5)

where δ is the corresponding effective binding rate constant of suspended cytoskeletal fragments to the lamella network. Equations 4 and 5 provide a minimal model for the kinetics of network assembly at the cell basis, and for the variations of the elastically relaxed radius, R₀(t), in particular. Although neglecting many details in this process, the simple model presented suffices us here as a minimal model for examining the consequences of network assembly on the mechanics of spreading. The progressive growth of R₀(t) relaxes the tension being created by the pulling of lamellipodia protrusions at the cell front (see Eq. 2). Consequently, the cell can initially spread with minor increase in force, providing a plausible explanation to the observed delay in force production (Fig. 1). Once the suspended material available for assembly has fully integrated into the network, a second, elastic phase begins where the force rapidly increases with cell area. This behavior explains why we may neglect the force-dependence of the rate constant δ, inasmuch as forces develop mainly after the assembly process is finished. A fit of this model to the experimental data is shown in Fig. 1 (red curves). The assembly model also predicts an interesting effect of cell volume on the spreading dynamics, as shown in the Supporting Material (see Fig. S2).

II: strengthening of actomyosin forces in the course of spreading

Whereas in our previous sections myosin activity has only implicitly been accounted for in contributing to the expansion modulus, κ_c, here we wish to explicitly represent myosin activity in our expression for the force and to demonstrate how the augmentation of actomyosin force in time may affect the evolution of cell area and total force during spreading. Generalizing Eq. 2, we write

$$f/h=2{\kappa }_c\left(R-R_0\right)/R_0+{\xi }_c\dot{R}/R_0-P\left(t\right),$$ (6)

where P(t) represents the radial myosin stress; the negative sign is here to indicate that the contractile activity of myosin (P(t) < 0) generates (positive) elastic tension in the cytoskeleton. To focus on the new effects arising from the polarization response of myosin contraction, we treat R₀ as a constant. Based on a variety of theoretical and experimental studies indicating that myosin activity responds to the local stress in the cytoskeleton (8), we write the following phenomenological relaxation response to account for its early-time dynamics (see Nisenholz et al. (9) for a more detailed treatment):

$${\tau }_p\dot{P}=-2{\kappa }_c\alpha \left(R-R_0\right)/R_0-\left[P-P_0\right].$$ (7)

Here, τ_p, represents the timescale of the polarization response (namely, of the increase in the magnitude of the actomyosin stress, P(t)); α reflects the susceptibility of the acto-myosin dipolar stress, P, to the evolving elastic stress; and P₀, is the initial acto-myosin dipolar stress. In the steady state,

$$\dot{P}=0\text{and}{P}_{\text{ss}}-P_0=-2\alpha {\kappa }_c\left(R-R_0\right)/R_0.$$

In cases where myosin polarization response is sufficiently strong (large α), and fast (τ_p small compared to overall spreading time), myosin forces would dominate the overall force, f, at early times, and one expects to find a characteristic acceleration of f in time. Such behavior is observed in Fig. 1 (green fit). Hence myosin polarization provides a second mechanism that may contribute to the apparent delay in force generation relative to area increase. However, we note that our data fitting should not be taken as a quantitative measurement of τ_p and α, inasmuch as all three mechanisms (I–III) might be operating simultaneously during spreading.

III: nonlinear elasticity of the cytoskeleton

A third mechanism that may inevitably contribute to the delay in force production is strain-stiffening of the cytoskeleton (9, 10). This is particularly expected in cases where initial spreading occurs with a relatively soft cytoskeleton, and consequently only weak tensile stresses are generated at early spreading. Strain-stiffening causes a delayed increase in cellular force. Replacing the Hookean term in Eq. 2 by an exponential strain-stiffening term (10), one writes

$$f/h=\left(2{\kappa }_c/\lambda \right)\left[e^{\lambda \left(R-R_0\right)/R_0}-1\right]+{\xi }_c\dot{R}/R_0.$$ (8)

Combining this equation with Eq. 3 reveals an analytically solvable equation for cell-spreading dynamics (5). The fit to experimental data is shown in Fig. 1 (blue curves).

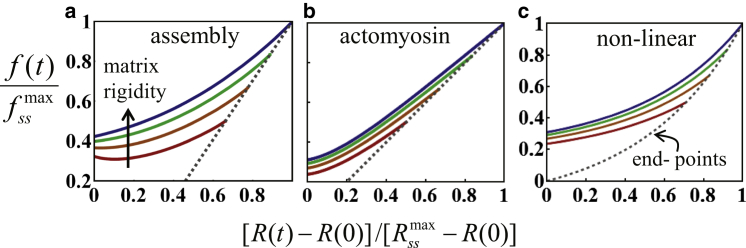
This mechanism is somewhat similar in effect to a slow assembly of the lamellar network, as considered in (I) above. However, the origin of the delay in force generation is different. In the current scenario, the nonlinear dependence of f(t) on R(t) arises from the passive constitutive relation of the cytoskeleton. In the assembly mechanism (I) and acto-myosin polarization mechanism (II), the apparent nonlinearity of f(R) is a consequence of the different dynamics of R(t) and f(t) but the cytoskeletal constitutive relation is linear. Because R and f cease to evolve in the steady state, systematic measurements of their steady-state values may shed light on the actual constitutive relation relevant for spreading, as demonstrated in Fig. 2. The dashed lines indicate the end-points of spreading on differently rigid substrates. For an intrinsically nonlinear cytoskeleton, all end-points must fall on a nonlinear curve that represents the cytoskeleton constitutive relation. In contrast, a linear relation between f_ss and R_ss is expected for (I) and (II) above. A scatter plot of cell area and force in the steady state is provided in Fig. S3; the overall trend is consistent with previous reports (4), which have suggested that F_ss scales linearly with A_ss. However, because the R² value in these plots is rather small, additional experiments would need to be carried out to reconcile to what extent the cytoskeleton behaves in a linear fashion during spreading.

Figure 2.

Comparison of the (scaled) f(t) versus R(t) plot for the three proposed models (a–c). Different curves correspond to different substrate rigidities. Dotted lines mark the steady-state. $R_{\text{ss}}^{\text{max}}$ and $f_{\text{ss}}^{\text{max}}$ are the steady-state radius and force for an infinitely rigid substrate, respectively. In all panels we took ξ_s/ξ_s^max = E_m/(E_m + E_c) = 0.5 (red), 0.67 (orange), 0.83 (green), and 0.99 (blue), where E_m and E_c are the respective Young’s moduli of the substrate and cell (5); see the Supporting Material for additional parameters used. To see this figure in color, go online.

Author Contributions

Yifat Brill-Karniely and Noam Nisenholz contributed equally to this article.

Editor: Christopher Yip.