Abstract
Histone tails play an important role in gene transcription and expression. We present here a systematic computational study of the role of histone tails in the nucleosome, using replica exchange molecular dynamics simulations with an implicit solvent model and different well-established force fields. We performed simulations for all four histone tails, H4, H3, H2A, and H2B, isolated and with inclusion of the nucleosome. The results confirm predictions of previous theoretical studies for the secondary structure of the isolated tails but show a strong dependence on the force field used. In the presence of the entire nucleosome for all force fields, the secondary structure of the histone tails is destabilized. Specific contacts are found between charged lysine and arginine residues and DNA phosphate groups and other binding sites in the minor and major DNA grooves. Using cluster analysis, we found a single dominant configuration of binding to DNA for the H4 and H2A histone tails, whereas H3 and H2B show multiple binding configurations with an equal probability. The leading stabilizing contribution for those binding configurations is the attractive interaction between the positively charged lysine and arginine residues and the negatively charged phosphate groups, and thus the resulting charge neutralization. Finally, we present results of molecular dynamics simulations in explicit solvent to confirm our conclusions. Results from both implicit and explicit solvent models show that large portions of the histone tails are not bound to DNA, supporting the complex role of these tails in gene transcription and expression and making them possible candidates for binding sites of transcription factors, enzymes, and other proteins.
Introduction
The nucleosome, discovered in 1974 (1, 2), constitutes the lowest-order packing of DNA. Since its discovery, considerable effort has been made to understand its structure and dynamics. High-resolution x-ray measurements have determined the nucleosome structure in detail to near-atomic resolution (1.9 Å) (3, 4), but its dynamics remain elusive. The nucleosome consists of 147 basepairs (bp) of DNA wrapped around a protein core. The core is made up of two copies each of four histone proteins, H3, H4, H2A and H2B, resulting in an octamer (see Fig. 1). Although this packing fits the genomic DNA into the small volume of the cell nucleus, it also hinders gene expression and gene transcription. For access to genomic DNA by proteins controlling and expressing the genome, the nucleosome must be remodeled, and such remodeling must include unwrapping of DNA from the nucleosome core.
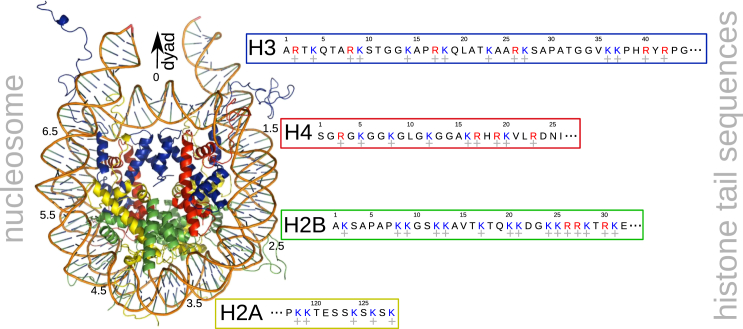
Figure 1.
The nucleosome and histone tail sequences, showing 147 bp of DNA wrapped around a protein core. The protein core is made up of four histone proteins, H3, H4, H2A, and H2B (blue, red, yellow, and green, respectively). We extended the nucleosome by 10 bp of DNA on each side. Sequences of N-terminal tails of histones H3, H4, and H2B and the C-terminal tail of histone H2A are also shown, with charged residues lysine and arginine indicated in blue and red, respectively. To see this figure in color, go online.
The positively charged N(C)-terminal tails of the histone proteins play a central role in this process; for a general discussion of histone tails, see Preez and Patterton (5). The compaction of chromatin into higher-order structures is mediated by the N-terminal tails of histones H3 and H4 through binding to DNA and/or to acidic regions on the histone octamer surface of neighboring nucleosomes (6, 7, 8). Knowing the structure and dynamics of these tails and their role in nucleosome architecture will help us to understand regulation of gene expression. Whether the tails are intrinsically disordered (9, 10) or have stable secondary structures, as proposed by circular dichroism experiments (11) and theoretical studies (12, 13), remains an open question. Intrinsically disordered histone tails might be able to change their conformation easily upon binding to other proteins or DNA, providing a framework to explain their multiple and complex roles.
Posttranslational modifications (PTMs) of the tails, i.e., acetylation, phosphorylation, and methylation, will change their structure and thus their function. Acetylation of H4-tail lysines results in reduced compactness of chromatin, allowing transcription factors to access the DNA in acetylated chromatin regions (14, 15, 16). A modification of histone tail H3 (K27M) has been correlated with the occurrence of cancer (17). A recently published study suggests that chromatin condensation on mitosis is triggered by a cascade of PTMs of the H3 and H4 tails (18).
The conformation and role of histone tails in the nucleosome have been examined in experimental studies using, e.g., circular dichroism (CD) (11, 19) or NMR and hydrogen-deuterium (H/D) exchange (20, 21, 22). Since the structural propensity of individual amino acid residues strongly depends on their environment (23), electrostatic interactions between histone tails and the nucleosomal DNA may affect the structure adopted by the histone domains in the nucleosome. Whether histone tails bind to DNA, and whether this interaction stabilizes or destabilizes a specific secondary structure (19), is still unclear. Wang et al. concluded that although in native tails the α-helical content appears to depend on interaction with DNA, acetylated tails show an increase in α-helical content relative to native tails, independent of DNA interaction (11).
Experiments on single nucleosomes using H/D exchange NMR methods (21) found that residues 16–22 of the H4 tail bind to DNA whereas the rest, i.e., residues 1–15, are mobile. Furthermore, a large part of the H3 tail was found to be highly flexible and disordered, a finding also confirmed by results from nucleosome arrays (22). However, the binding of residues 16–21 of the H4 tail to DNA of single nucleosomes was not observed in the arrays (22), in which the whole H4 tail was found to be highly flexible and mobile, suggesting that these domains have somewhat different properties in single nucleosomes (low concentration) than in highly concentrated arrays. The finding that H3 and H4 tails in condensed nucleosome arrays are highly flexible and mobile indicates that chromatin compaction does not require specific protein-protein or protein-DNA contacts. However, the authors of an H/D exchange NMR study of 12-mer nucleosome arrays (20) concluded that the H3 tail forms stable folded structures in highly condensed chromatin fibers, leaving the question open.
Other studies using various coarse-grained models have focused on internucleosomal interaction and chromatin compaction, including the role of histone tails. Although it might be asked to what extent modeling histone tails as simple beads on a chain can provide a correct picture of their role in chromatin compaction, these studies have provided a preliminary idea of the dynamics of this complex system (24, 25, 26, 27, 28, 29). Another coarse-grained study of DNA unwrapping showed long-lived DNA detachment (30), part of which involves binding of the H3 tail to the protein core, which blocks the DNA from rebinding to it. Removal of the H3 tails caused the long-lived detachment to disappear. This suggests that the H3 tail may stabilize DNA detachment during the initial stages of nucleosome remodeling.
There are a limited number of all-atom simulations (for a recent review, see Biswas et al. (31)), for example, the implicit solvent MD simulation by Ruscio and Onufriev (32), which focused on the flexibility of nucleosomal DNA, and the explicit solvent MD simulations of Roccatano et al. (33) and Biswas et al. (34), which examined the dynamics and the impact of a truncation of the histone tails. The truncation of the tails, similar to PTMs, resulted in a destabilization of the histone core, probably due to the absence of histone-histone and histone-DNA polar contacts (34). In a further study, by Ettig et al., steered MD simulations were used to investigate DNA-histone interactions and unwrapping of nucleosomal DNA (35).
Further all-atom studies focused on the structure of isolated histone tails (neglecting the nucleosome core particle) and the effect of PTMs (10, 12, 13). These studies used replica-exchange molecular dynamics (REMD) simulations together with explicit or implicit solvent models. The results suggested that specific secondary structures for histone tails: H3 and H2B were partly α-helical and that the H4 tail formed a stable β-sheet or α-helix. Modification of lysine residues was shown to alter the structure of the H3 and H4 N-terminal peptides. However, only one force field was used in these studies, making firm conclusions difficult, as secondary structural properties depend on the force field used (36, 37). Furthermore, none of these studies included the nucleosome core particle and the effect of the negatively charged DNA surface on the tail structure was not considered. Two recent simulations of the H4 tail and part of the nucleosomal DNA focused on interactions of the H4 tail with DNA and the effect of PTM on H4 binding to the DNA surface (38, 39). The latter study found that H4K16 acetylation partially orders the H4 tail and increases the probability of adopting α-helical configurations, resulting in stronger binding of the acetylated H4 tail to DNA compared to the nonacetylated form, perhaps contrary to what one might expect from electrostatic interactions. The difference in binding affinities was attributed to nonelectrostatic contributions, i.e., hydrophobic interactions, leading to more contacts with the DNA surface.
In this work, we study the role of histone tails in the nucleosome. Isolated tails tend to form a secondary structure in the simulation that disappears in the presence of the nucleosome. We observe that the positively charged tail residues, lysine and arginine, contact the phosphate groups or bind to the minor or major groove of DNA, resulting in stable binding configurations of the tails on the DNA surface. Special emphasis is placed on testing the robustness of results to variation of the force field.
Materials and Methods
Model structure
The nucleosome model contains the eight histone proteins with their tails and 147 bp of DNA (PDB ID 1KX5 (4)) plus 10 bp of linker DNA added at each end (for details, see Voltz et al. (30)). The choice of simulating the nucleosome core particle with 10-bp DNA linkers is motivated by the fact that H3 tails, which are at the entrance and exit points of the nucleosome, can also bind fully to DNA to model the behavior in oligonucleosomes, as described by Arya and Schlick (28). We simulated isolated histone tails and the whole nucleosome. The structure of the nucleosome and the sequences of the histone tails are shown in Fig. 1.
Simulation methods
We used REMD simulations to sample the configurational space (40, 41, 42). In REMD, multiple copies of the system are simulated at different temperatures and attempts are made routinely to exchange the configurations of two systems at neighboring temperatures based on the Monte Carlo Metropolis criterion. This enables the system to overcome high energy barriers between different states in conformational space (folded/unfolded or bound/unbound) and thus improves sampling. The simulations spanned a temperature range from 300 K to 550 K and the temperature spacing was chosen to reach a uniform exchange probability of ∼0.1. Using a step size of 0.002 ps and an exchange attempt every 100 steps (0.2 ps) results in an expected exchange every 2 ps. To obtain this exchange rate, we had to simulate 8–12 replicas depending on the number of atoms in the simulated histone tail (for more details about each histone tail, see Fig. S1 in the Supporting Material). We checked the robustness of results for the H2A tail against variations in the REMD parameters, i.e., a higher exchange probability (0.2), and less frequent exchange attempts. Details of these simulations can be found in the Supporting Material.
To accelerate conformational sampling even more, we used the generalized Born solvation model developed by Onufriev et al. (43) to mimic solvent effects in the simulations. For the intrinsic radii, we used modified Bondi van der Waals radii (mbondi2) from the Amber package (44, 45). The surface tension was set to 2.25936 kJ/mol/nm2 (43). The exterior solvent dielectric constant was set to 78.5. The salt concentration was set to 0.15 M and thus mimics the physiological environment.
We used the GROMACS 4.5.7 package (46, 47, 48, 49). The energy was minimized using the conjugate gradient method. To maintain the temperatures, a velocity rescaling with a stochastic term (50) was used (similar to Berendsen coupling), which ensures that a proper canonical ensemble is generated. The coupling constant, τt, was 2.0 ps. Conformations were saved every 10.0 ps. The LINCS algorithm (51) was applied to constrain the bonds to hydrogen atoms. The cutoff for nonbonded interactions and generalized Born pairwise summation was set to 1.5 nm. We performed two further REMD simulations for H2A and H3 using a cutoff of 2.5 nm to preclude a dependence of our results on the cutoff, as described in Anandakrishnan et al. (52). For both cutoffs, the tails bound to DNA and converged to the same number of DNA:tail contacts after 5 ns (see Supporting Material).
To save computational resources, we constrained the degrees of freedom of the whole nucleosome except the histone tail under investigation by defining them as a freeze group. Atoms that belong to this group were kept stationary in the simulation. Constraining the nucleosome results in a much smaller number of replicas needed to obtain the expected exchange probability. In this way, we include all interactions between the core and the tail residues and save resources at the same time. For H2A, we extended the tail (the nonfrozen part) by 13 residues (up to Q104) to give it more freedom to bind to the DNA surface. We also performed a test run relaxing a further 16 residues of the H4 histone to assess the robustness of the results with respect to the number of nonfixed residues (see the Supporting Material).
Simulations of all four histone tails were performed with and without the nucleosome core particle. The REMD simulations were conducted up to 160 ns for tails H3, H2A, and H2B and up to 120 ns for H4, depending on convergence. For analysis we have chosen the lowest temperature level of the REMD simulation, i.e., T = 300 K.
Currently available force fields are known to differ in their reproducing of experimental data and their predictions for observables like secondary structure. Some force fields are known to overstabilize certain types of secondary structure, e.g., helical structures with CHARMM27 (53) or Amber03 (54). For extensive studies comparing existing force fields, we refer the reader to Cino et al. (36) and Lindorff-Larsen et al. (37) or Best et al. (55). Further optimization of these force fields with direct use of the helical content of short peptides as fitting data resulted in an improvement of these deficiencies (see Tzanov et al. (56,), Huang and MacKerrell (57), and citations therein). It remains unclear whether these force fields provide a good description when extrapolating to the unknown region of intrinsically disordered proteins. This makes it necessary to test how robust the results are against variation of the force field. In our study, we were limited to force fields that also include parameters for nucleic acid. This limits our choice to different versions of Amber and Charmm force fields. Since first test runs of isolated histone tails using CHARMM27 have shown a high overstabilization of an α-helix, we excluded them. Finally, we limited our study to force fields Amber99SB (58), Amber03 (54), and Amber99SB-ILDN (59).
To examine the possible effect of explicit treatment of the solvent on the conclusions drawn from REMD with implicit solvent, we also performed MD simulations with an explicit solvent model (TIP3P). For this, we used the stable structure of the tails found in the REMD run as the initial structure. The water box was chosen such that the distances between the most distant atoms of the nucleosome and the box edges were 1.2 nm. The final size of the system, including water, was 594,113 atoms. The cutoff for nonbond interactions was set to 1.2 nm, and we used periodic boundary conditions and the particle mesh Ewald summation technique. Ions were added to neutralize the system, and further salt (NaCl) was added to represent 0.15 M ionic concentration. After the system was minimized using the conjugate gradient method, we equilibrated the system in the NVT ensemble (2 fs time step). Velocity rescaling with a stochastic term (50) and a coupling constant of τt= 1.0 ps was used. After 200 ps of NVT simulation, the system was equilibrated for 1 ns in an NPT ensemble. The LINCS algorithm (51) was applied to constrain the bonds to hydrogen atoms. In contrast to the implicit REMD simulations, no further constraints were used in the explicit REMD simulations.
REMD temperature space and convergence
The temperature trajectories of the REMD calculation are shown in Fig. S1. For the four simulations, all trajectories visit all temperature levels, indicating a sufficient exchange between temperature levels.
All simulations converged with respect to secondary structure (see Fig. S10), yielding a 120 ns trajectory for H4 and 160 ns trajectories for H3, H2A, and H2B.
Data analysis
We have chosen the first 10 ns as the equilibration phase.
Definition of secondary structure
The secondary structure content of histone tails was calculated using the DSSP algorithm (60), which measures the backbone hydrogen bonding pattern.
Cluster analysis
Structures with pairwise root mean-square deviations below the 0.2 nm cutoff were clustered in the same group, and the cluster center was selected as the representative structure. The root mean-square deviation was calculated based on Cα atom coordinates.
Definition of contacts
To define contacts between histone tail residues and the DNA surface, we used the VMD measure contacts tool. The threshold distance for a contact was set to 0.3 nm. We used the same cutoff to study the neutralization of positively charged lysine and arginine residues and the negative phosphate groups of DNA. When a positive side chain made contacts with two phosphate groups, or one phosphate group was in contact with two side chains, we always chose the pair with the smaller distance to count the neutralized charges.
Hydrogen bonds
For an analysis of hydrogen bonds within the histone tails, we used as criteria a donor-acceptor distance of <0.35 nm and a hydrogen-donor-acceptor angle of <30°.
Results and Discussion
Isolated tail results and comparison with previous results
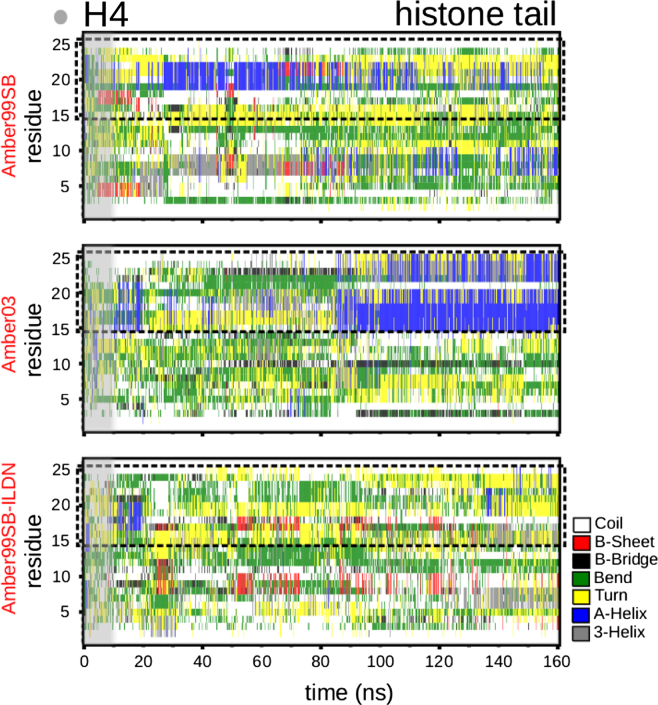
We first focus on the isolated histone tails and compare our results with those of previous studies (10, 12, 13, 39). Fig. 2 shows the secondary structure of the isolated histone tail H4 as a function of time from simulations using three force fields: Amber99SB (58), Amber99SB-ILDN (59), and Amber03 (54). Results for H2A and H2B can be found in the Supporting Material. Amber99SB-ILDN, and to some extent Amber99SB, forms a transient β-sheet in the H4 tail. However, although the β-sheet was stable in Potoyan and Papoian (10) using Amber99SB, it is not stable in our simulation of the isolated H4 tail. It disappears or switches to an α-helix for Amber99SB. Possible reasons for the higher stability found by Potoyan and Papoian (10) could be their use of explicit solvent or a shorter trajectory (60 ns). Results for the Amber03 force field in Fig. 2 clearly converge to stable α-helices between residues A15 and K20 and another one around residue 24, confirming the results reported in Yang and Arya (13) using Amber03. Amber03 seems to produce an energy surface with a distinct and clear minimum for an α-helix, whereas Amber99SB and Amber99SB-ILDN produce a more widely distributed configurational space for the secondary structure (showing a β-sheet, α-helix or coil).
Figure 2.
Secondary structure of the isolated H4 histone tail. Shown are results for the lowest temperature, 300 K, of the REMD calculation using Amber99SB (58), Amber03 (54), and Amber99SB-ILDN (59) force field. The gray area corresponds to 10 ns of equilibration. To see this figure in color, go online.
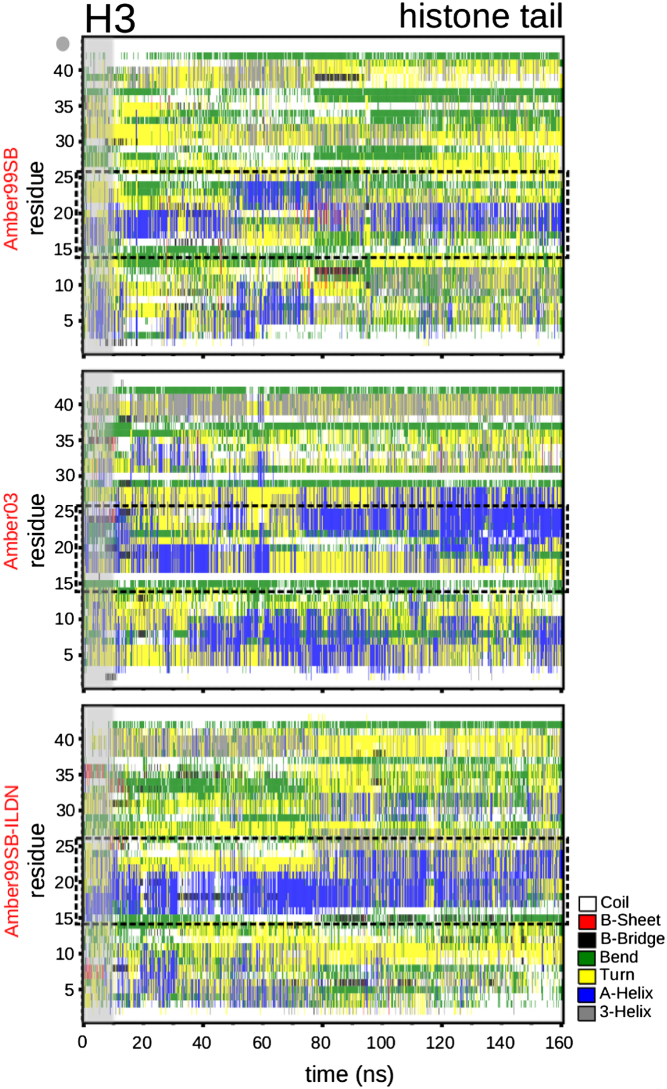
Fig. 3 shows the secondary structure of the isolated H3 tail. As reported in Liu and Duan (12), using force field Amber03, residues K4 and K9 are part of an α-helix. However, in our study, this α-helix is not stable with force fields Amber99SB and Amber99SB-ILDN, as it disappears after 80 ns. Further results in Fig. 3 show a stable α-helix for all three force fields between residues 14 and 26 (black box), also confirming previous results (10).
Figure 3.
Secondary structure of the isolated H3 histone tail. Shown are results for the lowest temperature level, 300 K, of the REMD calculation using force field Amber99SB (58), Amber03 (54), and Amber99SB-ILDN (59). The gray area corresponds to 10 ns of equilibration. To see this figure in color, go online.
Figs. S11 and S12 show the secondary structure of histone tails H2B and H2A, respectively. H2B forms a stable α-helix between residues 15 and 26 (black box) for Amber03 and Amber99SB-ILDN. Using AmberSB99 also tends to produce a helix in this region. The H2A tail forms a helix between residues 2 and 7 for all three force fields, in disagreement with the results of Potoyan and Papoian (10). A reason for this could again be the limited sampling in that study (10).
The results presented here indicate that it is risky to draw a conclusion about the secondary structure of histone tails based on only one force field, particularly for H4. The H4 tail may fold into an α-helix or a β-sheet, or may not have any ordered structure. H3, H2A, and H2B show a high tendency to form an α-helix for all tested force fields. The bias of certain force fields has been widely discussed in the literature (see, e.g., Lindorff-Larsen et al. (37)). Amber03 force field is known to overstabilize helical structures, whereas Amber99SB-ILDN is known to understabilize them (37). We therefore cannot draw firm conclusions regarding the stability of the secondary structures or in which configuration any given isolated tail exists. However, the results above are consistent with previous results for histone tails (12, 13), as well as with previous studies using an explicit solvent model (10), and they should be considered a benchmark justifying our methods (REMD and implicit solvent).
Secondary structure of histone tails on the nucleosome
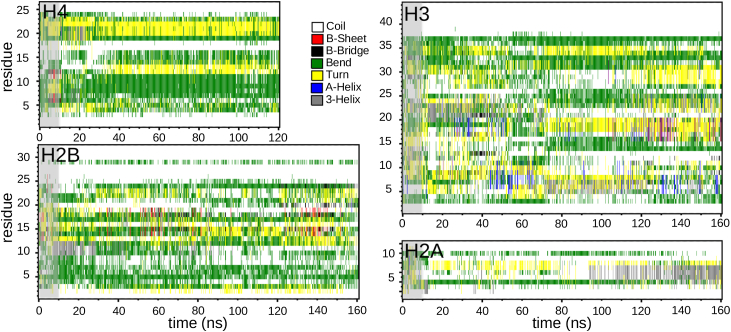
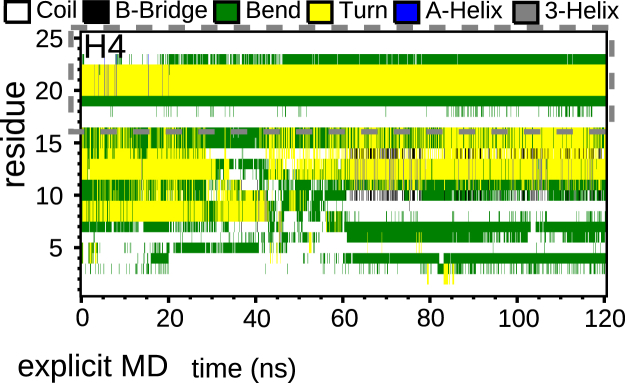
Histone tails are known to play an important role in nucleosome dynamics and thus in gene expression and transcription. We expect that the rest of the nucleosome, especially the negatively charged surface of the DNA, has a strong effect on the structure of the N(C)-terminal tails. Fig. 4 illustrates the secondary structure of all four histone tails in simulations of the whole nucleosome using force field Amber99SB (58). The configurations of all histone tails are dominated by bends (green), turns (yellow), and coils (white). In particular, H4 shows a stable bend for residues 7–11 over almost the whole trajectory. To preclude that in this case the tail is trapped in a local minimum, Fig. S13 shows the RMSD, dihedral angles, end-to-end distance, and radius of gyration of this segment (for results for other tails, see the Supporting Material). A transient α-helix or a β-sheet can be seen, but none is stable, with the exception of the H2A tail. For H2A, coils and bends dominate initially up to 90 ns, but afterward, a stable 310-helix forms between residues (4), 5, and 7, corresponding to residues (T120), E121, S122, and S123 situated between charged residues K119 and K124 (see also Fig. 1). In the isolated H2A tail, exactly this part forms a stable α-helix (see Fig. S12). Here, the binding of the lysines to the DNA surface shifts the α-helix to a 310-helix, with only the latter structure being compatible with the constraints given by the charged DNA phosphate groups. The effects of the charged DNA surface are even stronger for the H3, H4, and H2B tails. For these, although a high tendency to adopt secondary structure was noted in simulations of isolated tails, no secondary structure is found when simulating the whole nucleosome. The presence of the DNA (the negatively-charged phosphate groups) destroys the secondary structure of these tails (also predicted by the coarse-grained study (29)). The reason for this is the attraction of the side chains of lysines and arginines to the DNA phosphate groups, which is not compatible with a secondary structure. The tail configuration is thus governed by the charged phosphate groups. An explanation of this will be given later in the text. This shows that the whole nucleosome has to be considered for an understanding of the role of tails in nucleosome dynamics and PTM.
Figure 4.
Secondary structure of H4, H3, H2B, and H2A histone tails. The whole nucleosome was simulated and the Amber99SB force field (58) was used. Different types of structure are colored as indicated. The gray area corresponds to 10 ns of equilibration. To see this figure in color, go online.
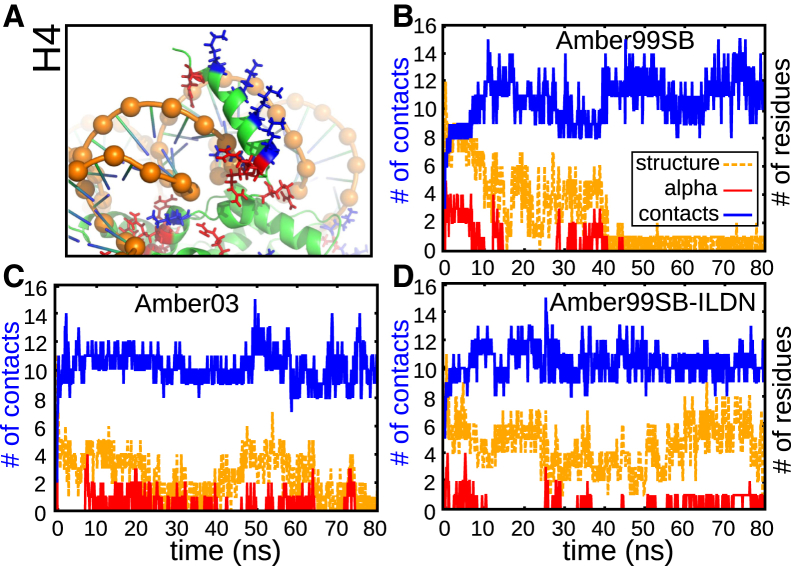
To examine whether the above results depend on the force fields and the initial structures used, we repeated the simulations for the H4 tail starting from a conformation in which residues 3–19 participate in an α-helix (the preparation was done by running the nucleosome without DNA using the CHARMM27 force field). Fig. 5 shows the results of 80 ns REMD simulations using Amber99SB (58), Amber03 (54), and Amber99SB-ILDN (59). For all force fields, the initial α-helix disappears. In Amber99SB-ILDN and Amber03, a small helical content remains, but a stable helical configuration is not found. The higher structure content for Amber99SB-ILDN and Amber03 is mainly due to their having a higher content of turns compared to Amber99SB. The α-helical content disappears with an increasing number of DNA:tail contacts, but no direct correlation exists between these two (see Fig. S15).
Figure 5.
Independence of results from initial configuration and force field used. (A) H4 tail initial configuration, consisting of DNA (orange), phosphate groups (orange beads), histone proteins (green), lysine (blue), and arginine (red). (B–D) Number of contacts with DNA (atom-based) and number of residues participating in a structure (α-helix + β-sheet + β-bridge + turn) or in an α-helix. Used are the Amber99SB, Amber03, and Amber99SB-ILDN force fields. Data were averaged over 10 frames (0.1 ns). To see this figure in color, go online.
The reason for the disappearance of the α-helix is that in the helical configuration shown in Fig. 5, the attractive interaction between phosphate groups and charged tail residues outcompetes the stabilization of the helix by hydrogen bonds. We show later that hydrogen bonds exist between histone tail residues and can be important for the stability of certain binding configurations of histone tails on the DNA surface, but do not result in an ordered structure such as an α-helix.
The secondary structure of histone tails derived from REMD simulation may be compared with the results of CD experiments. For H2A and H2B, we find no secondary structure, in agreement with experimental results presented by Banères et al. (19). However, our simulation results do not agree with the finding in that study (19), as well as a study by Wang et al. (11), that H3 and H4 tails have an α-helical conformation attributable to their interaction with DNA. Nevertheless, a variation of the salt concentration in Wang et al. (11) did not support the conclusion that the H4 tail adopts an α-helical conformation upon binding to DNA, as the salt-dependent dissociation should lead to a decrease of the α-helical content.
Contacts and cluster analysis
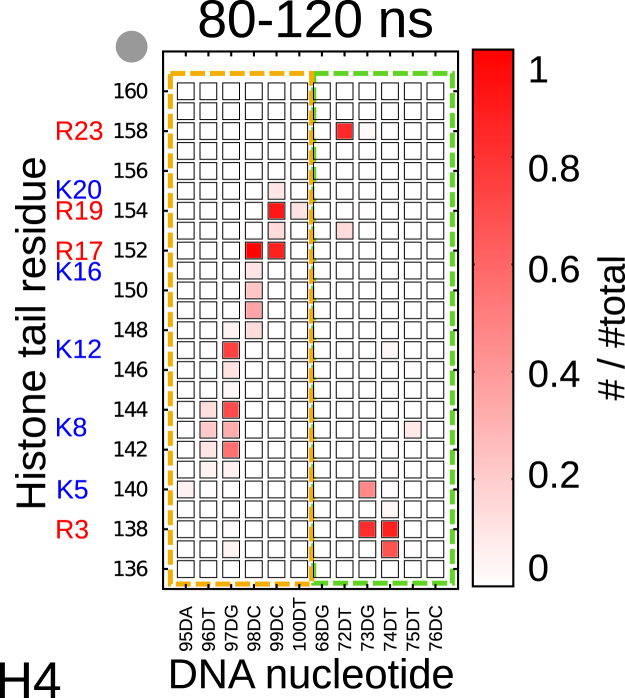
To determine at which DNA sites the charged and other residues of the histone tails bind, Fig. 6 shows the probability of contacts between H4 tail residues and DNA phosphates during the last 40 ns of the trajectory (for other histone-tail binding probabilities, see Figs. S17–S19). H4 tail residues make specific contacts with the two DNA strands (see also Fig. 7). Most contacts are between arginine and lysine residues and DNA. Arginines and lysines are also found between two phosphate groups. The remaining contacts are made by threonine and glycine, which are in most cases next to a lysine or arginine. Examples for the H4 tail are: G2, G7, G9, G13, and G14 (Gly137, Gly142, Gly147, Gly148, and Gly149). Fig. S16. shows a more detailed picture of these last 40 ns split into 5 ns intervals. The contacts are stable over the whole 40 ns interval apart from a fast jump back and forth of K8, G7, and G8 to neighboring nucleotides.
Figure 6.
Probability of contacts between histone tail residues and DNA phosphate for the H4 tail. The last part of the trajectory (80–120 ns) was studied and the threshold for a contact was 0.3 nm. Colored boxes indicate different DNA strands. To see this figure in color, go online.
Figure 7.
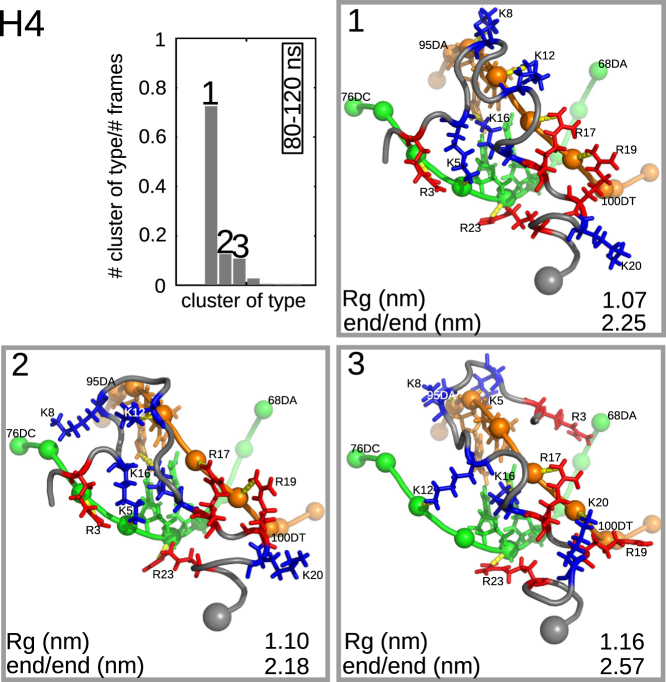
Results of a cluster analysis of the H4 tail trajectory. Probability and conformations of the cluster representative of the three most populated clusters are shown. The cutoff was 0.2 nm and the last part of the trajectory (80–120 ns) was used. The two DNA strands involved in binding of the H4 tail are colored orange and green. Spheres represent phosphate groups of DNA, and lysine and arginine residues are colored blue and red, respectively. The gray sphere is the end of the tail connected to the histone core. Yellow lines indicate interactions between the histone tail and the DNA. Radius of gyration, Rg, and end-to-end distance are given for each cluster. To see this figure in color, go online.
The same is true for histone tails H2A, H2B, and H3. For the latter two tails, however, contacts are distributed over more residues, especially for the free end of the tail (Figs. S17 and S18). H3 and H2B contain more charged lysine or arginine residues, thus enabling more combinations with phosphate groups. Interestingly, there are also charged lysine and arginine residues that do not make contacts with a phosphate group, i.e., K16 of the H4 tail and K24 and R30 of the H2B tail. The side chains of these residues are found in the DNA groove.
It is interesting to examine whether there are preferred stable binding configurations of the histone tails on the nucleosome surface. Fig. 7 shows the result of a cluster analysis over the last 40 ns of the trajectory of the H4 tail, illustrating the probability distribution and conformations of the three most populated clusters. The radius of gyration, Rg, and end-to-end distance of these clusters are also indicated. As expected, the side chains of lysine and arginine residues make contacts with the DNA phosphate groups. We recall, however, that K16 is found in the DNA groove in all clusters (as was found also by Potoyan and Papoian (39)). Although contacts between charged side chains and the phosphate groups originate from charge-charge interactions, the origin of the binding of K16 to the groove is cation-π interactions with the surrounding basepairs (see Fig. S20). For a study of cation-π interactions in protein-DNA complexes, we refer the reader to Gromiha et al. (61). Distances and angles between the cationic group of K16 and the basepair rings of surrounding adenine and guanine are in the same range found for ions (62). For further details about distances and angles, see Fig. S20.
To understand the occurrence of a dominant stable cluster in the H4 trajectory, we mapped the distances between tail residues and phosphate groups for each cluster in Fig. 7 (see Fig. 8). Such maps for the H2A, H2B, and H3 histone tails can be found in Figs. S21–S29. Furthermore, we also characterized the hydrogen bonds between the tail residues. Table 1 shows the data for all clusters of H4, as well as the other histone tails, including the probability of each cluster, the radius of gyration, Rg, the number of neutralized charges, and the number of tail residues in a DNA groove. The data for the other histone tails are shown in the same table.
Figure 8.
Key tail:DNA interactions of the H4 tail. (A) Distance map of tail residues and the phosphate group of each nucleotide for the three most populated clusters of the H4 tail. Orange and green boxes indicate the two strands of DNA, as in Fig. 7. Blue circles and red circles indicate contacts between lysines and arginines, respectively, and DNA phosphate (cutoff 0.3 nm). Green numbers denote the number of neutralized charges. (B) Schematic view of tail:DNA interactions. Gray boxes indicate interactions found in all three clusters. Red dashed line illustrate the cation-π interaction of K16. To see this figure in color, go online.
Table 1.
Results of a cluster analysis for all four histone tails
| H4 | |||||
| Cluster | Probability | H-bonds | Rg (nm) | Neutral (9) | Groove |
| 1 | 0.72 | 9 | 1.07 | 7 | 1 |
| 2 | 0.13 | 8 | 1.10 | 6 | 1 |
| 3 | 0.11 | 8 | 1.16 | 6 | 1 |
| H2A | |||||
| Cluster | Probability | H-bonds | Rg (nm) | Neutral (5) | Groove |
| 1 | 0.71 | 2 | 0.75 | 5 | 0 |
| 2 | 0.20 | 2 | 0.87 | 4 | 1 |
| H2B | |||||
| Cluster | Probability | H-bonds | Rg (nm) | Neutral (15) | Groove |
| 1 | 0.29 | 10 | 1.06 | 11 | 2 |
| 2 | 0.27 | 12 | 1.11 | 9 | 2 |
| 3 | 0.22 | 11 | 1.08 | 10 | 2 |
| 4 | 0.11 | 6 | 1.09 | 10 | 2 |
| H3 | |||||
| Cluster | Probability | H-bonds | Rg (nm) | Neutral (14) | Groove |
| 1 | 0.40 | 18 | 1.31 | 13 | 0 |
| 2 | 0.22 | 16 | 1.25 | 12 | 0 |
| 3 | 0.18 | 13 | 1.16 | 12 | 0 |
We present only clusters with a probability >0.1. Shown are number of hydrogen bonds between the histone tail residues (H-bonds), radius of gyration (Rg), and number of neutralized charges (Neutral) for each cluster representative, with the number of total positive charges on each histone tail in parentheses. The last column shows the number of residues found in the DNA groove.
For the H4 tail, we find a total of 7, 6, and 6 neutralized charges for clusters 1–3, respectively. In addition, we find 9, 8, and 8 hydrogen bonds between tail residues. Thus, the number of bound residues for both types of interaction agrees with the ranking of clusters found for H4 in Fig. 7. Similar behavior is seen for histone tail H2A. Cluster 1 has a population of 0.71 and has all charged side chains neutralized by contacts to phosphate groups, whereas cluster 2 has a population of 0.20 with only four charges neutralized. In the latter configuration, the remaining charged residue K126 is found in the major groove of DNA, indicating that binding to a phosphate group is more favored than binding to the DNA groove. Comparing the radii of gyration one can conclude that the more charges are neutralized, the more compact are the configurations, since the repulsive interaction between the positively charged tail residues decreases.
The same applies to the results of the H2B tail. H2B contains many more charged residues than H4 and H2A (see above), enabling more combinations with phosphate groups and resulting in a broader distribution of the cluster probability (see Table 1). Comparison of the number of neutralized charges does not explain the ranking of clusters: cluster 2, with nine neutralized charges, has a slightly higher probability than clusters 3 or 4, which have 10 neutralized charges. Here, hydrogen bonds between histone tail residues seem to become important, and could explain the probability distribution of the clusters found.
For the H3 histone tail, 13, 12, and 12 of the 14 charged residues are bound to a phosphate group in clusters 1–3, respectively. This, together with the number of hydrogen bonds, explains the ranking of the clusters. The high number of hydrogen bonds seems to lead to the opposite trend in the radius of gyration for H3 compared to the other three tails.
Comparing distance maps for different clusters of the H4 tail in Fig. 8, one can see that between residues A15 and I26 (Ala150 and Ile161), the maps do not differ. This indicates that this part of the tail is always bound to the DNA and is less flexible than the rest of the tail. H4 residues are bound up to K16, which is also a common target for PTMs. This is consistent with the results of H/D exchange NMR measurements on the single nucleosome (21), in which residues 1–15 in H4 were found to be flexible, whereas residues 16–22 fold onto the nucleosome core. Furthermore, Zhou et al. (21) found that a K16Q mutation in H4, a mimic of K16 acetylation, leads to structural disorder of the basic patch (K16R17H18R19). One could expect that mutation of K16, which in our results is bound to the minor DNA groove, could lead to a similar destabilization of this basic patch. This could be the focus of a future study of PTMs of the H4 tail.
Zhou et al. (21) also found that a major part of the H3 tail, i.e., residues 3–36, was highly flexible (mobile). Gao et al. found that H3 tail residues 1–35 (38) are flexible and not attached to the DNA surface, both in nucleosome arrays and high densities (22). A similar conclusion can be drawn from our results for H3 in Fig. S22. Distance maps 1–3 agree well for residues 34–44, but differ for the rest of the residues.
Results for an explicit solvent model
To examine whether the above conclusions still hold in the presence of explicit solvent at physiological salt concentrations, we performed MD simulations of the whole nucleosome with explicit solvent and 0.15 M salt, focusing on the H4 tail. As the initial configuration for the H4 tail, we used a representative of cluster 1 in Fig. 7. Fig. 9 shows results for the secondary structure of the H4 tail (results for the other tails can be found in Fig. S30). In general, the explicit solvent MD trajectory does not exhibit stable secondary structure. Results for the structure of the implicit solvent REMD (see Fig. 4) and explicit solvent MD simulations are almost identical between K16 and I26.
Figure 9.
Secondary structure of the H4 tail of a MD simulation with explicit solvent. Force field Amber99SB (58) was used. Different types of structures are color-coded as indicated. The simulation was initialized with the most probable configuration identified by the cluster analysis in Fig. 7. To see this figure in color, go online.
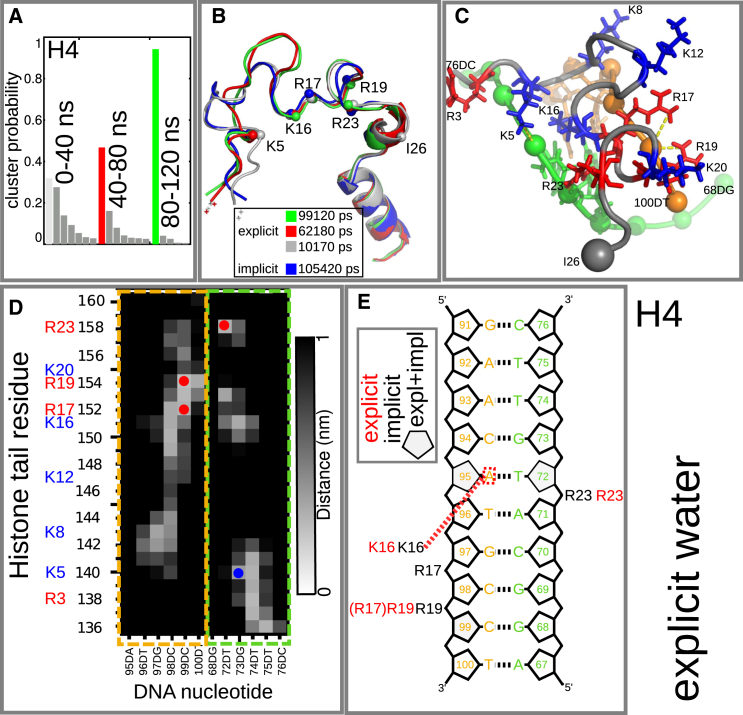
Fig. 10 shows the results of cluster analysis of the simulation with explicit solvent. We split the trajectory into 40-ns-long segments. The cluster population evolves from a broad distribution, where the most populated cluster still resembles the starting configuration, to a distribution dominated by one single configuration with a probability of 0.94. Comparing this dominant conformation and the starting configuration in Fig. 7, one sees that some lysines and arginines are no longer bound to the phosphate groups. However, the basic patch K16R17H18R19, which was bound to DNA in the REMD results and in the study by Zhou et al. (21), remains attached after 120 ns of MD simulations with explicit water. This can be seen more clearly in the distance map in Fig. 10. In addition to K16, R17, and R19, R23 remains attached (compare the discussion above and the results of Zhou et al. (21)), yielding the same conformation for residues K16–I26 in the implicit as in the explicit solvent simulations (see Fig. 10 B). A similar result can be seen for the H3 tail from K36 to G44, confirming results reported by Gao et al. (22) and for the H2B tail from K378 to E397, since the charged residues remain attached to DNA (see the Supporting Material). In the explicit-solvent simulation, K16 of H4 is still bound in the minor groove. This again brings up the question of whether acetylation of K16 would lead to detachment of the whole H4 tail. In contrast, we find that K8, K12, and K20 are not bound to DNA (K20 is also unbound in the implicit REMD simulation). This supports the candidacy of these residues for involvement in interactions with other proteins. Results of Hirano et al., for example, suggest that the Lamin B receptor, an inner nuclear membrane protein, interacts with the dimethylated K20 (H4K20me2) (63), which is essential for chromatin compaction.
Figure 10.
Results of the explicit MD simulation. (A) Evolution of cluster distribution. (B) Initial structure from implicit solvent REMD and cluster representatives of analysis in A. (C–E) Conformation (C), distance map (D), and DNA:tail interactions (E) of the cluster with highest population in the last time interval (including results from implicit solvent). To see this figure in color, go online.
Our simulation results disagree with an earlier experimental finding by Mangenot et al. (64), who observed a detachment of histone tails at physiological salt concentrations. They found, for a nucleosome containing 145 bp of DNA, a transition from a compact state, where all tails are attached to DNA, to a state where the tails are extended at 50 mM salt concentration. This transition was shifted to salt concentrations between 50 and 150 mM for nucleosomes with 165 bp, or to even higher concentrations for a longer DNA (65). We find a radius of gyration of Rg = 4.3 nm, slightly smaller than that of Mangenot and colleagues, Rg = 4.6 nm (64). The Rg value decreased during the first 20 ns, in agreement with the results of Roccatano et al. (33), and increased over the rest of the simulation time (see Fig. S34). Whether extending the simulation will increase the Rg further is not clear. Although the mesoscopic oligonucleosome model of Arya et al. (27) reproduced an increase in Rg, i.e., extension of the tails, with increasing salt concentration, no other computational study confirmed the extension of histone tails at physiological salt concentrations. Yang et al. (24), for example, found only a modest degree of detachment under a wide range of salt concentrations and concluded that a detachment is not induced by increased salt concentration but by the presence of other nucleosomes. However, all-atom MD simulations (33, 35) find histone tails stably attached to DNA at physiological salt concentration, which may indicate a general problem with MD simulations caused by periodic boundary conditions and lattice-sum techniques.
Conclusions
In this study, we performed REMD simulations using an implicit solvent model for all four histone tails, H4, H3, H2A, and H2B. An important goal was to test results against variation of the force fields. Our results for the secondary structures of isolated histone tails confirm those of previous studies (10, 12, 13, 39). We also show that for the H4 and H2B tails, the results depend strongly on the force field used. Further, we demonstrate that for most histone tails, a secondary structure is not compatible with the negatively charged DNA surface. An exception to this is H2A, which changes from an α-helix in the isolated tail to a 310-helix to fit onto the charged DNA surface. We also verified the robustness of the results for H4 by starting from an α-helical conformation, using different force fields, and using an explicit solvent model.
Results from contact maps, distance maps, and cluster analysis show that lysine and arginine residues make specific contacts with DNA. The positively charged side chains of histone tails were found at negatively charged phosphate groups or in the minor or major groove of the DNA, similar to the known behavior for ions (62). In cluster analysis, we found dominant binding conformations for H4 and H2A, whereas H3 and H2B show a broader probability distribution. The absence of a dominant binding conformation for the H3 tail supports the finding of Kan and Hayes (66) that H3 has multiple functions in chromatin compaction and regulation because it binds to neighboring nucleosomes and to the linker DNA of its own nucleosome. The H4 tail, however, is known to mediate internucleosomal interactions. We expect the binding behavior of the H4 tail in an oligonucleosome system to be different (see also Gao et al. (22)), which makes it difficult to draw a conclusion about general functions in the nucleosome from the binding configurations found. The ranking of the cluster, i.e., its population, is dominated mostly by the attractive interaction of lysine and arginine residues and phosphate groups, and thus the number of neutralized charges. However, hydrogen bonds between tail residues can also contribute to stabilizing the structures. Comparing the probabilities of clusters with different binding configurations of the H2A tail, we conclude that binding to a phosphate group is more favored than binding to the DNA groove.
Our results are compatible with H/D exchange NMR measurements on the single nucleosome (21) showing that part of the H4 tail is bound to DNA, whereas the rest is flexible and mobile. This part of the H4 tail stays attached to DNA in an explicit solvent MD simulation at physiological salt concentration. A similar result was found for the H3 tail. The flexibility and mobility of a major part of histone tails could enable the binding of enzymes or transcription factors, thereby explaining the complex role of these structures in nucleosome dynamics.
As a next step, we plan to investigate the role of PTMs. Further, spFRET measurements are planned to test our conclusions on conformations of histone tails and the binding of tails to the DNA surface.
Acknowledgments
Resources for this research were provided by the Oak Ridge Leadership Computing Facility at the Oak Ridge National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under contract no. DE-AC05-00OR22725. Computational resources were also provided by the HELICS computer cluster at the Institute for Scientific Computing at the University of Heidelberg.
This work was supported by Deutsche Forschungsgemeinschaft under Grant LA 500/14-2.
Editor: Nathan Baker.
Footnotes
Thirty-four figures and Supporting Materials and Methods are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(14)01156-4.
Supporting Material
References
- 1.Olins A.L., Olins D.E. Spheroid chromatin units (ν bodies) Science. 1974;183:330–332. doi: 10.1126/science.183.4122.330. [DOI] [PubMed] [Google Scholar]
- 2.Woodcock C.L., Frado L.-L., Ricciardiello L. Fine structure of active ribosomal genes. Chromosoma. 1976;58:33–39. doi: 10.1007/BF00293438. [DOI] [PubMed] [Google Scholar]
- 3.Luger K., Mäder A.W., Richmond T.J. Crystal structure of the nucleosome core particle at 2.8 Å resolution. Nature. 1997;389:251–260. doi: 10.1038/38444. [DOI] [PubMed] [Google Scholar]
- 4.Davey C.A., Richmond T.J. DNA-dependent divalent cation binding in the nucleosome core particle. Proc. Natl. Acad. Sci. USA. 2002;99:11169–11174. doi: 10.1073/pnas.172271399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Preez L.L., Patterton H.-G. Secondary structures of the core histone N-terminal tails: their role in regulating chromatin structure. In: Kundu T.K., editor. Epigenetics: Development and Disease. Springer; New York: 2013. pp. 37–55. [DOI] [PubMed] [Google Scholar]
- 6.Luger K., Richmond T.J. The histone tails of the nucleosome. Curr. Opin. Genet. Dev. 1998;8:140–146. doi: 10.1016/s0959-437x(98)80134-2. [DOI] [PubMed] [Google Scholar]
- 7.Dorigo B., Schalch T., Richmond T.J. Chromatin fiber folding: requirement for the histone H4 N-terminal tail. J. Mol. Biol. 2003;327:85–96. doi: 10.1016/s0022-2836(03)00025-1. [DOI] [PubMed] [Google Scholar]
- 8.Zheng C., Lu X., Hayes J.J. Salt-dependent intra- and internucleosomal interactions of the H3 tail domain in a model oligonucleosomal array. J. Biol. Chem. 2005;280:33552–33557. doi: 10.1074/jbc.M507241200. [DOI] [PubMed] [Google Scholar]
- 9.Hansen J.C., Lu X., Woody R.W. Intrinsic protein disorder, amino acid composition, and histone terminal domains. J. Biol. Chem. 2006;281:1853–1856. doi: 10.1074/jbc.R500022200. [DOI] [PubMed] [Google Scholar]
- 10.Potoyan D.A., Papoian G.A. Energy landscape analyses of disordered histone tails reveal special organization of their conformational dynamics. J. Am. Chem. Soc. 2011;133:7405–7415. doi: 10.1021/ja1111964. [DOI] [PubMed] [Google Scholar]
- 11.Wang X., Moore S.C., Ausió J. Acetylation increases the α-helical content of the histone tails of the nucleosome. J. Biol. Chem. 2000;275:35013–35020. doi: 10.1074/jbc.M004998200. [DOI] [PubMed] [Google Scholar]
- 12.Liu H., Duan Y. Effects of posttranslational modifications on the structure and dynamics of histone H3 N-terminal peptide. Biophys. J. 2008;94:4579–4585. doi: 10.1529/biophysj.107.115824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Yang D., Arya G. Structure and binding of the H4 histone tail and the effects of lysine 16 acetylation. Phys. Chem. Chem. Phys. 2011;13:2911–2921. doi: 10.1039/c0cp01487g. [DOI] [PubMed] [Google Scholar]
- 14.Shogren-Knaak M., Ishii H., Peterson C.L. Histone H4-K16 acetylation controls chromatin structure and protein interactions. Science. 2006;311:844–847. doi: 10.1126/science.1124000. [DOI] [PubMed] [Google Scholar]
- 15.Robinson P.J., An W., Rhodes D. 30 nm Chromatin fibre decompaction requires both H4-K16 acetylation and linker histone eviction. J. Mol. Biol. 2008;381:816–825. doi: 10.1016/j.jmb.2008.04.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Allahverdi A., Yang R., Nordenskiöld L. The effects of histone H4 tail acetylations on cation-induced chromatin folding and self-association. Nucleic Acids Res. 2011;39:1680–1691. doi: 10.1093/nar/gkq900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Schwartzentruber J., Korshunov A., Jabado N. Driver mutations in histone H3.3 and chromatin remodelling genes in paediatric glioblastoma. Nature. 2012;482:226–231. doi: 10.1038/nature10833. [DOI] [PubMed] [Google Scholar]
- 18.Wilkins B.J., Rall N.A., Neumann H. A cascade of histone modifications induces chromatin condensation in mitosis. Science. 2014;343:77–80. doi: 10.1126/science.1244508. [DOI] [PubMed] [Google Scholar]
- 19.Banères J.-L., Martin A., Parello J. The N tails of histones H3 and H4 adopt a highly structured conformation in the nucleosome. J. Mol. Biol. 1997;273:503–508. doi: 10.1006/jmbi.1997.1297. [DOI] [PubMed] [Google Scholar]
- 20.Kato H., Gruschus J., Bai Y. Characterization of the N-terminal tail domain of histone H3 in condensed nucleosome arrays by hydrogen exchange and NMR. J. Am. Chem. Soc. 2009;131:15104–15105. doi: 10.1021/ja9070078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zhou B.-R., Feng H., Bai Y. Histone H4 K16Q mutation, an acetylation mimic, causes structural disorder of its N-terminal basic patch in the nucleosome. J. Mol. Biol. 2012;421:30–37. doi: 10.1016/j.jmb.2012.04.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gao M., Nadaud P.S., Jaroniec C.P. Histone H3 and H4 N-terminal tails in nucleosome arrays at cellular concentrations probed by magic angle spinning NMR spectroscopy. J. Am. Chem. Soc. 2013;135:15278–15281. doi: 10.1021/ja407526s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zhong L., Johnson W.C., Jr. Environment affects amino acid preference for secondary structure. Proc. Natl. Acad. Sci. USA. 1992;89:4462–4465. doi: 10.1073/pnas.89.10.4462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Yang Y., Lyubartsev A.P., Nordenskiöld L. Computer modeling reveals that modifications of the histone tail charges define salt-dependent interaction of the nucleosome core particles. Biophys. J. 2009;96:2082–2094. doi: 10.1016/j.bpj.2008.10.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Arya G., Schlick T. A tale of tails: how histone tails mediate chromatin compaction in different salt and linker histone environments. J. Phys. Chem. A. 2009;113:4045–4059. doi: 10.1021/jp810375d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sun J., Zhang Q., Schlick T. Electrostatic mechanism of nucleosomal array folding revealed by computer simulation. Proc. Natl. Acad. Sci. USA. 2005;102:8180–8185. doi: 10.1073/pnas.0408867102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Arya G., Zhang Q., Schlick T. Flexible histone tails in a new mesoscopic oligonucleosome model. Biophys. J. 2006;91:133–150. doi: 10.1529/biophysj.106.083006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Arya G., Schlick T. Role of histone tails in chromatin folding revealed by a mesoscopic oligonucleosome model. Proc. Natl. Acad. Sci. USA. 2006;103:16236–16241. doi: 10.1073/pnas.0604817103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sharma S., Ding F., Dokholyan N.V. Multiscale modeling of nucleosome dynamics. Biophys. J. 2007;92:1457–1470. doi: 10.1529/biophysj.106.094805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Voltz K., Trylska J., Langowski J. Unwrapping of nucleosomal DNA ends: a multiscale molecular dynamics study. Biophys. J. 2012;102:849–858. doi: 10.1016/j.bpj.2011.11.4028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Biswas M., Langowski J., Bishop T.C. Atomistic simulations of nucleosomes. Wiley Interdiscip. Comput. Mol. Sci. 2013;3:378–392. [Google Scholar]
- 32.Ruscio J.Z., Onufriev A. A computational study of nucleosomal DNA flexibility. Biophys. J. 2006;91:4121–4132. doi: 10.1529/biophysj.106.082099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Roccatano D., Barthel A., Zacharias M. Structural flexibility of the nucleosome core particle at atomic resolution studied by molecular dynamics simulation. Biopolymers. 2007;85:407–421. doi: 10.1002/bip.20690. [DOI] [PubMed] [Google Scholar]
- 34.Biswas M., Voltz K., Langowski J. Role of histone tails in structural stability of the nucleosome. PLOS Comput. Biol. 2011;7:e1002279. doi: 10.1371/journal.pcbi.1002279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ettig R., Kepper N., Rippe K. Dissecting DNA-histone interactions in the nucleosome by molecular dynamics simulations of DNA unwrapping. Biophys. J. 2011;101:1999–2008. doi: 10.1016/j.bpj.2011.07.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Cino E.A., Choy W.Y., Karttunen M. Comparison of secondary structure formation using 10 different force fields in microsecond molecular dynamics simulations. J. Chem. Theory Comput. 2012;8:2725–2740. doi: 10.1021/ct300323g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lindorff-Larsen K., Maragakis P., Shaw D.E. Systematic validation of protein force fields against experimental data. PLoS ONE. 2012;7:e32131. doi: 10.1371/journal.pone.0032131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Korolev N., Yu H., Nordenskiöld L. Molecular dynamics simulations demonstrate the regulation of DNA-DNA attraction by H4 histone tail acetylations and mutations. Biopolymers. 2014;101:1051–1064. doi: 10.1002/bip.22499. [DOI] [PubMed] [Google Scholar]
- 39.Potoyan D.A., Papoian G.A. Regulation of the H4 tail binding and folding landscapes via Lys-16 acetylation. Proc. Natl. Acad. Sci. USA. 2012;109:17857–17862. doi: 10.1073/pnas.1201805109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hukushima K., Nemoto K. Exchange Monte Carlo method and application to spin glass simulations. J. Phys. Soc. Jpn. 1996;65:1604–1608. [Google Scholar]
- 41.Okabe T., Kawata M., Mikami M. Replica-exchange Monte Carlo method for the isobaric-isothermal ensemble. Chem. Phys. Lett. 2001;335:435–439. [Google Scholar]
- 42.Okamoto Y. Generalized-ensemble algorithms: enhanced sampling techniques for Monte Carlo and molecular dynamics simulations. J. Mol. Graph. Model. 2004;22:425–439. doi: 10.1016/j.jmgm.2003.12.009. (Conformational Sampling.) [DOI] [PubMed] [Google Scholar]
- 43.Onufriev A., Bashford D., Case D.A. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins. 2004;55:383–394. doi: 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
- 44.Bondi A. van der Waals volumes and radii. J. Phys. Chem. 1964;68:441–451. [Google Scholar]
- 45.Tsui V., Case D.A. Molecular dynamics simulations of nucleic acids with a generalized Born solvation model. J. Am. Chem. Soc. 2000;122:2489–2498. [Google Scholar]
- 46.Hess B., Kutzner C., Lindahl E. GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008;4:435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- 47.Van Der Spoel D., Lindahl E., Berendsen H.J.C. GROMACS: fast, flexible, and free. J. Comput. Chem. 2005;26:1701–1718. doi: 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
- 48.Lindahl E., Hess B., van der Spoel D. GROMACS 3.0: a package for molecular simulation and trajectory analysis. J. Mol. Mod. 2001:306–317. [Google Scholar]
- 49.Berendsen H., van der Spoel D., van Drunen R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995;91:43–56. [Google Scholar]
- 50.Bussi G., Donadio D., Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007;126:014101. doi: 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- 51.Hess B., Bekker H., Fraaije J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997;18:1463–1472. [Google Scholar]
- 52.Anandakrishnan R., Daga M., Onufriev A.V. An n log n generalized Born approximation. J. Chem. Theory Comput. 2011;7:544–559. doi: 10.1021/ct100390b. [DOI] [PubMed] [Google Scholar]
- 53.MacKerell A.D., Jr., Banavali N., Foloppe N. Development and current status of the CHARMM force field for nucleic acids. Biopolymers. 2000-2001;56:257–265. doi: 10.1002/1097-0282(2000)56:4<257::AID-BIP10029>3.0.CO;2-W. [DOI] [PubMed] [Google Scholar]
- 54.Duan Y., Wu C., Kollman P. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J. Comput. Chem. 2003;24:1999–2012. doi: 10.1002/jcc.10349. [DOI] [PubMed] [Google Scholar]
- 55.Best R.B., Buchete N.V., Hummer G. Are current molecular dynamics force fields too helical? Biophys. J. 2008;95:L07–L09. doi: 10.1529/biophysj.108.132696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Tzanov A.T., Cuendet M.A., Tuckerman M.E. How accurately do current force fields predict experimental peptide conformations? An adiabatic free energy dynamics study. J. Phys. Chem. B. 2014;118:6539–6552. doi: 10.1021/jp500193w. [DOI] [PubMed] [Google Scholar]
- 57.Huang J., MacKerell A.D., Jr. Induction of peptide bond dipoles drives cooperative helix formation in the (AAQAA)3 peptide. Biophys. J. 2014;107:991–997. doi: 10.1016/j.bpj.2014.06.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Hornak V., Abel R., Simmerling C. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins. 2006;65:712–725. doi: 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Lindorff-Larsen K., Piana S., Shaw D.E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins. 2010;78:1950–1958. doi: 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Kabsch W., Sander C. Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features. Biopolymers. 1983;22:2577–2637. doi: 10.1002/bip.360221211. [DOI] [PubMed] [Google Scholar]
- 61.Gromiha M.M., Santhosh C., Suwa M. Influence of cation-π interactions in protein-DNA complexes. Polymer. 2004;45:633–639. [Google Scholar]
- 62.Stewart M., Dunlap T., McFail-Isom L. Cations form sequence selective motifs within DNA grooves via a combination of cation-pi and ion-dipole/hydrogen bond interactions. PLoS ONE. 2013;8:e71420. doi: 10.1371/journal.pone.0071420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Hirano Y., Hizume K., Hiraoka Y. Lamin B receptor recognizes specific modifications of histone H4 in heterochromatin formation. J. Biol. Chem. 2012;287:42654–42663. doi: 10.1074/jbc.M112.397950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Mangenot S., Leforestier A., Livolant F. Salt-induced conformation and interaction changes of nucleosome core particles. Biophys. J. 2002;82:345–356. doi: 10.1016/S0006-3495(02)75399-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Mutskov V., Gerber D., Dimitrov S. Persistent interactions of core histone tails with nucleosomal DNA following acetylation and transcription factor binding. Mol. Cell. Biol. 1998;18:6293–6304. doi: 10.1128/mcb.18.11.6293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Kan P.-Y., Hayes J.J. Detection of interactions between nucleosome arrays mediated by specific core histone tail domains. Methods. 2007;41:278–285. doi: 10.1016/j.ymeth.2006.08.012. (Methods Related to the Structure and Function of Eukaryotic Chromatin.) [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.