A pH-Dependent Kinetic Model of Dihydrolipoamide Dehydrogenase from Multiple Organisms

Abstract

Dihydrolipoamide dehydrogenase is a flavoenzyme that reversibly catalyzes the oxidation of reduced lipoyl substrates with the reduction of NAD⁺ to NADH. In vivo, the dihydrolipoamide dehydrogenase component (E3) is associated with the pyruvate, α-ketoglutarate, and glycine dehydrogenase complexes. The pyruvate dehydrogenase (PDH) complex connects the glycolytic flux to the tricarboxylic acid cycle and is central to the regulation of primary metabolism. Regulation of PDH via regulation of the E3 component by the NAD⁺/NADH ratio represents one of the important physiological control mechanisms of PDH activity. Furthermore, previous experiments with the isolated E3 component have demonstrated the importance of pH in dictating NAD⁺/NADH ratio effects on enzymatic activity. Here, we show that a three-state mechanism that represents the major redox states of the enzyme and includes a detailed representation of the active-site chemistry constrained by both equilibrium and thermodynamic loop constraints can be used to model regulatory NAD⁺/NADH ratio and pH effects demonstrated in progress-curve and initial-velocity data sets from rat, human, Escherichia coli, and spinach enzymes. Global fitting of the model provides stable predictions to the steady-state distributions of enzyme redox states as a function of lipoamide/dihydrolipoamide, NAD⁺/NADH, and pH. These distributions were calculated using physiological NAD⁺/NADH ratios representative of the diverse organismal sources of E3 analyzed in this study. This mechanistically detailed, thermodynamically constrained, pH-dependent model of E3 provides a stable platform on which to accurately model multicomponent enzyme complexes that implement E3 from a variety of organisms.

Introduction

Dihydrolipoamide dehydrogenase (EC 1.8.1.4) is a member of the disulfide oxidoreductase family and reversibly catalyzes the oxidation of dihydrolipoamide with the reduction of NAD⁺ (1, 2, 3, 4) using a flavin adenine dinucleotide (FAD) cofactor.

$$\text{D}\text{i}\text{h}\text{y}\text{d}\text{r}\text{o}\text{l}\text{i}\text{p}\text{o}\text{a}\text{m}\text{i}\text{d}\text{e}+\text{N}\text{A}{\text{D}}^{+}\rightleftharpoons \text{L}\text{i}\text{p}\text{o}\text{a}\text{m}\text{i}\text{d}\text{e}+\text{N}\text{A}\text{D}\text{H}+{\text{H}}^{+}$$ (1)

Dihydrolipoamide dehydrogenase (E3) is a component of three different catabolic multienzyme complexes that oxidize pyruvate, α-ketoglutarate, or glycine, where E3 catalyzes the final step in a sequence of oxidative reactions (5). Of these, the pyruvate dehydrogenase (PDH) complex is at the interface of glycolysis and the tricarboxylic acid cycle and is key in switching between the use of glucose or fatty acids as the preferred substrate in skeletal muscle and heart (6, 7). The balance between glucose and fatty acid oxidation is critical in the prevention of lipotoxicity which can lead to hypertrophy in heart muscle and/or a diabetic state in skeletal muscle (6, 8). The PDH complex communicates between glucose and fatty acid oxidation by common substrates and products such as acetyl-CoA and the NAD⁺/NADH ratio (9, 10). The intracellular NAD⁺/NADH ratio contributes to the activation/inhibition of the complex by affecting E3 activity, most severely in Escherichia coli (11, 12) and plants (13), while also influencing regulation of PDH-specific kinase and phosphatase activity in mammals (14, 15, 16). The NAD⁺/NADH ratio is sensed directly through the E3 component of the PDH complex, so a detailed model that can predict E3 kinetic behavior as a function of lipoamide/dihydrolipoamide (Lipo/DHL), NAD⁺/NADH, and pH would be useful for predicting subsequent effects on the complex and on glycolytic/lipolytic balance (17, 18).

In the physiological direction, dihydrolipoamide, which is covalently tethered to another enzymatic subunit in the multienzyme complex (5), binds to the disulfide-exchange site near the si face of the FAD cofactor (4). Here, dihydrolipoamide is thought to donate a hydride to the disulfide and a proton to an active-site base forming a stable charge-transfer complex between the thiolate of the mixed disulfide and the oxidized FAD cofactor (1, 19, 20). In the presence of NAD⁺, electrons are passed to FAD and then to NAD⁺ on the re face of the flavin, forming NADH with the release of a proton (21). Thus, the mechanism is carried out between two substrate/product binding sites that are mediated by both sides of the FAD cofactor (4).

The E3 kinetic mechanism was first discussed by Massey, who concluded, from a parallel line pattern observed using Lineweaver-Burk plot analysis (LB) (1), that the enzyme from pig heart displays ping-pong-type kinetics. A ping-pong-type reaction was further confirmed using stopped-flow spectroscopy, which showed that the overall reaction sequence can be broken into reductive and oxidative half-reactions in the absence of the other substrate (1, 20, 21). A more extensive study employing initial velocity and product inhibition was carried out with rat liver E3 and yielded product-inhibition patterns that deviated from a simple one-site ping-pong mechanism (22).

Interestingly, early studies of E3 from E. coli (3), spinach (13), human liver (23), and pig heart (24) demonstrated an activating effect of NAD⁺ on the reverse reaction. It was also observed that initial NAD⁺ concentration could alter the pH dependence (11, 13, 25). It was hypothesized that the enzyme was being driven into a four-electron-reduced state (2e⁻ reduced mixed disulfide and 2e⁻ reduced FAD), which is considered to be a dead-end state (11, 26). The propensity to be regulated by this state is organism-specific. For instance, E. coli E3 displays a greater sensitivity to NAD⁺/NADH for the reverse reaction than do the pig heart and human liver enzymes (11, 23, 26). It is believed that an over-reduced E3 component is involved in regulating the overall activity of PDH, and thus having a metabolic regulatory impact (3, 17). The four-electron-reduced state not only ties up the complex in a simple dead-end state but may also increase the probability of down-regulation of the complex via phosphorylation of the pyruvate dehydrogenase component (E1). This can occur by reducing lipoamide moieties in the E2 component (dihydrolipoyl acetyltransferase), which then increases the affinity of PDH kinase binding (27, 28, 29).

Our main objective was to create a single model that synthesizes the pH-dependent kinetics of E3 observed from multiple organisms. Previous models do not account for pH, which is a crucial factor in the regulation of this enzyme and dictates the magnitude of the NAD⁺/NADH effect on activity (11, 22). Overall, we propose to our knowledge a new mechanism that is random and rapid in the extent of substrate and product binding and includes the reactions needed to produce and reverse a four-electron-reduced dead-end state. Our model incorporates pH such that a proton binds randomly and is treated much like a product in the overall reaction, as a proton is produced in the forward direction. In addition, the protonation states of both the active-site thiolate and base are considered based on their importance in catalysis (20, 26, 30).

The model explains initial velocity patterns in the presence and absence of products, shifts in pH-dependent velocity profiles as a function of NAD⁺, and observations of a lag in progress curve data as a function of NAD⁺ and pH. The model not only can describe these phenomena but is simultaneously consistent with a detailed representation of the enzyme active site proposed in a number of studies using thermodynamic constraints (31).

Methods

Model overview

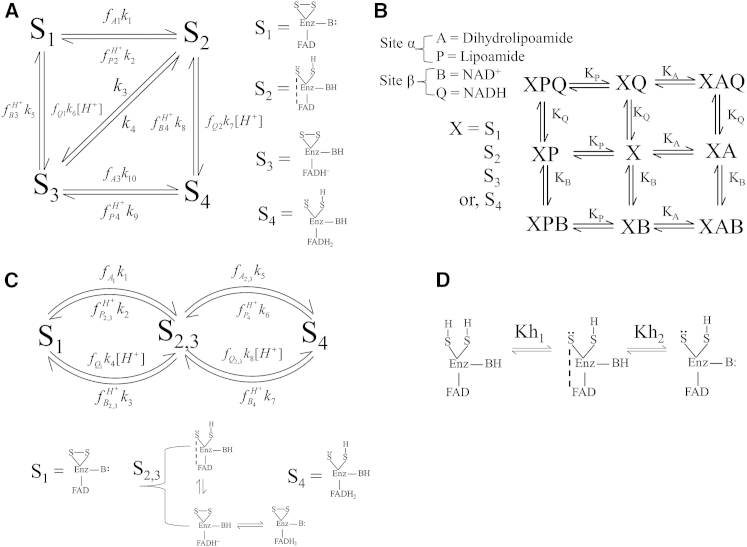
E3 can exist in one of four redox states (Fig. 1 A), including an oxidized state (S₁), a two-electron-reduced charge-transfer complex (S₂) or a two-electron-reduced FAD cofactor (S₃) state, and a four-electron-reduced dead-end state (S₄). The mechanism advances through these major redox states depending on the availability of substrates, products, and pH. Our model treats substrate/product binding to be random and in rapid equilibrium at two independent sites for Lipo/DHL (site α) and NAD/NADH (site β) (Fig. 1 B).

Figure 1.

(A) A four-state mechanism with rapid equilibrium binding of substrates and products, where S₁, S₂, S₃, and S₄ represent the oxidized, two-electron-reduced charge-transfer intermediate, hydride-reduced FAD, and four-electron-reduced dead-end states, respectively. Dihydrolipoamide, NAD⁺, lipoamide, NADH, and a proton are represented by A, B, P, Q, and H⁺, respectively. The fraction of each enzyme state bound to substrate or product is represented by f, subscript and superscript letters indicate the chemical species that is bound, and subscript numbers indicate the enzyme state. (B) Substrates and products are considered to randomly bind to either of two sites (α or β) and are in rapid equilibrium with each major state indicated by equilibrium dissociation constants of the corresponding substrates. As discussed in the main text, the added complexity of allowing the equilibrium dissociation constants for substrates and products to vary for each redox state of the enzyme was invoked to improve fits for certain data sets. (C) The mechanism shown in A was simplified to three states so that the two-electron-reduced states (S₂ and S₃ in A) are grouped into one state (S_2,3), according to previous observations that this step occurs very quickly (21, 33). (D) Proton binding sites on the thiolate (S:) and active-site base (B:), typically a histidine residue (4, 30), are modeled to further dictate whether certain substrate or product bound species can execute a chemical step in the mechanism.

In the forward direction (Fig. 1 A), a two-electron reduction of the enzyme from dihydrolipoamide results in a stable charge-transfer complex (S₁ to S₂) where an active-site base (Enz-B:), typically a histidine residue (4, 30), is thought to accept a proton from dihydrolipoamide that is critical for stabilizing the charge-transfer complex (20, 26). Electrons pass to the FAD cofactor, creating S₃, which is then oxidized to S₁ in the presence of NAD⁺. The model accounts for the possibility of turnover occurring through a ternary or ping-pong mechanism (32). A four-electron-reduced dead-end state (S₄) is produced from either of the two-electron-reduced states by pH-modulated reduction of S₂ by NADH or of S₃ by dihydrolipoamide.

A four-state model (Fig. 1 A) that distinguishes between the charge-transfer complex (S₂) and hydride-reduced FAD (S₃) states in the two-electron-reduced enzyme was simplified by creating a lumped two-electron-reduced state (Fig. 1 C, S_2,3). This simplification was made based on the fact that the hydride transfer from the mixed dithiol to the FAD cofactor has not been observed spectroscopically except in the Mycobacterium enzyme (21, 33). Moreover, a four-state model is not necessary to fit the data. The protonation state of the two-electron-reduced enzyme (Fig. 1 D) is critical in stabilizing hydride transfer between the disulfide and FAD sites. It is believed that hydride transfer can occur only when the active-site base is protonated (Enz-BH) and the thiolate is deprotonated (Enz-S:), so that the charge-transfer complex (Fig. 1 D, middle) between the thiolate and oxidized FAD is stabilized (19, 26, 30). These active-site details were incorporated into the model to more accurately describe the pH regulation of catalysis.

Model derivation

As shown previously, the fraction of each enzyme state occupied by substrates, products, and protons can be quantified by fractional occupancies (34, 35). In a general manner, assuming rapid equilibrium binding, we derived binding polynomials (Eq. 2) for dihydrolipoamide (A) and lipoamide (P) binding to site α and for NAD⁺ (B) and NADH (Q) binding to site β to either the oxidized (1), two-electron-reduced (2,3), or four-electron-reduced (4) enzyme species. Therefore, according to our nomenclature, D_1α is the polynomial for binding of dihydrolipoamide and lipoamide to site α of the oxidized enzyme state (S₁), whereas D_2,3α differs in that it determines the binding of these substrates to the two-electron-reduced enzyme state (S_2,3). Accordingly, K_A1 and K_P1 represent the equilibrium dissociation constants for dihydrolipoamide and lipoamide, respectively, to the oxidized enzyme state (S₁). Thus, our most general model accounts for possible differences in substrate and product binding affinities depending on the redox state of the enzyme. This possibility is often assumed in ordered redox enzyme mechanisms, but it is traditionally not incorporated into the model equations in the general form we present here. Binding polynomials for all substrates, products, and protons as they may depend on redox state of the enzyme are shown below.

$$\begin{array}{l}\begin{array}{c}{D}_h=\left(1+\frac{{\text{H}}^{+}}{K_{\text{H}1}}\right)\left(1+\frac{{\text{H}}^{+}}{K_{\text{H}2}}\right),\\ D_{1\alpha }=1+\frac{\text{A}}{K_{{\text{A}}_1}}+\frac{\text{P}}{K_{\text{P}1}},\\ D_{1\beta }=1+\frac{\text{B}}{K_{{\text{B}}_1}}+\frac{\text{Q}}{K_{{\text{Q}}_1}},\\ D_{\left(\mathrm{2,3}\right)\alpha }=1+\frac{\text{A}}{K_{{\text{A}}_{2\text{,}3}}}+\frac{\text{P}}{K_{{\text{P}}_{2\text{,}3}}},\\ D_{\left(\mathrm{2,3}\right)\beta }=1+\frac{\text{B}}{K_{{\text{B}}_{2\text{,}3}}}+\frac{\text{Q}}{K_{{\text{Q}}_{2\text{,}3}}},\\ D_{4\alpha }=1+\frac{\text{A}}{K_{{\text{A}}_4}}+\frac{\text{P}}{K_{{\text{P}}_4}},\\ D_{4\beta }=1+\frac{\text{B}}{K_{{\text{B}}_4}}+\frac{\text{Q}}{K_{{\text{Q}}_4}}\end{array}\end{array}$$ (2)

The binding polynomials represent all possible combinations of bound and unbound binding sites and are used to calculate the fractional occupancy of each state bound with substrate and product. The fractional occupancies (f) for each substrate and product are shown below; the subscript and superscript terms indicate what substrates or products are being represented, and subscript numbers identify the enzyme redox state bound as described above. The equilibrium dissociation constants for the proton-binding sites are represented by K_H1 for the thiolate and K_H2 for the active-site base.

$$\begin{array}{c}{f}_{{\text{A}}_1}=\frac{\left(\frac{\text{A}}{K_{{\text{A}}_1}}\right)}{D_{1\alpha }},f_{{\text{A}}_{2\text{,}3}}=\frac{\left(\frac{\text{A}}{K_{{\text{A}}_{2\text{,}3}}}\right)}{D_{\left(\mathrm{2,3}\right)\alpha }},\\ f_{{\text{B}}_{2\text{,}3}}^{{\text{H}}^{+}}=\frac{\left(\frac{\text{B}}{K_{{\text{B}}_{2\text{,}3}}}\right)}{D_{\left(\mathrm{2,3}\right)\beta }}\frac{\left(\frac{{\text{H}}^{+}}{K_{\text{H}2}}\right)}{D_h},f_{{\text{B}}_4}^{{\text{H}}^{+}}=\frac{\left(\frac{\text{B}}{K_{{\text{B}}_4}}\right)}{D_{4\beta }}\frac{\left(\frac{{\text{H}}^{+}}{K_{\text{H}2}}\right)}{D_h},\\ f_{{\text{P}}_{2\text{,}3}}^{{\text{H}}^{+}}=\frac{\left(\frac{\text{P}}{K_{{\text{P}}_{2\text{,}3}}}\right)}{D_{\left(\mathrm{2,3}\right)\alpha }}\frac{\left(\frac{{\text{H}}^{+}}{K_{\text{H}2}}\right)}{D_h},f_{{\text{P}}_4}^{{\text{H}}^{+}}=\frac{\left(\frac{\text{P}}{K_{{\text{P}}_4}}\right)}{D_{4\alpha }}\frac{\left(\frac{{\text{H}}^{+}}{K_{\text{H}2}}\right)}{D_h},\\ f_{{\text{Q}}_1}=\frac{\left(\frac{\text{Q}}{K_{{\text{Q}}_1}}\right)}{D_{1\beta }},f_{{\text{Q}}_{2\text{,}3}}=\frac{\left(\frac{\text{Q}}{K_{{\text{Q}}_{2\text{,}3}}}\right)}{D_{\left(\mathrm{2,3}\right)\beta }}.\end{array}$$ (3)

The fractional occupancies are then used to write the kinetic equations that govern the transitions between the three major enzyme states of the model. The equations are shown in matrix form in Eq. 4 and were solved analytically by computing the pseudoinverse of the state-transition matrix using MATLAB (2011b) Symbolic Math Toolbox, where S₁, S_2,3, and S₄ represent the major enzyme steady-state concentrations and E_t represents the total enzyme concentration.

$$\left[\begin{array}{ccc}-\left(f_{{\text{A}}_1}{k}_1+f_{{\text{Q}}_1}{k}_4\left[{\text{H}}^{+}\right]\right)& \left(f_{{\text{B}}_{2\text{,}3}}^{{\text{H}}^{+}}{k}_3+f_{{\text{P}}_{2\text{,}3}}^{{\text{H}}^{+}}{k}_2\right)& 0\\ \left(f_{{\text{A}}_1}{k}_1+f_{{\text{Q}}_1}{k}_4\left[{\text{H}}^{+}\right]\right)& -\left(f_{{\text{B}}_{2\text{,}3}}^{{\text{H}}^{+}}{k}_3+f_{{\text{P}}_{2\text{,}3}}^{{\text{H}}^{+}}{k}_2+f_{{\text{Q}}_{2\text{,}3}}{k}_8\left[{\text{H}}^{+}\right]+f_{{\text{A}}_{2\text{,}3}}{k}_5\right)& \left(f_{{\text{B}}_4}^{{\text{H}}^{+}}{k}_7+f_{{\text{P}}_4}^{{\text{H}}^{+}}{k}_6\right)\\ 0& \left(f_{{\text{Q}}_{2\text{,}3}}{k}_8\left[{\text{H}}^{+}\right]+f_{{\text{A}}_{2\text{,}3}}{k}_5\right)& -\left(f_{{\text{B}}_1}^{{\text{H}}^{+}}{k}_7+f_{{\text{P}}_1}^{{\text{H}}^{+}}{k}_6\right)\\ 1& 1& 1\end{array}\right]\left[\begin{array}{c}{\text{S}}_1\\ {\text{S}}_{2\text{,}3}\\ {\text{S}}_4\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\\ E_{\text{t}}\end{array}\right]$$ (4)

The net flux (J) of NADH, which is the major signal in the data sets, is expressed by considering the reactions that produce and consume it. The solution to Eq. 4 is then used to compute J.

$$\begin{array}{l}J=E_{\text{t}}\left(\left[{\text{S}}_{2\text{,}3}\right]f_{{\text{B}}_{2\text{,}3}}^{{\text{H}}^{+}}{k}_3-\left[{\text{S}}_1\right]f_{{\text{Q}}_1}{k}_4\left[{\text{H}}^{+}\right]+\left[{\text{S}}_4\right]f_{{\text{B}}_4}^{{\text{H}}^{+}}{k}_7-\left[{\text{S}}_{2\text{,}3}\right]f_{{\text{Q}}_{2\text{,}3}}{k}_8\left[{\text{H}}^{+}\right]\right)\\ =\frac{\left(\begin{array}{l}n1\text{ABP}+n2{\text{AB}}^2\text{PQ}+n3{\text{AB}}^2\text{P}\\ +n4{\text{AB}}^2\text{Q}+n5{\text{AB}}^2+n6{\text{AB}}^3\text{P}\\ +n7{\text{AB}}^3+n8{\text{A}}^2{\text{B}}^2\text{Q}+n9{\text{A}}^2{\text{B}}^2\\ +n10{\text{A}}^2{\text{B}}^3+n11{\text{ABQ}}^2+n12\text{ABQ}\\ +n13{\text{A}}^2{\text{BQ}}^2+n14{\text{A}}^2\text{BQ}+n15{\text{A}}^2\text{B}\end{array}\right)-\left(\begin{array}{l}n16{\text{APQ}}^3+n17{\text{APQ}}^2+n18\text{APQ}\\ +n19{\text{BP}}^2{\text{Q}}^2+n20{\text{B}}^2{\text{P}}^2\text{Q}+n21{\text{BP}}^2\text{Q}\\ +n22{\text{BPQ}}^2+n23\text{BPQ}+n24{\text{B}}^2\text{PQ}\\ +n25{\text{ABPQ}}^2+n26\text{ABPQ}+n27{\text{P}}^2\text{Q}\\ +n28{\text{P}}^2{\text{Q}}^2+n29{\text{PQ}}^2+n30{\text{PQ}}^3+n31{\text{P}}^2{\text{Q}}^3\end{array}\right)}{\begin{array}{l}d1{\text{A}}^2+d2{\text{Q}}^3+d3{\text{B}}^3+d4{\text{B}}^2+d5{\text{Q}}^2+d6{\text{P}}^2+d7{\text{BP}}^2{\text{Q}}^2+d8{\text{B}}^2{\text{P}}^2\text{Q}+d9{\text{BP}}^2\text{Q}+d10{\text{BPQ}}^2\\ +d11\text{BPQ}+d12{\text{B}}^2\text{PQ}+d13{\text{ABPQ}}^2+d14\text{ABPQ}+d15\text{ABP}+d16{\text{AB}}^2\text{PQ}+d17{\text{AB}}^2\text{P}\\ +d18{\text{AB}}^2\text{Q}+d19{\text{AB}}^2+d20{\text{AB}}^3\text{P}+d21{\text{AB}}^3+d22{\text{A}}^2{\text{B}}^2\text{Q}+d23{\text{A}}^2{\text{B}}^2+d24{\text{A}}^2{\text{B}}^3\\ +d25{\text{APQ}}^3+d26{\text{APQ}}^2+d27\text{APQ}+d28{\text{ABQ}}^2+d29\text{ABQ}+d30{\text{A}}^2{\text{BQ}}^2+d31{\text{A}}^2\text{BQ}\\ +d32{\text{A}}^2\text{B}+d33{\text{A}}^2\text{Q}+d34{\text{A}}^2{\text{Q}}^3+d35\text{QP}+d36\text{QB}+d37{\text{QB}}^2+d38{\text{Q}}^2\text{B}+d39\text{AP}\\ +d40\text{AB}+d41{\text{P}}^2\text{B}+d42{\text{P}}^2{\text{B}}^2+d43\text{PB}+d44{\text{PB}}^2+d45{\text{P}}^2{\text{B}}^3+d46{\text{PB}}^3+d47{\text{A}}^2{\text{Q}}^2\\ +d48\text{AQ}+d49{\text{AQ}}^2+d50{\text{AQ}}^3+d51{\text{P}}^2\text{Q}+d52{\text{P}}^2{\text{Q}}^2+d53{\text{PQ}}^2+d54{\text{PQ}}^3+d55{\text{P}}^2{\text{Q}}^3\end{array}}\end{array}$$ (5)

The expression for J is represented in coefficient form (36), using Maple 14 software (Maplesoft, Waterloo, Ontario, Canada), and contains 31 numerator (n) and 55 denominator (d) terms when the proton concentration terms are hidden in the coefficients for brevity. The analytical solutions of the model equations reveal higher-order terms in both the numerator and denominator, which was expected, considering that substrates and products are able to bind multiple times in the mechanism (37). Higher-order terms in the flux expression have the potential to produce so called non-Michaelis-Menten behavior (hyperbolic deviation), which alters the definition of the steady-state constants (37). Despite this, we derived and calculated the apparent Michaelis-Menten constants and the forward and reverse k_cat based on their traditional mathematical definitions (32, 38) from fitted rate and equilibrium constants as a function of pH. This procedure was carried out using MATLAB (2011b) Symbolic Math Toolbox according to a previously described protocol that implemented Maple symbolic software (38). These results are reported in the Supporting Material.

Model constraints

Thermodynamic loop constraints were derived as follows from the model scheme in Fig. 1 C. From the left loop in Fig. 1 C,

$${\text{S}}_1\underset{f_{{\text{P}}_{2\text{,}3}}^{{\text{H}}^{+}}{k}_2}{\overset{f_{{\text{A}}_1}{k}_1}{\rightleftharpoons }}{\text{S}}_{\mathrm{2,3}}.$$ (6)

At equilibrium, according to detailed balance,

$$\left[{\text{S}}_1\right]f_{{\text{A}}_1}{k}_1-\left[{\text{S}}_{2\text{,}3}\right]f_{{\text{P}}_{2\text{,}3}}^{{\text{H}}^{+}}{k}_2=0$$ (7)

After rearranging,

$$\frac{f_{{\text{A}}_1}{k}_1}{f_{{\text{P}}_{2\text{,}3}}^{{\text{H}}^{+}}{k}_2}=\frac{\left[{\text{S}}_{2\text{,}3}\right]}{\left[{\text{S}}_1\right]}.$$ (8)

In a similar way, from

$${\text{S}}_{\mathrm{2,3}}\underset{f_{\text{Q}1}{k}_4\left[{\text{H}}^{+}\right]}{\overset{f_{{\text{B}}_{2\text{,}3}}^{{\text{H}}^{+}}{k}_3}{\rightleftharpoons }}{\text{S}}_1,$$ (9)

$$\frac{f_{{\text{B}}_{2\text{,}3}}^{{\text{H}}^{+}}{k}_3}{f_{\text{Q}1}{k}_4\left[{\text{H}}^{+}\right]}=\frac{\left[{\text{S}}_1\right]}{\left[{\text{S}}_{2\text{,}3}\right]}.$$ (10)

Multiplying Eqs. 8 and 10 yields

$$\frac{f_{{\text{A}}_1}{k}_1{f}_{{\text{B}}_{2\text{,}3}}^{{\text{H}}^{+}}{k}_3}{f_{{\text{P}}_{2\text{,}3}}^{{\text{H}}^{+}}{k}_2{f}_{{\text{Q}}_1}{k}_4\left[{\text{H}}^{+}\right]}=1.$$ (11)

Substituting the fractional occupancies from Eq. 2,

$$\left(\frac{k_1{k}_3}{k_2{k}_4}\right)\frac{\frac{\left(\frac{\text{A}}{K_{{\text{A}}_1}}\right)}{D_{1\alpha }}\frac{\left(\frac{\text{B}}{K_{{\text{B}}_{2\text{,}3}}}\right)}{D_{\mathrm{2,3}\beta }}\frac{\left(\frac{{\text{H}}^{+}}{K_{\text{H}2}}\right)}{D_h}}{\frac{\left(\frac{{\text{H}}^{+}}{K_{\text{H}2}}\right)}{D_h}\frac{\left(\frac{\text{P}}{K_{{\text{P}}_{2\text{,}3}}}\right)}{D_{\mathrm{2,3}\alpha }}\frac{\left(\frac{\text{Q}}{K_{{\text{Q}}_1}}\right)}{D_{1\beta }}{\text{H}}^{+}}=1.$$ (12)

Rearranging yields the constraint

$$k_1=\left(\frac{k_2{k}_4}{k_3}\right)\left(\frac{K_{{\text{A}}_1}{K}_{{\text{B}}_{2\text{,}3}}}{K_{{\text{P}}_{2\text{,}3}}{K}_{{\text{Q}}_1}}\right)\left(\frac{D_{1\alpha }{D}_{\mathrm{2,3}\beta }}{D_{\mathrm{2,3}\alpha }{D}_{1\beta }}\right)K\text{eq}$$ (13)

The overall equilibrium constant, expressed in Eq. 14, was normalized to pH 7 by multiplying the righthand side of Eq. 14 by 10⁷.

$$K\text{eq}={\frac{{\text{PQH}}^{+}}{\text{AB}}|}_{\text{eq}}.$$ (14)

The same reasoning applies to the second loop in the overall reaction and yields the constraint

$$k_5=\left(\frac{k_6{k}_8}{k_7}\right)\left(\frac{K_{{\text{A}}_{2\text{,}3}}{K}_{{\text{B}}_4}}{K_{{\text{P}}_4}{K}_{{\text{Q}}_{2\text{,}3}}}\right)\left(\frac{D_{\mathrm{2,3}\alpha }{D}_{4\beta }}{D_{4\alpha }{D}_{\mathrm{2,3}\beta }}\right)K\text{eq}\text{.}$$ (15)

The midpoint potentials (E_m) at pH 7 and 25°C for the Lipo/DHL and NAD⁺/NADH couples are −0.287 and −0.320 V, respectively (2, 26). We used these midpoint potentials to calculate an overall equilibrium constant (Keq) of 0.0766:

$$K\text{eq}=e^{\frac{nF\text{Δ}{E}_{\text{m}}}{RT}},$$ (16)

where n is the number of electrons transferred, F is Faraday’s constant (96,485 C mol⁻¹), ΔE_m is the midpoint potential difference, R is the gas constant (8.315 J K⁻¹ mol⁻¹), and T is the temperature in Kelvin. The overall equilibrium constant was fitted for each data set (collected at 25°C) within a twofold range of 0.0766 using Eqs. 13 and 15. We applied a soft equilibrium constraint, since midpoint potentials can vary depending on the methods used to determine them (39), and this variability is amplified due to the exponential relationship between ΔE_m and Keq shown in Eq. 16. The twofold variation in Keq assumes that the error in the reported potentials is <1.5%. Notably, it was determined that it is possible to fit the data from all organisms at 25°C with values of Keq within a narrow range of 0.0383 to 0.05. However, because the rat liver data set was collected at 37°C (22), we allowed this Keq to vary beyond a twofold range.

Model fitting

Data were fitted using MATLAB 2011b software (The MathWorks, Natick, MA) using customized code of either a simulated annealing or genetic algorithm. They were then further optimized using the local nonlinear optimization function FMINCON. When data sets contained time-dependent data, the rate equations for A, B, P, and Q derived from the steady-state solution (solution to Eq. 4) were integrated using the numerical integrator ode45 (Runge-Kutta algorithm) in MATLAB and fitted simultaneously with initial rate data. Alternatively, the full solution (no steady-state assumption (40)), which contains time-dependent solutions of S₁, S_2,3, and S₄ using ode15s (a stiff solver in MATLAB) were also used to fit the data. Despite the added sophistication of the latter method, we did not see any improvement in fitting. Therefore, all results are shown using the former method. Data sets were obtained from previous publications (11, 13, 22, 23, 41, 42) using the freely available graph digitizing software ScanIt 1.06 (amsterCHEM). As errors were not given for any of the published data sets, the cost function (or error/fitting function) was weighted according to a general 10% error assumption as described previously (35). The extracted literature data and MATLAB code required to reproduce the figures in the main text and Supporting Material are included in the Supporting Material. It is important to note that data sets from each organism were fitted simultaneously, or globally, as compared to fitting individual data sets, the traditional approach to enzyme kinetic analysis (43, 44).

Each data set was fitted allowing all equilibrium dissociation constants to be either independent of or dependent on the redox state of the enzyme. This added sophistication in the model was implemented in an effort to better fit more expansive data sets, such as the E. coli and the spinach E3 data sets described below. Data sets such as the rat and human liver did not require the more detailed redox-dependent K_d model to fit the data.

In an effort to obtain the best fit, multiple fitting trials were conducted using the algorithms mentioned above (including global optimization) with random initial starting points. Fit results that fell within a certain cost-function value were saved (∼100 fits), and parameter values and their ranges were tabulated. This process gives insight into parameter uncertainty by showing parameter variation while still fitting the data. Results for this fitting procedure are displayed in the Supporting Material.

Results and Discussion

To our knowledge, Massey was the first to conclude that E3 from pig heart followed ping-pong-type kinetics based on LB plot analysis (1). Others have argued that this enzyme may also proceed via a ternary mechanism (25, 45), and recent structural data clearly show that two distinct sites are required to react with lipoyl and pyridine nucleotide substrates (4). An extensive steady-state kinetic data set with the rat liver enzyme, collected by Reed (22), offers a suitable challenge for our model through global fitting. Most enzyme kinetic studies lack proper global fitting analysis, which requires consistency among all data sets; therefore, we emphasize that this type of fitting procedure was implemented in fitting all of the data sets to our model.

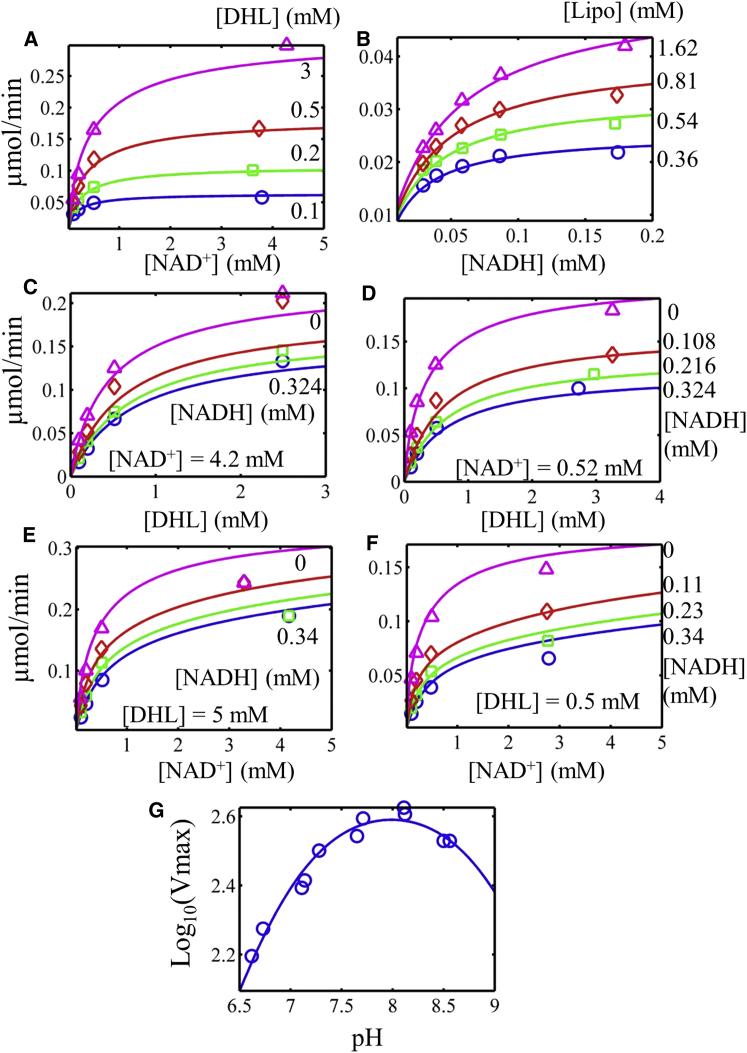
The data set collected by Reed includes initial velocity substrate profiles in the forward (Fig. 2 A) and reverse (Fig. 2 B) directions, as well as product-inhibition (Fig. 2, C–F) and pH-dependent (Fig. 2 G) data. In the analysis, Reed concluded that a simple ping-pong-type mechanism was not able to describe the observed product inhibition patterns (22). Although if lipoamide and NADH were considered to bind the oxidized and reduced forms of the enzyme, respectively, this would create LB patterns consistent with the data (22). Although it explains LB patterns, the model by Reed fails to account for the reversibility of the NADH inhibition step by NAD⁺ based on the active-site chemistry, assumes one binding site for both substrates and products (which is inconsistent with structural data (4, 46, 47)), and completely neglects any modulation of the reaction by pH, which is crucial for the regulation of this enzyme (Fig. 2 G). Furthermore, this enzyme is capable of producing product from either of two pathways shown in Fig. 1 C. Globally fitting the rat liver enzyme data (22) to the K_d redox-independent model demonstrates that the model can consistently explain all of the data, including the pH dependence of Vmax while being constrained by the known equilibrium constant and thermodynamic loop constraints.

Figure 2.

Global fitting of rat liver E3 activity as a function of substrates, products, and pH to data from Reed (22) (see Supporting Material). In all cases, the data are represented by symbols and the model by solid lines. (A) Initial velocity data in the absence of products in the forward direction, collected by varying NAD⁺ in different fixed concentrations of dihydrolipoamide (DHL) (top to bottom: 3, 0.5, 0.2, and 0.1 mM) at pH 8 were obtained from Fig. 1 A of Reed (22). (B) Initial velocity data in the absence of products in the reverse direction, with NADH varied and different fixed lipoamide concentrations (top to bottom: 1.62, 0.81, 0.54, and 0.36 mM) were obtained from Fig. 1 B of Reed (22). (C) Initial velocity data in the forward direction with DHL varied in a high NAD⁺ concentration (4.2 mM) with different fixed NADH (top to bottom: 0, 0.108, 0.216, and 0.324 mM) at pH = 8 were obtained from Fig. 3 of Reed (22). (D) Initial velocity data in the forward direction with DHL varied in low NAD⁺ concentration (0.52 mM) with different fixed NADH concentrations (top to bottom: 0, 0.108, 0.216, and 0.324 mM) at pH 8 were obtained from Fig. 4 of Reed (22). (E) Initial velocity data in the forward direction at high DHL concentration (5 mM) with different fixed NADH (top to bottom: 0, 0.11, 0.23, and 0.34 mM) at pH 8 were obtained from Fig. 5 of Reed (22). (F) Initial velocity data in the forward direction at low DHL (0.5 mM) in different fixed concentrations of NADH (top to bottom: 0, 0.11, 0.23, and 0.34 mM) at pH 8 were obtained from Fig. 6 of Reed (22). (G) Log10(Vmax) of the forward reaction with pH obtained from Fig. 9 of Reed (22). To see this figure in color, go online.

E. coli E3 is an example of an E3 that is strongly regulated by the NAD⁺/NADH ratio (11). As E3 is a component of the PDH complex, increased sensitivity to the NAD⁺/NADH ratio is thought to be important for compensating for the lack of regulation by phosphorylation of the E. coli PDH complex (12), which is present in mammalian PDH complexes (18). The enzyme’s sensitivity to the NAD⁺/NADH ratio is demonstrated by a number of experiments conducted by Wilkinson and Williams (11).

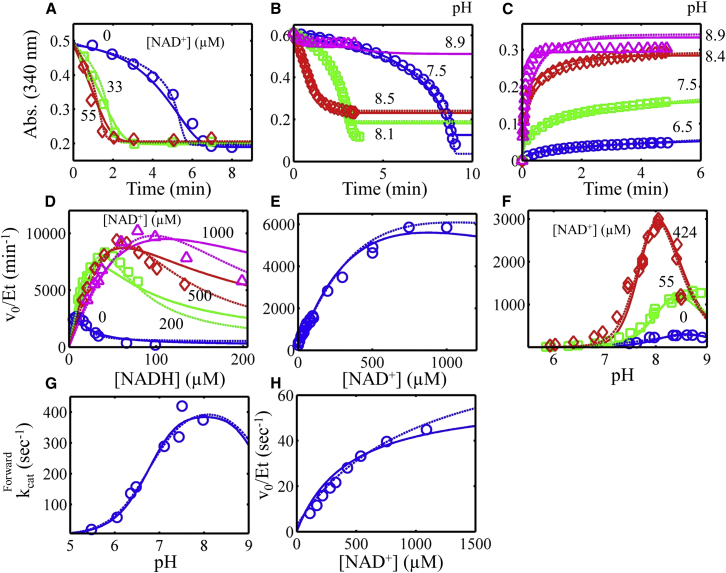
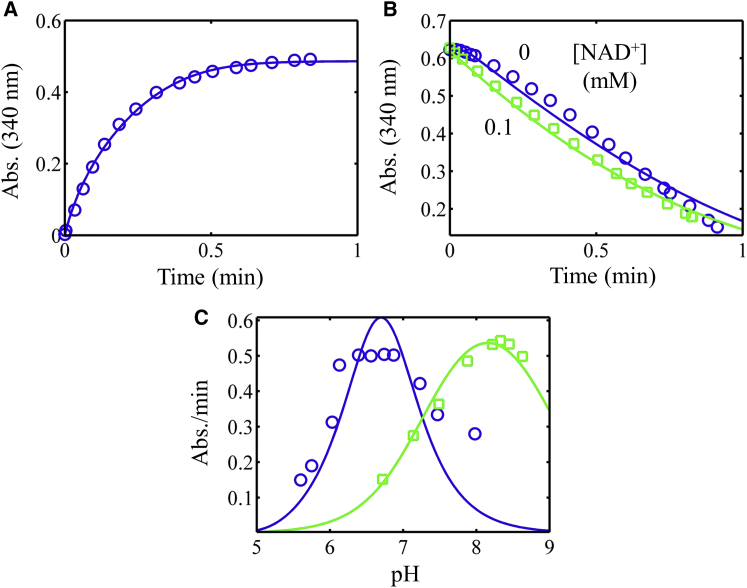
A substantial lag in progress curves has been observed in the reverse direction (Fig. 3, A and B) when NADH and lipoamide are utilized as substrates without initially added NAD⁺ (3, 11). The severity of this lag is modulated by both NAD⁺ and pH (Fig. 3, A and B). The lag is abated by either increasing initial amounts of NAD⁺ or increasing the pH (Fig. 3, A and B). This phenomenon was observed with pig heart E3 by Massey (24), who hypothesized that a four-electron-reduced dead-end state was responsible. The E. coli E3 data set from Wilkinson and Williams represents, among dihydrolipoamide dehydrogenases in general, one of the larger kinetic data sets displaying NADH inhibition that is rescued by added NAD⁺ (Fig. 3, A and D–F) (11). To incorporate data in the forward direction, including forward pH-dependent data (Fig. 3, C and G), we added E. coli E3 data from Sahlman and Williams (42) and Koike et al. (48) (Fig. 3, C, G, and H).

Figure 3.

Global fitting of the E. coli E3 progress curve, substrate inhibition, NAD⁺ activation, and pH-dependent data obtained from previous studies (3, 11, 42) (see Supporting Material). All data (symbols) were fitted to two models, where the K_d for substrates and products was either independent (solid lines) or dependent (dashed lines) on the enzyme redox state, as described in Methods. (A) Progress curves for the reverse reaction (pH 7.9) in different NAD⁺ concentrations, with data obtained from Fig. 1 of Wilkinson and Williams (11). (B) Progress curves for the reverse reaction, with pH varied, with data obtained from Fig. 5 of Koike et al. (3). (C) Progress curves in the forward direction with pH varied, with data obtained from Fig. 4 of Koike et al. (3). (D) Initial velocity divided by total enzyme concentration (v₀/E_t) in the reverse direction (pH 7.9) with varied NADH with different fixed NAD⁺ concentrations. Data were obtained from Fig. 6 of Wilkinson and Williams (11). (E) Activation of reverse v₀/E_t (pH 7.9) with increasing NAD⁺ concentration, with data obtained from Fig. 3 of Wilkinson and Williams (11). (F) v₀/E_t as a function of pH and NAD⁺ concentration, with data obtained from Fig. 2 of Wilkinson and Williams (11). (G) Forward k_cat as a function of pH, with data obtained from Fig. 4 A of Sahlman and Williams (42). (H) v₀/E_t as a function of NAD⁺ concentration (pH 6.05), with data obtained from Fig. 2 of Sahlman and Williams (42). To see this figure in color, go online.

The E. coli E3 data (11, 42, 48) were then globally fitted to the redox-independent (Fig. 3, solid lines) and redox-dependent (Fig. 3, dashed lines) K_d model. Fitting the E. coli data set illustrates that both the simpler and more complex models can capture all major features of the E. coli data; however, the more detailed model improves the fitting of the data, especially in Fig. 3 D. The E. coli initial-velocity pH-dependent data in Fig. 3 F reveal an interesting shift in the optimum pH from a basic to an acidic pH when NAD⁺ is added to the initial reaction mixture. This phenomenon can only be predicted by a model that accounts for the reversibility of the NADH inhibition by NAD⁺. In addition, the recovery of activity in the reverse direction by addition of NAD⁺ is predicted (Fig. 3 F). The model also predicts that activation by NAD⁺ (Fig. 3 E) will saturate and has the potential to inhibit at high enough NAD⁺ concentrations, depending on the parameterization of the model. Thus, our model can treat NAD⁺ as a partial activator or inhibitor (32, 37) when the net flux is favored in the reverse direction. Even though the simpler model can describe the major features of the data, the degree of inhibition/activation of NAD⁺ is more accurately described by the more detailed model (Fig. 3, D and E).

To explain their data, Wilkinson and Williams put forth a mechanistic hypothesis that included a model similar to that of Reed, discussed above (11). Their proposed model adds the possibility of NAD⁺ binding to the oxidized enzyme form (observed previously (25)) while excluding the possibility of lipoamide forming a dead-end complex with the oxidized enzyme form (11). In contrast to Reed (22), they do discuss effects of NADH reducing the two-electron-reduced enzyme state into the four-electron-reduced state (11). The method they used to test their model was again reasoning of LB plot patterns based on fitting individual data sets that may lack global parameter consistency (11). In addition, no parameters were even reported, so no information is available within the context of this publication to reproduce a model for E. coli E3 that accurately describes the data (11). Their model (11), although more advanced than that of Reed (22), also suffers from lack of consideration of pH, which greatly dictates the effects of the substrates and products on the enzyme state (Fig. 3, B, C, F, and G) and its propensity to catalyze the reaction in a preferred direction (Fig. 3, B and C). Interestingly, Wilkinson and Williams argued that the data shown in Fig. 3 H can be fitted significantly better using a cooperative model than a basic Michaelis-Menten model (see Fig. 2 in Sahlman and Williams (42)). A notable aspect of our model is that it reveals that the apparent cooperativity is an emergent property of the enzyme mechanism (Fig. 1 C) and is a consequence of higher-order terms in the steady-state expression (Eq. 5). Segel (37) has discussed similar behavior of cooperative and random mechanisms.

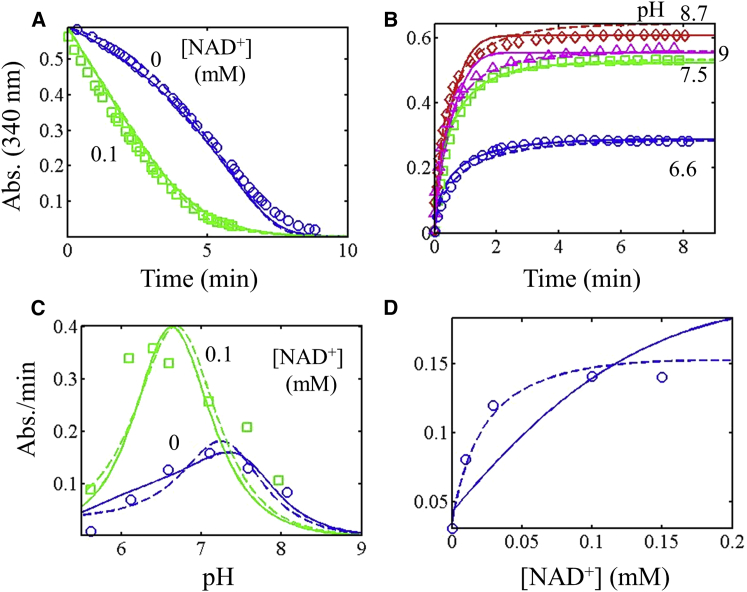
Similar observations made with E. coli E3 data have also been observed with E3 from spinach (Fig. 4) (13). A significant lag is observed in reverse progress curves in the absence of added NAD⁺ (Fig. 4 A), although it is somewhat less severe than with the E. coli enzyme (Fig. 3, A and B). Similar to the E. coli enzyme, spinach E3 forward-progress curve conditions that differ only in pH show an increase in the apparent equilibrium constant as a function of pH (Fig. 3 C). This behavior is consistent with the pH-dependent equilibria of the Lipo/DHL and NAD⁺/NADH redox couples, where the pH dependence of the apparent equilibrium constant is constrained by our model within a twofold range of the equilibrium constant normalized to Keq(pH 7) = 0.0766 at 25°C (see Model constraints).

Figure 4.

Global fitting of spinach E3 progress curves, NAD⁺ activation, and pH-dependent data obtained from Matthews and Reed (13) (see Supporting Material For data). All data (symbols) were fitted to two models in which the K_d for substrates and products was either independent (solid lines) or dependent (dashed lines) of the enzyme redox state, as described in Methods. (A) Progress-curve data for the reverse reaction in different NAD⁺ concentrations (pH 6.3), with data obtained from Fig. 4 in Matthews and Reed (13). (B) Progress-curve data for the forward reaction with varied pH, with data obtained from Fig. 7 of Matthews and Reed (13). (C) Initial velocity of the reverse reaction as a function of pH and NAD⁺ concentration, with data obtained from Fig. 6 of Matthews and Reed (13). (D) Activation of reverse initial velocity with increasing NAD⁺ concentration (pH 6.3), with data obtained from Fig. 5 of Matthews and Reed (13). To see this figure in color, go online.

The data set from spinach E3 (13) was then globally fitted to the redox-independent (Fig. 4, solid lines) and redox-dependent (Fig. 4, dashed lines) K_d model. The main deviation when fitting to the simpler redox-independent model occurs with the NAD⁺ activation data (Fig. 4 D), in the reverse direction, where the data show a tighter saturation compared to the model; however, when the K_d(s) are allowed to become dependent on the redox enzyme state, the model can accurately describe these data (Fig. 4 D, dashed lines). Other fits of the simpler model to the spinach enzyme (see Fig. S8 in the Supporting Material) demonstrate that the simpler model can accurately fit the data shown in Fig. 4 D but at the cost of deviating from the reverse-progress-curve data.

We also globally fitted a smaller data set available from human liver E3 to the redox-independent K_d model (Fig. 5) (23). An obvious difference between the human liver data set and the other data sets that contain progress-curve data is a much shorter observed lag in the reverse reaction (Fig. 5 B) in the absence of initially added NAD⁺. This difference can be explained by human liver having a smaller fraction of the E3 enzyme concentration than E. coli and spinach in the over-reduced dead-end state (Fig. 1 C, S₄). Previous investigators (11, 23) have made this qualitative conclusion to explain differences in the data, and it is consistent with our model, as discussed below.

Figure 5.

Global fitting of the human liver E3 progress curve and pH-dependent data from Ide et al. (23) (see Supporting Material). (A) Progress-curve data for the forward reaction (pH 8.5), with data obtained from Fig. 6 of Ide et al. (23). (B) Progress-curve data for the reverse reaction in different NAD concentrations (pH 6.5), with data obtained from Fig. 4 of Ide et al. (23). (C) Initial velocity as a function of pH for the forward (squares) and reverse reactions (circles), with data obtained from Fig. 5 of Ide et al. (23). To see this figure in color, go online.

To address the apparent difference in the steady-state redox enzyme state distributions of E3 components from different organisms, we used a multitude of parameter sets that fit the data (see Supporting Material) by means of the simpler redox-independent K_d model to calculate the enzyme fraction in each of the three major states (Fig. 1 C) as a function of the oxidized and reduced lipoamide (Lipo/DHL) and NAD ratio with pH and then calculated their mean distribution (Figs. 6 and 7). The greatest contrast is between the E. coli and human E3 distributions, as shown in the main text, whereas the spinach E3 distribution, which is more similar to the E. coli E3 distribution, is shown in the Supporting Material (see Fig. S11). We excluded the rat liver data set (Fig. 1) from the enzyme steady-state distribution analysis, since this data set did not contain progress-curve data, which includes information on the lag phase. The lag-phase data provides information on the S₄ state population, which greatly influences the calculated steady-state distributions and subsequent conclusions.

Figure 6.

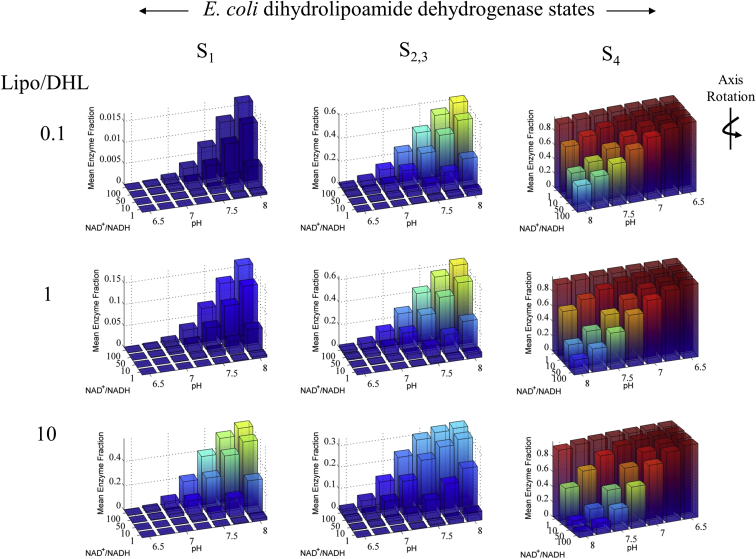
Mean E. coli E3 major redox steady-state distributions. E. coli E3 major redox steady-state distributions calculated from 100 parameter sets (see Supporting Material) with the redox-independent K_d model and Lipo/DHL and NAD⁺/NADH ratios as a function of pH. NAD⁺/NADH ratios were chosen based on literature data collected in aerobic conditions, and Lipo/DHL ratios were arbitrarily chosen (49). Total concentrations of lipoamide and NAD species were set to 10 mM and 3 mM, respectively. The total lipoamide concentration is based on a millimolar range approximation of the stoichiometry and volume of the pyruvate dehydrogenase complex (5). The total concentration of NAD species was chosen to compare with human liver state distribution calculations (Fig. 7). Note that plots in the S₄ column have been rotated with respect to those in other columns for a better view of the smaller bars, which would otherwise be hidden. To see this figure in color, go online.

Figure 7.

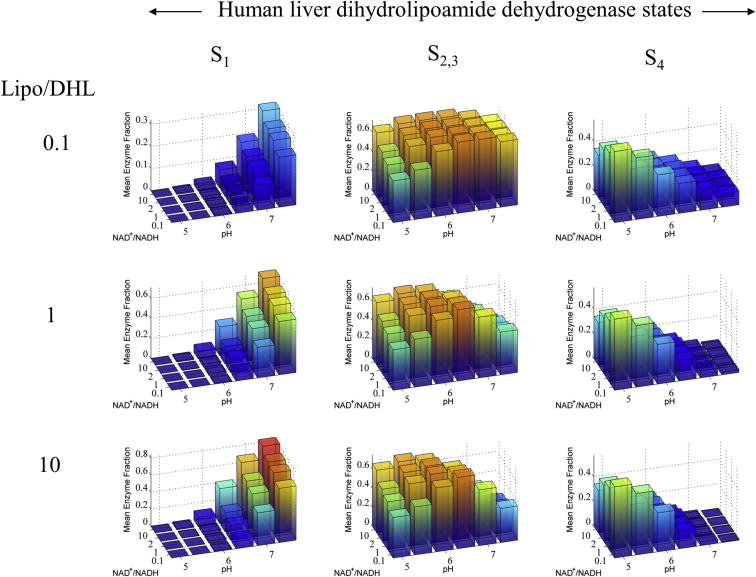
Mean human liver E3 major redox steady-state distributions as a function of pH, lipoamide, and NAD oxidized and reduced ratios calculated from 70 different parameter sets that fit the data (see Supporting Material). Human liver E3 major state distributions were calculated from 70 parameter sets from the redox-independent K_d model and Lipo/DHL and NAD⁺/NADH ratios as a function of pH. NAD⁺/NADH ratios were chosen based on literature data estimating a typical range of NAD⁺/NADH (50, 51, 52) and Lipo/DHL ratios were arbitrarily chosen. Total concentrations of lipoamide and NAD species were set to 10 mM and 3 mM (53), respectively. The total lipoamide concentration is based on a millimolar range approximation of the stoichiometry and volume of the pyruvate dehydrogenase complex (5). To see this figure in color, go online.

The mean steady-state redox enzyme state distribution calculated for E. coli E3 (Fig. 6) shows that at a low pH and NAD⁺/NADH ratio the four-electron dead-end state (S₄) is much more populated relative to the others. At pH 6.5, with all NAD⁺/NADH and Lipo/DHL ratios shown in Fig. 6, the four-electron-reduced dead-end state (S₄) represents >97% of the total enzyme concentration, showing the importance of pH in dictating this state.

The human liver E3 displays a shorter lag time compared to the E. coli and spinach enzymes, even at a lower pH (Fig. 5 B). To compare enzyme distributions, we also used a large parameter set that fits the human liver data (see Fig. S12) to calculate the mean steady-state redox enzyme-state distribution (Fig. 7). This calculation shows that in general, the enzyme mainly exists in the S₁, S_2,3, and S₄ states at pH ≥ 7, 5 ≤ pH ≤ 6.5, and pH ≤ 5, respectively. Although it appears that pH is the major regulator of the enzyme states compared to the NAD⁺/NADH ratio, it is important to remember that the pH is calculated on a logarithmic scale and that each pH unit thus represents a 10-fold change in proton concentration. Thus, changes from pH 5 to 7 represent 100-fold changes in the hydrogen ion concentration.

Overall, the progress-curve lag phase for the E. coli (Fig. 3, A and B), spinach (Fig. 4 A), and human liver (Fig. 5 B) E3 data sets vary substantially. Analysis of the mean steady-state redox enzyme-state distributions is consistent with the hypothesis that the underlying kinetic differences between these enzymes are indicative of their propensity to be driven into the four-electron-reduced state (S₄). Even though most E3 enzymes have about a 40% sequence homology (54), differences in the progress-curve lag phases cannot be explained using a single parameter set. However, as we have shown here, all of the kinetic data can be explained by a single mechanism.

Analysis of recent structural data does not give a clear explanation for kinetic differences among E3 homologs because active sites between homologs are conserved (54). However, there do not appear to be definitive structures of the four-electron-reduced state (S₄), which may reveal more information on regulatory differences. Structure-based kinetic predictions have shown that accounting for molecular fields such as the electrostatic potential is imperative for accurate prediction of simple steady-state kinetic parameters (55). E3s from various sources have been shown to vary in redox potential (see Table 2 of Argyrou et al. (33)). These variations in redox potential are consistent with differences in active-site electrostatic potentials, which then may explain some of the observed kinetic discrepancies.

Best-fit parameters and local sensitivity coefficients for each of the data sets are shown in Table 1. For more complicated data sets, such as E. coli and spinach, parameter values are given for additional K_d(s) that represent different enzyme redox states, as described above. In our attempts to fit each data set, we collected ∼100 fits from random starting points that fell within a certain cost function cutoff value (fval) with respect to the best fit (Figs. S1, S6, S9, and S13). The results for this trial typically show that a wide range of parameter values can fit these data sets, so the values shown in Table 1 are not well bounded by the data sets. Low confidence is expected for rate constants as compared to equilibrium dissociation constants, since the data used to fit the model are of the steady-state type and little information is available on the time dependency of enzyme states (56); however, rate constants can be calculated for certain simple mechanisms (32, 36, 37).

Table 1.

Best-fit examples of kinetic parameters for dihydrolipoamide dehydrogenase from various organisms

Parametera	Rat liver enzyme		Human liver enzyme		E. coli enzyme			Spinach enzyme
Single Kd set	Sensitivityb	Single Kd set	Sensitivityb	Single Kd set	Multiple Kd set	Sensitivityb	Single Kd set	Multiple Kd set	Sensitivityb
k1 (min−1)c	4.05 × 104	—	1.26 × 107	—	1.11 × 109	—	—	2.78 × 107	—	—
k2 (min−1)	294	0.183	9.91 × 104	0.349	2.76 × 104	2.52 × 104	0.393 (0.727)	3.17 × 106	1.95 × 105	0.308 (1.04)
k3 (min−1)	2.56 × 104	0.103	1.06 × 104	0.176	1.32 × 104	9.76 × 104	0.0518 (0.138)	103	106	0.184 (0.135)
k4 (min−1)	107	0.127	8.64 × 105	0.186	1.25 × 106	2.38 × 106	0.0905 (0.111)	6.33 × 103	5.86 × 103	0.255 (0.294)
k5 (min−1)c	1.22 × 104	—	1.15 × 10−5	—	2.49 × 106	—	—	3.42 × 105	—	—
k6 (min−1)	5.56 × 103	0.538	10−3	8.62 × 10−4	70.2	581	0.218 (0.2)	103	1.47 × 103	0.670 (0.128)
k7 (min−1)	1.33 × 105	0.236	4.97 × 106	0.0212	1.21 × 105	1.52 × 106	0.430 (0.676)	2.60 × 104	3.85 × 103	0.520 (0.901)
k8 (min−1)	8.30 × 105	0.371	3.69 × 104	0.0213	107	8 × 106	0.389 (0.696)	6.43 × 106	5.0 × 104	0.487 (0.950)
pKh1 (thiolate)	6.98	0.044	7.32	0.349	7.5	7.34	0.399 (0.566)	5.67	4	0.297 (0.01)
pKh2 (base)	9	0.042	9	0.0281	8.56	8.85	0.193 (0.14)	9	8.9	0.030 (0.017)
KA1 (μM)	920	0.307	2.5 × 103	1.15 × 10−4	104	104	10−3 (1.2 × 10−17)	155	4.88	0.040 (6.4 × 10−18)
KB1 (μM)	1.74 × 103	0.388	1.1	0.177	498	498	0.439 (5.6 × 10−3)	2.70	2.55	0.361 (0.163)
KP1 (μM)	758	0.657	1.15	0.002	3.44	3.44	0.01 (5.6 × 10−18)	3.26	33.3	0.0393 (6.4 × 10−18)
KQ1 (μM)	1.24 × 103	0.487	70.5	0.18	520	520	0.370 (0.11)	3.55	1	0.338 (0.166)
KA2,3 (μM)	—	—	—	—	—	55.6	9.9 × 10−4	—	5.05 × 103	0.0105
KB2,3 (μM)	—	—	—	—	—	1.04 × 103	0.115	—	26.2	0.0701
KP2,3 (μM)	—	—	—	—	—	1.67	0.254	—	19.6	0.0320
KQ2,3 (μM)	—	—	—	—	—	429	0.604	—	1	0.0654
KA4 (μM)	—	—	—	—	—	1.58	0.125	—	1	0.0610
KB4 (μM)	—	—	—	—	—	230	0.683	—	26.6	0.380
KP4(μM)	—	—	—	—	—	2.8 × 103	0.276	—	104	0.111
KQ4 (μM)	—	—	—	—	—	1.63	0.680	—	104	0.0028
Keq (pH 7)	0.206d	0.734	0.0418	0.0696	0.153	0.103	0.168 (0.667)	0.0383	0.0446	0.302 (0.115)

^aRate constants were constrained within the range 10⁻³ to 10⁹ min⁻¹ and equilibrium dissociation constants within the range 1 to 10⁴μM. pKh1 and 2 were generally in the range between 4 and 9.

^bSensitivities were calculated according to a previously described method (35); sensitivities in parentheses correspond to multiple K_d fits.

^cParameter was solved for based on thermodynamic cycle constraints.

^dRat liver enzyme data were collected at 37°C (22); thus, the equilibrium constant for these data was allowed to vary more from its known value at 25°C compared to the other data sets, which were collected at 25°C.

To analyze correlations between parameters, we constructed scatter plots of each parameter pair from the independently estimated set of parameter values. For the redox-independent K_d model, this exercise yields 105 different combinations of parameters (Figs. S2, S7, S10, and S14). This analysis explicitly shows linear and nonlinear relationships for each of the E3 parameter sets. Of the 127 fits to the rat liver E3 data set, three distinct parameter families were identified (Table S1). Since the estimates cluster into these three families, it is difficult to identify trends in the parameter scatter plots for the rat liver E3 parameter sets (Fig. S2). To better analyze correlations between rat liver E3 parameter sets, we computed correlation matrices (Fig. S3) for the average of three families of parameters that describes the overall parameter set (Table S1). These matrices demonstrate mostly moderate parameter correlation (average coefficients of 0.6 or −0.6 or less). In general, correlation was seen between parameters comprising the same mechanistic loop, such as k1 through k4, and between substrate and product equilibrium dissociation constants.

Despite variability and correlation in the parameters, the mean steady-state distributions of the enzyme redox states (Figs. 6 and 7) represent more stable pieces of information that can be extracted from these data. These distributions were calculated from all of the parameter sets we found that fit the data (see Supporting Material). Parameter values that change within a wide range but still fit the data in a similar way (see Supporting Material) still produce similar steady-state distributions of the different redox enzyme states. This is indicated by a low percent coefficient of variation for enzyme states that represent >80% of the total enzyme concentration (Fig. S16). We also intuit that fitting larger data sets that contain more information leads to less variable predictions of enzyme redox steady-state distributions (Fig. S16).

A major goal of our kinetic analysis was to constrain the fitting using a known value (0.0766) for the overall equilibrium constant at 25°C and pH 7 (2). We allowed this value to vary within a small range to account for differences in ionic strength and midpoint potential uncertainties. For example, a change of 1.5% in the midpoint potentials results in a twofold change in the equilibrium constant. To maintain a more consistent overall equilibrium constraint for all data sets collected at 25°C, which include the E. coli, spinach, and human liver data sets, we showed that we can fit these data sets within the narrow range of 0.0383 to 0.05 (Table 1). Although values of 0.153 and 0.103 are shown in Table 1 for the E. coli best-fit examples of the redox-independent (single K_d) and redox-dependent (multiple K_d) models, respectively, further fitting and constraining of the equilibrium constant shows that these data can be well fitted with values of 0.05 and 0.048 for each of these respective models (Fig. S5).

Definitions of steady-state constants in terms of rate and equilibrium dissociation constants were also derived using their typical mathematical definitions (32). The most widely used method for deriving steady-state constants as functions of microscopic rate constants and equilibrium dissociation constants for enzymatic reaction mechanisms is that of Cleland (36, 37). However, discussion of this method has not been extended to include complex reaction mechanisms that create numerous high-order terms in the denominator of the flux expression (see Eq. 5) (37). Typically, when this situation is confronted, attempts are not made to define steady-state constants (37).

Despite this, to further analyze our mechanism, we used MATLAB (2011b) Symbolic Math Toolbox to derive the steady-state-constant definitions in a manner similar to that of Straathof et al. (38). The MATLAB code for this procedure is provided in the Supporting Material. Steady-state parameters for the redox-independent K_d mechanism were calculated for rat liver, E. coli, spinach, and human liver E3 using all of approximately 100 parameter sets that fit each dataset (Figs. S3, S7, S10, and S14). The steady-state parameters are a function of pH, and they can vary substantially when there is a large parameter range that fits the data (Figs. S4, S8, S11, and S15). The calculated steady-state parameters for the rat liver (Fig. S4) and E. coli (Fig. S8) E3 parameter sets were less variable than the spinach (Fig. S11) and human liver (Fig. S15) E3 parameter sets. For the rat liver data, this is probably due to the fact that the data can be fit by three distinct families of parameters (Table S1). In addition, the experiments conducted with rat liver E3 contain more information on these parameters since they assay a wider range of substrate and product concentrations.

In general, the calculated reverse k_cat is low relative to the typical k_obs or v₀/E_t (Figs. S4, S8, S11, and S15). This is because k_cat is defined in the limit of substrates approaching infinity and is not a true maximum in flux (32). Since substrate inhibition is observed with NADH (Fig. 3 D), as the NADH concentration approaches infinity the catalytic rate is partially inhibited (36)); this issue has been pointed out previously with regard to E3 (57). Optimization of the flux expression to obtain an actual flux maximum may be a more appropriate and possibly a more physiologically relevant enzyme kinetic analysis.

Conclusions

Several independent kinetic sets of data on the E3 component from various organisms, including rat, E. coli, spinach, and human, were globally fitted to a pH-dependent model that accounts for a well-documented description of the active-site chemistry found in the literature. This model is able to reproduce a number of unique characteristics of the kinetic data sets, including NAD⁺-dependent pH optima, NAD⁺/NADH-dependent activation/inhibition, and NAD⁺/pH-dependent progress-curve lags. Although it is consistent with previous hypotheses that an over-reduced four-electron dead-end state is responsible for the unique regulation of this enzyme, the model now provides a quantitative means of simulating this behavior spanning three kingdoms of life.

The model incorporates active-site proton binding sites, such as an active-site base and thiolate, that are critical for pH regulation of its catalytic mechanism, and it provides a template for integrating these general features into other FAD-containing disulfide oxidoreductase enzymes (19, 26, 30). The model accounts for the possibility of the effect of redox-dependent binding of substrates and products to more accurately account for redox-related phenomena not well captured by simpler mechanisms. Moreover, NAD⁺/NADH-dependent enzymes are ubiquitous in redox metabolism and will be affected by pH in a similar manner. Therefore, to support efforts to model other enzymes, ranging from disulfide oxidoreductases to NAD⁺/NADH-dependent enzymes, we have supplied the model code in the Supporting Material. General MATLAB code has also been supplied in the Supporting Material for handling the derivation of steady-state constants for bi-bi reaction mechanisms (and easily adaptable to others).

Here, we also provide to our knowledge, a novel and rigorous demonstration that shows although the set of parameters that fit the data is large, all parameters predict similar enzyme redox steady-state distributions. This demonstration is to our knowledge unprecedented. Furthermore, this distribution calculation provides useful information that is not typically gleaned from steady-state-type data. Here we have used a range of what could be physiological or pathophysiological conditions to calculate steady-state redox enzyme distributions to predict the redox state of E3 during potential in vivo conditions. Therefore, in vitro quantitative knowledge of enzyme behavior and mechanism can be used to better quantitatively understand more elusive in vivo metabolic states.

Moreover, E3 is a component of the PDH complex, providing a layer of its regulation by sensing changes in the NAD⁺/NADH ratio, which in turn imparts regulation of central metabolism (6, 9, 14). Therefore, we look to incorporate this accurate E3 model into a larger multicomponent model of the PDH complex that will in turn provide better predictions of NAD ratio and pH effects on PDH-complex kinetic regulation. A detailed kinetic model of PDH-complex regulation that accounts for its individual components will yield a better quantitative understanding of the kinetic regulation of central metabolism.

Editor: Stanislav Shvartsman.