Capturing Transition Paths and Transition States for Conformational Rearrangements in the Ribosome

Abstract

To reveal the molecular determinants of biological function, one seeks to characterize the interactions that are formed in conformational and chemical transition states. In other words, what interactions govern the molecule’s energy landscape? To accomplish this, it is necessary to determine which degrees of freedom can unambiguously identify each transition state. Here, we perform simulations of large-scale aminoacyl-transfer RNA (aa-tRNA) rearrangements during accommodation on the ribosome and project the dynamics along experimentally accessible atomic distances. From this analysis, we obtain evidence for which coordinates capture the correct number of barrier-crossing events and accurately indicate when the aa-tRNA is on a transition path. Although a commonly used coordinate in single-molecule experiments performs poorly, this study implicates alternative coordinates along which rearrangements are accurately described as diffusive movements across a one-dimensional free-energy profile. From this, we provide the theoretical foundation required for single-molecule techniques to uncover the energy landscape governing aa-tRNA selection by the ribosome.

Introduction

During biological functioning, molecular assemblies interconvert between energetically competing configurations where the kinetics are determined by the relative stabilities of the endpoints and the scale of the intervening free-energy barriers. Thus, quantifying the energetic and structural content of the transition state ensembles (TSEs) is central to understanding the mechanisms that govern biological regulation. This has long been recognized in the area of protein dynamics, where decades of theoretical and experimental efforts have aimed to describe the underlying energy landscapes associated with folding, binding, and conformational rearrangements (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13). These studies have provided the field of biophysics with a rich set of general methods that are grounded in statistical mechanics, which may now be applied to quantitatively probe a wide range of biological processes. Accordingly, here, we have adopted these tools to elucidate the character of the energy landscapes associated with conformational transitions in the ribosome (Fig. 1).

Figure 1.

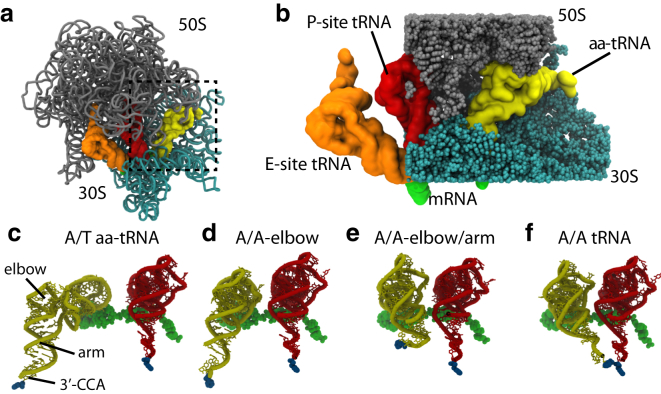
Structural description of accommodation. (a) The large subunit rRNA (gray) and small subunit rRNA (cyan) are shown in cartoon representation, with the aa-tRNA (yellow), P-site tRNA (red), and E-site tRNA (orange) shown in surface representation. (Green) mRNA. (Dashed box) Accommodation corridor. (b) Close-up perspective of the A/T (preaccommodation) configuration of aa-tRNA; (spheres) accommodation corridor atoms (rRNA and ribosomal proteins). (c) aa-tRNA and P-site tRNA shown in the A/T configuration. View rotated relative to panel b. (c–f) During aa-tRNA accommodation, the incoming amino acid is delivered to the PTC. Previous theoretical and experimental studies have implicated a multistep accommodation process, where intermediate elbow-accommodated (d) and arm-accommodated (e) configurations are transiently populated. In this study, we probe elbow accommodation, because it is monitored by single-molecule methods.

The ribosome is a large (2.4 MDa) RNA-protein assembly, and it is the sole producer of proteins in the cell. To translate messenger RNA (mRNA) sequences into protein sequences, each aminoacyl-transfer RNA (aa-tRNA) molecule is delivered to the ribosome by the prokaryotic EF-Tu (i.e., elongation factor-thermo unstable), after which it may add an amino acid to the growing protein chain. During initial association of the ternary complex (aa-tRNA⋅EF-Tu⋅GTP), codon-anticodon interactions are formed between the aa-tRNA and mRNA. Through thermodynamic discrimination alone, correct (cognate) aa-tRNA molecules can be selected over incorrect (near/noncognate) ones by a factor of ∼100. However, the fidelity of aa-tRNA selection is roughly 1:3000 to 1:10,000, thus implicating the presence of a subsequent free-energy barrier that serves as a proofreading step (14).

The putative conformational change responsible for proofreading is known as aa-tRNA accommodation (15), where the incoming amino acid is displaced ≈100 Å from the periphery of the ribosome to the peptidyltransferase center (Fig. 1). The biological significance of this process has motivated many investigations with cryo-electron microscopy (16, 17), x-ray crystallography (18, 19), biochemical kinetic techniques (20, 21), single-molecule methods (22, 23), simulations (24, 25), and bioinformatics (26, 27). These studies have elucidated the structural content of the endpoints and overall rates of interconversion, and have provided qualitative descriptions of accessible pathways. Despite this progress, it is still unclear precisely where the TSE is that governs the dynamics of accommodation, and what coordinates most accurately describe it. By addressing these points, experimental approaches will be able to more precisely probe the physical-chemical interactions that govern this biological process.

With an energy landscape perspective, one may systematically describe the structural and energetic characteristics of the TSEs associated with ribosomal conformational transitions. However, to do so, one should first ask:

• 1.When is it appropriate to describe aa-tRNA movement as diffusion across an energy landscape?
• 2.Which coordinates most accurately describe movement along the dominant (i.e., lowest free-energy) pathway/s?

One way to answer these questions is to analyze the properties of the transition paths associated with each rearrangement. In the diffusive regime, the dynamics is Markovian and configurations in the TSE are equally likely to continue to the product or reactant states. Quantitatively, this may be phrased as: The conditional probability of being on a transition path (TP), expressed as $P\left(TP|\overrightarrow{x}\right)$ (where $\overrightarrow{x}$ is the configuration of the system in the full phase space), is equal to 0.5 for configurations that are in the TSE. While biological dynamics are described in the full 6N-dimensional phase space (coordinates and velocities), when an appropriate set of reaction coordinates {ρ_i} is chosen, P(TP|{ρ_i}) will also be equal to 0.5 for configurations in the TSE. Reducing the dimensionality is often advantageous/required in experimentation and computation. In single-molecule experiments, it is necessary to have accurate low-dimensional representations, because it is only possible to probe a small number of degrees of freedom simultaneously (22, 28, 29, 30, 31).

From a theoretical perspective, the choice of a particular coordinate can allow for a more intuitive description to emerge, where common low-dimensional projections are based on atomic distances (7, 32, 33, 34) or collective variables (35, 36, 37, 38, 39, 40, 41, 42, 43). Regardless of the technique, it is important that the true dynamics are not masked when projected onto a specific coordinate. To determine whether there is an experimentally accessible one-dimensional coordinate that captures the essential features of aa-tRNA accommodation, we use long molecular dynamics simulations of aa-tRNA accommodation movement, and from them calculate P(TP|ρ), i.e., the conditional probability of being on a transition path as a function of each reaction coordinate ρ. As already mentioned, when a coordinate accurately measures movement over the free-energy barrier, P(TP|ρ) will reach a peak value of 0.5 (44, 45). Accordingly, we have used P(TP|ρ) as an unbiased metric to measure each coordinate’s ability to accurately capture barrier-crossing events, while also pinpointing the location of the TSE. From this analysis, we have identified numerous coordinates that can be used in experiments or simulations to more precisely characterize the free-energy landscape of aa-tRNA accommodation.

Materials and Methods

Energy function

We simulated the movement of aa-tRNA elbow accommodation using an all-atom structure-based SMOG model (46, 47). All nonhydrogen atoms were explicitly represented, and the A/A configuration (PDB:3I8F (48)) was defined as the global potential energy minimum, similar to our earlier simulations of the ribosome (25). Input files for the model were generated using the SMOG-SERVER.ORG webtool (47). For completeness, we provide a detailed description of the energy function used here, including all parameters necessary to reproduce the model. All calculations employed reduced units, where each atom is represented as a single bead of unit mass. The covalent geometry is maintained through harmonic interactions that maintain bond lengths, bond angles, improper dihedral angles, and planar dihedral angles. Nonbonded atom pairs that are in contact in the native configuration (in this case, the A/A configuration) between residues i and j, where i > j + 3 for proteins and i ≠ j for RNA, are given a 6-12 potential, where the minimum corresponds to the distance in the A/A configuration. All other nonlocal interactions between atoms that do not interact through bonded terms are repulsive. Contacts were defined according to a 4 Å cutoff criterion (49). The functional form of the potential is

$$V=\sum _{\text{bonds}}{ϵ}_r{\left(r_i-r_{i,o}\right)}^2+\sum _{\text{angles}}{ϵ}_{\theta }{\left({\theta }_i-{\theta }_{i,o}\right)}^2+\sum _{\text{impropers}}{ϵ}_{{\chi }_{\text{imp}}}{\left({\chi }_i-{\chi }_{i,o}\right)}^2+\sum _{\text{planar}}{ϵ}_{{\chi }_{\text{planar}}}{\left({\chi }_i-{\chi }_{i,o}\right)}^2+\sum _{\text{backbone}}{ϵ}_{BB}{F}_D\left({\varphi }_i\right)+\sum _{\text{side}\text{chains}}{ϵ}_{SC}{F}_D\left({\varphi }_i\right)+\sum _{\text{contacts}}{ϵ}_C\left[{\left(\frac{{\sigma }_{ij}}{r}\right)}^{12}-2{\left(\frac{{\sigma }_{ij}}{r}\right)}^6\right]+\sum _{\text{noncontacts}}{ϵ}_{NC}{\left(\frac{{\sigma }_{NC}}{r_{ij}}\right)}^{12},$$ (1)

where

$$F_D\left(\varphi \right)=\left[1-\text{cos}\left({\varphi }_i-{\varphi }_{i,o}\right)\right]+1/2\left[1-\text{cos}\left(3\left({\varphi }_i-{\varphi }_{i,o}\right)\right)\right]$$ (2)

and

$${ϵ}_r=50{ϵ}_0,{ϵ}_{\theta }=40{ϵ}_0,{ϵ}_{{\chi }_{\text{imp}}}=10{ϵ}_0,{ϵ}_{{\chi }_{\text{planar}}}=40{ϵ}_0,\text{and}{ϵ}_{NC}=0.1{ϵ}_0$$

(ϵ₀ = 1 for all calculations).

$$r_{i,o},{\theta }_{i,o},{\chi }_{i,o},{\varphi }_{i,o},\text{and}{\sigma }_{i,j}$$

are given the values found in the native state, σ_NC = 2.5 Å. To assign dihedral interaction weights, dihedrals are first grouped if they share a common middle bond. In a protein backbone, there are up to four dihedral angles that possess the same C – C_α bond as the middle bond. Each dihedral group is given a summed weight of ϵ_BB or ϵ_SC. R_BB/SC was defined as ϵ_BB/ϵ_SC and was set to 1 for nucleic acid dihedrals and 2 for protein dihedrals. The weights of protein and nucleic acid backbone dihedrals were set to be equal. Finally, dihedral strengths and contact strengths were scaled such that the ratio of total contact energy to total dihedral energy is

$$R_{C/D}=\frac{\sum {ϵ}_C}{\sum {ϵ}_{BB}+\sum {ϵ}_{SC}}=2,$$

and the total stabilizing energy is

$$\sum {ϵ}_C+\sum {ϵ}_{BB}+\sum {ϵ}_{SC}=N{ϵ}_0,$$

where N is the number of atoms in the system.

After generating the default structure-based model, there was one atypical modification that was necessary to obtain sufficient statistics of elbow-accommodation events. Specifically, intermolecular contacts in the A/A configuration between aa-tRNA and the ribosome (rRNA and proteins) were rescaled by a factor of F_A/A. The precise value of F_A/A was determined phenomenologically. That is, single-molecule experiments indicate that the aa-tRNA elbow undergoes reversible fluctuations between A/T and A/A-like configurations before full aa-tRNA entry into the ribosome (23).

To describe these fluctuations, multiple values of F_A/A < 1.0 were employed in shorter trajectories to identify a value for which reversible fluctuations were observed in the simulation. Using a factor F_A/A < 1 can be interpreted in terms of effective energetics. Specifically, structure-based models define the crystal structure as the lowest effective-energy configuration, based on the observation that the crystallized structure necessarily represents a stable configuration of the complex. However, because tRNA molecules only transiently associate with the ribosome and undergo rearrangements between binding sites, the tRNA-ribosome interactions are effectively less stable than interactions that maintain the secondary and tertiary structures of the ribosome. By rescaling tRNA-ribosome interactions by a factor of F_A/A < 1, our model mimics this difference in effective stabilities.

Simulation details and boundary conditions

By using modified weights for the bond angle and bond lengths, relative to our earlier implementation of the model (46, 47), we were able to use a timestep of 0.002 (reduced units) to be used without the introduction of numerical artifacts, whereas earlier simulations employed a timestep of 0.0005. Control simulations were performed for small proteins to ensure that the dynamics are not sensitive to these modifications. To reduce computational demand, only atoms near the accommodation corridor were included in each calculation. To avoid the introduction of boundary effects, isotropic spatial harmonic restraints were imposed on each atom i possessing native interactions with atoms in the full ribosome which were not included in the truncated system. The value of the restraint on each atom k_i was iteratively tuned until the mean-squared fluctuations of each atom i in the truncated system was consistent with the values obtained from simulations of a complete ribosome (see the Supporting Material for details). Each simulation was performed using the GROMACS Ver. 4.6.1 software package (50, 51), and constant temperature was maintained through the use of Langevin dynamics protocols. Each simulation was performed using 128 computer cores of the Texas Advanced Computing Center STAMPEDE Cluster and the Northeastern University Discovery Cluster.

To test the robustness of the analysis of reaction coordinates, we performed two independent simulations at different temperatures (0.42 and 0.5, in reduced units). Earlier calculations showed that the scale of atomic fluctuations at these temperatures are consistent with fluctuations observed in all-atom explicit-solvent simulations (25). Because there is a decrease in configurational entropy as the aa-tRNA accommodates, increasing the temperature stabilizes the A/T ensemble in our model, relative to the A/A ensemble. To compensate for this and ensure that the A/A and A/T ensembles have comparable free energies, F_A/A was larger for the higher-temperature simulation. For the lower-temperature simulation (T = 0.42), F_A/A was set to 0.25, and 2 × 10¹⁰ timesteps were simulated (95 barrier crossing events). For the higher temperature simulation (T = 0.5), F_A/A was set to 0.375, and 1.5 × 10¹⁰ timesteps were simulated (38 barrier crossing events). All analysis was performed for both parameter-temperature sets, which showed robustness of the results.

Results

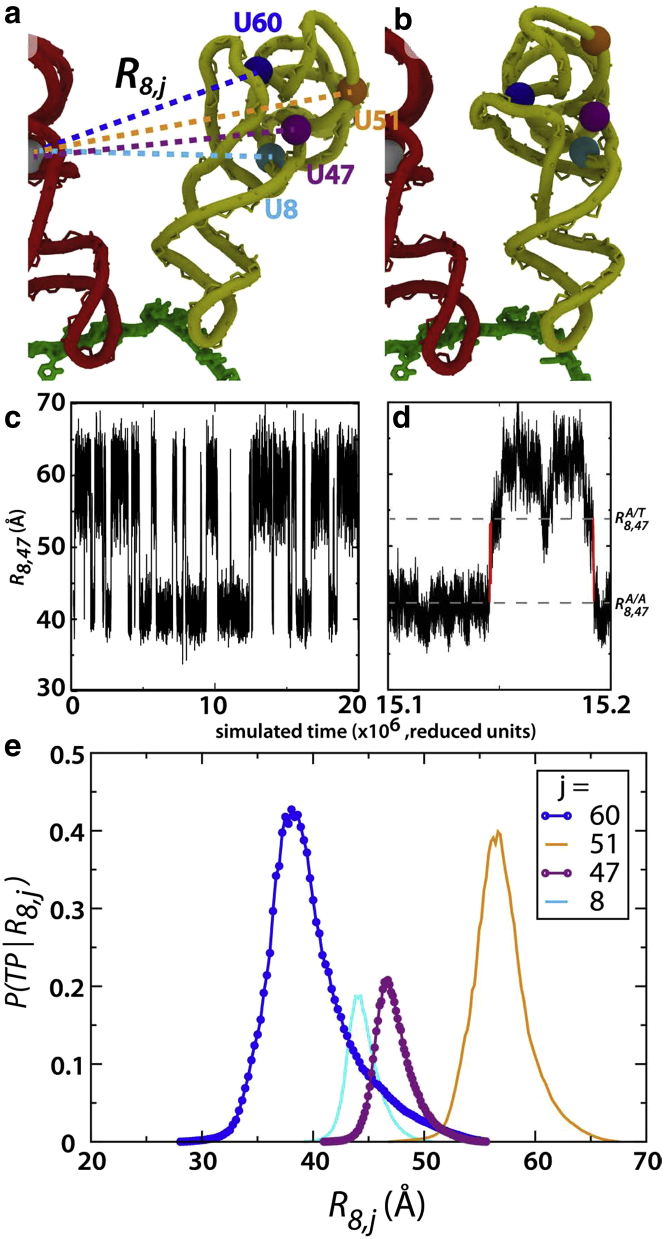
Using an all-atom structure-based model (46, 47) of the ribosome in complex with aa-tRNA^Phe, we simulated the first step of aa-tRNA accommodation (Fig. 1) and generated a trajectory with ≈100 spontaneous barrier crossing events. To identify whether any atom-atom distances R_i,j accurately capture the accommodation TSE, we calculated the probability of being on a transition path P(TP|R_i,j) for a wide range of atom pairs i,j (Fig. 2). We focused on distances between Uracil residues because these residues are often accessible for labeling with Förster resonance energy transfer (FRET) dyes.

Figure 2.

Different atomic distances R_i,j capture the transition state with varied accuracy. (a) The A/T configuration of the aa-tRNA, shown with four Uracil residues (spheres). Several R_i,j distances, where i is the P-site tRNA residue index ( $=$ 8) and j is the aa-tRNA residue index (dotted lines). The O3′ of U8 on the P-site tRNA (white sphere). (b) The elbow-accommodated configuration, shown with the same representation as panel a. By comparing the dynamics projected along different coordinates R_i,j, one may assess the ability of each to capture the transition state associated with aa-tRNA elbow accommodation. (c) R_8,47, which is monitored in our smFRET studies, is shown as a function of time for one-half of the simulated trajectory. There is a visible distinction between the A/T (R_8,47 ≈ 60 Å) and elbow-accommodated (R_8,47 ≈ 40 Å) ensembles, where transitions appear to be two-state in character. (d) Same as panel c, with the timescale dilated. (Dashed lines) $R_{\mathrm{8,47}}^{A/T}$ and $R_{\mathrm{8,47}}^{A/A}$. Two transition paths (red), as identified with R_8,47. (e) The conditional probability of being on a transition path as a function of each interatomic distance, P(TP|R_i,j), is shown for distances between U8 of the P-site tRNA and different aa-tRNA residues j. Of the 169 coordinates studied, R_8,60 most precisely captures transition paths and performs significantly better than the experimentally employed coordinate R_8,47. While P(TP|R_8,47) reaches a maximum value $P_{\text{max}}^{TP}$ of only 0.2, P(TP|R_8,60) exceeds 0.4 (blue).

Before discussing the results, it is valuable to first consider the energetic model that serves as a foundation for the simulations. In this study, all nonhydrogen atoms are explicitly represented, and the potential energy landscape has a global minimum corresponding to the A/A configuration (i.e., the endpoint of accommodation; Fig. 1). Because the global minimum is assigned based on a crystallographic structure, the models are commonly referred to as “structure-based energy functions” (52). In this model, electrostatics and solvation effects are implicitly accounted for, insofar as the stabilizing interactions in the model describe the effective atomic interactions after averaging over all interactions that stabilize the A/A configuration.

This effective description is consistent with the observation that the crystallographic structure represents a stable configuration (i.e., free-energy minimum) on the ribosome’s landscape, allowing the tRNA to act as a molecular spring (53) that accumulates and releases strain energy during the elongation cycle. Because our model does not include nonspecific energetic roughness, the primary contributors to the simulated dynamics are molecular flexibility and steric effects. As described below, these two properties are sufficient to ensure that there is a single dominant sequence of events during accommodation. In addition, because the representation of sterics and flexibility is consistent between this model and all-atom explicit-solvent simulations (see the Supporting Material of Whitford et al. (25)), this model provides an overall description that is consistent with more computationally demanding methods.

Using an all-atom structure-based (SMOG (46, 47)) model, our earlier simulations of the ribosome found a specific ordering of conformational events during aa-tRNA accommodation (25), and the A/A-ensemble was only marginally more stable than the A/T ensemble. Both features are supported by observations from experimentation, as described below. Although the model describes the potential energy as having a global minimum at the A/A (aa-tRNA accommodated) configuration, steric and entropic contributions give rise to distinct free-energy barriers. By characterizing the dynamics for a range of parameters, it was shown that the ordering of conformational events is model-independent and follows a specific sequence (Fig. 1):

• 1.aa-tRNA elbow accommodation,
• 2.aa-tRNA arm accommodation, and
• 3.3′-CCA entry into the peptidyltransferase center (PTC).

This ordering was also observed in simulations that employed targeted MD protocols with an explicit-solvent force field (24). Physically, the late entry of the 3′-CCA tail can be understood as being the result of molecular flexibility. Specifically, as the 3′-CCA tail enters the ribosome, a large decrease in configurational entropy serves as a penalizing factor that delays entry of the tail. Consistent with the flexibility exhibited by this model, flexibility of the aa-tRNA 3′-CCA end has been noted in crystallographic studies, where it has elevated B-factors (54) (or is not resolved (55)), and cryo-EM reconstructions typically have lower densities for the tail (56), suggesting conformational heterogeneity within each identified state. Evidence of sequential motion during accommodation also comes from single-molecule FRET experiments, where changes in the amino-acid composition impact elongation rates while having negligible impact on elbow movement (57). Other single-molecule (sm) FRET measurements suggest that the elbow-accommodated conformation is only slightly more stable than the A/T ensemble, which leads to reversible accommodation-like fluctuations of the elbow before incorporation of the amino acid (23), as also seen in simulations with the SMOG model. Together, these theoretical and experimental studies strongly implicate a sequential accommodation process that begins with elbow movement into the A site, consistent with the description provided by this simple model.

With evidence implicating a separation of aa-tRNA elbow and 3′-CCA accommodation, we will focus our attention on the former. One reason for doing so is that because smFRET experiments can monitor elbow displacements (23, 58, 59), insights from the presented analysis have immediate experimental utility. In contrast, we are unaware of single-molecule approaches that can directly monitor movement of the 3′-CCA end. An additional reason for first focusing on elbow movement is that simulations have shown there are at least three accessible routes for 3′-CCA entry into the PTC (25). Although it may be possible to extend the methods discussed here and construct collective coordinates that can distinguish between these routes, it is unclear how such coordinates would aid the design of more precise experiments.

In the following sections, we systematically compare the ability of 256 different atomic distances (R_i,j) to capture transition events associated with aa-tRNA elbow accommodation. By subjecting each coordinate to several tests, we identified 21 high-performing coordinates that may be explored using single-molecule methods. The following criteria were used as metrics to identify optimal coordinates:

• 1.The atomic distances in the A/T and elbow-accommodated configurations differ by at least 10 Å, which focuses the discussion on coordinates that are likely to yield detectable changes in FRET signal;
• 2.The number of transition paths is minimized (i.e., the number of false-positives is minimized);
• 3.P(TP|R_i,j) is maximized; and
• 4.Movement along R_i,j exhibits diffusive characteristics.

We will close the discussion by providing a brief structural description of the TSE, as identified by the optimal coordinate.

Identifying transition paths

The first criterion that we used to compare coordinates was that an optimal coordinate should maximally separate the endpoints (i.e., minimize the number of identified transitions N_T). For a poorly chosen coordinate, nonreactive (i.e., nonbarrier crossing) fluctuations may be perceived to be transitions between the endpoints. To detect these events, we use simulations to directly count the number of projected transitions along each coordinate. To monitor for barrier-crossing events, we first defined the endpoints by two reference configurations: 1), the A/T configuration (60), and 2), a structural model of an A/A-elbow configuration (Fig. 1). Each interatomic pair distance R_i,j (distance between the O3′ atom of residue i on the P-site tRNA and residue j of the aa-tRNA) was then calculated for the endpoint configurations ( $R_{i,j}^{A/T}$ and $R_{i,j}^{A/A}$ ). Next, we calculated the distance as a function of simulated time R_i,j(t).

A transition path (TP) was defined as having occurred when R_i,j(t) moved from $R_{i,j}^{A/T}$ to $R_{i,j}^{A/A}$ without recrossing $R_{i,j}^{A/T}$, or when it moved from $R_{i,j}^{A/A}$ to $R_{i,j}^{A/T}$ without recrossing $R_{i,j}^{A/A}$. It is important to note that the results presented below were not sensitive to minor (10–20%) changes in the endpoint distances used for TP analysis. To further confirm robustness of the results, we repeated the analysis for a second simulation, which was performed at a temperature that was elevated by 20%. Changing temperature significantly perturbs the free-energy landscape, because it alters the balance between energy and configurational entropy. Even though entropic changes have been implicated during accommodation (25), this major alteration to the simulation parameters did not lead to notable differences in our evaluation of coordinates.

The TP analysis was performed for distances between all inter-tRNA U-U pairs. With 16 U residues in each tRNA^Phe, 256 U-U distances were considered. Of these, $\left|R_{i,j}^{A/T}-R_{i,j}^{A/A}\right|>10$ Å for 169 pairs. For those, we calculated R_i,j(t), $R_{i,j}^{A/T}$, and $R_{i,j}^{A/A}$ to evaluate the number of transition paths detected with each. According to our analysis, 40 coordinates minimized the number of crossing events, with N_T = 95 (see Table S1 in the Supporting Material). To provide evidence that N_T = 95 represents the number of true barrier crossing events, and does not include false positives, we employed a more stringent measure of transitions that is based on all 169 coordinates.

Specifically, we counted the number of times that the tRNA transitioned from a configuration where $R_{i,j}\left(t\right)<R_{i,j}^{A/A}$ simultaneously for all 169 coordinates and then later adopted a configuration where $R_{i,j}\left(t\right)>R_{i,j}^{A/T}$ for all coordinates (reverse transitions were also counted). Using this strict definition of what constitutes a transition, which describes the collective movements of U residues that are present throughout the elbow and arm regions of the tRNA molecules (see Fig. S5 in the Supporting Material), we found N_T = 95, indicating that all 95 transition events apparent with R_8,60 are common to every coordinate.

Perhaps surprising is that despite its intuitive positioning, the residue pair commonly used in smFRET experiments (U8–U47 (23, 58, 59)) overestimated the N_T value by >10% (N_T = 107). Although one may argue that this casts doubts on the interpretation of earlier experiments, timescale considerations suggest it is unlikely that false positives would have resulted purely from the use of R_8,47 as a coordinate. Because single-molecule experiments provide measures that are averaged over finite time intervals (typically milliseconds), we performed TP analysis for time-averaged values of R_i,j(t). We averaged each R_i,j(t) over N = 2^m sampled frames (M = 1, 2,…,12) and recounted the number of apparent transitions. For R_8,60, N_T = 95 for M < 11 (see Fig. S4). For M ≥ 11, almost all coordinates capture <95 transitions, because this window is approaching the average dwell time of the endpoint ensembles.

Because there is a range of averaging windows for which N_T = 95, if experimentally accessible timescales are not far below the timescale of accommodation (1/k_acc), our analysis suggests false positives are unlikely to arise from the use of R_8,47. However, because quantitative methods are being developed that can remove features arising from instrumentation noise and time-averaging (61, 62), single-molecule methods may soon begin to probe timescales well below 1/k_acc, at which point artifacts arising from the use of less optimal coordinates are expected to significantly impact the measured statistics.

Isolating the transition state ensemble

To determine how well each coordinate can capture the TSE, we calculated the conditional probability of being on a transition path as a function of each coordinate P(TP|R_i,j), which may be related to the splitting probabilities ϕ_A(R_i,j) and ϕ_B(R_i,j) (44, 45). For a coordinate describing a transition between states A and B (with R_i,j values of $R_{i,j}^A$ and $R_{i,j}^B$ ), ϕ_B(R_i,j) is the probability that given a particular value of R_i,j, the system will reach $R_{i,j}^B$ before returning to $R_{i,j}^A$.

When the movement in the full phase space is Markovian and the coordinate accurately captures the underlying barrier, P(TP|R_i,j) = 2ϕ_A(R_i,j)ϕ_B(R_i,j). Then, at the TSE $\left(R_{i,j}\equiv R_{i,j}^{TSE}\right)$, ${\varphi }_B\left(R_{i,j}^{TSE}\right)={\varphi }_A\left(R_{i,j}^{TSE}\right)=0.5$, and $P\left(TP|R_{i,j}^{TSE}\right)=0.5$. When the coordinate does not accurately capture the TSE, nonreactive fluctuations can lead to reduced values of $P\left(TP|R_{i,j}^{TSE}\right)$. In protein folding studies this property has found significant utility, where maximizing $P\left(TP|R_{i,j}^{TSE}\right)$ has been used as a strategy for constructing collective reaction coordinates for coarse-grained models (45) and for all-atom explicit-solvent simulations (35, 63).

To determine the extent to which a coordinate can uniquely identify the TSE, we calculated P(TP|R_i,j) for each. We found that for 10 coordinates $P_{\text{max}}^{TP}>$ 0.4, whereas most others are relatively poor indicators of when the aa-tRNA is on a transition path, with P(TP|R_i,j) values <0.3. A striking observation is that out of the top 10 performing coordinates, eight measure the position of U60 in the aa-tRNA (R_i,60: i = 8, 16, 20, 45, 47, 50, 59, 60). In fact, only three different aa-tRNA residues (j) were implicated in the top 21 coordinates: U51, U59, and U60. This demonstrates that the choice of an appropriate coordinate is not arbitrary, and that results are strongly dependent upon which aa-tRNA residue is being monitored. In stark contrast, there was not a single P-site tRNA residue that consistently performed best. Although the most relevant coordinates are narrowly distributed across the aa-tRNA, there is more degeneracy in the choice of P-site tRNA residue. This finding is critical for the design of more accurate single-molecule experiments. Nonetheless, it is also rather intuitive, because accommodation is associated with movement of the aa-tRNA, and the P-site tRNA is treated as a point of reference.

The dependence of P(TP|R_i,j) on the choice of aa-tRNA residue being monitored is depicted in Fig. 2, which shows P(TP|R_8,j) for four different atomic distances involving U8 of the P-site tRNA. In Fig. 2, only the choice of the aa-tRNA residue is varied. As already noted, R_8,60 is a relatively accurate indicator of when aa-tRNA is on a transition path, where $P_{\text{max}}^{TP}=0.43$ (red). In contrast, movement along R_8,47 is a not a strong indicator of when the system is on a transition path, with $P_{\text{max}}^{TP}\approx 0.2$. Together, our analysis indicates that R_8,47 only overestimates the number of crossing events by 10%, making it a reasonable metric for discerning between the endpoints. However, although this allows R_8,47 to have utility in experiments, its low $P_{\text{max}}^{TP}$ value indicates that it is unlikely to provide precise information regarding the TSE. To resolve this limitation in the experiments, the presented analysis suggests that by labeling aa-tRNA at U60, observed signals will be more strongly correlated with barrier-crossing events.

Because experimental measurements provide time-averaged coordinates $\left({\overline{R}}_{i,j}\right)$, it is interesting to consider the impact of time averaging on the presented calculation of P(TP|R_i,j). We found that the peak value of $P\left(TP|{\overline{R}}_{i,j}\right)$ increases for all coordinates when time-averaging is employed, although this should not necessarily be interpreted as suggesting improved performance of a particular coordinate. That is, time-averaging can introduce memory into the projected dynamics. For example, consider a time-averaged coordinate $\overline{R}$ that initially adopts a value corresponding to state A, followed by a value corresponding to the TSE. In this case, if the time-averaging window is long relative to the timescale of an individual barrier crossing event (which is not to be confused with the mean first passage time), when a TSE value of $\overline{R}$ is observed, it is likely that within a single time window the molecule will have initially resided in state A and transited fully to state B. Under these conditions, the peak value of $P\left(TP|\overline{R}\right)$ may exceed 0.5. Unfortunately, when averaging over such long times, the dynamics along $\overline{R}$ will not be Markovian, making a diffusive description inappropriate. Nonetheless, we computed $P\left(TP|{\overline{R}}_{i,j}\right)$ for relatively short time intervals (N < 100) and found that the maximal value was always larger for ${\overline{R}}_{\mathrm{8,60}}$ than for ${\overline{R}}_{\mathrm{8,47}}$, consistent with our analysis of nonaveraged dynamics.

Diffusive versus subdiffusive dynamics at the TSE

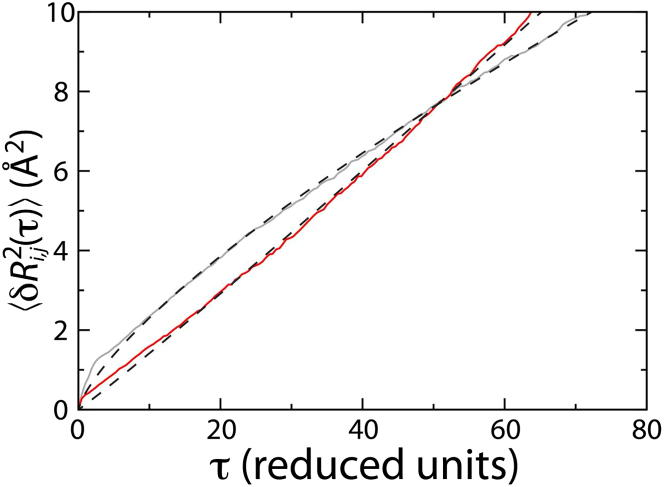
Analysis of P(TP|R_i,j) suggests that motion along some coordinates is likely to be diffusive at the TSE. To directly evaluate the degree to which motion is diffusive, we calculated the displacement squared as a function of the lag time $\langle \delta R_{i,j}^2\left(\tau \right)\rangle$ for each coordinate. To specifically characterize the TSE, we only included starting frames (i.e., τ = 0) for which $R_{i,j}\left(t\right)=R_{i,j}^{TSE}$. We fit each curve to R₀²τ^α, where the value of α indicates whether the motion is subdiffusive (< 1), diffusive (= 1), or superdiffusive (> 1). For R_8,47 (the coordinate measured in our smFRET experiments), we found a distinctly subdiffusive character, with α ≈ 0.75, which is consistent with the relatively low value of P(TP|R_8,47).

In contrast, when the dynamics was projected along R_8,60, α ≈ 1, providing further evidence of diffusive dynamics (Fig. 3). When α = 1, the diffusion coefficient D is given by $D=R_0^2/2$. Although there is a correlation between $P_{\text{max}}^{TP}$ and α (see Fig. S1), very few coordinates maximize both quantities. Further, some coordinates that do not minimize the number of transitions also have relatively high values of α and $P_{\text{max}}^{TP}$. By considering all three metrics (N_T, $P_{\text{max}}^{TP}$, and α), this analysis strongly supports R_8,60 as an appropriate coordinate for describing accommodation as diffusive movement across a one-dimensional free-energy barrier.

Figure 3.

The dynamics is diffusive along R_8,60 at the TSE. To assess the degree to which motion at the TSE is diffusive, the mean-squared displacement was calculated as a function of lag time 〈δR²_i,j(τ)〉 for R_8,47 (gray) and R_8,60 (red). Each curve was fit to R²₀τ^α (dashed lines). For R_8,47, the dynamics is subdiffusive, with α ≈ 0.75. In contrast, the dynamics along R_8,60 is diffusive (α ≈ 1), consistent with P(TP|R_8,60) approaching a value of 0.5 (see Fig. 2).

Kinetics and rate-limiting barriers

Because the projected dynamics along R_8,60 suggest it is an accurate indicator of when the aa-tRNA is on a transition path, and movement about the TSE is diffusive, we will use it to describe the kinetics of accommodation. Under these conditions, it is possible to interconvert between the free-energy profile G(ρ) and rate k according to (64)

$$1/k=\langle \tau \rangle =\underset{{\rho }_{A/T}}{\overset{{\rho }_{A/A}}{\int }}d\rho {\int }_{\infty }^{\rho }d{\rho }^{\text{′}}\frac{\text{exp}\left[\left(G\left(\rho \right)-G\left({\rho }^{\prime }\right)\right)/k_{\text{B}}T\right]}{D_{\rho }\left(\rho \right)},$$ (3)

where D_ρ(ρ) is the diffusion coefficient along ρ as a function of ρ and 〈τ〉 is the mean first passage time between points ρ_A/T and ρ_A/A. In our previous study of aa-tRNA diffusion during accommodation, we estimated the diffusion coefficient of the aa-tRNA elbow from explicit-solvent simulations (65). We then used Eq. 3 to infer a relationship between the rates and barriers, under the assumption that the employed coordinate was appropriate. In that study, R_8,47 was measured. Because we now see that R_8,47 performs more poorly than R_8,60, we can illustrate the strength of R_8,60 by comparing the projected free-energy profiles and observed mean first passage time. From Eq. 3, we calculated the mean first passage time $\langle {\tau }_{i,j}^{\text{calc}}\rangle$ using the free energy and diffusion coefficient along R_8,60. For this calculation D_ρ was assumed constant and the value obtained for the TSE was used, because the value at the TSE provides the largest contribution to the integral. For an appropriately chosen coordinate, $\langle {\tau }_{i,j}^{\text{calc}}\rangle$ will be consistent with the observed time for interconversion between states: 〈τ^obs〉. We find that R_8,60 provides an accurate description of the overall rate with

$$\frac{\langle {\tau }_{8\text{,}60}^{\text{calc}}\rangle }{\langle {\tau }^{\text{obs}}\rangle }\approx 0.5-1,$$

further supporting its use when describing aa-tRNA accommodation.

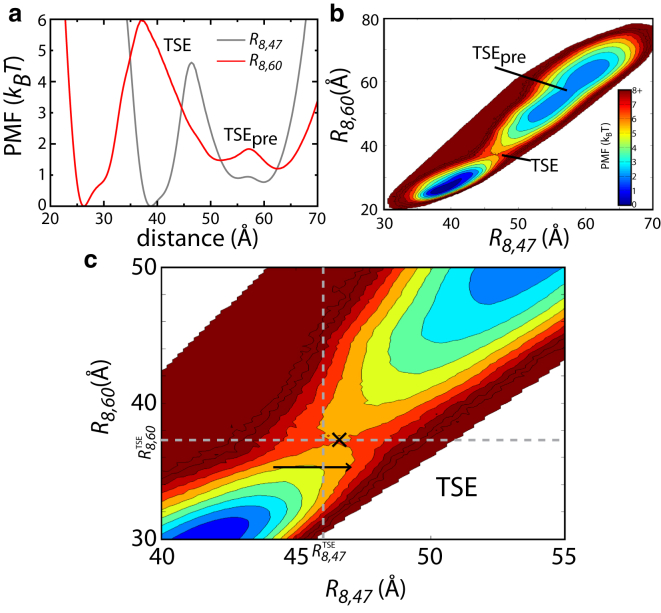
Differences between the projections along each coordinate, including reduced values of P(TP|R_8,47) and subdiffusive dynamics along R_8,47, can be further rationalized by plotting the two-dimensional potential of mean force: PMF (R_8,47, R_8,60) (Fig. 4). In the PMF, there is a visible separation of the basins along R_8,60 at the TSE ($R_{\mathrm{8,60}}^{TSE}=37.3$ Å). When the aa-tRNA adopts the value of R_8,47 that corresponds to the TSE ($R_{\mathrm{8,47}}^{TSE}=46.5$ Å), the tRNA is not necessarily at a saddle point on the free-energy surface, but it may be in either of the endpoint basins (A/T, or accommodated elbow basins). As already discussed, this leads to an underestimate of the free energy when projected along R_8,47, as compared to R_8,60. To further illustrate this, the values of $R_{\mathrm{8,60}}^{TSE}$ and $R_{\mathrm{8,47}}^{TSE}$ are indicated by dotted lines in Fig. 4 c. The $R_{\mathrm{8,47}}^{TSE}$ line visibly intersects the endpoint basins, where the lowest free-energy points along $R_{\mathrm{8,47}}^{TSE}$ correspond to the endpoint basins. In contrast, $R_{\mathrm{8,60}}=R_{\mathrm{8,60}}^{TSE}$ visibly separates the basins and the lowest free-energy point along the line (at R_8,47 ≈ 46.7 Å) corresponds to a saddle point on the surface, consistent with it being a free-energy TSE.

Figure 4.

The projected free-energy barrier is larger when a more appropriate coordinate is used. (a) The PMF, or free energy, as a function of R_8,47 (gray) and R_8,60 (red). The accommodation-related TSE is indicated. Interestingly, there is an additional TSE (TSE_pre) that is apparent in the PMF, although it falls outside the bounds of the A/T and A/A configurations, and it therefore does not impact the presented analysis. (b) The PMF plotted against both coordinates. (c) Zoomed-in perspective of panel b. (Dotted lines) Positions of the maximum free energy $R_{8,j}^{\text{TSE}}$ when plotted against each coordinate individually, as shown in panel a. Here, $R_{\mathrm{8,60}}^{TSE}=37.3$ Å and $R_{\mathrm{8,47}}^{TSE}=46.5$ Å. The reduced value of the free-energy barrier and lower values of P(TP|R_8,47) is due to the presence of large-scale nonreactive fluctuations (i.e., nonbarrier crossing events) along R_8,47 that are capable of crossing the apparent TSE without moving to the other free-energy basin. (Arrow) Example of such a fluctuation. In contrast, fluctuations along R_8,60 are more likely to be associated with barrier-crossing transitions. The point of lowest free energy along $R_{\mathrm{8,60}}^{TSE}$ (i.e., the most probable point of crossing) is marked with an X.

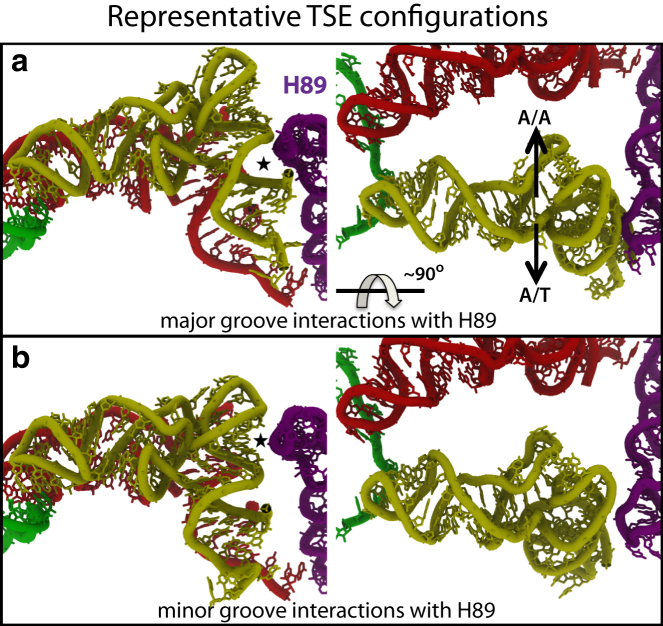
Structural composition of the TSE

In Fig. 5 we show two representative structural snapshots taken from the TSE, as identified by R_8,60. In the TSE, the aa-tRNA minor groove, or major groove, closely interacts with the stem loop of H89, consistent with previous biochemical and simulation studies (24, 25, 66). In contrast to earlier simulation studies, the identification of the appropriate coordinate and the associated TSE here was based entirely on the properties of the projected dynamics, and not construction of coordinates that are crafted for illustrative purposes. Visual inspection of earlier simulated trajectories, and the use of R_8,47 as a coordinate, generally suggested that H89 acts as a steric barrier during elbow accommodation (25). However, as shown in Fig. 4, for TSE configurations identified with R_8,60 (= 37 Å), there are multiple minima along R_8,47 (ranging from 43 to 50 Å). This inherent uncertainty that is introduced by R_8,47 is alleviated by moving to an alternate coordinate, R_8,60.

Figure 5.

Two representative configurations from the TSE. Both configurations correspond to the point of lowest free energy along $R_{\mathrm{8,60}}^{TSE}$, marked by an X in Fig. 4c. (a) A TSE configuration where the major groove of aa-tRNA (yellow) interacts with H89 (purple). P-site tRNA (red) and mRNA (green). (b) A TSE configuration where the aa-tRNA minor groove contacts H89. (Star) The relevant aa-tRNA-H89 interaction. The same configurations are shown in the right panels, each rotated by ≈90°. (Arrows) Relative positions of the aa-tRNA in the A/A and A/T configurations.

Discussion

As we seek to develop deeper insights into the origins of the energy landscapes that govern biological function, theoretical concepts will prove invaluable. In the case of the ribosome, the theoretical framework for interpreting and analyzing its dynamics is nascent, relative to other biological processes such as protein folding. Fortunately, the theoretical tools developed for folding are grounded in the statistical mechanics of biomolecular dynamics, allowing them to be adapted and applied to other biological phenomena. Here, we have demonstrated how the analysis of projected dynamics can be used to identify the kinetically and thermodynamically relevant coordinates for describing the ribosome’s energy landscape. These results provide a clear foundation, upon which to devise new experiments that can be unambiguously compared to theoretical and computational predictions. This integration of experimental and theoretical tools will be mutually beneficial, and will allow the field to precisely describe the energetic properties of increasingly complex biological phenomena.

Editor: Matthias Rief.