Feedback Mechanism for Microtubule Length Regulation by Stathmin Gradients

Abstract

We formulate and analyze a theoretical model for the regulation of microtubule (MT) polymerization dynamics by the signaling proteins Rac1 and stathmin. In cells, the MT growth rate is inhibited by cytosolic stathmin, which, in turn, is inactivated by Rac1. Growing MTs activate Rac1 at the cell edge, which closes a positive feedback loop. We investigate both tubulin sequestering and catastrophe promotion as mechanisms for MT growth inhibition by stathmin. For a homogeneous stathmin concentration in the absence of Rac1, we find a switchlike regulation of the MT mean length by stathmin. For constitutively active Rac1 at the cell edge, stathmin is deactivated locally, which establishes a spatial gradient of active stathmin. In this gradient, we find a stationary bimodal MT-length distribution for both mechanisms of MT growth inhibition by stathmin. One subpopulation of the bimodal length distribution can be identified with fast-growing and long pioneering MTs in the region near the cell edge, which have been observed experimentally. The feedback loop is closed through Rac1 activation by MTs. For tubulin sequestering by stathmin, this establishes a bistable switch with two stable states: one stable state corresponds to upregulated MT mean length and bimodal MT length distributions, i.e., pioneering MTs; the other stable state corresponds to an interrupted feedback with short MTs. Stochastic effects as well as external perturbations can trigger switching events. For catastrophe-promoting stathmin, we do not find bistability.

Introduction

Microtubules (MTs), an essential part of the cytoskeleton of eukaryotic cells, are involved in many cellular processes. These include cell division (1), intracellular positioning processes (2) such as positioning of the cell nucleus (3) or chromosomes during mitosis, establishment of cell polarity (4), and regulation of cell length (5). In all of these processes, the MT cytoskeleton has to be able to change shape and adjust the MT length distribution by polymerization and depolymerization. MT polymerization and depolymerization also plays a crucial role in the constant reorganization of the cytoskeleton of motile cells such as fibroblasts (6) or cells growing into polar shapes such as neurons (7). In motile cells, protrusion forces are often generated by the actin lamellipodium at the cell edge, but MTs interact with the actin cytoskeleton and actively participate in the regulation of motility (6). As a result, the MT cytoskeleton shape has to adjust to changing cell shapes during locomotion.

The fast spatial reorganization of MTs is based on the dynamic instability: phases of elongation by polymerization are stochastically interrupted by catastrophes that initiate phases of fast depolymerization; fast depolymerization terminates stochastically in a rescue event followed again by a polymerization phase (8).

Regulation of MT length is crucial for the MT cytoskeleton to change shape. MT length regulation by depolymerases and polymerases such as kinesin-8 or XMAP215, which directly bind to the MT, has been studied both experimentally (see Howard and Hyman (9) and Tolić-Nørrelykke (10) for reviews) and theoretically (11, 12, 13, 14, 15). Here, we want to explore and analyze models for cellular MT length regulation by the signaling proteins Rac1 and stathmin, which do not directly associate with MTs but are localized at the cell edge or in the cytosol, respectively.

Experiments have shown that dynamic MTs participate in regulation mechanisms at the lamellipodium of protruding cells through interaction with Rac1 (6, 16, 17). Rac1 is a signaling molecule that controls actin dynamics and is essential for cell motility (18). It is a GTPase of the Rho family that has been found to be active (phosphorylated) at the edge of protruding cells (6, 16) as it becomes membrane-bound in its active state (19). Rac1 activation at the cell edge has been shown to be correlated with MT polymerization (6). Therefore, it has been suggested that polymerizing MTs play an important role in activating Rac1 at the cell edge (17). The activation of Rac1 by MTs could involve their guanine-nucleotide-exchange factors. For the following, we will assume that Rac1 is activated by contact of MTs with the cell edge.

MTs are also targets of cellular regulation mechanisms, which affect their dynamic properties (20). The dynamic instability of MTs enables various regulation mechanisms of MT dynamics. In vivo, various MT-associated proteins have been found that either stabilize or destabilize MTs by direct interaction with the MT lattice, and regulate MT dynamics both spatially and temporally (21).

MT polymerization can also be regulated by the soluble protein stathmin, which diffuses freely in the cytosol and inhibits MT polymerization (22). The mechanism of MT inhibition by stathmin is still under debate (23) with the discussion focusing on two mechanisms (22, 23):

• 1.Stathmin inhibits MT growth via sequestering of free tubulin. One mole of active (nonphosphorylated) stathmin binds two moles of free tubulin and thereby lowers the local tubulin concentration (24, 25, 26, 27). Consequently, the growth velocity of the MT is suppressed and the catastrophe rate, increased.
• 2.At high pH values, stathmin does not affect the growth velocity but only increases the MT catastrophe rate (27), possibly by direct interaction with the MT lattice (23).

Stathmin can be regulated by deactivation upon phosphorylation (22). One pathway of stathmin regulation is the Rac1-Pak pathway, where Rac1 deactivates stathmin through the intermediate protein Pak (28, 29). Similar to Rac1, Pak has also been found to be localized in the leading edge of motile cells (30). Because the active form of Rac1 is situated at the cell edge, this introduces a spatial gradient of stathmin phosphorylation and thereby stathmin tubulin interaction (31).

Thus, there is a positive feedback loop of MT regulation (32, 33, 34) consisting of the activation of localized Rac1 by polymerizing MTs at the cell edge, the inhibition of cytosolic stathmin by active Rac1 via the Rac1-Pak pathway at the cell edge, and, finally, the inhibition of MT polymerization by stathmin, which sequesters tubulin or promotes catastrophes. The overall result is a positive feedback loop consisting of one positive (activating) and a doubly negative (inhibitory) interaction (Fig. 1, A and B). Polymerizing MTs are an essential part of this feedback loop. Therefore, this feedback system represents a seemingly novel type of spatially organized biochemical network, which could give rise to new types of spatial organization (35). In this article, we will formulate and analyze a theoretical model for this feedback loop for tubulin-sequestering stathmin and for purely catastrophe-promoting stathmin. Using this model, we address the question how the feedback loop regulates the MT length.

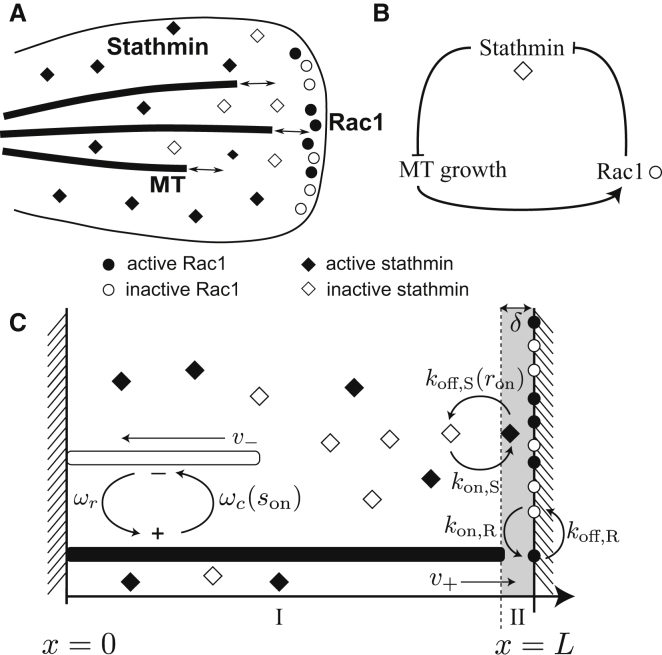
Figure 1.

(A) Sketch of the feedback loop for MT growth regulation by Rac1 and stathmin in a cell. (B) Abstract scheme of the feedback loop. (C) Sketch of the one-dimensional model. The MT switches between growing (solid bar) or shrinking state (open bar) with rescue and catastrophe rates ω_r and ω_c, respectively. Rac1 proteins (circles) are located at the cell edge x = L in active or inactive form (solid and open circles, respectively). Rac1 is activated with a rate k_on,R only if the MT enters the shaded region II of size δ representing the cell edge, and deactivated at all times with the rate k_on,R. Stathmin deactivation only takes place in the shaded region II with a rate proportional to the fraction of active Rac1 k_off,Sr_on. The local concentration of active stathmin inhibits MT growth by tubulin sequestering, which reduces the MT growth velocity v₊ locally, or by direct catastrophe promotion.

The general structure of the described positive feedback mechanism suggests two hypotheses for MT regulation, which we investigate within our model:

• 1.The positive feedback increases MT growth and, thus, MT length.
• 2.Nonlinearities in the positive feedback loop can give rise to a bistable switching between states of inhibited and increased MT growth.

Regarding Hypothesis 1, we will confirm that the regulation loop enhances MT growth. We will also show that polymerizing MTs as one part of the loop result in a particular spatial organization of the feedback loop with bimodal MT length distributions. This allows us to successfully explain the occurrence of pioneering MTs as they have been observed in Waterman-Storer and Salmon (36) and Wittmann et al. (32). Such pioneering MTs grow into the leading edge of migrating cells and exhibit a decreased catastrophe frequency. In the experiments in Wittmann et al. (32), this pioneering behavior could be promoted by introducing constitutively active Rac1 and suppressed by introducing constitutively inactive Rac1 into the cells indicating that the mechanism underlying the pioneering MTs involves regulation by Rac1. Our model shows there is a window of stathmin concentrations for which the MT length distribution is bimodal, and which consists of two subpopulations: fast growing, long pioneering MTs near the cell edge; and collapsed MTs with suppressed growth rates distant from the cell edge. This bimodality is caused by a gradient in stathmin phosphorylation.

Regarding Hypothesis 2, we will show that our model exhibits bistability only if stathmin inhibits MT growth by tubulin sequestering. The stathmin activation gradient, which upregulates MT growth near the cell edge, represents one stable state of the switch; complete stathmin deactivation with shorter MTs represents the other state. If stathmin acts by promoting MT catastrophes, we do not find bistability.

Materials and Methods

We formulate an effective model in which we focus on MT regulation through Rac1 and stathmin. We do not model the Rac1 activation pathway through MTs at the cell edge explicitly (which requires most likely the action of additional guanine-nucleotide-exchange factors), and we do not model the pathway of stathmin deactivation by Rac1 explicitly (which also involves Pak and, most likely, other signaling molecules). The following experimental facts are included: MT growth is inhibited by active stathmin; we consider both tubulin sequestering and catastrophe promotion as inhibition mechanisms. Dynamic MTs activate localized Rac1 upon contacting the cell edge. Activated Rac1, in turn, inhibits stathmin at the cell edge. Our effective model then reduces to an amplifying positive feedback loop, which is composed of one positive and two inhibitory interactions (see Fig. 1 B).

We describe this regulation mechanism as a modified reaction-diffusion process that includes directed MT polymerization and approach the problem by particle-based stochastic simulations and analytical mean-field calculations. For simplicity, we consider one spatial dimension, i.e., regulation in a narrow box of length L along the x axis of the growing MT. The model includes m independent MTs confined within the box, Rac1 proteins, which are localized at the right boundary of the box representing the cell edge, and stathmin proteins, which diffuse freely along the box (Fig. 1 C). Our model for MT regulation is characterized by a number of parameters, for many of which experimental information is already available, which we collected in Table 1 (37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48).

Table 1.

Literature values for parameters

Parameter	Values	References
Microtubule
Growth velocity v+	7–80 nm/s	(37, 38, 39, 40)
Shrinking velocity v−	0.18–0.5 μm/s	(37, 38, 39)
Effective dimer length d	8/13 nm ≃ 0.6 nm
Tubulin association rate ωon = κ∞[T0] for [T0] = 7 – 20 μM	62–178 1/s	(39)
Rescue rate ωr	0.05–0.5 1/s	(39, 41, 42)
Catastrophe rate ωc = 1/a + bv+	b = 1.38 × 1010 s2 m−1; a = 20 s	(52)
Rac
Intrinsic hydrolysis rate koff,R	0.0018–0.0023/s	(43, 44)
Hydrolysis rate koff,R in the presence of GAP	0.039/s	(43)
Stathmin
Diffusion coefficient D	13(COPY)-73(RB3) μm2/s	(24, 31)
Stokes radius Rs	33–39 Å	(26, 45, 46)
Activation gradient length scale χs	4–8 μm	(31)
Phosphatase activity kon,S	0.3–0.7 1/s	(31)
Sequestering equilibrium constant K0 = 1/KD	1.43–169/μM2	(25, 26, 31, 47, 48)
Catastrophe promotion constant kc	0.002 s−1μM−1	(27)

Single microtubule in a box

The MT dynamics in the presence of the dynamic instability is described in terms of a stochastic two-state model (49, 50): In the growing state, a MT polymerizes with an average velocity v₊. The MT stochastically switches from the growing state to a shrinking state with the catastrophe rate ω_c. In the shrinking state, it rapidly depolymerizes with an average velocity v₋. With the rescue rate ω_r, the MT stochastically switches back to the growing state.

The stochastic time evolution of an ensemble of independent MTs, growing along the x axis, can be described by two coupled master equations for the probabilities p₊(x,t) and p₋(x,t) of finding a MT with length x at time t in a growing or shrinking state (50):

$${\partial }_t{p}_{+}\left(x,t\right)=-{\omega }_c{p}_{+}\left(x,t\right)+{\omega }_r{p}_{-}\left(x,t\right)-v_{+}{\partial }_x{p}_{+}\left(x,t\right),$$ (1)

$${\partial }_t{p}_{-}\left(x,t\right)={\omega }_c{p}_{+}\left(x,t\right)-{\omega }_r{p}_{-}\left(x,t\right)+v_{-}{\partial }_x{p}_{-}\left(x,t\right).$$ (2)

We confine the MT within the one-dimensional cell of length L by reflecting boundary conditions: shrinking back to zero length gives rise to a forced rescue and contacting the boundary at x = L gives rise to an instantaneous catastrophe event. This corresponds to

$$v_{+}{p}_{+}\left(0,t\right)-v_{-}{p}_{-}\left(0,t\right)=v_{+}{p}_{+}\left(L,t\right)-v_{-}{p}_{-}\left(L,t\right)=0.$$

Forced rescue at x = 0 is equivalent to immediate renucleation of MTs, which are anchored at a MT organizing center. Our model does not apply to unanchored treadmilling MTs.

For a x-independent catastrophe rate ω_c, the steady-state probability density function of finding a MT of length x can be determined analytically (12, 51), as

$$p\left(x\right)=p_{+}\left(x\right)+p_{-}\left(x\right)=N\left(1+\frac{v_{+}}{v_{-}}\right)e^{x/\lambda },$$ (3)

with a normalization

$$N^{-1}=\lambda \left(1+v_{+}/v_{-}\right)\left(e^{L/\lambda }-1\right),$$

where λ is a characteristic length parameter of

$$\lambda \equiv \frac{v_{+}{v}_{-}}{v_{+}{\omega }_r-v_{-}{\omega }_c}.$$ (4)

If λ < 0, the average length loss after catastrophe exceeds the average length gain; if λ > 0, the average length gain exceeds the average length loss. The resulting average MT length is given by

$$\langle x_{\text{MT}}\rangle ={\int }_0^{L}xp\left(x\right)dx=\frac{L}{1-e^{\lambda /L}}-\lambda .$$ (5)

In the growing state, GTP-tubulin dimers are attached to any of the 13 protofilaments with the rate ω_on, which is proportional to the local concentration of free GTP-tubulin [T], ω_on = κ_on[T]. GTP-tubulin dimers are detached with the rate ω_off. The resulting growth velocity is obtained by multiplication with the effective tubulin dimer size d ≈ 8 nm/13 ≈ 0.6 nm,

$$v_{+}=\left({\kappa }_{\text{on}}\left[T\right]-{\omega }_{\text{off}}\right)d.$$ (6)

In the classical model of the MT catastrophe mechanism, the catastrophe rate ω_c is determined by the hydrolysis dynamics of GTP-tubulin with each loss of the stabilizing GTP-cap due to hydrolysis causing a catastrophe. Experimental results (52) show that the average time spent in the growing state, 〈τ₊〉 = 1/ω_c, is a linear function of the growth velocity v₊,

$${\omega }_c=\frac{1}{a+b{v}_{+}},$$ (7)

with constant coefficients a = 20 s and b = 1.38 × 10¹⁰ s² m⁻¹. All of our results will be robust against the choice of the catastrophe model (see the Supporting Material).

Rac model

Rac1 (in the following called “Rac”) proteins are small GTPases, whose activity is regulated by GTP-binding (activation) and intrinsic hydrolysis (deactivation). Rac proteins are localized at the edge of protruding cells (6, 16, 19), and polymerizing MTs activate Rac at the cell edge (17).

We model Rac proteins as pointlike objects situated at the boundary x = L, which can exist in two states, activated or deactivated. We denote the fraction of activated Rac by r_on. A boundary region x ∈ [L – δ, L] of small size δ represents the cell edge (region II in Fig. 1 C); because the details of the Rac activation are not known, we include δ << L as a reaction distance. Rac activation takes place with a constant rate k_on,R, and only if one of the m MT contacts the right boundary region in its growing state. The deactivation of Rac, on the other hand, happens independently of the MT growth state with the constant rate k_off,R.

The chemical kinetics of Rac at the cell edge can be described by

$$\frac{\partial r_{\text{on}}}{\partial t}=p_{\text{MT}}{k}_{\text{on},R}\left(1-r_{\text{on}}\right)-k_{\text{off},R}{r}_{\text{on}},$$ (8)

where the Rac activation rate is analogous to a second-order reaction with the mean MT cell-edge contact probability (for contact in the growing state)

$$p_{\text{MT}}\left(t\right)=m{\int }_{L-\delta }^L{p}_{+}\left(x,t\right),$$ (9)

playing the role of a MT concentration, and the Rac deactivation rate is first-order. Equations 8 and 9 describe the Rac kinetics at the mean-field level neglecting temporal correlations between MT cell-edge contacts and Rac number fluctuations. In a stationary state, Eq. 8 gives a Rac activation level

$$r_{\text{on}}=\frac{1}{1+k_{\text{off},R}/p_{\text{MT}}{k}_{\text{on},R}}.$$ (10)

Because Rac activation requires MT contact, changes in the activation rate k_on,R (for which there is no experimental data yet) can always be compensated by changing the number of MTs m, as it is apparent from Eq. 10.

Stathmin model

Stathmin is a soluble protein that diffuses freely in the cytosol and inhibits MT growth. We consider two possible inhibition mechanisms (22): 1) tubulin sequestering and 2) catastrophe promotion. MT growth inhibition is turned off by stathmin phosphorylation through the Rac-Pak pathway (28, 29).

Gradient in stathmin activation

The interplay of stathmin diffusion and phosphorylation by active Rac at the cell edge establishes a spatial gradient of stathmin activation.

Stathmin proteins are modeled as pointlike objects in an active or inactive state. Unlike Rac proteins, stathmin proteins diffuse freely within the whole simulation box x ∈ [0; L] assuming concentration profiles S_on(x) in the active dephosphorylated state, which can inhibit MT growth, and S_off(x) in the inactive phosphorylated state (with a total stathmin concentration S_tot(x) = S_on(x) + S_off(x)). We assume the diffusion coefficient D to be constant and equal for both states. Switching between active and inactive states is a stochastic process with rates k_on,S and k_off,S, respectively.

Rac acts through Pak as a stathmin kinase. We describe stathmin deactivation by Rac at the cell edge x = L as a simple second-order reaction with a rate proportional to r_on (note that including Michaelis-Menten-like enzyme kinetics for stathmin deactivation does not alter the results qualitatively).

We assume that the phosphatase responsible for stathmin activation is homogeneously distributed within the cytosol such that stathmin dephosphorylates everywhere within the box with the constant rate k_on,S (53). The distribution of deactivated stathmin in the one-dimensional box is then described by a reaction-diffusion equation (see the Supporting Material for details).

In the steady state, we find a stathmin activation gradient with a profile

$$\frac{S_{\text{on}}\left(x\right)}{S_{\text{tot}}}=1-2A\text{cos}\text{h}\left(x/{\chi }_S\right),$$ (11)

which decreases with increasing x toward the cell edge x = L because stathmin is deactivated at the cell edge by Rac. The characteristic decay length for the stathmin activation gradients is given by

$${\chi }_S=\sqrt{D/k_{\text{on},S}}$$

and arises from the competition of stathmin reactivation in the bulk of the box and diffusion. The integration constant

$$A=1/2\frac{r_{\text{on}}{k}_{\text{off},\text{S}}}{\left(D/\delta {\chi }_S\right)\text{sin}\text{h}\left(L/{\chi }_S\right)+\left(r_{\text{on}}{k}_{\text{off},\text{S}}+k_{\text{on},\text{S}}\right)\text{cos}\text{h}\left(L/{\chi }_S\right)}$$ (12)

depends on the degree of stathmin deactivation by Rac at the cell edge x = L and, thus, on the fraction r_on of activated Rac (see the Supporting Material).

Experimentally, a characteristic stathmin gradient length scale χ_s = 4–8 μm has been measured using fluorescence resonance energy transfer with fluorescent stathmin fusion proteins (COPY) (31). Values for the diffusion constant D = 13–18 μm²/s of the fluorescent COPY proteins (31) are consistent with activation or dephosphorylation rates k_on,s = 0.3–0.71/s by phosphatase activity.

Tubulin-sequestering stathmin

One possible pathway for stathmin to inhibit MT growth is sequestering of free tubulin, which lowers the MT growth velocity v₊ by decreasing the local concentration of free tubulin. It also alters the catastrophe rate ω_c via the growth velocity, as described by Eq. 7 (26).

One active stathmin protein sequesters two tubulin proteins (24, 25, 26, 27),

$$2T+1S\rightleftharpoons S{T}_2,$$ (13)

and the growth velocity v₊ depends on the concentration [T] of free tubulin as described in Eq. 6. Solving the chemical equilibrium equations, we find the normalized concentration of free tubulin t ≡ [T]/[T₀] (normalized by the total tubulin concentration [T₀] = [T] + 2[ST₂]) as a function of normalized active stathmin s_on ≡ S_on[T₀],

$$\begin{array}{c}t\left(s_{\text{on}}\right)=1/3\left[1-2s_{\text{on}}+\frac{-3+k{\left(1-2s_{\text{on}}\right)}^2}{k\alpha \left(s_{\text{on}}\right)}+\alpha \left(s_{\text{on}}\right)\right]\\ \text{with}\\ \alpha \left(s_{\text{on}}\right)\equiv [{\left(1-2s_{\text{on}}\right)}^3+\left(9/k\right)\left(1+s_{\text{on}}\right)\\ {+3\sqrt{\left(3/k^3\right)\left(1+k^2{\left(1-2s_{\text{on}}\right)}^3+k\left(2+10s_{\text{on}}-s_{\text{on}}^2\right)\right)}]}^{1/3},\end{array}$$ (14)

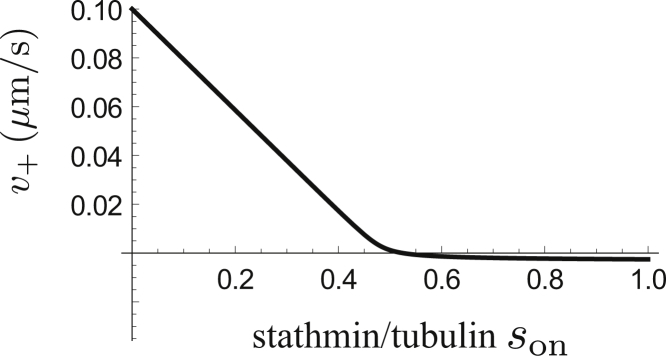
where k ≡ K₀[T₀]² denotes the normalized equilibrium constant of the reaction (Eq. 11). The resulting curve t(s_on) is strongly nonlinear, and agrees well with experimental results on the amount 1 − t of bound tubulin in Jourdain et al. (25).

Inserting the result [T] = [T₀]t(s_on) in the linear Eq. 4 for the growth velocity), we also obtain a strongly nonlinear dependence of the growth velocity on active stathmin (see Fig. 2). Assuming that tubulin-stathmin association is fast compared to the other processes, a local concentration s_on(x) of active stathmin also gives rise to a local concentration [T](x) = [T₀]t(s_on(x)) of free tubulin, and Eq. 6 determines the local growth velocity:

$$v_{+}=v_{+}\left(\left[T\right]\left(x\right)\right)=v_{+}\left(\left[T_0\right]t\left(s_{\text{on}}\left(x\right)\right)\right).$$ (15)

Figure 2.

Growth velocity v₊ as a function of the normalized concentration of active stathmin s_on = S_on/[T₀] as given by inserting [T] = [T₀]t(s_on) according to Eq. 14 into Eq. 6 for k = K₀[T₀]² = 9400 corresponding to K₀ = 25 μM² and [T₀] = 19.4 μM (see Table 2). The sharp crossover at s_on ≃ 0.5 is a result of the tubulin sequestering in a 1:2 complex.

Catastrophe-promoting stathmin

Another possible pathway for stathmin to inhibit MT growth is by directly promoting catastrophes, possibly via direct interaction with the MT lattice (23). This pathway might be more relevant at high pH values, whereas tubulin sequestering dominates at lower pH values (27). For high pH, the data of Howell et al. (27) are consistent with a linear increase of the catastrophe rate with the concentration of active stathmin,

$${\omega }_c\left(S_{\text{on}}\right)={\omega }_c\left(0\right)+k_c{S}_{\text{on}}={\omega }_c\left(0\right)+k_c\left[T_0\right]s_{\text{on}},$$ (16)

with a catastrophe promotion constant k_c = 0.002 s⁻¹ μM⁻¹. An activation gradient of stathmin S_on(x) then gives rise to a local MT catastrophe rate ω_c(S_on(x)).

We will use both the catastrophe promotion pathway of stathmin and the sequestering pathway in our model, and compare the resulting MT growth behavior.

Stochastic simulations

The model outlined in the previous section is the basis for our one-dimensional stochastic simulations (employing equal time steps Δt = 0.001 s). We model the MTs as straight polymers with continuous length x, and Rac and stathmin distributions via discrete particles, which can be activated and deactivated according to the rates specified above. The N_S stathmin particles can diffuse freely within the simulation box, whereas the N_R Rac particles are localized at the cell-edge region of size δ. Details of the simulation are described in the Supporting Material.

In Table 2 we present our choice of parameters to perform simulations. We assume a tubulin concentration [T₀] = 19.4 μM. We choose a simulation box of length L = 10 μm with a cell-edge region of size δ = 20 nm, where Rac can be activated by MTs. In the Supporting Material, it is shown that our results are qualitatively similar for larger lengths L.

Table 2.

Parameter values used for simulation

Description	Parameter	Value/Reference
Time step	Δt	0.001 s
System length	L	10 μm
Cell-edge region	δ	0.02 μm
Microtubule
Tubulin concentration	[T0]	19.4 μM
Effective dimer length	d	8/13 nm ≃ 0.6 nm
Growth velocity (Son = 0)	v+	0.1 μm/s
Shrinking velocity	v−	0.3 μm/s
Tubulin association rate	ωon = κon[T0]	173/s (39)
Dissociation velocity	voff	3.6 nm/s (40)
Rescue rate	ωr	0.1/s
Catastrophe rate (Son = 0)	ωc	0.0007/s
Number of tubulin dimers	NT	10,000
Corresponding to a volume	V	0.86 μm3
Rac
Number of Rac molecules	NR	1000
Activation rate	kon,R	5/s
Deactivation rate	koff,R	0.002/s
Stathmin
Activation rate	kon,S	1/s
Deactivation rate	koff,S	300/s
Diffusion coefficient	D	15 μm2/s
Sequestering equilibrium constant	K0	25/μM2
k = K0[T0]2	9400 with [T0] = 19.4 μM
Catastrophe promotion constant	kc	0.002 s−1μM−1

Results and Discussion

Interrupted feedback for constitutively active stathmin in the absence of Rac

In a first step, we investigate how constitutively active stathmin alters the MT dynamics, which is equivalent to interrupting the feedback loop by removing Rac (r_on = 0) such that stathmin cannot be deactivated and is homogeneously distributed, S_tot = S_on = const, due to diffusion. Because Rac is absent, all results are independent of the membrane contact probability of MTs, and we can limit the MT number to m = 1.

For homogeneously distributed stathmin, the MT growth rate v₊ and the catastrophe rate ω_c are homogeneous both for tubulin-sequestering and catastrophe-promoting stathmin. Then, we can calculate the MT length distribution from the analytical solution 3 for a position-independent parameter λ (see Eq. 4). We find good agreement between the analytical result Eq. 5 for the MT mean length and stochastic simulation results as a function of the stathmin/tubulin s ≡ S_tot/[T₀] (s = s_on for constitutively active stathmin) both for tubulin-sequestering and catastrophe-promoting stathmin (Fig. 3). Deviations are due to stochastic fluctuations of the local stathmin concentration because of diffusion.

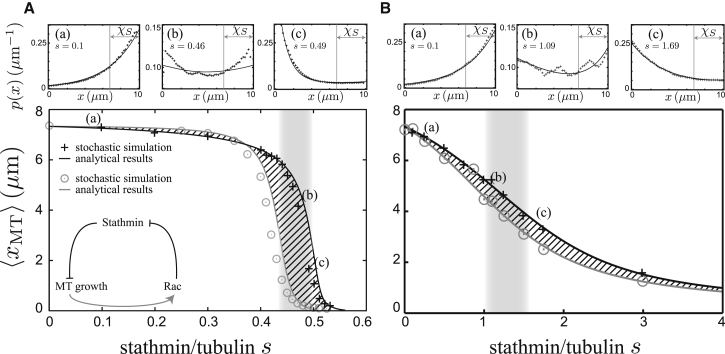
Figure 3.

Stochastic simulation data (data points) and analytical master equation results (solid lines) for the mean MT length 〈x_MT〉 as a function of stathmin/tubulin s = S_tot/[T₀]. We compare the system with constitutively active Rac (r_on = 1, solid lines and crosses) to the system without Rac (r_on = 0, shaded lines and circles) both for tubulin-sequestering stathmin (A) and catastrophe-promoting stathmin (B). (Hatched area) Possible MT length gain by Rac regulation. (Shaded area) Region in which MTs exhibit bimodal length distributions for constitutively active Rac. (Insets a–c) Corresponding MT length distributions for three particular values of s with (a) s < s_λ, (b) s = s_λ, and (c) s > s_λ.

Our main finding is that stathmin regulates MT growth in a switchlike manner if stathmin both sequesters tubulin and promotes catastrophes. For tubulin-sequestering stathmin the switch is much steeper, and we can define two stathmin concentrations, S_λ and S_v, which characterize the steepness of the switch. At the critical concentration S_λ, the characteristic length parameter λ (see Eq. 4) changes sign, i.e., λ⁻¹ (S_tot = S_λ) = 0. The condition λ⁻¹ = 0 results in a flat MT length distribution (Eq. 1) and, thus, an alternative definition of S_λ is 〈x_MT〉(S_tot = S_λ) = L/2.

Above the critical stathmin concentration S_λ, we find the MT length distributions to be negative exponentials. At the second, higher critical concentration S_v, the MT growth velocity v₊ (see Eqs. 6 and 14) changes sign, i.e., v₊(S_tot = S_v) = 0. Above S_v, the MT cannot grow at all and 〈x_MT〉 = 0 for S ≥ S_v. For catastrophe-promoting stathmin, the switch is much broader because the MT growth velocity is not affected, formally resulting in an infinite S_v. A critical concentration S_λ can be defined in the same way as for tubulin-sequestering stathmin.

For tubulin-sequestering stathmin, the critical stathmin/tubulin s_λ and s_v are generally close to 0.5 as a result of the 1:2 tubulin sequestering. For catastrophe-promoting stathmin, s_λ approaches the [T₀]-independent limit s_λ ≈ κ_ondω_r/v₋k_c = 0.91, which is >>0.5 (for more details, see the Supporting Material). The values s_λ and s_v are only weakly [T₀]-dependent, which motivates using the stathmin/tubulin s = s_on as a control parameter.

We find that constitutively active stathmin regulates MT growth in a switchlike manner for a fixed tubulin concentration [T₀] as characterized by the critical concentration S_λ, which is approximately linear in the tubulin concentration [T₀] for both models of stathmin action. Vice versa, we conclude that, at a fixed stathmin concentration S_tot, the tubulin concentration [T₀] can regulate MT growth in a switchlike manner with a critical concentration [T] ∼ s_λ/S_tot, which can be controlled by the stathmin concentration S_tot. Without stathmin regulation, a critical tubulin concentration [T] = κ_on/ω_off for MT growth at the plus-end exists, but this concentration is fixed by the rate constants of the growth velocity v₊ appearing in Eq. 6. Moreover, the switchlike behavior becomes sharpened by stathmin regulation.

In vivo, the picture will be complicated if additional populations of treadmilling MTs exist apart from the end-anchored MTs, which we consider here. For tubulin-sequestering stathmin, treadmilling MTs will act as additional tubulin buffer. Upon sequestering by stathmin the length of treadmilling MTs will adjust such that the concentration of free tubulin is maintained at the critical concentration for treadmilling.

For a system that contains constitutively active stathmin and no Rac, the growth velocity v₊ is homogeneous, and we always expect exponential MT length distributions as in Eq. 1. In particular, we do not find bimodal MT length distributions in the absence of Rac (see also the Supporting Material).

Interrupted feedback for constitutively active Rac

Now we reinclude Rac into our analysis of the feedback mechanism. We start with constitutively active Rac (r_on = 1), which is analogous to interrupting the feedback between MTs and Rac by making the level of Rac activation independent of the cell-edge contacts of the MTs. Thus, we can limit the MT number to m = 1 in this section.

Constitutively active Rac establishes a gradient of active stathmin, constant in time, which can be quantified by the analytical result from Eq. 11 with r_on = 1. As shown in the Supporting Material, it agrees very well with stochastic simulation results. The decreasing profile S_on(x) of activated stathmin is essential for MT length regulation because it leads to an increasing growth velocity v_x(x) (for tubulin-sequestering stathmin) and/or a decreasing catastrophe rate ω_c(x) (for tubulin-sequestering and catastrophe-promoting stathmin), which modulates the MT length distribution.

We can calculate the MT length distribution starting from the negative stathmin gradient

$$s_{\text{on}}\left(x\right)=S_{\text{on}}\left(x\right)/\left[T_0\right]=s\left(S_{\text{on}}\left(x\right)/S_{\text{tot}}\right)$$

(with the total stathmin/tubulin s = S_tot/[T₀]) as given by Eq. 11. For tubulin-sequestering stathmin, this results in an increasing tubulin concentration of

$$\left[T\right]\left(x\right)=\left[T_0\right]t\left(s_{\text{on}}\left(x\right)\right)$$

through Eq. 14, which gives rise to both an increasing growth velocity v₊(x) according to Eq. 15 and a decreasing catastrophe rate ω_c = ω_c(v₊ (x)). For catastrophe-promoting stathmin, only the catastrophe rate ω_c = ω_c(S_on) becomes decreasing via Eq. 16. For both stathmin models, this results in an increasing inverse characteristic length parameter of

$${\lambda }^{-1}\left(x\right)={\omega }_r/v_{-}-{\omega }_c\left(x\right)/v_{+}\left(x\right)$$

(see Eq. 4). The master equations (Eqs. 1 and 2) then give the steady-state probability distribution for the MT length (51),

$$p\left(x\right)=p_{+}\left(x\right)+p_{-}\left(x\right)=N\left(1+\frac{v_{-}}{v_{+}\left(x\right)}\right)\text{exp}\left({\int }_0^{x}d{x}^{\prime }/\lambda \left(x^{\prime }\right)\right),$$ (17)

with a normalization

$$N^{-1}={\int }_0^{L}dx\left(1+\frac{v_{-}}{v_{+}\left(x\right)}\right)\text{exp}\left({\int }_0^{x}d{x}^{\prime }/\lambda \left(x^{\prime }\right)\right).$$

In contrast to the system without Rac, position-dependent MT growth velocity and/or catastrophe rates can give rise to more complex MT length distributions because the decreasing profile S_on(x) of active stathmin gives rise to an inverse parameter λ⁻¹(x), which is an increasing function of x for both stathmin models. The most interesting situation then arises if λ⁻¹(x) changes its sign on 0 < x < L. Then, we find λ(x) < 0 or MTs shrinking on average for small x and λ(x) > 0 or MTs growing on average for large x. The decreasing profile S_on(x) of active stathmin thus leads to unstable MT growth because it promotes growth of long MTs, and shrinkage of short MTs. In fact, we find bimodal MT length distributions for this case as a result of the negative gradient or decreasing profile of active stathmin according to Eq. 11 (and see Fig. 3 insets, b).

These bimodal MT length distributions correspond to two populations of MTs: long fast-growing MTs and short collapsed MTs. The subpopulation of long fast-growing MTs resembles the experimentally observed long pioneering microtubules (32, 36). Pioneering MTs have been observed to grow into the leading edge of migrating cells and exhibit a decreased catastrophe frequency. Because of the reduced growth velocity by deactivated stathmin, these are exactly the properties of the subpopulation of long MTs. We conclude that the bimodal MT length distribution occurring at high active Rac fractions can explain the phenomenon of pioneering MTs.

It is instructive to compare the impact of the decreasing active stathmin profile S_on(x) on the MT length distribution with the effect of an external force F(x), which opposes MT growth and increases with x, for example, as for an elastic obstacle (51, 54). Whereas an opposing force F(x), which increases with x, gives rise to a decreasing growth velocity v₊(x) and a decreasing parameter λ⁻¹(x), it is found that a decreasing profile S_on(x) always gives rise to an increasing parameter λ⁻¹(x). This difference leads to very different behavior. For an opposing force F(x), the MT length x_MT with λ⁻¹(x_MT) = 0 represents a stable equilibrium: shorter MTs grow on average, whereas longer MTs shrink. Therefore, we find a pronounced maximum in the MT length distribution at x ∼ x_MT (51, 54). For stathmin-regulated MT growth, a decreasing profile S_on(x) leads to an unstable equilibrium as outlined above. As a result, we find a bimodal MT length distribution with a minimum in the MT length distribution around the MT length x_MT with λ⁻¹(x_MT) = 0.

In Fig. 3, we show the average length 〈x_MT〉 of the MT as a function of the stathmin/tubulin s = S_tot/[T₀] for the two subsystems with constitutively active Rac (black lines and symbols) and without Rac (shaded lines and symbols) for both tubulin-sequestering and catastrophe-promoting stathmin. The black lines correspond to the analytical steady-state solution following the calculation outlined before; black data points are results from fully stochastic simulations. Also for active Rac, the total stathmin concentration regulates MT growth in a switchlike manner, and we can define a critical stathmin concentration S_λ from the condition 〈x_MT〉(S_tot = S_λ) = L/2. The corresponding values are slightly higher than in the absence of Rac. We find bimodal MT length distributions for stathmin concentrations close to the critical value s_λ because the condition 〈x_MT〉 = L/2 implies that there exists an MT length x_MT with λ⁻¹(x_MT) = 0.

The deviation between the stochastic simulation results and the analytical master equation solution in Fig. 3 is due to fluctuations in the local concentration of active stathmin. Also in stochastic simulations, we find bimodal MT length distributions and, thus, pioneering MTs for stathmin/tubulin S_tot/[T₀] in the gray-shaded area in Fig. 3 around the critical value s_λ.

Closed feedback

Now we consider the full system with closed feedback, where the activation of Rac proteins depends on cell-edge contacts of the MTs and changes with the number of MTs m in the system.

For the closed feedback loop, we expect that the average MT length will lie in between our results without Rac (r_on = 0) and for full Rac activation (r_on = 1), as indicated by the hatched areas in Fig. 3. For a closed regulation feedback loop, the system can vary the MT length between these two bounds, for example, by increasing the number m of MTs and, thus, the Rac activation level. The MT length is most sensitive to regulation in the vicinity of the switchlike behavior, i.e., for stathmin/tubulin S_tot/[T₀] ∼ s_λ.

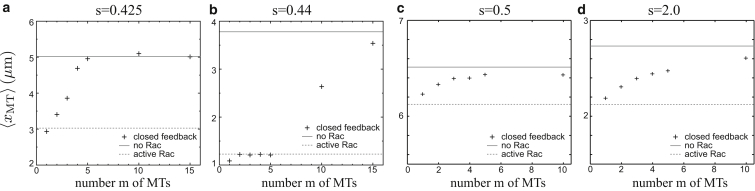
Using fully stochastic simulations we investigate the dependence of the mean MT length 〈x_MT〉 on the number m of MTs for stathmin/tubulin S_tot/[T₀] ∼ s_λ (s ≈ 0.4–0.5 for tubulin-sequestering stathmin and s ≈ 1.0–1.5 for catastrophe-promoting stathmin). The results are shown in Fig. 4. For a closed feedback loop, the mean MT length increases with the number m of MTs between the two bounds given by a system without Rac and a system with complete Rac activation, because the strength of the feedback increases with m via the cell-edge contact probability as given by Eq. 7. If the MT contact probability is sufficiently high, the system will stabilize long MTs by Rac activation. For tubulin-sequestering stathmin, the average MT length increases linearly only above a critical number m_c of MTs. This critical number m_c increases with the stathmin concentration. For catastrophe-promoting stathmin, there is no critical number of MTs necessary, and the length increases gradually as a function of MT number m.

Figure 4.

The average MT length 〈x_MT〉 as a function of the number of MTs m in a system with closed feedback for tubulin-sequestering stathmin (a and b) and catastrophe-promoting stathmin (c and d) at different stathmin/tubulin s = s_tot/[T₀] values: (a) s = 0.425, (b) s = 0.44, (c) s = 0.5, and (d) s = 2.0. (Horizontal solid and dashed lines) Mean MT length for systems without Rac (r_on = 0) and constitutively active Rac (r_on = 1), respectively.

We can rationalize these results by the bifurcation behavior of the stationary state of the feedback system at the mean-field level, which is qualitatively different for tubulin-sequestering stathmin and catastrophe-promoting stathmin. For a fixed mean concentration r_on of activated Rac, we can follow the same steps as in the previous section to calculate the resulting stationary stathmin profile (Eq. 9) with an arbitrary 0 ≤ r_on ≤ 1 in Eq. 12 for the parameter A and, then, the steady-state probability distribution p(x) for the MT length (Eq. 15) given the velocity profile in Eq. 13. From p(x) we obtain the MT cell-edge contact probability p_MT in the stationary state using Eq. 9. All in all, we can calculate p_MT from any given fixed Rac activation level r_on. On the other hand, for a closed feedback loop, the MT contact probability p_MT feeds back and determines the Rac activation level r_on via Eq. 10 in the stationary state. At the stationary state of the closed feedback loop both relations have to be fulfilled simultaneously, which is only possible at certain fixed points of the feedback system.

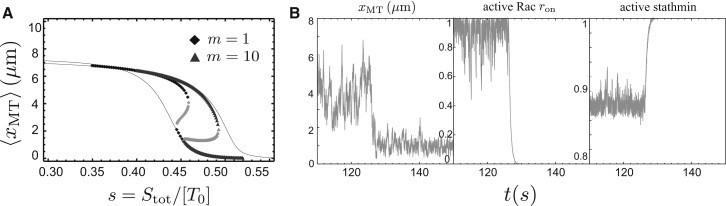
For tubulin-sequestering stathmin, there are up to three fixed points, which exhibit two saddle-node bifurcations typical for a bistable switch (see the Supporting Material for more details). For small stathmin concentrations, there is only a single fixed point at a high level r_on ≈ 1 of active Rac, corresponding to upregulated MT growth resulting in a large mean MT length 〈x_MT〉 and bistable length distributions, i.e., pioneering MTs. At this fixed point, 〈x_MT〉 is described by the black curve in Fig. 3. For high stathmin concentrations, there exists only a single fixed point at low active Rac r_on ≈ 0, corresponding to an interrupted feedback loop with short MTs. At this fixed point, 〈x_MT〉 is given by the shaded curve in Fig. 3. The upper critical stathmin/tubulin increases with the MT number m. In between, we find a hysteresis with three fixed points, one of which is unstable, corresponding to a bistable switch behavior. The hysteresis loop widens for increasing MT numbers m, which is why the critical m_c rises as a function of s (see Fig. 4). This also gives rise to hysteresis in the mean MT length, as shown in Fig. 5 A.

Figure 5.

(A) Average MT length 〈x_MT〉 at the fixed points as a function of stathmin/tubulin s = S_tot/[T₀] value for tubulin-sequestering stathmin (diamonds, m = 1; triangles, m = 10; gray, unstable fixed point). (Lines) 〈x_MT〉 for a system without Rac (lower line, r_on = 0) and for constitutively active Rac (upper line, r_on = 1). (B) Time evolution of a feedback system with m = 1 MT for tubulin-sequestering stathmin and x = 0.44. Plots show MT length, the fraction r_on of active Rac, and the total fraction of active stathmin $L^{-1}{\int }_0^{L}dx{S}_{\text{on}}\left(x\right)/S_{\text{tot}}$ as a function of time. At t ∼ 130 s, the system switches from the high active Rac fixed point to an interrupted feedback fixed point.

We conclude that for tubulin-sequestering stathmin, closure of the positive feedback mechanism leads to a bistable switch. This switch locks either into a high concentration of active Rac with upregulated MT growth and pioneering MTs, or into a low concentration of active Rac with quasi-interrupted feedback and short MTs. This bistable behavior requires a certain threshold value mk_on,R > 1.9/s such that the feedback is strong enough. As of this writing, there is no experimental data for k_on,R; values k_on,R < 1.9/s would require more than one MT to trigger bistability. In our model, this bistable switching behavior occurs even in the absence of a nonlinear Michaelis-Menten kinetics for stathmin phosphorylation because the dependence of the contact probability p_MT on the Rac activation level r_on is strongly nonlinear for tubulin-sequestering stathmin. The observed bifurcation is a stochastic bifurcation (of P-type) (55) in the sense that the MT length distribution undergoes a qualitative change at the bifurcation.

This bistability is also observed in our stochastic simulations for tubulin-sequestering stathmin (see Fig. 5 B), where stochastic fluctuations give rise to switching from the high active Rac fixed point (r_on ≈ 1) to an interrupted feedback at low active Rac (r_on ≈ 0). If we start in a state at the high Rac fixed point and the time between successive cell-edge contacts becomes comparable to the time constants k_off,R for Rac deactivation and k_on,S for stathmin reactivation, the feedback can be interrupted by stochastic fluctuations. Then the system falls into the low Rac fixed point, as can be seen in Fig. 5 at t ∼ 130 s. Because the MT length distribution is exponentially decreasing at the low Rac fixed point, the reverse event of switching back to a high Rac value is improbable. Stochastic switching events as shown in Fig. 5 for m = 1 MT become increasingly rare for large numbers m of MTs, which effectively stabilizes the fixed point of upregulated MT growth.

The main source of stochasticity is the growth dynamics of MTs and the resulting time-dependence of the contact probability: for small numbers m, the constant average value p_MT is only established as average over many contacts with relatively long times between successive contacts. Therefore, we expect the mean-field results to become correct only for large MT numbers m. For small m, we find pronounced stochastic effects. Furthermore, the gradual linear increase of 〈x_MT〉 above the critical MT number m_c in Fig. 4 is the result of averaging bistable switching over many realizations.

For catastrophe-promoting stathmin, there is only a single fixed point, which explains the gradual upregulation of MT growth by the MT number m. The reason for the absence of any bistability is the strictly linear dependence of the inverse characteristic length parameter

$${\lambda }^{-1}\left(x\right)={\omega }_r/v_{-}-{\omega }_c\left(x\right)/v_{+}\left(x\right)$$

on the concentration of active stathmin (see Eqs. 4 and 16). This gives rise to a quasi-linear dependence of the contact probability p_MT on the Rac activation level r_on for catastrophe-promoting stathmin.

Our theoretical findings show the following:

• 1.Rac activation in the cell-edge region can establish the feedback, increase MT growth, and trigger MT pioneering behavior in accordance with experimental findings in Wittmann et al. (2), and
• 2.Surprisingly, simply increasing the number m of participating MTs can also upregulate growth of these MTs, inasmuch as this increases the feedback strength and the level of active Rac.

Conclusions

We formulated and investigated a theoretical model for the influence of a doubly negative feedback mechanism on MT growth involving the signaling proteins Rac1 and stathmin. MTs activate Rac1 in the cell-edge region; activated localized Rac1 inhibits stathmin, which freely diffuses in the cytosol and is an inhibitor for MT growth. We studied and compared two models for the MT inhibiting effect of stathmin, tubulin sequestering, and catastrophe promotion. The resulting positive feedback loop is of particular interest because of the prominent role spatial organization: MTs grow along a particular direction and stathmin organization along this direction is essential.

For high concentrations of active Rac1, our model produces a stathmin activation gradient, which leads to an increased mean MT length and bimodal MT length distributions. This explains the phenomenon of pioneering MTs that have been observed experimentally (32, 36). We find bimodal MT length distributions both for tubulin-sequestering and for catastrophe-promoting stathmin. Our model shows that the stathmin activation gradient requires a local activation of Rac1 at the cell edge. Local Rac1 activation can happen by MT contacts for closed feedback, but an external local Rac1 activation should also trigger a stathmin activation gradient and, thus, pioneering MTs in accordance with experimental observations (32). Localized activation of other kinases that inactivate stathmin could have a similar effect, whereas stathmin-targeting kinases, which are active throughout the cytoplasm, will not give rise to stathmin activation gradients or pioneering MTs.

For constitutively active and inactive Rac1, we find a switchlike dependence of the mean MT length on the overall concentration ratio of stathmin to tubulin. We find such a switchlike dependence both for tubulin-sequestering and catastrophe-promoting stathmin with a characteristically steeper switch for tubulin-sequestering stathmin. This qualitative difference between tubulin-sequestering and catastrophe-promoting stathmin should be amenable to experimental testing, which might help to settle the yet-unresolved question of the MT-inhibiting mechanism of stathmin.

The positive feedback mechanism involving Rac1 and stathmin allows us to upregulate MT growth within the bounds set by constitutively active and inactive Rac1. Based on our theoretical model, we predict a qualitatively different effect of the positive feedback for tubulin-sequestering and catastrophe-promoting stathmin. For tubulin-sequestering stathmin, we identify a bistable switch with two stable fixed points within a mean-field theory. One fixed point corresponds to high active Rac1, upregulated MT mean length, and bimodal MT length distributions, i.e., pioneering MTs; the other fixed point corresponds to an interrupted feedback at low active Rac1 concentrations, with short MTs. Stochastic fluctuations can give rise to spontaneous stochastic switching events, which we also observed in simulations.

Interestingly, we find bistable switching behavior even in the absence of a nonlinear Michaelis-Menten kinetics for stathmin phosphorylation. The bistability is due to nonlinear dependencies of the MT cell-edge contact probability on the active Rac1 concentration via the free tubulin concentration and the stathmin concentration. For catastrophe-promoting stathmin, this nonlinearity is absent and we find a gradual increase of MT length by the positive feedback mechanism. These qualitative differences between tubulin-sequestering and catastrophe-promoting stathmin in the theoretical model could give important indications for experiments to resolve the issue of the mechanism of MT growth inhibition by stathmin: experimental observations of bistability would clearly hint toward the tubulin-sequestering mechanism.

We checked that all of our results are robust against changes of the catastrophe model and the cell length L (see the Supporting Material). Based on our model, we suggest three mechanisms to influence the overall MT growth behavior or the Rac1-induced upregulation of MT growth in vivo or by external perturbation in experiments:

• 1.The overall MT length can be controlled via the total tubulin or stathmin concentrations. Raising the tubulin concentration or lowering the stathmin concentration upregulates MT growth.
• 2.Rac1 activation in the cell-edge region increases MT growth and can trigger pioneering MTs.
• 3.Increasing the number m of participating MTs can also increase MT growth and trigger pioneering MTs.

All of these mechanisms should be accessible in perturbation experiments. Moreover, our results on MT length distributions can be checked against future quantitative length measurements on pioneering MTs.

Our results have implications for the polarization of the MT cytoskeleton as well. In a population of MTs growing in different directions, the investigated positive feedback mechanism via Rac1 and stathmin regulation can select and amplify a certain MT growth direction, such as one triggered by a locally increased Rac1 concentration in the cell-edge region. This issue remains to be investigated in the future.

Editor: David Odde.

Supporting Citations

References (56, 57) appear in the Supporting Material.