Mapping Diffusion in a Living Cell via the Phasor Approach

Abstract

Diffusion of a fluorescent protein within a cell has been measured using either fluctuation-based techniques (fluorescence correlation spectroscopy (FCS) or raster-scan image correlation spectroscopy) or particle tracking. However, none of these methods enables us to measure the diffusion of the fluorescent particle at each pixel of the image. Measurement using conventional single-point FCS at every individual pixel results in continuous long exposure of the cell to the laser and eventual bleaching of the sample. To overcome this limitation, we have developed what we believe to be a new method of scanning with simultaneous construction of a fluorescent image of the cell. In this believed new method of modified raster scanning, as it acquires the image, the laser scans each individual line multiple times before moving to the next line. This continues until the entire area is scanned. This is different from the original raster-scan image correlation spectroscopy approach, where data are acquired by scanning each frame once and then scanning the image multiple times. The total time of data acquisition needed for this method is much shorter than the time required for traditional FCS analysis at each pixel. However, at a single pixel, the acquired intensity time sequence is short; requiring nonconventional analysis of the correlation function to extract information about the diffusion. These correlation data have been analyzed using the phasor approach, a fit-free method that was originally developed for analysis of FLIM images. Analysis using this method results in an estimation of the average diffusion coefficient of the fluorescent species at each pixel of an image, and thus, a detailed diffusion map of the cell can be created.

Introduction

The mobility of biological macromolecules inside cells has been a focus of scientific inquiry for a long time (1, 2, 3, 4). Anomalous diffusion and constrained diffusion have been the subjects of ongoing debate in the scientific community (1, 2, 3, 4). Historically, the diffusion of biological macromolecules has been investigated using fluorescence, anisotropy, correlation spectroscopy (5, 6, 7, 8, 9, 10, 11, 12, 13, 14), and fluorescence recovery after photobleaching (15, 16, 17, 18). More recently, raster image correlation spectroscopy (RICS) and various other image correlation spectroscopic techniques have been used to investigate diffusion inside the cell (12, 13, 14, 19, 20). Single-particle tracking has also been employed for this purpose (21, 22, 23, 24, 25, 26). RICS enables us to look at diffusion in various sections of cells. However, it is limited to an area much larger than one pixel, and usually, a picture of diffusion at each pixel of a cell cannot be obtained, as the pixel size is limited (∼50 nm) for a spatiotemporal correlation function like RICS (13, 14). Single-point fluorescence correlation spectroscopy (FCS) enables us to measure diffusion of a fluorophore at each pixel of an image. Nonetheless, measuring single-point FCS at each pixel of the 256 × 256 image of a cell requires a very long acquisition time (∼180 h for acquisition of 10 s at each point) and results in bleaching of the cell or cell death. Hence, there is a need for a technique by which diffusion information at each pixel of an image can be obtained.

Calculation of diffusion constants at each pixel of a cell image is achieved in this study by determining the correlation function from the fluorescence intensity obtained for a very short time sequence. The main difference between this method and single-point FCS is that the time of acquisition at each pixel is much shorter with this method (∼0.8–10 ms) than with traditional FCS (10–100 s). The shape and amplitude of these short-time correlation functions are very different from those determined using the common one-photon FCS decays and hence require a different type of analysis. In this work, such analysis is achieved by transforming the correlation functions to the Fourier space into the phasor plot. This new (to our knowledge) method, which we call phasor FCS (short-time-sequence FCS), enables us to measure the diffusion map of a fluorescent species inside the cell with pixel resolution, giving the most detailed map possible of diffusion inside the cell.

Theory and simulations

Fluorescence autocorrelation function is defined as (27, 28, 29)

$$G\left(\tau \right)=\frac{\langle F\left(t\right)\times F\left(t+\tau \right)\rangle }{\langle F{\left(t\right)}^2\rangle }-1,$$ (1)

where τ is the lag time and F(t) and F(t + τ) are the fluorescence intensities at time t and time t + τ. The intensity at time t, F(t), can be defined as

$$F\left(t\right)=\kappa \times Q\times {\int }_0^{\infty }d\overrightarrow{r}\times w_{\overrightarrow{r}}\times C\left(\overrightarrow{r},t\right).$$ (2)

In the above equation, κ is a constant that depends on the instrument settings, and $C\left(\overrightarrow{r},t\right)$, Q, and $w_{\overrightarrow{r}}$ represent the concentration function, quantum yield, and point spread function (PSF), respectively.

In single-point FCS, the acquisition time is much longer than the characteristic diffusion time (by at least two orders of magnitude), and the fluorescence correlation function, resulting from diffusion of the fluorescence particles in and out of the PSF and in different positions of the PSF, decays to zero. Assuming a three-dimensional (3D) Gaussian excitation volume, single-photon excitation, and 3D diffusion, these data can be analyzed using the common FCS autocorrelation equation (27, 28, 29),

$$G\left(\tau \right)=\frac{\gamma }{\langle N\rangle }\times {\left(1+\frac{4\times D\times \tau }{{\omega }_0^2}\right)}^{-1}\times {\left(1+\frac{4\times D\times \tau }{z_0^2}\right)}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},$$ (3)

where N, D, τ, ω₀, and z₀ represent the average number of molecules in the confocal volume, the diffusion constant of the fluorescent species, the lag time, and the waist and height of the Gaussian beam, respectively. The γ factor is related to the shape of the illumination profile.

It should be noted that Eq. 3 is only valid if the time of the fluorescence intensity acquisition at each pixel is long enough, and as a rule of thumb, the acquisition time has to be at least two orders of magnitude longer than the characteristic correlation time for fitting of the correlation decay with Eq. 3. In comparison, the autocorrelation function calculated for a very short period of time has a very different shape, and its decay is usually beyond zero, to negative values. This is due to the limited sampling interval of the relaxation of the fluctuation. Thus these correlation functions cannot be analyzed using Eq. 3, and a different type of approach is required.

This believed new approach to analyzing correlation decays obtained from short-time-sequence acquisition involves transforming the correlation functions to phasor plots using Fourier transformation. This is similar to the phasor approach developed earlier by Digman et al. for fluorescence lifetime imaging (FLIM) (30, 31, 32, 33). With this method, the autocorrelation function is calculated from short-time acquisition at each pixel using the expression in Eq. 1, but because the average is obtained from a short sequence, the fluctuation might not yet have completely relaxed. The obtained autocorrelation functions, (G(τ)), are then transformed to the phasor plot as follows:

$$g=\frac{{\int }_0^T\text{cos}\left(2\pi t\right)\times G\left(\tau \right)dt}{{\int }_0^{T}G\left(\tau \right)dt}$$ (4a)

$$s=\frac{{\int }_0^T\text{sin}\left(2\pi t\right)\times G\left(\tau \right)dt}{{\int }_0^{T}G\left(\tau \right)dt}.$$ (4b)

In comparison to the FLIM method (30, 31, 32, 33), however, the amplitude is kept constant in the phasor FCS method using the relation

$$\sqrt{s^2+g^2}=\mathrm{0.5.}$$ (5)

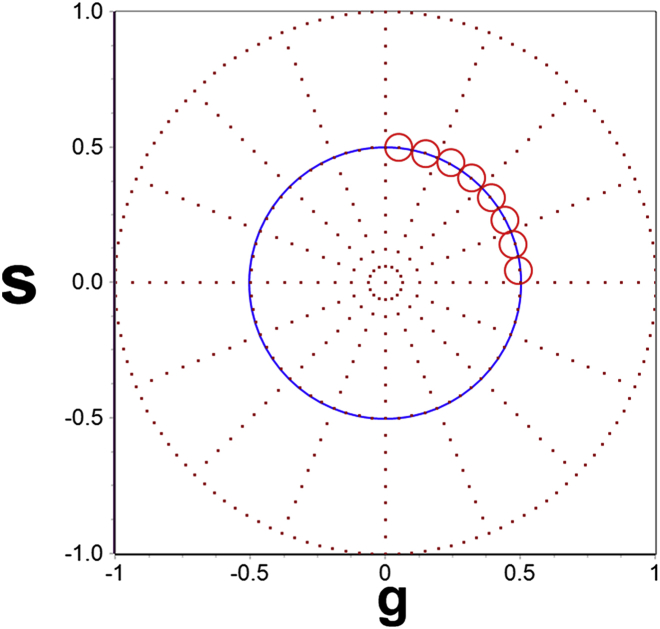
Thus, after the phasor transformation, the correlation decays obtained at each pixel of an image get converted to individual points in the polar plot (Fig. 1) and appear along the blue circle in the first quadrant (shown by the position of the cursors (Fig. 1, red circles)). The phasor plot is the histogram of values of the short correlation function, G(τ), at each pixel of the image. In this process of phasor transformation, the correlation-time information of the autocorrelation decay is preserved in the Fourier space. However, the amplitude information, and consequently the number and brightness information, are lost. The short correlation function could be negative at some correlation time, but after calculation of the Fourier components, negative values of the correlation function do not change the phase of the transformed point, and thus, the relaxation timescales determined by the phasor method remain unaffected. After transformation to the phasor plot, slowly diffusing particles appear at high s and low g values (larger phase angles) and the faster-diffusing species appear at high g and low s values (small phase angles).

Figure 1.

Transformation of the autocorrelation function calculated from the short-time intensity acquisition to the phasor plot. The autocorrelation functions, after transformation to the phasor plot, appear along the blue circle in the first quadrant of the phasor (s against g) plot and appear in the areas shown by the red cursors (circles). Slow diffusion appears at large phase angles and fast diffusion at smaller phase angles. To see this figure in color, go online.

Different components of the distribution of diffusion populations can then be selected by choosing a set of points in the phasor plot with colored cursors (see Fig. 1, red circles), and the intensity images can be painted accordingly. This is achieved simply by identifying the chosen phasor points with the corresponding pixels of the image. In this process, the intensity image is painted with the chosen cursor color, and regions of different diffusion populations can be easily identified. Up to this point, the data analysis does not involve any fitting or assumptions, because all that is involved is calculation of the correlation function, G(τ), using Eq. 1, and mathematical transformation of G(τ) to the phasor space using Eqs. 4a and 4b.

Estimate the value of the diffusion coefficient from a position in the phasor histogram requires a forward calculation, which is obtained by calculating the expected position of a species diffusing with a given diffusion coefficient under the conditions of the experiment. For this forward calculation, we need the shape of the PSF, ω_p, a model for diffusion, $C\left(\overrightarrow{r},t\right)$, the pixel dwell time, and the specific scanning path employed. For 3D diffusion, Eq. 3 gives the value of G(τ) for a given beam waist, D, and the time delay used for data acquisition. To calculate the phasor position, we must account for the limited range of the time sequence acquired. For example, we calculate Eq. 3 for N points at a repetition time of τ₀ per point and insert the values calculated in Eqs. 4a and 4b. This calculation provides the position in the phasor plot of a molecule diffusing with a given diffusion coefficient, D. Then, for each diffusion-coefficient value plotted in the x axis (in a semilogarithmic fashion), we count in the phasor plot the number of pixels (y axis) that fall in the proximity of that value. The number of pixels counted depends on the size of the circular cursor used to analyze the phasor plot. The end result is the calculation of the diffusion coefficient present at each pixel of the image falling within the circle used to analyze the diffusion phasor plot. The radius of the circle determines the resolution used to estimate the diffusion coefficient.

Simulation

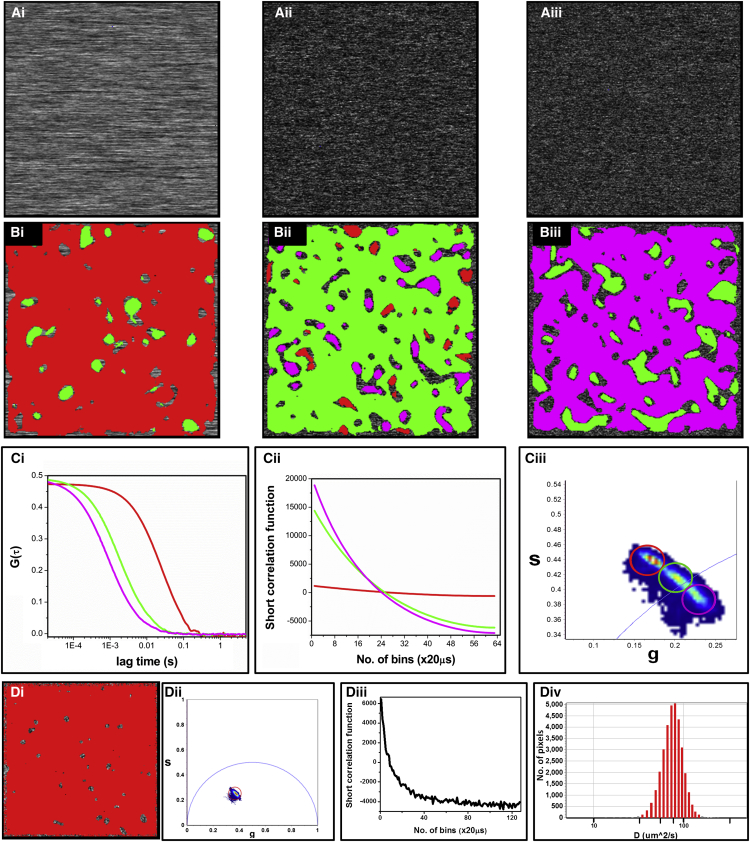
Simulations were performed to distinguish the resolvability of the diffusion phasor and the position of the different diffusion coefficient for a given pixel dwell time. This involved simulation of the fluorescence intensity traces of fluorophores diffusing freely through an observation volume. The molecules were allowed to move in a 2D plane and the PSF was approximated to a 3D Gaussian (ω₀ = 0.3 μm and z₀ = 1.2 μm). Three different intensity images corresponding to diffusion coefficients of 1 μm²/s, 10 μm²/s, and 20 μm²/s were simulated with a pixel dwell time of 20 μs and 128 repeat points (see Fig. 2 A). The single-point FCS and phasor FCS decays (Fig. 2 C, i and ii, respectively) were calculated from the simulated intensity data. In these two figures, red, green, and purple represent the single-point FCS and phasor FCS for diffusion coefficients of 1 μm²/s, 10 μm²/s and 20 μm²/s, respectively. The difference in the correlation times for the single-point FCS data can be noticed very easily. In the phasor FCS plot (Fig. 2 C, ii), the slope of the correlation decay decreases with increasing diffusion constant, as can be seen from the decay for the diffusion coefficient of 1 μm²/s, which is much flatter compared to the decay for 20 μm²/s. However, compared to the correlation decays for single-point FCS (Fig. 2 C, i), which have the same amplitude, the G(0) values for phasor FCS decay are different, and as a result, the number and brightness information cannot be calculated from these measurements. Transformation of the phasor FCS decays to the phasor plot is shown in Fig. 2 C, iii; colored cursors can be used to choose the different distributions of points in the phasor plot and paint the intensity images accordingly. The images in Fig. 2 B, i–iii, are intensity images corresponding to Fig. 2 A, i–iii, respectively, color mapped by the chosen cursors of Fig. 2 D, iii. These images show that phasor FCS can be used to easily separate the pixels belonging to fluorophores with different diffusion coefficients and then paint them accordingly to give a detailed diffusion map.

Figure 2.

Intensity image and single point phasor FCS calculation from the simulated fluorescence intensity. (A) Simulated intensity images for a sample with diffusion coefficients of 1 μm²/s (i), 10 μm²/s (ii), and 20 μm²/s (iii) with a pixel dwell time of 20 μs and 128 repeats per pixel. (B) Intensity images of the populations selected in C. (C) Calculated single-point FCS decays (i) of 1 μm²/s (red), 10 μm²/s (green), and 20 μm²/s (purple). Colored circles (iii) in accordance with the FCS-decay color scheme (Ci) were used to select different populations in the diffusion phasor plot, and the intensity images (Bi, Bii, and Biii) were painted accordingly. The prevalence of red, green, and purple in the images in B shows that diffusion can be resolved using the phasor FCS approach. (D) Specific analysis of the simulated case for diffusion of 20 μm²/s. Also shown are the short FCS decays (Diii) and transformation to the diffusion phasor (Dii), where the image (Di) is colored according to the color selection in (Dii) and the recovered diffusion histogram (Div) according to a model for one-species diffusion. To see this figure in color, go online.

Materials and Methods

Cell culture and transfection

Chinese hamster ovary (CHOK1) cells stably transfected with paxillin-enhanced green fluorescent protein (Pax-EGFP) were cultured and maintained at 37°C in a humidified 5% CO₂ atmosphere in Dulbecco’s modified Eagle’s medium/F12 (1:1) (11320-033, Life Technologies, Carlsbad, CA), supplemented with 10% fetal bovine serum and 1% penicillin streptomycin to maintain selection. Freshly split cells were plated onto 35-mm glass-bottom dishes (Mattek, Ashland, MA) for the optical experiments.

Label free CHOK1 cells were cultured in Dulbecco’s modified Eagles medium/F12 (1:1) supplemented with 10% fetal bovine serum and 1% penicillin streptomycin. Freshly split cells were plated onto 35-mm Mattek glass-bottom dishes for the optical experiments. These cells were transected with human insulin receptor plasmid (hIR) (addgene, Cambridge, MA) using Lipofectamine 2000 (Life Technologies) according to the manufacturer’s instructions. Generally, 1 μg of the plasmid was incubated with 5 μL of Lipofectamine 2000 in fully supplemented media. Samples were used within 24 h of transfection.

Microscopy

The phasor FCS measurements were carried out using a modified commercial Olympus FV1000 (Center Valley, PA) laser scanning microscope. In this modified instrument, the galvanometric scanning mirrors of the commercial microscope were controlled by an IOtech card. The signal from the photomultiplier tube was sent back externally to the IOtech card after being transformed into photon counts using an amplifier and discriminator. Scanning and acquisition were controlled using the SimFCS software developed by Prof. Enrico Gratton at the Laboratory for Fluorescence Dynamics in Irvine, CA (software available at www.lfd.uci.edu). A 60× water immersion objective, 1.2 NA (Olympus, PA) was used to excite and collect fluorescence. Pax-EGFP and hIR-GFP were excited with the 488 nm line of the Ar-laser. The volume of the PSF was obtained by measuring the single-point FCS correlation function of 50 nM GFP in Dulbecco’s phosphate-buffered saline (DPBS) buffer and fitting those decays with the diffusion constant of 90 μm²/s. A typical value of ω₀, defining the value of the PSF, was on the order of 0.24 μm. The coverslips for the GFP measurements were treated with bovine serum albumin to prevent surface absorption of the GFP.

Data acquisition for single-point FCS of the beads involved a total acquisition time of ∼300 s with 10 μs pixel dwell time. The correlation functions were calculated from the obtained intensity traces and fitted to obtain the diffusion constant for a given ω₀ using SimFCS. RICS images were obtained in a 256 × 256 pixel image with pixel resolution of 50 nm and pixel dwell time of 40 μs. At each measurement point, 100 images were taken for the analysis. The images were corrected by subtracting the moving average. To calculate the diffusion constant at different parts of the image, different regions of interest were selected and fitted using the SimFCS.

The data acquisition and analysis for the short-time-sequence FCS are different from conventional RICS measurements, as explained below in more detail.

Data acquisition for phasor FCS

Data acquisition for the short-time-sequence FCS (phasor FCS) was controlled by SimFCS. Two different modes of acquisition, the point-scan mode and line-scan mode, were used. The point-scan mode resembles single-point FCS at each pixel of an image and requires continuous measurements at the same pixel before moving to the adjacent pixel. The main difference is that the acquisition time for phasor FCS in this mode is much shorter (1–8 ms) than that for single-point FCS (10–100 s). The time difference between two continuous measurements at the same pixel in this mode is the pixel dwell time.

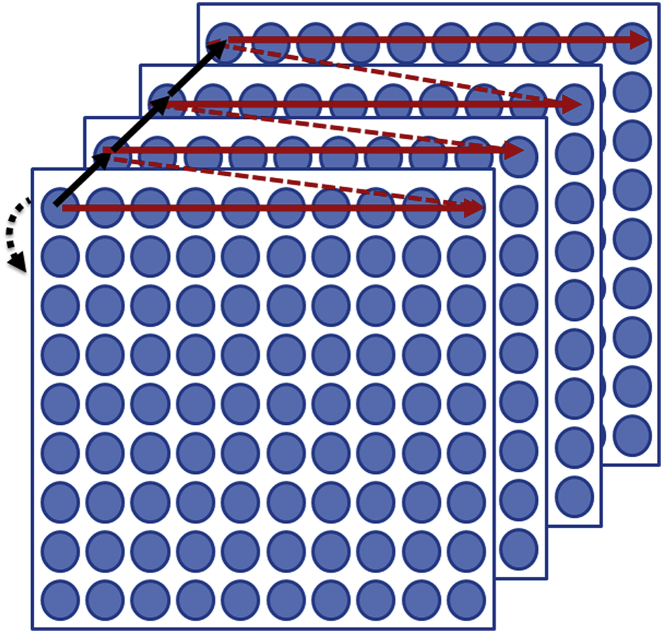
Data acquisition in the line-scan mode is in principle similar to raster scanning. The main difference from a conventional RICS acquisition is that with this technique, each line of the image was scanned multiple (64/128) times with a fixed pixel dwell time. After the repeats of the line scan were finished, the acquisition was moved to the next line and that line was then scanned multiple times. This was repeated until the whole area of the image had been scanned. The time difference between two sequential measurements at the same pixel was equal to the line time. This mode of acquisition enables us to measure the intensity at a particular pixel for a longer time without increasing the total image acquisition time. It is also very useful for measuring the diffusion of proteins in a cell, where diffusion is usually slow and intensity fluctuations due to the movement of the molecules happen at a slower timescale than in solution. The total acquisition time required for the whole image is much less than the time required with single-point FCS at each point of the image. This data acquisition scheme is pictorially represented in Fig. 3.

Figure 3.

Schematic representation of data acquisition for the phasor FCS method. The blue circles represent the pixels of an image. In this scanning mode, each line is scanned multiple times. The line time and the retracing time are represented by the solid and dashed red lines, respectively. The time between two consecutive acquisitions at the same pixel is shown by the solid black line and is equal to the sum of line time plus retracing time. After the line scans are completed, the scanner moves to the next line (black dashed arrow). To see this figure in color, go online.

The pixel repeat time for the phasor FCS method depends on the diffusion coefficient of the fluorophore. Fast-moving molecules create fluctuations in the fluorescence intensity at a faster timescale, and if the repeat time is too slow then the fluctuations are lost between two continuous measurements at the same pixel. On the other hand, if acquisition is too fast, data may be acquired before the fluctuations are being manifested. In these cases, diffusion coefficients calculated from phasor FCS can have large errors. Thus, there is a need to match the pixel dwell time with the expected diffusion coefficient. This is shown in Fig. S1 in the Supporting Material. The left y axis represents the characteristic correlation time of a fluorophore for a given diffusion coefficient (x axis) and a given PSF of 0.3 μm waist. The pixel dwell time required to measure a given diffusion coefficient is shown on the right y axis. These pixel dwell times are calculated for 128 repeats at the same pixel. The larger pixel dwell times can be determined using the line-scan mode and the smaller pixel dwell times using the point-scan mode. Thus, a combination of the two methods allows us to calculate diffusion coefficients in any range.

Data analysis for phasor FCS

The data analysis for phasor FCS was accomplished using SimFCS (available at www.lfd.uci.edu). The data were transposed so that the different time points originating from acquisitions at the same pixel were aligned, and the intensity image was constructed using the average intensity. The image was then corrected for the background, and only pixels of the image above a given threshold were used for the analysis. The correlation functions at each pixel of the image for the short-time sequence acquisition were calculated and transferred to the phasor plot using Fourier transformation as described in above (see Theory). Different phasor points in the phasor plot were chosen with colored cursors, and the corresponding pixels in the intensity image were masked with the color of the cursor. Up to this point of the analysis, the original data have only been transformed, with no fitting or interpretation of their meaning involved. A 3D plot was then constructed using the intensity image as the wire frame, with the level of intensity representing the height of the image and the wire frame painted with the cursor color corresponding to the pixel chosen in the phasor plot. This enabled us to visually determine whether there was any relationship between the different pixels of the diffusion phasor plot and the intensity image. Finally, the diffusion coefficient at the individual pixel was calculated based on a 3D diffusion model and plotted in a log-diffusion plot, where the x and y axes represent the diffusion constant in the log scale and the number of pixels that belong to a particular diffusion constant, respectively. To correctly calculate the diffusion-coefficient histogram, GFP in DPBS buffer was used for the calibration. The waist of the PSF was calculated by fitting the RICS measurements with the diffusion coefficient of GFP (90 μm²/s) (34). This calculated ω₀ value is used for phase-angle correction of the diffusion phasor measurements. Application of this phase-angle correction and a proper diffusion range results in quantitatively correct estimation of diffusion coefficients using phasor FCS. The end result is an intensity image of the cell painted according to the diffusion coefficients corresponding to populations obtained from the phasor plot.

Results

Measurements of diffusion of GFP in solutions

To demonstrate that the measurements using the short-time sequence method analyzed with the phasor FCS approach can yield the same result as that of other fluctuation-based techniques, diffusion of GFP in DPBS buffer was measured using both RICS and the phasor FCS approach. RICS measurements and phasor FCS were carried out using a pixel size of 32 nm and a pixel dwell time of 10 μs. One hundred frames were recorded for the RICS measurements and the phasor FCS measurements were done in the point-scan mode. Both types of acquisition were carried out using the IOtech card and controlled by SimFCS, and the data were analyzed using the same software. Fig. S2 A describes the fitting from the RICS measurements. The diffusion coefficient of GFP for the RICS measurement was fixed at 90 μm²/s and the calculated ω₀ (0.25 μm) was used for fitting the phasor FCS. The histogram of diffusion coefficients calculated from phasor FCS (Fig. S2 B) has a maximum at 91 μm²/s. This shows the agreement between RICS and phasor FCS measurements and proves that phasor FCS can be used to quantitatively calculate the diffusion coefficients.

The goal of this technique is to create a pixel-resolved map of diffusion of biological macromolecules inside the cell. To achieve this goal, we measured two different types of fluorescently labeled proteins, Pax-EGFP and hIR-GFP, both of which are expressed in CHOK1 cells.

Measurements of diffusion of Pax-EGFP in the cytoplasm of CHOK1 cells in line scan mode

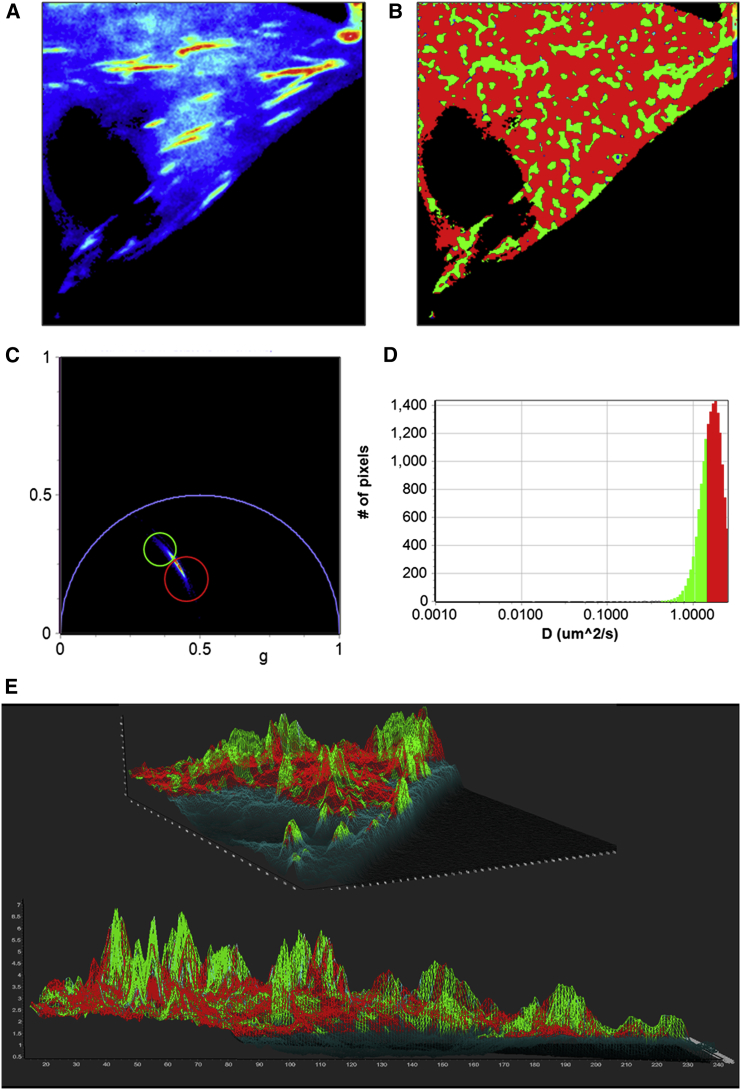
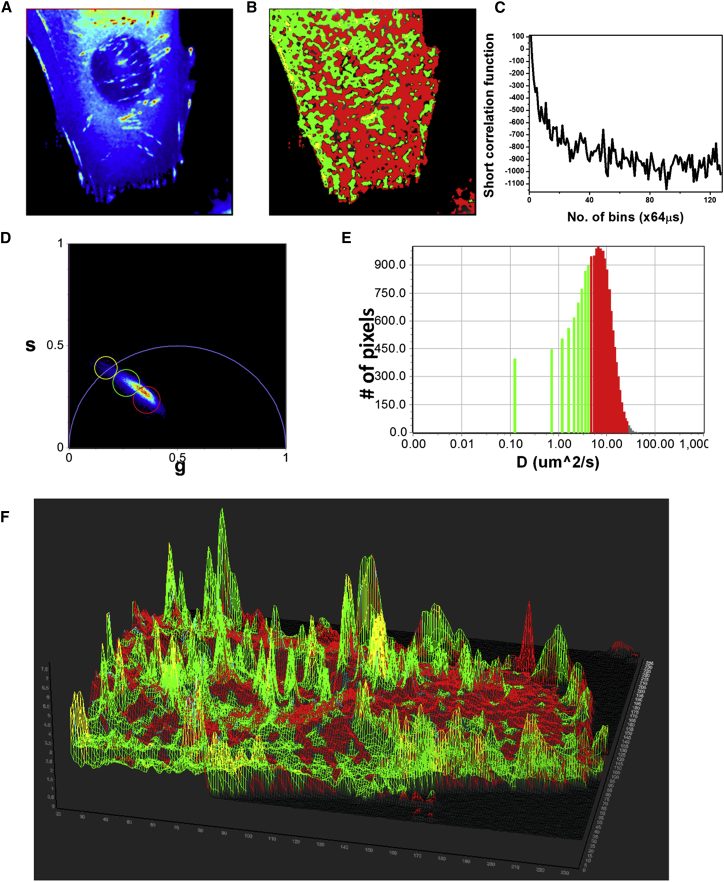
Paxillin-EGFP is a comparatively faster-moving molecule in the cytoplasm of the cells. Thus, to measure the diffusion of Pax-EGFP in the cell, two different modes of data acquisition were used. In the line-scan mode, a comparatively faster data acquisition of 8 μs/pixel or 16 μs/pixel was selected and the scans were carried out in line-scan mode for 64 or 128 repeats/line. Fig. 4 represents the analysis using the phasor FCS approach. The intensity image (Fig. 4 A) shows the presence of focal adhesion sites where the Pax-EGFP binds that have a higher concentration than the rest of the cell. Fig. 4 C shows the position of the cursors in the diffusion phasor plot used to select different sections of the distribution of the diffusing species. These colors are used to paint the intensity image (Fig. 4 A) to create the diffusion image (Fig. 4 B). A close inspection of the intensity image (Fig. 4 A) and the diffusion image (Fig. 4 B) shows that the areas of the highest intensity, i.e., the areas of focal adhesion, have slower diffusion (Fig. 4 B, green) and the rest of the cell has faster diffusion (Fig. 4 B, red). It has been shown previously by Digman et al. (35) that the diffusion of paxillin is appreciably slower near focal adhesion sites. This means that at the focal adhesion site, the intensity is highest and the diffusion slowest (Fig. 4 B). To verify this finding, a 3D image (Fig. 4 E and Movie S1) was constructed where the intensity was used as the wireframe and the colors of the chosen cursors were mapped to the image. Thus, the higher-intensity regions are represented as the peaks in this 3D image. It can be seen that the peaks are green and yellow color, representing slower diffusion, and the valleys are mostly red, characteristic of faster diffusion. The distribution of the diffusion coefficients is presented in the diffusion histogram (Fig. 4 D). This result is in agreement with the results of Digman et al. (14, 35, 36). Measurements were repeated for N = 40 Pax-EGFP-labeled CHOK1 cells, and the differences in diffusion behavior between the cytoplasm far from the adhesions and the regions near the adhesions were consistent over all the measurements.

Figure 4.

Diffusion analysis of the Paxillin-EGFP in CHOK1 cells acquired using the line-scan method. (A) Fluorescence intensity map of Pax-EGFP. Bright spots represent the focal adhesion sites. (B) Diffusion map of the cell, with color coding based on the cursors in C (colored circles). (C) The phasor plot. (D) Diffusion histogram calculated based on a 0.4 μm ω₀ and 3D diffusion profile. (E) 3D intensity map of the cell, where the intensity was used as the wire frame. The height on the z plane represents intensity. The image was then color-coded based on the cursor colors in C. The color of the mask at the peaks is mostly green, representing slow diffusion in the focal adhesion sites. To see this figure in color, go online.

Measurements of diffusion of Pax-EGFP in the cytoplasm of CHOK1 cells in point-scan mode

The diffusion of Pax-EGFP in the CHOK1 cells was also measured using the point scan approach. For this approach, the intensity was measured with a 64 μs pixel time for 256 continuous measurements at the same pixel. Once the measurements at the same pixel were completed, the acquisition was moved to the adjacent pixel and repeated. This resembles acquisition by single-point FCS at each point of an image but has a much shorter data collection time. The phasor FCS data analysis was carried out on the collected images, and the results are presented in Fig. 5.

Figure 5.

Diffusion analysis of the Paxillin-EGFP in CHOK1 cells acquired using the point-scan method. (A) Fluorescence intensity map of Pax-EGFP. Bright spots represent the focal adhesion sites. (B–D) Diffusion map of the cell (B) color-coded to match the cursor colors in the phasor plot (D) and representative short decay correlation function (C). (E) Diffusion histogram calculated based on a 0.4 μm ω₀ and 3D diffusion profile. (F) 3D intensity map of the cell, where the intensity was used as the wire frame. The height in the z plane represents intensity. The image was then color-coded to match the cursors in D. The color of the peaks is mostly green, representing slow diffusion in the focal adhesion sites. To see this figure in color, go online.

Fig. 5 D shows the position of the cursors in the diffusion phasor plot that were used to select different sections of the distribution of the diffusing species. These colors are used to paint the intensity image (Fig. 5 A) to create the diffusion image (Fig. 5 B), and the diffusion image shows that diffusion is faster in the cytoplasm (red) and slower at the highest-intensity areas, i.e., the focal adhesion sites (green and yellow). This can be seen much more clearly in the 3D intensity wireframe (Fig. 5 F), where the z axis represents the level of intensity and is color mapped with the phasor colors chosen in Fig. 5D. The peaks in Fig. 5 F are colored yellow or green, representing slow diffusion, and the valleys are presented in red, showing faster diffusion. This is similar to the line-scan-mode analysis for the Pax-EGFP described previously. These data were analyzed using the ω₀ value (0.25 μm) and phase-angle correction (0°) calculated by fitting of the GFP in DPBS buffer used for the calibration. The histogram of diffusion coefficients (Fig. 5 E) shows that the diffusion coefficients in the cytoplasm (red bars) and focal adhesion sites (green bars) are on the order of 10 μm²/s and 1 μm²/s, respectively, similar to the values obtained for the diffusion phasor measurements in line-scan mode.

Measurements of diffusion of hIR in CHOK1 cells in line-scan mode

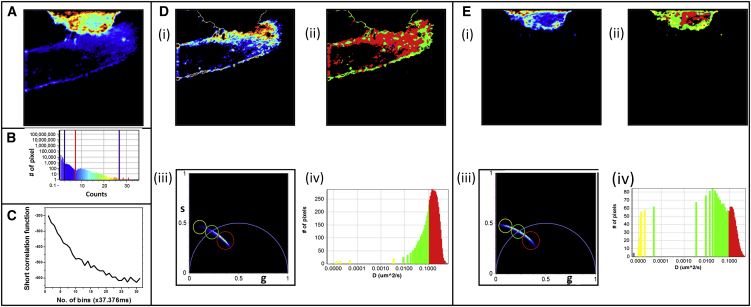
The second type of biological measurement involved hIR-GFP in the CHOK1 cells. This protein (hIR) is present in the endoplasmic reticulum and in cell membranes and is known to have a much slower diffusion than GFP in the cytoplasm (16, 18, 37). Thus, the scanning speed was changed to 64–128 μs/pixel and the line was repeated 64–128 times. The resulting measurements are presented in Fig. 6. The different cells (Fig. 6, C and D) can be chosen based on the different intensity levels from the histogram (Fig. 6 B). The diffusion analysis suggests that the slower-moving population of the hIR-GFP is present on the cell surface and the faster-moving population is present inside the cells. A series of measurements show the presence of inhomogeneity in the diffusion of hIR-GFP in these cells (Fig. S4). The position of the cluster of points in the phasor plot shifts from measurement to measurement for the cells transfected with hIR-GFP, showing heterogeneity in diffusion of hIR-GFP among the different cells (Fig. S4 C). However, one can see that among the different areas of the cell, the diffusion in the cell membrane is always slower than diffusion in the endoplasmic reticulum, and the calculation of the diffusion phasor is independent of the intensity of the cell.

Figure 6.

Diffusion analysis of hIR-GFP in CHOK1 cells. (A) Fluorescence intensity image of the hIR-GFP-labeled cells. (B), Intensity histogram used to choose the dimmer or brighter cells. (C) Diffusion measurements in the dimmer cells chosen by the histogram in B. (D) Intensity map (i), diffusion map (ii), diffusion phasor (iii), and diffusion histogram for the dimmer cell. (E) Intensity map (i), diffusion map (ii), diffusion phasor (iii), and the diffusion histogram (iv) for the brighter cell chosen by the histogram in B. To see this figure in color, go online.

The values calculated from the diffusion phasor have been compared with values measured by RICS in different areas of the cell and published values measured using fluorescence recovery after photobleaching (37). RICS measurements around the cell membrane yield diffusion constant values of −0.18∼0.20 μm²/s, and measurements at the interior of the cell have a value of ∼1.0 μm²/s. Diffusion measurements using the phasor FCS method, yielded similar values, as can be seen from the histogram of diffusion coefficients (Figs. 6 C, iv, 6 D, iv, and S4 B). The similarity between the values obtained from these two separate measurements shows the agreement between these different techniques.

Discussion

In this article, we have presented a to our knowledge new method of data acquisition and analysis for mapping the diffusion of molecules in cells using a common commercially available laser scanning microscope. Conventional methods, including single-point FCS and other scanning correlation microscopy techniques (e.g., spFCS and RICS), are capable of elucidating diffusion of a fluorescent species in the cell, but not at a per-pixel resolution of the image and not for every pixel of the image. In principle, single-point FCS at each pixel of an image could provide the diffusion coefficient at each pixel. However, the total exposure time for measuring each pixel of an image is prohibitively long and leads to eventual bleaching of the sample. For single-point FCS, there are two possibilities: either to measure fewer points or to measure each point for less time. If molecules are diffusing slowly, we could measure the intensity at a single point for a brief time and then measure the intensity at many other points before returning to measure the intensity at the original point. If we properly multiplex the time and location of the measurement, we could measure many locations quasisimultaneously and still extract the value of the diffusion coefficient using the correlation point at one location. A simple way to accomplish this multiplexing is to repeat a line in the raster scan microscope several times, for example, 128 times, and then move to the next line, as shown schematically in Fig. 3. For example, if we sample a pixel at 8 μs dwell time and we acquire 256 points along a line, it will take ∼2 ms/line (neglecting retracing time). In this case, the same pixel is measured again every 2 ms. If we repeat the line 128 times (128 ms total), we have a short time sequence, but still we could calculate the correlation function of this sequence. Then, 256 lines are measured in an image for a total measurement time of 64 s. The short-time-sequence correlation function obtained at each pixel has a different form than the correlation functions normally used to fit single-point FCS correlation functions, which assume that the time sequence is very long. In principle, we could fit each of the 256 × 256 correlation functions with a modified G(τ) that accounts for the short time sequence. However, we found that the amplitude of the short-time-sequence correlation function is very noisy, whereas the characteristic relaxation of G(τ) for the short time sequences is more robust.

To account for these limitations, and to avoid the noise arising from the fit, we created the diffusion phasor approach based on the correlation of a very short time sequence, which is sufficient to recover the distribution of diffusion coefficients throughout the cell and create a detailed diffusion map. This to our knowledge new technique has been tested in various different environments, i.e., GFP in DPBS, Pax-EGFP in CHOK1 cells, and hIR-GFP in CHOK1 cells. In all cases, the phasor FCS measurements are consistent with measurements using other conventional methods and match the values reported previously. The total acquisition time for a 256 × 256 frame is rather short and depends on the line time needed to match the characteristic diffusion time at one pixel (3–10 min) and can be used to create a detailed diffusion map with a pixel resolution for an entire image.

The phasor approach, because it is fit-free, provides instantaneous representation of the diffusion map of a cell, and it could be used to analyze hundreds of images simultaneously, since the time to map diffusion values for an image is extremely short. Although we have discussed using the phasor approach to estimate the diffusion coefficient at each pixel, we could use other models for the calculation of the forward problem, such as binding of blinking. Our method can equally well be applied to cross-correlation of the fluctuations between two or more detection channels.

Editor: Paul Wiseman.