Silicon coupled-resonator optical-waveguide-based biosensors using light-scattering pattern recognition with pixelized mode-field-intensity distributions

Abstract

Chip-scale, optical microcavity-based biosensors typically employ an ultra-high-quality microcavity and require a precision wavelength-tunable laser for exciting the cavity resonance. For point-of-care applications, however, such a system based on measurements in the spectral domain is prone to equipment noise and not portable. An alternative microcavity-based biosensor that enables a high sensitivity in an equipment-noise-tolerant and potentially portable system is desirable. Here, we demonstrate the proof-of-concept of such a biosensor using a coupled-resonator optical-waveguide (CROW) on a silicon-on-insulator chip. The sensing scheme is based on measurements in the spatial domain, and only requires exciting the CROW at a fixed wavelength and imaging the out-of-plane elastic light-scattering intensity patterns of the CROW. Based on correlating the light-scattering intensity pattern at a probe wavelength with the light-scattering intensity patterns at the CROW eigenstates, we devise a pattern-recognition algorithm that enables the extraction of a refractive index change, Δn, applied upon the CROW upper-cladding from a calibrated set of correlation coefficients. Our experiments using an 8-microring CROW covered by NaCl solutions of different concentrations reveal a Δn of ~1.5 × 10⁻⁴ refractive index unit (RIU) and a sensitivity of ~752 RIU⁻¹, with a noise-equivalent detection limit of ~6 × 10⁻⁶ RIU.

Due to the increasing demand of healthcare, various chip-scale, label-free optical biochemical sensing technologies have been proposed and studied over the past two decades¹,²,³,⁴,⁵. Specifically, optical microresonator-based biochemical sensors have been attracting significant attention over the past decade. Conventional biochemical sensing techniques using optical microresonators typically employ two ways to quantitatively derive real-time information of the analyte on the microresonator surface. One is to monitor ultra-high-quality (ultra-high-Q) cavity resonance wavelength shifts in the transmission spectrum through scanning the input laser wavelength in the proximity of the resonance⁶,⁷,⁸,⁹,¹⁰,¹¹,¹²,¹³,¹⁴. The other is to monitor the transmission intensity change around a cavity resonance at a fixed wavelength⁷. However, both approaches working in the spectral domain typically require a precision spectrum scanning system such as a wavelength-tunable diode laser.

Previously, our research group has proposed an alternative microresonator-based biochemical sensing scheme working in the spatial domain by using a coupled-resonator optical waveguide (CROW) excited at a fixed wavelength and monitoring the analyte-induced discrete modulations of the pixelized light-scattering intensity patterns among the CROW eigenstates¹⁵,¹⁶. Such a sensing scheme only requires a relatively simple optical read-out system including a fixed-wavelength laser and a camera. The simultaneous imaging of the spatially distributed coupled microresonators allows such a scheme to be more immune to the equipment noise that equally affects each microresonator but does not change the relative intensity distribution. Other researchers have also recently studied CROWs through imaging the out-of-plane elastic light scattering intensity patterns in the far field¹⁷,¹⁸,¹⁹. Nonetheless, our initial proposal fell short in measuring only discrete modulations in refractive index applied on the CROW surface, and only considered an ideal CROW structure.

Here, we propose and demonstrate as a proof of concept an improved CROW-based biochemical sensing scheme working in the spatial domain using albeit imperfect coupled microring resonators on the silicon-on-insulator (SOI) platform. The choice of the SOI platform in 1550 nm wavelengths is primarily motivated by the maturing complementary metal-oxide-semiconductor (CMOS)-compatible SOI technology available to silicon photonics. We devise a correlation analysis of the pixelized mode-field-intensity distributions to extract from a library of calibrated correlation coefficients a refractive index change, Δn, applied upon the CROW surface from a known cladding refractive index, n₀. We model the CROW sensor assuming an imperfect CROW with fabrication-imperfection-induced randomly disordered coupled microresonators. Our experiments using a SOI 8-microring CROW in 1550 nm wavelengths reveal a Δn of ~1.5 × 10⁻⁴ refractive index unit (RIU). Upon a specific probe wavelength, we demonstrate a sensitivity in terms of correlation coefficient change per unit RIU of ~752 RIU⁻¹ and a noise-equivalent detection limit (NEDL) of ~6 × 10⁻⁶ RIU.

Results

Principle

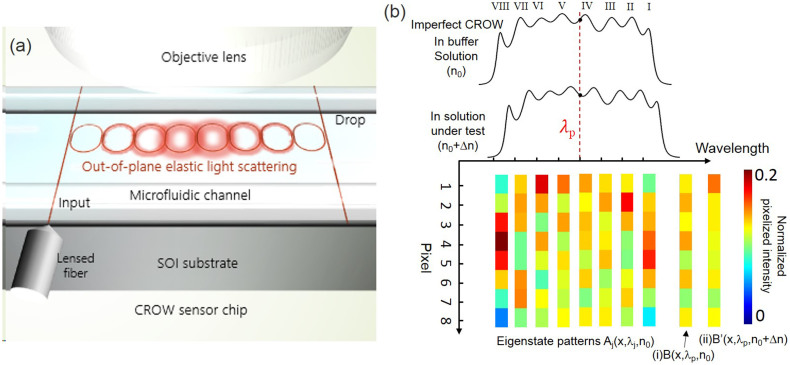
Fig. 1 illustrates the proposed CROW-based biochemical sensor. Fig. 1(a) shows the device schematic of a SOI CROW sensor comprising eight identically designed coupled microring resonators symmetrically coupled to input and output bus waveguides in an add-drop filter configuration. The out-of-plane elastic light scattering of the CROW is imaged by a top-view objective lens into an infrared (IR) camera in the far field. The sensor is integrated with a microfluidic channel on the top.

Figure 1. Working principle of CROW-based biochemical sensors in the spatial domain.

(a) Schematic of a SOI CROW sensor comprising eight coupled microring resonators in an add-drop filter configuration. (b) Illustration of an imperfect eight-element CROW, including the inhomogeneously broadened transmission bands in a buffer solution and a solution under test, and the complete set of eigenstate normalized pixelized mode-field-intensity distributions upon n₀, {A_j}. Insets: (i) Pixelized mode-field-intensity distribution upon n₀, B(λ_p). (ii) Pixelized mode-field intensity distribution upon a small Δn, B′(λ_p).

In the case that the dimensional disorders are small and the identically designed coupled microresonators are singlemode, the number of CROW eigenstates within each transmission band equals to the number of microresonators. A perfect CROW without dimensional disorders only exhibits at half of its complete set of eigenstates (within half of the transmission band) distinctive mode-field intensity distributions. The pair of symmetric and anti-symmetric intercavity-coupling-induced split modes have identical mode-field intensity distributions but distinctive mode-field amplitude distributions and eigenfrequencies. In practice, each coupled microresonator displays certain deviations from the design due to fabrication imperfection. This breaks the symmetry between the pair of symmetric and anti-symmetric split modes. An imperfect CROW thus exhibits distinctive mode-field amplitude and intensity distributions among its complete set of eigenstates. Fig. 1(b) illustrates for an imperfect 8-element CROW the inhomogeneously broadened transmission bands upon n₀ and n₀ + Δn, and the complete set of distinctive eigenstate pixelized mode-field intensity distributions upon n₀, denoted as {A_j}.

We integrate the mode-field intensity of each microring to form a pixelized one-dimensional (1D) pattern for the ease of analysis. Trading-off some detailed features of the distributions makes the pattern-recognition analysis of the mode-field-intensity distributions computationally efficient. Any mode-field amplitude profile at an arbitrary wavelength, λ_p, within the CROW transmission band upon n₀ can be given by a linear superposition of the complete set of the eigenstate mode-field amplitude distributions upon n₀. Therefore, it is conceivable to uniquely identify by a correlation analysis any pixelized mode-field intensity profile, B(λ_p), as shown in inset (i), with {A_j}. Likewise, assuming a weak perturbation, we can uniquely identify by the correlation analysis any pixelized mode-field-intensity distribution upon a small global Δn in the cladding, B′(λ_p), as shown in inset (ii), with {A_j}.

Correlation analysis and the sensing algorithm

A unique feature in our correlation analysis is the use of the CROW eigenstate mode-field intensity distributions as intrinsic references. We adopt the Pearson's correlation coefficient, ρ, in order to quantify the correlation between a pixelized pattern at an arbitrary wavelength λ_p, B(λ_p), and the eigenstate pixelized patterns at the eigenstate wavelengths λ_j, A(λ_j). For an N-element CROW, we define the correlation coefficient as follows:

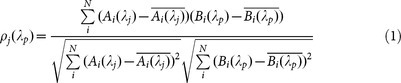where j = 1, 2, …, N is the eigenstate number, i = 1, 2, …, N is the cavity or pixel number, the pixel values A_i and B_i are normalized respectively to the total intensity of the entire patterns, the bar sign denotes the mean of the pixelized pattern over the number of pixels.

Previously²⁰, Pearson's product-moment correlation approach has been used to describe the dependence of a measured optical field intensity distribution to calibrated reference intensity distributions. Here, we utilize its property of invariance to change of level and scale in the two distributions under comparison. The Pearson's correlation coefficient allows the noise that are common to all pixels, including equipment noise and waveguide guided power fluctuation, to be effectively normalized. Thus, this approach allows our sensing scheme to be tolerant to the equipment noise.

Here we detail our sensing algorithm. We first generate a library of {ρ_j′(λ₀)} calibrated at a wavelength λ₀ centered at the CROW transmission band, with ρ_j′ defined by replacing from equation (1) the B(λ_p) terms with the pixelized patterns B′(λ₀). The library is taken over a range of calibrated Δn values, with a refractive index interval of Δn_i, and the range Δn_d is given by an integral multiple of Δn_i. The {ρ_j′(λ₀)} thus comprises a data array of N (rows) × M (columns), where M is given by Δn_d/Δn_i. We then generate a column of {ρ_j(λ_p)} according to equation (1) for an arbitrary baseline pattern B(λ_p) upon n₀. We next find the closest match of {ρ_j(λ_p)} with a particular column of {ρ_j′(λ₀)}. We can derive by interpolation for the baseline pattern a unique equivalent Δn_B that is associated with the wavelength offset between λ_p and λ₀. The interpolation enhances the resolution of Δn_B, given a certain Δn_i. We repeat the same process for the sensing pattern B′(λ_p) to uniquely extract an equivalent Δn_B′. Finally, we obtain Δn = (Δn_B′ − Δn_B).

In order to uniquely identify {ρ_j(λ_p)} from the library, we find from our modeling that it is sufficient to use only the principal component, ρ^p, and the second-principal component, ρ^s, of {ρ_j(λ_p)}, for N up to at least 28 (See Methods and Supplementary Information S1–S3). This streamlines the algorithm linearly by a factor of 2/N.

Modeling results

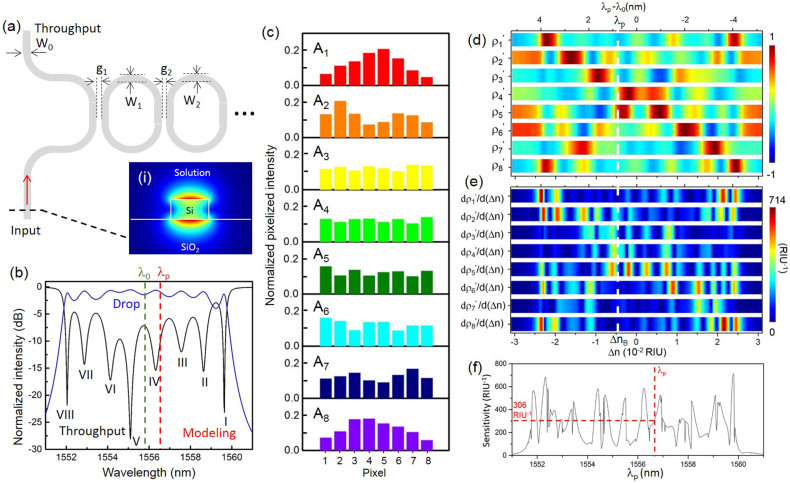
We use transfer-matrix method to model the imperfect SOI CROW (see Methods and Supplementary Information S1). Fig. 2(a) shows the schematic of the imperfect SOI CROW. Inset shows the cross-sectional view of the numerically calculated transverse-magnetic (TM)-polarized waveguide mode-field amplitude profile. We choose the TM polarization mode in order to obtain a good mode-field exposure into the analyte on the CROW top surface. We assume n₀ = 1.318 (water cladding). According to our numerical modelling using finite-element method (FEM), the fraction of the optical mode into the water is 14.4%, which is much higher than the value of 5.0% in the transverse-electric (TE) mode. Fig. 2(b) shows the modeled transmission spectra of an imperfect CROW. The imperfect CROW comprises eight non-identical microring resonators. The measured waveguide width and coupling gap spacing of each microresonator vary following Gaussian distributions (see Methods and Supplementary Information S2). Fig. 2(c) shows the modeled eigenstate pixelized patterns. Fig. 2(d) shows the calculated {ρ_j′(λ₀)} as a function of Δn, with Δn_d = 6.204 × 10⁻² RIU and Δn_i = 1.2 × 10⁻⁴ RIU. Fig. 2(e) shows the calculated differential correlation coefficients per unit Δn, given as (d(ρ′(λ₀))/d(Δn)).

Figure 2.

(a) Schematic of an imperfect CROW model with disordered waveguide widths W₁, W₂,…W_N and coupling gap widths g₁, g₂, … g_{N + 1}. Inset (i): Simulated cross-sectional view of the waveguide mode-field amplitude profile. (b) Modeled throughput- and drop-port transmission spectra of an imperfect CROW using transfer-matrix modeling. Green dashed line: reference wavelength λ₀ of 1555.82 nm. Red dashed line: probe wavelength λ_p of 1556.66 nm. (c) Modeled pixelized intensity patterns at eigenstates I–VIII. (d) Calculated library of the correlation coefficients ρ₁′–ρ₈′ as a function of Δn at λ₀. (e) Calculated library of the differential correlation coefficients as a function of Δn. (f) Calculated sensitivity as a function of probe wavelength. The red dashed line indicates a sensitivity of 306 RIU⁻¹ at 1556.66 nm.

When λ_p is offset from λ₀, the zero-point of Δn is offset in the opposite direction to Δn_B. We define the sensitivity at an arbitrary probe wavelength λ_p as the larger (d(ρ′(λ_p))/d(Δn)) of ρ^p and ρ^s, in units of RIU⁻¹. Therefore, we can directly extract the sensitivity for λ_p from the library of differential correlation coefficients at Δn_B in Fig. 2(e). Fig. 2(f)) shows a highly non-uniform distribution of the modeled sensitivity as a function of λ_p. The sensitivity spans a range of 1.6 RIU⁻¹ and 715 RIU⁻¹ over the spectral 3 dB-bandwidth with an average sensitivity of ~279 RIU⁻¹. It is highly dependent on the choice of λ_p. For modeling the sensing in the spatial domain, we first arbitrarily choose a fixed probe wavelength λ_p at 1556.66 nm near the center of the CROW transmission band (Fig. 2(b)). The sensitivity at λ_p is ~306 RIU⁻¹.

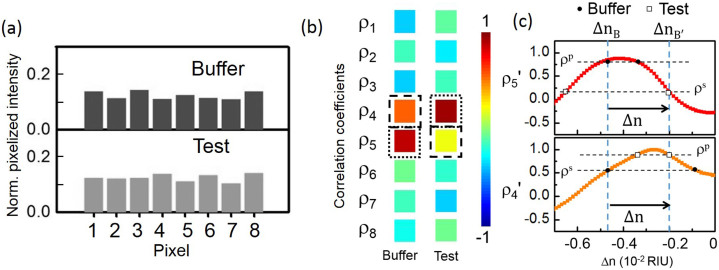
Fig. 3 illustrates the modeling of the CROW-based sensing using the correlation analysis. Fig. 3(a) shows the modeled pixelized patterns at λ_p without (buffer) and with (test) applying a Δn that is arbitrarily chosen as 2.68 × 10⁻³ RIU. Fig. 3(b) shows the two sets of modeled correlation coefficients of the two pixelized patterns without and with Δn. The ρ^p and ρ^s without Δn are ρ₅ and ρ₄, respectively. The ρ^p and ρ^s with Δn are ρ₄ and ρ₅, respectively. Fig. 3(c) shows a zoom-in view of the calculated library of ρ₅′ and ρ₄′ as a function of Δn and mapping of ρ₅ and ρ₄. We extract from the library Δn = Δn_B′ − Δn_B = 2.68 × 10⁻³ RIU, which agrees with the arbitrarily chosen Δn value.

Figure 3.

(a) Modeled pixelized patterns at probe wavelength λ_p (1556.66 nm) upon the buffer solution and the test solution. (b) Calculated sets of correlation coefficients upon the buffer solution and the test solution. The dotted-line boxes indicate ρ^p and the dashed-line boxes indicate ρ^s. (c) A zoom-in view of the calibrated ρ₅′ and ρ₄′ as a function of Δn and the extracted Δn_B, Δn_B′ and Δn.

Calibration of the CROW sensor

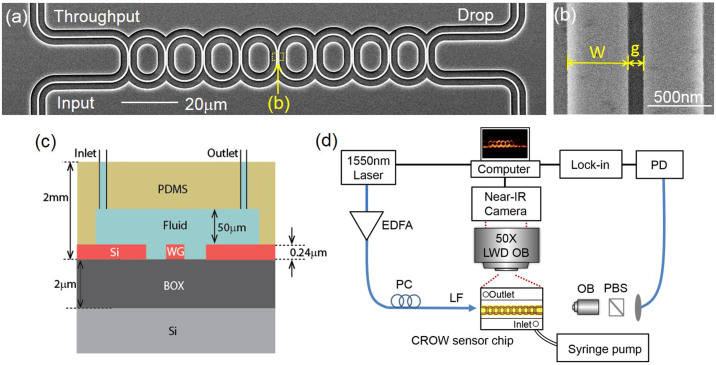
Fig. 4(a) shows the scanning-electron microscope (SEM) picture of the fabricated 8-element microring-based CROW. The racetrack microring comprises two half circles with a radius of 6.5 μm and two straight waveguides with an interaction length of 3.5 μm and a designed coupling gap spacing of 100 nm. We design the inter-cavity coupling in the strong-coupling regime in order to obtain a wide inhomogeneously broadened transmission band. This enables a large sensing dynamic range Δn_d and a wide spectral range for choosing an arbitrary probe wavelength. Fig. 4(b) shows a representative zoom-in-view image of the inter-cavity coupling region.

Figure 4.

(a) Scanning-electron microscope image of the fabricated eight-element microring-based CROW. (b) Zoom-in-view image of an inter-cavity coupling region. (c) Schematic of the cross-sectional view of the optofluidic chip. (d) Schematic of the experimental setup. EDFA: erbium-doped fiber amplifier, PC: polarization controller, PBS: polarized beam splitter, LWD OB: long-working-distance objective lens, OB: objective lens, PD: photodetector.

Fig. 4(c) schematically shows the cross-sectional view of the optofluidic chip. The fabricated SOI chip is bonded with a polydimethylsiloxane (PDMS) layer, with a microfluidic channel of 50 μm-height and 1 mm-wide encompassing the CROW sensor. Fig. 4(d) schematically shows the experimental setup (see Methods).

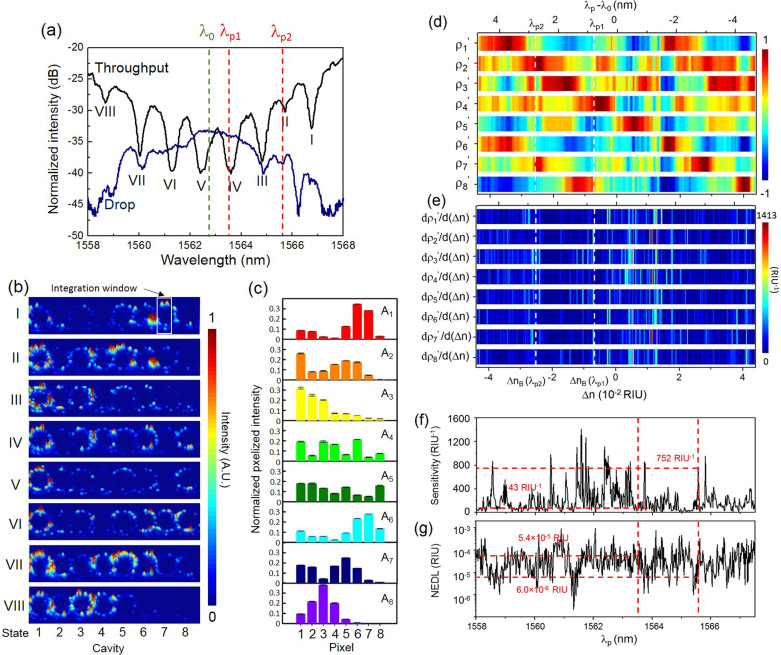
Fig. 5(a) shows the measured TM-polarized transmission spectra of the CROW sensor covered by deionized (DI) water as the upper cladding. The CROW sensor exhibits an inhomogeneously broadened transmission band with a 3 dB bandwidth of ~8.1 nm. The measured free spectral range of 11.2 nm is consistent with the microring circumference. We discern the eight eigenstates as the eight resonance dips in the throughput spectrum (labelled by I to VIII).

Figure 5.

(a) Measured TM-polarized transmission spectra of the 8-element CROW device with DI water as the upper-cladding. Green dashed-line: reference wavelength λ₀ of 1562.72 nm. Red dashed-lines: probe wavelengths, λ_p1 (1563.50 nm) and λ_p2 (1565.56 nm). (b) Measured infrared light-scattering images of the CROW with DI water upper-cladding at eigenstates I-VIII. The white-line box indicates the integration window for the pixelized patterns. (c) Pixelized mode-field intensity patterns at eigenstates I–VIII. (d) Calibrated library of the correlation coefficients ρ₁′–ρ₈′ as a function of Δn. White dashed-lines indicate the Δn_B values at λ_p1 and λ_p2. (e) Calculated differential correlation coefficients as a function of Δn. (f) Calculated sensitivity as a function of probe wavelength. Red dashed-lines indicate a sensitivity of 43 RIU⁻¹ at λ_p1 and 752 RIU⁻¹ at λ_p2. (g) Calculated noise-equivalent detection limit as a function of probe wavelength. Red dashed-lines indicate a NEDL of 5.4 × 10⁻⁵ RIU at λ_p1 and 6 × 10⁻⁶ RIU at λ_p2.

Fig. 5(b) shows the measured light-scattering images of the CROW with DI water upper cladding at eigenstates I–VIII. We observe from the images highly non-uniform light-scattering profiles across each microring. We attribute such a non-uniformity to random variations of the surface roughness on each microring (see Supplementary Information S4). Such surface-roughness-induced scattering modulates the out-of-plane elastic light scattering patterns from the original mode-field distributions.

We integrate the out-of-plane scattering light intensity from each microring within a fixed integration window to form a pixel (Fig. 5(b)). The integration window covers both arcs of a microring, but excludes the two coupling regions in order to minimize the crosstalk between adjacent microring cavities. We correct the integrated patterns by normalizing with the estimated contributions of the surface-roughness-induced scattering (see Supplementary Information S4). Fig. 5(c) shows the corrected pixelized mode-field intensity patterns at the eight eigenstates, which are clearly distinguishable. Fig. 5(d) shows the measured library of the calibrated correlation coefficients as a function of Δn. We calibrate by scanning the input laser wavelength by ±Δλ about the center of the CROW transmission band upon a fixed buffer solution (DI water) with minimum wavelength interval of 0.02 nm. This wavelength interval corresponds to a Δn_i of ~1.87 × 10⁻⁴ RIU, based on the calibrated linear spectral sensitivity of ~106.82 nm/RIU of the CROW sensor (see Supplementary Information S5). We convert Δλ to Δn using the calibrated linear spectral sensitivity. We choose Δλ = 4.7 nm such that the corresponding Δn ranging from −4.40 × 10⁻² RIU to 4.40 × 10⁻² RIU (Δn_d = 8.80 × 10⁻² RIU), which sequentially yields a unity value for ρ₁′ to ρ₈′.

Fig. 5(e) shows the calculated differential correlation coefficients, dρ_j′/d(Δn), as a function of Δn. Fig. 5(f) shows the calculated sensitivity as a function of λ_p. The calculated sensitivity shows a highly non-uniform profile, ranging from 5 to 1412 RIU⁻¹, with an average value of 199 RIU⁻¹ over the 3 dB bandwidth of the CROW transmission band.

We define the NEDL at λ_p as the uncertainty of extracted Δn (see Methods). We extract the NEDL from the measured uncertainty of each ρ^p and ρ^s of the library {ρ_j′(λ₀)} at Δn_B. Fig. 5(g) shows the calculated NEDL as a function of λ_p. NEDL is highly dependent on the choice of λ_p. We show an average NEDL over the entire transmission band as ~6 × 10⁻⁵ RIU.

Sensing in the spatial domain with correlation analysis

We first implement a blind test with an arbitrarily set probe wavelength λ_p1 (1563.50 nm) near the center of the CROW transmission band. The sensitivity at λ_p1 is only ~43 RIU⁻¹ (see Fig. 5(f)). The NEDL at λ_p1 is 5.4 × 10⁻⁵ RIU (see Fig. 5(g)). We prepare one buffer solution (DI water) and two NaCl solutions, X and Y, with mass concentrations unknown to the person conducting the sensing experiment.

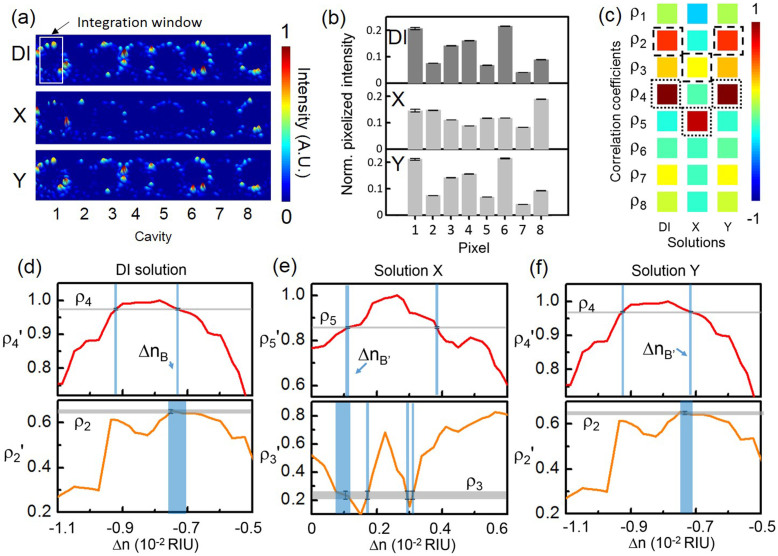
Fig. 6 shows the experimental sensing results at λ_p1. Fig. 6(a)) shows the measured light-scattering images of the CROW upon the buffer solution and the test solutions at λ_p1. Fig. 6(b) shows the corresponding pixelized patterns. Fig. 6(c) shows the corresponding calculated correlation coefficients. Fig. 6(d) shows the mapping of ρ^p and ρ^s in the buffer solution. When we are mapping ρ^p and ρ^s to the corresponding Δn, we use linear interpolation between Δn_i. We obtain ρ^p as ρ₄ (0.974 ± 0.003) and ρ^s as ρ₂ (0.652 ± 0.008). By mapping ρ₄ and ρ₂ to the library, we uniquely identify Δn_B as (−7.30 ± 0.07) × 10⁻³ RIU.

Figure 6.

(a) Measured infrared light-scattering images of the CROW at an arbitrary probe wavelength λ_p1 (1563.50 nm) near the center of the CROW transmission band upon the buffer solution and the blind-test solutions X and Y. White-line box indicates the integration window for the pixelized patterns. (b) Pixelized patterns upon the buffer solution and the blind-test solutions X and Y. (c) Corresponding calculated correlation coefficients upon the buffer solution and solutions X and Y. Dotted-line boxes: ρ^p, dashed-line boxes: ρ^s. (d)–(f) Mapping of ρ^p and ρ^s with the library to extract Δn. (d) Upon the buffer solution. (e) Upon solution X. (f) Upon solution Y.

For solution X (Fig. 6(e)), we observe a significant pattern change from the buffer solution. We obtain ρ^p as ρ₅ (0.857 ± 0.004) and ρ^s as ρ₃ (0.24 ± 0.04). By mapping ρ₅ and ρ₃ to the library, we uniquely identify Δn_B′ as (1.11 ± 0.12) × 10⁻³ RIU. Thus, we acquire for solution X a Δn = Δn_B′ − Δn_B = (8.41 ± 0.18) × 10⁻³ RIU, corresponding to a mass concentration of (4.67 ± 0.10) %. This agrees with the prepared concentration of solution X ((4.80 ± 0.01) %).

For solution Y (Fig. 6(f)), we find ρ^p as ρ₄ (0.969 ± 0.002) and ρ^s as ρ₂ (0.650 ± 0.006). These values are close to those observed from the buffer solution, suggesting a very small Δn. By mapping ρ₄ and ρ₂ to the library, we uniquely identify Δn_B′ as (−7.15 ± 0.1) × 10⁻³ RIU. Thus, we obtain for solution Y a Δn = (1.5 ± 1.2) × 10⁻⁴ RIU, corresponding to a mass concentration of (0.08 ± 0.06) %. The central value of the extracted Δn agrees with the prepared concentration of solution Y ((0.0800 ± 0.0003) %). However, the uncertainty of the extracted Δn is limited by the NEDL at λ_p1, which is close to the Δn in the test.

We implement another blind test using the same solutions X and Y at a specifically chosen wavelength λ_p2 (1565.56 nm) within the transmission band. At λ_p2, we obtain a higher sensitivity of ~752 RIU⁻¹ (see Fig. 5(f)) and a lower NEDL of 6 × 10⁻⁶ RIU (see Fig. 5(g)) compared with those obtained at λ_p1.

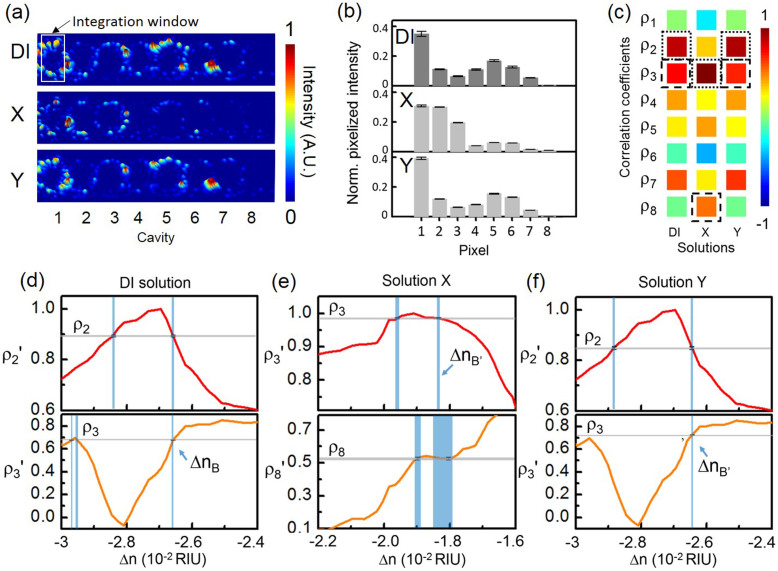
Fig. 7 shows the experimental results measured at λ_p2. Fig. 7(a) shows the measured light-scattering images of the CROW upon the buffer solution and the test solutions. Fig. 7(b) shows the corresponding pixelized patterns. Fig. 7(c) shows the corresponding calculated correlation coefficients. Fig. 7(d) shows the mapping of ρ^p and ρ^s in the buffer solution. We obtain ρ^p as ρ₂ (0.893 ± 0.003) and ρ^s as ρ₃ (0.679 ± 0.001). By mapping ρ₂ and ρ₃ to the library, we uniquely identify Δn_B as (−2.6587 ± 0.0008) × 10⁻² RIU. For solution X (Fig. 7(e)), we obtain ρ^p as ρ₃ (0.985 ± 0.002) and ρ^s as ρ₈ (0.527 ± 0.009). By mapping ρ₃ and ρ₂ to the library, we uniquely identify Δn_B′ as (−1.834 ± 0.05) × 10⁻² RIU. Thus, we acquire for solution X a Δn = Δn_B′ − Δn_B = (8.25 ± 0.03) × 10⁻³ RIU, corresponding to a mass concentration of (4.58 ± 0.02) %. The extracted Δn value is consistent with that measured at λ_p1. This confirms that our CROW-based sensor can work at different probe wavelengths within the transmission band.

Figure 7.

(a) Measured infrared light-scattering images of the CROW at a specifically chosen probe wavelength λ_p2 (1565.56 nm) upon the buffer solution and the blind-test solutions X and Y. White-line box indicates the integration window for the pixelized patterns. (b) Pixelized patterns upon the buffer solution and the blind-test solutions X and Y. (c) Corresponding calculated correlation coefficients upon the buffer solution and solutions X and Y. Dotted-line boxes: ρ^p, dashed-line boxes: ρ^s. (d)–(f) Mapping of ρ^p and ρ^s with the library to extract Δn. (d) Upon the buffer solution. (e) Upon solution X. (f) Upon solution Y.

For solution Y (Fig. 7(f)), we find ρ^p as ρ₂ (0.849 ± 0.005) and ρ^s as ρ₃ (0.726 ± 0.001), similar to the buffer solution case. By mapping ρ₂ and ρ₃ to the library, we uniquely identify Δn_B′ as (−2.6439 ± 0.0004) × 10⁻² RIU. Thus, we obtain for solution Y a Δn = (1.48 ± 0.09) × 10⁻⁴ RIU, corresponding to a mass concentration of (0.082 ± 0.005) %. We obtain a consistent value of Δn with that measured at λ_p1, with a much improved uncertainty. We attribute this to the higher sensitivity and NEDL at λ_p2 than those at λ_p1.

Discussion

We compare the sensitivity of the CROW sensor with the sensitivity of the traditional waveguide-based refractive-index sensor in a Mach-Zehnder interferometer (MZI) configuration as a baseline device (see Supplementary Information S6). We assume the same SOI waveguide dimensions and sensing in the TM mode. For a MZI sensor with the same sensing waveguide length as our 8-ring CROW total circumference length (~382.7 μm), the calculated sensitivity is ~110 (2π RIU⁻¹). This value is comparable to the modeled sensitivity of the CROW sensor (~1.6–~715 RIU⁻¹) (see Fig. 3).

We also compare the detection limit of the CROW sensor with the detection limit of various optical microresonator-based sensors in the spectral domain. A detection limit down to ~10⁻⁴–~10⁻⁷ RIU has been demonstrated using various optical microresonators in different material platforms. The demonstrated NEDL ranging from ~9 × 10⁻⁴–~2 × 10⁻⁷ RIU (see Fig. 5(g)) of the CROW sensor is comparable with the mainstream microresonator-based sensors performance.

The CROW sensor sensitivity can be further optimized by (i) reducing the waveguide propagation loss (α), (ii) increasing the number of coupled cavities (N), and (iii) reducing the inter-cavity coupling coefficient (κ). Given the same fixed cavity circumference (47.8 μm) following our experiments and assuming the same degree of imperfection, our transfer-matrix modeling results suggest an optimized average sensitivity of ~641 RIU⁻¹, with α = 2.2 dB/cm, N = 12, and κ ≈ 0.3, with a reduced Δn_d ≈ 1.7 × 10⁻² RIU (see Supplementary Information S7).

The choice of the SOI platform, along with the use of a 1550 nm laser, amplifier and an expensive InGaAs camera in our experimental setup is, however, not practical for point-of-care optical biosensing applications. A practical sensing system should be low cost, and the sensing window is likely to be in the visible to near-infrared wavelengths. Thus, a future direction for practically implementing our sensing scheme is to adopt a silicon-based material platform that is transparent to the visible and near-infrared wavelengths, is compatible with CMOS processes, and offers a sufficiently high refractive index for a small device footprint. A possible choice is silicon nitride (SiN). The operational wavelength can then be below ~1000 nm, which allows the use of a low-power diode laser source and a standard silicon charge-coupled device (CCD) or CMOS camera to image the light scattering. The relatively low refractive index contrast between the SiN waveguide and the analyte also enables a better exposure of the TM mode to interact with the analyte.

In summary, we report a paradigm-shift biochemical sensing scheme in the spatial domain using chip-scale, microresonator-based CROWs on a SOI chip. Instead of using narrowband microresonator resonances, we use an inhomogeneously broadened transmission band of an imperfect CROW and the out-of-plane elastic light scattering patterns to attain a good average sensitivity (~199 RIU⁻¹) and a low detection limit (~9 × 10⁻⁴–~2 × 10⁻⁷ RIU) over a large refractive index range (8.8 × 10⁻² RIU). The correlation analysis employed takes into account of the whole mode-field-intensity distribution across the CROW. This sensing scheme is immune to the common external noise affecting all the coupled cavities, and thus enabling an improved tolerance to the equipment noise. Our blind tests using a SOI 8-microring CROW at fixed probe wavelengths and NaCl solutions with different mass concentrations showed the detection of a cladding refractive index change of 1.5 × 10⁻⁴ RIU. We showed a noise-equivalent detection limit of ~6 × 10⁻⁶ RIU at a specific fixed probe wavelength. We therefore envision that our demonstrated CROW-based sensing scheme using light-scattering pattern recognition and the correlation analysis can potentially offer an alternative route toward a high-performance, reliable and relatively compact integrated label-free optical biochemical sensor.

Methods

Transfer-matrix modeling on an imperfect CROW

We model an imperfect microring CROW using transfer-matrix method with empirical and numerical inputs (see Supplementary Information S1). We accumulate statistics of the measured waveguide widths and coupling gap widths from SEM characterization over the nine coupling regions of a representative 8-microring CROW (see Supplementary Information S2). For each coupling region, we sample six waveguide widths and three coupling gap spacing. The statistics of the waveguide widths and the coupling gap widths approximately follow Gaussian distributions. We obtain the mean values and the standard deviations of fabricated waveguide widths and coupling gap widths. We assume that the Gaussian distributions of the waveguide widths and the coupling gap widths are independent. We use the Gaussian number generator in Matlab to generate a set of randomized waveguide widths and coupling gap widths distributed along an imperfect CROW. We study 200 sets of such randomly generated parameters for the 8-microring CROW (see Supplementary Information S7).

We calculate using FEM (COMSOL RF module) the waveguide effective refractive index, n_eff, of a SOI waveguide with a water upper-cladding as a function of the waveguide width, at a fixed waveguide height of 240 nm. The mean value of the calculated n_eff is 1.839 ± 0.002. We calculate using two-dimensional (2D) finite-difference time-domain (FDTD) simulations the coupling coefficient in each coupling region as a function of the coupling gap width, with the waveguide width fixed at its mean value of 470 nm. The mean value of the calculated coupling coefficient is 0.910 ± 0.004. In the simulations, we choose the TM polarization mode. Based on our experiments, we estimate the waveguide propagation loss to be relatively high at 22 dB/cm, which we attribute primarily to surface-roughness-induced scattering losses. We assume that each microring follows the designed racetrack arc radius of 6.5 μm and the designed interaction length of 3.5 μm. In order to convert the cladding refractive index change into the effective index change of the sensor, we calculate the intrinsic sensitivity, S_i, using the FEM. S_i is calculated as 0.45 using the effective refractive index change divided by the cladding refractive index change (see Supplementary Information S1). We extract from the transfer-matrix modeling assuming the above parameters the mode-field intensity distributions of an imperfect CROW through adding the intensities right before and after each coupling region.

Fabrication process

We fabricate the CROW devices in commercial SOI wafers (SOITEC). The 6-inch SOI wafer has a 240 nm-thick silicon device layer on a 3 μm-thick buried-oxide (BOX) layer. We pattern the CROW devices by electron-beam (E-beam) lithography (JEOL JBX-6300FS) using photoresist ZEP-520. We transfer the device pattern to the silicon device layer by inductively coupled plasma (ICP) etching (STS ICP DRIE Silicon Etcher).

We fabricate a microfluidic chamber with an inlet and an outlet on a PDMS layer. In order to form the microfluidic channel by imprinting, we use SU8 patterned by contact photolithography as the PDMS mold to transfer the pattern to the PDMS. We use a puncher to make an inlet and an outlet, each with a diameter of 1 mm.

The SOI chip and the PDMS microfluidic layer are treated with oxygen plasma and directly bonded, with the microfluidic channel aligned with the CROW devices. The bonded PDMS-silicon interface is stable enough for repeating the sensing experiments under a relatively high pump pressure.

Experimental setup

The wavelength-tunable laser light in the 1550 nm wavelength range is coupled into a 33 dB-gain erbium-doped fiber amplifier. The amplified laser light is polarization-controlled to the TM polarization and is end-fired into a tapered silicon waveguide through a singlemode polarization-maintaining lensed fiber.

We prepare NaCl solutions with mass concentrations from 1% to 5% (in steps of 1%) in order to calibrate the CROW transmission band spectral shifts upon a refractive index change from the cladding solution. All the measurements are repeated three times, with DI water as the reference cladding solution. Between two measurements, we rinse the chip by DI water for one time. We determine the resonance spectral shifts by fitting the throughput- and drop-transmission spectra with a sum of multiple Lorentzian lineshapes, with each Lorentzian lineshape centered at the CROW eigenstate wavelength. The overall transmission band shift is taken as the average value of the spectral shifts of eigenstates I–VIII.

Imaging of elastic light scattering

We use a long-working-distance microscope objective lens (50× Mitutoyo Plan Apo, NA = 0.55) and an InGaAs camera (Hamamatsu C10633-23) with 320 × 256 pixels (a 30 μm pixel size) to image the light scattering patterns from the top. The camera has a high responsivity at the 1000–1700 nm wavelength range with a 14 bit analog-to-digital conversion in data readout. We set the camera exposure time as 6 ms with a calibrated gamma factor of ~1. Each microring is imaged onto an area of 44 × 25 pixels. The integration window for each microring includes 44 × 19 pixels. We set the probe wavelength far away from the CROW transmission band and obtain a background image for background subtraction.

In order to acquire the calibrated correlation coefficients, we scan the laser wavelength and record 8 successive images for each wavelength step over a time interval of 0.8 s and take average for reducing the equipment noise contribution. In the blind sensing tests, we record and take average over 100 successive images during a time period of 10 s at a fixed probe wavelength after the buffer or the test solution is injected and the scattering pattern is stabilized.

Author Contributions

A.W.P. initiated and supervised all of the work. T.L. designed the device and conducted the initial experimental work. J.W. and T.L. carried out the device fabrication. J.W. conducted the experiment and the data analysis. Z.Y. and J.W. performed the numerical modeling. A.W.P., J.W. and Z.Y. wrote the manuscript.

Supplementary Material

Supplementary Information

Supplementary information