An Interactive, Web-based High Performance Modeling Environment for Computational Epidemiology

Abstract

We present an integrated interactive modeling environment to support public health epidemiology. The environment combines a high resolution individual-based model with a user-friendly web-based interface that allows analysts to access the models and the analytics back-end remotely from a desktop or a mobile device. The environment is based on a loosely-coupled service-oriented-architecture that allows analysts to explore various counter factual scenarios. As the modeling tools for public health epidemiology are getting more sophisticated, it is becoming increasingly hard for non-computational scientists to effectively use the systems that incorporate such models. Thus an important design consideration for an integrated modeling environment is to improve ease of use such that experimental simulations can be driven by the users. This is achieved by designing intuitive and user-friendly interfaces that allow users to design and analyze a computational experiment and steer the experiment based on the state of the system.

A key feature of a system that supports this design goal is the ability to start, stop, pause and roll-back the disease propagation and intervention application process interactively. An analyst can access the state of the system at any point in time and formulate dynamic interventions based on additional information obtained through state assessment. In addition, the environment provides automated services for experiment set-up and management, thus reducing the overall time for conducting end-to-end experimental studies.

We illustrate the applicability of the system by describing computational experiments based on realistic pandemic planning scenarios. The experiments are designed to demonstrate the system's capability and enhanced user productivity.

1. Introduction

Epidemiology aims to study the spatio-temporal patterns of health in a population and the factors that contribute to these patterns. Computational epidemiology is the development and use of computer models to generate appropriate spatio-temporal patterns as well as methods for controlling these patterns. Computational models may be descriptive, e.g., static estimates of correlations within large databases, or generative, e.g., computing the spread of a disease via person-to-person interactions through a large population. The infectious disease may represent an actual disease, or it may represent a more general reaction-diffusion process, such as the diffusion of innovation. The populations of interest depend on the disease, including humans, animals, plants, and computers. Similarly, the interactions that must be represented depend on the disease and the populations, including physical proximity for aerosol-borne diseases, sexual contact for sexually transmitted diseases, and insect feeding patterns for mosquito-borne diseases.

Computational epidemiology allows analysts and epidemiologists to undertake counterfactual in silico experiments as well as study the efficacy of various intervention strategies. Potential interventions for controlling infectious diseases include pharmaceutical interventions, social distancing designed to reduce interactions between individuals, and eradication of vectors. Efficient use of these interventions requires targeting critical subpopulations that inhibit disease spread. Computational models can be used to identify such critical subpopulations. The models can also be used to assess the feasibility and effectiveness of proposed interventions.

Useful computational environments that support epidemiologists need to satisfy important requirements, including: (i) model validity, (ii) computational efficiency, (iii) ability to represent a wide variety of diseases and interventions and (iv) ease of use. Some of the requirements are often in conflict and thus are challenging.

1.1. Contributions

In this paper, we describe the architecture and a prototype implementation of DISimS (Distributed Interactive Simulation System), a flexible epidemiological modeling environment. DISimS combines high resolution individual-based epidemic and intervention modeling environment with web-based user-friendly analytics. DISimS can be used by policy makers and epidemiologists for undertaking a broad range of counterfactual computer experiments and for analyzing results through detailed graphs and plots inside the system. It also allows export of result data in standard formats for analysis using other tools. Additionally, the modeling environment can be used for training analysts in the use of complex epidemiological models.

DISimS is an interactive modeling environment and interactivity is one of its key technical strengths. DISimS allows an analyst to start, stop, pause, resume and roll back previously applied intervention strategies and disease propagation processes. Users can ask complicated spatio-temporal queries in support of situation assessment. DISimS aids policy makers interested in developing dynamic health policies – policies that can adapt to new data that become available via surveillance. This is an important issue in epidemiology. See a recent paper by Yaesoubi and Cohen [Yaesoubi and Cohen 2011] for additional discussion. Developing such interactive simulations and computational steering environments, especially for parallel simulations, is a well known challenging problem. DISimS achieves this by exploiting the problem specific semantics that allow one to achieve these features using a relatively small data footprint.

DISimS uses existing software modules that are re-engineered appropriately to achieve the design goals. The data storage and communication mechanisms ensure that there is no bottleneck due to large scale data movement. The software sub-systems that were part of the integration effort include EpiFast [Bisset et al. 2009] – an HPC-based simulation engine, that simulates disease propagation process over a given region; ISIS [Beckman et al. ] – a web-based visual interface tool, that can be used for experiment set-up and analysis of the role of different parameters in disease propagation; and a database repository, storing and operating on the demographic and geographic information, extended from Indemics [Bisset et al. 2014]. We analyzed feasibility of the existing middleware platforms such as Simfrastructure [Bisset et al. 2013] and the middleware used in the implementation of Indemics, to support integration of these distinct system components and remodeled the middleware for supporting optimal data movement and interactivity.

DISimS is specifically designed to improve user experience. This includes ease of use of the system and user productivity. Care has been taken so that a user can drive computational experiments by accessing complicated mathematical models without having to become a computing expert. For instance, the environment provides automated services for experiment set-up and management, thus reducing the overall time of conducting end-to-end experimental studies. It also allows reuse of past epidemiological experiments and their results, which avoids duplication of efforts. Also, using DISimS, users can view and analyze partial and complete simulation results through graphs and plots without having to perform manual analysis. This automates the analysis to a large extent and leads to considerable gain in productivity of users.

We demonstrate the applicability of DISimS by describing two computational experiments. The experiments are motivated by real-world policy case studies and highlight important features of DISimS.

2. Background and Related Work

Computational models used in the study of epidemics is comprised of two broad categories – aggregate based models and individual based network models.

Aggregate differential equation based models partition individuals into separate classes such as Susceptible, Exposed, Infectious and Recovered (SEIR model), depending on the model of infection dynamics chosen. These models assume homogeneous mixing of populations and use differential equations to study the changes in epidemic states of populations over time. Some examples of aggregate differential equation based models used for studying disease propagation include epidemiological models developed by [Rvachev and Longini 1985; Hufnagel et al. 2004]. Another tool based on this differential equation based approach is the open source tool called Spatio-Temporal Epidemiological Modeler- STEM[Edlund and Kaufman 2012 ], developed by IBM in collaboration with Eclipse, Johns Hopkins University and others.

Individual based networked models explicitly represent individuals within a population. The individuals interact via an interaction network. Recent research in this area includes work by [Meyers 2007; Meyers and Dimitrov 2010; Pastor-Satorras and Vespignani 2002; Barrat et al. 2008; Newman et al. 2002]. This work involves deriving closed form analytical results on random graphs for finding epidemiological patterns of interest. Another type of individual based model uses important statistics of a region such as density of individuals in a region using land scan data and basic census information to get demographic distribution of individuals in a region, in order to model epidemic propagation. Research in this area includes work by [Germann et al. 2006; Ferguson et al. 2006; Ferguson et al. 2003]. Some researchers have also explored a hybrid approach where counties are represented as nodes and the movement of individuals represent the edges. Coupled rate simulations are used for propagation simulation between counties. Example of a high-performance agent-based simulation based on this approach is the Global-Scale Agent Model (GSAM) [Parker and Epstein 2012], which simulates propagation of epidemics over billions of agents.

The last category of individual based models try to model individual level interaction between people based on their day-to-day activities and generate a graph of social contact network used for epidemic propagation. Research in this area includes work by [Keeling and Eames 2005; Meyers 2007; Barrett et al. 2008; Eubank 2002]. The backend models used in the implementation of DISimS also broadly fit in this category. DISimS also builds on the work previously carried out in this domain of modeling individual-level interactions including EpiFast [Bisset et al. 2009], which implements individual level interactions affecting disease propagation and intervention strategies for disease containment, using high performance computational code; and Indemics [Bisset et al. 2014], which uses databases for intervention implementation on individuals and can be accessed by public health decision makers through query based IQL scripts.

Recent work in computing technologies and ubiquitous computing has enabled relatively easy access to remote computing resources including on grids, clouds or clusters. One such recent work also discusses providing access to high performance computing resources as a service [AbdelBaky et al. 2012]. There has been significant research in the area of accessing models and simulations through web-based systems, so that simulation complexity is hidden from users. Research has also been conducted in the broader area of applying different visualization techniques for representing high-end simulations on web-based user interfaces. Some examples of graph visualization techniques and tools developed include Gephi [Bastian et al. 2009] and Pajek [Batagelj and Mrvar 1998]. Easy accessibility through visualization is particularly important in public health epidemiology because domain specialists have limited technical expertise to execute and analyze complex simulations on high end computing platforms like clusters and grids.

Some examples of research conducted in developing web-based systems and visualization platforms for epidemic simulations include Epinome [Livnat et al. 2012], Gryphon [Yu et al. 2010], FRED (Framework for Reconstructing Epidemiological Dynamics) [Grefenstette et al. ], GLEaMviz [Broeck et al. 2011] and ISIS (Interface to Synthetic Information Systems) [Beckman et al. ]. Epinome is a user centric system with visual analytics support for epidemiology that helps users evaluate intervention strategies based on available information. Gryphon presents a modeling environment to represent geographic spread of the SARS outbreak, based on published data, but it supports relatively smaller scale models. FRED is an open source modeling system developed collaboratively by University of Pittsburgh and Carnegie Mellon University that captures interacting effects of mitigation strategies, behavioral changes of people and evolution of virus. GLEaMviz is a desktop based visualization and analytical software that simulates disease propagation based on integration of data at three levels - data on global population, data on population mobility and model of infection based on disease dynamics. Both FRED and GLEaMviz however, do not provide a web-based interface for easy adoptation by epidemiologists and health professionals. Table I compares the features of existing epidemic systems with DISimS based on several design principles.

Table I. Comparison of DISimS features with existing tools.

System Name	Web interface	User interactivity	Analytical Capability	Scalability
FRED [Grefenstette et al. ]	No	No	Yes	Large scale models
EPINOME [Livnat et al. 2012]	Yes	Partial	Yes	Pre-run simulated disease outbreak models
Gryphon [Yu et al. 2010]	Yes	Yes	Yes	Relatively smaller scale models
GSAM [Parker and Epstein 2012]	No	No	Partial	Highly scalable with high resolution models
Flute [Chai et al. 2010]	No	No	Yes	Large scale individual-based models
GLEaMviz [Broeck et al. 2011]	Desktop based visualizations	Yes	Yes	Large scale hybrid models
DISimS	Yes	Yes	Yes	Large scale high resolution individual-based models

One of the earlier web interface tools developed by our lab called “ISIS” [Beckman et al. ] allowed access to a limited set of high-performance simulation models through a user-friendly web-based interface without interactivity or rollback features.

We developed the modeling environment, DISimS, that not just embeds the features of ISIS but also also provides additional interactive features such as pause-resume-roll and access to improved simulation models. We present the architecture of DISimS in the following sections.

3. Architecture and Implementation

DISimS (Distributed Interactive Simulation System) is an interactive high-performance modeling environment for epidemiological simulations that integrates real-time information based on surveillance data into the simulation. DISimS leverages three distinct modeling components built by our group: (i) EpiFast [Bisset et al. 2009] – an HPC-based simulation engine for epidemic propagation simulation; (ii) Indemics [Bisset et al. 2010], an interactive modeling platform that provides a database repository for intervention selection and application, external to the propagation simulation engine. DISimS also extends the interactive client and the loosely coupled Middleware Platform introduced in Indemics; (iii) and ISIS [Beckman et al. ] – a web-based visual interface tool, to develop a truly interactive modeling environment. Each of the three modules was extended and re-engineered to support the functionality of DISimS. In addition, the Simfrastructure Middleware Platform[Bisset et al. 2013] was reengineered to support interactivity and communication between the component modules.

We implemented the following new features to achieve the architectural goals of DISimS-

1. Abstracting the complexity of writing query scripts written in Indemics Query Language (IQL), that we had developed earlier, behind a web-based interface, for ease-of-use by epidemiologists and public health decision makers.

2. Extending ISIS such that it is able to provide analytics on partial simulation results, allowing users to integrate real-time information in the analysis.

3. New methods for analyzing the current state of an epidemic during a simulation run and new program abstractions to support rollback of previously applied intervention strategies without adversely affecting system response time and efficiency.

4. Design and development of the Indemics broker as an important backend component to facilitate interactivity. The broker plays a crucial role in orchestrating the interaction between the database and the diffusion simulator to support start, stop, pause and resume operations.

The overall architecture of DISimS is designed such that it balances conflicting system requirements. For instance, speed of simulation versus usability and user experience. An epidemic simulation has to process large scale data ranging in several gigabytes at very high speeds (several GBs per second) so that it produces results in a timely manner. However, the information has to be presented to the users in a coherent way such that users can consume the information and make decisions for further simulation execution. Hence usability considerations often conflict with high speed processing goals, since the former requires slower processing for convenience of users while later requires fast processing of large scale data. Since DISimS is also a multi-user system where several users can submit requests for simulation execution at the same time, the architecture has to cache the output for different users separately. The middleware of DISimS handles communication between the components such that optimal rate of interaction is supported and the data is presented in an aggregated form to every user.

Similarly, high-performance analytics requirements conflict with real-time information integration. Real-time information becomes available at different rates from the environment based on availability of surveillance data. A tightly-coupled analytics environment requires complete information during processing for providing accurate analytical results. However, real-time information is obtained at a much slower rate and hence integrating it into a high performance analytics environment is non-trivial. DISimS is designed as a loosely-coupled architecture such that information is integrated as and when it becomes available into the relational database component and analytical results are updated based on new information. This ensures that the performance of analytics environment does not degrade while integrating real-time data from different sources.

The DISimS architecture has two parts: (i) Functional components of DISimS architecture, and (ii) Middleware platforms to support the movement of data and control between components.

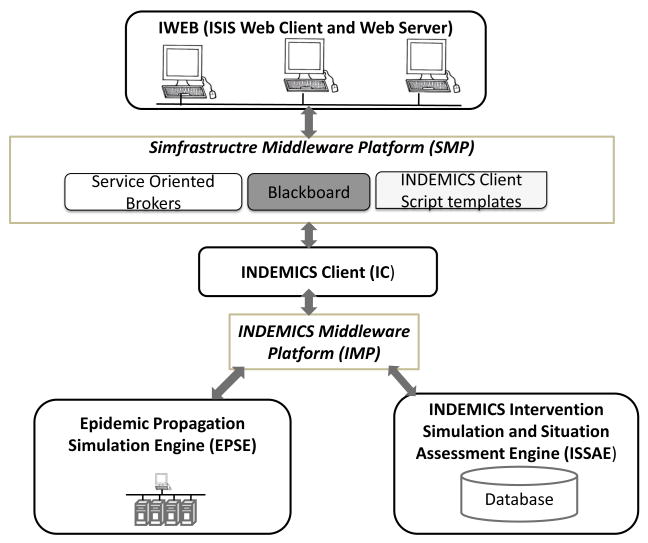
Figure 1 shows the high level architecture of DISimS. The functional components are represented by black boxes whereas the middleware platforms are represented with brown boxes.

Fig. 1.

High Level Architecture of DISimS.

In the subsequent sections, we describe these architectural components of DISimS in detail.

3.1. Functional components of DISimS architecture

The DISimS architecture is comprised of three primary functional components:

• —Epidemic Propagation Simulation Engine (EPSE) extended from EpiFast
• —Indemics Intervention Simulation and Situation Assessment Engine (ISSAE) and Indemics Client extended from Indemics
• —ISIS Web Client and Web Server (IWEB) extended from ISIS

Table II lists the implementation technology and design concerns supported by these functional components. Among these functional components, the Indemics Client, EPSE and ISSAE form the back-end infrastructure whereas IWEB forms the front-end infrastructure.

Table II. Functional Components of DISimS, corresponding technologies and primary design concern.

Component system	Description	Implementation Technology	Design Concern
EPSE	High performance simulation engine	C++/MPI	Performance and Efficiency
ISSAE and Indemics Client	Intervention Selection and Situation Assessment engine and client interface	Oracle Relational DBMS and Scripting language embedding SQL	Flexibility and Dynamic Interactions
ISIS Web Client and Server	Web-based visual interface tool	Google Web Toolkit	Usability and Interactivity

3.1.1. EPSE

EPSE is a high performance simulation engine that simulates the spread of epidemics through large scale populations, capturing the co-evolution of individual health, behavior, and disease transmission. It also has the capability to execute multiple replicates in order to capture the variability of the results due to the stochastic nature of the phenomena being modeled. In DISimS, EPSE is implemented using an extended version of the propagation simulation engine, EpiFast [Bisset et al. 2009]. EPSE can execute the propagation process at a very rapid pace, simulating disease spread over multiple time-steps (i.e., simulated days). For instance, EPSE can execute epidemic simulation on a cluster of 10 nodes with eight cores each, for a city with a population of about two million, in less than 30 seconds. The speed of simulation can be further improved by adding more nodes to the cluster.

EpiFast was initially designed to run to completion without stopping. To support interactivity, the EPSE component was engineered to support pause, resume and roll-back operations. Furthermore, when the system is paused, an analyst can examine the state of the system as well as modify the currently active set of interventions.

Formal Abstraction

The propagation simulation, represented by the EPSE component, is a concrete implementation of the extended CGDDS framework described in [Ma et al. 2011]. Modeling social network dynamics using discrete graphical dynamical systems was earlier described in [Barrett et al. 2006], [Barrett et al. 2007] and [Barrett et al. 2011]. The primary input is a social contact network that represents proximity relationships between individuals of the population in a certain region for which epidemic propagation has to be simulated. The region information is represented at a county, city and state level and stored in separate files. The file storing social contact network at a county level is a subset of the contact network at the city level, which in turn is a subset of the contact network at state level. Depending on the region selected by the users through ISIS web-based front-end, the corresponding contact network file is loaded by EPSE.

The social contact network of individuals in a region is represented by the graph G(V, E), where V is a set of vertices representing the individuals of the population and E represents contact between them. Each vertex υ ∈ V has an associated vector V = (pid, h, t₁, t₂, l₁) where

• —pid is the person identifier for the given vertex,
• —h is the health state based on SEIR model,
• —t₁ is the time at which the vertex is infected,
• —t₂ is the time of recovery and
• —l₁ is the list of interventions applied on the vertex.

Each edge E is represented as a vector E = (V₁, V₂, p) where

• —V₁ and V₂ are the vertices on which the edge is incident and
• —p is the probability of transmission between the vertices as defined in the propagation algorithm.

EPSE reads the entire graph G(V, E) into the distributed main memory from a flat file at the beginning of the simulation, based on the value of the parameter region, selected by the user through ISIS. G(V, E) remains more or less unchanged throughout the simulation. Interventions change the edge attributes, in particular the probability of transmission. Edge deletion can be simulated marking the edge label as “Deleted”.

The other input to EPSE is the list of interventions selected by users through the ISIS interface and retrieved from the RDBMS-based INDEMICS Intervention Simulation and Situation Assessment Engine. This is given by the vector intv- (subpop,intvAction). (subpop) represents the subpopulation on which an intervention has to be applied represented as a list of person identifiers, whereas (intvAction) represents the intervention action. For implementation inside EPSE, interventions are represented as I = (pid, A), where

• —pid represents the identifier of the person to be intervened, and
• —A represents the intervention action to be implemented. A is a vector given by (type, del, eff, dur, compl), where
  • —type is the type of intervention to be applied such as vaccination, social distancing, or anti-viral,
  • —del represents the delay in implementing the intervention action in real world, and
  • —dur, eff and compl represent fixed values for duration, efficacy and compliance rate respectively of the intervention action applied on the targeted population.

The intervention I is obtained from ISSAE through the Indemics middleware as input at every time-step, typically represented as one day. EPSE then runs the propagation simulation and computes disease propagation, returning the results in the form of a list of individuals infected during the time-step. This list is a vector O of infections, each of the form (infected, infector, infDur, diagnosed, incDur) where

• —infected represents the set of newly infected vertices in the current time-step,
• —infector represents the corresponding vertex identifiers that infected them,
• —infDur is the duration for which the vertex would remain in the Infectious disease state,
• —diagnosed are the vertex identifiers that are diagnosed with the disease but not yet symptomatic and
• —incDur is the period for which the diagnosed vertices remain asymptomatic.

The output O from EPSE is passed to ISSAE through the Indemics Middleware Platform (IMP) at every time-step, represented as a day.

A single simulation run is performed for several simulation days or time-steps. Since the data between EPSE and ISSAE is passed back at every time-step and contains a set of PIDs, which may run into thousands of vertices, depending on the extent of the infections in the population, the scale and frequency of data transfer is large. For instance, a typical epidemic simulation is carried out for a period of 200-300 days, over which an analyst can study the effects of different mitigation strategies on epidemic spread in a particular region. If the simulation is run for a city with a population of say 2 million people, then it is possible that the number of infected individuals can run into several thousands on any particular day or days. This infection information is captured in EPSE and needs to be passed back to ISSAE within milliseconds if the entire simulation has to complete within a reasonable time of minutes. For simulations over larger regions such as state level, the scale of infections would be higher per day and hence the data to be transferred between EPSE and ISSAE modules would be higher. The typical amount of data transferred between EPSE and ISSAE modules for simulation at a city level for a city with a population of about 2-5 million individuals, is around 15-20 KB/time-step.

Handling this scale of data requires a specialized middleware platform implemented using the Indemics Middleware Platform (IMP) explained in Section 3.2.

Whenever a user requests a simulation to be paused after a certain duration to be able to analyze the results of the intervention strategy applied till that point, then EPSE holds the connection with the Indemics Middleware Platform just like it is expecting data for the next iteration. When a new Indemics client script is generated through the SMP it is passed to IMP and IMP makes the necessary data conversions to pass data to EPSE without having to make any other changes. We discuss the specialized middleware - Indemics Middleware Platform (IMP) and Simfrastructure Middleware Platform (SMP) in Section 3.2.

3.1.2. ISSAE and Indemics Client

ISSAE simulates application of intervention strategies during an ongoing epidemic simulation externally to the high-performance simulation engine. ISSAE component of DISimS is implemented using a relational database management system, extended from the Indemics architecture. ISSAE stores demographic and social contact information along with time-varying infection data about individuals in relational format. Use of relational databases to represent ISSAE provides atomicity, consistency, isolation and durability to the data along with features such as indexing for fast retrieval. This allows real-time information to be incorporated quickly into the system so that the users can perform situation assessment. The ISSAE is updated with information of infected individuals at each time-step by EPSE. To get updated data on subpopulations to be intervened based on situation assessment, ISSAE can be queried using scripts written in Indemics query language (IQL), which is an extension of SQL (Please refer to the Appendix for an example of an IQL script template).

The Indemics Client component of DISimS is closely associated with ISSAE. This component reads the Indemics Client scripts or IQL scripts written in Indemics Query Language and feeds the queries to ISSAE through the middlware, IMP (Indemics Middleware Platform). To hide the complexity of writing and executing IQL scripts from users, the DISimS architecture automates the creation of dynamic IQL scripts based on predefined Indemics client script templates. These templates are stored in a database of intervention scripts in the Simfrastructure middleware and invoked based on user selection dynamically. Also, the actual parameters of execution selected by users using the ISIS Web Client are substituted in the invoked script during run-time. With this feature, analysts and epidemiologists are freed from the burden of writing complicated IQL scripts and can focus on finding optimal intervention strategies for containing epidemics.

Separating the ISSAE component from simulation engine provides users with the flexibility to choose different type of interventions dynamically and also to choose the subpopulation to apply interventions on.

Formal Abstraction

ISSAE stores and processes four kinds of datasets: the social contact network data N, demographic data R, infection dendogram data D and intervention data I_n.

Demographic data for each region is stored in a simple relational format in a table given by the tuple R = (pid, age, gender, income). Region information is stored at county, city and state levels to support the selection made by users.

R is static and remains unchanged for the duration of a simulation. New demographic value sets can be added to the tuple based on availability of information for the population.

The social contact network data N is stored as a tuple N = (pid₁, pid₂), where pid₁ and pid₂ represent the end points of an edge in the social contact network. This is a copy of the data used by EPSE to simulate epidemic propagation in a relational format. It is stored in the RDBMS so that interventions based on social contact network structure can be formulated.

The temporal data related to infections is stored in a separate table which can be directly updated based on the output received from EPSE. This data can be represented by the tuple T = (infected,infector, infDur) where

• —infected represents the set of newly infected vertices in the current time-step,
• —infector represents the corresponding set of vertices that infected them and
• —infDur is the duration for which the vertex would remain in the infectious disease state.

ISSAE is used to support situation assessment and intervention simulation. The output obtained from ISSAE is given by I(S′, A) where the set S′ contains person identifiers on whom to apply interventions and A represents the intervention actions. IMP sends this to EPSE. When EPSE resumes computation, it uses the new vertex and edge labels to evaluate the epidemic propagation for the next time-step. In case of interactive computations, the IMP receives a new Indemics intervention script and queries ISSAE based on specified IQL (Indemics Query Language) in the script. (Please refer to the Appendix for an example of an IQL script template written in IQL). IMP then fetches data from ISSAE based on the query and signals EPSE to resume operation for next time-step with new data.

Implementation of rollback feature

Design of the rollback feature is one of the major contributions of DISimS. The rollback operation allows users to rollback the system state to a particular day in the past and resume operation with a different set of interventions or system state. For example, a user may receive surveillance information that several school-age children were infected in about 20 days after an epidemic started. Based on this information, if the simulation has already moved to day 40, then the user may decide to roll-back to day 20, infect a few additional individuals and close schools as an intervention strategy going forward.

The roll-back feature of DISimS was supported by re-engineering the EPSE and ISSAE modules. One of the design considerations to support this feature was how to store information needed to execute rollback of a sequence of changes to system state over several time-steps. For rollback execution, the system needs a mechanism to store the intermediate information at each time-step of the simulation (typically represented as a day) about: (1) state changes of each node and (2) interventions applied. However, storing complete state information at each time-step of the entire social contact network would be a huge overhead to the system, increasing memory usage and impacting performance significantly. The data needed to be stored in this case would be O(t · k · (n + m)), where t is the number of time-steps; k is the number of interventions; n and m are the number of nodes and the number of edges, respectively, of the social contact network.

To avoid this, we leverage the known information about the S-E-I-R model, that a node representing an individual of a social contact network is in a Susceptible state under normal circumstances. Once the node moves from Susceptible(S) to Exposed(E) state, it will change its state from Exposed(E) to Infectious(I) after ∂_E time-steps; and from Infectious(I) to Recovered(R) after ∂_I time-steps, where ∂_E is the node's incubation duration and ∂_I is the node's infectious duration; and ∂_E and ∂_I are heterogeneous between nodes.

We define a variable for each of the E, I, R states of each node and assign it a value, representing the time-step at which the node enters that state (infinity if it has not entered the state yet). For instance, the value of variable E(υ) is the day on which node υ changes state to Exposed from Susceptible. In addition, whenever a node is computed to be infected after getting exposed (entering Exposed state), then two new variables - incubation duration ∂_E(υ) and infectious duration ∂_I(υ) are assigned to it. Incubation duration corresponds to how long before a node can start infecting others i.e. move into Infectious state. Infectious duration represents the time for which a node is infected, after which it moves to Recovered state. Thus, whenever a node υ enters into the Exposed state, the value of E(υ) is assigned to it at the current time-step; and the values of I(υ) and R(υ) can be computed. Those variables are initialized to ∞ by default for each node.

If we want to know the state of a node υ at time t, then we retrieve the values of the variables associated with the node. For example, suppose that the current day is day 30 and the retrieved values for node υ are E(υ)=28, I(υ)=31 and R(υ)=35 (where I(υ) and R(υ) are derived from E(υ), given that Incubation duration associated with the node is 3 days and Infectious duration is 4 days). From this information, we can infer that υ is in Exposed state on day 30. To rollback the state of node υ to for example day 20, we scan the variables and reset the variables with values greater than the rollback point (day 20). In this case, values of variables E(υ), I(υ) and R(υ) are reset to ∞. Thus the node υ goes back to susceptible state on day 20 after roll-back operation.

For storing information on interventions, we keep track of the time-step at which an intervention is applied and during what time period it is effective for each node of the social contact network. This information is stored as an intervention tuple I = (I_t,I_a,I_e), corresponding to the intervened node, where I_t is the Intervention type, I_a is the Intervention application time and I_e is the duration for which intervention is effective. For instance, if a school closure intervention is applied to node υ on day 20 and it is effective from day 30 to day 40, then this intervention information is stored as a tuple I = (school closure, 20, 30 – 40), associated with node υ.

With this information, the system can figure out what interventions are effective on a node at any time. For example, the system knows that school closure intervention is effective for node υ on day 35. To rollback to a previous day (e.g. to day 25), the system has information that the intervention was already applied (since 25 > 20) and it is not yet effective; so no change needs to be made. But if rollback is requested by a user to day 15, then the system knows that this intervention was not executed (since 15 < 20). Hence the intervention will be removed for node υ.

In addition to state information and interventions, the system also stores random seed information associated with the stochastic epidemic simulation, so that the simulation path is replicated if the same trace of interventions is repeated after roll-back. Changes associated with state change for rollback are required in both EPSE and ISSAE, whereas the changes associated with interventions are required only in EPSE. Since the intervention information is stored in ISSAE, it has complete information present in it to execute a roll-back.

Space Complexity

By storing only the state change information for nodes affected by epidemic propagation or due to an applied intervention inside EPSE, we avoid storing node states at each time-step or a snapshot of the entire social contact network graph for each time-step. With this approach, the amount of data stored in memory related to propagation is O(s · n), where s is the number of states that a node can be in. In our case s = 3 corresponding to E, I and R. S is considered as the default state. The space complexity for storing intervention information is O(k · (n + m)), where k is the number of interventions; n and m are the number of nodes and number of edges of the social contact network respectively. In addition, the space complexity for storing random seed information for the stochastic simulation process inside memory is O(t). The total space complexity of our approach is significantly smaller than O(t · k · (n + m)) which is the space complexity without our problem-specific optimizations. Hence our approach leads to considerable performance benefits for the high performance simulation execution.

3.1.3. ISIS Web Client and Server (IWEB)

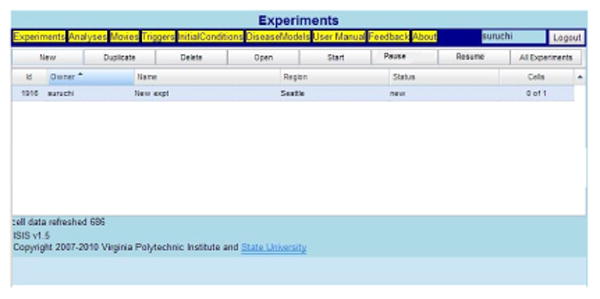
IWEB is the user-interface component of DISimS which includes a combination of ISIS Web Client and Web Server. It is an extension of the original ISIS system developed by our lab based on several years of research and extensive interactions with policy analysts over a 10 year period. Our early work in [Eubank et al. 2004] led to a realization that models can be made more useful only when they are easily accessible to end-users. ISIS allows users access to models such as EpiFast [Bisset et al. 2009] and EpiSimdemics [Barrett et al. 2008] through a web-based interface. It allows selection and analysis based on a range of parameters such as disease models, efficacy of interventions, compliance rate and so on, that play an important role in epidemic propagation. In addition, ISIS provides embedded management and storage of experiments that saves time to set-up and manage epidemiological experiments. Figure 2 shows a screen shot of ISIS.

Fig. 2.

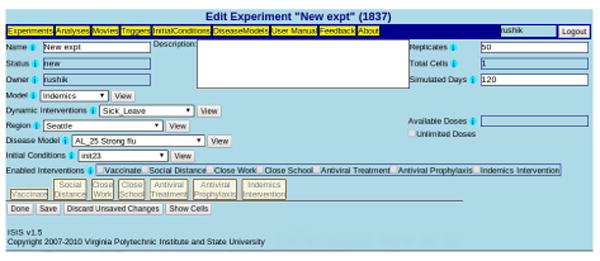
ISIS-based UI for automated experiment set-up and management in DISimS with provision for selection of input parameters such as region, disease model, number of replicates, dynamic interventions and so on.

We extended the original ISIS Web client to support interactive features such as pause resume and roll-back operations. Earlier, users could only save an experiment and start the experiment by clicking the “Start” button. We added additional buttons on the user interface - “Pause” and “Resume”, that provide the flexibility to make a single simulation run interactive. See Figure 3 for a snapshot of the available buttons on the UI. Users can also specify running the simulation for a small duration by selecting the “Duration” parameter in the Interventions tab, after which the simulation pauses automatically. The constraint here is that the specified duration has to be smaller than the total number of simulated days. When the user clicks the “Resume” button, the simulation resumes back again with same or different set of parameters, selected by the user.

Fig. 3. Start, Pause and Resume buttons of DISimS to allow pausing an ongoing simulation and resuming with a different set of input parameters in a single experimental simulation run.

This added functionality allows users to analyze the effects of multiple intervention strategies on disease propagation in a single simulation run. Users can analyze partial simulation results by viewing analytical plots and graphs that are generated in the “Analyses” tab of ISIS. Based on the results, they can decide whether to continue the simulation with different parameters or roll back to a time-step in the past and resume with different set of interventions. Please refer to Figures 5 and 6 for an example of output graphs obtained through ISIS web-system in the “Analyses” tab.

Fig. 5.

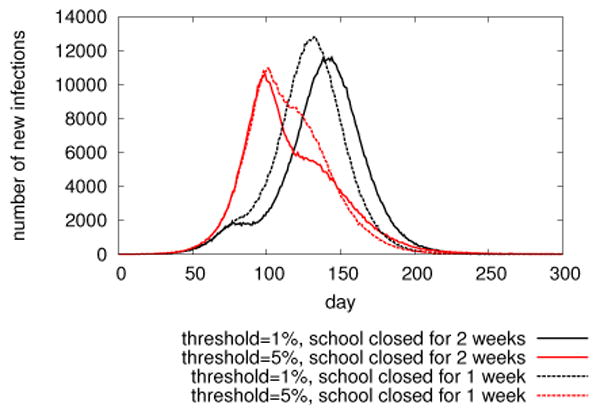
Example of DISimS generated plots: epicurves in a 2 by 2 experiment with different parameter settings of school closure intervention in Miami during a catastrophic flu.

Fig. 6.

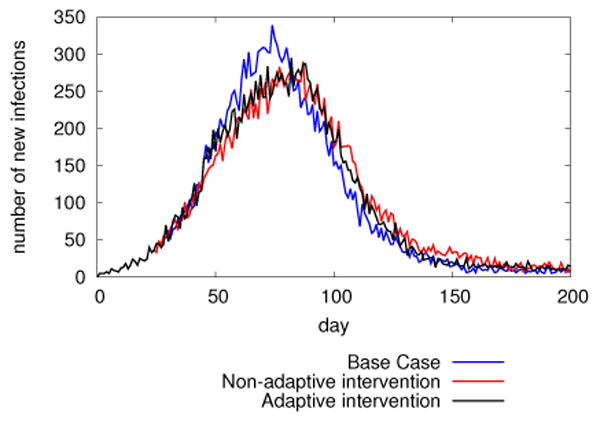
DISimS supported optimization study: Comparison of epidemic curves obtained in non-adaptive vs. adaptive cases.

Analysis of partial simulation results also enables better situation assessment and real-time information integration. For instance, if it is known that limited quantity of anti-virals would be available in the market only 15 days after the epidemic starts propagating, an analyst can pause the simulation on day 14 and analyze which sub-population is the most affected and can benefit from the dose of anti-virals. The subpopulation may be based on age group, gender or other demographics. The simulation can then resume with a new set of anti-viral interventions applied to the particular sub-population.

Formal Abstraction

The data selected through ISIS Web Client that is passed back to EPSE at the backend through ISIS Web Server can be represented as a vector (simtype,param,intv*) where

• —simtype is the type of propagation simulation that is to be executed at the back end such as EPSE
• —param is the set of parameters that represent the epidemic simulation including region, disease model, initial conditions and so on.
• —intv is a set of one or more intervention strategies that can be applied.

param is a vector given by (region,dismodel,initial,simdays), where

• —region is the region on which the epidemic simulation has to be executed. Region may be at a county, city or state level.
• —dismodel represents the disease model such as catastrophic flu, mild flu, H1N1, H1N2 and so on.
• —initial represents the initial conditions of the epidemic
• —simdays represents the total number of simulated days

intv is a vector given by (subpop,intvAction), where subpop represents the subpopulation on which the interventions have to be applied and intvAction is a vector given by (type,del,eff,dur,compl) where

• —type is the type of intervention to be applied such as vaccination, social distancing, anti-viral.
• —del represents the delay in implementing the intervention action in real world.
• —dur, eff and compl represent the duration, efficacy and compliance rate respectively of the intervention action applied on the targeted population.

The data represented by the vector (simtype,param,intv) is passed from the ISIS web server to the Interface broker of the Simfrastructure Middleware Platform (SMP), described in Section 3.2. Based on the selections made by the user, a request is submitted on the blackboard to start a propagation simulation of type simtype at the back end. The Indemics broker (Refer Section 3.2) reads the request and the parameters along with the intervention strategy. It places a request to start the propagation simulation of type simtype and the execution broker starts the simulation.

Intervention strategy - intv is used for creating the client script from the appropriate Indemics client template. The template parameters are replaced by actual values represented by objects of vector intv. Objects of param are also used to replace template parameters as values in the dynamic Indemics client script.

Whenever an interactive simulation is paused by the user after a fixed duration, the user can request an analysis to be run on the intermediate results. The output from the analysis is displayed to the user in the form of graphs. Based on the outcome of the analysis, the user might decide to submit new intervention strategies for the next duration. This new data is also represented similar to the original vector (simtype,param,intv) and is passed to the Interface broker of SMP.

3.2. Middleware platforms to support data movement and interaction

Design and development of middleware platforms is an important part of DISimS architecture to support communication and movement of data between the functional components described in Section 3.1. The backend infrastructure, consisting of the EPSE, ISSAE and Indemics Client has extremely high data speed requirements as described in Section 3.1 to maintain simulation performance, whereas the front-end infrastructure, IWEB is used for interaction with users. These systems have varied performance requirements and hence a single middleware platform cannot be used as a common means of communication throughout the system.

At a macro level, there is need for data and control passing middleware mechanism between the front-end and the back-end infrastructure; and a platform to support high performance speed requirements between components of the back-end infrastructure.

The IWEB including the ISIS Web Client and ISIS Web Server interface represent data and operations at a higher level of abstraction for the convenience of end users. ISIS Web server is typically deployed on a single dedicated web server that hosts the ISIS application. EPSE, on the other hand, implements an MPI based algorithm operating at low levels of abstraction and requires high-performance computing resources such as grids or multi-node clusters for execution. Hence, the ISIS Web Server and the HPC-based EPSE simulation engine cannot be co-located on the same machine instance.

The input parameters selected by users through ISIS Web Client and passed to the ISIS Web server, need to be relayed to the EPSE through some communication mechanism. The amount of data passed as parameters is usually small in scale. Once the propagation simulation starts at the EPSE, it may run for a long time depending on the parameters of execution or until it is paused or rolled-back. Hence the nature of communication between ISIS Web Server and EPSE is largely asynchronous. Moreover, even with interactions, the EPSE has to execute for some time-steps before the user can analyze the effects of any intervention. Hence the frequency of communication between the ISIS Web Server and EPSE is small.

We evaluated the applicability of “Simfrastructure” [Bisset et al. 2013] for achieving communication between the front-end and back-end infrastructure of DISimS. Please refer to the Appendix for details on Simfrastructure. Simfrastructure uses a distributed coordinated blackboard mechanism for message passing between varied system components. Simfrastructure is based on the concept of Service brokers that can handle the request for a particular service and return back the results to the blackboard.

To enable communication between ISIS Web Server and EPSE, we extended the blackboard and interface broker components of Simfrastructure. We engineered a new service broker component called the Indemics broker inside Simfrastructure. The Indemics broker is one of the most important components of DISimS. It automates the process of starting, stopping or pausing the simulation. The Indemics broker maintains a database of several distinct client program templates written in IQL, corresponding to different intervention studies.

The Indemics broker continually monitors the blackboard for new simulation requests for DISimS. When a new request is found on the blackboard, it invokes the appropriate template from the database and overwrites the actual parameters selected by users on the script template. When a user pauses, resumes or rolls-back a simulation, the Indemics broker interrupts the EPSE, which then handles the change in state as described in Section 3.1.1. The design of Indemics broker is one of the important contributions of DISimS. Overall, with extension of Simfrastructure, DISimS is able to support support variability in the implementation of its functional components and provide asynchronous mode of communication between them.

The other aspect of the DISimS architecture is to deal with large scale data communication between the EPSE and the ISSAE, implemented using the relational database. If ISSAE is directly connected to the EPSE, then any change in the implementation of ISSAE would need changes to the high performance code of EPSE. For making the system modular, flexible and adaptable, the EPSE and ISSAE have to be connected through an optimized middleware platform. Since EPSE executes a simulation over several time-steps (typically represented as days), data has to be retrieved from the database and passed to EPSE over many time-steps. This data passed back and forth can range up to several megabytes, as explained before. An orchestration mechanism of a service oriented architecture can slow the speeds of the EPSE. Also, a service oriented abstraction such as the one provided by Simfrastructure, where service requests are made asynchronously cannot be used since consistency of data has to be guaranteed in ISSAE.

Indemics [Bisset et al. 2014] introduced the concept of using a high-performance middleware platform that is optimized for communication between the relational database component and high-performance simulation engine. We decided to reengineer the Indemics Middleware Platform for our communication needs between ISSAE and EPSE.

Using IMP as the additional middleware, large scale data volumes can be supported per time-step across multiple simulation runs. IMP has an optimized queuing mechanism to queue data to be passed back and forth between the EPSE and the ISSAE. IMP also has features for data interpretation to speed up data mapping and transfer process. This ensures optimal performance of the simulation engine within DISimS. As can be seen in Figure 1, the presence of two middleware systems - SMP and IMP connected together in DISimS, instead of a single generic middleware, allows the simulation system to accomplish its usability goals along with performance.

Table III provides a comparison of the two middleware platforms - SMP and IMP, their main objectives, the data size that each of them support and the granularity of computation. As can be seen from the table, these two middleware have been specialized and optimized based on performance and functional needs.

Table III.

Middleware platforms and their speed comparison. Note: A single simulation experiment is carried out over multiple temporal iterations or time-steps (typically days) to study epidemic spread patterns over a period of time

Middleware Platform	Simfrastructure Middleware Platform	Indemics Middleware Platform
Description	Spaces-based middleware for high performance distributed systems between ISIS and HPC simulations	Java based middleware for data transfer between database system and high performance computing simulation system
Usage	Message-oriented data transfer	Large scale raw data transfer
Typical Comm. Data Size	140B per simulation	16KB per iteration of simulation
Design concern	Loose coupling and Modularity	Performance and efficiency

3.3. DISimS User workflow

In this section, we describe a detailed user workflow of DISimS and its effect on the data and context flow within DISimS. The DISimS platform can be accessed by users using any standard web browser. The ISIS Web Client of DISimS allows users to set-up and execute a simulation experiment. Figure 4 shows the sequence of events that take place inside DISimS, when a user submits a request to start a new epidemiological simulation experiment. The sequence of events can be described as a series of steps 1 to 19 as follows:

Fig. 4.

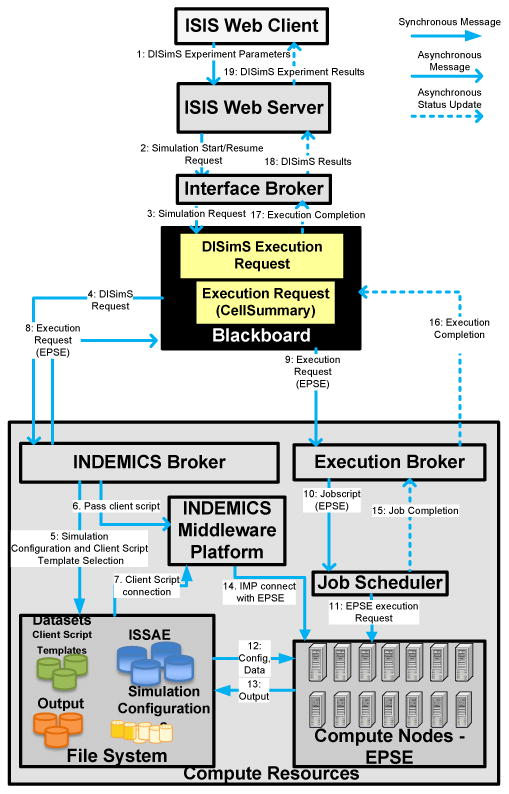
Workflow diagram showing the sequence of events that take place inside DISimS when a request for simulation execution is submitted at the beginning of the simulation or resumed from Paused state.

• —Step 1: As the first step to start a simulation experiment, a user has to select the parameters of simulation execution. Parameters of execution include the region of experimental study, number of days of simulation, number of replicates of simulation, disease model, initial conditions and so on. In addition, users can select intervention strategies to be applied to the propagation process such as vaccination, social distancing and so on. Requests can also be submitted to perform some complex epidemiological experiments by applying dynamic interventions such as the Block-based intervention strategy. Refer Section 6 for definition of the Block-based intervention strategy and an example of an IQL script written for Block-based intervention.
• —Step 2 : Once the experiment is set-up and submitted using the ISIS Web-client, the request is received by the ISIS Web server to start a simulation with input parameters. The ISIS Web server passes this information as input to the interface broker of the Simfrastructure Middleware Platform (SMP).
• —Step 3: The interface broker interprets the data, bundles the parameters as a ‘Simulation request’ and submits it on to the blackboard of the SMP.
• —Steps 4-5 : The Indemics broker, engineered as one of the sub-components of SMP, continually monitors the blackboard for new simulation requests for DISimS. Once a service request embedded with the required parameters is found on the blackboard, it unpacks the request, invokes the correct Indemics script template from the SMP database and replaces the template parameters with the actual parameters selected by users.
• —Steps 6-7 : During the same time, the Indemics broker hands over the created Indemics client script, written in IQL to the Indemics Middleware Platform (IMP) to communicate directly with ISSAE and EPSE. The dynamically generated IQL-based client script can be interpreted by the Indemics Middleware Platform.
• —Step 8 : The Indemics broker creates a new bundled execution request for EPSE and places it on the blackboard for starting the propagation simulation on EPSE.
• —Steps 9-11 : The execution broker monitors the blackboard for any new execution requests. When it finds a request, it starts execution of propagation simulation on the available compute resources such as a cluster or cloud, through a local job scheduler.
• —Steps 12-13 : The required data sets and configuration parameters for job execution are read from the file system and the intermediate results are written back for further processing.
• —Step 14 : The IMP is configured as a background process that is always in a running state. Once it receives an IQL script in Step 7, it monitors to see if the EPSE has started execution. If the EPSE has started execution, then IMP establishes connection with it. Based on the invoked intervention script, the IMP connects to appropriate database tables, retrieves intervened population data and passes it as an intervention to the EPSE. The EPSE continues to execute over several time-steps in this manner, receiving intervention data from IMP and executes until completion or until paused.
• —Steps 15-19 : Once the simulation is completed, the results are written back on the blackboard as shown in Figure 4 and are displayed to the users through the ISIS Web Client.

DISimS has a component called the “Analysis broker” that is configured to run analysis scripts based on the analysis request made by a user, similar to the execution broker,. The request for analysis of a particular experiment is made to an Analysis server that runs the R statistical software tool and follows similar workflow as above. The results of analysis are written on to the blackboard and consequently passed to the ISIS Web Client through the interface broker, where the corresponding graphs are plotted for analysis by the user. The user may also decide to use DISimS interactively by pausing the simulation after a certain duration and running analysis on partial simulation execution. Based on results of the analysis, the user may decide to apply a different set of parameters including a new intervention strategy or continue with the same parameters for the rest of the simulation. A resume request issued by the user after pausing a simulation follows similar flow of data as given in Steps 1 through 19.

If a new dynamic intervention strategy is selected by the user, then the Indemics broker invokes a new client script starting from the day/time-step the simulation was paused. This new client script connects to the same session with the Indemics Middleware Platform. The IMP is capable of storing state information for each simulation session. It holds its connection with the EPSE corresponding to an ongoing simulation for a user and sends out new interventions to the EPSE by selecting new subpopulation data from ISSAE.

In this way, an end-to-end interactive simulation can be executed using DISimS.

4. Computational Experiments

In this section we illustrate the capability of DISimS with two computational experiments. The first one is a real world case study to evaluate the effectiveness of school closure intervention in containing an ongoing epidemic with DISimS. The second one is to illustrate online optimization of intervention strategies along a decision tree via interactions with a DISimS-run simulation.

4.1. Computational Experiment 1

In this computational experiment, we evaluated the school closure intervention strategy applied during an epidemic of catastrophic flu in a region. School closure has been deemed as an effective measure to contain a flu pandemic. For example, during the 2009 H1N1 flu outbreak, New York city officials ordered the closure of 30 schools “after an increase of reports of students with flu-like symptoms” [CNN 2009]. School closure reduces the overall transmission within a school and is a well known and effective non-pharmaceutical intervention [Cauchemez et al. 2009; Wu et al. 2010].

For a school closure intervention, the potential risk of within-school flu outbreak if schools remain open has to be evaluated against the large social costs associated with school closures. The decision to close schools is based on such evaluation. For example, the Centers for Disease Control and Prevention (CDC) revised its earlier recommendation of shutting down schools immediately when a few students became ill to keeping schools open even with flu outbreaks during the later period of the 2009 H1N1 pandemic [Time 2009].

The school closure policy works as follows. If in a school, the fraction of students diagnosed with flu exceeds a certain threshold then the school is closed for a certain number of days, and for each diagnosed student below a certain age, one parent or care giver must stay at home. School closure is not a binary decision, but based on a number of parameters. We analyzed an event-triggered school closure policy for an experimental study on a flu outbreak in Miami, to assist analysts in their decision making in the real world. We considered two parameters in this measure: threshold and duration. The former determines the severity of the epidemic to make it necessary to close schools; the latter determines how long schools need to be closed. We chose two values for each of the two parameters to form four configurations of the school closure intervention. In contrast to previous studies where we examined the course of epidemic dynamics, the main objective of this study was to study and provide an effective comparison between a variety of settings of an intervention policy. We point out that the study provides an illustration of possible interventions that can be easily simulated by DISimS but difficult for either EpiFast or Indemics.

The complexity of the school closure intervention comes from two aspects: each school is determined to be closed individually instead of universal closures; for the affected subpopulation (students of the closed school) we need to identify another subpopulation consisting of people of appropriate demographic properties (age and household), who represent the care givers of the children.

When we were requested to perform the school closure study, our simulation engines such as EpiSimdemics and EpiFast did not have features to integrate supplemental information at that time and hence could only simulate simplified but less realistic versions of the school closure intervention. The code of these high performance simulation engines would have had to be modified to support such interventions. Our simulation engine developers and the intervention experiment strategy designers would have had to work together to precisely interpret the strategies and code them into the high performance engines. The estimated development time including requirements gathering, implementation, and testing would be several weeks, in contrast to the estimated experiment execution time of only one week. This approach would have been time-consuming and it would have been difficult to report simulation results and make policy recommendations in time.

To overcome this problem, we used Indemics, a database supported epidemic simulation framework, to run the study. In contrast to the epidemic simulation engine like EpiFast, the implementation of interventions in Indemics is modeled by data query algebra, and the interventions are completely computed using the Indemics Query Language (IQL), as described before. Experiment strategy designers only need to describe their scenarios in IQL and submit the simulation jobs to Indemics for execution. The experiment development process of Indemics takes a few days to map the interventions into IQL. Indemics incurs marginal execution time overhead, but it needs no significant code development or testing for the HPC simulation engine. We adopted this solution to run the study and it greatly reduced the study period and saved a significant human effort.

Although the development time for implementing the intervention was shortened remarkably by Indemics, Indemics did not have a module to automatically set up experiments, monitor the state of an experiment and manage experimental inputs and results. There was no provision for re-usability and sharing by checking if an appropriate Indemics intervention script was previously written by some other user. Also, when the intervention had to be simulated with different parameter settings, using Indemics became cumbersome. For example, a script to run a factorial experiment by changing multiple parameter values had to be prepared manually, which was error-prone. The simulation inputs and outputs had to be well organized to avoid overwriting or misreading. The simulation jobs also had to be monitored by the experiment executors. Such tasks needed considerable manual effort. Reading and understanding raw simulation results was difficult since Indemics did not have statistical analysis or data visualization modules. We realized that when the user has minimum knowledge and experience in preparing Indemics scripts (in IQL) and running simulations in a high-performance computing environment, which is often true for public health domain experts, executing complex experimental studies such as the one to implement school closure intervention, is difficult even with Indemics.

From the experience of implementing the School closure intervention study, we realized that the usability of the simulation system had to be leveraged further. Hence we developed DISimS, with features like user interactivity, simple interface, experiment data management, job monitoring and analysis in addition to the attributes that were already provided by Indemics and EpiFast. Employing DISimS for the school closure intervention study could have reduced the overall experiment set-up and management time and enhanced the human productivity considerably.

Using DISimS, the users now only need to select the intervention scripts and parameters of execution using a intuitive web-based graphical interface. The data files for the factorial experiments are well-organized and well-archived and the simulation jobs are automatically monitored and scheduled. DISimS introduces a marginal overhead of execution as compared to Indemics, which is equivalent to the communication time between the web-based front end to the Indemics server middleware. Table IV shows the comparison of the efforts for the school closure intervention experiments using EpiFast, Indemics and DISimS on the city of Miami. As can be seen in the table, the total human effort for experiment design and analysis is reduced significantly by DISimS compared to previous systems, and the total increase in the experiment execution time is negligible. This table shows the value of DISimS for improving the productivity of epidemiologists and public policy decision makers. They can now set up, manage, and execute complex intervention case studies without much help from the computational scientists.

Table IV.

Comparison of efforts for school closure intervention case study on Miami city. Experiment execution is carried out over multiple iteration days. *For DISimS, the expt. execution time excludes communication time between the web-server and Indemics Middleware Platform, which is negligible compared to actual expt. execution

Case study	System Name	Development time	Analysis set-up time	Expt. set-up+analysis time	Expt. execution time
School	EpiFast	hard to implement	unknown	unknown	unknown
Closure	Indemics	1 day	0.5 day	1.5 days	3-4 min/iteration
intervention	DISimS	5 minutes	20-25 mins	30 min	3-4 min/iteration*

Figure 5 shows epicurves in different intervention settings. It is an example of visualization that user can obtain directly from the DISimS system. In this plot, we can see that applying school closure too early (with 1% threshold) may suppress the disease outbreak temporarily but the epidemic takes off soon. But it indeed postpones the epidemic peak; and the gained time may be useful for taking other measures. Analysts are able to conduct such in-depth analysis using DISimS and make decisions regarding the epidemic mitigation strategies to apply in real world.

DISimS has been in use by the analysts in our lab to execute a number of simulation experiments with a variety of intervention strategies to contain epidemics. The analysts have reported that they are able to execute intervention strategies using DISimS that were previously not possible to be executed within a stipulated time range. The analysts have also reported that DISimS provides much greater capabilities in terms of analysis and range of experiments, that were not possible using any of the previous systems.

For instance, using DISimS analysts can write Intervention script templates for new types of interventions and quickly incorporate them as part of the system. Other analysts can reuse the same scripts with a wide range of parameters such as number of replicates and different regions, and perform a factorial study design with increased accuracy. Such study was not possible before without several changes and manual analysis. DISimS makes it easier to conduct complex experimental studies on high-end computational resources in a timely manner with graphical analytical results. DISimS also frees the analysts from the burden of understanding details of the computing infrastructure or the need to write complicated simulation scripts.

4.2. Computational Experiment 2

In this computational experiment, we demonstrate the utility of DISimS to train public health decision makers in evaluating the effectiveness of various intervention strategies. DISimS provides a specific type of interactivity while executing realistic large scale simulations. This interactivity allows users to pause a simulation after a specific duration, analyze the evolution of the epidemic in the current scenario and then come up with a new strategy that can work best for containing the epidemic in the given scenario.

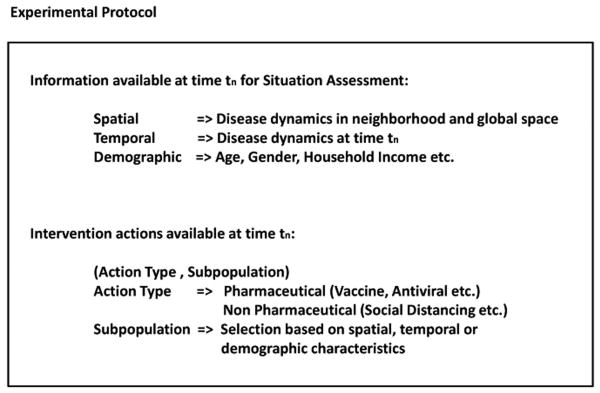
At every time-step at which the simulation is paused, the analyst has to make a decision about which intervention strategy to apply for the next duration ranging across several time-steps, so that the epidemic can be contained effectively. This decision is based on situation assessment of the epidemic dynamics at the current time-step, which is made possible because of the ISSAE component of DISimS. The various choices available to the analyst for decision making and the actions taken by the analyst (that could affect availability of future choices), can be represented in the form of a decision tree. This decision tree is based on the experimental protocol of information available to users and the range of intervention actions that can be executed. The experimental protocol of an adaptive epidemiological experiment is shown in Figure 7.

Fig. 7.

Experimental protocol of the information available to a public health analyst for situation assessment at any time-step when the simulation is paused and the range of options available for intervention application for the remainder of the simulation.

Experiment design

We have designed a computational experiment for training purposes to study a case of strong flu epidemic in the Montgomery County of Virginia. The county has a population of about 75,000 people. The public health decision maker has antivirals to distribute but the supply is limited. Starting from the beginning of the epidemic, every 25 days, 1,000 more units of antivirals become available. This is to address the limited pharmaceutical manufacturing capacities and latency of massive distribution of drugs. The antivirals are effective for 14 days once applied and they reduce probability of getting infected (for healthy people) or probability of infecting others (for ill people) by 80%.

A group of experts are chosen to participate in the experiment. Each expert can ask DISimS questions about the current epidemic dynamics and can decide how to distribute the available antiviral supply based on the answers to the questions. For illustration, we pause the simulation every 25 time-steps (25 simulation days) to allow the experts to query and intervene based on age groups and current health state of each person in the Montgomery County. We point out, however, that the simulation can be paused at any time-step and the user interaction can be based on any data available from the simulation or in the database.

A public health analyst, at each decision point, can decide to do nothing, or apply K units of antivirals, where K is bounded by the current antiviral supply, to people randomly chosen in certain age groups. The possible decisions and the random epidemic trajectory formulates a stochastic decision tree, where at each decision point an analyst may decide to take different branches depending on the epidemic dynamics.

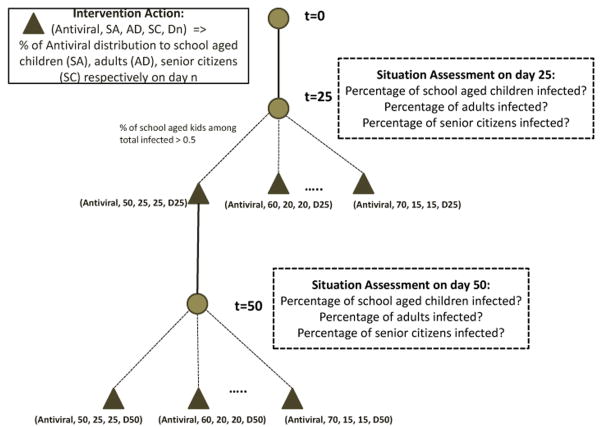
We ran this scenario with a public health analyst. Figure 8 shows the representation of the decision tree available to the analyst at the various decision points that he paused the simulation. In this case, the analyst paused the simulation on day 25 and day 50 respectively. The figure also shows the corresponding choices available for intervention application. For the sake of simplicity of the experiment, we made only limited choices available to the analyst for situation assessment and intervention application based on age groups. However, in reality the analyst can choose from a large range of information for situation assessment and intervention application, based on the Experiment protocol described in Figure 7.

Fig. 8.

Decision tree representation of the choices available to a public health analyst for applying interventions based on situation assessment. The analyst can pause the simulation periodically, analyze the situation and take actions that affect the course of the epidemic.

Figure 6 shows epidemic curves generated from the DISimS system for the experiment. In the non-Adaptive case, antivirals are evenly distributed among each age group - School age, Adults and Senior Citizens on day 25 and day 50. In the adaptive case, antivirals are distributed based on situation assessment on day 25 and day 50. Since it was observed by the analyst that higher percentage of school children were infected in the first few days compared to other age groups, greater percentage of AVs were distributed to school children. As can be seen in the Figure 6, the peak time of the epidemic shifted to the right in the non-adaptive and adaptive cases and the peak infection count also went down. There is not much difference observed in the epi curves plotted for non adaptive vs. adaptive cases, since there is only a small difference in the percentage distribution of antivirals in both cases. Hence, this may not cause a significant difference to the epidemic dynamics. However, if the adaptive technique is used for training the analysts such that they can infer more about the epidemic dynamics and apply intervention actions at the right decision points, then there is a possibility of seeing change in propagation dynamics of the epidemic.

This experiment illustrates the following capabilities of the DISimS system: (i) A user can pause and resume a simulation at any time-step. (ii) A user can interact with the simulation online, query the system and make decisions accordingly. DISimS enables adaptive interventions that address both uncertainty of epidemics and that of the human decision process. (iii) DISimS supports realistic scenarios of public health level decision making. (iv) DISimS supports simulations of realistic, implementable but complex intervention strategies, based on dynamic epidemic data, as well as demographic and other data.

5. Conclusion

In this paper, we have presented the architecture and implementation details of DISimS– an integrated, high performance computing oriented epidemic modeling environment. DISimS focuses on three important user level goals: (i) improving user productivity and ease of use, (ii) supporting interactive modeling and (iii) pervasive web-based access to the models. We described two computational experiments that illustrate the applicability of DISimS for addressing practical public health policy questions. We hope to deploy a prototype of DISimS for use by a broader scientific community in the near future. DISimS can be extended in several different directions. We mention three important ones here: (i) extending DISimS to further support optimal dynamic interventions, (ii) an evolved scripting language that allows a user to specify broad classes of situation assessment queries, and (iii) allowing multiple stake holders to interact with a single instance of the system to support distributed decision making.

More generally, modeling environments to study other socio-technical and biological systems, including urban transport systems, telecommunication systems and immune modeling systems, often exhibit similar modeling requirements as discussed here for epidemiological modeling environments. We believe that DISimS and its extensions can thus provide applicability beyond the specific application domain described in this paper.

We discuss a specific extension that we are currently investigating – development of an educational gaming technology based on the epidemic modeling environment. Gaming systems not only need fast computations at run-time along with changing parameters, but also very detailed graphical interfaces for the convenience of users. Performance is a key requirement for such gaming systems along with a high resolution user-friendly graphical interface to keep the attention of the users.

Appendix

In this section, we describe some of the terms used extensively in the paper that need more detailed explanation. We also briefly describe the architecture of Simfrastructure and the Indemics Intervention Language (IQL) used to specify the intervention strategies in ISSAE.

A.1. Simfrastructure

Simfrastructure[Bisset et al. 2013] is a distributed middleware platform that decouples compute resources such as clouds, grids and clusters from the simulation models, digital library components and web user interface systems. (Refer Figure 9) Simfrastructure was conceptualized as a high performance distributed system mechanism that could handle asynchronous communication between various service components distributed across different networks. It is based on tuple spaces based architecture with associative memory paradigm and provides distributed coordination framework to allow a consumer to request service fulfillment from a service provider. Simfrastructure that supports its service oriented model is the Blackboard, on which service requests are placed by the consumer. The other important component of Simfrastructure is called the Service Broker. Each Service Broker provides service fulfillment of a particular service that it is specialized to serve. The Service Broker continuously monitors the blackboard and when a service request placed by a consumer is found, it reads the request and fulfills it.

Fig. 9.

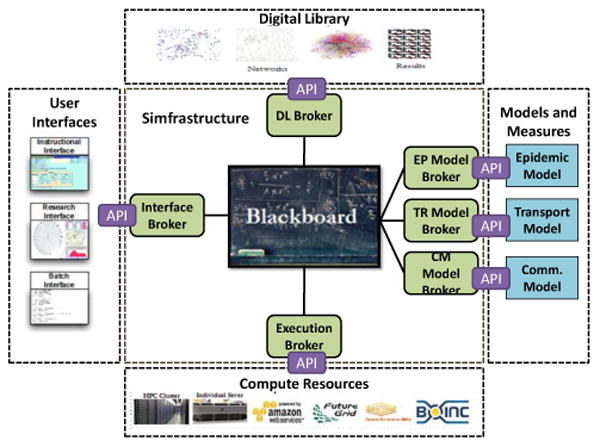
Modeling and simulation environment using Simfrastructure as the central communication and coordination middleware. Simfrastructure coordinates data and context flow between user interfaces, digital library, compute resources and simulation models and measures.

A.2. Block-based intervention strategy

Block-based intervention: This mitigation strategy specifies that if a fraction of people diagnosed with a disease in a census block exceeds a certain threshold, then quarantine or give medical treatment to individuals in the entire block. This strategy is often used by epidemiologists and public health decision makers when several cases of an outbreak are reported in a certain census block.

Algorithm 1: Indemics Client Script template of Block-based intervention using IQL

connect session: session_name = block-based-intervention

day from 0 to last_simulation_day do

copy data: to set ISISTMP, from select b.block, count(b.pid) as total diagnosed, day from BLOCK b,

DIAGNOSED_PERSON d where diagnosed_time =day and b.pid = d.pid group by b.block

define set: infected_block_day as select block from ISISTMP where day = day and total diagnosed/total persons >0.02

update set: update INTERVENED_BLOCK set intervened = day where block in infected_block_day

define set: intervened_population_day as select pid from PERSON_HOME_LOCATION where home_location in (select block from INTERVENED_BLOCK where intervened = day)

set interventions: action= StayHome, compliance=1.0, duration=7 days, delay=0 days on

intervened_population_day

stop session:

stop client:

A.3. Indemics Query Language (IQL)

The Indemics Query Language is used to fetch data related to interventions from ISSAE and use it to apply interventions to propagation simulation in EPSE. The commands available in Indemics Query Language can be classified into two types: Simulation Setting/Cleaning Commands (SSCs) and Simulation Interaction Commands (SICs). As shown in the given example, connection session, stop session and stop client are SSCs; define set, update set and set interventions are SICs.

Both SSC and SIC are composed of two parts: the command operator and its parameter. For the SSCs, the command parameter is very simple. For example, the parameter of “connection session” command is the session name, which is the name of the session that the client is supposed to interact with. (Since Indemics client and EPSE are distributed modules, they need to be connected first before further interaction). The situation assessment and intervention strategies are specified by set operators in Indemics Query Language. The command parameters of SIC are the data sets to apply set operators on. If relational database is used to implement ISSAE in Indemics, the data sets in the SIC command parameters represent tables in the database. Client may define a set, copy data to the set and update an existing data set. What operation to perform on the data sets is specified in the command parameters. In the current version of Indemics Query Language (IQL), we borrow much of the syntax from the structured query language (SQL) for data set operations. For example, in the given client script, data is copied from existing data sets to a target data set by applying filters similar to that in SQL.

An example client template script for a block-based intervention written in Indemics Query Language is given here. The SMP replaces the dummy variables with actual parameters creating a dynamic Indemics client script at run-time.