Abstract
We report a study of the wetting and ordering of thermotropic liquid crystal (LC) droplets that are trapped (or “caged”) within micrometer-sized cationic polymeric microcapsules dispersed in aqueous solutions of surfactants. When they were initially dispersed in water, we observed caged, nearly spherical droplets of E7, a nematic LC mixture, to occupy ∼40% of the interior volume of the polymeric capsules [diameter of 6.7 ± 0.3 μm, formed via covalent layer-by-layer assembly of branched polyethylenimine and poly(2-vinyl-4,4-dimethylazlactone)] and to contact the interior surface of the capsule wall at an angle of ∼157 ± 11°. The internal ordering of LC within the droplets corresponded to the so-called bipolar configuration (distorted by contact with the capsule walls). While the effects of dodecyltrimethylammonium bromide (DTAB) and sodium dodecyl sulfate (SDS) on the internal ordering of “free” LC droplets are similar, we observed the two surfactants to trigger strikingly different wetting and configurational transitions when LC droplets were caged within polymeric capsules. Specifically, upon addition of SDS to the aqueous phase, we observed the contact angles (θ) of caged LC on the interior surface of the capsule to decrease, resulting in a progression of complex droplet shapes, including lenses (θ ≈ 130 ± 10°), hemispheres (θ ≈ 89 ± 5°), and concave hemispheres (θ < 85°). The wetting transitions induced by SDS also resulted in changes in the internal ordering of the LC to yield states topologically equivalent to axial and radial configurations. Although topologically equivalent to free droplets, the contributions that surface anchoring, LC elasticity, and topological defects make to the free energy of caged LC droplets differ from those of free droplets. Overall, these results and others reported herein lead us to conclude that caged LC droplets offer a platform for new designs of LC-droplet-based responsive soft matter that cannot be realized in dispersions of free droplets.
Introduction
Aqueous dispersions of micrometer-sized droplets of thermotropic liquid crystals (LCs) provide versatile platforms for the design of stimuli-responsive soft matter systems.1−14 The responsiveness of these droplet-based LC systems to various types of stimuli results from the fine scale of energetics that controls the equilibrium ordering of LCs. Specifically, past studies have established that the ordering of LCs within micrometer-sized droplets reflects contributions to the free energy that arise from orientation-dependent anchoring of the LC at the surfaces of the droplets, elastic strain of the LC associated with the accommodation of surface anchoring, and the formation of topological defects.1−14 Recent studies, however, have also led to observations involving LC droplets in aqueous dispersions that reveal our understanding of factors controlling the ordering of LC droplets to be incomplete. In particular, existing theories of LC droplets cannot account for (i) changes in the internal configurations of the LC droplets that occur with changes in droplet size,6,8,15 (ii) the effects of simple salts on the ordering of the LCs,8 or (iii) the partitioning of amphiphiles to the defects of LC droplets.8,9,16 In this paper, we seek to advance our understanding and ability to design aqueous dispersions of stimuli-responsive LC droplets by exploring the properties of LC droplets encapsulated (or “caged”) inside thin and porous polymeric membranes. Our results reveal that the interactions of the LC droplets with the interfaces of the polymeric cages give rise to surfactant-triggered shape changes and resulting internal ordering transitions that are not seen in free LC droplets.
Of particular relevance to this article are recent studies that have investigated the ordering of spherical LC droplets encapsulated in capsules composed of polyelectrolyte multilayers (PEMs).5−7 In those studies, the spherical polymeric capsules were formed using noncovalent interactions (e.g., electrostatic interactions or hydrogen bonding), and the LCs were observed to fill the interiors of the capsules completely. The study reported in this article moves to investigate the ordering of LCs within multilayer capsules prepared by covalent reactions of branched polyethylenimine (PEI) and poly(2-vinyl-4,4-dimethylazlactone) (PVDMA). In contrast to capsules formed from PEMs, multilayer capsules formed using PEI and PVDMA have been found to fill only partially with LC, resulting in the formation of micrometer-sized LC droplets that are trapped or caged in aqueous solutions contained within the polymer capsule.13 These systems are a particularly interesting class of responsive soft matter, as the capsules can be designed to bind to the surfaces of mammalian cells, with the caged LC droplets undergoing changes in optical appearance upon exposure to cytotoxic analytes (thus providing the basis for sensors of local concentrations of toxic analytes near cells, etc.).13
The work reported here sought to provide insight into some of the observations reported above and explore further the properties of caged LC droplets in the presence of aqueous solutions of surfactants. First, we report on the origins of the partial filling of PEI/PVDMA capsules by the nematic LC E7. In this context, we describe the design of new amphiphilic polymeric capsules that were prepared to present a hydrophobic inner surface to the LC droplet (to promote filling) and a charged (cationic) outer surface to promote the dispersal of the capsules in water. We establish that the partial filling of the capsules by E7 is also observed with amphiphilic capsules and that it arises largely from the swelling of the capsules upon transfer into water from the bulk LC phase after filling of the capsules with LC. Second, because the capsules are partially filled by LC (the remainder of the internal volume of the capsule is an aqueous solution), we explore changes in the shapes of the caged LC droplets that are driven by surfactant-induced changes in the wetting of the LC on the inner surfaces of the capsules. As detailed below, we observed the addition of surfactants to aqueous solutions of caged LC droplets to promote wetting and ordering transitions of a complexity not observed in free LC droplets, which may permit new designs of stimuli-responsive LC-droplet-based systems.
Experimental Section
Fabrication and Functionalization of Polymer Multilayers on Silica Microparticles and Creation of Hollow Capsules
The fabrication of hollow polymer microcapsules was performed according to a previously published procedure for the layer-by-layer (LbL) formation of covalently assembled polymeric capsules.17 On the basis of a past report,6 we used monodisperse silica microspheres with a diameter of 4.99 ± 0.22 μm as a template for the polymer microcapsules to produce LC droplets of a size that is sensitive to amphiphilic adsorbates. Solutions of PEI and PVDMA (or PVDMAFL labeled with 6-aminofluorescein to facilitate fluorescence-based imaging) (Figure 1A) were prepared in acetone (20 mM with respect to the molecular weight of the polymer repeat unit). SiO2 microparticles (100 μL in plastic microcentrifuge tubes) were rinsed with 1 mL of acetone and centrifuged prior to the addition of polymer. In brief (see SI and past reports13,17 for details), an initial layer of PEI was adsorbed onto the silica microparticles through electrostatic interactions, and subsequent layers of PVDMA (or PVDMAFL) and PEI were sequentially added, layer-by-layer, to build up a covalently cross-linked multilayer film. Between the addition of each polymer layer, particles were rinsed three times by centrifugation (2 min at 1500 rpm) and resuspension in acetone.
Figure 1.
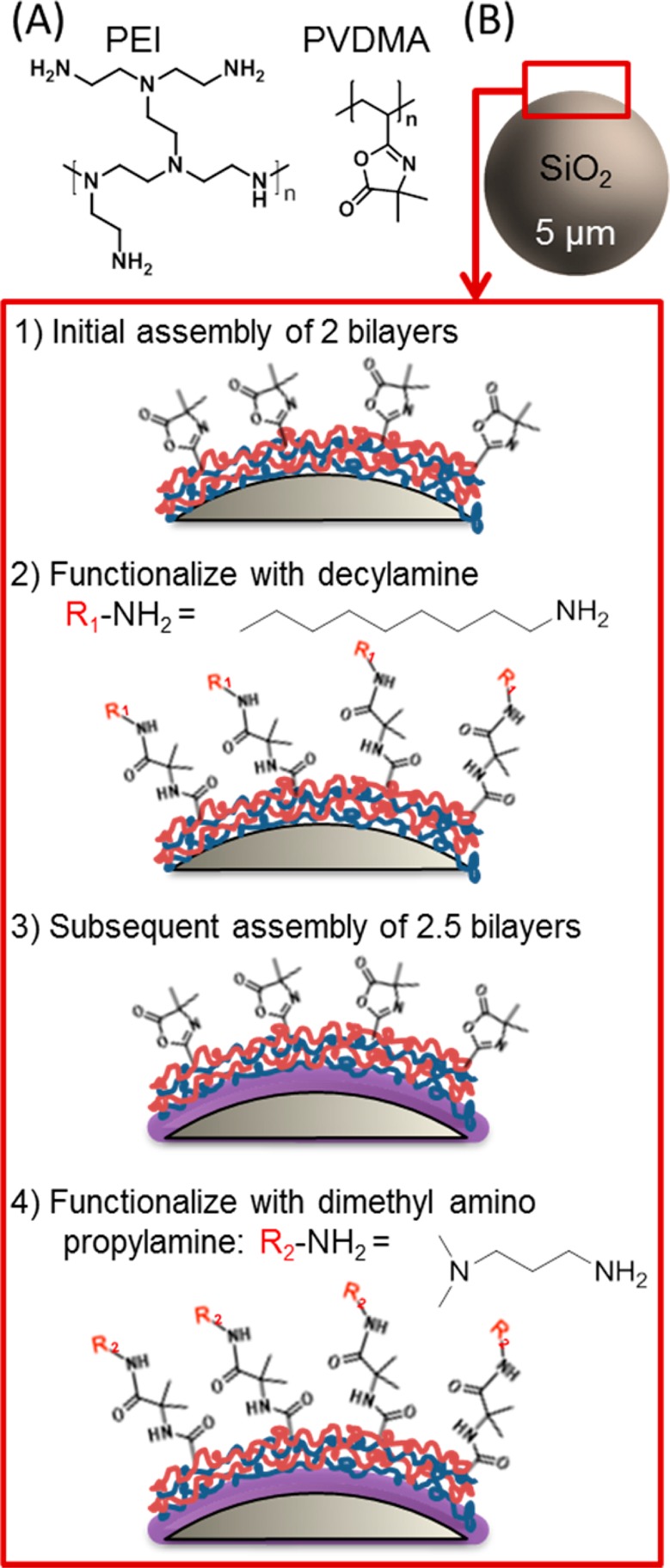
(A) Chemical structure of branched PEI and PVDMA used for the covalent layer-by-layer assembly of multilayer films. (B) Schematic showing the steps in film fabrication. Chemical functional groups: decylamine (denoted R1 or DA) was used to functionalize the first two bilayers, and dimethylaminopropylamine (denoted R2 or DM) was used to functionalize the outer 2.5 bilayers (see text).
Films fabricated using this method have been shown previously to contain residual azlactone groups, providing a reactive handle for postfabrication functionalization with other chemical functionalities. We selected two different structural motifs, shown in Figure 1B; further discussion is included below. After the fabrication of two PEI/PVDMA bilayers, the coated microparticles were rinsed with tetrahydrofuran (THF) and functionalized by adding 1 mL of decylamine (DA, Figure 1B) in THF (20 mM) for 1 h to install the hydrophobic functionality. These DA-functionalized coated microparticles were then rinsed with THF three times and dispersed in acetone prior to resuming the fabrication of an additional 2.5 bilayers of PEI and PVDMA. Finally, to functionalize these outer 2.5 bilayers with protonatable hydrophilic functional groups, the microparticles were washed with THF three times and then dispersed in 1 mL of 3-(dimethylamino)propylamine (DM) in THF (20 mM) for 1 h.
Polymer-coated silica microparticles were rinsed with THF three times by centrifugation and then suspended in a small volume of water (∼100 μL) in preparation for aqueous etching. The silica core was removed from the polymer membrane by treatment with a commercially available buffered oxide etching (BOE, 10:1) solution containing hydrofluoric acid (HF); see Materials section in SI. (Warning! Extreme care should be taken when handling HF. HF solutions and vapors are extremely poisonous and corrosive and may cause extreme burns that are not immediately painful. Handle with extreme caution in a chemical fume hood, and use appropriate protective equipment (gloves, face/eye protection, laboratory coat, etc.), and neutralize waste appropriately.) The samples were incubated with 800 μL of BOE at room temperature for 5–10 min. The resulting hollow capsules were centrifuged (4500 rpm for 5 min) and rinsed five times in 1 mL of water.
Filling of Polymeric Capsules with LC
After the silica template was removed to obtain hollow polymeric microcapsules, the microcapsules were filled with LC following a previously reported protocol.5,6,13 In brief, the capsules were rinsed with ethanol twice, centrifuged to remove as much of the supernatant ethanol as possible, and suspended in a mixture of 5% ethanol and 95% E7. This mixture of ethanol and E7 forms an isotropic phase that can infiltrate the polymeric capsules. The ethanol was slowly evaporated from the sample by leaving the tube containing the sample uncapped on a shaker plate for 24 h, resulting in a nematic phase containing the capsules. The capsules were then extracted into an aqueous phase by removing excess E7 by centrifugation, contacting the sample with water, and shaking gently. This procedure resulted in the spontaneous transfer of capsules containing LC droplets to the aqueous phase.
Characterization of LC Droplets and Polymer Capsules by Microscopy
Dispersions of either bare or coated microparticles, hollow capsules, and LC-containing capsules were placed on a coverslip and optically imaged in bright-field polarized light (crossed polarizers) using fluorescence modes with an Olympus IX-71 inverted microscope (Center Valley, PA) with a 100× oil-immersion objective (with or without an additional 1.6× optical zoom) and equipped with a 100 W mercury lamp. For fluorescence-based imaging of capsules fabricated using PVDMAFL, an Olympus U-MNB2 fluorescence filter cube was used with a 470–490 nm excitation filter and a 520 nm emission filter. A monochrome Hamamatsu 1394 ORCA-ER CCD camera (Bridgewater, NJ) was controlled with SimplePCI software (Compix, Inc., Cranberry Twp., NJ). Images were later analyzed using ImageJ software (NIH, Bethesda, MD). For each sample, the bulk solution was imaged using polarized light microscopy to determine the ordering of LC droplets in capsules that were freely diffusing. However, since the diffusion quickly moved the capsules out of the plane of focus or the field of view, capsules could be imaged in all three imaging modes (bright field, crossed polarizers, and fluorescence) only after sedimentation onto the coverslip surface. In our experiments, we did not observe any orienting effect on the LC resulting from contact with the coverslip, as reported in a past study.18
Results
Partial Filling of Multilayer Capsules with LC
In contrast to prior studies described in the Introduction, the capsules used in this current investigation were prepared to have walls with hydrophobic functionality facing the interior of the capsule and hydrophilic functionality on the outer surface. This was accomplished by functionalizing the interior with decylamine (DA) and the exterior with dimethylaminopropylamine (DM) such that the hydrophobic interior contacted the LC and the hydrophilic exterior surface contacted the bulk aqueous phase. (See Figure 1 and the Experimental Section for details.) In the remainder of this article, we refer to these capsules as having an amphiphilic structure and by using the acronym DADM to identify the DA and DM motifs decorating the interior and exterior walls of the capsules. In the interest of brevity, the confirmation of the successful synthesis of these DADM capsules is detailed in the Supporting Information (SI). Specifically, we present evidence of the incorporation of the DA and DM into the capsule walls (Figure S1) and show scanning electron micrographs of polymer-coated microparticles and hollow capsules (Figure S2). Measurements made using the scanning electron micrographs reveal the size of the dried, polymer-coated microparticles to be 4.9 ± 0.2 μm.
After treatment with LC using methods that lead to the complete filling of PEM-based capsules in past studies, we observed the DADM-functionalized PEI/PVDMA capsules used here to be only partially filled with LC (see Figure 2F, middle row). Specifically, we measured the average diameters of the DADM capsules and the LC droplets to be 6.7 ± 0.3 and 4.9 ± 0.5 μm, respectively; that is, the LC filled approximately 40% of the internal volume of the capsules. To provide insight into the reasons underlying partial filling, we imaged the film-coated microparticle precursors and the hollow capsules in each step of the synthesis (Figure 2). The images in the middle row of Figure 2 are bright-field micrographs, and images in the bottom row are fluorescence micrographs of fluorescein-labeled capsules that clearly define the sizes and shapes of the capsules. An inspection of Figure 2 reveals several key points. First, the DADM-coated silica microparticles in water were measured to have a diameter of 5.3 ± 0.3 μm (Figure 2B), a value that is indistinguishable from the diameter measured for the bare silica microparticles in water (5.2 ± 0.3 μm as in Figure 2A). Second, after etching of the silica templates, we measured the diameter of the resulting hollow capsules to vary significantly depending upon the solvent in which they were suspended (Figure 2C–E). Specifically, we measured capsule diameters to be 6.7 ± 0.3 μm in water, 5.6 ± 0.3 μm in 90% acetone/10% water, and 4.7 ± 0.2 μm in nematic E7. Third, upon extraction of LC-containing DADM capsules into an aqueous phase, the capsule diameter was again measured to be 6.7 ± 0.3 μm (Figure 2F), a value that is indistinguishable from that of empty capsules in water. Overall, these observations reveal that the volume of the LC encapsulated within the polymeric shell is determined by the size of the capsule when it is present in the nematic LC (i.e., during filling; compare panels E and F of Figure 2). When LC-filled capsules are extracted into an aqueous phase, the capsules swell, thus resulting in capsules that are only partially filled. We emphasize that the volume of the LC droplets caged within the polymer capsules when dispersed in water is roughly equal to the interior volume of the capsules when they are dispersed in nematic LC during filling.
Figure 2.
The top row shows a cartoon of the sample composition, the middle row consists of bright-field images, and the bottom row contains the corresponding fluorescence microscopy images of (A) bare silica microparticles in water, (B) DADM-coated silica microparticles in water, (C) empty DADM capsules in water (after HF treatment and rinsing), (D) empty DADM capsules in a solution of ∼90% acetone and ∼10% water, (E) DADM capsules in nematic E7, and (F) DADM capsules partially filled with E7 in water. The average capsule size is noted below the fluorescence microscopy image, and the LC droplet size is also denoted below (F). Bright-field and fluorescence microscopy images are not shown for all states, e.g., where the sample was not in focus or not fluorescent. Scale bars are 5 μm.
Finally, we comment that a fraction of capsules observed in nematic E7 (approximately one in six capsules prior to extraction into water) possessed nonspherical crescent shapes, consistent with a buckling instability in the capsule wall (Figure 3).19 For these nonspherical capsules, we measured the long axis (i.e., the largest diameter that could be measured) to be 4.5 ± 0.3 μm, corresponding to a diameter similar to that of the spherical capsules (4.9 ± 0.5 μm), and the short axis (perpendicular to the long axis) was measured to be 2.3 ± 0.6 μm. This small subpopulation impacted the underfilling of the capsules with LC and contributed to heterogeneity in the size and shape of the capsules and droplets. We note that the majority of capsules that we observed to be nonspherical in the E7 phase returned to a spherical shape when transferred to the aqueous phase; a very small percentage of capsules (approximately 2%) remained nonspherical in shape.
Figure 3.
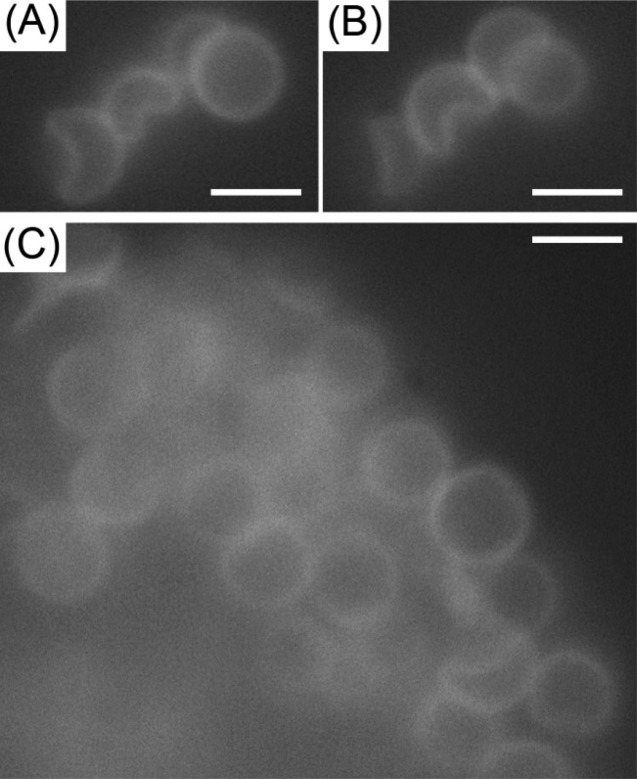
Fluorescence micrographs of DADM capsules suspended in nematic E7. (A, B) Micrographs of the same group of capsules imaged with different locations of the focal plane such that in (A) the circular capsule on the right of the image was in focus and in (B) the crescent-shaped capsule in the center of the group was in focus. (C) Micrograph of a separate region showing a group of capsules with more spherical than nonspherical capsules. Scale bars are 5 μm.
Ordering of Caged LC Droplets
Figure 4A–C shows representative caged LC droplets imaged in bright-field and polarized light modes as well as schematic illustrations of the ordering of the LC in the droplets. A number of features of the droplets imaged between crossed polarizers led us to conclude that the orientational ordering of the LC within these droplets corresponds to a so-called bipolar configuration. In this configuration, the LC lies tangential to the LC–aqueous interface with two point defects at diametrically opposite poles, as depicted schematically in the right column of Figure 4.2−5,20−23 In Figure 4A, the key identifying features are the two dark spots on the left and right sides of the droplet, bright lobes above and below these spots, and a relatively dark center of the droplet, indicating that the LC in the center is aligned with either the polarizer or analyzer. The narrow dark spots correspond to point defects on the droplet surface known as boojums that define the poles and, thus, the symmetry axis of the bipolar nematic droplet. (The angle that this symmetry axis makes with the polarizer is indicated on the polarized light images.) Typically, boojum defects can be seen in bright-field images as dark regions because they possess a local refractive index environment that is distinct from that of the rest of the LC droplet and thus scatter light. However, optical distortions resulting from the polymer capsule prevented us from identifying the boojums in many of our bright-field images.
Figure 4.
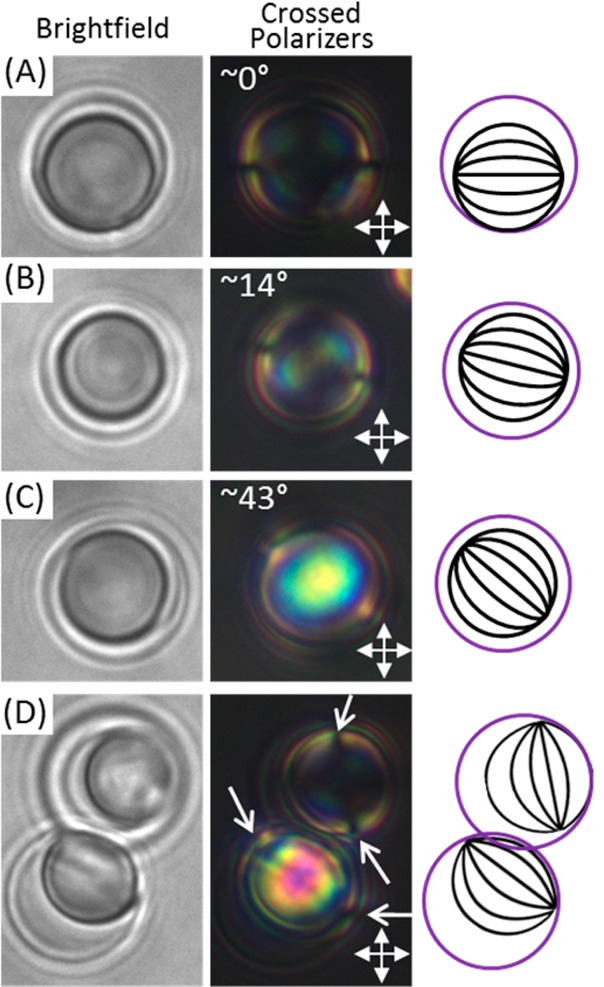
Bright-field and polarized light micrographs of DADM capsules in water (left and center columns, crossed polarizers indicated by white arrows). Corresponding schematic illustrations of the LC director profiles are shown in the right column. The angle that the axis of symmetry of the droplet makes with the polarizer is 0° in (A), 14° in (B), and 43° in (C). (D) Two droplets with asymmetric shapes also exhibit signature features of bipolar ordering with arrows indicating the locations of boojum defects.
Figure 4B shows a droplet that has its symmetry axis, defined again by dark spots that correspond to the boojums, at an angle between the polarizer and analyzer. The rotation of the symmetry axis away from the polarizer/analyzer results in a birefringent texture within the droplet that is brighter than that shown in Figure 4A. This droplet also has curved dark bands within the bright central region in a baseball-like pattern, a characteristic that is frequently used to identify bipolar droplets.2,24 Figure 4C shows a bipolar LC droplet within a capsule aligned with its axis of symmetry at an angle of ∼43° from the polarizer and analyzer. In this image, we observed only one bright region next to each boojum, as the other lobe is more closely aligned with a polarizer. In summary, the observations reported above are consistent with a bipolar configuration of roughly spherical LC droplets within the capsules.
While the majority of the caged LC droplets appeared to be spherical, we also observed a subpopulation of nonspherical, asymmetric droplets (approximately one in four droplets was asymmetric; see Discussion below for a further analysis of shape). Figure 4D shows an example of two capsules that contain nonspherical LC droplets. In these images, it appears that the LC has partially wet the inner surface of the capsules, causing the droplets to distort to asymmetric lemonlike shapes. Droplets that assumed this asymmetric shape, however, still exhibited birefringent textures that closely resembled those of the spherical droplets. We conclude that the LC ordering in these cases is a distorted bipolar configuration (Figure 4D), with the two boojums located close to the contact line defined by the LC–polymer interface. Here, we also note that the shape of the polymeric capsules did not appear to be perturbed by partial wetting of the inner surface of the capsule by the LC.
Surfactant-Induced Transitions in Caged LC Droplets
Previous studies have shown that addition of surfactants to aqueous dispersions of LC droplets can trigger a bipolar-to-radial ordering transition within the droplets.5,6 Inspired by these results, we investigated the response of LC droplets confined within DADM capsules to model anionic and cationic surfactants (sodium dodecyl sulfate (SDS) and dodecyl trimethylammonium bromide (DTAB)). The first section below describes LC wetting transitions within amphiphilic capsules induced by SDS and DTAB, and the second section describes changes in the internal ordering that occur in response to each of the two surfactants. We note that the highest concentrations of surfactant used in the experiments described below were less than the critical micelle concentrations to avoid the solubilization of the LC.
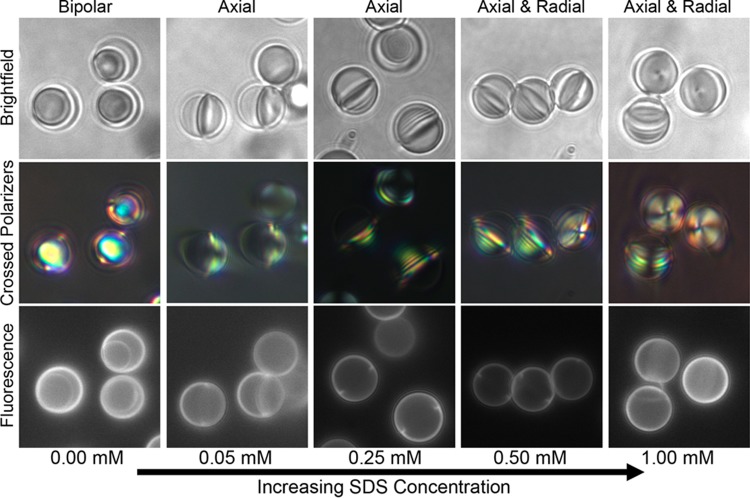
Figure 5 shows the appearance of LC droplets within DADM capsules upon exposure to increasing concentrations of SDS. An inspection of Figure 5 reveals that the addition of SDS caused a continuous decrease in the contact angle (θ) of the LC on the inner surfaces of the capsules (see Figure 6 for the definition of θ and values of θ measured from bright-field micrographs), resulting in a change in the shape of the LC droplet. Figures 5 and 6, when combined, first reveal that low concentrations of SDS (∼0.05–0.25 mM) caused the LC droplets to adopt a convex lens shape (θ ≈ 130 ± 10°). At moderate SDS concentrations (∼0.25–1 mM), we observed hemispherically shaped LC droplets (θ ≈ 89 ± 5°), with approximately planar (low curvature or a large radius of curvature (Rc), see Discussion below) LC–aqueous interfaces inside the capsules. We note that the shape (and internal ordering) of the LC droplets was not homogeneous within a sample; for example, at 0.25 mM SDS, we observed both lens-shaped droplets and nearly hemispherical droplets. (See also Figure S3 for information regarding the distribution of θ for samples in water or at different surfactant concentrations.) Lastly, at higher SDS concentrations (∼0.5–10 mM), we observed a large population of droplets that adopted a concave LC–aqueous interface within the capsules (θ < 85°; measurements on these samples were difficult because the angle was occluded by the LC when the interface was concave; see also a representative video included in the SI). These observations of a continuous change in the contact angle of the LC droplet on the inner wall of the polymeric capsule suggest that the interaction of SDS with the capsule walls triggered this wetting transition.
Figure 5.
Bright-field (top row), polarized light (middle row, crossed polarizers), and fluorescence (bottom row) micrographs of representative regions showing LC ordering and wetting in partially filled capsules as a function of increasing SDS concentration (indicated below each column). Labels above each column indicate the internal ordering of the LC at each concentration.
Figure 6.
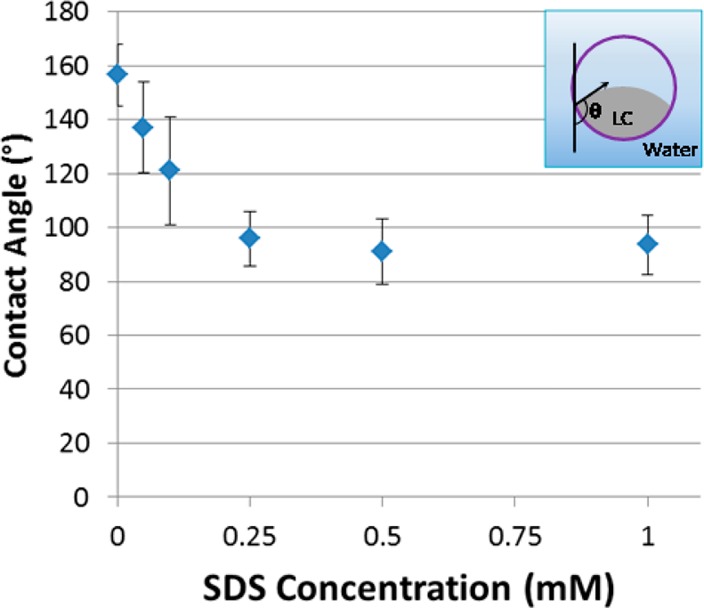
Plot of contact angles of caged LC droplets on the interiors of polymeric microcapsules as a function of SDS concentration (number of droplets measured N > 30 for each data point). The inset defines the contact angle (θ).
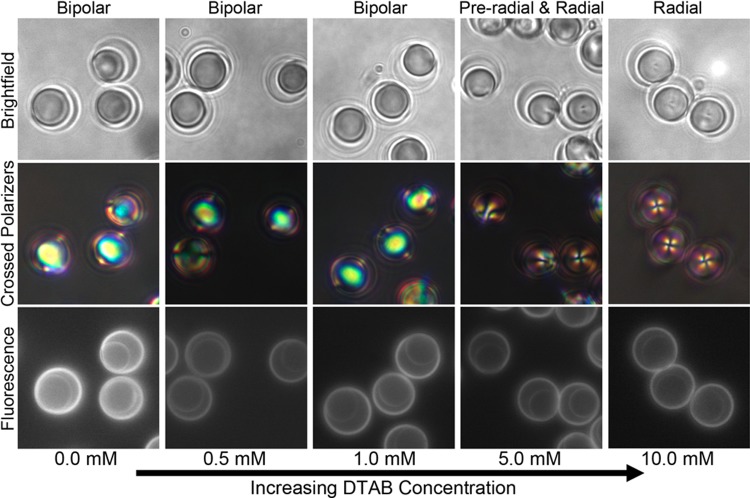
In contrast to the above-described influence of SDS on the wetting of LC on capsule walls, we did not observe a substantial change in the shape or wetting of LC droplets in the presence of DTAB (see Figure 7; the average θ increased from 157 ± 11° in water to 162 ± 10° in 10 mM DTAB; see also the SI for histograms of θ). In contrast to our results using SDS, this result suggests that DTAB permeates but does not adsorb to the wall of the capsule to an extent that it leads to measurable changes in the contact angle, likely because of the positive charge of the dimethylamine functional groups decorating the outer walls of the DADM capsules.
Figure 7.
Bright-field (top row), polarized light (middle row, crossed polarizers), and fluorescence (bottom row) micrographs of representative regions showing LC ordering and wetting within partially filled capsules as a function of increasing DTAB concentration (indicated below each column). Labels above each column indicate the internal ordering of the LC at each concentration.
Concurrent with the surfactant-induced wetting transitions on the inner surfaces of the capsules, we observed the ordering of the LC within the droplets to change with the addition of SDS and DTAB (middle row of images in Figures 5 and 7). As discussed above, the encapsulated LC droplets exhibited bipolar ordering in water (i.e., no surfactant, see Figure 4). When DTAB was added to an aqueous dispersion of encapsulated LC droplets, we observed very little change in the shapes of the droplets (Figure 7), and the sequence of internal configurational states that we observed was similar to that of free LC droplets. The states observed include (i) Saturn-ring disclination line-containing states (at 2.5 mM DTAB), (ii) preradial configurations with a single point defect on the surface (from 2.5 to 5 mM), and (iii) radial configurations (from 5 to 10 mM). We note, in particular, that the appearance of the radial configuration is consistent with very weak interactions between the LC droplets and the inner surfaces of the capsules. Past studies have noted that the contact of LC droplets with surfaces often pins the configurational state of LC droplets at high surfactant concentration in the preradial state.25
Next, we characterized the ordering states of the LC within the lens- and hemispherical-shaped LC droplets (θ ≈ 85–127°) that formed in the presence of SDS. Figure 8A–D shows selected LC droplets in the presence of 0.25 mM SDS (θ ≈ 90°). We interpret the optical appearance of these droplets to indicate that they possess ordering consistent with an axial or Saturn-ring configuration in which the axis of symmetry of the LC ordering follows the axis of symmetry of the droplet shape. (See the Discussion below for further analysis of the proposed ordering.) We note that this optical texture is observed for lens-shaped droplets in the presence of 0.05 mM SDS (Figure 5), and it is also observed in samples at higher concentrations of SDS (up to 1.0 mM). As seen from a side view (Figure 8C,D), this director profile exhibits a disclination line near the planar interface such that the profile resembles that of a Saturn-ring configuration. (See Figure S4 for images of bare E7 droplets with Saturn-ring and radial configurations.)
Figure 8.

Schematic director profiles (left column) with corresponding bright-field (middle column) and polarized light (right column, crossed polarizers indicated by white arrows) micrographs of (A) top, (B) tilted, and (C, D) side views (at different angles with respect to the polarizer/analyzer) of hemispherical LC droplets contained within DADM capsules in 0.25 mM SDS. (E, F) Side views at different angles of hemispherical LC droplets in 1 mM SDS. (G, H) Schematics show possible director configurations for inhomogeneous boundary conditions.
Additionally, the top view (Figure 8A) of the hemispherical droplets has four white lobes surrounding a dark cross, consistent with the axial symmetry15,21 indicated in Figure 8. As the SDS concentration was increased, the LC droplets transitioned to an internal configuration that resembled a deformed radial droplet (Figure 8E,F, 1 mM SDS, see also the video in the SI) with a point defect clearly visible in the bright-field and polarized light micrographs. We note that another possible director configuration that is consistent with the micrographs is shown in Figure 8G, as further discussed below.
Discussion
The key results of the study reported in this article relate to the response of caged LC droplets to surfactants. In contrast to free LC droplets, where SDS and DTAB trigger qualitatively similar configurational transitions and cause a minimal change in shape, we observed DADM-caged LC droplets to undergo wetting transitions in the presence of SDS but not DTAB. The change in droplet shape that accompanied the wetting transition resulted in differential effects of the two surfactants on the internal configurations of the LC within the droplets. We emphasize that this situation also differs from past reports that examined the anchoring of LCs confined to capillaries (diameter ≈ 10–200 nm),26−28 microgrooves,29 silica pores,30 polymer-dispersed cavities,21−24,31−33 and so forth because the internal volumes of those structures were completely filled with LC. (Thus, changes in shape were not observed; see ref (34) for one exception.) Below, we discuss in more detail the coupled wetting transitions and ordering transitions described in this article.
To provide insight into the wetting transitions, we calculated the shapes of the caged droplets by solving the Laplace equation under the assumption that gravity and the elasticity of the LC have a negligible influence on shape. The neglect of gravity is justified by an evaluation of the Bond number, calculated as Bo = ΔρgL2/γ, where Δρ is the difference in densities of the fluid phases, g is the acceleration due to gravity, L is the characteristic length (for which we use the droplet radius), and γ is the interfacial tension. For our experimental system, we estimate Bo to be ∼10–8. As noted above, we also neglect the effect of the elasticity of the LC on the shape of the LC droplets since the ratio of the elastic energy to the surface energy, given as K/γV1/3 (where K is either the splay or bend elastic constant and K ≈ 10–11 N), is ∼10–4 for our experimental system.35,36 Overall, these two approximations lead us to conclude that the LC–aqueous interface will have constant curvature within the caged LC droplets, as predicted by the Laplace equation under the above-stated conditions.
The results of our calculations are shown in Figure 9. Figure 9A shows the shapes of LC droplets on (i) planar surfaces and (ii) the curved interior surfaces of the microcapsules, both calculated as a function of θ [and by assuming that the capsules are rigid (see experimental observations above) and of constant size]. For these calculations, we used a volume of LC that corresponded to ∼40% of the interior of the capsule volume (also consistent with the experiments reported in this article). To enable comparisons of the LC droplet behavior on a flat substrate and in a spherical cavity, Figure 9B shows a plot of the interfacial area between the LC and polymer (i.e., the wall of the capsule or the surface of the flat substrate) and between the LC and aqueous phase, both as a function of θ. Finally, Figure 9C shows the radii of curvature of the LC–aqueous interfaces, plotted as a function of θ for the two geometries.
Figure 9.
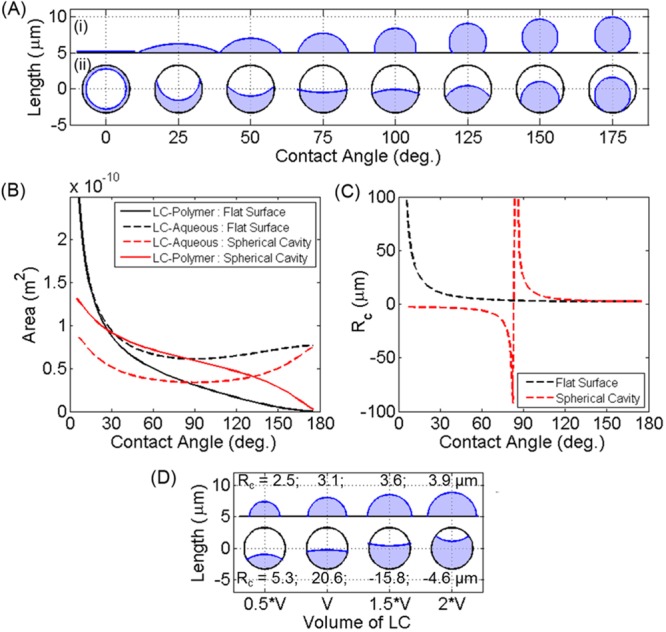
(A) Calculated shapes for LC droplets of constant volume (using the average experimental volume) with varying contact angle for two geometries: (i) on a flat surface and (ii) within a spherical cavity equal in size to the DADM capsules in water. Black lines represent the flat surface or spherical cavity, and blue lines represent the LC–aqueous interface. Axes are square, with the grid on the x axis marking 10 μm (each droplet is plotted with centers 10 μm apart), and contact angles are used to label the x axis. (B) Graph of interfacial areas; interfaces are indicated within the legend. (C) Graph of the radius of curvature (Rc) of the LC–aqueous interface for each geometry. (D) Shapes plotted for a constant contact angle of 90° for varying volumes of LC, denoted on the plot relative to V, the average volume measured experimentally. The Rc of the LC–aqueous interface is also indicated next to the corresponding droplet.
From Figure 9A–C we make two key points. First, an inspection of Figure 9B reveals that, within a spherical cavity defined by the polymer capsule, there exists a crossover at which the interfacial area between the LC and polymer capsule exceeds the interfacial area of the LC–aqueous interface. For the LC volume and capsule size used in our calculations, this occurs at θ ≈ 130°. In contrast, on a planar surface, the interfacial area between the droplet and supporting substrate is always less than the aqueous interface. We also note that, on a planar substrate, the areas of the two interfaces of the LC droplets approach each other only in the limit of θ → 0°. In this limit, a thin film of infinite area is predicted. In contrast, however, in a spherical cavity, a thin film of finite thickness (∼0.5 μm thick, as shown in Figure 9A) is formed on the interior surface of the capsule wall in the limit of θ → 0°. From this result, we conclude that the caging of droplets within capsules provides, in general, the basis of a versatile method for control of the relative interfacial areas of liquids that is not possible on flat surfaces.
The second set of observations that we make from Figure 9 relates to the radius of curvature (Rc) of the LC interface. Specifically, an examination of Figure 9C reveals that the caging of LC droplets within capsules leads to radii of curvature of the LC interfaces that are strikingly different from those on planar substrates. In particular, as the contact angle of the LC with the capsule wall approaches ∼84°, we calculate Rc of the LC–aqueous interface to diverge to positive or negative infinity. (See also experimental observations in Figure 5.) In contrast, the Rc of LC on a planar interface diverges only in the limit of θ → 0°. This fundamental difference in the behavior of Rc is significant, as Rc dictates the Laplace pressure difference, Δρ = Pin – Pout = 2γ/Rc, across the interface of the droplet. Thus, Rc also affects the chemical potential of the LC inside a droplet, which is given by μi(Rc) = μi(∞) + 2γV̅i/Rc, where μi(∞) is the chemical potential of species i with a flat interface and V̅i is the molar volume of species i.37 In particular, we note that for all contact angles (Figure 9C), the Rc of the LC–aqueous interface for LC contained within a spherical cavity is either negative (at θ < 84°) or larger (84° < θ < 180°) than that of the LC on a flat surface. This observation, when combined with the influence of the Laplace pressure on the chemical potential of the LC, leads us to conclude that the chemical potential of caged LC is lower than that of an LC droplet on a flat surface. If two such droplets were present in a system, then we would predict that Ostwald ripening would cause the growth of the encapsulated droplet at the expense of decreasing the size (and Rc) of the droplet of the same volume on a flat surface. The effects of changes in droplet volume for caged LC droplets and LC droplets supported on flat surfaces are shown in Figure 9D (for constant θ = 90°). For caged droplets, an increase in volume leads to an increase in Rc before turning negative. Significantly, the chemical potential of the LC in the caged droplet decreases more rapidly with increasing volume as compared to droplets on flat surfaces. This observation leads us to predict that capsules containing droplets with Rc < 0 will be stable with respect to both uncaged droplets as well as bulk LC.
A second key result reported in this article is that the wetting transitions described above are coupled to changes in the internal ordering and topological defects of the LC. In order to discuss this coupling, two key concepts need to be introduced, namely, the topological charge of defects and the Euler characteristic of closed surfaces.3,4,38−41 The topological charge (N) of a defect is related to the number of times the LC director rotates through all possible angles encountered on a surface that encompasses the defect. For example, in the case of a bipolar droplet, a topological charge of N = +1/2 is assigned to each of the boojum defects by placing a hemispherical surface around the boojum and evaluating the director orientations. For the case of a radial droplet with a central point defect,42,43 the defect can be surrounded by a spherical surface that encounters all possible angles of the director, and it therefore has a topological charge of N = +1. For droplets in transition states that connect the bipolar and radial configurations of spherical LC droplets and possess uniform boundary conditions (the tilt angle with respect to the surface normal is the same everywhere on the droplet surface), Gauss’s theorem requires the conservation of topological charge. For example, the transition state that comprises a Saturn-ring disclination line located slightly inside the surface of the droplet must have a topological charge of +1 (it can be encompassed by a spherical surface that encounters all orientations of the LC director). Another commonly encountered transition state that lies between the bipolar and radial configurations is the preradial configuration with a topological charge of N = +1.
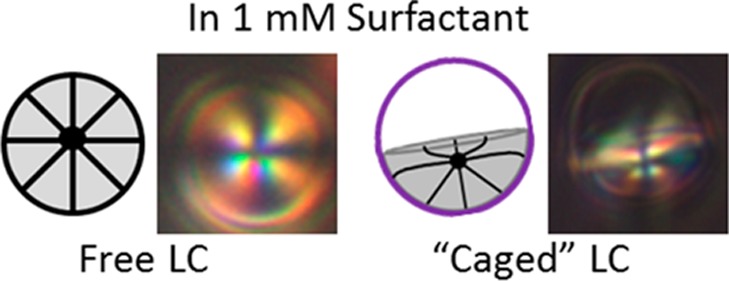
The above-described discussion addresses the well-studied case of configurational transitions in spherical droplets whereas the experiments reported in this article address the more complicated situation where changes in the shapes of the LC droplets accompany internal configurational transitions. To address this situation, we consider the Euler characteristic of a closed surface. The Euler characteristic of a sphere, and any surface that can smoothly be transformed into a sphere (e.g., a football and a bowl are both topologically equivalent to a sphere), is two.39−41 This result is useful because, for uniform boundary conditions, the sum of the topological charges (N) must be half of the Euler characteristic of a closed surface.3,4 This leads us to conclude that the Euler characteristic of the caged LC droplet shapes observed in our experiments is unaltered as compared to that of spherical droplets because all shapes observed for the caged LC droplets can be smoothly transformed into a sphere. Thus, the wetting transitions reported in this article do not change the conservation of topological charge discussed in the context of past studies of free (spherical) droplets.3,4 Specifically, for LC droplets exposed to SDS (Figures 5 and 8), the wetting transition results in multiple shapes (lenses, hemispheres, and concave hemispheres), all of which are smooth deformations of a spherical surface. Thus, if the boundary conditions are uniform at all surfaces of the LC, then the internal configurations of the LC in the presence of SDS will be topologically equivalent to bipolar, axial/Saturn-ring, and radial configurations (schematics in Figures 4 and 8A–F).
Whether the anchoring of the LC at all surfaces of the caged droplets is uniform, however, remains to be established. It is possible that the caged LC droplets possess inhomogeneous anchoring, for example, due to differential adsorption of SDS between the LC–aqueous interface or the LC–polymer interface (Figure 8G,H). In this scenario, due to inhomogeneous anchoring, the relationship of the topological charge and the Euler characteristic is changed from that discussed above. The topological charges, however, will still satisfy Gauss’s theorem and will be determined by the specific profile of the director at the surfaces of the LC droplets. In Figure 8G,H, we present two possible director configurations in the caged LC droplets that are consistent with the nonuniform anchoring of the LC at its surfaces. In each case, there is a boojum on either the LC–aqueous interface or LC–polymer interface, providing a net topological charge of +1/2 (see above). As noted in the Results section, the LC anchoring shown schematically in Figure 8G is consistent with the experimental observations shown in the micrographs in Figure 8E,F. However, we do not observe birefringent textures that are consistent with the configuration in Figure 8H.
We end by noting that in the limit of θ → 0 the complete wetting of LC on the inner surface of the capsule would lead to the formation of a shell of LC. This transition, although not yet observed in our experiments, leads to the creation of a new surface and thus the shell possesses an Euler characteristic of +4 (and thus a topological charge of +2). For additional discussion of this geometry, we refer the reader to studies of LC shells created from double emulsions.1,44,45
Conclusions
In summary, the key advances reported in this article are two-fold. First, we provide insight into the physical processes that underlie the formation of caged LC droplets contained within cross-linked polymer multilayer capsules. We demonstrate that DADM capsules swell reversibly and that the extent of swelling correlates with the dielectric constant of the solvent. This result suggests principles by which the extent of filling of the capsules can be systematically varied in future studies. We emphasize that the partial filling of the capsules reported here underlies our observations of the LC wetting transitions. The second key advance involves surfactant-induced changes in both the wetting and ordering of caged LC droplets. Whereas the effects of DTAB and SDS on the internal ordering of free LC droplets are similar, we reveal that the two surfactants trigger strikingly different wetting and configurational transitions when the LC droplets are caged within the polymeric capsules. Specifically, the addition of anionic SDS resulted in a progression of complex droplet shapes as the contact angle of the LC on the inner surfaces of the capsules decreased; in contrast, no significant change in droplet shape was observed upon addition of cationic surfactant DTAB. Although additional measurements are needed to quantify the orientation of the LC at the surfaces of the complex shapes formed by the caged LC in the presence of the SDS, under the assumption of uniform anchoring the various internal states of the droplets are topologically equivalent to axial and radial configurations (i.e., consistent with the conservation of topological charge). Although topologically equivalent to free droplets, the contributions that surface anchoring, LC elasticity, and topological defects make to the free energy of caged LC droplets will differ from those of free droplets. As a result, caged LC droplets offer the promise of new and versatile sources for the design of LC-droplet-based responsive soft matter that cannot be realized in dispersions of free droplets. We also note that the physics of caged LC droplets is conceptually similar to that of liquid-crystalline DNA toroids confined in viral capsids.46 As such, caged LC droplets may offer the basis of a model system for understanding some aspects of DNA packing in viruses.
Acknowledgments
This work was supported by the National Science Foundation (under awards DMR-1121288 (MRSEC) and CBET-1263970), the National Institutes of Health (CA108467 and AI092004), and the Army Research Office (W911-NF-11-1-0251 and W911-NF-14-1-0140).
Supporting Information Available
Experimental materials and additional details for layer-by-layer fabrication of polymer multilayers. Video of rotating and translating capsules containing LC droplets with a concave-hemisphere shape in 1 mM SDS (details and caption in SI pdf). This material is available free of charge via the Internet at http://pubs.acs.org.
The authors declare the following competing financial interest: NLA has a financial interest in Platypus Technologies LLC, a for-profit company that has developed liquid-crystal-based sensors.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Lopez-Leon T.; Fernandez-Nieves A. Drops and shells of liquid crystal. Colloid Polym. Sci. 2011, 289, 345–359. [Google Scholar]
- Drzaic P. S.Liquid Crystal Dispersions; World Scientific Publishing Company: Singapore, 1995. [Google Scholar]
- Volovik G. E.; Lavrentovich O. D. The Topological Dynamics of Defects - Boojums in Nematic Drops. Zh. Eksp. Teor. Fiz. 1983, 85, 1997–2010. [Google Scholar]
- Lavrentovich O. D. Topological defects in dispersed liquid crystals, or words and worlds around liquid crystal drops. Liq. Cryst. 1998, 24, 117–125. [Google Scholar]
- Gupta J. K.; Zimmerman J. S.; de Pablo J. J.; Caruso F.; Abbott N. L. Characterization of adsorbate-induced ordering transitions of liquid crystals within monodisperse droplets. Langmuir 2009, 25, 9016–9024. [DOI] [PubMed] [Google Scholar]
- Gupta J. K.; Sivakumar S.; Caruso F.; Abbott N. L. Size-dependent ordering of liquid crystals observed in polymeric capsules with micrometer and smaller diameter. Angew. Chem., Int. Ed. 2009, 48, 1652–1655. [DOI] [PubMed] [Google Scholar]
- Zou J. H.; Bera T.; Davis A. A.; Liang W. L.; Fang J. Y. Director configuration transitions of polyelectrolyte coated liquid-crystal droplets. J. Phys. Chem. B 2011, 115, 8970–8974. [DOI] [PubMed] [Google Scholar]
- Carlton R. J.; Hunter J. T.; Miller D. S.; Abbasi R.; Mushenheim P. C.; Tan L.; Abbott N. L. Chemical and Biological Sensing Using Liquid Crystals. Liq. Cryst. Rev. 2013, 1, 1–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin I. H.; Miller D. S.; Bertics P. J.; Murphy C. J.; de Pablo J. J.; Abbott N. L. Endotoxin-induced structural transformations in liquid crystalline droplets. Science 2011, 332, 1297–1300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alino V. J.; Pang J.; Yang K. L. Liquid Crystal Droplets as a Hosting and Sensing Platform for Developing Immunoassays. Langmuir 2011, 27, 11784–11789. [DOI] [PubMed] [Google Scholar]
- Bera T.; Fang J. Y. Polyelectrolyte-coated liquid crystal droplets for detecting charged macromolecules. J. Mater. Chem. 2012, 22, 6807–6812. [Google Scholar]
- Bera T.; Fang J. Y. Optical Detection of Lithocholic Acid with Liquid Crystal Emulsions. Langmuir 2013, 29, 387–392. [DOI] [PubMed] [Google Scholar]
- Manna U.; Zayas-Gonzalez Y. M.; Carlton R. J.; Caruso F.; Abbott N. L.; Lynn D. M. Liquid crystal chemical sensors that cells can wear. Angew. Chem., Int. Ed. 2013, 52, 14011–14015. [DOI] [PubMed] [Google Scholar]
- Khan W.; Choi J. H.; Kim G. M.; Park S. Y. Microfluidic formation of pH responsive 5CB droplets decorated with PAA-b-LCP. Lab Chip 2011, 11, 3493–3498. [DOI] [PubMed] [Google Scholar]
- Zumer S.; Kralj S. Influence of K24 on the Structure of Nematic Liquid-Crystal Droplets. Liq. Cryst. 1992, 12, 613–624. [Google Scholar]
- Mondiot F.; Wang X.; de Pablo J. J.; Abbott N. L. Liquid crystal-based emulsions for synthesis of spherical and non-spherical particles with chemical patches. J. Am. Chem. Soc. 2013, 135, 9972–9975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saurer E. M.; Flessner R. M.; Buck M. E.; Lynn D. M. Fabrication of covalently crosslinked and amine-reactive microcapsules by reactive layer-by-layer assembly of azlactone-containing polymer multilayers on sacrificial microparticle templates. J. Mater. Chem. 2011, 21, 1736–1745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinsinger M. I.; Buck M. E.; Abbott N. L.; Lynn D. M. Immobilization of Polymer-Decorated Liquid Crystal Droplets on Chemically Tailored Surfaces. Langmuir 2010, 26, 10234–10242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jose J.; Kamp M.; van Blaaderen A.; Imhof A. Unloading and reloading colloidal microcapsules with apolar solutions by controlled and reversible buckling. Langmuir 2014, 30, 2385–2393. [DOI] [PubMed] [Google Scholar]
- Miller D. S.; Carlton R. J.; Mushenheim P. C.; Abbott N. L. Introduction to optical methods for characterizing liquid crystals at interfaces. Langmuir 2013, 29, 3154–3169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ondris-Crawford R.; Boyko E. P.; Wagner B. G.; Erdmann J. H.; Zumer S.; Doane J. W. Microscope textures of nematic droplets in polymer dispersed liquid-crystals. J. Appl. Phys. 1991, 69, 6380–6386. [Google Scholar]
- Prischepa O. O.; Shabanov A. V.; Zyryanov V. Y. Transformation of director configuration upon changing boundary conditions in droplets of nematic liquid crystal. JETP Lett. 2004, 79, 257–261. [Google Scholar]
- Prishchepa O. O.; Shabanov A. V.; Zyryanov V. Y. Director configurations in nematic droplets with inhomogeneous boundary conditions. Phys. Rev. E 2005, 72, 031712. [DOI] [PubMed] [Google Scholar]
- Drzaic P. S. Polymer dispersed nematic liquid-crystal for large area displays and light valves. J. Appl. Phys. 1986, 60, 2142–2148. [Google Scholar]
- Whitmer J. K.; Wang X. G.; Mondiot F.; Miller D. S.; Abbott N. L.; de Pablo J. J. Nematic-field-driven positioning of particles in liquid crystal droplets. Phys. Rev. Lett. 2013, 111, 227801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crawford G. P.; Ondris-Crawford R. J.; Doane J. W.; Zumer S. Systematic study of orientational wetting and anchoring at a liquid-crystal-surfactant interface. Phys. Rev. E 1996, 53, 3647–3661. [DOI] [PubMed] [Google Scholar]
- Cloutier S. G.; Eakin J. N.; Guico R. S.; Sousa M. E.; Crawford G. P.; Xu J. M. Molecular self-organization in cylindrical nanocavities. Phys. Rev. E 2006, 73, 051703. [DOI] [PubMed] [Google Scholar]
- Kityk A. V.; Wolff M.; Knorr K.; Morineau D.; Lefort R.; Huber P. Continuous paranematic-to-nematic ordering transitions of liquid crystals in tubular silica nanochannels. Phys. Rev. Lett. 2008, 101, 187801. [DOI] [PubMed] [Google Scholar]
- Ohzono T.; Fukuda J.; Suzuki K.; Yamaguchi T. +/- 1/2 wedge disclinations stabilized by a sinusoidal boundary in a thin hybrid nematic liquid-crystal film. Phys. Rev. E 2012, 86, 030701. [DOI] [PubMed] [Google Scholar]
- Castellon E.; Zayat M.; Levy D. Molecular configuration transitions of a nematic liquid crystal encapsulated in organically modified silicas. Phys. Chem. Chem. Phys. 2009, 11, 6234–6241. [DOI] [PubMed] [Google Scholar]
- Higgins D. A. Probing the mesoscopic chemical and physical properties of polymer-dispersed liquid crystals. Adv. Mater. 2000, 12, 251–264. [Google Scholar]
- Amimori I.; Eakin J. N.; Qi J.; Skacej G.; Zumer S.; Crawford G. P. Surface-induced orientational order in stretched nanoscale-sized polymer dispersed liquid-crystal droplets. Phys. Rev. E 2005, 71, 031702. [DOI] [PubMed] [Google Scholar]
- Wang J.; Xia J.; Hong S. W.; Qiu F.; Yang Y.; Lin Z. Phase separation of polymer-dispersed liquid crystals on a chemically patterned substrate. Langmuir 2007, 23, 7411–7415. [DOI] [PubMed] [Google Scholar]
- Huber P.; Busch M.; Całus S.; Kityk A. V. Thermotropic nematic order upon nanocapillary filling. Phys. Rev. E 2013, 87, 042502. [DOI] [PubMed] [Google Scholar]
- Kaznacheev A. V.; Bogdanov M. M.; Taraskin S. A. The nature of prolate shape of tactoids in lyotropic inorganic liquid crystals. J. Exp. Theor. Phys. 2002, 95, 57–63. [Google Scholar]
- Prinsen P.; van der Schoot P. Shape and director-field transformation of tactoids. Phys. Rev. E 2003, 68, 021701. [DOI] [PubMed] [Google Scholar]
- Kabalnov A. Ostwald ripening and related phenomena. J. Disper. Sci. Technol. 2001, 22, 1–12. [Google Scholar]
- Mermin N. D. Topological theory of defects in ordered media. Rev. Mod. Phys. 1979, 51, 591–648. [Google Scholar]
- Kamien R. D. The geometry of soft materials: a primer. Rev. Mod. Phys. 2002, 74, 953–971. [Google Scholar]
- Richeson D. S.Euler’s Gem: The Polyhedron Formula and the Birth of Topology; Princeton University Press: Princeton, NJ, 2008. [Google Scholar]
- Lakatos I.Proofs and Refutations: The Logic of Mathematical Discovery; Cambridge University Press: Cambridge, U.K., 1976. [Google Scholar]
- Bodnar V. G.; Lavrentovich O. D.; Pergamenshchik V. M. The Threshold for the Hedgehog - Ring Structural Transition in Nematic Drops in an Alternating Electric-Field. Zh. Eksp. Teor. Fiz. 1992, 101, 111–125. [Google Scholar]
- Gartland E. C.; Mkaddem S. Instability of Radial Hedgehog Configurations in Nematic Liquid Crystals under Landau-de Gennes Free-Energy Models. Phys. Rev. E 1999, 59, 563–567. [Google Scholar]
- Fernandez-Nieves A.; Vitelli V.; Utada A. S.; Link D. R.; Marquez M.; Nelson D. R.; Weitz D. A. Novel defect structures in nematic liquid crystal shells. Phys. Rev. Lett. 2007, 99, 157801. [DOI] [PubMed] [Google Scholar]
- Lopez-Leon T.; Fernandez-Nieves A. Topological transformations in bipolar shells of nematic liquid crystals. Phys. Rev. E 2009, 79, 021707. [DOI] [PubMed] [Google Scholar]
- Leforestier A.; Šiber A.; Livolant F.; Podgornik R. Protein-DNA interactions determine the shapes of DNA toroids condensed in virus capsids. Biophys. J. 2011, 100, 2209–2216. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.