Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2014 Apr 16;1(5):464–470. doi: 10.1021/ph500091h

Individual Template-Stripped Conductive Gold Pyramids for Tip-Enhanced Dielectrophoresis

Jincy Jose †, Stephan Kress ‡, Avijit Barik †,§, Lauren M Otto †, Jonah Shaver †, Timothy W Johnson †, Zachary J Lapin ∥, Palash Bharadwaj ∥, Lukas Novotny ∥, Sang-Hyun Oh †,§,*
PMCID: PMC4270414  PMID: 25541619

Abstract

graphic file with name ph-2014-00091h_0007.jpg

Gradient fields of optical, magnetic, or electrical origin are widely used for the manipulation of micro- and nanoscale objects. Among various device geometries to generate gradient forces, sharp metallic tips are one of the most effective. Surface roughness and asperities present on traditionally produced tips reduce trapping efficiencies and limit plasmonic applications. Template-stripped, noble metal surfaces and structures have sub-nm roughness and can overcome these limits. We have developed a process using a mix of conductive and dielectric epoxies to mount template-stripped gold pyramids on tungsten wires that can be integrated with a movable stage. When coupled with a transparent indium tin oxide (ITO) electrode, the conductive pyramidal tip functions as a movable three-dimensional dielectrophoretic trap which can be used to manipulate submicrometer-scale particles. We experimentally demonstrate the electrically conductive functionality of the pyramidal tip by dielectrophoretic manipulation of fluorescent beads and concentration of single-walled carbon nanotubes, detected with fluorescent microscopy and Raman spectroscopy.

Keywords: template stripping, gradient force, dielectrophoresis, particle trapping, plasmonics

Gradient forces generated by spatially nonuniform electromagnetic fields can be used to facilitate trapping1−5 and sorting6−10 of particles and molecules. Particle manipulation via electric field gradients, known as dielectrophoresis (DEP),1 is widely used for lab-on-a-chip applications due to its ease of implementation and utility in label-free manipulation of both charged and neutral species. In DEP, the force acting on a polarizable object in a nonuniform electric field attracts (positive DEP) or repels (negative DEP) the object from the field maximum in proportion to its relative polarizability with respect to the surrounding medium. The time-averaged dielectrophoretic force acting on a spherical particle of radius R is given by

graphic file with name ph-2014-00091h_m001.jpg 1

Here εm denotes the real permittivity of the suspending medium, E is the total electric field, and fCM(ω) is the frequency-dependent Clausius-Mossotti factor:

graphic file with name ph-2014-00091h_m002.jpg 2

with particle and medium complex permittivities, ε*p and ε*m.

The electric field gradient distribution and strength is determined by electrode shape and spatial configuration. Generation of DEP forces large enough to trap, that is, overcome Brownian motion, single molecules often requires nanometer-sized gaps made using advanced nanofabrication tools such as electron-beam lithography.11 Various electrode shapes, such as gaps, interdigitated electrodes, and quadrupoles have been utilized for DEP trapping of particles in two-dimensional (2D), static configurations.9 These kinds of electrodes are easy to fabricate, but are limited by their static, planar nature, and relatively small DEP forces. A three-dimensional (3D), mobile trap could be used to transfer trapped particles from one site to another, enabling new applications in microfluidics, nanolithography,12 and biology. Three-dimensional structures, such as metallic posts and tips, in conjunction with a ground plane can also create strong field gradients, and were a mainstay of the field before the development of lithographically patterned samples with finer features.13 Metallic tips in particular are interesting as the sharpness of tip itself creates a strong field gradient. Recent developments in sharp tip fabrication,14 primarily for scanning probe microscopy applications, have led to more efficient DEP trapping of a variety of objects such as nanoparticles15 and carbon nanotubes.16

In addition to their ability to generate strong gradient electric fields for DEP, sharp tips made with noble metals can also localize surface plasmons,2,17 density fluctuations of conduction electrons on metallic surfaces.18 This effect is utilized for plasmonic trapping,5 near-field scanning optical microscopy (NSOM),14 and nonlinear spectroscopy.19 A combination of the spectroscopic sensing capability of metallic tips with DEP trapping of molecules will give high fidelity data and could result in novel scanning probe techniques.

While considerable effort has been devoted to the fabrication of sharp metallic tips, the production of high-quality metallic probes is not a trivial task. Traditionally, tips are made via electrochemical etching technique,14 a low-throughput technique with quality and reproducibility issues. Etched tips are prone to nanoscale surface roughness, which results in unwanted trapping sites20 and random “hot spots” in tip-enhanced Raman spectroscopy.21 We utilize template stripping22 for wafer-scale production of nanometrically smooth, ultrasharp metallic pyramids for NSOM and tip-enhanced Raman spectroscopy.21,23−25 When compared with etched tips, these template-stripped pyramids demonstrate higher reproducibility, smoother surfaces (roughness below 1 nm), and sharper tips (radius below ∼20 nm). Here we expand the functionality of pyramidal tips by attaching them to metallic wires using electrically conductive epoxy, thereby creating a DEP electrode (Figure 1). We demonstrate dielectrophoretic manipulation, trapping, movement, and release, of fluorescently labeled polystyrene beads (2 μm and 190 nm diameters) at the pyramid apex. We also demonstrate concentration of single-walled carbon nanotubes (SWCNTs) near the tip by simultaneous detection of real-time Raman and photoluminescence signals.

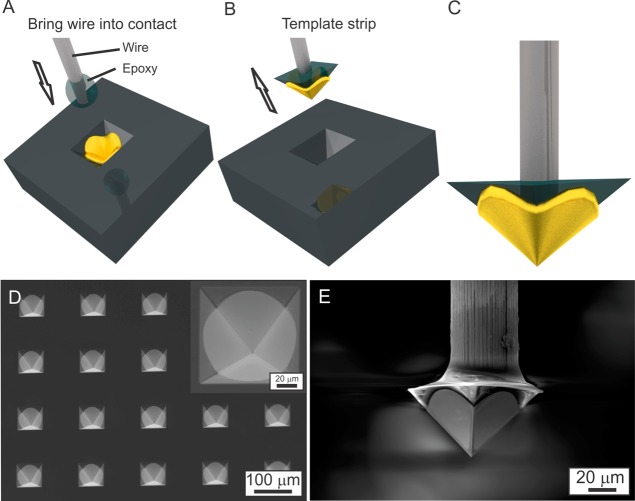
Figure 1.

Figure 1

Open in a new tab

Fabrication of a template-stripped gold pyramid and connection to a metal wire. (A) Tungsten wire is dipped in conductive epoxy and aligned on top of the gold pyramid in the silicon mold. (B) After curing the epoxy, the pyramid is pulled by raising the wire. (C) A pulled gold pyramid attached to the tungsten wire. Scanning electron microscopy (SEM) images of (D) gold pyramids (in silicon mold) fabricated over an entire wafer and (E) single pyramid pulled out using a 50 μm tungsten wire and conductive epoxy. The inset in (D) shows a zoomed-in image of a single gold pyramid in the silicon mold.

Results and Discussion

Computational Modeling

To better understand the electrostatic properties of a sharp gold pyramid, we performed finite-element modeling using COMSOL Multiphysics 4.3a (Figure 2). The angle between opposite facets of our template-stripped pyramidal tip is 70.5°, determined by {111} crystal planes of the silicon template.26 An indium tin oxide (ITO) counter electrode is placed at a distance of d (electrode gap) from the apex of the pyramid. The sharp, 20 nm tip radius of curvature, r, and 50 μm electrode gap, generates a strong electric field intensity gradient, ∇|E|2, whose magnitude is shown in Figure 2a. The electric field intensity gradient reaches values of 1023 V2 m–3 at the tip and decreases rapidly with increasing distance in both x and z directions (Figure 2b). The variation of ∇|E|2 with electrode gap, d, measured at 5 nm below the tip apex was also modeled (Figure 2c). For d ≤ 1 μm, the field gradient shows 1/d0.88 dependence. It has been analytically shown that for electrode gap sizes smaller than the tip radius of curvature (here d < r = 20 nm), the apex of the tip can be approximated as a sphere of radius r and its electrostatic image yielding a 1/d dependence in ∇|E|2.27 For d ≥ 100 μm, the field gradient shows 1/d1.95 dependence. Electrode gap sizes approximately larger than the tip length require compensation for the entire shape of the tip (including its half angle) in addition to the sphere-image approximation and therefore yield a 1/d2 dependence in ∇|E|2. Since our calculations extend only down to 10 nm electrode gap size, we can approximate the 1/d0.88 dependence to an intermediate regime affected by the entire structure including its opening half angle, finite size, and finite tip radius of curvature.27 Due to practical limitations, such as crashing the tip, we performed the experiments in the electrode gap region of 50–70 μm. Reducing the electrode gap to submicrometer distances (e.g., 0.5 μm) will further increase the DEP force by one or 2 orders of magnitude.

Figure 2.

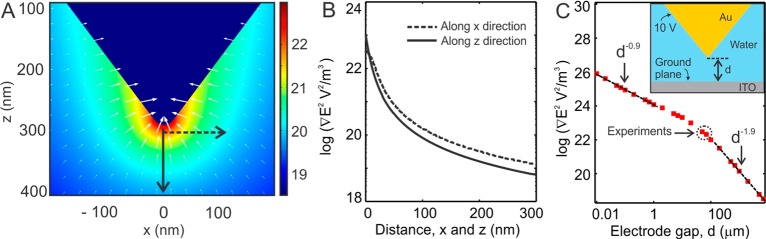
Figure 2

Open in a new tab

Finite-element method calculations of the tip-plane geometry. (A) Magnitude (colors, logarithmically scaled) and direction (white arrows, also logarithmically scaled) of ∇|E|2 for 10 V potential and 50 μm electrode gap. (B) Magnitude of ∇|E|2 plotted along the black solid (z direction at x = 0 nm) and dotted (x direction at z = 5 nm below the tip) arrows in (A). (C) Electric field gradient as a function of the distance between the tip and the counter electrode (ITO). The experiments were performed in the region (black dotted circle) spanning over 50–70 μm. The inset shows the modeling design with gold tip and ITO counter electrode separated by an electrode gap, d.

Conductive Pyramid Fabrication

To create our DEP electrodes, we modified a previously demonstrated template-stripping technique to produce ultrasmooth metallic pyramidal tips.21−23,28 Instead of template-stripping single metallic pyramid using dielectric epoxy,23 we used a conductive epoxy, resulting in electrically conductive probes. This process is not a trivial extension of previous techniques due to the nature of conductive epoxy. Silver particles dispersed above the percolation threshold in a nonconductive epoxy matrix give the final connection its electrical connectivity. The fabrication steps are depicted in Figures 1a–c. The pyramids are made over an entire 4 in. Si wafer (Figure 1d) that can be stored for an extended time with single pyramids template-stripped on demand. Scanning electron micrograph (SEM) of a template-stripped gold pyramid is shown in Figure 1e. The radius of curvature of the tip is ∼20 nm. A short piece of 50 μm diameter tungsten wire (Alfa Aesar) was dipped in a droplet of electrically conductive epoxy (NCA 130, Norland) mixed with a two-component fast-curing epoxy (UHU Schnellfest) before attaching to the 65 μm pyramid base with a micrometric XYZ stage. After curing, the metallic pyramid was detached (template-stripped) by pulling the wire and pyramid from the Si template. The conductive epoxy, holding the pyramid to the wire, was thermally cured at 100 °C for 1 h. The tungsten wire was then soldered to a Cu wire and mounted to a separate XYZ micropositioning stage on an inverted microscope for DEP trapping experiments.

Dielectrophoretic Trapping of Particles

Our DEP trapping system (illustrated in Figure 3a) consists of a conductive gold pyramid, a drop of the particle solution in a PDMS ring, an ITO-coated glass ground plate, and a function generator. The tip was positioned with a micrometer driven XYZ stage. To demonstrate DEP trapping, we used fluorescently labeled polystyrene beads of diameters of 2 μm (Sigma-Aldrich) and 190 nm (Bangs Laboratories). A 5 μL drop of beads diluted in water was injected between the pyramid and ITO electrode with the tip fixed at a distance of approximately 70 μm from the electrode. The electrode gap was determined at the end of the experiment by using the micrometer readings on the Z stage of the tip mount, with the tip touching the ITO as a reference point. The applied AC voltage is 10 Vpp for all experiments reported in this work.

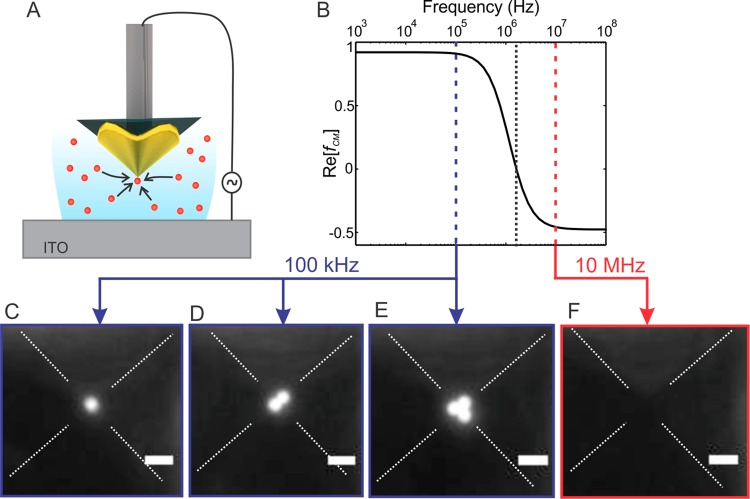
Figure 3.

Figure 3

Open in a new tab

Reversible dielectrophoretic manipulation of fluorescently labeled polystyrene beads. (A) Illustration of dielectrophoretic trapping of particles suspended in water at the apex of the gold pyramidal tip. (B) Real part of fCM(ω) for polystyrene bead in water (conductivity of the mixed solution = 0.28 mS/m) plotted as a function of frequency. The dotted line near 1.67 MHz is the transition from positive to negative DEP. (C–E) Fluorescence snapshots of dielectrophoretic manipulation of labeled polystyrene beads (2 μm) suspended in water using the template-stripped gold pyramidal tip. The applied potential was fixed at 10 Vpp. (C–E) 100 kHz (trapping, positive DEP), and (F) 10 MHz (releasing, negative DEP). The scale bar is 5 μm.

The different frequency regimes for reversible DEP manipulation of polystyrene beads suspended in water (relative permittivity = 80 and conductivity = 0.28 mS/m) are depicted in the fCM(ω) plot in Figure 3b. The cross over frequency, when Re[fCM(ω)] = 0, for the bead-water system is around 1.67 MHz. For frequencies lower than the cross over frequency, where Re[fCM(ω)] > 0, the polarizability of the beads is higher than water and therefore the beads will be drawn toward the region of highest electric field (i.e., apex of the pyramid). For frequencies higher than the cross over frequency, Re[fCM(ω)] < 0, the beads are repelled from the high field region since their polarizability drops below that of water. To demonstrate reversible manipulation of beads, we acquired fluorescence images (800 ms exposure time) for two different applied frequencies. When a 100 kHz AC signal was applied, a single 2 μm bead was trapped on the tip of the pyramid in less than 1 s (Figure 3c). As time goes on, more beads are subsequently trapped on the tip (Figure 3d,e). We attribute this site-specific trapping of beads on the tip to the strong electric field gradient concentrated at the pyramid apex with very weak field intensity on the edges and facets of the pyramid. Upon increasing the frequency to 10 MHz, which is above the cross over frequency for DEP trapping, beads were released into the solution (see Figure 3f). Since the tip is mounted on a XYZ micropositioner, we can move the pyramidal tip while trapping particles at the tip apex (see Supporting Information, video).

At high voltages, such as 10 Vpp, the average electric field per particle is enough to trap multiple particles on the tip of the pyramid. However, reducing the voltage reduces the effective trapping volume leading to the ejection of subsequent particles from the DEP trap and only a single particle remains in the lowest energy configuration. We observed trapping of a single particle for longer duration for an applied voltage as low as 2 Vpp.

Accumulation of particles on the facets of the pyramid was also observed (not shown) at very low frequencies (1–10 kHz). Such low-frequency accumulation of particles on top of electrodes, similar to our pyramid’s facets, was observed for planar microelectrodes29,30 and attributed to electrohydrodynamic effects.31 Low-frequency electrohydrodynamic effects can inhibit trapping at sharp electrode features (e.g., like the tips and edges) and promote trapping on the flat part of the electrode. For higher frequencies, these effects diminish and geometrical features govern the electric field distribution.32 As flat facets do not generate high electric field gradients, particles under positive DEP are pulled away from these regions. More in-depth discussion about the low-frequency particle manipulation is outside the scope of this work. As we focus on reversible particle manipulation, an effect in the ∼100 s of kHz, our experiments are not influenced by low-frequency electrohydrodynamic effects.

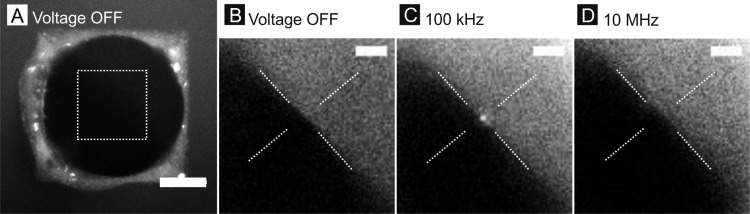
Next, we scaled down the particle size by a factor of 10. Reducing the particle diameter from 2 μm to 190 nm, assuming a constant electrode gap and tip radius, will scale down the DEP force by approximately a factor of 1000 (eq 1). The reduced DEP force can increase the time it takes to trap a single bead. Fluorescence snap shots of a template-stripped gold pyramid immersed in the bead solution (with approximately 50 μm electrode gap) were taken at an exposure time of 400 ms (see Figure 4a–d). At approximately 60 s after applying a potential (10 Vpp, 100 kHz), a single 190 nm bead was trapped on the tip of the pyramid. The trapped bead was released back into solution when the frequency was increased to 10 MHz due to negative DEP (Figure 4d). Unlike the 2 μm bead experiment, where multiple beads were easily trapped in less than a second, trapping multiple 190 nm beads was found to take longer; unless a higher voltage was used.

Figure 4.

Figure 4

Open in a new tab

Fluorescence snapshots of dielectrophoretic manipulation of labeled polystyrene beads (190 nm diameter) suspended in water using template-stripped gold pyramidal tip. Fluorescence images of the pyramid before applying potential with (A) focusing on the pyramid base and (B–D) focusing on the pyramid apex. Fluorescence images of the pyramid with applied potential of 10 Vpp and frequency of (C) 100 kHz (positive DEP) and (D) 10 MHz (negative DEP). In (C) a single 190 nm bead is trapped at the apex. The white dotted square in (A) marks the region showed in (B–D). The scale bar is 20 μm in (A) and 5 μm in (B–D).

Dielectrophoretic Trapping of Single-Walled Carbon Nanotubes

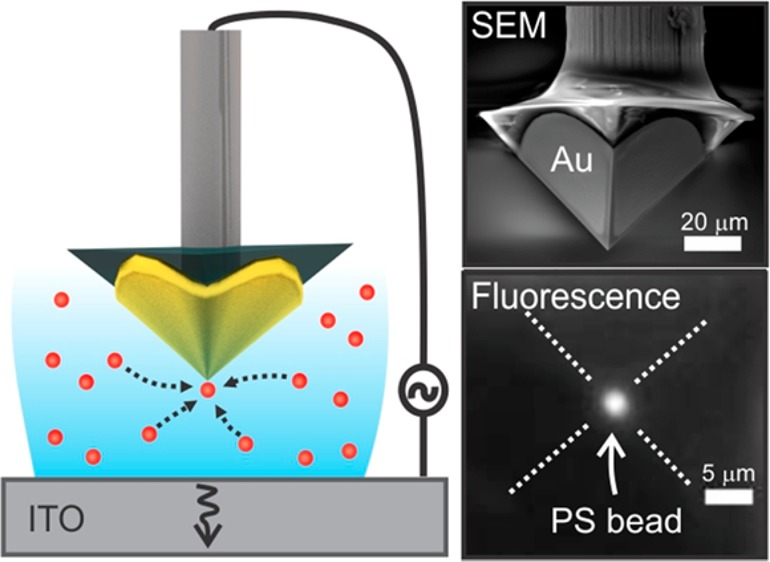
Finally, we demonstrate the spectroscopic sensing capability of our gold pyramid by dielectrophoretic concentration of SWCNTs on the tip of the pyramid and simultaneous spectral detection. The experimental scheme is illustrated in Figure 5a with the tip held at ∼50 μm above the ITO counter electrode. A 10 μL suspension of diluted, sodium deoxycholate suspended SWCNTs (see Methods) was injected between the pyramid and the ITO electrode. Linearly polarized 785 nm laser light (4.7 mW) is focused on the tip of the gold pyramid using a 50× microscope objective lens. The far-field, scattered light was collected in reflection geometry, filtered, and sent to a fiber-optic spectrometer (Ocean Optics) for detection. Spectra taken with a 2 s integration time every 20 s with 10 Vpp, 100 kHz applied potential are shown in Figure 5b. A spectrum (inset, Figure 5b) taken at 0 V, before DEP, shows a broad background photoluminescence signal attributed to the glass/ITO substrate, and this background was subtracted from subsequent collections. As the DEP force concentrates SWCNTs in the vicinity of the tip, Raman G-band (1595 cm–1) and photoluminescence (PL) signal intensities (758, 1411, and 1898 cm–1; corresponding to 835, 883, and 923 nm) are seen to increase. Background-subtracted spectra, along with superimposed fitting (consisting of three Gaussians for PL and one Lorentzian for Raman) are shown in Figure 5B. The G-band33 is characteristic of all SWCNTs, and the three PL peaks are assigned to (5,4), (6,4), and (9,1).34,35 These small diameter tubes are nonresonantly excited by our 785 nm laser, and the emission wavelengths overlap with our Raman spectrometer’s detection range. The spectral identification of the Raman band and the PL peaks corresponding to SWCNTs demonstrates DEP induced concentration of carbon nanotubes on the tip of the pyramid. The Raman and PL signal can be boosted further by exciting localized plasmonic field at the tip of the pyramid by using a radially polarized beam.36

Figure 5.

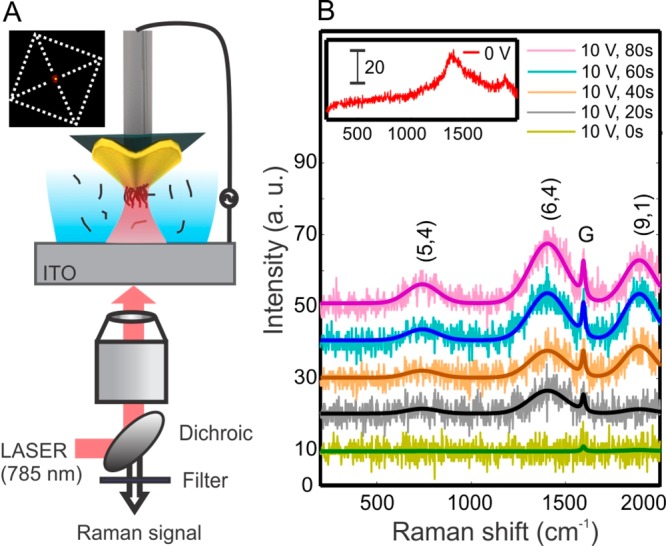
Figure 5

Open in a new tab

Raman spectroscopy of dielectrophoretically trapped SWCNTs on the tip of a template-stripped gold pyramid. (A) Illustration of the experimental setup. The laser light (785 nm) is focused on the tip of the gold pyramid and the reflected light is filtered and detected using a Raman spectrometer. Inset shows the laser light scattered by the tip of the gold pyramid, which is immersed in the SWCNT solution. (B) Background-subtracted Raman spectra (2 s acquisition time) for an applied potential of 10 Vpp and 100 kHz at different time sequences indicating the clear emergence of the Raman G band at 1595 cm–1 and the three different photoluminescence peaks. The spectra are vertically offset for clarity. The inset shows the Raman spectrum collected before applying the potential.

In summary, we have demonstrated site-specific, reversible dielectrophoretic trapping based on template-stripped gold pyramid tips. A single pyramidal tip was template-stripped using conductive epoxy coated on a thin tungsten wire. This was made possible by mixing two kinds of epoxy and verifying the conductive path to the exterior of pyramid. The pyramid was integrated to a XYZ micropositioner and immersed in a solution of fluorescently labeled beads on an ITO electrode. AC voltage applied between the pyramid and the ITO electrode generated an electric field intensity gradient at the apex of the pyramid that allowed us to reversibly manipulate 2 μm and 190 nm beads. Furthermore, we utilized DEP to concentrate single-walled carbon nanotubes at the tip apex and demonstrated simultaneous Raman and photoluminescence detection. The conductive gold pyramidal tips are of potential use for many applications, including electrochemistry,37−39 scanning probe microscopy,40−43 and photoemission studies.44 Being a mobile single-electrode DEP trap, our design can be extended further for dielectrophoretic manipulation of single molecules and nanoparticles.

Methods

Pyramid Fabrication

A standard (100) Si wafer was coated with 100 nm thick low-stress Si3N4 and spun-coat with MEGAPOSIT SPR-955 photoresist (Rohm and Haas). The wafer was then exposed with an i-line stepper (Canon 2500 i3) using a mask to produce 35, 45, 55, and 65 μm holes and developed for 70 s in MF CD 26 (Rohm and Haas) using a EE 200X (Brewer Science) spray developer. The exposed Si3N4 layer was etched using RIE (STS model 320) with CF4, followed by resist removal with O2 plasma. The wafer was then dipped in a bath of 30% KOH, 10% isopropyl alcohol, and water for 90 min for anisotropic etching of Si. After etching, the wafer was rinsed for 30 min and cleaned with a 1:1 solution of sulfuric acid and hydrogen peroxide. 200 nm of gold was evaporated on the wafer using an e-beam evaporator (CHA, SEC600). After metal deposition, the wafer was soaked in 49% HF for 20 min to remove the Si3N4 mask, giving isolated gold pyramids.

Computational Modeling

Finite-element modeling (FEM) of our pyramid–ITO electrode system was performed using COMSOL Multiphysics 4.3a. The pyramid is approximated as a cone in a 2D axisymmetric model with base half-width of 32.5 μm and height of 44.7 μm. The radius of the apex of the tip and the tip-electrode gap were set to 20 nm and 50 μm, respectively, which closely resembles the experimental setup. A 10 V DC signal was applied to the tip. Since the nanoscale curvature of the tip and the micron size of the pyramid are much smaller than the wavelength of the 100 kHz AC signal (10 Vpp) applied in the experiments, a DC voltage approximation was used.

Preparation of Single-Walled Carbon Nanotube Solution

HiPco single-walled carbon nanotubes (batch HPR195.1, Rice University) were dispersed at 1 mg/mL in a 2 wt % solution of sodium deoxycholate45 (Sigma-Aldrich). This suspension was tip-sonicated at 1 W/mL for 10 min before centrifuging at 50000 rpm (166000g) for 4 h in a Beckman TL 100 ultracentrifuge with TLS 55 swing bucket rotor. The resulting supernatant was decanted and diluted 100-fold in 2% sodium deoxycholate solution to suppress a pre-DEP trapping signal.

Acknowledgments

This work was supported by grants from the Office of Naval Research (ONR) Young Investigator Award (N00014-11-1-0645) and the National Science Foundation (NSF CAREER Award; DBI 1054191). L.M.O. acknowledges the College of Science and Engineering Fellowship from the University of Minnesota, the National Institutes of Health (NIH) Biotechnology Training Grant, and the NSF Graduate Research Fellowship. T.W.J. acknowledges support from the NIH Biotechnology Training Grant and the University of Minnesota Doctoral Dissertation Fellowship. J.S. and S.-H.O. acknowledge support from Seagate Technology. Device fabrication was performed at the University of Minnesota Nanofabrication Center, which receives support from the NSF through the National Nanotechnology Infrastructure Network. Computational modeling using COMSOL was performed through the University of Minnesota Supercomputing Institute. We thank Adrian Hegeman for use of the ultracentrifuge and sonicator for SWCNT sample preparation, Seon Namgung for help with the preparation of SWCNTs, and David Norris for helpful comments.

Supporting Information Available

Videos showing dielectrophoretic manipulation of polystyrene beads suspended in water using a template-stripped gold pyramid electrode. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States

Supplementary Material

ph500091h_si_001.avi (12.6MB, avi)
ph500091h_si_002.avi (4.9MB, avi)
ph500091h_si_003.avi (6.4MB, avi)

References

  1. Pohl H. A.Dielectrophoresis: the Behavior of Neutral Matter in Nonuniform Electric Fields; Cambridge University Press: New York, 1978. [Google Scholar]
  2. Novotny L.; Bian R.; Xie X. Theory of Nanometric Optical Tweezers. Phys. Rev. Lett. 1997, 79, 645–648. [Google Scholar]
  3. Ashkin A. History of Optical Trapping and Manipulation of Small-Neutral Particle, Atoms, and Molecules. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 841–856. [Google Scholar]
  4. Juan M. L.; Gordon R.; Pang Y.; Eftekhari F.; Quidant R. Self-Induced Back-Action Optical Trapping of Dielectric Nanoparticles. Nat. Phys. 2009, 5, 915–919. [Google Scholar]
  5. Pang Y.; Gordon R. Optical Trapping of a Single Protein. Nano Lett. 2012, 12, 402–406. [DOI] [PubMed] [Google Scholar]
  6. Gascoyne P. R. C.; Vykoukal J. V. Particle Separation by Dielectrophoresis. Electrophoresis 2002, 23, 1973–1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Krupke R.; Hennrich F.; von Lohneysen H.; Kappes M. Separation of Metallic From Semiconducting Single-Walled Carbon Nanotubes. Science 2003, 301, 344–347. [DOI] [PubMed] [Google Scholar]
  8. Inglis D. W.; Riehn R.; Austin R. H.; Sturm J. C. Continuous Microfluidic Immunomagnetic Cell Separation. Appl. Phys. Lett. 2004, 85, 5093. [Google Scholar]
  9. Burke P. J. Nanodielectrophoresis: Electronic Nanotweezers. Encycl. Nanosci. Nanotechnol. 2004, 6, 623–641. [Google Scholar]
  10. Hu X.; Bessette P.; Qian J.; Meinhart C.; Daugherty P. S.; Soh H. T. Marker-Specific Sorting of Rare Cells Using Dielectrophoresis. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 15757–15761. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Hölzel R.; Calander N.; Chiragwandi Z.; Willander M.; Bier F. F. Trapping Single Molecules by Dielectrophoresis. Phys. Rev. Lett. 2005, 95, 128102. [DOI] [PubMed] [Google Scholar]
  12. Salaita K.; Wang Y.; Mirkin C. A. Applications of Dip-Pen Nanolithography. Nat. Nanotechnol. 2007, 2, 145–155. [DOI] [PubMed] [Google Scholar]
  13. Pethig R.; Markx G. H. Applications of Dielectrophoresis in Biotechnology. Trends Biotechnol. 1997, 15, 426–432. [DOI] [PubMed] [Google Scholar]
  14. Novotny L.; Hecht B.. Principles of Nano-Optics, 2nd ed.; Cambridge University Press: New York, 2012. [Google Scholar]
  15. Yeo W.-H.; Kopacz A. M.; Kim J.-H.; Chen X.; Wu J.; Gao D.; Lee K.-H.; Liu W.-K.; Chung J.-H. Dielectrophoretic Concentration of Low-Abundance Nanoparticles Using a Nanostructured Tip. Nanotechnology 2012, 23, 485707. [DOI] [PubMed] [Google Scholar]
  16. Hulman M.; Tajmar M. The Dielectrophoretic Attachment of Nanotube Fibres on Tungsten Needles. Nanotechnology 2007, 18, 145504. [DOI] [PubMed] [Google Scholar]
  17. Maier S. A.; Kik P. G.; Atwater H. A.; Meltzer S.; Harel E.; Koel B. E.; Requicha A. A. G. Local Detection of Electromagnetic Energy Transport Below the Diffraction Limit in Metal Nanoparticle Plasmon Waveguides. Nat. Mater. 2003, 2, 229–232. [DOI] [PubMed] [Google Scholar]
  18. Barnes W. L.; Dereux A.; Ebbesen T. W. Surface Plasmon Subwavelength Optics. Nature 2003, 424, 824–830. [DOI] [PubMed] [Google Scholar]
  19. Bouhelier A.; Beversluis M.; Hartschuh A.; Novotny L. Near-Field Second-Harmonic Generation Induced by Local Field Enhancement. Phys. Rev. Lett. 2003, 90, 013903. [DOI] [PubMed] [Google Scholar]
  20. Yeo W.-H.; Chung J.-H.; Liu Y.; Lee K.-H. Size-Specific Concentration of DNA to a Nanostructured Tip Using Dielectrophoresis and Capillary Action. J. Phys. Chem. B 2009, 113, 10849–10858. [DOI] [PubMed] [Google Scholar]
  21. Lindquist N. C.; Nagpal P.; Lesuffleur A.; Norris D. J.; Oh S.-H. Three-Dimensional Plasmonic Nanofocusing. Nano Lett. 2010, 10, 1369–1373. [DOI] [PubMed] [Google Scholar]
  22. Nagpal P.; Lindquist N. C.; Oh S.-H.; Norris D. J. Ultrasmooth Patterned Metals for Plasmonics and Metamaterials. Science 2009, 325, 594–597. [DOI] [PubMed] [Google Scholar]
  23. Johnson T. W.; Lapin Z. J.; Beams R.; Lindquist N. C.; Rodrigo S. G.; Novotny L.; Oh S.-H. Highly Reproducible Near-Field Optical Imaging with Sub-20-Nm Resolution Based on Template-Stripped Gold Pyramids. ACS Nano 2012, 6, 9168–9174. [DOI] [PubMed] [Google Scholar]
  24. Cherukulappurath S.; Johnson T. W.; Lindquist N. C.; Oh S.-H. Template-Stripped Asymmetric Metallic Pyramids for Tunable Plasmonic Nanofocusing. Nano Lett. 2013, 13, 5635–5641. [DOI] [PubMed] [Google Scholar]
  25. Henzie J.; Lee J.; Lee M. H.; Hasan W.; Odom T. W. Nanofabrication of Plasmonic Structures. Annu. Rev. Phys. Chem. 2009, 60, 147–165. [DOI] [PubMed] [Google Scholar]
  26. Lindquist N. C.; Nagpal P.; McPeak K. M.; Norris D. J.; Oh S.-H. Engineering Metallic Nanostructures for Plasmonics and Nanophotonics. Rep. Prog. Phys. 2012, 75, 036501. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Belaidi S.; Girard P.; Leveque G. Electrostatic Forces Acting on the Tip in Atomic Force Microscopy: Modelization and Comparison with Analytic Expressions. J. Appl. Phys. 1997, 81, 1023–1030. [Google Scholar]
  28. Yang J.-C.; Gao H.; Suh J. Y.; Zhou W.; Lee M. H.; Odom T. W. Enhanced Optical Transmission Mediated by Localized Plasmons in Anisotropic, Three-Dimensional Nanohole Arrays. Nano Lett. 2010, 10, 3173–3178. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Ramos A.; Morgan H.; Green N. G.; Castellanos A. AC Electrokinetics: a Review of Forces in Microelectrode Structures. J. Phys. D: Appl. Phys. 1998, 31, 2338–2353. [Google Scholar]
  30. Wu J.; Ben Y.; Battigelli D.; Chang H.-C. Long-Range AC Electroosmotic Trapping and Detection of Bioparticles. Ind. Eng. Chem. Res. 2005, 44, 2815–2822. [Google Scholar]
  31. Morgan H.; Green N. G.. AC Electrokinetics: Colloids and Nanoparticles; Research Studies Press: Champaign, IL, 2003. [Google Scholar]
  32. Castellanos A.; Ramos A.; González A.; Green N. G.; Morgan H. Electrohydrodynamics and Dielectrophoresis in Microsystems: Scaling Laws. J. Phys. D: Appl. Phys. 2003, 36, 2584–2597. [Google Scholar]
  33. Saito R.; Hofmann M.; Dresselhaus G.; Jorio A.; Dresselhaus M. S. Raman Spectroscopy of Graphene and Carbon Nanotubes. Adv. Phys. 2011, 60, 413–550. [Google Scholar]
  34. Weisman R. B.; Bachilo S. M. Dependence of Optical Transition Energies on Structure for Single-Walled Carbon Nanotubes in Aqueous Suspension: an Empirical Kataura Plot. Nano Lett. 2003, 3, 1235–1238. [Google Scholar]
  35. Nugraha A. R. T.; Saito R.; Sato K.; Araujo P. T.; Jorio A.; Dresselhaus M. S. Dielectric Constant Model for Environmental Effects on the Exciton Energies of Single Wall Carbon Nanotubes. Appl. Phys. Lett. 2010, 97, 091905. [Google Scholar]
  36. Cancado L. G.; Jorio A.; Ismach A.; Joselevich E.; Hartschuh A.; Novotny L. Mechanism of Near-Field Raman Enhancement in One-Dimensional Systems. Phys. Rev. Lett. 2009, 103, 186101. [DOI] [PubMed] [Google Scholar]
  37. Fan F.-R. F.; Bard A. J. Electrochemical Detection of Single Molecules. Science 1995, 267, 871–874. [DOI] [PubMed] [Google Scholar]
  38. Oja S. M.; Wood M.; Zhang B. Nanoscale Electrochemistry. Anal. Chem. 2013, 85, 473–486. [DOI] [PubMed] [Google Scholar]
  39. Comstock D. J.; Elam J. W.; Pellin M. J.; Hersam M. C. High Aspect Ratio Nanoneedle Probes with an Integrated Electrode at the Tip Apex. Rev. Sci. Instrum. 2012, 83, 113704. [DOI] [PubMed] [Google Scholar]
  40. Odom T. W.; Huang J.-L.; Kim P.; Lieber C. M. Atomic Structure and Electronic Properties of Single-Walled Carbon Nanotubes. Nature 1998, 391, 62–64. [Google Scholar]
  41. Dai H.; Hafner J. H.; Rinzler A. G.; Colbert D. T.; Smalley R. E. Nanotubes as Nanoprobes in Scanning Probe Microscopy. Nature 1996, 384, 147–150. [Google Scholar]
  42. Tang J.; Yang G.; Zhang Q.; Parhat A.; Maynor B.; Liu J.; Qin L.-C.; Zhou O. Rapid and Reproducible Fabrication of Carbon Nanotube AFM Probes by Dielectrophoresis. Nano Lett. 2005, 5, 11–14. [DOI] [PubMed] [Google Scholar]
  43. Kim J.-E.; Park J.-K.; Han C.-S. Use of Dielectrophoresis in the Fabrication of an Atomic Force Microscope Tip with a Carbon Nanotube: Experimental Investigation. Nanotechnology 2006, 17, 2937–2941. [Google Scholar]
  44. Bharadwaj P.; Bouhelier A.; Novotny L. Electrical Excitation of Surface Plasmons. Phys. Rev. Lett. 2011, 106, 226802. [DOI] [PubMed] [Google Scholar]
  45. Wenseleers W.; Vlasov I. I.; Goovaerts E.; Obraztsova E. D.; Lobach A. S.; Bouwen A. Efficient Isolation and Solubilization of Pristine Single-Walled Nanotubes in Bile Salt Micelles. Adv. Funct. Mater. 2004, 14, 1105–1112. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ph500091h_si_001.avi (12.6MB, avi)
ph500091h_si_002.avi (4.9MB, avi)
ph500091h_si_003.avi (6.4MB, avi)

Articles from ACS Photonics are provided here courtesy of American Chemical Society

RESOURCES