Skip to main content
PMC home page
Springer logoLink to Springer
. 2010 Jan 27;3(4):285–294. doi: 10.1007/s12080-009-0069-x

The inverse niche model for food webs with parasites

Christopher P Warren 1,2,✉, Mercedes Pascual 1,3, Kevin D Lafferty 4, Armand M Kuris 5
PMCID: PMC4270433  PMID: 25540673

Abstract

Although parasites represent an important component of ecosystems, few field and theoretical studies have addressed the structure of parasites in food webs. We evaluate the structure of parasitic links in an extensive salt marsh food web, with a new model distinguishing parasitic links from non-parasitic links among free-living species. The proposed model is an extension of the niche model for food web structure, motivated by the potential role of size (and related metabolic rates) in structuring food webs. The proposed extension captures several properties observed in the data, including patterns of clustering and nestedness, better than does a random model. By relaxing specific assumptions, we demonstrate that two essential elements of the proposed model are the similarity of a parasite’s hosts and the increasing degree of parasite specialization, along a one-dimensional niche axis. Thus, inverting one of the basic rules of the original model, the one determining consumers’ generality appears critical. Our results support the role of size as one of the organizing principles underlying niche space and food web topology. They also strengthen the evidence for the non-random structure of parasitic links in food webs and open the door to addressing questions concerning the consequences and origins of this structure.

Electronic supplementary material

The online version of this article (doi:10.1007/s12080-009-0069-x) contains supplementary material, which is available to authorized users.

Keywords: Food webs with parasites, Food web structure, Niche model

Introduction

There is a large body of work describing the structure of food webs that exclude parasites (Pimm et al. 1991; see Dunne 2006, for a recent review). Several simple models have played an important role characterizing the non-random structure of food webs, including the cascade model (Cohen et al. 1990a), the niche model (Williams and Martinez 2000), and the nested-hierarchy model (Cattin et al. 2004). These are essentially static models based upon a one-dimensional ordering or hierarchy for species. Despite their simple rules, the niche and nested-hierarchy models have been able to capture several structural properties of empirical food webs. Of all the food webs Williams and Martinez analyzed for their assessment of the niche model, only the Ythan Estuary food web included parasites (Huxham and Raffaelli 1995), and that was the food web most poorly captured by the niche model, though apparently, this was due to a preponderance of top predators (birds) in this system (Williams and Martinez 2000). Huxham et al. (1996) point out the two aspects of parasitism that potentially result in poor fits to existing models of structure: a reversed ordering on the niche dimension due to their feeding on resources with larger body sizes and complex life cycles, which reduces intervality.

Although parasites can have profound effects on the structure and dynamics of ecological networks (Marcogliese and Cone 1997; Lafferty et al. 2006a, b; Lafferty et al. 2008), they have usually been excluded from food web research due to the perception that they contribute little to energy flow, do not kill their hosts; in addition, they are out of sight for ecologists, can be laborious to detect and have complex trophic life cycles, challenging placement in a web (Lafferty et al. 2008). Increasingly, their impact on host populations and communities has been recognized, and the recent quantification of their biomass in estuarine ecosystems shows that infectious agents may make a substantial energetic contribution to ecosystems (Kuris et al. 2008).

Few field and theoretical studies have addressed the role of parasitic links in food webs. The exceptions in field studies include the Ythan Estuary food web (Huxham and Raffaelli 1995), the Company Bay food web (Thompson et al. 2005), and the Carpinteria Salt Marsh food web (Lafferty et.al. 2006a). For the Ythan Estuary food web, only helminths were systematically detected, and the food web of the Company Bay intertidal mudflat includes only nine parasites. The Carpinteria Salt Marsh web is the most comprehensive web including parasites. It has the benefit of extensive sampling of both hosts and parasites and extensive information on the complex life cycles of the parasites (Lafferty et al. 2006a; Kuris et al. 2008).

Initial analyses have shown that consideration of parasites in food webs significantly modifies general topological properties of the network. Not surprisingly, the addition of parasites increases species richness, the number of links, trophic level, and chain length (Huxham and Raffaelli 1995; Thompson et al. 2005). More interestingly, parasites increase connectance, an important metric measuring the density of links in the network (Lafferty et al. 2006a, b; Lafferty et al. 2008). Recognizing and including predator–parasite and parasite–parasite links further increases this metric and dramatically increases relative nestedness (Lafferty et al. 2006a, b), a global measure that characterizes how interactions between species in two different levels (e.g., plants and pollinators or hosts and parasites) are distributed among species with different degrees of specialization. A nested network possesses a cohesive core of interacting species, composed largely of generalists, and a high asymmetry in that specialists interact primarily with generalists (Bascompte et al. 2003). Parasitic links, like predator–prey links, are non-randomly distributed, with an overdispersed number of parasites per host and with hosts tending to occupy higher trophic levels (Chen et al. 2008). The detailed analyses of a series of new empirical networks by Dunne et al. (personal communication) show that the inclusion of parasites pushes the overall food web structure away from the niche model’s expectation.

Though the niche model suggests that much of the structure of food webs can be explained by a one-dimensional ordering, what that ordering factor is remains an open question. Potential candidates include body mass (Warren and Lawton 1987; Cohen et al. 1993; Petchey et al. 2008) and related quantities such as metabolic rates and trophic level (Stouffer et al. 2007). Predators are generally larger than their prey, and parasites are nearly always smaller than their hosts (Lafferty and Kuris 2002). Leaper and Huxham (2002) argue that this size relationship for parasites and hosts eliminates the prospects of body size as the hierarchy factor in a model with a strict ordering, such as the cascade model, but, as we will describe here, the same factor and ordering can be used when considering parasites if one distinguishes parasitic and predatory links by ordering them by different (but related) rules.

To further address the non-random structure of parasitic links, we consider a series of network properties related to the links themselves, in particular, those describing the degree of clustering, nestedness, and generality. To explain the non-random structure of host–parasite links revealed by these analyses, we propose an extension of the niche model. This model captures the observed clustering, nestedness, and several food web indices of the parasitic links, significantly better than a series of null models, including a random assignment of parasites to hosts. The proposed model essentially reverses the hierarchy of the niche model (Williams and Martinez 2000), but only for parasite–host links; this is the constraint by which the range of prey for a given consumer must be centered below its own position in the one-dimensional niche axis. It also reverses the axis of generality for parasites. Comparisons to a series of models that relax these assumptions show that only the reversal of the generality rule appears essential. We discuss interpretations of these results in relation to body size and future directions for models of food web structure.

Data

The Carpinteria Salt Marsh food web (Lafferty et al. 2006a, b) comprises free-living species chosen from quantitative surveys and generally included those metazoan species common enough to comprise 99.58% of the individuals from a particular taxonomic group (birds, fishes, large invertebrates, small invertebrates). Published, observed, and inferred diet relationships were used to recognize predator–prey links. Infectious agents were included based on extensive parasitological investigations of hosts in this marsh (thousands of hosts of almost all the predator and prey species in the web were dissected for infectious agents). Parasites included macroparasites mostly parasitic helminths, parasitic castrators, parasitoids, pathogens, and trophically transmitted parasites (sensu Lafferty and Kuris 2002). Some natural enemies were underestimated. For instance, microbial pathogens were not typically detected; plant pathogens were excluded, and avian parasites, pathogens, and ectoparasites were under-sampled. Parasites of plants were not included in the analysis. Very small invertebrates (<∼1 mm), free-living protozoans, bacteria, and fungi were not included, nor were their infectious agents. These detailed data on web structure are available at the National Center for Ecological Analysis and Synthesis Interaction Web Database, which is free and accessible to the public.

We consider two types of links in this network: predator–prey links and parasite–host links. Predator–prey links (and predation) refer throughout the paper to non-parasitic interactions between free-living species, including herbivory. Many of the parasites possess complex life cycles. To simplify the analysis, two versions of the Carpinteria food web were analyzed. In the species version, life stages of a particular species were grouped into one entity or “species.” In the life stage version, each life stage of a species is treated as a separate “trophic unit.” The trophic “species” convention was used, where all species that share identical predators, prey, parasites, and hosts were grouped. This convention has been used in food web studies to reduce methodological and statistical variation due to uneven resolution (Briand and Cohen 1984) and insufficient sampling (Martinez et al. 1999) of taxa and to focus on functionally distinct components of food webs (Williams and Martinez 2000). Micropredators feed on multiple preys as do predators, but take a small meal as do parasites. These functional affinities to both parasites and predators pose a classification dilemma. For example, mosquitoes are micropredators interacting with many “prey”, totaling 79 links. They were classified as predators in our analyses.

The Carpinteria data include two other types of links that are not explicitly considered in our analyses: predators feeding on parasites and parasites feeding on parasites. Consumption of parasites in the Carpinteria’s web occurs primarily as the result of predators eating infected prey. This is the main form of transmission for parasites with complex life cycles whose different stages parasitize different host species. The reason not to include such links in the model explicitly is that links that result from predators feeding on infected hosts can be easily generated from the two types of links we do generate, for example, by estimating the probability of “incidental” or “concomitant” predation of parasites based on the existence of a prey with links to both a predator and a parasite. This would take into account the great majority of the links for the consumption of parasites, the exception being the links to free-living stages of parasites, exclusively cercariae in our system. We also do not consider parasite–parasite links since these represent primarily competitive interactions within the host and do not affect the network of species interactions between hosts and parasites or between consumers and their resources.

Finally, hyperparasitism is absent from our analyses as it is also very rare in the data. However, this is not a limitation of the proposed model itself which could generate such links by establishing a parasite–parasite link when a parasite falls into the host range of another parasite.

Statistical measures

To evaluate clustering properties of the network when two different types of links (predation and parasitism) are present, we introduce the following two statistics:

The feed-forward loop motif is a particular directed triad form of clustering. We specifically compute the probability, given that a parasite parasitizes a particular trophic species and a predator preys upon that species, that the parasite parasitizes that predator as well (see Fig. 1a). This motif was studied earlier by (Shen-Orr et al. 2002) in their analysis of the regulatory network of Escherichia coli. Our version of the motif is a bit different in that there are two types of nodes—parasite and nonparasite.

Fig. 1.

Fig. 1

Open in a new tab

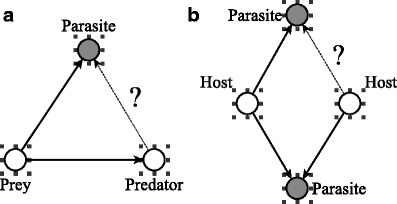
Food web motif statistics analyzed: a The feed-forward loop statistic looks for two chains of a prey/host being both parasitized and preyed upon. The statistic is the probability that the respective predator is also parasitized by the respective parasite. b The bi-fan statistic looks for parasites that share a host. The statistic is the probability, if one of the parasites has another host, that the other parasite also shares that host

The bi-fan motif characterizes another higher form of clustering. Given that two parasites parasitize the same host and one of the parasites parasitizes another host, we evaluate the probability that the second parasite parasitizes the second host as well (Fig. 1b). This is a measure of the contiguity of the niche space, related to the notion of intervality in food webs (Cohen 1977; Cattin et al. 2004; Stouffer et al. 2007). For interval networks, there exists a suitable ordering of the species for which all the prey of each predator are contiguous.

A macroscopic characterization of structure, in terms of the distribution of parasitic links on their hosts, is evaluated with the statistic nestedness for bipartite networks. Nestedness measures how well the groups of hosts of specialist parasites can be successively nested, like matryoshka dolls or Chinese boxes, into the host groups of increasingly more generalist parasites (see Atmar and Patterson (1993) or Bascompte et al. (2003) for details). Nestedness was originally developed to analyze how species are distributed on a set of small islands (Atmar and Patterson 1993). Applying this species–island analogy, Bascompte et al. (2003) used nestedness to characterize how animals were distributed in plant–animal mutualistic networks. We used the Nestedness Calculator software created by W. Atmar and B. D. Patterson and converted the “temperature” T obtained with it into a nestedness measure using the convention of Bascompte et al. (2003), \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ N = \left( {100 - T} \right)/100 $$\end{document}. The nestedness of the sample food web is compared with that of a network produced by a null model in which the links are randomized in such a way as to preserve the degree distribution of the entire web (Fischer and Lindenmayer 2002). We also considered a null model in which the same number of parasite–host links was randomly assigned to parasites and hosts. Nestedness has the unique feature of being not merely a local measure (e.g., feed-forward loop) or a global measure (e.g., connectivity) of the food web, but rather a measure across many scales.

A number of global measures or indices have been used to characterize the fit of food web models (Williams and Martinez 2000). For the same purpose, we also re-define several of these previously used measures to characterize the structure of the parasitic links in the network (details are given in Appendix S1). For instance, the fraction of basal, intermediate, and top species can be defined exclusively for parasites, to mean the fraction of parasites of basal, intermediate, and top free-living (host) species. Similarly, the standard deviation of generality provides a measure of the variability in the number of hosts per parasite species. The complete list of measures and their definitions can be found in Appendix S1. Note that we consider vulnerability statistics both (a) with respect to predator–prey links and parasite–host links and (b) with respect to parasite–host links only, in order to more specifically evaluate our model.

Proposed models

We consider that the niche model as originally proposed by Williams and Martinez (2000) applies to the food web part of the network composed only of non-parasitic interactions between consumers and resources. This model first establishes a hierarchy by ordering species along a one-dimensional axis, which determines potential prey species. Actual predation links are then assigned through contiguous ranges along this same axis selected to preserve the chosen connectance (Fig. 2). Importantly, the size of these ranges is an increasing function of the position of the predator in the niche axis, which makes them increasingly less specialized (Fig. 2).

Fig. 2.

Fig. 2

Open in a new tab

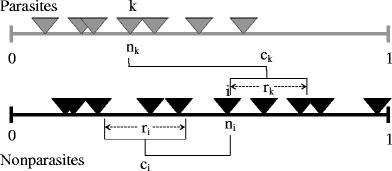
The niche model (Williams and Martinez 2000) is used to model the underlying predator–prey food web, and, as described below, parasites were added to the web. The niche model uses two fundamental parameters, connectance and species richness, and relies on a one-dimensional niche space or hierarchy. Species are given a random niche value n i ∼ Uniform (0.1) in the hierarchy. Diets are assigned to each species independently by generating a center and a range as follows. Firstly, the feeding range is given by r i = n i x i where x is a random number drawn from a Beta distribution, with\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {x_i}\sim Beta\left( {\alpha = 1,\beta } \right) $$\end{document}. The distribution is chosen to obtain, on average, the desired connectance. Secondly, the centers of the feeding ranges are chosen randomly from species further down in the hierarchy, with \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {c_i}\sim {{Uniform}}\left( {{r_i}/2,{n_i}} \right) $$\end{document}. Once a feeding range is established for a given species, all species in that range become its prey. We add parasites to this model, by reversing the above rules as follows. First, a niche value ñ k ∼ Uniform (0.1) is assigned to each parasite trophic species k. Parasites are also assigned feeding range sizes, but now these decrease as we move up the hierarchy, with \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {r_k} = \left( {1 - n} \right){y_k} $$\end{document}, where y k is chosen from a Beta distribution properly chosen to obtain on average the observed connectance of the parasitic links. Parasites infect any nonparasite in their feeding range. However, now, the center of the parasites feeding range is drawn randomly from a position higher on the hierarchy, with \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\tilde c_k}\sim {{Uniform}}\left( {{{\tilde n}_k},1 - {{\tilde r}_k}/2} \right) $$\end{document}. The larger feeding range is motivated by the concept that, if the hierarchy is related to size, parasites lower in the hierarchy, smaller in size, will typically have a larger potential feeding range, a larger set of hosts that can energetically support them. The parameters of the inverse niche model are: the number of parasites, the number of non-parasitic species, and the respective connectances of the parasite–nonparasite and nonparasite–nonparasite subwebs. Although for graphical convenience the niche axis is represented separately here for parasites and free-living species, this is in fact the same axis. Additional parameters could be introduced to restrict the parasitic niche space to map only onto a part of this segment

The niche model, without any extension to distinguish parasitic from non-parasitic links, could be applied to the full Carpinteria webs with all types of interactions included. We note, however, that the niche model considers only two parameters, corresponding respectively to connectance and species richness for the whole network. Because of this, the resulting subwebs generated by this model lack the proper connectance for the four corresponding submatrices defined by the different types of interactions (parasite–nonparasite, nonparasite–nonparasite, nonparasite–parasite, and parasite–parasite; see Table S3, Supplement). This is not surprising since the model lacks enough information to generate an expected number of links in each submatrix that matches their observed values. Because the empirical web is composed of these subwebs and their connectance differs, we can expect the simulated networks to deviate for a number of properties from the data. We can also expect that assigning parasites at random to these simulated networks would fail to capture basic properties of the network, such as the fraction of intermediate and top consumers, as well as parasites (see Results).

We extend the niche model to introduce parasitic links by considering the same single dimension and the same two general concepts of a hierarchy and interaction ranges. However, the model effectively reverses the hierarchy for the parasite species that determine potential and realized hosts as illustrated in Fig. 2. The center of host ranges are now placed above the parasite in the niche axis, and the size of the host range decreases instead of increasing with the position of the parasite in this axis. Effectively, parasites become increasingly specialized the higher their ranking. We refer to this extension of the niche model as the inverse niche model.

Besides the null model that assigns parasites randomly to the nonparasites in the web, we simulated a series of alternative models described below that generate non-random structures of the parasitic links. To see which elements of the inverse niche model were essential, three simpler variants were considered: First, all parasites were given a constant range, but the ordering of hosts relative to their parasites was preserved. A constant range eliminates from the model the relationship between generality and position in the niche axis. Second, this relationship was preserved, but the hierarchy itself was not. In this case, hosts can be above or below the parasite’s placement in the niche axis, with range centers chosen randomly. Third, both the hierarchy and the decreasing host range were eliminated. All parasites were given a constant range and the range centers were chosen randomly. Random centers break down the assignment of parasites to hosts that are higher up in the niche axis.

Simulation

Monte Carlo simulations generated 1,000 webs with the same number of nonparasites S NP and parasites S P. To obtain the 1,000 webs, we followed the rejection criteria introduced by Williams and Martinez for the niche model. Thus, we rejected those webs whose connectance was not within 3% of the observed value for the nonparasite–nonparasite links and parasite–nonparasite links. Species that were isolated from the rest of the web, having no prey, predators, parasites, or hosts, were discarded and replaced. Extra species that had identical interactions were also discarded and replaced.

Results

Statistics of the two food web versions, life stage and species, were compared with those of a null model where the same number of parasite–host links were randomly assigned to parasites and nonparasites or hosts. As shown in Tables 1 and 2, and consistent with Chen et al. (2008), both versions of the Carpinteria food web differed greatly from their random counterparts. Both the bi-fan and the average maximum similarity (MaxSim) statistics show a food web with parasites having much more similar diets than would be predicted from random, suggesting a low-dimensional or otherwise clumpy, compartmentalized niche space.

Table 1.

Comparison of the different models for the species version of the Carpinteria food web based on a number of food web statistics

Statistics Carpinteria Carp. web + random links Constant range with hierarchy Inverse niche model (1−n)y range with no hierarchy
Web Mean SD z value Mean SD z value Mean SD z value Mean SD z value
Proportion of completed bi-fans 0.586 0.145 0.0056 78.166 0.652 0.018 −3.562 0.513 0.037 2.013 0.539 0.039 1.186
Proportion of completed FFLs 0.434 0.146 0.0092 31.315 0.249 0.066 2.820 0.298 0.072 1.892 0.310 0.064 1.918
Nestedness 0.843 0.512 0.0231 −14.350 0.533 0.059 −5.215 0.818 0.0405 −0.632 0.715 0.043 2.981
Ave. basal 0.123 0.123 – – 0.173 0.036 −1.364 0.168 0.035 −1.288 0.175 0.035 −1.481
Ave. intermediate 0.852 0.852 – – 0.780 0.065 1.119 0.786 0.063 1.038 0.775 0.067 1.144
Ave. top 0.025 0.025 – – 0.051 0.059 −0.451 0.049 0.056 −0.436 0.055 0.063 −0.489
Rate of p-basal connection 0.011 0.123 0.0149 −7.485 0.098 0.036 −2.413 0.091 0.038 −2.112 0.154 0.041 −3.486
Rate of p-intermediate connection 0.971 0.852 0.0161 7.386 0.829 0.102 1.400 0.825 0.114 1.279 0.798 0.076 2.282
Rate of p-top connection 0.018 0.025 0.0067 −1.052 0.075 0.095 −0.602 0.086 0.106 −0.643 0.048 0.067 −0.458
Ave. cannibal rate 0.000 0.000 – – 0.090 0.031 −2.908 0.092 0.030 −3.114 0.089 0.030 −2.940
p–h SD generality 0.868 0.265 0.0301 20.061 0.261 0.064 9.446 0.914 0.104 −0.436 0.901 0.102 −0.323
p–h SD vulnerability 1.000 0.388 0.0302 20.275 0.697 0.101 3.004 0.822 0.125 1.426 0.366 0.094 6.770
SD vul (p–h & predator–prey) 0.540 0.55 0.0195 −0.488 0.285 0.049 5.204 0.289 0.052 4.834 0.355 0.076 2.456
p–h ave. max similarity 0.591 0.226 0.0094 39.050 0.842 0.017 −15.119 0.615 0.031 −0.765 0.578 0.038 0.363
Loop proportion 0.259 0.259 – – 0.102 0.036 4.318 0.104 0.036 4.255 0.100 0.037 4.302
Ln (no. of chains) 5.210 5.210 – – 5.559 0.699 −0.499 5.800 0.751 −0.785 5.516 0.686 −0.445
Ave. food chain length 6.716 6.716 – – 8.557 1.753 −1.050 8.985 1.810 −1.255 8.432 1.703 −1.007
SD of chain length 1.379 1.379 – – 2.079 0.264 −2.651 2.128 0.256 −2.923 2.069 0.264 −2.609
Ln (no. of p. chains) 6.198 5.955 0.0341 7.122 6.516 0.705 −0.451 6.746 0.758 −0.723 6.248 0.692 −0.073
Average p. food chain length 7.659 7.715 0.0524 −1.063 9.547 1.741 −1.084 10.000 1.794 −1.305 9.368 1.698 −1.006
SD of p. chain length 1.313 1.378 0.0205 −3.192 2.063 0.268 −2.803 2.109 0.260 −3.058 2.071 0.267 −2.840
Proportion of omnivory 0.714 0.714 – – 0.947 0.044 −5.227 0.949 0.042 −5.551 0.945 0.048 −4.802
Proportion of p. omnivory 0.937 0.999 0.0030 −20.852 1.000 0.000 NAN 0.999 0.006 −10.610 0.988 0.020 −2.515
Open in a new tab

The values of these statistics are first shown for the empirical data. Those of the mean and standard deviation for the simulated networks are then given for (1) a null random model in which the parasitic links are assigned at random to the predator and prey of the empirical food web, (2) a model with a parasite hierarchy but constant host ranges, (3) the inverse niche model, and (4) a model with decreasing host ranges \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {r_i} = (1 - {n_i}){y_i} $$\end{document} but no parasite hierarchy. Italicized statistics include only host–parasite links in the calculations. Results for the simulations of the model with a constant host range and no parasite hierarchy are shown in Table S1. Normalized errors (t scores), obtained by dividing the raw errors by the SD of the properties’ distributions in the model simulations, are also given.

FFLs feed-forward loops, p parasite, p–h parasite–host links

Table 2.

Comparison of the different models for the life stages version of the Carpinteria food web

Statistics Carpinteria Carp. web + random links Constant range with hierarchy Inverse niche model (1−n)y range with no hierarchy
Web Mean SD z value Mean SD z value Mean SD z value Mean SD z value
Proportion of completed bi-fans 0.604 0.092 0.006 87.618 0.628 0.018 −1.281 0.513 0.037 2.512 0.504 0.044 2.293
Proportion of completed FFLs 0.120 0.092 0.007 3.868 0.159 0.048 −0.808 0.298 0.072 −2.487 0.212 0.051 −1.787
Nestedness 0.862 0.668 0.017 11.261 0.644 0.041 5.280 0.823 0.033 1.191 0.805 0.025 2.262
Ave. basal 0.120 0.120 – – 0.167 0.034 −1.374 0.168 0.035 −1.373 0.171 0.036 −1.386
Ave. intermediate 0.831 0.831 – – 0.788 0.063 0.687 0.786 0.063 0.714 0.785 0.065 0.715
Ave. top 0.048 0.048 – – 0.048 0.058 0.009 0.049 0.056 −0.016 0.0492 0.058 −0.018
Rate of p-basal connection 0.013 0.120 0.016 −6.553 0.098 0.035 −2.429 0.091 0.038 −2.067 0.147 0.042 −3.239
Rate of p-intermediate connection 0.974 0.831 0.019 7.479 0.833 0.101 1.400 0.825 0.114 1.308 0.806 0.077 2.182
Rate of p-top connection 0.013 0.049 0.010 −3.495 0.071 0.096 −0.604 0.086 0.106 −0.690 0.048 0.065 −0.538
Ave. cannibal rate 0.000 0.000 – – 0.092 0.030 −3.051 0.092 0.030 −3.114 0.090 0.031 −2.922
p–h SD generality 1.105 0.339 0.033 22.854 0.325 0.064 12.178 0.914 0.104 1.826 0.936 0.109 1.539
p–h SD vulnerability 1.076 0.434 0.032 20.031 0.668 0.091 4.478 0.822 0.125 2.032 0.427 0.097 6.654
SD vul (p–h & predator–prey) 0.537 0.549 0.019 −0.643 0.290 0.050 4.909 0.289 0.052 4.770 0.363 0.072 2.426
p–h ave. max similarity 0.523 0.221 0.001 31.148 0.796 0.016 −17.080 0.615 0.031 −2.980 0.554 0.033 −0.946
Loop proportion 0.000 0.000 – – 0.104 0.036 −2.887 0.104 0.036 −2.865 0.102 0.038 −2.675
Ln (no. of chains) 4.265 4.265 – – 5.771 0.751 −2.006 5.800 0.751 −2.045 5.735 0.727 −2.023
Ave. food chain length 4.272 4.272 – – 8.939 1.808 −2.581 8.985 1.807 −2.608 8.811 1.803 −2.517
SD of chain length 1.118 1.118 – – 2.122 0.264 −3.800 2.128 0.256 −3.942 2.100 0.266 −3.687
Ln (no. of p. chains) 4.846 4.935 0.083 −1.070 6.647 0.755 −2.384 6.746 0.758 −2.507 6.441 0.736 −2.167
Average p. food chain length 4.697 5.262 0.085 −6.599 9.927 1.792 −2.917 10.000 1.794 −2.955 9.769 1.801 −2.817
SD of p. chain length 1.033 1.116 0.013 −6.439 2.107 0.267 −4.019 2.109 0.260 −4.134 2.097 0.268 −3.962
Proportion of omnivory 0.7069 0.707 – – 0.947 0.047 −5.128 0.949 0.042 −5.726 0.945 0.048 −4.908
Proportion of p. omnivory 0.882 0.996 0.009 −13.039 0.999 0.004 −28.595 0.999 0.006 −20.188 0.983 0.024 −4.125
Open in a new tab

The values of the food web statistics for the empirical data are shown first. The mean and standard deviation of these properties for the simulated networks are then given for the inverse niche model and a number of null models described in the text. Italicized statistics include only host–parasite links in the calculations. Results for the simulations of the model with constant host ranges and no parasite hierarchy are shown in Table S2.

FFLs feed-forward loops, p parasite, p–h parasite–host links

The number of feed-forward loops for the species version of the web was also significantly high, reflecting the common pathway of parasites from prey to predator. With the host species embedded in a trophic hierarchy, this high value indicates that a sizable number of parasites should be sufficiently generalist to parasitize both predator and prey. The significantly lower value of the number of feed-forward loops for the life stage web should not be surprising since the life stage separation segregates many of these triangle-completing links.

Both versions of the food web are much more nested than the degree distribution-preserving null model. The less strict null model originally used by Atmar and Patterson (1993) yielded even more statistically significant values of nestedness. Other indices further reflect significant departures from a random assignment of parasitic links to the predator–prey food web. In both web versions, the empirical values of vulnerability of hosts to parasites are significantly higher than those obtained in the model that randomly assigns parasites to hosts. Significantly higher values are also seen for the generality of parasites and for their maximum similarity. The above comparisons for clustering, nestedness, and other general statistics describe in detail how the structure of the parasitic links in the food web differs from random.

A similarly poor fit to the data is obtained if we use the original niche model to generate the whole food web (with the connectance and species richness determined by all four types of interactions) and assign parasites at random (Table S3, Supplement). This result is to be expected since the number of links in each of the four possible submatrices (defined by the four types of links) is significantly different from its expected value (Table S3, Supplement).

We evaluate next whether the proposed inverse niche model captures this structure.

Results in Tables 1 and 2 show that the inverse niche model is significantly better than the random null model. Bi-fan and feed-forward loop clustering were captured better in both versions of the food web and so were nestedness and the standard deviation of generality. The MaxSim generated by the inverse niche model was closer to that of the empirical web than that generated by the random model, although the difference between simulations and data remains significant. Fig. 3 shows the normalized error between observed and predicted values of the different measures. These errors for the inverse niche model exhibit for the most part a large decrease relative to their values for the random model (compare 1 and 4 in Fig. 3). The fact that a number of errors are still larger than 1 (or 2) in absolute magnitude shows, however, that there are still significant differences between the data and the model-generated webs. The models with constant ranges, including the model with no hierarchy (Tables S1 and S2, Supplement), exhibit the worse performance. Interestingly, the hierarchy itself can be relaxed, and the performance of the model with random centers and decreasing ranges is comparable to that of the inverse niche model. Thus, the degree of specialization of the parasites as a function of their position in the niche axis appears to be the key property in the performance of the inverse model.

Fig. 3.

Fig. 3

Open in a new tab

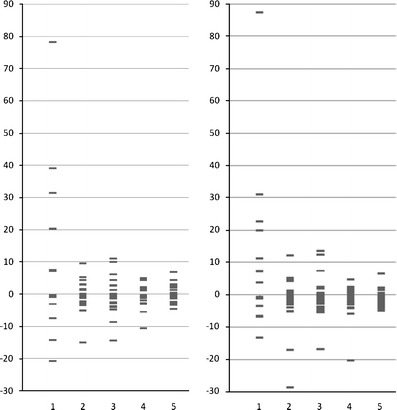
Normalized errors of various models with respect to the a species and b life stage versions of the Carpinteria food web with the following models: (1) Carpinteria food web with random parasitic links, (2) constant host range with parasite hierarchy, (3) constant host range with random centers (detailed statistics shown in S1 and S2), (4) inverse niche model, and (5) decreasing host range model \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \left( {{r_i} = (1 - {n_i}){y_i}} \right) $$\end{document} with random centers (no parasite hierarchy). Normalized errors are obtained by dividing the raw errors by the SD of the properties’ distributions in the model simulations. Their values are listed in Tables 1, 2, S1, and S2 for the different models

Discussion

Our results demonstrate that parasites are far from randomly distributed to the underlying predator–prey food web, extending the findings by Chen et al. (2008). As emphasized by Bascompte et al. (2003), higher nestedness implies a more cohesive network consisting primarily of interactions among generalists and a degree of asymmetry in the interaction between specialists and generalists. At a more local level, we have found that clustering measures, based on the feed-forward loop motifs and bi-fan motifs, were also high. The decrease of the proportion of feed-forward loops when the life cycles are disaggregated reflects that this quantity in the species version of the web capture trophic transmission of parasites from prey to predators. The high fraction of completed bi-fans provides further evidence for a non-random structure and justifies the notion of a contiguous “niche” as considered in the proposed inverse niche model. Contiguous host ranges make it more likely that if two parasites parasitize the same host and one of them parasitizes another host, the second parasite parasitizes the second host as well.

A significant part of this non-random structure can be captured by extending the niche model to include parasites in a way that reverses the rules of the original formulation. In the original niche model, placing the center of feeding ranges at or below the consumer’s niche value ensures that species feed primarily on resources that are lower in the hierarchy. In addition, having the size of feeding ranges grow in proportion to consumers’ positions in the hierarchy ensures that species with higher niche values are increasingly general in their feeding habits. Size or the related metabolic rate must be an important component of the single dimension underlying both the ordering of species and the concept of contiguous ranges for predation and parasitism. Parasitism constitutes a diverse set of strategies which may feed on distinctly different relative sizes of resources (Lafferty and Kuris 2002). One could expand our approach to consider, for example, that parasitoids and parasitic castrators have different relative and absolute body size associations with their hosts compared with typical parasites (macroparasites). In particular, their feeding niche would be narrower and closer to their own niche.

Comparisons of the inverse niche model with the alternative formulations that relax specific assumptions indicate that the key feature of the model for the parasitic links is the increasing specialization of the parasites with their position in the niche axis. However, the tendency of parasites to interact with hosts that occupy a higher position (Chen et al. 2008) does not appear essential. Body mass may thus influence the specificity of parasites and the vulnerability of hosts, but not the range of potential hosts. The inverse niche model further captures the average maximum similarity of parasites, particularly for the species web and less well for the life stage web.

Our analysis has not addressed the performance of the original niche model for food webs that incorporate parasites. In this case, no distinction would be made between parasitic and feeding links. We would then consider a single type of link and a single type of node. This was not the scope of our analysis because we specifically chose to focus on the structure of the parasitic links and on a model of structure that could generate the two distinct types of links. This distinction is essential for a number of future applications of the model, including questions on secondary extinctions and dynamical stability that incorporate different properties of parasitic and free-living species. We have also noted, however, that the original niche model cannot be expected to reproduce the connectance of each of the four subwebs that become possible when parasites are introduced. This limitation should lead to a number of other discrepancies in the fit of the model to data, as confirmed by the detailed analyses of Dunne et al. (personal communication) who show that a number of properties of new webs that include parasites, including the Carpinteria one, appear to deviate from the niche model’s expectations and to do so more strongly for the whole web than for the standard subweb composed of free-living species.

The exclusion of parasites of the basal species in the original data will lead to some biases in measured statistics. For instance, the proportional rate of parasites parasitizing basal species has been underestimated as zero while rates of parasitizing intermediate and top species have been overestimated. The average path length for parasites will be increased, and the number of paths will be decreased. However, these biases are mitigated by the fact that these measures are weighted by the number of paths from parasite to basal species. There are typically multiple paths to the basal species for parasites of non-basal species but only one path for parasites of basal species. The other statistical implications of this exclusion are not clear.

A more conclusive assessment of simple models of food web structure that do not include parasites to empirical food web data is now possible based on likelihoods instead of a collection of indices (Allesina et al. 2008). The likelihood that a specific model has generated the observed network has been derived for the cascade, niche, and nested-hierarchy models. Future work should derive a likelihood for the inverse niche model and extend the genetic algorithm of Allesina et al. (2008) to find a one-dimensional order of both the parasitic and non-parasitic species. Because of the computational complexity of the problem, this will be better achieved by reformulating the models to consider a discrete niche axis (Allesina, personal communication). Such an analysis would also allow the further exploration of the biological properties that underlie the niche axis and the hierarchy of predators and parasites. It would provide an ordering of the species which can then be compared with specific biological properties of interest. Alternatively, different biological properties could be used to order the species, to then compare the resulting likelihoods of the models. Besides size and metabolic rate, the role of phylogenetic relationships should be examined. Likelihood-based approaches would also allow us to consider future extensions of the model(s) we have proposed, as well as alternative formulations. Clearly, there is room for improvement in the fits we have reported. More importantly, future studies should consider all types of links defined by the three (or four) different subwebs that become possible once parasites are introduced, including predation of parasites, parasitism, predation (and parasite–parasite interactions, if present in the data).

Predation on parasites by predators that feed on their hosts is an emergent property of the predator–prey and parasite–host webs and, therefore, can be computed exactly without need for a model. Approximately 30% of the parasites have complex life cycles. Some of these are vector borne; but, in Carpinteria Salt Marsh, most are predator–prey-transmitted. For just those parasites with complex life cycles, 50% of the links involve transmission to a host. To more accurately account for complex life cycles, one would first add parasites to a niche web according to the inverted model (but first negating links to final hosts for parasites with complex life cycles). One would then construct a predator–parasite link for each predator–host link. One could then randomly identify an appropriate fraction (e.g., 30% for Carpinteria Salt Marsh) of the parasites as complex life cycle parasites. One could then assume that the predator served as a final host for another appropriate fraction of the preyed-on parasites (e.g., 50% for Carpinteria Salt Marsh), implying a complex life cycle. Once this is done, assessment of the models to data by use of a long list of indices for the different types of links will be problematic and will benefit from parallel statistical approaches that consider network structure as a whole.

As with its predecessors, the model presented here is static. This type of model can suggest main factors behind the non-random structure of ecological networks and be used to investigate the robustness of the network to species extinctions (Dunne et al. 2002; Dunne et al. 2004; Srinivasan et al. 2007). Beyond static considerations, the cascade and the niche models have been used to formulate large dynamical models of food webs by mapping a set of nonlinear differential equations upon the generated non-random structure of links (Cohen et al. 1990b; Chen and Cohen 2001; Williams and Martinez 2004; Martinez et al. 1999). The model proposed here opens the possibility to pursue similar connections between structure and dynamics in large ecological networks encompassing both predators and parasites.

Acknowledgements

M. P. thanks the support of the James S. McDonnell Foundation through a Centennial Fellowship in Global and Complex Systems. C. W. would like to thank the Center for the Study of Complex Systems for computer resources. This work was conducted as a part of the Parasites and Food Webs Working Group supported by the National Center for Ecological Analysis and Synthesis, a Center funded by NSF (Grant #DEB-0553768), the University of California, Santa Barbara, and the State of California. The NSF/NIH Ecology of Infectious Diseases Program, Grant DEB-0224565 and the NSF Theory in Biology, Grant N, also supported aspects of the research. R. Hechinger and J. McLaughlin provided helpful comments on the manuscript. Any use of trade, product, or firm names in this publication is for descriptive purposes only and does not imply endorsement by the US government.

Open Access

This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.

Supporting information

The following Supporting Information is available for this article:

Appendix S1 (24KB, doc)

Description of food web statistics (DOC 24 kb)

Table S1 (59.5KB, doc)

Statistical comparison of all species models, including a model with constant ranges and no hierarchy (DOC 59 kb)

Table S2 (60KB, doc)

Statistical comparison of all life stage models, including a model with constant ranges and no hierarchy (DOC 60 kb)

Table S3 (45.5KB, doc)

Observed vs. predicted statistics for networks generated by simulating the original niche model and randomly assigning parasites to the resulting nodes (DOC 45 kb)

Additional Supporting Information may be found in the online version of this article.

Contributor Information

Christopher P. Warren, Email: warrencp@umich.edu

Mercedes Pascual, Phone: +1-734-6159808, Email: pascual@umich.edu.

Kevin D. Lafferty, Email: lafferty@lifesci.ucsb.edu

Armand M. Kuris, Email: kuris@lifesci.ucsb.edu

References

  1. Allesina S, Alonso D, Pascual M. A general model for food web structure. Science. 2008;320:658–661. doi: 10.1126/science.1156269. [DOI] [PubMed] [Google Scholar]
  2. Atmar W, Patterson BD. The measure of order and disorder in the distribution of species in fragmented habitat. Oecologia. 1993;96:373–382. doi: 10.1007/BF00317508. [DOI] [PubMed] [Google Scholar]
  3. Bascompte J, Jordano P, Melian CJ, Olesen JM. The nested assembly of plant-animal mutualistic networks. Proc Natl Acad Sci USA. 2003;100:9383–9387. doi: 10.1073/pnas.1633576100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Briand F, Cohen JE. Community food webs have scale-invariant structure. Nature. 1984;307:264–266. doi: 10.1038/307264a0. [DOI] [Google Scholar]
  5. Cattin MF, Bersier LF, Banasek-Richter C, Baltensperger R, Gabriel JP. Phylogenetic constraints and adaptation explain food-web structure. Nature. 2004;427:835–839. doi: 10.1038/nature02327. [DOI] [PubMed] [Google Scholar]
  6. Chen X, Cohen JE. Transient dynamics and food-web complexity in the Lotka–Volterra cascade model. Proc R Soc Lond B Biol Sci. 2001;268:869–877. doi: 10.1098/rspb.2001.1596. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Chen HW, Liu WC, Davis AJ, Jordan F, Hwang MJ, Shao KT. Network position of hosts in food webs and their parasite diversity. Oikos. 2008;117:1847–1855. doi: 10.1111/j.1600-0706.2008.16607.x. [DOI] [Google Scholar]
  8. Cohen JE. Food webs and dimensionality of trophic niche space. Proc Natl Acad Sci USA. 1977;74:4533–4536. doi: 10.1073/pnas.74.10.4533. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Cohen JE, Briand F, Newman CM. Community food webs: data and theory. Berlin, New York: Springer-Verlag; 1990. [Google Scholar]
  10. Cohen JE, Luczak T, Newman CM, Zhou ZM. Stochastic structure and nonlinear dynamics of food webs—qualitative stability in a Lotka Volterra cascade model. Proc R Soc Lond B Biol Sci. 1990;240:607–627. doi: 10.1098/rspb.1990.0055. [DOI] [Google Scholar]
  11. Cohen JE, Pimm SL, Yodzis P, Saldana J. Body sizes of animal predators and animal prey in food webs. J Anim Ecol. 1993;62:67–78. doi: 10.2307/5483. [DOI] [Google Scholar]
  12. Dunne JA. The network structure of food webs. In: Pascual M, Dunne JA, editors. Ecological networks: linking structure to dynamics in food webs. New York: Oxford University Press; 2006. pp. 27–86. [Google Scholar]
  13. Dunne JA, Williams RJ, Martinez ND. Food-web structure and network theory: the role of connectance and size. Proc Natl Acad Sci USA. 2002;99:12917–12922. doi: 10.1073/pnas.192407699. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Dunne JA, Williams RJ, Martinez ND. Network structure and robustness of marine food webs. Mar Ecol Prog Ser. 2004;273:291–302. doi: 10.3354/meps273291. [DOI] [Google Scholar]
  15. Fischer J, Lindenmayer DB. Treating the nestedness temperature calculator as a “black box” can lead to false conclusions. Oikos. 2002;99:193–199. doi: 10.1034/j.1600-0706.2002.990121.x. [DOI] [Google Scholar]
  16. Huxham M, Raffaelli D. Parasites and food-web patterns. J Anim Ecol. 1995;64:168–176. doi: 10.2307/5752. [DOI] [Google Scholar]
  17. Huxham M, Beaney S, Raffaelli DG. Do parasites reduce the chances of triangulation in a real food web? Oikos. 1996;76:284–300. doi: 10.2307/3546201. [DOI] [Google Scholar]
  18. Kuris AM, Hechinger RF, Shaw JC, Whitney KL, Aguirre-Macedo L, Boch CA, Dobson AP, Dunham EJ, Fredensborg BL, Huspeni TC, Lorda J, Mababa L, Mancini FT, Mora AB, Pickering M, Talhouk NL, Torchin ME, Lafferty KD. Ecosystem energetic implications of parasite and free-living biomass in three estuaries. Nature. 2008;454:515–518. doi: 10.1038/nature06970. [DOI] [PubMed] [Google Scholar]
  19. Lafferty KD, Kuris AM (2002) Trophic strategies, animal diversity and body size. Trends in Ecology & Evolution, 17, PII S0169-5347(02)02615-0.
  20. Lafferty KD, Dobson AP, Kuris AM. Parasites dominate food web links. Proc Natl Acad Sci USA. 2006;103:11211–11216. doi: 10.1073/pnas.0604755103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Lafferty KD, Hechinger RF, Shaw JC, Whitney K, Kuris A. Food webs and parasites in a salt marsh ecosystem. In: Collinge SK, Ray C, editors. Disease ecology: community structure and pathogen dynamics. Oxford; New York: Oxford University Press; 2006. pp. 119–134. [Google Scholar]
  22. Lafferty KD, Allesina S, Arim M, Briggs CJ, De Leo G, Dobson AP, Dunne JA, Johnson PTJ, Kuris AM, Marcogliese DJ, Martinez ND, Memmott J, Marquet PA, McLaughlin JP, Mordecai EA, Pascual M, Poulin R, Thieltges DW. Parasites in food webs: the ultimate missing links. Ecol Lett. 2008;11:533–546. doi: 10.1111/j.1461-0248.2008.01174.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Leaper R, Huxham M. Size constraints in a real food web: predator, parasite and prey body-size relationships. Oikos. 2002;99:443–456. doi: 10.1034/j.1600-0706.2002.10888.x. [DOI] [Google Scholar]
  24. Marcogliese DJ, Cone DK. Food webs: a plea for parasites. Trends Ecol Evol. 1997;12:320–325. doi: 10.1016/S0169-5347(97)01080-X. [DOI] [PubMed] [Google Scholar]
  25. Martinez ND, Hawkins BA, Dawah HA, Feifarek BP. Effects of sampling effort on characterization of food-web structure. Ecology. 1999;80:1044–1055. doi: 10.1890/0012-9658(1999)080[1044:EOSEOC]2.0.CO;2. [DOI] [Google Scholar]
  26. Petchey OL, Beckerman AP, Riede JO, Warren PH. Size, foraging, and food web structure. Proc Natl Acad Sci USA. 2008;105:4191–4196. doi: 10.1073/pnas.0710672105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Pimm SL, Lawton JH, Cohen JE. Food web patterns and their consequences. Nature. 1991;350:669–674. doi: 10.1038/350669a0. [DOI] [Google Scholar]
  28. Shen-Orr SS, Milo R, Mangan S, Alon U. Network motifs in the transcriptional regulation network of Escherichia coli. Nat Genet. 2002;31:64–68. doi: 10.1038/ng881. [DOI] [PubMed] [Google Scholar]
  29. Stouffer DB, Camacho J, Jiang W, Amaral LAN. Evidence for the existence of a robust pattern of prey selection in food webs. Proc R Soc B-Biol Sci. 2007;274:1931–1940. doi: 10.1098/rspb.2007.0571. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Srinivasan UT, Dunne JA, Harte J, Martinez ND. Response of complex food webs to realistic extinction sequences. Ecology. 2007;88:671–682. doi: 10.1890/06-0971. [DOI] [PubMed] [Google Scholar]
  31. Thompson RM, Mouritsen KN, Poulin R. Importance of parasites and their life cycle characteristics in determining the structure of a large marine food web. J Anim Ecol. 2005;74:77–85. doi: 10.1111/j.1365-2656.2004.00899.x. [DOI] [Google Scholar]
  32. Warren PH, Lawton JH. Invertebrate predator–prey body size relationships—an explanation for upper-triangular food webs and patterns in food web structure. Oecologia. 1987;74:231–235. doi: 10.1007/BF00379364. [DOI] [PubMed] [Google Scholar]
  33. Williams RJ, Martinez ND. Simple rules yield complex food webs. Nature. 2000;404:180–183. doi: 10.1038/35006555. [DOI] [PubMed] [Google Scholar]
  34. Williams RJ, Martinez ND. Stabilization of chaotic and non-permanent food-web dynamics. Eur Phys J B. 2004;38:297–303. doi: 10.1140/epjb/e2004-00122-1. [DOI] [Google Scholar]

Articles from Theoretical Ecology are provided here courtesy of Springer

RESOURCES