A “Fuzzy”-Logic Language for Encoding Multiple Physical Traits in Biomolecules

Abstract

To carry out their activities, biological macromolecules balance different physical traits, such as stability, interaction affinity, and selectivity. How such often opposing traits are encoded in a macromolecular system is critical to our understanding of evolutionary processes and ability to design new molecules with desired functions. We present a framework for constraining design simulations to balance different physical characteristics. Each trait is represented by the equilibrium fractional occupancy of the desired state relative to its alternatives, ranging from none to full occupancy, and the different traits are combined using Boolean operators to effect a “fuzzy”-logic language for encoding any combination of traits. In another paper, we presented a new combinatorial backbone design algorithm AbDesign where the fuzzy-logic framework was used to optimize protein backbones and sequences for both stability and binding affinity in antibody-design simulation. We now extend this framework and find that fuzzy-logic design simulations reproduce sequence and structure design principles seen in nature to underlie exquisite specificity on the one hand and multispecificity on the other hand. The fuzzy-logic language is broadly applicable and could help define the space of tolerated and beneficial mutations in natural biomolecular systems and design artificial molecules that encode complex characteristics.

Graphical abstract

Highlights

• •Complex combinations of physical constraints shape the evolution of biomolecules.
• •An analytical system based on equilibrium thermodynamics and fuzzy logic is proposed to embody these constraints.
• •Computational design simulations subject to fuzzy-logic design recapitulate elements observed in natural proteins.
• •This design language can be used to analyze natural biomolecular systems and design new ones exhibiting complex traits.

Introduction

The physical properties of biological macromolecules are subject to evolutionary selection to improve organism fitness. In all cases, more than one biomolecular property is under selection, and complex tradeoffs between competing traits often constrain the evolutionary optimization process. As a very general example, all enzymes need to fold into stable three-dimensional structures in order to function. Therefore, all enzyme sequences, regardless of their functional class, encode favorable free-energy changes for folding [1], [2], [3], [4], as well as for their catalytic function, which itself presents a complex tradeoff among substrate, transition state, and product binding affinities [5]. Stability, selectivity, and higher catalytic efficiency are often opposing objectives in the selection of biomolecules, such as proteins or RNAs. Thus, mutations that improve stability often come at the price of reduced binding affinity [6] and catalytic efficiency [7], [8], [9], [10], [11], [12] and vice versa [13]. Biomolecular specificity, where an enzyme or receptor recognizes a set of substrates or ligands while excluding noncognate molecules of similar structure, is often encoded by features, including sequence and backbone changes, that destabilize undesirable contacts even at the expense of lower affinity or catalytic efficiency for the desired partners [14], [15]. Conversely, multispecific enzymes and receptors exhibit similar affinities for a range of ligands rather than the highest possible affinity for one [16]. These and many other examples demonstrate the universal importance of encoding multiple constraints and tradeoffs for understanding and engineering biomolecular systems [15].

By controlling all inputs into the process, computational protein design could provide a way to rigorously formulate and test our understanding of the physical constraints that shape biological molecules and particularly of tradeoffs between these constraints [17]. To date, however, most design strategies explicitly maximized one desired physical property through a strategy broadly known as positive design [18], where the sequence and structure are optimized to lower the energy of the target state. Positive design strategies have led, among other applications, to the design and experimental validation of thermostabilized protein variants [19], [20], a highly thermostable novel protein fold [21], idealized natural folds [22], enzymes [23], [24], and protein binders [25], [26], [27], [28]. However, the strategy of maximizing molecular traits stands to reason when only one molecular trait, such as stability, is optimized [19], [20], [21], [22] or when molecular traits do not tradeoff, that is, come at the expense of one another. When tradeoffs apply, maximizing any subset of properties can have the undesired consequence of disfavoring sequences that could simultaneously optimize all desired traits, at least to sufficiency [29].

Computational design methods that explicitly encode multiple constraints have been suggested to design and analyze specificity and multispecificity. These methods consider several different states for the designed molecule in a strategy broadly known as multistate design. A particularly influential concept has been to maximize the energy gap between the target (positive) state and undesired (negative) states to generate pairs of molecules that interact more favorably with one another than with homologous natural partners [30], [31], [32]. Conversely, multispecificity has been analyzed by computationally optimizing the sum of energies computed for complexes formed between a hub protein and its ligands, rather than maximizing the binding energy between any particular pair [33]. Recent progress in de novo binder design relied on optimizing the designed binders' rigidity at the price of losing favorable contacts with the target molecule, thus encoding some elements of the biomolecular tradeoff [34], [35], [36], [37], [38]. While these strategies share in common the concept of encoding multiple physical traits and tradeoffs between them, they use fundamentally different analytical frameworks and heuristics, each tailored to the particular design objective under consideration.

Here, we develop a general framework for optimizing biomolecular systems operating under conditions where tradeoffs emerge. Our framework is based on equilibrium-thermodynamics principles and is supported by recent observations on the natural and laboratory evolution of biomolecules. In another paper, we used this new framework to encode both stability and binding in the design of antibody binders (Lapidoth et al., unpublished results). Here, we develop the theoretical grounds for this framework, generalize it to more complex relationships between physical traits (including tradeoffs between constraints), and subject it to two classic tests of multiconstrained design: the design of protein-binding specificity and multispecificity. We find that designed complexes qualitatively recapitulate the energy and structure features observed in their natural counterparts.

Results

Quantifying physical traits using fractional occupancies

We consider cases where evolutionary selection operates on molecular properties that are under chemical equilibrium such as folding, binding, or conformational changes. Most generally, we can describe these properties as an equilibrium between two states, A and B, where one state, say B, exhibits the desirable molecular function and thereby promotes “fitness”. For example, A and B could represent, respectively, the unfolded and folded states of a protein or an RNA molecule, the unbound and bound states of a receptor-ligand complex, the inactive conformation relative to the active conformations of an enzyme, and so on.

The equilibrium, A ⇌ B, is characterized by an equilibrium constant

$$K_{\mathrm{eq}}={\mathrm{e}}^{-\Delta G/RT}$$ (1)

where ΔG is the free-energy difference between the two states, R is the gas constant, and T is the absolute temperature. Evolution acts on this equilibrium by favoring sequences that increase the fractional occupancy of B, the desirable state. The fractional occupancy, f, is defined as

$$f=\frac{\left[\mathrm{B}\right]}{\left[\mathrm{A}\right]+\left[\mathrm{B}\right]}$$ (2)

where [A] and [B] are the concentrations of the two states at chemical equilibrium [39]. Combining Eqs. (1), (2) and the thermodynamics definition

$$K_{\mathrm{eq}}=\frac{\left[\mathrm{B}\right]}{\left[\mathrm{A}\right]}$$ (3)

provides that the fractional occupancy of the desirable molecular state as a function of free-energy change of the process exhibits a sigmoidal relationship:

$$f=\frac{1}{1+{\mathrm{e}}^{\Delta G/RT}}$$ (4)

More generally, we rephrase Eq. (4) by adding an offset free-energy term ΔG_offset, at which the target state is half occupied (i.e., where [A] = [B]; Fig. 1a):

$$f=\frac{1}{1+{\mathrm{e}}^{\left(\Delta G-\Delta G_{\mathrm{offset}}\right)/RT}}$$ (5)

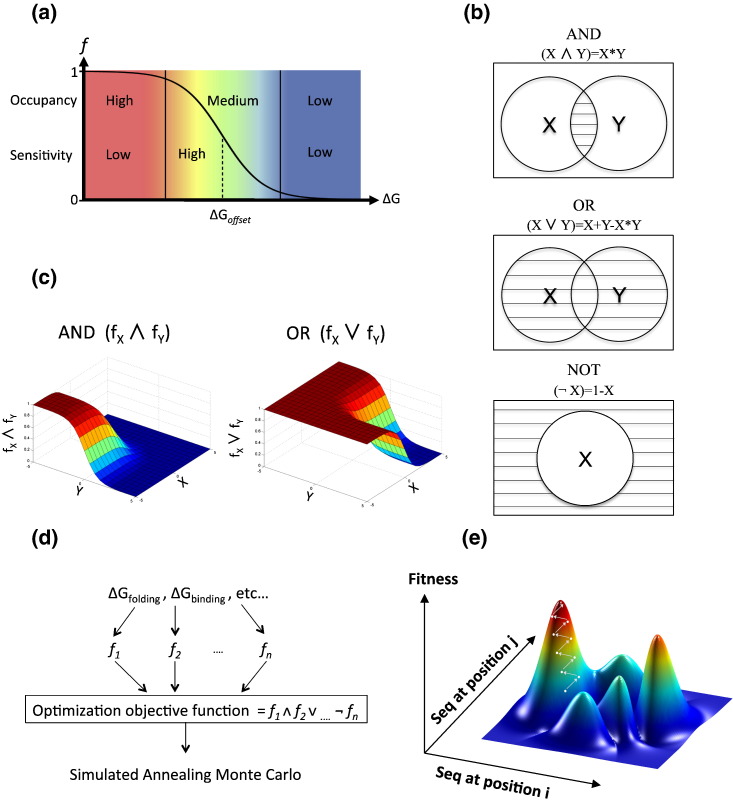
Fig. 1.

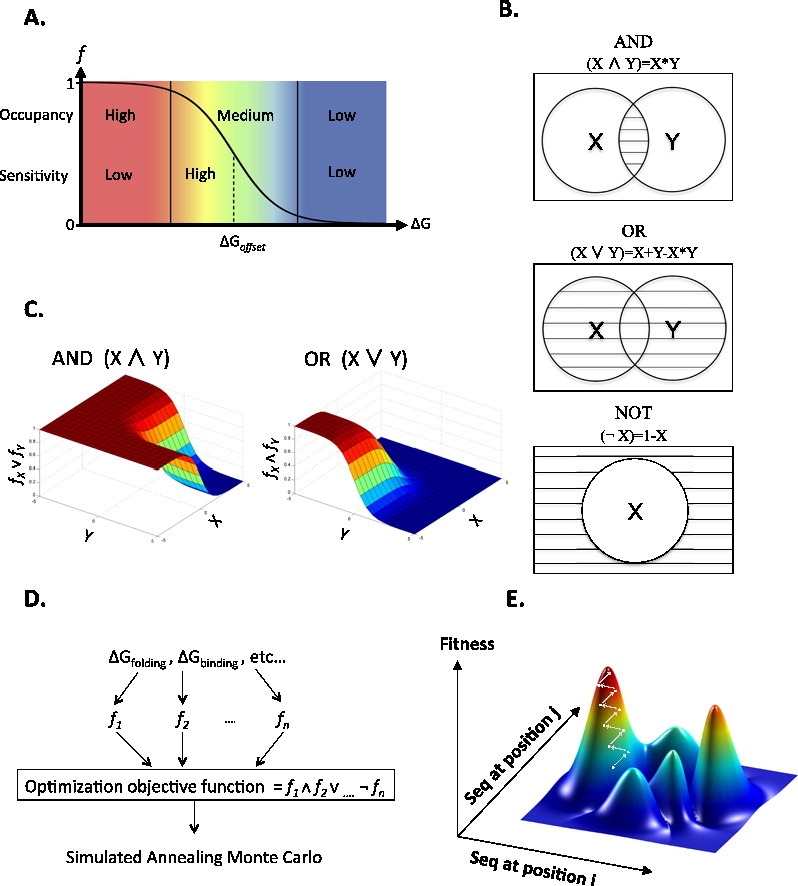
Overview of the design algorithm. (a) Fractional occupancy shows a sigmoidal dependence on ∆G, the equilibrium free-energy change [Eq. (4)]. ∆G_offset is the free-energy offset at which the target state, for example, the bound receptor, is half occupied. The plot illustrates three regimes: left, high occupancy (95–100%) and low sensitivity, where the fractional occupancy remains largely unaffected by mutations that induce moderate changes in ∆G; middle, medium occupancy (5–95%) and high sensitivity, where there is significant change in the fractional occupancy due to changes in ∆G; and right, low occupancy (0–5%) and low sensitivity, where the fractional occupancy is negligible and remains thus despite moderate improvements in ∆G. (b) Venn diagram graphically demonstrates the Boolean operators AND, OR, and NOT. AND and OR gates act on two states X and Y, whereas the NOT gate acts on one state, X. All states are drawn as circles and the selected area is marked in stripes. (c) Boolean operators (NOT, AND, and OR) are used to integrate the variables into an optimization objective function. By defining the three fundamental logical operators, we can formulate arguments encoding combinations of physical properties, including where properties tradeoff with one another. (d) The design flow chart exemplified for designing for stability and ligand binding, in four steps: first, the relevant properties of the system (stability of individual components and affinities between components) are defined. Second, for each property, the steepness and offset are defined and the sigmoidal function is set [Eq. (6)]. Third, the objective function is calculated by integrating the sigmoidal functions using Boolean operators. Fourth, the objective function is used by simulated annealing Monte Carlo sequence optimization. (e) Fitness is a complex function of biomolecular properties (such as binding, stability, etc.) exemplified here as a function of sequence exchanges at two positions only; in reality, fitness is a function in n-dimensional space, where n is the number of mutable protein or RNA residues. The landscape's ruggedness is the outcome of the nonadditive fitness effects of mutations, the limited choice of natural amino acids, and of tradeoffs between different molecular properties.

ΔG_offset reflects the energy requirements of a particular characteristic, namely, how favorable should the optimized trait's energy ΔG be to achieve a target occupancy (e.g., to obtain f > 0.5, ΔG must be smaller than ΔG_offset). For example, the receptor-ligand binding energy required to achieve half-maximal receptor occupancy depends on the ligand concentration; the lower the ligand concentration is, the higher ΔG_offset is, as well as the more favorable the required binding affinity must be to achieve a certain degree of occupancy [39], [40]. Equation (5) asymptotically approaches 1 at negative ΔG values and 0 at positive ΔG values with an inflection point at ΔG = ΔG_offset (Fig. 1a).

We further rephrase the sigmoidal relationship of Eq. (5) as:

$$f_x=\frac{1}{1+{\mathrm{e}}^{\left(x-o\right)s}}$$ (6)

where x and o are ΔG and ΔG_offset of Eq. (5), respectively, and s determines the slope of the sigmoidal response to free-energy changes around the inflection point.

Equation (6) generalizes the chemical equilibrium description of the fractional occupancy into the concept of biomolecular “fitness”, reflecting the molecule's activity or functionality within an organism. The actual functionality of a biomolecule could have a sharper or a more attenuated dependence on the equilibrium free-energy change than Eq. (5) dictates. As an example, a molecule that has irreversible effects on cell fate, such as a nuclease, a protease, or a gene master regulator, may have large biological effects even at low fractional occupancies; the biomolecular output in this scenario is reproduced by low o and high s values. Conversely, two competing effector molecules, which bind overlapping sites on their target molecule, may only exert their biological effects at high occupancy [41] and would be modeled with high o and low s values (guidelines for determining o and s values are provided in the supplement). For simplicity, in what follows, we refer to fractional occupancy and biological “fitness” interchangeably, noting that both concepts could be modeled within the suggested framework.

The fractional occupancy of the desired state is certainly but one of many factors affecting the molecule's contribution to organism fitness, and expression levels, half-lives, post-translational modifications, and compartmentalization, play important complementary roles [42], [43], [44], [45]. The sigmoidal relationship of Eqs. (5), (6) is nevertheless a fundamental property of biomolecular systems, which can quantitatively describe numerous observations in natural and laboratory evolution, including the response to mutations [46]. Consider a concrete example of protein stability in mesophilic organisms. Many proteins have ΔG_folding values of − 5 kcal/mol [47] meaning that, under standard conditions, more than 99.97% of the protein is in its folded state [Eq. (4)]. If protein misfolding [10], quality control [48], expression levels, post-translational modifications, and other extrinsic factors [49] are held constant, a mutation that decreases ΔG_folding by 2 kcal/mol would increase the folded fraction by less than 0.03% and would not be subject to strong evolutionary selection; thus, the high fractional occupancy regime exhibits relatively low sensitivity to mutation (Fig. 1a). By contrast, a protein with ΔG_folding of − 1 kcal/mol is 84% folded, and a mutation that decreases ΔG_folding by 2 kcal/mol would increase the folded fraction by an appreciable 13% and would be strongly favored by selection, leading to high sensitivity to mutation around the sigmoid inflection point (Fig. 1a). Protein engineering is routinely used to successfully thermostabilize natural proteins [19], [20], [50], [51], demonstrating that protein stability plateaus in evolution and that natural molecules can be readily engineered for higher stability. For other examples where physical traits plateau in evolution, see Supplemental Data.

A fuzzy-logic model for the selection of biomolecules with multiple physical traits

From the considerations mentioned above, we infer that a general model for representing multiple constraints selecting a biomolecule should exhibit two properties: first, a biomolecule's contribution to organism fitness is not only a function of the free-energy change associated with a physical trait but also a function of the fractional occupancy of the desirable state (Fig. 1a); and second, the constraints operating on the evolution of intrinsic physical traits are a complex, nonadditive function of the relevant target-state occupancies. To model the combination of constraints that shape a biomolecule through evolution, we borrow a concept from “fuzzy” or many-valued logic systems [52], [53]. Fuzzy-logic formulations have been applied to produce graded rather than all-or-none responses to changes in input. It extends conventional Boolean logic by proposing that truth (1) and falsehood (0) are only extremes in a continuum of evaluations (0–1) with states that have intermediate values of truth and falsehood. The combination of molecular constraints, based on the fractional occupancies described above, lends itself naturally to fuzzy-logic treatment, in which the fractional occupancy f [Eq. (6)] of any energy term is treated as a Boolean variable and the standard Boolean operators (NOT, AND, and OR) are used to combine the variables into an optimization objective function (Fig. 1b): for any two target states (e.g., folded molecule, bound receptor, etc.), the individual fractional occupancies, f_x and f_y, are computed using Eq. (6). We thus define, as in Boolean algebra, ¬f_x = 1 − f_x(NOT f_x), f_x∧f_y = f_x*f_y (f_x AND f_y), and f_x∨f_y = f_x + f_y − f_x*f_y (f_x OR f_y) (Fig. 1b). In fuzzy logic, values approaching 1 satisfy the constraints embodied in the argument and values approaching 0 fail to satisfy them (Fig. 1c). By defining the three fundamental logical operators (Boolean NOT, AND, and OR), any argument comprising any number of constraints relating to energy evaluations of biomolecular states can be formulated in a statement that resembles natural language. The fuzzy-logic arguments then serve as objective functions (Fig. 1d) in stochastic sequence optimization in search for sequences that best conform to the encoded constraints (Fig. 1e). As in a natural language, the objective functions are an approximate model or representation of reality, and a completely accurate description of the fitness landscape, accounting for all of the constraints bearing on the biomolecular system, is impossible.

Despite this caveat, the fuzzy-logic system provides a framework for testing our understanding of the main constraints observed in biomolecular systems by integrating the fractional occupancies of Eq. (6) for each of the optimized energy criteria (e.g., binding and stability) using Boolean operators (Fig. 1c). In the supplement, we demonstrate that, under certain conditions, multistate design [30], which optimizes the energy gap between a target state and its competitors, describes a special case of the sigmoid relationship, assuming one target and several off-target states. Optimizing the energy gap suffers from a weakness, though, since mutations are favored even if they lead to the unwanted destabilization of the designed molecule or of the desired complex. In the context of the discussion mentioned above, energy-gap optimization, when applied with no additional constraints, fails to take into account that biomolecules need to stably fold in order to function correctly. Indeed, previous studies augmented energy-gap optimization with cutoffs that prevent energy terms from deteriorating beyond a certain limit [54], [55]. Setting strict cutoffs on energy values is, however, more likely to funnel sampling to regions of sequence space where physical properties are on the border between optimality and suboptimality, potentially resulting in nonfunctional molecules. Using sigmoidal constraints and tradeoffs rather than strict cutoffs directs the search toward compromises that raise the chances of satisfying each of the individual constraints at least to sufficiency.

The fuzzy-logic design framework also allows framing constraints other than of the energy gap between states. For instance, several successful binder design studies selected sequences based on whether they encode both active-site side-chain rigidity and high-affinity binding [34], [35], [36], [37], [38]. Applying the fuzzy-logic strategy, we can explicitly optimize these properties during design simulations using the objective function:

$$\mathrm{O}=\mathrm{B}\left(a,b\right)\wedge \mathrm{S}\left(a\right)$$ (7)

(Fig. 1c), where a and b are the designed protein and the target molecule, respectively, and B and S are the sigmoidal functions [Eq. (6)] for binding energy and stability, respectively. Indeed, in another paper, we demonstrated that, by optimizing Eq. (7), during antibody-design simulations, one can select antibody backbone conformations and sequences that exhibit features seen in natural antibody binders, such as conserved backbone conformations, hydrogen-bonding patterns, and van der Waals packing arrangements observed both within and between antibodies and their target molecules (Lapidoth et al., unpublished results). Encouragingly, by optimizing Eq. (7), side-chain conformation stability at the designed binding surface was comparable and exceeded that observed in natural antibodies, even though, unlike previous design of function studies [37], side-chain rigidity was not explicitly used to select models. These results suggest that fuzzy-logic optimization could address some of the challenges of de novo design of function.

Here, we focus on additional uses for the fuzzy-logic framework and specifically on cases where tradeoffs between different molecular properties are prominent, such as binding specificity. We note, however, that this framework can be applied to situations where optimizing one property does not come at the expense of other properties and to situations where maximizing one trait is deleterious (as such in Ref. [29]). In the latter case, two sigmoid functions [Eq. (6)] can be applied to constrain the same physical trait, for example, S₁(a) and S₂(a), where S₁ defines the lower energy bound (with a low o parameter) and S₂ defines the upper bound (high o parameter) of the same energy criterion. The optimization objective function is then defined as:

$$\mathrm{O}={\mathrm{S}}_2\left(\mathrm{a}\right)\wedge \neg {\mathrm{S}}_1\left(\mathrm{a}\right)$$ (8)

biasing sequence search toward values intermediate between the two extremes.

Empirical tests of the fuzzy-logic design language

We subject the fuzzy-logic framework to two classic tests of computational protein design: the design of multispecificity and of orthogonal specificity. These tasks previously required different heuristics and optimization frameworks [30], [31], [32], [33], [54], [55], [56], [57], [58], [59], [60], but here we show that the fuzzy-logic language provides a unified framework for analyzing both phenomena.

Multispecificity design

As a model for multispecificity design, we select the protein human H-RAS, which has been co-crystallized with five natural partners [61], [62], [63], [64] and was previously subjected to multispecificity analysis [33]. RAS is a member of the family of small GTP-binding proteins and is involved in regulating signal-transduction processes leading to cell growth and differentiation by directly controlling multiple pathways [65], [66]. H-RAS presents special challenges to single-state design because it interacts via overlapping surfaces with several proteins, some of which have different folds and molecular functions, and because the backbone conformation of H-RAS varies when bound to its different partners [61], [62], [63], [64]; the designed H-RAS sequences must therefore be compatible with all of H-RAS's backbone conformations and encode favorable contacts with all of its partners. To demonstrate the shortcomings of single-state design, that is, design toward any one of the H-RAS-bound structures, we select for stochastic sequence optimization eight amino acid positions on the H-RAS binding surface, four in switch region I (Ile36, Glu37, Asp38, and Ser39), two in switch region II (Gln61 and Glu63), and two outside of these regions (Ile21 and Gln25). With the use of RosettaDesign (Experimental Procedures), single-state, positive-only design of H-RAS toward each of its partners separately leads to sequences that increase H-RAS stability and its binding affinity for that particular target. However, single-state design clearly violates the requirements of stability in the alternative H-RAS conformations and binding affinity for the other partners (Table S1). In some cases, the energy violations are severe [more than 10 R.e.u. (Rosetta energy units); Table S1 and Fig. 2], suggesting that optimizing H-RAS to bind any one of its partners alone increases specificity (as has been observed in other systems [67]) and protein rigidity, at the cost of binding to its other natural partners.

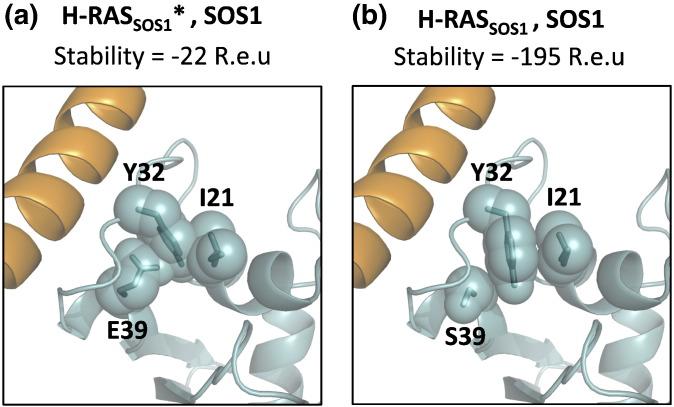
Fig. 2.

Single-state, positive-only design violates the requirement for stability in alternative conformations. The single-state designed sequence of H-RAS_PI3K (H-RAS designed to target PI3K) was threaded on H-RAS_SOS1 backbone (H-RAS in the SOS-1 bound backbone, cyan), producing the H-RAS_SOS1*,SOS1 structure (SOS1 is in orange) (a) after side-chain and rigid-body minimization. This designed sequence compromises the stability of H-RAS_SOS1 monomer (b) by + 173 R.e.u. mainly due to steric overlap among Y32, E39, and I21.

To model the multiple physical requirements on H-RAS, we use the new framework to encode energy constraints on all of the observed H-RAS backbone conformations and on binding affinities for all of its partners:

$$\begin{array}{l}\mathrm{O}=\mathbf{B}\left(\mathrm{H}‐{\mathrm{RAS}}_{\mathrm{SOS1}}\ast ,\mathrm{SOS1}\right)\mathbf{\wedge }\mathbf{B}\left(\mathrm{H}‐{\mathrm{RAS}}_{\mathrm{PI}3\mathrm{K}}\ast ,\mathrm{PI}3\mathrm{K}\right)\wedge \mathrm{B}\left(\mathrm{H}‐{\mathrm{RAS}}_{{\mathrm{B}\mathrm{R}\mathrm{Y}‐2\mathrm{R}\mathrm{B}\mathrm{D}}^{\cdot }}\ast ,\mathrm{B}\mathrm{R}\mathrm{Y}‐2\mathrm{R}\mathrm{B}\mathrm{D}\right)\mathbf{\wedge }\\ \mathbf{B}\left(\mathrm{H}‐{\mathrm{RAS}}_{\mathrm{B}\mathrm{R}\mathrm{Y}‐2\mathrm{R}\mathrm{B}\mathrm{D}}\ast ,\mathrm{B}\mathrm{R}\mathrm{Y}‐\mathrm{2}\mathrm{R}\mathrm{B}\mathrm{D}\right)\mathbf{\wedge }\mathbf{B}\left(\mathrm{H}‐{\mathrm{RAS}}_{\mathrm{R}\mathrm{a}\mathrm{l}‐\mathrm{G}\mathrm{D}\mathrm{S}}\ast ,\mathrm{R}\mathrm{a}\mathrm{l}‐\mathrm{G}\mathrm{D}\mathrm{S}\right)\mathbf{\wedge }\mathbf{B}\left(\mathrm{H}‐{\mathrm{RAS}}_{\mathrm{R}\mathrm{A}\mathrm{S}‐\mathrm{G}\mathrm{A}\mathrm{P}}\ast ,\mathrm{R}\mathrm{A}\mathrm{S}‐\mathrm{G}\mathrm{A}\mathrm{P}\right)\mathbf{\wedge }\mathbf{S}\left(\mathrm{H}‐{\mathrm{RAS}}_{\mathrm{S}\mathrm{O}\mathrm{S}1}\ast \right)\mathbf{\wedge }\mathbf{S}\\ \left(\mathrm{H}‐\mathrm{RAS}{}_{\mathrm{PI}3\mathrm{K}}\ast \right)\mathbf{\wedge }\mathbf{S}\left(\mathrm{H}‐{\mathrm{RAS}}_{\mathrm{B}\mathrm{R}\mathrm{Y}‐2\mathrm{R}\mathrm{B}\mathrm{D}}\ast \right)\mathbf{\wedge }\mathbf{S}\left(\mathrm{H}‐{\mathrm{RAS}}_{\mathrm{R}\mathrm{a}\mathrm{l}‐\mathrm{GDS}}\ast \right)\mathbf{\wedge }\mathbf{S}\left(\mathrm{H}‐{\mathrm{RAS}}_{\mathrm{RAS}‐\mathrm{GAP}}\ast \right)\end{array}$$ (9)

where O is the optimization objective function, H-RAS* is the designed H-RAS protein, and B and S are sigmoidal functions for binding and stability, respectively (see Experimental Procedures). Subscripts in Eq. (9) denote which backbone conformation is used for modeling H-RAS; thus, H-RAS_SOS1* denotes the designed H-RAS sequence modeled on the SOS1-bound backbone conformation.

Each of the functions (B and S) of Eq. (9) requires parameterization of the offset (o) and slope (s) as defined in Eq. (6). The offset and slope parameters were determined according to the guidelines in the supplement. We conduct 4000 independent design simulations starting from two single-state designed complexes as representatives of two different H-RAS-bound complexes, H-RAS,SOS1 and H-RAS,Ral-GDS, whereby the eight selected H-RAS positions are optimized to bind to each partner separately. In each simulation, the H-RAS sequence is subjected to nondeterministic simulated annealing Monte Carlo optimization with Eq. (9) serving as the optimization objective function (Fig. 1d and Experimental Procedures), and the resulting design variants are ranked according to the objective function [Eq. (9)]. In both cases, the top-ranked designs have binding affinities and stabilities similar to those computed for the natural H-RAS structures. Further, the top-ranked designs show favorable H-RAS-ligand molecular contacts as observed in the natural H-RAS (Fig. 3).

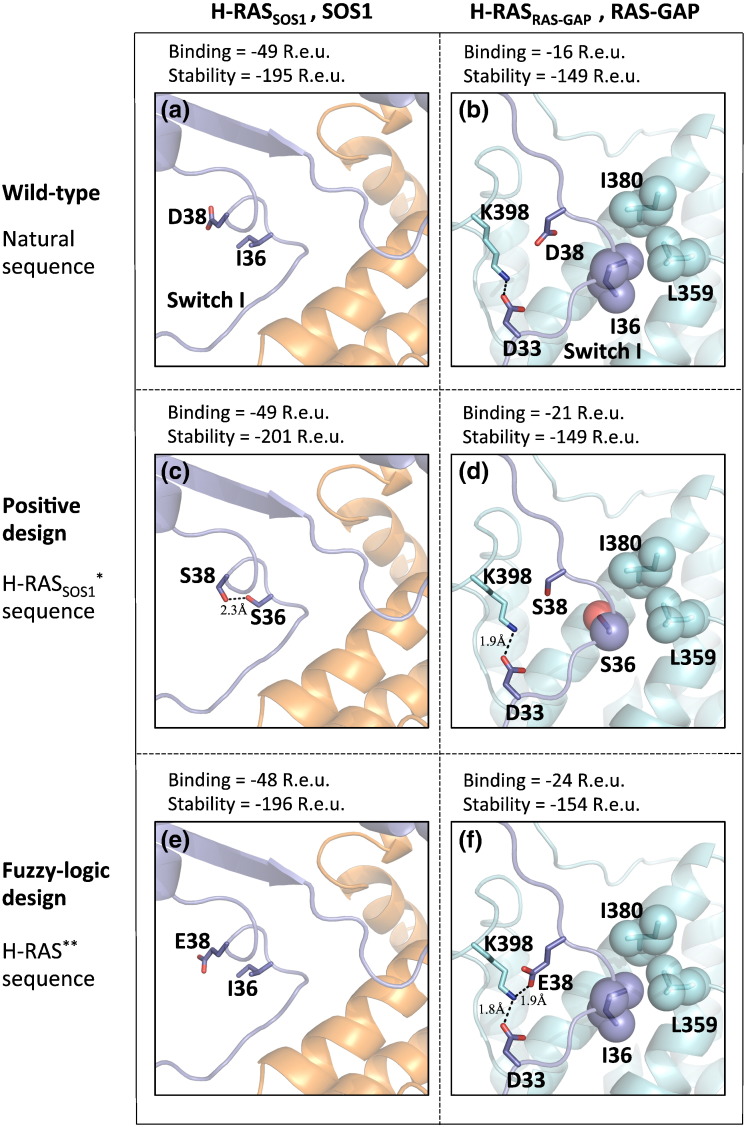
Fig. 3.

Single-state design versus fuzzy-logic design of the multispecific hub protein H-RAS. This view focuses on H-RAS switch I loop. The two H-RAS complexes presented here, H-RAS_SOS1 (a–e) and H-RAS_RAS-GAP (b–f), have different backbone conformations. Upper panel: structures of the native complexes of H-RAS_SOS1 (violet) and SOS1 (orange) complex (a) and H-RAS_RAS-GAP (violet) and RAS-GAP (cyan) complex (b), where I380, L359, and I36 form favorable van der Waals contacts and K398 and D33 form a salt bridge. Middle panel: single-state design of H-RAS_SOS1*,SOS1 complex, where D38S and I36S are introduced to form a hydrogen bond (c), and the designed sequence of H-RAS_SOS1* threaded on H-RAS_RAS-GAP backbone, where I36S packing with I380 and L359 is compromised (d). Bottom panel: fuzzy-logic design of H-RAS in complex with SOS1 (e) and with RAS-GAP (f). Position 36 was restored to Ile, which is the natural identity, while position 38 was designed to Glu, which forms a new electrostatic interaction with K398 in H-RAS_RAS-GAP*,RAS-GAP structure (f), resulting in a sequence that is similar to the wild type.

As expected, Monte Carlo sequence optimization does not converge on a single solution but rather produces a large landscape of sequences that are compatible with the constraints defined by the objective function. As the objective function of Eq. (9) encodes 10 different fractional occupancies (five each for binding and H-RAS stability), we set the threshold for favorable sequences at an objective value above 0.95¹⁰ = 0.59, equivalent to requiring roughly 95% occupancy on all the terms of Eq. (9). For the case where we started with the H-RAS-SOS1 single-state designed model, 75% of the trajectories passed this threshold yielding approximately 1400 unique sequences. Notably, none of the H-RAS sequences optimized by single-state design to bind only SOS1 (H-RAS*,SOS1) (Fig. 3 and Table S1) overlapped any of the fuzzy-logic designed sequences. Further, the objective function calculated for the single-state designed H-RAS was 0.35, well below the acceptance threshold of 0.59, indicating that this design is suboptimal with respect to the set of constraints encoded in Eq. (9). Even though the resulting sequence space is large, on a position-by-position basis, the designed H-RAS proteins converge on amino acid identities that are physicochemically similar to the natural H-RAS (Fig. 4). Further, in several trajectories, produced from simulations that started with H-RAS designed solely to bind SOS1 and optimized using Eq. (9), the natural H-RAS sequence was retrieved as is and was ranked in the top 15% of all designed sequences. Although the natural H-RAS sequence is ranked high, there are 108 unique sequences in the set that converge to similar but not identical sequences (Fig. 4) and are predicted to have superior objective function values [Eq. (9)] compared to the natural H-RAS. Inaccuracies in the energy function and in the optimization objective function could account for this result, and other H-RAS properties that were not encoded by Eq. (9) might be compromised by these nonnatural sequences; alternatively, these solutions comprise variants predicted to have comparable or better stability and binding properties relative to the natural H-RAS for the chosen partners. Thus, the use of a gradual response curve [the sigmoid of Eq. (6) and Fig. 1a], rather than all-or-none thresholds, enables ranking the optimized sequences and provides testable hypotheses for structure–function studies.

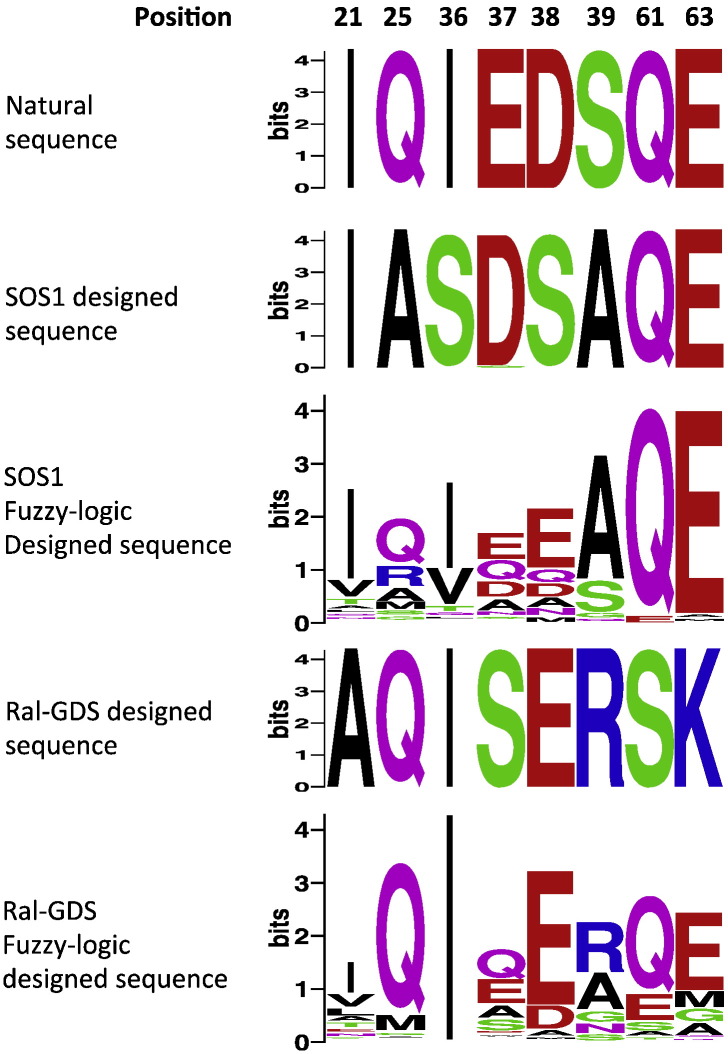
Fig. 4.

Fuzzy-logic design converges on amino acids with physicochemical properties that resemble those of the natural H-RAS. Sequence logos [68] of the natural, positive-only, and fuzzy-logic designed sequences of two structures with distinct conformations: H-RAS_SOS1 and H-RAS_Ral-GDS. All designable positions exhibit two features: (i) a different sequence is compatible with each structure after positive design and (ii) the sequences of the two converge after the design to identities physicochemically similar to those observed in the natural sequence.

Orthogonal-specificity design by combining positive and negative design constraints

The challenge in orthogonal-specificity design is generally defined as follows: starting from a natural complex of known structure, design a pair of proteins that bind as tightly as the natural complex but will bind their natural partners more weakly. Orthogonal specificity is a crucial determinant of the function of biological systems, insulating homologous signaling and metabolic pathways from one another, and has received several treatments from computational protein design [31], [32], [58], [60], [67].

To test the new design strategy in this context, we analyze two complexes from the bacterial E colicin endonuclease-immunity family, endonuclease-immunity 2 (E2,Im2) and endonuclease-immunity 9 (E9,Im9) [69]. The two pairs share the same overall folds, binding mode, and an identical set of residues at the core of the binding site (the interaction hotspot). There are, however, significant differences in the identities of interface residues outside the core. Additionally, one of the interfacial loops on the immunity protein differs in conformation, resulting in a 5.6° reorientation of the partners in one complex relative to the other [70]. The net effect of these molecular differences is that both cognate pairs are highly specific and bind with femtomolar dissociation constants, while the noncognate pairs interact with 6–7 orders of magnitude lower affinities [71], [72]. This colicin family has been subjected previously to a specialized heuristic for specificity design producing designed partners that bound one another 2–3 orders of magnitude more tightly than their interactions with the noncognate natural partners and with 2–4 orders of magnitude lower affinity than observed for natural colicin pairs [56], [58].

Here, we show that subjecting the E9-Im9 naturally occurring high-affinity complex to the orthogonal-specificity design objective function defined below reproduces the required energy and structure characteristics seen in natural high-specificity pairs and in more specialized computational specificity-design heuristics:

$$\mathrm{O}=\mathbf{B}\left(\mathrm{E}9\ast ,\mathrm{I}\mathrm{m}9\ast \right)\wedge \mathbf{S}\left(\mathrm{E}9\ast \right)\wedge \mathbf{S}\left(\mathrm{I}\mathrm{m}9\ast \right)\wedge \neg \mathbf{B}\left(\mathrm{E}9\ast ,\mathrm{I}\mathrm{m}9\right)\wedge \neg \mathbf{B}\left(\mathrm{E}9,\mathrm{I}\mathrm{m}9\ast \right)$$ (10)

where B and S are the binding and stability fractional occupancies determined from Eq. (6), E9 and Im9 are the natural sequences, and E9* and Im9* are the designed sequences. The first three terms in Eq. (10) ensure that the designed complex affinity and the designed monomer stabilities are maintained close to their levels in the natural complex, while the last two terms disfavor cross-binding of each of the designed partners to its original natural partner. Thus, Eq. (10) demonstrates the flexibility and expressiveness of the fuzzy-logic framework, which can be readily extended to situations where some target states are disfavored.

The colicin pairs 2 and 9 present a unique case, where molecular structures for two cognate pairs [70], [73] and one of the noncognate pairs (E9, Im2) [74] are available. These structures allow us to estimate the computed energies that are required for establishing high-affinity cognate binding and medium-affinity noncognate binding in our simulations. The two cognate pairs (E2,Im2 and E9,Im9) have calculated binding affinities below − 32 R.e.u., whereas the noncognate pair (E9,Im2) has calculated binding affinity of − 27 R.e.u. We therefore set the offset value for noncognate binding [o in Eq. (6)] to − 27 R.e.u., meaning that the fractional occupancy value [Eq. (6)] for a designed noncognate pair with computed binding energy as the natural noncognate E9,Im2 pair would be one-half (all other parameters are provided in Supplemental Experimental Procedures).

Starting from the molecular structure of the E9-Im9 complex [73], we select nine positions at the binding surfaces of the immunity and endonuclease pair that were experimentally shown to contribute to specificity [four on the immunity (Thr27, Leu33, Val34, Thr38) and five on the endonuclease (Ser77, Ser78, Tyr83, Lys97, Val98)] [71]. These positions are subjected to stochastic sequence optimization using the objective function defined in Eq. (10). Unlike the specialized schemes used previously [58], we employ the same simulated annealing Monte Carlo sampling method used above for the calculation of multispecificity. The difference between the H-RAS multispecificity implementation above and colicin orthogonal-specificity design here is restricted solely to the objective function [Eqs. (9), (10), respectively].

As in the design of multispecificity mentioned above, orthogonal-specificity design does not converge on a single solution, but rather it produces hundreds of sequences that meet the threshold values for individual partner stabilities, high cognate binding affinity, and low affinities toward the respective natural (noncognate) partners (Fig. 5). In fact, for the top designs, the resulting energy gap between the designed cognate and designed noncognate pairs (> 10 R.e.u.; Fig. 5) is calculated to be larger than that computed for the natural pairs. The molecular details of the designed complexes reproduce the hallmarks of high-affinity and high-specificity complexes, as seen in natural colicin complexes [74], including intricate van der Waals packing and hydrogen-bonding networks in the designed cognate complexes (E9*,Im9*). Conversely, the modeled noncognate complexes (E9*,Im9 and E9,Im9*) exhibit electrostatic and steric frustration (Fig. 5). Even though we use only a single design heuristic and objective function, different trajectories result in quite different solutions to encoding specificity; these include, in the two cases highlighted in Fig. 5, one that employs knobs-into-holes to introduce steric overlaps in noncognate pairs and another that uses electrostatic frustration to achieve the same goal. Fuzzy-logic design can therefore define several physicochemically distinct ways of achieving the same desired function. We note, however, that, in the natural colicin family, specificity is also encoded by backbone conformation changes and perturbations to the rigid-body orientations [74] and that recapitulating natural sequences in this family likely requires modeling these degrees of freedom. The objective function defined in Eq. (10) can indeed be used to guide an optimization algorithm that samples sequence, as well as backbone and rigid-body conformations (Lapidoth et al., unpublished results) [56], [75].

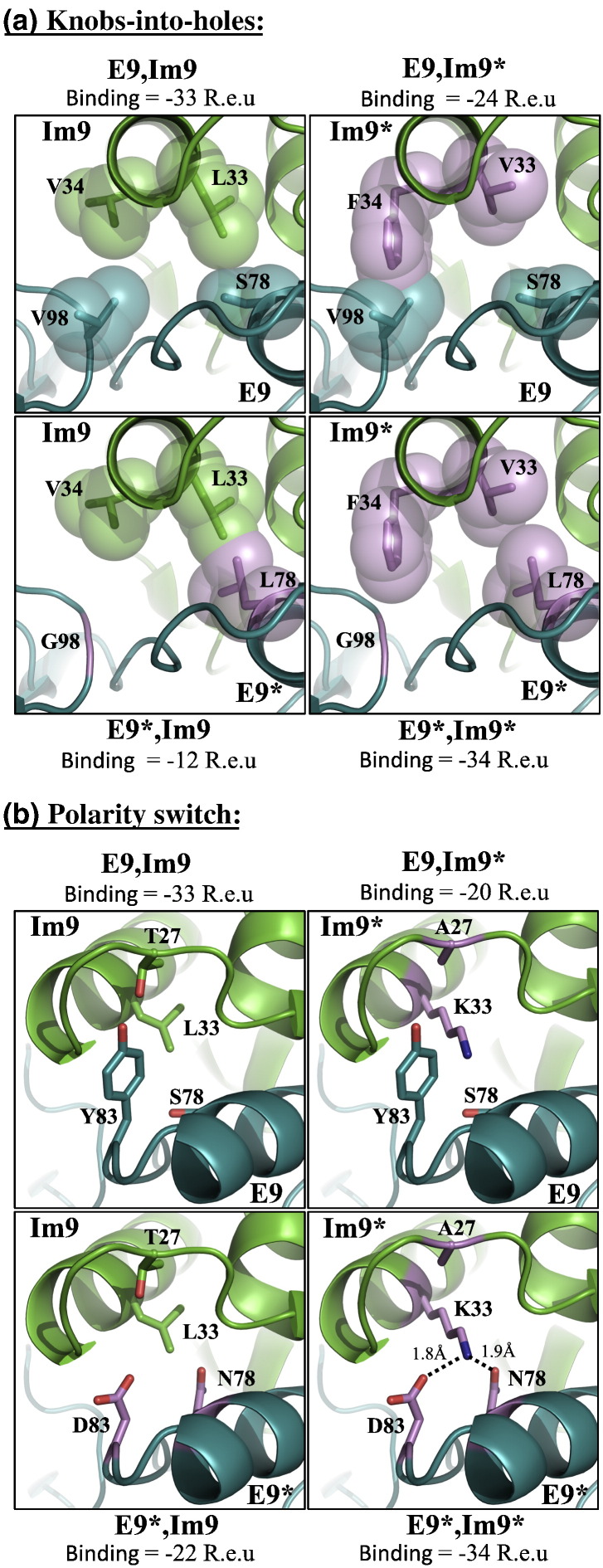
Fig. 5.

Two designed specificity switches in the colicin endonuclease-immunity pair E9-Im9. Interactions with binding energy greater than or equal to − 27 R.e.u. are noncognate (see Results), while interactions with binding energy less than or equal to − 33 are expected to be as favorable as the natural pairs. Im9 and E9 are shown in green and deep-teal cartoons, respectively. The mutated residues in the design pair are shown in violet. (a) A design pair in which specificity is encoded by knobs-into-holes features. In the natural pair (upper left panel), L33 and V34 of Im9 pack against S78 and V98 of E9, respectively. In the design pair (lower right panel), L33V mutation introduces a smaller side chain, and the complementary S78L mutation maintains packing density as in the natural pair. Similarly, V34F introduces a large side-chain in the designed Im9* while V98G removes a side-chain. In the designed noncognate pair E9,Im9*, V34F forms a steric overlap with E9's V98, thus destabilizing the bound state. Similarly, in the designed noncognate pair E9*, Im9 mutation S78L forms a steric overlap with Im9's L33. (b) A design pair, in which specificity is encoded through a switch in polarity features. The natural interaction is mainly based on hydrophobic packing. In the designed pair (bottom right), K33 forms hydrogen bonds with D83 and N78, as well as a salt bridge with D83. In the designed noncognate pairs, the hydrogen bonds are not formed and polar residues pack against hydrophobic ones leading to electrostatic frustration similar to the observation in the natural noncognate pair [74]. Also, there are steric overlaps in the designed noncognate pairs that further destabilize the bound state. In E9*, Im9's (bottom left) D83 and N78 pack against the hydrophobic L33. A steric overlap is formed between L33 and N78. In the design noncognate pair E9,Im9*, K33 packs against S78 and Y83, resulting in steric overlap.

Discussion

The evolution of a biological macromolecule is subject to selection pressures that bear on its physical properties, such as stability, binding affinity, specificity, and activity. We presented a framework for encoding each physical constraint based on the equilibrium-thermodynamics concept of fractional occupancy of the target state within an ensemble of states. In the example of H-RAS, multispecificity design specified a large number of physical properties, overall encoding 10 different constraints relating to both stability and binding affinity. These 10 constraints were combined using Boolean operators to recapitulate sequences and conformations observed in nature, including the natural H-RAS sequence. By changing the objective function only and without changing the underlying optimization algorithm, we can also model competition with alternative states, as seen in specificity-switch modeling. The result is a general language for encoding different physical traits, including ones that exhibit tradeoffs with one another, as logical expressions that can be translated into a numerical objective function for optimization. In reality, the tradeoffs between different physical properties extend beyond purely thermodynamics properties and also involve kinetics [15], [76] and, specifically, association and dissociation rate constants. Where structural data are available on kinetic intermediates and parameters, kinetic constraints could also be modeled using the same framework, as could other important properties such as selectivity. We expect the fuzzy-logic design scheme to work well in cases where large structural differences between the alternative states exist and where the desired energy gaps between target and off-target states are large, as in the case studies selected here. Encoding fine discrimination between structurally similar states or small energy gaps may require refined energy functions.

Not all properties of biological systems are explained within the context of optimality and adaptation [77]; however, the physical constraints shaping biomolecules and biomolecular structures are largely known. The computational framework suggested here can be useful for a quantitative analysis of these constraints and for the design of novel biomolecules with desired functions. The design of novel or rewired signaling and metabolic networks [78], for instance, inevitably invokes complex tradeoffs between different molecules and their properties, and these can also be encoded within the framework presented here. Recent advances in the application of deep sequencing to libraries of natural protein variants [79], [80] and of in vitro mutational repertoires selected for complex combinations of physical features, including stability, binding, and specificity profiles [34], [36], [81], [82], [83] are generating datasets comprising thousands of mutants that relate sequence changes to function at unprecedented resolution and coverage [84]. The fuzzy-logic design framework described here can be used to test hypotheses relating sequence, structure, and energetics to function, as well as in turn to fitness. Interpreting these empirical data through fuzzy-logic design may ultimately lead to a better understanding and ability to manipulate the multiple physical properties and tradeoffs that shape the evolution of biomolecular functions. More broadly, tradeoffs in biology extend beyond the molecular level to the evolution of organism phenotypes [85]; the use of sigmoid functions to represent the levels at which individual traits reach sufficiency and fuzzy logic to integrate these into optimization objective functions that resemble natural language could thus be generalized beyond the molecular level explored here.

Experimental Procedures

Sequence optimization

For both multispecificity and orthogonal-specificity design, we start from wild-type complexes of solved molecular structure, relaxed using procedures described in Supplemental Experimental Procedures, and compute the binding and stability energies of each component in the natural system. For each design objective, the o and s parameters of the fractional occupancy equation [Eq. (6)] are computed to reflect the desired energies of each modeled state (see Results and Supplemental Experimental Procedures). Each design task is assigned a different objective function [e.g., Eqs. (9), (10)] to reflect its unique biomolecular constraints. We then select a set of interface residues for stochastic sequence optimization. At each step of the optimization trajectory, a single position is chosen at random out of the set of positions allowed to optimize (including on both sides of the interface in the case of orthogonal-specificity design), and a substitution to a randomly chosen identity is introduced in all modeled protein states (i.e., unbound for stability calculations and bound to each of the partners in the case of binding calculations); each state is then subjected to the same energy-relaxation protocol, including combinatorial side-chain packing and side-chain and rigid-body minimization. All energies are computed with the Rosetta all-atom energy function, which is dominated by contributions from van der Waals packing, hydrogen bonding, and solvation [86]. A new state is accepted subject to the Metropolis criterion and the mutation and selection process is repeated. Additional implementation details are provided in Supplemental Experimental Procedures, including complete RosettaScripts [87] and execution instructions for each design task.

Binding and stability calculations

Binding energies are computed as the difference in system energy between the bound repacked model and the repacked monomers when taken apart from one another and are substituted for x in Eq. (6) to produce the bound fractional occupancy [B in Eqs. (7), (8), (9), (10)]. Monomer stability is the system energy of the monomer in its bound conformation but dissociated from the ligand, and it is likewise substituted for x in Eq. (6) to produce the folded fractional occupancy [S in Eqs. (7), (8), (9), (10)]. For example, B(H-RAS_partner*,partner) of Eq. (9) is the fractional occupancy as a function of the binding energy of the H-RAS mutant for its partner and S(H-RAS_partner*) is the fractional occupancy as a function of the stability of the H-RAS mutant monomeric form modeled on the backbone observed in the partner-bound molecular structure.

Edited by S. A. Teichmann

Appendix A. Supplementary data

Supplementary material