Abstract
Studies of DNA from ancient samples provide a valuable opportunity to gain insight into past evolutionary and demographic processes. Bayesian phylogenetic methods can estimate evolutionary rates and timescales from ancient DNA sequences, with the ages of the samples acting as calibrations for the molecular clock. Sample ages are often estimated using radiocarbon dating, but the associated measurement error is rarely taken into account. In addition, the total uncertainty quantified by converting radiocarbon dates to calendar dates is typically ignored. Here we present a tool for incorporating both of these sources of uncertainty into Bayesian phylogenetic analyses of ancient DNA. This empirical calibrated radiocarbon sampler (ECRS) integrates the age uncertainty for each ancient sequence over the calibrated probability density function estimated for its radiocarbon date and associated error. We use the ECRS to analyse three ancient DNA data sets. Accounting for radiocarbon-dating and calibration error appeared to have little impact on estimates of evolutionary rates and related parameters for these data sets. However, analyses of other data sets, particularly those with few or only very old radiocarbon dates, might be more sensitive to using artificially precise sample ages and should benefit from use of the ECRS.
Keywords: age estimation error, ancient DNA, phylogenetic dating, BEAST
Introduction
Genetic analysis of ancient and historic samples provides access to valuable information that is not available from modern samples alone. For example, phylogenetic and phylogeographic analyses incorporating serially-sampled data have allowed estimates of the relationships between extinct species (e.g., Bunce et al. 2003), inference of past population dynamics (e.g., Lorenzen et al. 2011), and insights into hominin evolution (e.g., Fu et al. 2013; Reich et al. 2011). Ancient DNA data can also be used to estimate evolutionary rates and associated timescales, using the ages of the ancient samples to calibrate the molecular clock (Drummond et al. 2003; Rambaut 2000). Molecular-clock analyses of ancient DNA have been particularly informative about evolutionary rates over population timescales (Ho et al. 2011), providing estimates, for example, of the timing of migration events (Debruyne et al. 2008; Edwards et al. 2011).
With the exception of historical samples that have documented dates of collection, the ages of ancient samples are typically unknown and need to be estimated. Radiocarbon dating (dating using decay of 14C), by scintillation counting or by accelerator mass spectrometry (AMS), is a common method for estimating sample ages and has a theoretical and methodological foundation that provides a quantifiable amount of uncertainty that can be rather considerable (Guilderson et al. 2005). In phylogenetic analyses of ancient DNA, sample ages are typically assigned the mean or median single value of the age distribution and the rest of the uncertainty information is ignored. Methods were recently implemented in the software package BEAST (Drummond et al. 2012) to allow radiocarbon-dating or other sources of error to be taken into account, by specifying a prior distribution on the age of each sample (Ho & Phillips 2009; Shapiro et al. 2011). This approach has been used to incorporate uncertainty when direct AMS radiocarbon dates are not available, for example where ages are inferred from stratigraphic information (e.g., Orlando et al. 2013; Stiller et al. In press).
Previous work has suggested that incorporating error associated with AMS radiocarbon age estimates tends to have a limited impact on estimates of evolutionary and demographic parameters (Molak et al. 2013). However, there might be instances in which this error plays an important role in the analysis. For example, if the estimated error is large (as it tends to be for many samples towards the upper limit of ca. 40–50,000 years for 14C dating) or when only one or a few ancient sequences are used, ignoring the error could lead to artificially precise estimates of the evolutionary rate. As a consequence, estimates of the timing of demographic events would be misleadingly precise.
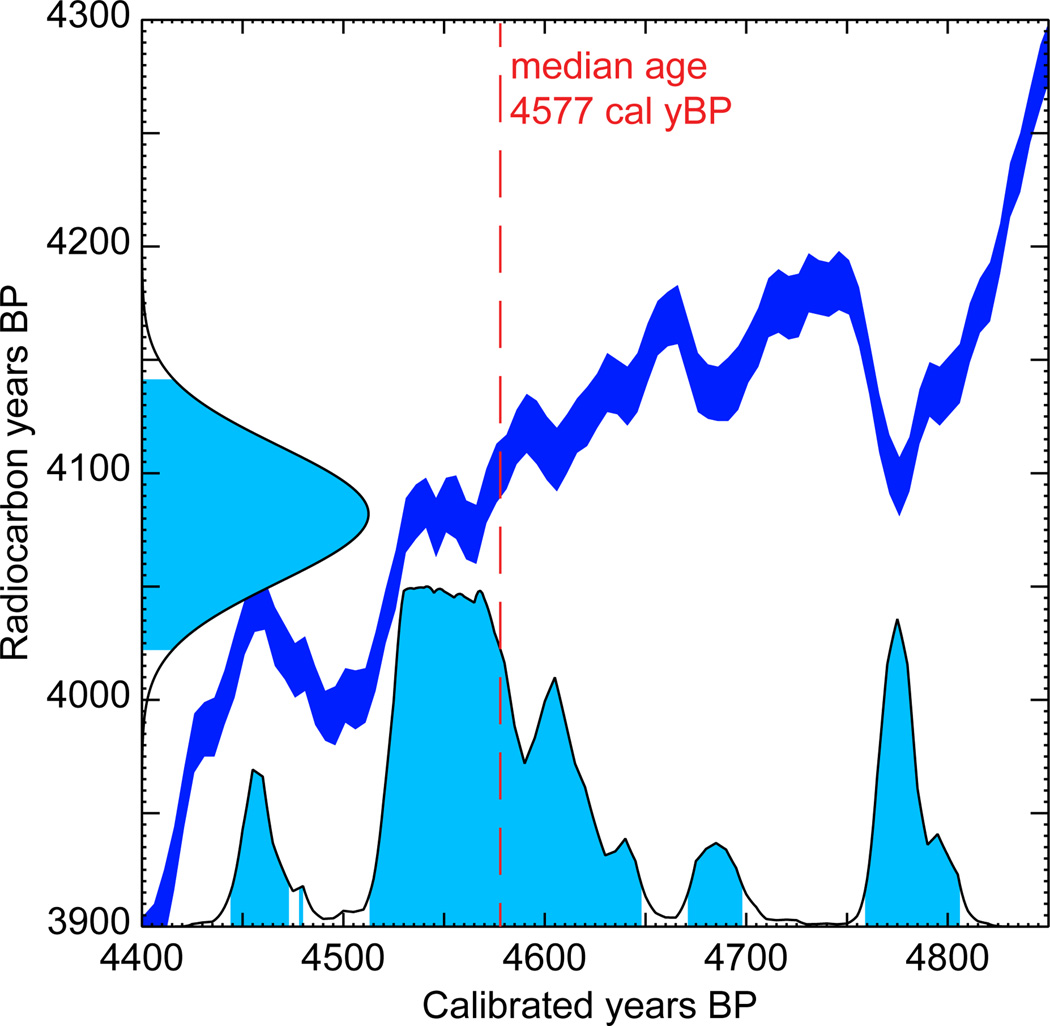
Moreover, radiocarbon ages determined from 14C values and the accepted radioisotope half life differ from absolute (calendar) ages because the atmospheric concentration of 14C has varied through time. If calendar ages are desired, then the radiocarbon ages need to be converted using a calibration curve. Calibration curves are based on analysis of growth patterns correlated with calendar years, such as those observed in tree rings or coral, and comparison of these with their radiocarbon ages. Obtaining a calibration curve for the entire age range spanned by radiocarbon-dating methods requires the combination of several sources of calibration, and curves continue to improve as more data become available and methodology improves (Reimer et al. 2013; Stuiver & Reimer 1993). Importantly, the uncertainty quantified by converting radiocarbon years before present (14C yBP) to calendar years before present (cal yBP) is compounded with that of the initial 14C measurement error (Figure 1). Probability distributions of calibrated ages usually do not follow a simple parametric distribution and are often multimodal, making it a challenge to incorporate this uncertainty into a phylogenetic analysis.
Figure 1.
Example of a calibration plot with a multimodal probability distribution. The radiocarbon age estimate of the sample is 4082±30 14C yBP. The median calibrated age estimate of the sample is 4577 cal yBP. The probability density functions of the uncalibrated and calibrated ages are plotted along the y- and x-axes, respectively. Conversion between the two is performed using IntCal13 calibration curve (in dark blue).
Here we present the empirical calibrated radiocarbon sampler (ECRS), which we have implemented in the Bayesian phylogenetic software BEAST v1.8 (Drummond et al. 2012). The ECRS allows the uncertainty in calibrated radiocarbon dates to be taken into account directly as non-parametric prior information. This is achieved by providing the software with an empirical description of the probability density function for the calibrated age estimate for each radiocarbon-dated sample. The age of that sample is then integrated over this probability distribution through a Markov chain Monte Carlo (MCMC) algorithm. We introduce a simple method to incorporate age uncertainty into Bayesian phylogenetic analysis by using the probability density functions generated through the calibration program CALIB (Stuiver & Reimer 1993).
Methods
BEAST analysis with the ECRS
We implemented in BEAST v1.8 a novel non-parametric probability distribution to model empirical information about uncertainty and systematic error in specifying tip ages. The ECRS takes as input age probability density files generated by CALIB 7.0.0 (or newer) that provide a finite grid of ages and their associated probability masses (alternative software can be used to generate equivalent probability density files). The novel BEAST implementation reads in these values, assumes a 1st-order spline fit between these grid values to allow for continuous ages, places zero density outside the minimal and maximal grid values, and renormalizes to generate an integrable density function for use with MCMC.
In making this transformation for our examples in this paper, the ECRS applies an offset of 60 years to the age values in the probability density text files. Data reporting conventions for 14C dating are such that ages are given in “years before 1950”. Therefore, the ECRS assumes that modern (age=0) samples were collected in 2010. For evolutionary rate estimation, any disparity between 2010 and the real age of the modern samples used should be negligible. This offset was introduced in the ECRS to avoid age distributions of young radiocarbon-dated samples extending to negative values.
The age distributions cannot be easily applied to data sets that include no modern samples (e.g. extinct species). When there is no stable zero-height point, the current implementation of BEAST will reassign the timescale of the tree according to the youngest sequence sampled in any given MCMC step. This problem can be avoided by fixing the age of the youngest sample in the data set to a point value, provided that none of the other sample age distributions can cross this point. Otherwise, they too will cause the tree to be rescaled. In such circumstances, we advise fixing the ages of all the sequences of which age distributions cross the value of the age of the youngest sample.
The BEAST input file needs to be edited to define the age prior for each ancient DNA sample as the probability density defined in the age probability density text file. Instructions on how to use the ECRS, along with all used XML files, are available as Supporting Information.
Testing the ECRS
We tested the ECRS on three published ancient DNA data sets: bison (Shapiro et al. 2004), muskox (Campos et al. 2010), and human (Fu et al. 2013). Sequence alignments of the mitochondrial control region were used for bison (591 bp, 159 sequences) and muskox (682 bp, 131 sequences), whereas whole mitochondrial genomes were used for humans (16,564 bp, 64 sequences). Ages of ancient DNA sequences ranged from 125 to 43,400 14C yBP for bison (142 samples), 115 to 45,900 14C yBP for muskox (117 samples), and 690 to 39,475 14C yBP for humans (10 samples).
We performed a Bayesian phylogenetic analysis of each data set, using either the median calibrated ages of the samples or with the ECRS using the age distributions obtained with the IntCal13 calibration curve (Reimer et al. 2013). The probability density for the calibrated age of each radiocarbon-dated specimen was obtained using CALIB 7.0.0 (Stuiver & Reimer 1993). Because the ECRS adds 60 years to the age of each ancient DNA sequence, we added 60 years also to the median calibrated ages of the ancient DNA sequences for ECRS testing. This allowed us to compare directly the analyses using median calibrated sample ages and using the age probability densities.
For each data set, the best-fitting model of nucleotide substitution was chosen according to the Bayesian Information Criterion using ModelGenerator (Keane et al. 2006). Each analysis was performed in BEAST v1.8 using a conditional reference prior (Ferreira & Suchard 2008) for the substitution rate. The sample ages were the only source of calibrating information for the molecular clock. For each data set, we performed analyses using both a constant-size coalescent model and the skygrid model (Gill et al. 2013). Owing to the intraspecific nature of the data, we assumed a strict molecular clock. Markov chains were run for at least 107 steps, with parameters subsampled every 103 steps. Chains were run for longer if required until all parameter estimates converged and achieved effective sample sizes of >100. In each analysis, the first 10% of steps were discarded as burn-in. For each data set, we compared marginal likelihoods estimated for both coalescent models using stepping-stone and path sampling protocols (Baele et al. 2012; Baele et al. 2013). This Bayes-factor analysis supported the Bayesian skygrid model for bison and human, and a constant-size model for muskox.
We used Bayes factors (estimated as above) to compare the analyses calibrated using median sample ages and those based on the ECRS (Suchard et al. 2001). We also investigated estimates of substitution rates and the age of the root, as well as the duration of the analysis.
Results of ECRS testing
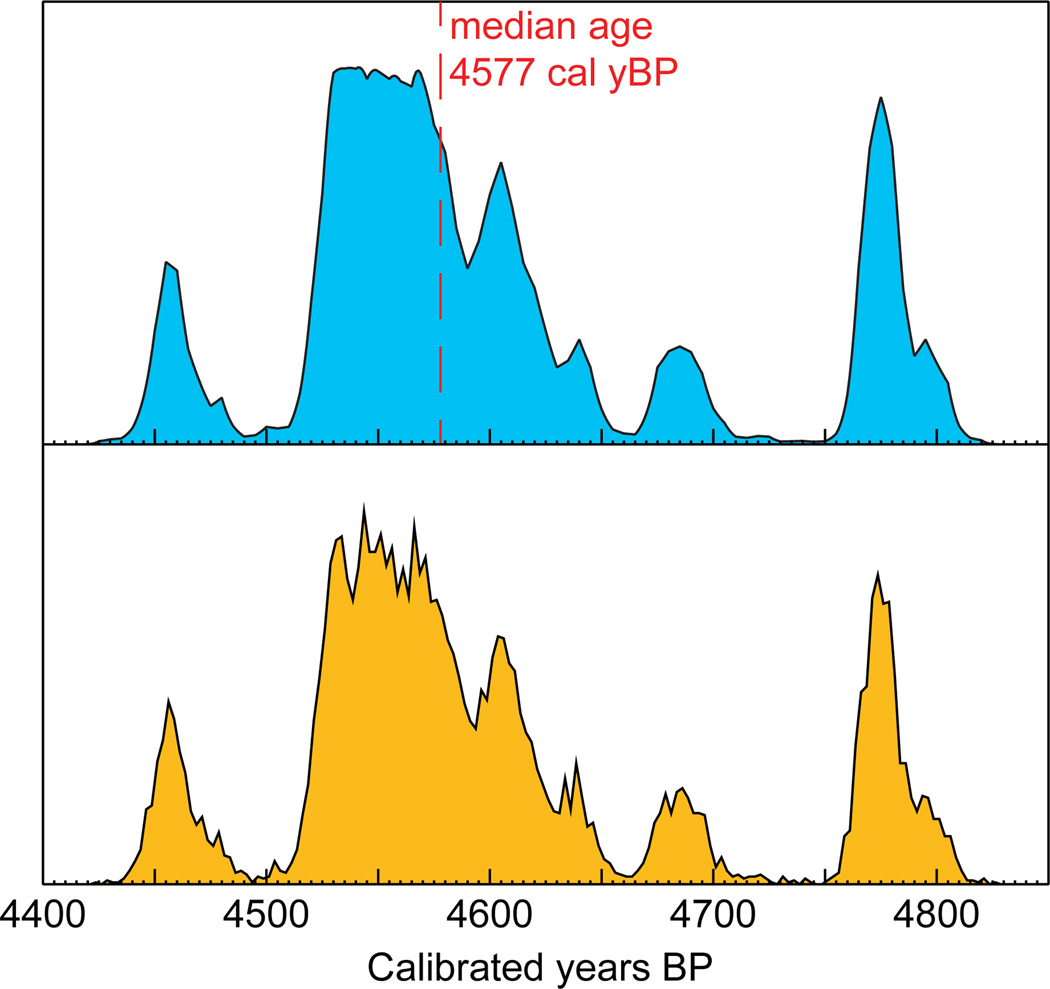
The ECRS, as implemented in the BEAST phylogenetic framework, makes it possible to account for the uncertainty in radiocarbon measurement and age calibration when estimating evolutionary rates. The model performs as expected, as is reflected in the posterior distributions of sample ages, which accurately recapitulate the probability density associated with the calibrated age of each specimen (Figure 2).
Figure 2.
Example of a posterior distribution of a sample age (bottom plot, orange) compared with the calibration plot obtained in CALIB (top plot, blue) and used as a prior for Bayesian phylogenetic analysis. The vertical axis represents the probability density. Note that the figure shows ages in yBP (before 1950), whereas ECRS yields posterior ages in years before 2010.
Accounting for this uncertainty in the sample ages did not lead to a substantial improvement in marginal likelihood for any of the three data sets analysed (Table 1). The 95% credibility intervals for the substitution rate and age of the root were of similar widths to or slightly narrower (up to 8%) than the ones obtained using median sample ages for molecular-clock calibration. We also note that, as expected, the computation time (per effective sample size of 100) was longer for the ECRS model than for the model that used median sample age for two out of the three data sets (bison and muskox). The amount of computation time will depend on specific characteristics of the data sets, such as alignment length and number of sequences, and on the availability of resources.
Table 1.
Comparison of Bayesian phylogenetic analyses made using the empirical calibrated radiocarbon sampler (ECRS) and median sample ages. Data shown include estimates and 95% highest posterior density (HPD) intervals for the substitution rate and age of the root; speed of the BEAST run; and Bayes factors for the ECRS compared with median sample ages, with marginal likelihoods calculated using stepping-stone and path sampling.
| Substitutions/site/year | Time to most recent common ancestor | Run speed |
Bayes factors | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Population model |
Substitution model |
Sample ages used |
Median estimate |
95% HPD | 95% HPD width |
95% HPD width ratioa |
Median estimate |
95% HPD | 95% HPD width |
95% HPD width ratioa |
Run speed ratiob |
Via stepping- stone samplinga |
Via path samplinga |
|
| Bison | skygrid | TRN+G6 | Median | 4.39×10−7 | 3.26×10−7 – 5.60×10−7 | 2.34×10−7 | 1.01 | 1.08×105 | 8.81×104 – 1.37×105 | 4.86×104 | 1.03 | 2.47 | 0.00 | 0.00 |
| ECRS | 4.39×10−7 | 3.25×10−7 – 5.60×10−7 | 2.35×10−7 | 1.08×105 | 8.86×104 – 1.37×105 | 5.03×104 | ||||||||
| Human | skygrid | TRN+G6 | Median | 1.99×10−8 | 1.58×10−8 – 2.42×10−8 | 8.37×10−9 | 0.94 | 1.54×105 | 1.22×105 – 1.96×105 | 7.36×104 | 0.92 | 0.62 | 1.63 | 2.22 |
| ECRS | 2.03×10−8 | 1.64×10−8 – 2.43×10−8 | 7.90×10−9 | 1.53×105 | 1.22×105 – 1.90×105 | 6.74×104 | ||||||||
| Musk ox | constant | TVM+G6 | Median | 8.16×10−7 | 6.20×10−7 – 1.02×10−6 | 3.99×10−7 | 0.94 | 8.04×104 | 6.78×104 – 9.51×104 | 2.72×104 | 1.00 | 4.45 | 0.91 | 0.10 |
| ECRS | 8.09×10−7 | 6.23×10−7 – 9.99×10−7 | 3.76×10−7 | 8.05×104 | 6.74×104 – 9.47×104 | 2.72×104 | ||||||||
ECRS vs median age
ECRS vs median age run speed calculated as hours per 100 ESS for rate estimate
Discussion
We have presented the ECRS, a tool implemented in the BEAST software package that enables the uncertainty from radiocarbon measurement and age calibration to be taken into account in Bayesian phylogenetic analysis. Concordance between the prior and posterior distributions of sample ages indicates that there is no conflict between the prior age distribution and the genetic signal in the data set. However, it also indicates that the genetic signal is not strong enough in any of our three data sets to improve the precision of the age estimate, even for the human data set which comprises complete mitochondrial genomes.
Accounting for the uncertainty in sample ages in Bayesian phylogenetic analysis appears to have had a limited impact on estimates of key evolutionary parameters, including the evolutionary rate and the age of the root of the tree. This result is consistent with previous findings from a range of ancient DNA data (Molak et al. 2013), and suggests that the common practice of ignoring errors in sample-age estimation and radiocarbon calibration in phylogenetic analyses of ancient DNA likely does not introduce significant error into these analyses. Nevertheless, implementing the ECRS is an important step towards more accurate models of biological parameters for phylogenetic analysis.
The ECRS is simple to implement and reduces the potential effect of disregarding sample-age estimation error in Bayesian phylogenetic analyses. If the sequence ages used to calibrate the molecular clock are artificially precise, our confidence in phylogenetic estimates of rates and timescales could be overstated. Consequently, accounting for radiocarbon-dating and calibration error might be most useful in analyses of data sets that include only a small number of ancient DNA sequences, where each sample age constitutes a considerable proportion of the overall tree-calibrating information. This effect will be particularly pronounced when the sequences have ages for which calibration curves produce large age-estimation errors, as is typically the case for samples that are near the upper age limit for radiocarbon dating.
Supplementary Material
Acknowledgements
MM is supported by the University of Sydney International Scholarship. MAS is supported in part by National Institutes of Health grants R01 AI107034 and R01 HG006139 and National Science Foundation grants DMS 1264153 and IIS 1251151. SYWH is supported by the Australian Research Council. DWB is supported in part by National Science Foundation grants 1108116 and 1246359. BS is supported by The Packard Foundation.
Footnotes
Data accessibility
All the genetic and radiocarbon dating data used in the analyses used have been previously published and are available alongside the original publications (with DNA sequences available via GenBank): bison – Shapiro et al. 2004, human – Fu et al. 2013, muskox – Campos et al. 2010. For the ECRS testing we chose from these data sets only samples for which there were provided 14C ages and errors and of which ages did not exceed the limits of the IntCal13 calibration curve.
All input XML files used to test the ECRS (including the script required to run BEAST with ECRS) and information about the ages of the samples (provided as CALIB input files), which will allow the readers to fully replicate our analyses are available as Supporting Information.
Author contributions
MM planned and performed the analyses, wrote the manuscript.
MAS developed the new empirical distribution, implemented this distribution in BEAST, planned the analyses, and wrote the manuscript.
SYWH planned the analyses and wrote the manuscript.
DWB provided calibration data and wrote the manuscript.
BS planned and performed the analyses and wrote the manuscript.
References
- Baele G, Lemey P, Bedford T, et al. Improving the accuracy of demographic and molecular clock model comparison while accommodating phylogenetic uncertainty. Molecular Biology and Evolution. 2012;29:2157–2167. doi: 10.1093/molbev/mss084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baele G, Li WLS, Drummond AJ, Suchard MA, Lemey P. Accurate model selection of relaxed molecular clocks in Bayesian phylogenetics. Molecular Biology and Evolution. 2013;30:239–243. doi: 10.1093/molbev/mss243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bunce M, Worthy TH, Ford T, et al. Extreme reversed sexual size dimorphism in the extinct New Zealand moa Dinornis. Nature. 2003;425:172–175. doi: 10.1038/nature01871. [DOI] [PubMed] [Google Scholar]
- Campos PF, Willerslev E, Sher A, et al. Ancient DNA analyses exclude humans as the driving force behind late Pleistocene musk ox (Ovibos moschatus) population dynamics. Proceedings of the National Academy of Sciences of the United States of America. 2010;107:5675–5680. doi: 10.1073/pnas.0907189107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Debruyne R, Chu G, King CE, et al. Out of America: ancient DNA evidence for a new world origin of late quaternary woolly mammoths. Current Biology. 2008;18:1320–1326. doi: 10.1016/j.cub.2008.07.061. [DOI] [PubMed] [Google Scholar]
- Drummond AJ, Pybus OG, Rambaut A, Forsberg R, Rodrigo AG. Measurably evolving populations. Trends in Ecology and Evolution. 2003;18:481–488. [Google Scholar]
- Drummond AJ, Suchard MA, Xie D, Rambaut A. Bayesian phylogenetics with BEAUti and the BEAST 1.7. Molecular Biology and Evolution. 2012;29:1969–1973. doi: 10.1093/molbev/mss075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards CJ, Suchard MA, Lemey P, et al. Ancient hybridization and an Irish origin for the modern polar bear matriline. Current Biology. 2011;21:1251–1258. doi: 10.1016/j.cub.2011.05.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferreira MAR, Suchard MA. Bayesian analysis of elapsed times in continuous-time Markov chains. Canadian Journal of Statistics. 2008;36:355–368. [Google Scholar]
- Fu Q, Mittnik A, Johnson PL, et al. A revised timescale for human evolution based on ancient mitochondrial genomes. Current Biology. 2013;23:553–559. doi: 10.1016/j.cub.2013.02.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gill MS, Lemey P, Faria NR, et al. Improving Bayesian population dynamics inference: a coalescent-based model for multiple loci. Molecular Biology and Evolution. 2013;30:713–724. doi: 10.1093/molbev/mss265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guilderson TP, Reimer PJ, Brown TA. The boon and bane of radiocarbon dating. Science. 2005;307:362–364. doi: 10.1126/science.1104164. [DOI] [PubMed] [Google Scholar]
- Ho SYW, Lanfear R, Bromham L, et al. Time-dependent rates of molecular evolution. Molecular Ecology. 2011;20:3087–3101. doi: 10.1111/j.1365-294X.2011.05178.x. [DOI] [PubMed] [Google Scholar]
- Ho SYW, Phillips MJ. Accounting for calibration uncertainty in phylogenetic estimation of evolutionary divergence times. Systematic Biology. 2009;58:367–380. doi: 10.1093/sysbio/syp035. [DOI] [PubMed] [Google Scholar]
- Keane TM, Creevey CJ, Pentony MM, Naughton TJ, McLnerney JO. Assessment of methods for amino acid matrix selection and their use on empirical data shows that ad hoc assumptions for choice of matrix are not justified. BMC Evolutionary Biology. 2006;6:29. doi: 10.1186/1471-2148-6-29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorenzen ED, Nogues-Bravo D, Orlando L, et al. Species-specific responses of Late Quaternary megafauna to climate and humans. Nature. 2011;479:359–364. doi: 10.1038/nature10574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molak M, Lorenzen ED, Shapiro B, Ho SYW. Phylogenetic estimation of timescales using ancient DNA: the effects of temporal sampling scheme and uncertainty in sample ages. Molecular Biology and Evolution. 2013;30:253–262. doi: 10.1093/molbev/mss232. [DOI] [PubMed] [Google Scholar]
- Orlando L, Ginolhac A, Zhang G, et al. Recalibrating Equus evolution using the genome sequence of an early Middle Pleistocene horse. Nature. 2013;499:74–78. doi: 10.1038/nature12323. [DOI] [PubMed] [Google Scholar]
- Rambaut A. Estimating the rate of molecular evolution: incorporating non-contemporaneous sequences into maximum likelihood phylogenies. Bioinformatics. 2000;16:395–399. doi: 10.1093/bioinformatics/16.4.395. [DOI] [PubMed] [Google Scholar]
- Reich D, Patterson N, Kircher M, et al. Denisova admixture and the first modern human dispersals into Southeast Asia and Oceania. American Journal of Human Genetics. 2011;89:516–528. doi: 10.1016/j.ajhg.2011.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reimer PJ, Bard E, Bayliss A, et al. IntCal13 and Marine13 radiocarbon age calibration curves 0–50,000 years cal BP. Radiocarbon. 2013;55:1869–1887. [Google Scholar]
- Shapiro B, Drummond AJ, Rambaut A, et al. Rise and fall of the Beringian steppe bison. Science. 2004;306:1561–1565. doi: 10.1126/science.1101074. [DOI] [PubMed] [Google Scholar]
- Shapiro B, Ho SYW, Drummond AJ, et al. A Bayesian phylogenetic method to estimate unknown sequence ages. Molecular Biology and Evolution. 2011;28:879–887. doi: 10.1093/molbev/msq262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stiller M, Molak M, Prost S, et al. Mitochondrial DNA diversity and evolution of the Pleistocene cave bear complex. Quaternary International. (In press) [Google Scholar]
- Stuiver M, Reimer PJ. Extended 14C data base and revised CALIB 3.0 14C age calibration program. Radiocarbon. 1993;35:215–230. [Google Scholar]
- Suchard MA, Weiss RE, Sinsheimer JS. Bayesian selection of continuous-time Markov chain evolutionary models. Molecular Biology and Evolution. 2001;18:1001–1013. doi: 10.1093/oxfordjournals.molbev.a003872. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.