Impact of copula directional specification on multi-trial evaluation of surrogate endpoints

Abstract

Evaluation of surrogate endpoints using patient-level data from multiple trials is the gold standard, where multi-trial copula models are used to quantify both patient-level and trial-level surrogacy. While limited consideration has been given in the literature to copula choice (e.g., Clayton), no prior consideration has been given to direction of implementation (via survival versus distribution functions). We demonstrate that evenwith the “correct” copula family, directional misspecification leads to biased estimates of patient-level and trial-level surrogacy. We illustrate with a simulation study and a re-analysis of disease-free survival as a surrogate for overall survival in early stage colon cancer.

1 Introduction

Surrogate endpoints are desirable in clinical trials where clinical endpoints are expensive or difficult to obtain, or where substantial follow-up would be required to observe the primary endpoint in a sufficient number of patients to draw meaningful trial conclusions. While numerous methods for evaluating and validating surrogate endpoints have been proposed, recent consensus has supported evaluation of potential surrogates based on patient-level data from multiple similar trials, where performance is traditionally assessed both within and across trials. Specifically, multi-trial copula models are commonly employed, as they allow estimation of trial- and endpoint-specific marginal parameters (e.g., treatment effects) concurrent with estimation of the possibly nonzero association between the true clinical end-point (T) and candidate surrogate (S). In all published copula-based surrogacy evaluations to date, associations between pairs of endpoints have been modeled using so-called “survival copulas,” i.e., copulas directly constructed from marginal survival functions rather than from cumulative distribution functions (CDFs), presumably to simplify the task of deriving the multi-trial likelihood components required to accommodate possibly right-censored data. It is equally common in practice to assume that (S, T) association does not vary by trial, resulting in a convenient single-number summary of patient-level surrogacy. Estimates of marginal treatment effects on S and T obtained by fitting these equal-association survivalcopulas are traditionally carried forward into a second-stage, across-trial surrogacy estimation procedure, where another single-number summary denoting surrogate performance at the trial level is derived. A surrogate is deemed promising if both the patient-level and trial-level performance quantities are sufficiently high.

The existing multi-trial, survival copula, and equal-association approach described above was introduced by Burzykowski et al. (2001) for time-to-event endpoints, and was subsequently used to validate both disease-free survival (DFS) and progression-free survival (PFS) as surrogates for overall survival (OS) in the adjuvant colon cancer and advanced colorectal cancer settings, respectively (Sargent et al., 2005, 2007; Buyse et al., 2007; de Gramont et al., 2010). This approach was also used by Collette et al. (2005) to evaluate candidate surrogate endpoints in prostate cancer, by Burzykowski et al. (2008) for endpoints in breast cancer, by Foster et al. (2011) and Mauguen et al. (2013) for endpoints in lung cancer, by Michiels et al. (2009) for endpoints in head and neck cancer, by Buyse et al. (2011) for endpoints leukemia, by Burzykowski et al. (2008b) and Chibaudel et al. (2011) to evaluate endpoints for other classes of treatments in colorectal cancer, plus other applications. Furthermore, this approach has been extended to account for estimation error of treatment effects at the first stage, based on both frequentist and Bayesian points of view (Burzykowski et al., 2001; Renfro et al., 2012). Importantly, both DFS and PFS are currently being utilized as primary endpoints in clinical trials for experimental therapeutic agents, based in part on their promising performance in multi-trial survival copula modeling, which is now considered a gold standard approach to surrogate endpoint assessment.

However, in our own recent explorations, we found (as we will describe hereafter) that this long-employed multi-trial modeling approach assuming a survival copula relationship between S and T and equal (S, T) association across trials may produce systematically biased estimates of both marginal treatment effects and the copula association parameter when the shape of the association is not well-represented by the survival copula, or when the level of (S, T) association truly differs across trials, or both. For example, the popular multi-trial Clayton survival copula (which assumes strong upper-tail and weak lower-tail association of S and T) is commonly applied in settings where S and T exhibit strong lower-tail and weak upper-tail association (as is assumed by the Clayton CDF copula). We show that under this directional misspecification, bias worsens as the association between S and T grows stronger–precisely the case desired when evaluating promising candidate surrogates. Furthermore, biased treatment effect estimates are carried forward to construct (biased) estimates of trial-level surrogacy, resulting in potentially untrustworthy comprehensive (patient-level and trial-level) surrogacy evaluations. In addition, the impact of assuming equal (S, T) association across trials, where such strict homogeneity is unlikely, has not been previously addressed in the literature.

Herein, we assess the consequences of these surrogacy evaluation practices separately and jointly by comparing the estimation performance of survival-based versus CDF-based multi-trial copula models in settings where S and T truly arise from a CDF copula (which we will argue is more likely in practice). While the arguments presented in this paper are relevant when any radially asymmetric copula is considered for surrogacy modeling, for both ease of exposition and relevance to our applications of interest, we focus on a single copula–Clayton–as the strong lower-tail dependence and weak upper-tail dependence it assumes under the CDF framework is most similar to relationships observed between surrogate and true endpoints in our application of interest: time-to-event endpoints in clinical trials. Throughout, we will compare the multi-trial Clayton survival copula proposed by Burzykowski et al. (2001) to a set of alternative multi-trial Clayton CDF copulas, for which either common or trial-specific association parameters may be assumed. Furthermore, we explore the accuracy and efficiency of simultaneous (marginal and association) versus two-stage (marginal, then association) multi-trial copula modeling.

The remainder of the paper evolves as follows. In Section 2, we review the traditional survival copula, single association parameter approach to multi-trial surrogacy evaluation, and we present four alternative CDF-based copula strategies intended to show improved performance when lower-tail dependence of S and T is present. These four strategies were derived from the possible combinations of two important copula modeling decisions: equal versus trial-specific patient-level association, and simultaneous versus two-stage estimation. We demonstrate the relative advantages of our proposed strategies, including improved patient-level and trial-level surrogacy estimation, in a simulation study presented in Section 3. In Section 4, we compare these methods in a re-evaluation of DFS as a surrogate for OS, using patient-level data from 18 trials in adjuvant colon cancer originally published by Sargent et al. (2005). We conclude with a discussion in Section 5.

2 Copula Approaches for Surrogacy Evaluation

2.1 Multi-Trial Clayton Survival Copula

First, we provide a general review of the multi-trial Clayton survival copula modeling approach that is commonly used in practice (Burzykowski et al., 2001), but note that the same developments apply to other radially asymmetric copulas. To remain consistent with past implementations of this approach, we assume trial-specific marginal models (e.g., Weibull) for a time-to-event surrogate endpoint S and a true endpoint T, which in turn depend on covariates such as treatment assignment. When the Clayton copula C(u, v) ={u^1−γ+v^1−γ−1}^1/(1−γ), (u, v) ∈ [0, 1]² with association parameter γ Clayton (1978) is selected to model the association between S and T, it may optionally be used to construct the joint survival function S(s, t) from the marginal survival functions S_s(s)and S_T(t):

$$S(s,t)=C\{S_S(s),S_T(t);\gamma \}={\{S_S{(s)}^{1-\gamma }+S_T{(t)}^{1-\gamma }-1\}}^{1/(1-\gamma )},\gamma >1$$ (1)

The bivariate survival function (1) represents the likelihood contribution when both S and T are right-censored. For the case where both S and T are observed, the likelihood contribution is

$$f(s,t)=\frac{{\partial }^{2}S(s,t)}{\partial s\partial t}=\gamma {\{S_S{(s)}^{1-\gamma }+S_T{(t)}^{1-\gamma }-1\}}^{\gamma /(1-\gamma )-1}{S}_S{(s)}^{-\gamma }{f}_S(s)S_T{(t)}^{-\gamma }{f}_T(t),$$

where f_S(s)and f_T(t)are the marginal density functions.When S is observed and T is right-censored, the likelihood contribution becomes

$$f_S(s,t)=-\frac{\partial S(s,t)}{\partial s}={\{S_S{(s)}^{1-\gamma }+S_T{(t)}^{1-\gamma }-1\}}^{\gamma /(1-\gamma )}{S}_S{(s)}^{-\gamma }{f}_S(s).$$

Similarly, for T observed and S right-censored, the contribution is

$$f_T(s,t)=-\frac{\partial S(s,t)}{\partial t}={\{S_S{(s)}^{1-\gamma }+S_T{(t)}^{1-\gamma }-1\}}^{\gamma /(1-\gamma )}{S}_T{(t)}^{-\gamma }{f}_T(t).$$

For a patient-level sample (s_ij, t_ij), j = 1, …, n_i with corresponding censoring indicators $({\partial }_{ij}^S,{\partial }_{ij}^T)$ from trials indexed by i ∈ {1, …, N}, the likelihood function may be constructed:

$$\mathcal{ℒ}=\prod _{i=1}^N\prod _{j=1}^{n_i}{f}_i{(s_{ij},t_{ij})}^{{\delta }_{ij}^S{\delta }_{ij}^T}{S}_i{(s_{ij},t_{ij})}^{(1-{\delta }_{ij}^S)(1-{\delta }_{ij}^T)}{f}_{S,i}{(s_{ij},t_{ij})}^{{\delta }_{ij}^S(1-{\delta }_{ij}^T)}{f}_{T,i}{(s_{ij},t_{ij})}^{{\delta }_{ij}^T(1-{\delta }_{ij}^S)}.$$ (2)

In practice, the joint likelihood terms of (2) and their marginal components and parameters are further indexed by trial, and the likelihood products are taken over trials and patients within trials. Traditionally for the survival copula approach, a single association parameter γ is assumed across trials, and simultaneous estimation of all trial-specific marginal parameters and the single copula association parameter is performed via maximum likelihood.

2.2 Multi-Trial Clayton CDF Copula

Continuing to assume trial-specific marginal models for S and T that depend on covariates such as treatment assignment, we may alternatively use the Clayton copula with association parameter γ to construct the joint distribution function F*(s, t) from the marginal distribution functions F_S(s) and F_T(t):

$$F^{\ast }(s,t)=C\{F_S(s),F_T(t);\gamma \}={\{F_S{(s)}^{1-\gamma }+F_T{(t)}^{1-\gamma }-1\}}^{1/(1-\gamma )},\gamma >1.$$ (3)

Note we use asterisks (*) to differentiate the cumulative distribution function (CDF) copula (3) and its derived likelihood terms below from the survival copula (1) and its derived terms presented in Section 2.1. The joint probability density function representing the likelihood contribution when both S and T are observed is then given by

$$f^{\ast }(s,t)=\frac{{\partial }^2{F}^{\ast }(s,t)}{\partial s\partial t}=\gamma {\{F_S{(s)}^{1-\gamma }+F_T{(t)}^{1-\gamma }-1\}}^{\gamma /(1-\gamma )-1}{F}_S{(s)}^{-\gamma }{f}_S(s)F_T{(t)}^{-\gamma }{f}_T(t),$$

where f_S(s) and f_T(t) are the marginal density functions. When S is observed and T is right-censored, the likelihood contribution is

$$f_S^{\ast }(s,t)={\int }_t^{\infty }{f}^{\ast }(s,y)\mathit{\text{dy}}=f_S(s)[1-F_S{(s)}^{-\gamma }]{\{F_S{(s)}^{1-\gamma }+F_T{(t)}^{1-\gamma }-1\}}^{-\gamma /(1-\gamma )}.$$

Similarly, the likelihood contribution for T observed and S right-censored is

$$f_T^{\ast }(s,t)={\int }_s^{\infty }{f}^{\ast }(x,t)\mathit{\text{dx}}=f_T(t)[1-F_T{(t)}^{-\gamma }]{\{F_S{(s)}^{1-\gamma }+F_T{(t)}^{1-\gamma }-1\}}^{-\gamma /(1-\gamma )}.$$

The joint survivor function for S and T both right-censored is also obtained from f(s, t) by

$$S^{\ast }(s,t)={\int }_s^{\infty }{\int }_t^{\infty }{f}^{\ast }(x,y)dxdy=1-F_S(s)-F_T(t)+{\{F_S{(s)}^{1-\gamma }+F_T{(t)}^{1-\gamma }-1\}}^{1/(1-\gamma )}.$$

For a sample (s_ij, t_ij), j= 1, …, n_i with corresponding censoring indicators $({\delta }_{ij}^S,{\delta }_{ij}^T)$ from trials indexed by i ∈ {1,…, N}, the likelihood function is constructed as:

$${ℒ}^{\ast }=\prod _{i=1}^N\prod _{j=1}^{n_i}{f}_i^{\ast }{(s_{ij},t_{ij})}^{{\delta }_{ij}^S{\delta }_{ij}^T}{S}_i^{\ast }{(s_{ij},t_{ij})}^{(1-{\delta }_{ij}^S)(1-{\delta }_{ij}^T)}{f}_{S,i}^{\ast }{(s_{ij},t_{ij})}^{{\delta }_{ij}^S(1-{\delta }_{ij}^T)}{f}_{T,i}^{\ast }{(s_{ij},t_{ij})}^{{\delta }_{ij}^T(1-{\delta }_{ij}^S)}.$$ (4)

In (4), we similarly index the joint likelihood terms, marginal components, and marginal parameters by trial and take the likelihood product over trials and patients within trials. As will be described in Section 2.4, we will separately consider equal association γ across trials and trial-specific (S, T) association, for which γ is further indexed by i ∈ {1,…, N}.

2.3 Survival Versus CDF Copula Implementation

From the developments in Sections 2.1 and 2.2 above, it can be readily seen that the choice of survival copula versus cumulative distribution function (CDF) copula leads to fundamentally different likelihoods given by (2) and (4), respectively. It is important to note that this feature is dissimilar from the traditional linkage of the “survival copula” and traditional (CDF) copula (see, e.g., Nelson (2006)), where a survival copula C̃{S_S(s), S_T(t)} corresponds to an associated CDF copula C{F_S(s), F_T(t)} via C̃{S_S(s), S_T(t)}= S_S(s)+S_T(t)− 1 +C{F_S(s), F_T(t)}, such that C̃{S_S(s), S_T(t)}and C{F_S(s), F_T(t)} jointly refer to the same model and maintain the same shape and direction of (S, T) association.

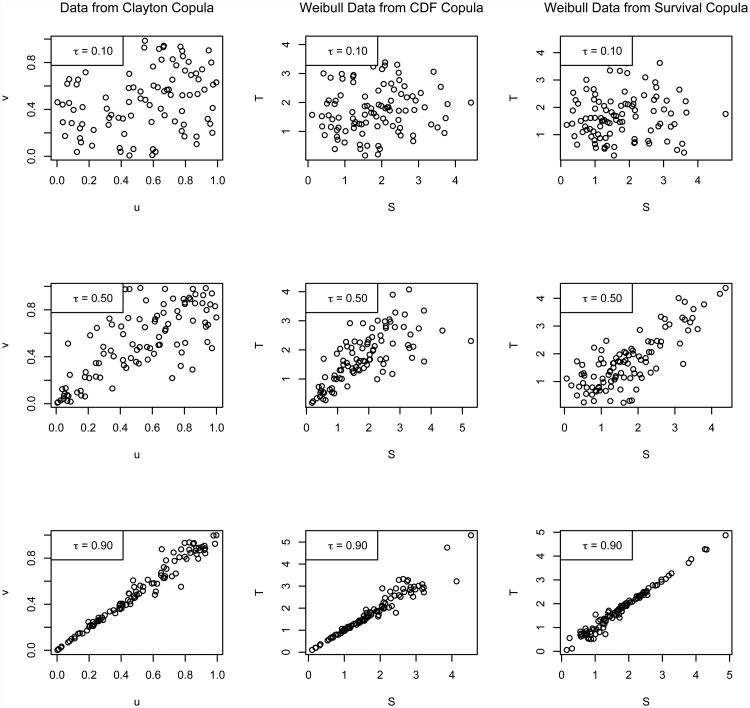
In practice, when choosing the direction of implementation (survival versus CDF) for a particular dataset and copula (e.g., Clayton), the general association pattern assumed by the copula should be taken into account, as demonstrated in Figure 1 for varying strengths association expressed in terms of Kendall's τ. The general form of the Clayton copula C(u,v) = (u^1−γ+v^1−γ)^1/(1−γ) defined on [0, 1]² assumes strong lower-tail dependence near (u,v) = (0,0) and weak upper-tail dependence near (u,v) = (1,1); that is, the association pattern is not symmetric over the line v= 1 −u, as shown in the first column of Figure 1. Modeling S and T using the CDF implementation of the Clayton copula given by (3) with arguments (u,v) = {F_S(s), F_T(t)} assumes the same direction of association is expected for S and T; specifically, stronger (S,T) association is expected near {F_S(s), F_T(t)}= (0,0), or where event times are smallest, while relatively weaker (S,T) association is expected near {F_S(s), F_T(t)}= (1,1), where event times are largest (see the second column of Figure 1). On the other hand, modeling S and T using the Clayton survival copula (1) with arguments (u,v) = {S_S(s), S_T(t)}assumes that stronger (S,T) association is expected near {S_S(s), S_T(t)}= (0, 0), or where event times are largest, relative to weaker association near {S_S(s), S_T(t)}= (1,1), where event times are smallest; see the third column of Figure 1. Thus, in practical terms, the choice of the Clayton survival copula for (S,T) implies that true and surrogate events are expected to be more highly associated at the end of a trial than at the beginning, while choice of the Clayton CDF copula implies that true and surrogate events are expected to be more highly associated at the beginning of a trial than at the end. In either case, the copula association parameter γ controls the overall level of association between S and T, while the specific copula form (Clayton) and direction of implementation (survival versus CDF) jointly describe the shape of the association.

Figure 1.

Scatterplots of random draws from the Clayton copula for τ ∈ {0.10, 0.50, 0.90} (first column), presented with corresponding Weibull generates from the Clayton CDF copula (second column) and Clayton survival copula (third column), obtained via marginal application of the inverse-CDF method and inverse-survival method, respectively.

2.4 Summary of Modeling and Estimation Approaches

We henceforth refer to the Clayton survival copula modeling approach with single association parameter and simultaneous (marginal and association) maximum likelihood estimation of Section 2.1 as Method 0. For the Clayton CDF-based copula model described in Section 2.2, we separately consider both a common association parameter γ across trials and trial-specific association parameters. In the latter case, construction of the likelihood function (4) will require additional indexing of the association parameter by trial i ∈ {1, …, N}. Also for the CDF-based approach, we will investigate the performance of simultaneous (marginal and association) versus two-stage (marginal, then association) maximum likelihood estimation,where the latter method's second-stage estimation of the copula association parameter(s) will optimize the likelihood function evaluated at the first-stage marginal parameter estimates (see Shih and Louis (1995)). The traditional survival and new CDF-based approaches are summarized together in Table 1.

Table 1.

Existing (Method 0) and newly-proposed (Methods 1-4) multi-trial copula modeling and estimation methods.

Name	Copula Type	Association Modeling	Estimation
Method 0	Clayton - Survival	Equal across trials	Simultaneous
Method 1	Clayton - CDF	Equal across trials	Simultaneous
Method 2	Clayton - CDF	Trial-specific	Simultaneous
Method 3	Clayton - CDF	Equal across trials	Two stage
Method 4	Clayton - CDF	Trial-specific	Two stage

3 Simulation Study

3.1 Data Generation and Settings

Motivated by published multi-trial surrogacy evaluations which may have relied on directionally misspecified copula models, we performed a simulation to study the consequences of fitting a survival copula (Method 0) to truly CDF copula data generated from multiple trials. In the same study, we also compare the estimation performance of different multi-trial copula strategies assuming proper directional specification (Methods 1-4; see Table 1). Throughout, we assume a time-to-event endpoint S is a candidate surrogate to replace a time-to-event primary endpoint T based on a collection of 10 historical trials indexed by i ∈ {1, …, N} with N = 10. Within the ith trial, we assume n_i= 1,000 patients indexed by j ∈ {1, …, n_i}, equally randomized to two treatment arms Z, where Z = 1 for experimental and Z = 0 for control. While S and T may follow any parametric or semi-parametric models, here we assume each marginally follows a Weibull distribution parameterized as

$$f(x|r,\lambda )=(r/\lambda ){(x/\lambda )}^{r-1}exp\{-{(x/\lambda )}^r\},r,\lambda ,x\ge 0.$$

Allowing unique baseline hazard functions for each trial and endpoint, the surrogate and true clinical endpoints for patient j from trial i are marginally modeled as

$$S_{ij}~\text{Weibull}(r_i^S,{\lambda }_{ij}^S)$$ (5)

$$\text{and}{T}_{ij}~\text{Weibull}(r_i^T,{\lambda }_{ij}^T),$$ (6)

where $r_i^S$ and $r_i^T$ are trial-specific shape parameters, and regressors z_ij and corresponding treatment coefficients α_i and β_i are introduced through trial and patient-specific scale parameters ${\lambda }_{ij}^S=exp(-{\mu }_i^S-{\alpha }_i{z}_{ij}/r_i^S)$ and ${\lambda }_{ij}^T=exp(-{\mu }_i^T-{\beta }_i{z}_{ij}/r_i^T)$. This model parameterization was chosen for comparability of its treatment coefficients with those resulting from Cox proportional hazards models (see Cox (1972)). Trial treatment effect pairs (α_i, β_i) are assumed to arise from a bivariate normal distribution with mean (0,0), variances var(α_i) = var(β_i) = 0.50, and squared correlation $R_{\mathit{\text{trial}}}^2={\{\mathit{\text{corr}}({\alpha }_i,{\beta }_i)\}}^2=0.90$, where R_trial denotes the true trial-level surrogacy of S for T (Burzykowski et al., 2001). We further assume ${\mu }_i^S={\mu }_i^T=1$ and $r_i^S=r_i^T=5$, and within each trial, we generate patient-level bivariate Weibull data (s_ij, t_ij) by converting correlated uniformly-distributed paired variates (u_ij,v_ij) from the Clayton CDF copula (3) to random Weibull variates via the inverse-CDF method, where trial-specific marginal CDFs F_Si(s_ij) and F_Ti(t_ij) follow the parameterization given in (5) and (6).

We consider a range of simulation scenarios with equal (S, T) association across trials given by Kendall's τ_i = τ ∈ {0.1, 0.3, 0.5, 0.7, 0.9} according to the relationship τ= (γ − 1)/(γ+1), where γ is the copula association parameter described in (3). We further consider a scenario where the 10 trials are comprised of τ_i= 0.20 for i ∈ {1, …, 5} and τ_i= 0.80 for i ∈ {6, …, 10}. Finally, we consider scenarios with equal τ_i= τ= 0.90 and approximately 30% or 70% independent uniform censoring on S and T. The effects of trial size and true trial-level surrogacy on estimation performance were also explored in preliminary simulations, but neither was found to have significant differential impact among the methods presented.

3.2 Simulation Results

We performed 500 iterations for each scenario and computed summary statistics for several quantities of interest across all methods considered. Maximum likelihood estimation for all copula approaches was performed using the Broyden-Fletcher-Goldfarb-Shanno (BFGS) optimization method (Nocedal and Wright, 1999). Because Methods 2 and 4 involve likelihoods that are separable by trial, trial-specific optimization was performed for efficiency. For the purpose of comparing quantities estimated from joint copula models with those originating from traditional marginal models, we also present results based on trial-specific independent Cox proportional hazards models for S and T.

3.2.1 Estimation of Marginal Treatment Effects

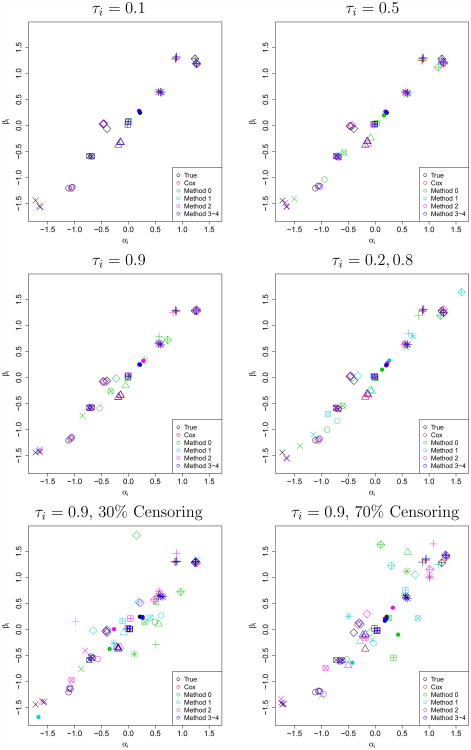
First, estimated trial-specific treatment effects (α̂_i, β̂_i) were visually compared to the “true” generated treatment effects (α_i, β_i) for a single iteration under each scenario, as shown in Figure 2. We observed that as τ_i=τ→1, (α̂_i, β̂_i) → (0, 0) under Method 0 (survival copula). This phenomenon was verified both by plotting additional iterations and moving the mean of (α_i, β_i) away from (0, 0). Because traditional bias computations for estimates of α_i and β_i will fail to reveal this symmetric shrinkage, we instead compute the absolute bias (average absolute value of the errors) for estimates of α_i and β_i, which are presented with mean-squared error (MSE) of the estimates in the first two sections of Table 2.

Figure 2.

Scatterplots of true and estimated (α_i, β_i) across methods (colors) for 10 trials (shapes) from a single iteration for τ_i=0.1, 0.5, 0.9 or an equal mix of {0.20, 0.80} without censoring, and for τ_i = 0.9 with 30% or 70% censoring.

Table 2.

Top panel: average absolute error (absolute bias) and mean squared error (MSE) for α̂_i and β̂_i. Middle panel: bias and MSE for τ̂ (single association methods) or τ̂_i (trial-specific association methods), where computations for methods with trial-specific association are further averaged across trials. Lower panel: bias and MSE for $R_{\mathit{\text{trial}}}^2$ relative to generated $R_{\mathit{\text{trial}},\mathit{\text{gen}}}^2$.

		Absolute Bias (×10−3)						MSE (×10−3)
τi	Cens	Cox	M0	M1	M2	M3	M4	Cox	M0	M1	M2	M3	M4
							α̂i
0.1	0%	53.8	53.4	52.7	52.7	53.1	53.1	4.6	4.4	4.3	4.4	4.4	4.4
0.3	0%	53.3	56.6	50.1	50.3	52.6	52.6	4.5	5.0	4.0	4.0	4.4	4.4
0.5	0%	53.0	72.8	47.3	47.9	52.2	52.2	4.4	8.3	3.5	3.6	4.3	4.3
0.7	0%	53.3	119.0	45.4	46.1	52.7	52.7	4.5	22.1	3.2	3.3	4.3	4.3
0.9	0%	53.1	258.8	41.4	42.4	52.3	52.3	4.5	104.8	2.7	2.9	4.3	4.3
0.2 & 0.8	0%	53.5	79.9	174.2	48.7	52.5	52.5	4.5	10.2	47.7	3.7	4.3	4.3
0.9	30%	64.3	751.4	773.6	306.0	64.9	64.5	6.6	911.2	941.9	163.3	6.6	6.6
0.9	70%	97.6	652.1	706.0	228.1	97.1	97.5	15.4	701.1	784.2	83.8	15.2	15.2
							β̂i
0.1	0%	53.6	52.8	52.4	52.4	52.7	52.7	4.5	4.3	4.3	4.3	4.3	4.3
0.3	0%	53.9	56.1	50.9	51.2	53.1	53.1	4.6	5.0	4.0	4.1	4.4	4.4
0.5	0%	54.6	73.3	48.6	49.2	53.7	53.7	4.7	8.4	3.7	3.8	4.5	4.5
0.7	0%	54.7	119.2	45.9	46.8	53.8	53.8	4.7	22.3	3.3	3.4	4.5	4.5
0.9	0%	53.1	258.6	41.5	42.5	52.2	52.2	4.5	105.1	2.7	2.9	4.3	4.3
0.2 & 0.8	0%	53.9	79.3	175.7	49.0	52.9	52.9	4.6	10.1	48.5	3.7	4.4	4.4
0.9	30%	62.7	734.9	767.5	305.8	63.5	63.1	6.3	875.6	929.0	162.6	6.4	6.4
0.9	70%	97.7	644.5	694.9	227.5	97.6	97.5	15.0	667.1	759.2	83.4	14.9	14.9
		Bias (×10−3)						MSE (×10−4)
τi	Cens	Cox	M0	M1	M2	M3	M4	Cox	M0	M1	M2	M3	M4
							τ̂ (or τ̂i)
0.1	0%	-	−49.9	0.5	0.4	−79.7	−83.6	-	25.3	0.3	3.0	79.3	88.2
0.3	0%	-	−115.9	0.1	−0.0	−0.5	−0.4	-	134.9	0.3	2.5	0.3	2.6
0.5	0%	-	−159.2	0.3	0.2	−0.7	−0.6	-	253.8	0.2	1.9	0.2	2.0
0.7	0%	-	−153.3	0.4	0.2	−1.0	−0.9	-	235.6	0.1	1.0	0.1	1.0
0.9	0%	-	−38.7	0.2	0.1	−2.2	−2.1	-	15.0	0.0	0.2	0.2	0.2
0.2 & 0.8	0%	-	−100.6	78.4	0.3	-66.6	-0.6	-	1001.7	961.6	1.7	944.7	1.8
0.9	30%	-	−307.5	−290.2	−90.3	−110.7	−65.5	-	1243.9	973.4	106.3	131.7	50.0
0.9	70%	-	−185.3	−344.3	−102.6	−128.2	−86.5	-	660.5	1272.2	116.1	172.9	83.0
		Bias (×10−3)						MSE (×10−3)
τi	Cens	Cox	M0	M1	M2	M3	M4	Cox	M0	M1	M2	M3	M4
	${\widehat{R^2}}_{\mathit{\text{trial}}}$ compared to $R_{\mathit{\text{trial}},\mathit{\text{gen}}}^2$
0.1	0%	−13.7	−13.5	−13.1	−13.2	−13.5	−13.5	1.2	1.2	1.2	1.2	1.2	1.2
0.3	0%	−9.2	−9.0	−7.7	−7.8	−8.8	−8.8	0.8	0.8	0.6	0.6	0.8	0.8
0.5	0%	−7.5	−8.0	−3.9	−4.0	−7.3	−7.3	0.7	0.8	0.3	0.4	0.7	0.7
0.7	0%	−4.5	−4.8	−0.1	−0.2	−4.3	−4.3	0.4	0.6	0.1	0.2	0.4	0.4
0.9	0%	−2.3	1.2	−0.1	0.0	−2.1	−2.1	0.3	0.6	0.1	0.1	0.3	0.3
0.2 & 0.8	0%	−8.5	−9.0	−7.3	−6.1	−8.4	−8.4	0.7	0.9	2.7	0.5	0.7	0.7
0.9	30%	−7.1	−506.2	−508.3	−33.3	−8.1	−7.8	0.6	327.2	329.7	6.1	0.7	0.7
0.9	70%	−34.8	−542.9	−617.2	−24.2	−34.7	−35.1	3.9	355.7	435.8	3.6	3.8	3.9

Across the scenarios considered, the two-stage estimation approaches (Methods 3 and 4) yield the most accurate and precise estimates of marginal treatment effects. In the top panel of Table 2, we find that CDF-based copula Methods 1-4 perform well at estimating the true treatment effects in cases of equal τ_i across trials and no censoring, yielding the smallest absolute bias and MSE, similar to the marginal Cox approach. When τ_i=τ is low, the directional misspecification of Method 0 has little impact on absolute bias and MSE, but as τ_i= τ increases to 0.90, absolute bias and MSE of α̂_i and β̂_i under this traditional approachincrease dramatically, with absolute bias more than 5 times larger and MSE more than 30 times larger than those quantities given by the best performing CDF-based approaches (Methods 1 and 2).

When τ_i varies across trials, with half of trials demonstrating low (τ_i= 0.20) and half demonstrating high (τ_i= 0.80) association between S and T, Methods 0 and 1 are unable to capture the differences in association across trials and both suffer in terms of absolute bias and MSE for estimating the marginal treatment effects. Interestingly for this scenario, Method 0's additional misspecification of the direction of (S, T) association offers a protective advantage against extreme bias and MSE relative to Method 1. Methods 2 and 4, which allow for trial-specific association, yield improved performance with Method 2 (simultaneous estimation) showing slight gains over Method 4 (two-stage estimation). Because the first-stage marginal estimation step is identical for two-stage estimation Methods 3 and 4, the single association parameter assumption of Method 3 does not negatively affect marginal treatment effect estimation.

When τ_i = τ = 0.90 and S and T are subject to 30% or 70% censoring, Methods 0 and 1 (and to a lesser extent, Method 2) struggle to estimate the true marginal treatment effect pairs (α_i, β_i)relative to the other approaches. This is likely due to the following three reasons, in combination: censored data dramatically increases the complexity of both likelihood functions (2) and (4) to include the second, third, and fourth terms inside the products, which otherwise vanish to one; likelihood functions for the equal-association approaches (Methods 0, 1, and 3) do not have the advantage of being separable by trial and thus require estimation of 6N + 1 parameters from a single likelihood, rather than estimation of 7 parameters from each trial-specific likelihood as in Methods 2 and 4; among the three equal-association approaches (Methods 0, 1, and 3) likely to suffer in the presence of censoring for the reasons previously mentioned, Methods 0 and 1 call for simultaneous estimation of marginal effects and association parameters, and are unable to benefit fromthe protective effect of a two-stage approach in estimation of treatment effects at the first stage. The reduced performance of Method 2 in estimating marginal treatment effects in the presence of censoring is likely due to the increased likelihood complexity, in combination with its simultaneous (versus two-stage) estimation of the treatment effects with the trial-specific association parameters. It should be noted that introduction of right-censoring further reduces the weak upper-tail association assumed for S and T, where Method 0 continues to assume strong S,T association at later event times.

3.2.2 Estimation of Patient-Level Surrogacy

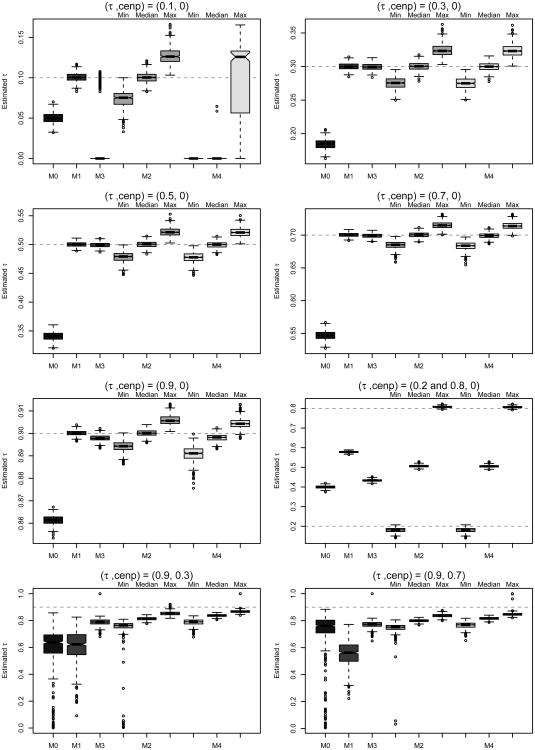
Next we compare performance of the copula methods in estimation of patient-level surrogacy, or equivalently, estimation of the trial-specific (S, T) association, τ_i, as shown in the middle panel of Table 2 and in Figure 3. For methods assuming trial-specific associations (Methods 2 and 4), bias and MSE computations for trial-specific estimates of τ_i are further averaged across trials, which we assert produces conservative estimates of these quantities for comparison with those from the other methods.

Figure 3.

Boxplots of τ_i (trial-specific association) or τ (equal association) estimates across iterations for each copula method and scenario considered. For methods assuming trial-specific associations, boxplots are given for the minimum, median, and maximum value of τ̂_i across trials.

Aside from one exceptional scenario not likely to be encountered in practice, Method 4 demonstrated the most consistent performance in terms of bias and MSE across the scenarios considered. We find that when equal association is assumed across trials (τ_i = τ) without censoring, all CDF-based methods perform well at estimating patient-level surrogacy except for the case when patient-level association between S and T is near zero. In this case, which is unlikely to be encountered for truly promising surrogates, the two-stage estimation Methods 3 and 4 struggle to estimate a truly low τ_i= τ after fixing the marginal parameters at their first-stage estimates. In general, the traditional evaluation approach (Method 0) consistently underestimates the (S, T) association by as much as τ − τ̂= 0.15, due to the incorrect relationship pattern between S and T it assumes in this simulation. It is interesting to observe that as τ_i = τ approaches a boundary of τ = 0 or τ= 1, Method 0's performanceat estimating patient-level association actually improves relative to its performance for moderate values of τ. This is because the shape of (S, T) relationship assumed by the Clayton survival copula and the opposing shape assumed by the Clayton CDF-copula near similarity for values of τ near the boundaries of [0, 1], as can be seen in Figure 1.

When τ_i truly varies across trials, Method 0 (and to a lesser extent, Methods 1 and 3) struggle to estimate patient-level surrogacy. This is not surprising, as these are the approaches that assume equal (S, T) association across trials. Instead, these methods effectively estimate an average τ across trials, though it should be noted the bias associated with estimating (τ̄= 0.50) is largest for Method 0 due to the directional misspecification of (S, T) association. Methods 2 and 4, which allow for trial-specific patient-level association, perform equally well in this case.

In the presence of censoring, Methods 0 and 1 yield the worst performance for estimating patient-level surrogacy, while Methods 2-4 continue to benefit from simplified likelihoods and/or two-stage estimation as described in Section 3.2.1. Of the latter approaches, Method 4 demonstrates the best patient-level surrogacy estimation performance in terms of bias and MSE; however, all methods underestimate patient-level surrogacy to some degree under censoring, as shown in Figure 3.

3.2.3 Estimation of Trial-Level Surrogacy

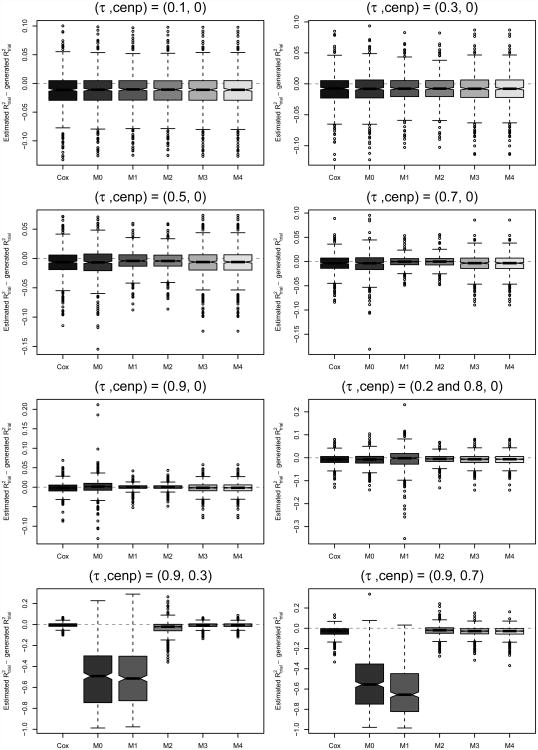
An important quantity of interest in a multi-trial surrogacy evaluation is trial-level surrogacy, $R_{\mathit{\text{trial}}}^2$, defined as the squared Pearson correlation of the treatment effect pairs (α_i, β_i) across trials, optionally weighted by trial size (Burzykowski et al., 2001). In practice, estimates ${\widehat{R^2}}_{\mathit{\text{trial}}}$ are computed from the estimated copula treatment effects (α̂_i, β̂_i), possibly after adjustment for estimation error (see, e.g., Burzykowski et al. (2001); Renfro et al. (2012)). Here, given the possibly biased estimation of (α_i, β_i) as discussed in Section 3.2.1, we investigate the subsequent impact on $R_{\mathit{\text{trial}}}^2$ estimation. Because generated treatment effect pairs vary at each simulated iteration, generated values of trial-level surrogacy, denoted $R_{\mathit{\text{trial}}–\mathit{\text{gen}}}^2$, also vary and in some cases may not be near $R_{\mathit{\text{trial}}}^2$; thus, for each method, we compare estimates ${\widehat{R^2}}_{\mathit{\text{trial}}}$ to the value of trial-level surrogacy generated at each iteration, where $R_{\mathit{\text{trial}}–\mathit{\text{gen}}}^2\in [0,1]$. Results are presented in the bottom panel of Table 2, as well as in Figure 4. We note that comparisons of ${\widehat{R^2}}_{\mathit{\text{trial}}}$ to true trial-level surrogacy $R_{\mathit{\text{trial}}}^2=0.90$ were also considered for all scenarios, but as qualitative differences from the results presented herein were not observed, these results are omitted for brevity.

Figure 4.

Boxplots of differences ${\widehat{R^2}}_{\mathit{\text{trial}}}$ – $R_{\mathit{\text{trial}}–\mathit{\text{gen}}}^2$ across iterations for each method (Cox and copula) and scenario considered.

Across the scenarios considered, both trial-specific association approaches (Methods 2 and 4) as well as the equal-association, two-stage estimation approach (Method 3) perform well at estimating generated trial-level surrogacy, $R_{\mathit{\text{trial}}–\mathit{\text{gen}}}^2$. Among the equal-association and trial-specific association scenarios without censoring, we find that all copula-based and Cox methods perform similarly well at $R_{\mathit{\text{trial}}–\mathit{\text{gen}}}^2$ estimation in terms of bias, while Method 0 demonstrates slightly increased variability as τ_i=τ→1. When (S, T) association varies across trials, Method 1 shows increased variability, and when censoring is introduced, both Methods 0 and 1 struggle to accurately estimate trial-level surrogacy due to their trouble estimating the marginal treatment effects used in the ${\widehat{R^2}}_{\mathit{\text{trial}}}$ computations.

It is noteworthy that for Method 0, the survival copula approach commonly used in practice, the shrinkage of the estimated treatment effects toward (0, 0) as τ_i=τ→1 as discussed in Section 3.2.1 does not alter the strength of their relationship (as shown in 2), and thus estimation of $R_{\mathit{\text{trial}}}^2$ is not severely affected. This is partly because the shrinkage is symmetric by design, as we center the generated treatment effect pairs around (0,0) throughout our simulations. However, in our experience, when the treatment effect pairs are centered away from (0, 0), the shrinkage becomes asymmetric (simulations not shown), distorting the trial-level surrogacy relationship and negatively impacting $R_{\mathit{\text{trial}}}^2$ estimation under the survival copula approach (Method 0) when data truly originate from a CDF copula.Furthermore, it is often desired in practice to predict a treatment effect on a trueendpoint, β_i, conditional on an observed value of the treatment effect associated with a promising surrogate endpoint, α_i. By definition, a promising surrogate requires both ${\widehat{R^2}}_{\mathit{\text{trial}}}$ near 1 and τ̂ near 1, precisely the condition where treatment effect pairs shrink the most under the traditional survival copula approach. In this case, we caution that application of a directionally misspecified copula (e.g., Method 0 when data resemble a Clayton CDF copula) may accurately estimate $R_{\mathit{\text{trial}}}^2$ to be high despite its biased treatment effect estimates, which in turn could yield erroneous conditional treatment effect predictions of interest. This phenomenon of observed high trial-level surrogacy based on biased treatment effects will be evident in the colon cancer surrogacy analysis presented in Section 4.

4 Example: Evaluation of DFS as Surrogate for OS in ACCENT Trials

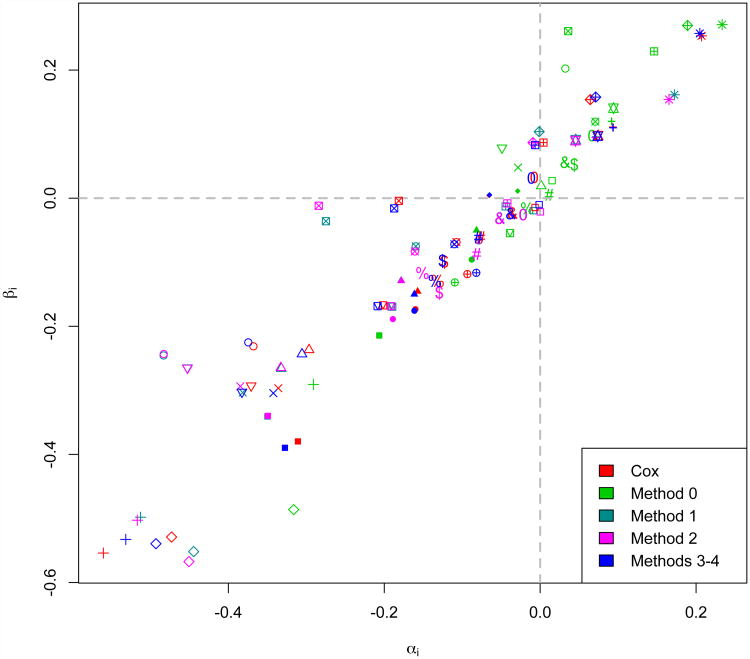
To compare the surrogacy conclusions that would be drawn from survival-based and CDF-based implementations of the same multi-trial copula (Clayton) in practice, we assessed the surrogacy of DFS for OS using patient-level data from 18 randomized phase III trials for adjuvant therapies in stage II and stage III colon cancer. Previously, using data from the same collection of trials belonging to the Adjuvant Colon Cancer Endpoints (ACCENT) group, Sargent et al. (2005) demonstrated that DFS with a median of 3 years follow-up is a valid surrogate for OS with a median of 5 years follow-up in the adjuvant setting. This validation of DFS to replace OS as a primary endpoint in adjuvant colon cancer was based in part on the Clayton survival copula approach assuming a single association parameter across trials (Method 0). The original set of ACCENT trials were conducted from 1977 to 1999, and collectively include 20,898 patients assigned to 43 treatment arms, composed of 34 active treatment arms (with at least one fluorouracil (FU)-based chemotherapy arm per trial) and 9 surgery-only arms.Censoring longer-term patient follow-up at 8 years, and maintainingthe natural ordering of the treatment arms in the original trial designs, we consider pairwise comparisons of experimental to control arms for a total of N= 25 trial units. Results are presented numerically in Table 3 and graphically in Figure 5, with all estimates of trial-level surrogacy weighted by trial size.

Table 3.

Estimates of $R_{\mathit{\text{trial}}}^2$ weighted by trial size, associated standard errors (SE), and estimates of τ (or range of estimated τ_i) under Cox and copula surrogacy evaluation methods for the ACCENT trials.

	Estimate (SE)
	Cox	M0	M1	M2	M3	M4
${\widehat{R^2}}_{\mathit{\text{trial}}}$	0.928	0.874	0.864	0.852	0.930	0.930
SE( ${\widehat{R^2}}_{\mathit{\text{trial}}}$)	0.108	0.138	0.143	0.148	0.107	0.107
τ̂ or range of τ̂i	-	0.891	0.692	(0.540 - 0.789)	0.648	(0.482 - 0.753)

Figure 5.

Estimated treatment effect pairs (α̂_i, β̂_i) presented by estimation method (colors) for 25 individual ACCENT trial comparisons (symbols). Reference lines at α_i= 0 and β_i= 0 support the bias of Method 0 effects positively along the α_i= β_i diagonal.

4.1 ACCENT Results: Trial-Level Surrogacy

First, we note from graphical exploration that DFS and OS for this dataset are more highly associated at earlier event times than at later event times, which motivated use of the Clayton CDF copula for data generation in the simulation study of Section 3. This shape and direction of association, which we commonly encounter for joint time-to-event endpoints, similarly indicate a CDF-based Clayton copula could be a reasonable modeling approach for this surrogacy analysis. In practice, one would evaluate a number of copulas (e.g., Clayton, Hougaard, Plackett) for a given dataset, through preliminary (not necessarily meta-analytic) goodness-of-fit examinations. Such copula selection methods have been widely discussed elsewhere (see, e.g., Wang and Wells (2000) or Genest, Rmillard, and Beaudoin (2009) for an overview); here, we focus attention on the Clayton copula previously utilized and published for these data, and provide a re-analysis to include both traditional (survival-based) and alternative proposed (CDF-based) approaches.

In general, we find that DFS exhibits high trial-level surrogacy for OS across the methods considered, generally consistent with the published validation of DFS as a surrogate for OS (Sargent et al., 2005). However, copula Methods 0-2 yield considerably lower $R_{\mathit{\text{trial}}}^2$ estimates (range: 0.85–0.87) than the Cox and two-stage estimation copula Methods 3 and 4 (all equal to 0.93). This is consistent with our simulation findings that copula Methods 3 and 4 best agree with the Cox approach in terms of treatment effect estimation (and thusterms of treatment effect estimation (and thus $R_{\mathit{\text{trial}}}^2$ estimation) in the presence of early S, T association, a large amount of right-censoring, and unequal (S, T) association across trials, which are each potentially relevant features ofthe ACCENT trials. Additionally, Methods 3 and 4 yield the smallest standard errors for trial-level surrogacy estimation (both equal to 0.11) compared to the other copula methods (range: 0.14–0.15).

Although trial-level surrogacy estimates are similar across trials, Figure 5 demonstrates that when Cox-based treatment effects are trusted for comparison, the two-stage copula estimation approach utilized by Methods 3 and 4 consistently estimates treatment effect pairs (α̂_i,β̂_i) to be in close agreement with Cox effect pairs, while treatment effect pairs are substantially biased positively under Method 0. We hypothesize that for this analysis, the bias observed under the traditional and previously published method (Method 0) is largely due to misspecification of the direction of implementation of the Clayton copula. Because the ACCENT treatment effect pairs are not centered around (0,0) as they were in the simulation study, this bias is asymmetric and thus has a more profound effect on $R_{\mathit{\text{trial}}}^2$ estimation. When trial-specific estimates (α̂_i, β̂_i) are used in a leave-one-out fashion to predict an unobserved treatment effect on OS in a “new” trial (β₀) given the observed effect on DFS (α̂₀), we find that 95% confidence intervals for β̂₀ contain the unobserved value 88% of the time for Methods 0-2 and 92% of the time for Cox and Methods 3-4. Thus, we would expect the two-stage CDF-based approaches (Methods 3 and 4) to yield the best predictions of unobserved treatment effects on OS in future adjuvant colon cancer trials using DFS as a primary endpoint, where these predictions are of particular interest to regulatory authorities.

Though the purpose of this data analysis is to highlight the differences in surrogacy that could emerge from opposite (CDF versus survival) implementations of a single copula (Clayton), in practice, one could perform a model selection test such as the Vuong (1989) test to choose between non-nested models such as the Clayton CDF versus Clayton survival multi-trial copulas. The Vuong test, unlike the copula goodness-of-fit tests available in existing software packages, may be used to directly compare non-nested models of any level of complexity, and is additionally capable of handling censored data. We performed Vuong teststo compare the first-stage estimation fit of Clayton survival versus Clayton CDF multi-trial copula models, M0 versus M1, for both the DFS/OS and TTR/OS surrogacy relationships. For DFS/OS, the null hypothesis of no difference in model fit was not rejected (p = 0.41), but for TTR/OS, the Clayton CDF copula demonstrated a better fit than the Clayton survival copula (p = 0.039).

4.2 ACCENT Results: Patient-Level Surrogacy

Estimation of patient-level surrogacy for the ACCENT trials yields greater disagreement among the copula methods examined. It is reasonable to assume that (S, T) association might be trial-specific in practice, and indeed, Methods 2 and 4 estimate the range of τ_i to be quite large, respectively (0.54 – 0.79) and (0.48 – 0.75) across the 25 trial units. Methods 1 and 3, which assume equal association across trials, yield pooled (S, T) association estimates of τ̂= 0.69 and τ̂= 0.65, respectively. It is interesting that the pooled patient-level surrogacy estimate given by Method 0, τ̂ = 0.89, is even higher than the largest trial-specific association estimate observed (under Method 2) by a difference of over 0.10. In this case, patient-level surrogacy estimation under the traditional survival copula approach, Method 0, may be untrustworthy and adversely affected by its simultaneously poor estimation of the marginal treatment effects.

5 Discussion

Through both simulation studies and re-analysis of DFS as a surrogate for OS in adjuvant colon cancer, we have demonstrated that a multi-trial copula model traditionally used to evaluate time-to-event surrogate endpoints may produce biased estimates of patient-level association, marginal treatment effects, and/or trial-level surrogacy when careful attention is not paid to match the shape of (S, T) association apparent in the data with the direction of association assumed by the copula. Specifically, we have shown that even when the correct (or in practice, the best possible) copula family is chosen for modeling, large bias may result from directional misspecification, i.e., the wrong choice of survival versus CDF copula implementation. Furthermore, this bias be exacerbated by the presence of those factors likely to be encountered in applications involving a promising surrogate: a high level of patient-level (S, T) association, unequal patient-level (S, T) association across trials, and possibly high levels of censoring for one or both endpoints.

In multi-trial copula analyses published to date, only survival copula implementations of radially asymmetric copulas (e.g., Clayton and Hougaard) have been considered, thereby excluding at least half of association patterns that might be more appropriate for a given dataset. Even when the correct direction of copula implementation is selected, two-stage copula estimation may improve estimation performance compared to simultaneous estimation, and models allowing for trial-specific (S, T) association yield a clearer picture of surrogacy relationships likely to exist in practice. Better estimation of (S, T) association will yield reliable information regarding patient-level surrogacy, while improved estimates of trial-specific treatment effects will in turn yield both reliable estimates of trial-level surrogacy and improved prediction of the hypothetical treatment effect on the true endpoint in a new trial given the effect on the surrogate–a quantity of special interest and importance to regulators when surrogate endpoints are to be used in large confirmatory trials.

Based on the simulation results and data analyses presented here, we make the following 4 recommendations:

Recommendations for Multi-Trial Copula Modeling of Surrogate Relationships

1. Careful selection of a specific copula (e.g., Clayton) informed by the shape of (S, T) association present in the data for a given application

2. Equally careful selection of either a survival-based or CDF-based implementation of the copula, given the chosen copula and direction of the (S, T) association

3. A two-stage estimation approach for large problems involving right-censoring

4. Relaxing the assumption of equal (S, T) association across trials where such an assumption is likely to be violated

As implied by recommendations (1) and (2) above, the arguments presented in this paper are relevant for all copulas C(u, v) defined on [0, 1]² that exhibit asymmetry over the line v= 1−u, i.e., copulas lacking radial symmetry. This includes, e.g., the Clayton and Gumbel copulas from the popular Archimedean family of copulas. Radially symmetric copulas for which recommendation (2) may be less of a concern (when such copulas are appropriate for the data) include the Frank copula from the Archimedean family, as well as the Gaussian copula and t-copula (Nelson, 2006). In general, goodness-of-fit tests developed for selecting from among various copula models (see, e.g., the review provided by Genest, Rmillard, and Beaudoin (2009)) may be useful during preliminary copula selection, prior to initiating the multi-trial modeling steps discussed in this paper. During either preliminary pooled copula modeling or formal subsequent multi-trial modeling, use of a model selection test for non-nested models such as the Vuong test may be particularly useful for selecting an appropriate copula family and choosing between the survival versus CDF implementation in the presence of right-censored data (Vuong, 1989). When comparing several radially asymmetric copulas for a given application is of interest, the concept of tail order as described by Hua and Joe (2011) for summarizing the strength of (asymmetric) upper and lower tail dependence for specific copulas, may lend some additional intuition.

Another important discussion point is whether copula models as a whole offer any advantages over simple application of marginal Cox models for evaluating candidate surrogate endpoints. We would argue that copula modeling of surrogacy relationships in general–and improved copula modeling of these relationships more specifically–do remain relevant, as they are widely used in such evaluations (as discussed in Section 1), with only results based on survival copula implementations published to date. Additionally, there exists widespread agreement that both patient-level and trial-level surrogacy must be sufficiently high for a new surrogate endpoint to become used in practice, i.e., resulting in designation of the surrogate as the primary endpoint in a future trial within the same disease setting. While straight-forward modeling of S and T (and associated treatment effects on each endpoint) via Cox models may yield reliable estimates of trial-level surrogacy, a separate model–presumably a copula or other bivariate alternative–must then be fitted to assess patient-level surrogacy. In (most) cases where patient-level surrogacy is being evaluated jointly with trial-level surrogacy, and where a copula approach is capable of producing reliable estimates of both, we would argue that a multi-trial copula model eclipses the need for additional Cox modeling. However, in rare instances where patient-level surrogacy is believed to be well-established and only trial-level surrogacy is of interest, foregoing copula modeling in favor of the Cox approach is appropriate. In general, we recommend performing both approaches, where the estimated treatment effects (and resulting trial-level surrogacy estimate) derived from the Cox approach may compared against and used to gauge the performance of a chosen copula approach, similar to the strategy taken in Section 4.

It should also be noted that complementary multi-trial methods for evaluating candidate surrogate endpoints do exist, and the change of practice for copula-based surrogacy evaluations suggested in this paper will also directly improve applications of the complementary methods. For example, the so-called surrogate threshold effect (STE), a multi-trial measure defined by Burzykowski and Buyse (2006) as the minimum treatment effect on the surrogate endpoint in a new trial necessary to predict a non-zero effect on the (incompletely observed) true endpoint, depends directly on prior unbiased estimation of marginal treatment effects from a joint (patient-level and trial-level) surrogacy model. When the issues addressed bythe recommendations above are not considered during preliminary application of the joint model, the resulting value of STE–an arguably important quantity, particularly for regulatory purposes–may be derived from an unrepresentative S, T association pattern and lead to incorrect predictions regarding the efficacy of a new treatment.

Finally, we note that our findings and recommendations extend to any surrogacy evaluation setting requiring copula modeling, for example where one endpoint is not time-to-event, or where two uncensored endpoints are not amenable to some other joint distribution (e.g., bivariate Normal). Multi-trial copulas such as those described in this paper, when carefully chosen to reflect and address the nature of the application at hand, are powerful tools capable of simultaneously evaluating patient-level and trial-level association from a single model. Based on our findings, we encourage their continued use in accordance with the provided recommendations.