Methods for Multilevel Ordinal Data in Prevention Research

Abstract

This paper discusses statistical models for multilevel ordinal data that may be more appropriate for prevention outcomes than are models that assume continuous measurement and normality. Prevention outcomes often have distributions that make them inappropriate for many popular statistical models that assume normality, and are more appropriately considered ordinal outcomes. Despite this, the modeling of ordinal outcomes is often not well understood. This article discusses ways to analyze multilevel ordinal outcomes that are clustered or longitudinal, including the proportional odds regression model for ordinal outcomes, which assumes that the covariate effects are the same across the levels of the ordinal outcome. The article will cover how to test this assumption and what to do if it is violated. It will also discuss application of these models using computer software programs.

1. Introduction

In many prevention science studies the outcome of interest is measured in a series of ordered categories. Such outcomes are termed “ordinal” and can represent a variety of graded responses such as ratings of severity (e.g., none, mild, moderate, severe), agreement ratings (disagree, undecided, agree), and in particular Likert scales (e.g., strongly disagree, disagree, neither agree nor disagree, agree, strongly agree). In other cases, the outcome may represent a count (e.g., number of cigarettes smoked) that has a large number of zero responses (i.e., no cigarettes), many values in the one to five-cigarette range, and a few extreme values. In these cases, an ordinal variable can be constructed with ordered categories of, say, 0, 1, 2, 4, 5, and 6 or more cigarettes.

Researchers sometimes analyze ordinal outcomes, like Likert scale outcomes, assuming a normal (continuous) distribution for the outcome. However, treating the outcome as normal assumes that the intervals between the categories of the Likert scale are all equal, which is clearly a dubious assumption. Also, as will be described, the ordinal model takes into account the ceiling and floor effects of the dependent variable, whereas models for continuous data do not. For example, if the outcome is coded in categories 1 to 5, a model for normal data can easily yield estimates below 1 and above 5. In this case, as [22] point out, biased estimates of the regression slopes and incorrect conclusions can easily result. Furthermore, as [42] note, the advantage of ordinal models in accounting for ceiling and floor effects of the ordinal variable is most critical if the variable is highly skewed, which is often the case in prevention research where many of the responses are observed in the lowest and/or highest category of the ordinal outcome. Recently, [4] conducted an extensive simulation study addressing these issues and concluded that continuous models were only reasonable when the ordinal outcome had seven or more response categories and its distribution was approximately normal. Thus, for example, if one has a Likert-scale outcome with five categories (e.g., strongly disagree, disagree, neither agree nor disagree, agree, strongly agree) an ordinal model should be used. Alternatively, researchers sometimes dichotomize an ordinal outcome and analyze it using (binary) logistic regression. [35] provided a simulation study in which an ordinal outcome with 5 categories was dichotomized and observed rather large losses of precision and power resulting from this practice. Also, [40] showed that the regression estimates can be poorly estimated when dichotomizing an ordinal outcome in datasets of limited size. Since power is a critical issue in small datasets, it therefore behooves researchers to analyze ordinal outcomes with ordinal models, rather than losing power and information by dichotomizing them. The ordinal logistic regression model, described as the proportional odds model by [21], provides a useful approach for analyzing ordinal outcomes. For multilevel data, where observations are nested within clusters (e.g., classes, schools, clinics) or are repeatedly assessed across time within subjects, mixed-effects regression models (aka multilevel or hierarchical linear models) are often used to account for the dependency inherent in the data [7,13,30]. Mixed-effects models for ordinal data have been developed for quite some time [11,41,2], including software [12], making such analysis accessible to prevention researchers.

Models for ordinal outcomes often include the proportional odds assumption for model covariates. For an ordinal response with C categories, this assumption states that the effect of the covariate is the same across the C-1 cumulative logits of the model (or proportional across the cumulative odds). The idea is that if one did dichotomize the ordinal outcome and used a (binary) logistic regression model, the regression slopes would be equal, regardless of how one did the dichotomization (e.g., for an ordinal variable with 3 categories there are two possible dichotomizations: 1 vs 2 & 3, and 1 & 2 vs 3). In previous papers [15,16], we have described an extension to allow for non-proportional odds for the covariates. This extension provides a way of testing the proportional odds assumption. Namely, one can compare a model that relaxes the proportional odds assumption (i.e., allows covariates to have different effects) to one that makes this assumption (i.e., does not allow covariates to have different effects) using a likelihood-ratio test.

In terms of the organization, the mixed model for clustered ordinal data will be described in Section 2. Both 2- and 3-level models will be considered, and Section 3 will illustrate application of the model using a smoking prevention dataset where students are nested within both classrooms and schools. Section 4 will detail the mixed model for longitudinal ordinal data, and Section 5 will illustrate use of this model with a longitudinal psychiatric dataset in which a patient’s level of depression is classified on an ordinal scale. Section 6 will describe aspects related to software, and Section 7 will conclude with some discussion.

2. Mixed Proportional Odds Model for Clustered Data

Suppose that subjects are clustered or nested within some kind of cluster (e.g., providers, hospitals, schools, families, etc.) and let i denote the cluster (i = 1,…, N ) and j denote the subject ( j = 1,…,n_i ). In the multilevel structure, level-1 subjects are clustered within level-2 clusters. There are a total of N clusters, each with n subjects, so that the total number of subjects is ${\sum }_i^N{n}_i$. Let Y_ij denote the ordinal outcome from subject j in cluster i, and let the ordered response categories be coded as c = 1, 2,…, C. Ordinal regression models often utilize cumulative comparisons of the categories. For this, define the cumulative probabilities for the C categories of the outcome Y as $P_{\mathit{ijc}}=Pr(Y_{ij}\le c)={\sum }_{m=1}^c{p}_{\mathit{ijm}}$, where p_ijm represents the probability of response in category m. For example, with three categories, we would have P_ij1 = p_ij1 as the probability of a response in category 1, and P_ij2 = p_ij1 + p_ij2 as the probability of a response in categories 1 and 2. The probability of a response in category 3 would be obtained by subtraction as p_ij3 = 1 − P_ij2.

The mixed-effects logistic regression model for the cumulative probabilities is expressed as a cumulative logit (i.e., log odds) model as

$$log\left[\frac{P_{\mathit{ijc}}}{1-P_{\mathit{ijc}}}\right]={\gamma }_c-\left[{\mathrm{x}}_{ij}\beta +{\upsilon }_i\right],$$ (1)

with C-1 strictly increasing model thresholds γ_c. These thresholds are akin to intercepts and represent the cumulative logits when the covariates and random effects equal 0. Basically, the thresholds indicate how many responses are in the different categories (when the covariates and random effects equal 0), and are usually not of great interest. The distribution of responses in the ordered categories is completely arbitrary. As usual, x_ij are the covariates and β are the regression slopes (i.e., effects of the covariates). The effect of the cluster on the subject’s outcome is represented by υ_i, and these cluster effects (i.e., one for each cluster) are assumed to be distributed in the population as $N(0,{\sigma }_{\upsilon }^2)$. The sample of clusters in a particular dataset represent the population of clusters that one wants to make inferences about, and so the cluster effects are “random” effects and have a distribution in the population. Alternatively, the regression coefficients β (and the thresholds γ_c) are “fixed” parameters because they do not have a distribution; they are unknown constants in the population that we use our sample data to estimate. As a result, the model is a “mixed” model because it includes both fixed and random parameters.

1. Proportional Odds Assumption

Since the slopes β do not carry the c subscript, they do not vary across categories. That is, the effect of each covariate in x is assumed to be the same across the C-1 cumulative logits. For example, if Y has three categories, it is as if one ran two binary logistic regressions (with dichotomized outcomes 1 vs 2 & 3 and 1 & 2 vs 3) and assumed that the covariate effects were the same for these two analyses. [21] calls this assumption the proportional odds assumption. Relaxing the proportional odds assumption is possible; [15] described a mixed non-proportional odds model, and [16] illustrate its use for substance use outcomes. In this case, the covariates have different effects on the C-1 cumulative logits. Tests of the proportional odds assumption can then be performed by running and comparing models: (a) assuming proportional odds vs. (b) relaxing proportional odds assumption. Comparing the model deviances (i.e., −2 log likelihood values) that are obtained from these two analyses provides a likelihood ratio test of the proportional odds assumption for the set of covariates under consideration.

2. Intraclass Correlation

For a multilevel model, it is often of interest to express the cluster variance in terms of an intraclass correlation (ICC). The ICC indicates the proportion of unexplained variance that is at the cluster level, and is given by $\mathit{ICC}={\sigma }_{\upsilon }^2/\left({\sigma }_{\upsilon }^2+{\sigma }^2\right)$, where ${\sigma }_{\upsilon }^2$ is the cluster or level-2 variance and σ² is the level-1 variance. For a logistic regression model (either binary or ordinal), the level-1 variance, which is not estimated, equals the variance of the standard logistic distribution π²/3 [1].

3. Three-level Model

In some cases, subjects might be clustered within more than one hierarchy. For example, students might be clustered within classrooms within schools, or patients may be clustered within providers within clinics. Such an extension for ordinal data is described in [29]. For this, the model can be written as

$$log\left[\frac{P_{\mathit{ijkc}}}{1-P_{\mathit{ijkc}}}\right]={\gamma }_c-\left[x_{\mathit{ijk}}B+{\upsilon }_{ij}+{\upsilon }_i\right],$$ (2)

for the level-1 subject k nested within the level-2 cluster j (e.g., classroom) and level-3 cluster i (e.g., school). In this model, a subject’s response is influenced by both the classroom (υ_ij) and school (υ_i) that he/she belongs to. The level-2 random effects υ_ij have variance ${\sigma }_{\upsilon (2)}^2$, and the level-3 random effects have variance ${\sigma }_{\upsilon (3)}^2$. For a three-level model, the ICC for the level-3 clustering effect is

$${\mathit{ICC}}_{(3)}=\frac{{\sigma }_{\upsilon (3)}^2}{{\sigma }_{\upsilon (3)}^2+{\sigma }_{\upsilon (2)}^2+{\sigma }^2},$$

which represents the proportion of variance at the third level (e.g., school). The ICC for the level-2 clustering effect includes both the level-2 and level-3 variances (since subjects who are within a given classroom are also within the school that the classroom is part of):

$${\mathit{ICC}}_{(2)}=\frac{{\sigma }_{\upsilon (2)}^2+{\sigma }_{\upsilon (3)}^2}{{\sigma }_{\upsilon (3)}^2+{\sigma }_{\upsilon (2)}^2+{\sigma }^2}.$$

Thus, unless the level-3 variance equals 0 (e.g., a student’s school has no effect on their outcome), the level-2 ICC is larger than the level-3 ICC.

3. Clustered Data Example

The Television School and Family Smoking Prevention and Cessation Project (TVSFP) study (Flay et.al., 1988) was designed to test independent and combined effects of a school-based social-resistance curriculum and a television-based program in terms of tobacco use prevention and cessation. The study sample consisted of 7th-grade students who were pretested in January, 1986 and post-tested in April, 1986. Randomization to various design conditions was at the school level, while much of the intervention was delivered to students within classrooms. Specifically, the 28 Los Angeles schools were randomized to either: (a) a social-resistance classroom curriculum (CC), (b) a media (TV) intervention, (c) a combination of CC and TV, and (d) a no-treatment control group. These conditions form a 2 x 2 design of CC (= yes or no) by TV (= yes or no). Note that the variables that will represent these conditions are at the school-level (i.e., they don’t vary within schools, but only between schools), and that the number of schools, which will be treated as a level in the analysis, is not terribly large. Thus, statistical power is of concern here as in other small sample studies.

A tobacco and health knowledge scale (THKS) score was one of the study outcome variables. The scale consisted of seven items used to assess tobacco and health knowledge, and a student’s score was the number of items that they answered correctly. Subjects were included in the analysis if they had complete data on the THKS at both pre and post-test; there were 1600 students from 135 classrooms and 28 schools who met this criterion. The dataset had a range of 1 to 13 classrooms per school, and 2 to 28 students per classroom. The frequency distribution of the post-intervention THKS total scores suggested four ordinal classifications corresponding to 0–1, 2, 3, and 4–7 correct responses. Student frequencies for these categories of the THKS, broken down by condition subgroups, are given in Table 1.

Table 1.

Tobacco and Health Knowledge Scale Post-Intervention Scores Subgroup Frequencies (and percentages)

subgroup		THKS score				total
CC	TV	0–1	2	3	4–7
no	no	117 (27.8)	129 (30.6)	89 (21.1)	86 (20.4)	421
no	yes	110 (26.4)	105 (25.2)	91 (21.9)	110 (26.4)	416
yes	no	62 (16.3)	78 (20.5)	106 (27.9)	134 (35.3)	380
yes	yes	66 (17.2)	86 (22.5)	114 (29.8)	117 (30.5)	383
total		355 (22.2)	398 (24.9)	400 (25.0)	447 (27.9)	1600

Three ordinal logistic regression models were fit to these data. Results from these analyses are given in Table 2. For all, the post-intervention THKS score was modeled in terms of the baseline THKS score, dummy-coded (no = 0 and yes = 1) effects of CC and TV, and the CC by TV interaction. The first column of Table 2 lists results ignoring the clustering of students and treating each student’s outcome as an independent observation. This analysis clearly indicates the positive effect of the social-resistance classroom curriculum as well as the television part of the intervention. However, the interaction of CC by TV is also observed to be statistically significant, thus, student-level analysis suggests that while TV intervention is effective in increasing THKS scores for those not receiving the CC component, it has a slight negative effect on those exposed to both components.

Table 2.

THKS Post Intervention Ordinal Scores Proportional Odds Model Estimates (standard errors)

parameter	Student-level	2-level multilevel	3-level multilevel
threshold γ1	−0.040 (0.121)	−0.076 (0.147)	−0.096 (0.169)
threshold γ 2	1.185** (0.123)	1.198** (0.149)	1.178** (0.171)
threshold γ 3	2.345** (0.134)	2.403** (0.158)	2.384** (0.179)
baseline THKS β1	0.422** (0.038)	0.415** (0.039)	0.409** (0.040)
CC β 2	0.863** (0.129)	0.861** (0.174)	0.885** (0.210)
TV β 3	0.253* (0.125)	0.206 (0.171)	0.237 (0.205)
CC × TV β 4	−0.367* (0.182)	−0.301 (0.245)	−0.372 (0.296)
class variance ${\sigma }_{{\upsilon }_{(2)}}^2$		0.189** (0.064)	0.148* (0.064)
school variance ${\sigma }_{{\upsilon }_{(3)}}^2$			0.045 (0.043)
−2 log L	4250.21	4230.77	4229.18

^**p < 0. 01

^*p < 0.05

The next two columns of Table 2 list results from multilevel ordinal logistic regression models allowing for (a) nesting of students within classrooms, and (b) nesting of students within classrooms within schools. The latter is a 3-level model in which students (level-1) are nested within classrooms (level-2) which are nested within schools (level-3). Results from these multilevel analyses are somewhat different from those obtained from the student-level analysis. Unlike ordinary student-level analysis, either multilevel analysis indicates that both the TV effect and the interaction of CC by TV are not statistically significant. Additionally, the variability attributable to the classes is highly significant and when expressed as an intra-class correlation equals 0.0543, reflecting the degree of non-independence for this clustered dataset. Finally, the likelihood-ratio ${\chi }_1^2$ equals 4250.21 – 4230.77 = 19.44, which clearly supports the significance of including the random classroom effect in the model.

Comparing the 2- and 3-level models yields a likelihood-ratio ${\chi }_1^2=4230.77-4229.18=1.59$, which is not significant. However, because the schools were the unit of randomization, one can make the case that the clustering attributable to schools should be in any statistical modeling of these data, regardless of the statistical significance of this clustering effect. Also, because the intervention was delivered in the classrooms, including the classroom cluster effect is important. Thus, based on the design of the study, the 3-level analysis provides the most valid approach. With only 28 schools, as noted, this represents a somewhat small sample, though of a typical number in school-based prevention research. Clearly, the effect of clustering attributable to the schools is rather small:

$${\mathit{ICC}}_{(3)}=\frac{0.045}{0.045+0.148+{\pi }^2/3}=0.0129,$$

while the clustering attributable to classrooms equals

$${\mathit{ICC}}_{(2)}=\frac{0.045+0.148}{0.045+0.148+{\pi }^2/3}=\mathrm{0.0554.}$$

These values are consistent with published results [38] that considered ICCs evaluated across variable type, time, race, and gender.

Finally, we can test the proportional odds assumption by additionally estimating a model that relaxes this assumption. The logic is that we compare the model that assumes proportional odds to the model that relaxes this assumption. If the latter fits the data (statistically) better, then the assumption of proportional odds is rejected. Table 3 presents the covariate estimates for both models, as well as the model deviances (−2 log L ) from these two models. These deviance statistics are obtained as a standard part of the computer output. Notice that the non-proportional odds model includes three estimates for each of the covariates, one for each of the three cumulative logits. Comparing the deviance statistics, we obtain a likelihood-ratio ${\chi }_8^2=4229.18-4220.46=8.72$, which is not statistically significant. Thus, the proportional odds assumption is not rejected for these data, and so assuming that the four covariates have the same effect on the three cumulative logits is reasonable. The degrees of freedom for this test represents the difference in the number of estimated covariate effects: 12 under the non-proportional odds model versus 4 under the proportional odds model. Notice that, for a given covariate, the estimate from the proportional odds model is essentially an average of the non-proportional odds model estimates (it is not precisely an average because it depends on the category frequencies associated with different levels of the covariate). In statistics, one typically gains precision by averaging, and so it is not surprising that the standard errors are appreciably smaller in the proportional odds model as compared to their counterparts in the non-proportional odds model. This shows why one loses statistical power if an ordinal outcome is dichotomized and analyzed as a dichotomy (rather than as an ordinal outcome).

Table 3.

THNKS Post-Intervention Ordinal Scores Proportional and Non-Proportional Odds 3-level Multilevel Models Estimates of Covariate Effects (standard errors)

parameter	Proportional Odds	Non-Proportional Odds
		1 vs 2,3,4	1,2 vs 3,4	1,2,3 vs 4
baseline THKS β1	0.409** (0.040)	0.369** (0.055)	0.400** (0.046)	0.444 ** (0.049)
CC β 2	0.885** (0.210)	0.772** (0.243)	1.000** (0.221)	0.850 ** (0.234)
TV β 3	0.237 (0.205)	0.096 (0.226)	0.282 (0.215)	0.327 (0.234)
CC × TV β 4	−0.372 (0.296)	−0.1518 (0.342)	−0.385 (0.311)	−0.526 (0.328)
−2 log L	4229.18	4220.46

^**p < 0. 01

^*p < 0.05

4. Mixed Proportional Odds Model for Longitudinal Data

Here, subjects are denoted as i (where i = 1,…, N subjects) and the repeated observations are denoted as j (where j = 1…, n_i). The number of repeated observations per subject is n_i, and so there is no assumption that each subject is measured on the same number of timepoints. In longitudinal studies, it is common to have incomplete data across time, so it is important that the model allows for this. The mixed-effects logistic regression model for the cumulative probabilities of subject i at timepoint j is given in terms of the C-1 cumulative logits as

$$log\left[\frac{P_{\mathit{ijc}}}{1-P_{\mathit{ijc}}}\right]={\gamma }_c-\left[{\mathrm{x}}_{ij}\beta +{\upsilon }_i\right],$$ (3)

where the random effects υ_i reflect each subject’s influence on their repeated observations. This model is referred to as a random-intercept model as the subject effects do not vary across time. These are assumed to be distributed in the population of subjects as $N(0,{\sigma }_{\upsilon }^2)$, and so the sample of subjects are thought to represent a population of subjects that one wants to make inferences about.

In terms of the effects of time on the repeated outcomes, typically the covariate(s) x_ij would include at least a linear effect of time. For example, suppose that subjects are measured at baseline, 6 months, and 12 months. Then, one of the covariates in x_ij might be a variable t_ij (and coded 0, 1, 2) to represent the linear effect of time (in 6 month intervals). With more timepoints, the model might also include quadratic effects to allow for curvilinear effects of time. That is, the response across time might be a decelerating or accelerating trend, rather than a simple linear trend. For this, one could include both t_ij and its square $t_{ij}^2$ to represent the linear and quadratic components of the trend across time. Alternatively, in some cases, it might be of interest to compare each follow-up to baseline and therefore to create dummy variables for each of the follow-ups treating baseline as the reference cell. Whether one uses polynomials for trends or dummy codes to represent the effects of time depends on the scientific questions of interest.

Interactions with the time effects are usually of interest in longitudinal models in order to assess, for example, the degree to which trends vary across groups of subjects. So, if there is a grouping variable G_i, say coded 0 for a control group and 1 for an intervention group, and one simply included a linear effect of time, the following model might be posited:

$$log\left[\frac{P_{\mathit{ijc}}}{1-P_{\mathit{ijc}}}\right]={\gamma }_c-\left[{\beta }_1{T}_{ij}+{\beta }_2{G}_i+{\beta }_3(G_i\times T_{ij})+{\upsilon }_i\right].$$ (4)

Here, β₂ represents the group difference when T_ij equals 0, and β₃ indicates how the group difference varies with time. Or, β₁ represents the time trend for the control group (when G_i equals 0), and β₃ represents the difference in the trend for the intervention group relative to the control group. Thus, testing the significance of β₃ is of great interest as it represents how the trends differ between the two groups.

Thus far, the model only includes a single random subject effect υ_i and assumes that a subject’s effect on their responses is the same across all timepoints. This is often an unreasonable assumption because subjects often vary in their trends across time. To permit this, we can extend the model by including a random subject trend:

$$log\left[\frac{P_{\mathit{ijc}}}{1-P_{\mathit{ijc}}}\right]={\gamma }_c-\left[{\beta }_1{T}_{ij}+{\beta }_2{G}_i+{\beta }_3(G_i\times T_{ij})+{\upsilon }_{0i}+{\upsilon }_{1i}{T}_{ij}\right].$$ (5)

Here, υ_1i is essentially an interaction of subject by time, indicating the degree to which subjects have different time trends. In this model, υ_0i represents the subject effect when T_ij equals 0, and υ_1i indicates how a subject’s effect varies with time. Subjects have different time trends to the extent that the υ_1i parameters are non-zero. Both random effects are usually assumed to be normally distributed in the population of subjects with variances ${\sigma }_{{\upsilon }_0}^2$ and ${\sigma }_{{\upsilon }_1}^2$, respectively. The covariance between a subject’s intercept and trend, σ_υ01, indicates the degree to which a subject’s starting point is associated with their trend.

Notice that the random-intercept model in Equation (4) is a special case of the random trend model in Equation (5). By not including the random time effect υ_1i, the random intercept model assumes that these are all zero and thus that the variance ${\sigma }_{{\upsilon }_1}^2$ and covariance σ_υ01 both equal zero. Thus, comparison of the two models via a likelihood ratio test can be performed to test whether these two parameters equal zero. If the test is non-significant, then the simpler random-intercept model is supported and there is no appreciable subject heterogeneity in their time trends (other than the random intercept υ_0i). Alternatively, if this test is significant it indicates that subjects do vary in their trends, and the simpler random-intercept model would be rejected in favor of the random trend model.

In some studies, there might be time-varying covariates which are thought to influence the ordinal outcome. In this case, the model might be

$$log\left[\frac{P_{\mathit{ijc}}}{1-P_{\mathit{ijc}}}\right]={\gamma }_c-\left[{\beta }_1{T}_{ij}+{\beta }_2{X}_{ij}+{\upsilon }_{0i}+{\upsilon }_{1i}{T}_{ij}\right],$$ (6)

where X_ij represents the time-varying covariate. One might also examine whether there is an interaction of X_ij with time, by including the product term X_ij × T_ij into the model, which would suggest that the relationship between the covariate and the outcome varies with time. When time-varying covariates are included in the model, as in Equation (6), an assumption is made that the between and within-subjects effects of the covariate are equal. To see this, express the time-varying covariate X_ij as X_ij = X̄_i +(X_ij − X̄_i), where X̄_i is the mean of the time-varying covariate (averaged across time) for each subject (i.e., a between-subjects variable). The term ( X_ij − X̄_i) represents the subject’s deviation around their mean (i.e., a within-subjects variable). Including both of these terms into the model yields:

$$log\left[\frac{P_{\mathit{ijc}}}{1-P_{\mathit{ijc}}}\right]={\gamma }_c-\left[{\beta }_1{T}_{ij}+{\beta }_2{\overline{X}}_i+{\beta }_3(X_{ij}-{\overline{X}}_i)+{\upsilon }_{0i}+{\upsilon }_{1i}{T}_{ij}\right],$$ (7)

The total effect of X_ij, β₂X̄_i + β₃ (X_ij − X̄_i), is partitioned into its between- and within-subjects effects (i.e., β₂ and β₃, respectively). The between-subjects part indicates the degree to which the subject’s average covariate level is related to their average outcome level, averaging across time. The within-subjects component represents the degree to which change in a subject’s covariate level is associated with change in their outcome (i.e., a within-subject change). If these two are equal (β₃ = β₂), then the effect is exactly as in Equation (6). Thus, model (6) makes the assumption that the within- and between-subjects effects of the covariate are the same. This assumption can be assessed by comparing the models specified by (6) and (7) via a likelihood ratio test. If these two models are significantly different, then the assumption is rejected and the more general model (7) is preferred; whereas if the models are not significantly different then the assumption is reasonable and model (6) can be used.

5. Longitudinal Data Example

Data from a psychiatric study described in [32] are considered here. This study focused on the longitudinal relationship between imipramine (IMI) and desipramine (DMI) plasma levels and clinical response in 66 depressed inpatients. Imipramine is the prototypic drug in the series of compounds known as tricyclic antidepressants, and was commonly prescribed for the treatment of major depression at the time of this study [37]. Since imipramine biotransforms into the active metabolite desmethylimipramine (or desipramine), measurement of desipramine was also done. The study design was as follows. Following a placebo period of 1 week, patients received 225 mg/day doses of imipramine for four weeks. In this study, subjects were rated with the Hamilton depression (HD) rating scale [9] twice during the baseline placebo week (at the start and end of this week) as well as at the end of each of the four treatment weeks of the study. Plasma level measurements of both IMI and DMI were made at the end of each week. The total number of subjects was 66, but the number of subjects measured at each week fluctuated: 61 at pre1 (start of placebo week), 63 at pre2 (end of placebo week), 65 at week 1 (end of first drug treatment week), 65 at week 2 (end of second drug treatment week), 63 at week 3 (end of third drug treatment week), and 58 at week 4 (end of fourth drug treatment week). Here, we concentrate on the relationship between the drug levels and depression and focus on the four timepoints of the drug treatment period (after the placebo period). [10] presents several analyses treating the HD outcome as continuous. Here, as in [32], the outcome is ordinalized with 0 = full response (HD score below 8), 1 = partial response (HD score from 8 to 15), and 2 = non response (HD score above 15). We do this for illustrative purposes since, as noted, this leads to a loss of information and statistical power. To further simplify the analysis, we will consider a dichotomization of the time-varying metabolite DMI in terms of a median split on this variable.

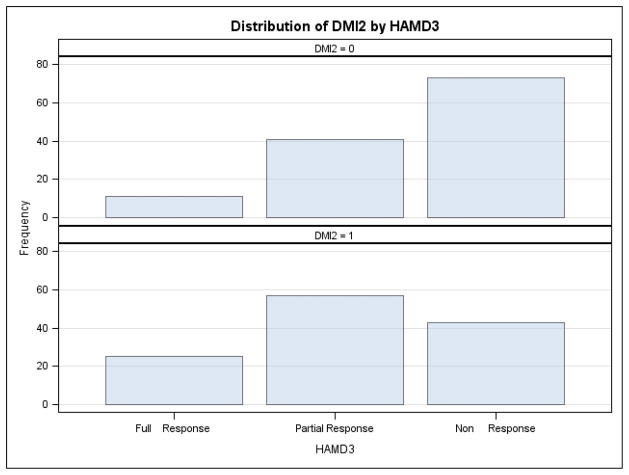
Figure 1 presents the ordinal outcome frequencies (HAMD3) for the two groups of dichotomized DMI observations (DMI2). As DMI is a time-varying variable, a given subject could have both above and below median observations across the four weeks of the study. As Figure 1 suggests, there appears to be a beneficial effect of the drug, in that a better response profile is observed for the above median DMI observations (DMI2=1) than for the below median DMI observations (DMI2=0).

Figure 1.

Frequency distribution of the ordinal Hamilton Depression Scale outcome (HAMD3) by the dichotomized Desipramine plasma levels (DMI2)

Table 4 presents the results of random trend models both assuming and relaxing the proportional odds assumption. Both models include a linear effect of time (Week) and the dichotomized desipramine variable (DMI2) as covariates. Comparing these models yields a likelihood-ratio ${\chi }_2^2=3.18$, which is not statistically significant, and so the proportional odds assumption is not rejected for these data. As can be seen, both the estimates for time and DMI2 are negative and significant, indicating that subjects have lower responses (i.e., more in the full response category) as time goes on and as the drug level is higher. Testing for whether there is an interaction of DMI2 by time yields a highly non-significant result, as does testing for the equality of the between-subjects and within-subjects effects of DMI2. Thus, there is no evidence of a differential effect of drug across the four weeks of the study, and no evidence that the within-subject and between-subject effects are different. Finally, comparing the random trend model to a simpler random intercept model (not shown) yields a likelihood-ratio ${\chi }_2^2=6.89$, which is significant and rejects the simpler random intercept model. Thus, there is evidence that subjects vary significantly in their trends across time.

Table 4.

Hamilton Depression Ordinal Scores Proportional and Non-Proportional Odds 2-level Multilevel Models Parameter Estimates (standard errors)

parameter	Proportional Odds	Non-Proportional Odds
		1 vs 2,3	1,2 vs 3
threshold γ1	−7.269** (1.157)	−8.360 ** (1.520)
threshold γ 2	−2.431** (0.723)		−2.423 ** (0.769)
Week β1	−1.375** (0.304)	−1.965 ** (0.480)	−1.218 ** (0.302)
DMI2 β 2	−1.706* (0.670)	−1.607 (0.898)	−1.958 ** (0.744)
Intercept variance ${\sigma }_{{\upsilon }_0}^2$	8.348 (4.593)	10.853 (5.781)
Week variance ${\sigma }_{{\upsilon }_1}^2$	1.186 (0.780)	0.979 (0.732)
Intercept, Week covariance συ01	−0.581 (1.205)	−1.212 (1.494)
−2 log L	377.52	374.34

^**p < 0. 01

^*p < 0.05

6. Computational Issues

Variants of maximum likelihood are typically used to estimate the models presented in this article, and the solutions are usually more computationally demanding than similar models for normal outcomes. Software programs vary in the approaches they use, with some approaches being more approximate than others. Here, several of the most common approaches will be briefly described. More information about these different approaches can be found in [34].

Perhaps the most frequently used methods are marginal quasi-likelihood (MQL) and penalized or predictive quasi-likelihood (PQL) [8]. These quasi-likelihood approaches are computationally less-intense, unfortunately, several authors [6,33,31] have reported biased estimates using these procedures in certain situations, especially for MQL. Several software programs provide either MQL and PQL as their default estimation approach (MLwiN, HLM, IBM SPSS, SAS PROC GLIMMIX), though some also offer other approaches. In general, PQL is preferred to MQL, though neither do well if the correlation of the clustered outcomes is high or the number of clusters and/or clustered observations are small. In longitudinal studies, the correlation is typically high and there are not that many clustered observations within subjects. Thus, for longitudinal data, MQL and PQL can produce biased results. However, as noted by [4], for situations in which the correlation is not that high and there are moderate numbers of individuals in clusters (e.g., students in classrooms and/or schools), PQL provides good results and can be relied upon. A disadvantage of both MQL and PQL is that one does not obtain a deviance statistic that can be used for likelihood ratio tests.

The most accurate approach is to use what is called adaptive quadrature in the estimation procedure [20,23,5,26]. Simulations show that adaptive quadrature performs well in a wide variety of situations [28]. Several software packages have implemented adaptive quadrature, including SuperMix [14], GLLAMM [27], Stata [39], and SAS PROCs GLIMMIX and NLMIXED [36]. For the most accurate and reliable results, adaptive quadrature is advised. Additionally, this approach yields a deviance that can be readily used for likelihood-ratio tests. It is worth noting that not all of the software programs listed support estimation of the non-proportional odds models that were presented in this article. Also, some programs are restricted to 2-level models and cannot estimate 3-level models (e.g., the students within classrooms within schools model presented). Because this is constantly changing with software updates, the limitations of a given software program are worth checking into before undertaking a series of analyses. All of the models presented in this article were estimated with adaptive quadrature using the SuperMix software program. A student version of this program is freely available via the Scientific Software website, and all of the syntax scripts and datasets used in this article are available from the first author upon request.

7. Discussion

Mixed ordinal regression models have been described for analysis of clustered and longitudinal ordinal data. For clustered data, random cluster effects characterize the dependency of subjects’ responses from the same cluster. In our example, students were clustered within both classrooms and schools, and analyses of 2- and 3-level models were presented. For longitudinal data, repeated observations are clustered within subjects and random subject intercepts and trends are often considered. These allow subjects to vary in terms of their starting points and trajectories across time. In our example of subjects’ depression ratings across time, there was evidence for random subject trends in addition to random intercepts.

Models assuming and relaxing the proportional odds assumption were presented and compared. By comparing the two, one can perform a test of the proportional odds assumption. In this article, the proportional odds assumption was deemed reasonable for the examples considered. However, that is not always the case and more general models that relax the proportional odds assumption are sometimes required [16]. In these non-proportional odds models, covariates have different effects on each of the C-1 cumulative logits of the model. For example, suppose that the ordinal outcome is measured according to the Transtheoretical Model of Change (or Stages of Change Model) [24,25] with stages of, say, pre-contemplation, contemplation, and action. Then, it certainly could be the case that a covariate has an effect on moving subjects from pre-contemplation to contemplation, but does not produce effects on action. For such cases, we have described a “Thresholds of Change Model” using an ordinal non-proportional odds modeling approach [15,18].

Another area of application is for time to event data in which the timing is not known precisely but only within time periods. For example, one might be interested in modeling time until initiation of smoking in students who are measured annually in grades 5 to 8. Here, the ordered outcome is the grade in which smoking initiation began. We have described such multilevel survival analysis using the ordinal modeling approach [19,17]. Rather than using a logit link function, these survival models typically use a complementary log-log link function in order to yield a proportional hazards interpretation. Also, in this scenario one needs to consider the possibility of right-censoring in which the time of the event is unknown beyond a certain timepoint.

Certainly, researchers are more familiar with normal models and software, and so often treat ordinal outcomes as normal outcomes. One might wonder about whether this is a reasonable practice or not. In this regard, a comprehensive examination of this practice was performed by [4]. They examined the performance of mixed normal and ordinal models to ordinal outcomes with 3 to 7 categories, and distributions that were symmetric, skewed, and polarized. In terms of bias, these authors concluded that the mixed normal model only gave reasonable results if there were 7 categories and the distribution was symmetric. In all other cases, the mixed normal model yielded unduly biased estimates of regression coefficients. In comparison, the mixed ordinal model (i.e., the same model as presented in the current paper) produced unbiased estimates regardless of the number or shape of the distribution across the ordered categories.

For datasets of limited size, another concern is the issue of statistical power. For this, [3] ordinalized a continuous outcome and reported efficiency (i.e., power) of 94% to 99% for 4 to 9 categories, respectively, as compared to the continuous outcome. Thus, even if the outcome is continuous, there is little efficiency loss, especially as the number of categories is increased. Conversely, if one dichotomizes an ordinal outcome, there can be appreciable loss in statistical power. [40] dichotomized an ordinal outcome with 5 categories, and for which the power level was 78%. The dichotomized outcomes had power levels between 38% to 68% depending on the cutpoint chosen. Thus, blindly dichotomizing an ordinal outcome can severely reduce power.

This article has attempted to present the ordinal model clearly and in relatively non-technical terms. Certainly the use of ordinal models is not as popular as use of normal and binary models, despite the fact that ordinal outcomes are often obtained. The tools are available in terms of methods and software, so hopefully this situation will change as researchers become more familiar with application of the ordinal model.