Integrative approaches for predicting protein function and prioritizing genes for complex phenotypes using protein interaction networks

Abstract

With the rapid development of biotechnologies, many types of biological data including molecular networks are now available. However, to obtain a more complete understanding of a biological system, the integration of molecular networks with other data, such as molecular sequences, protein domains and gene expression profiles, is needed. A key to the use of networks in biological studies is the definition of similarity among proteins over the networks. Here, we review applications of similarity measures over networks with a special focus on the following four problems: (i) predicting protein functions, (ii) prioritizing genes related to a phenotype given a set of seed genes that have been shown to be related to the phenotype, (iii) prioritizing genes related to a phenotype by integrating gene expression profiles and networks and (iv) identification of false positives and false negatives from RNAi experiments. Diffusion kernels are demonstrated to give superior performance in all these tasks, leading to the suggestion that diffusion kernels should be the primary choice for a network similarity metric over other similarity measures such as direct neighbors and shortest path distance.

INTRODUCTION

In recent years, many large-scale functional interaction networks among genes and their protein products have been generated. These networks include protein physical interactions for a number of species [1–7], gene regulatory networks [8], genetic interaction networks [9–14] and co-expression networks from a large number of gene expression studies using either microarray technologies or next-generation sequencing. Several protein interaction databases are available, including MIPS [15], PID [16], BioGRID [17] and STRING [18]. Moreover, species–specific interaction networks, such as the Human Protein Reference Database (HPRD) [19], the Comprehensive Drosophila Interactions Database (DroID) [20] and the Yeast Protein database (YPD) [21], are also available.

Molecular networks can be represented mathematically as networks or graphs with nodes indicating molecules and edges indicating relationships between molecules, such as protein physical interactions, genetic interactions, gene regulation or gene co-expression. For a given graph, many similarity or dissimilarity measures between nodes have been defined. The geodesic/Dijkastra distance calculates the length of the shortest path between any two nodes [22]. Kondor and Lafferty [23] first introduced the exponential kernel and Laplacian exponential diffusion (LED) kernel over networks. Several variants of the exponential kernels and similarity measures have then been developed and carefully studied, such as the regularized Laplacian kernel [24, 25], the von Neumann diffusion kernel [26], the commute-time kernel [27, 28] and the random-walk-with-restart similarity matrix [29–31]. Fouss et al. [32] reviewed nine forms of kernels and similarity matrices on graphs and their applications to the collaborative recommendation task. However, we are not aware of reviews on the use of kernels or similarity matrices for biological studies, in particular, for protein function prediction and prioritization of genes related to complex phenotypes.

To gain a more complete understanding of a given biological system, it is necessary to integrate different networks with other data, such as molecular sequences, gene ontologies, gene expression profiles and RNAi outcomes. Molecular networks have been widely used to study a variety of problems in basic biological science, biomedicine and public health. In this review, we focus on the definition of similarity among proteins over the network, as exemplified by four problems. The first is the classical problem of predicting protein function based on the functions of known proteins and protein interaction networks. Here, the assumption is that interacting proteins are more likely to have similar functions. The second problem involves prioritizing genes related to a complex phenotype given a set of seed genes that have been shown to be related to the phenotype. The principle is that a gene close to seed genes in the network is more likely to be related to the phenotype. However, in the event that no seed genes are available, the third case calls for integrating gene expression profiles and networks to prioritize genes related to a phenotype. More specifically, if a gene and most of its neighbors are differentially expressed, then that gene is most likely to be related to the phenotype. The fourth and final question is the identification of false positives and false negatives in RNAi experiments. The commonality that unites all these problems is based on how we define similarity between nodes over the network. We have found through previous studies that diffusion kernels over networks can usually yield superior results compared with the use of standard similarity measures, such as direct neighbors and shortest path distance. The objective of this review is to demonstrate the power of diffusion kernels over networks in solving various biological problems.

The organization of the article is as follows. We first introduce the definitions of exponential diffusion kernel and Laplacian diffusion kernels over networks of Kondor and Lafferty [23], as they form the bases for all the following applications. We also include the definitions of several other diffusion kernels and similarity measures over networks that have been used for protein function prediction or gene prioritization for complex phenotypes. Then we review the use of diffusion kernels and similarity measures to solve the four aforementioned problems. We point out that there is a large body of research literature and review articles for each of the topics [33–36]. This review differs from others in that we focus on the use of kernels and similarity measures of nodes over networks to these problems.

DIFFUSION KERNELS AND NODE SIMILARITY MEASURES OVER NETWORKS

Many different forms of kernels and similarity measures between nodes over networks have been developed during the past decade. Kondor and Lafferty [23] first developed the LED kernel that can be conveniently introduced using random walks over a network (Figure 1). Denote the unweighted network as

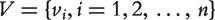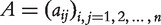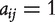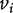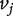where are nodes and E indicates the set of edges. A graph can also be represented by an adjacency matrix where means there is an edge connecting nodes and and 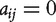otherwise. The 1s in the ith row of A represent all nodes connecting to node i. We assume that the graph of interest is connected. It is easy to see that the adjacency matrix A of an undirected graph is symmetric, that is 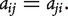The degree of the ith node 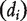, which measures how many other nodes are immediately connected to it, can be found by taking the sum of the ith row (or column) of the adjacent matrix A. Let D be the diagonal matrix with the ith diagonal term being 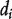and the off-diagonal terms being 0.

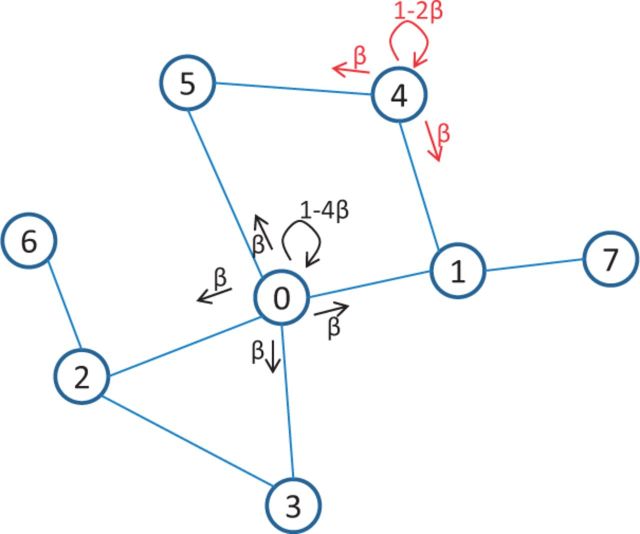
Figure 1:

Random walk on a graph. At each step, the walker will move to its neighbor nodes according to the direct neighbors of the current node. For example, if the current node is 0, the walker will randomly move to one of its four neighbors with probability β (<<1), and stay in current node with probability 1 − 4β. If the current node is 4, the walker will move to one of its neighbors with probability β (<<1), and stay in current node with probability 1 − 2β.

To define similarity between nodes, we consider random walks over a network (Figure 1; also see [37]). Starting from a node at each time interval 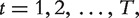the walker chooses either to move to one of the neighbors of node 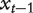according to a small probability β, or to stay at the current node with probability In other words, the transition probability matrix of this walker’s movement is

where 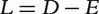is the unnormalized graph Laplacian [38]. Let 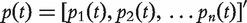be the column probability vector where 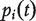is the probability that the walker is at node i at time t. Then

Therefore, 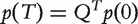, where p(0) is the initial probability distribution of finding the walker at the nodes. As it is desirable to measure the similarity between nodes without explicitly specifying T, Kondor and Lafferty [23] proposed to break the time of moving away from a node into an infinitesimally small number and to increase the number of steps to infinity

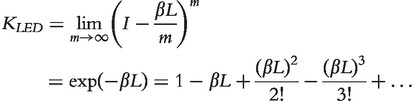(1)

The matrix 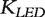is called a LED kernel.

A few properties of the LED kernel on graphs can be listed here. First, as it is calculated based on the entire network, it is a global measure of similarity rather than a metric that uses immediate neighbors. Second, for certain learning problems based on the LED kernel, the parameter β can be fine-tuned during training to achieve high-learning accuracy. As mentioned in Kondor and Vert [39], shortest path distance similarity is extremely sensitive to random insertion/deletion of edges. On the other hand, the LED kernel is less affected by such problems. Therefore, it is expected that the LED kernel can be more useful in propagating information on a network, as will be shown later from real applications of diffusion kernels.

In addition to the LED kernel, Kondor and Lafferty [23] also studied the exponential diffusion kernel (ED) defined by

(2)

Since the publication of [23], many other diffusion kernels have been developed and studied. Corresponding to the LED kernel defined in Equation (1), Smola and Kondor [25] considered the regularized Laplacian (L) kernel by replacing the coefficient of (−L)^k in Equation (1) to β^k , thus increasing the contribution of higher power of –L.

(3)

The matrix K_L is defined for with 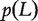being the largest eigenvalue in absolute value of matrix L.

Similarly, by changing the coefficient of A^k in Equation (2) to β^k, the von Neumann diffusion (VND) kernel, 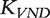, was defined previously [26, 40]

(4)

The matrix 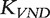is defined for 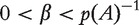with 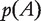being the largest eigenvalue in absolute value of matrix A.

By replacing the identify matrix in Equation (4) with the diagonal degree matrix D, Fouss et al. [41] defined the regularized commute time (RCT) kernel

(5)

By replacing the Laplacian matrix L in Equation (1) with the normalized Laplacian matrix 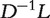, the heat diffusion (HD) kernel [42] is defined as

(6)

The random-walk-with-restart (RWR) similarity [30, 31] matrix is defined by

(7)

Note that 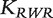is not a kernel as it is not symmetric.

In this article, we review the applications of the kernels and similarity matrices for protein function prediction and gene prioritization for complex phenotypes using molecular networks.

Application 1: predicting protein functions based on functions of known proteins and protein interaction networks

Sequence comparison had been the dominant method for protein function prediction before high-throughput protein interaction data were available in the early 2000s [1–6]. Basically, if sequences of two proteins are similar, they are more likely to have similar functions. However, over two-thirds of the proteins had no similarity with proteins having known functions in the early 2000s, prompting the search for alternative approaches to predict protein functions. Along with the rapid development of high-throughput protein interaction profiling technologies such as yeast-two-hybrid [2, 3] and affinity profiling [4, 6, 43–45], protein function prediction methods based on large-scale protein interaction data sets have been under intensive study during the past decade. For example, functions of a new protein may be extrapolated by assigning the most frequently annotated functions among its direct interaction partners [46, 47]. However, these methods have three major limitations. First, only direct interacting proteins with known functions are considered, and functions of high order interacting proteins are ignored. Second, these methods do not take the degrees of the proteins into consideration. Third, neighbor proteins with unknown functions are not used in these methods. To overcome these limitations, many methods have been developed to predict protein functions using protein interaction networks based on the ideas of message propagation over networks, and several excellent reviews are now available [34–36]. Here, we concentrate on the use of diffusion kernels over networks for protein function prediction. As the use of diffusion kernels over protein interaction networks for protein function prediction is closely related to early applications of Markov random field (MRF) for the same purpose, we first introduce the MRF model.

Consider a specific function of interest and a protein interaction network with nodes indicating proteins and edges indicating interactions between proteins. Denote the binary labeling of functional annotations of all proteins as (X₁, X₂, … , X_n, X_n+1, … , X_n+m), where the first n nodes are un-annotated and the last m nodes are annotated, where 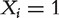indicates the ith protein having the function and otherwise. Deng et al. [48] proposed to model all the labels of the proteins for a particular function of interest as a MRF with the probability of a configuration for the annotation of all the proteins proportional to

where N₁ is the number of proteins having the function of interest; N₁₀, N₁₁ and N₀₀ are the numbers of interacting protein pairs with exactly one, both or none having the function of interest, respectively; and a, b₁₀, b₁₁ and b₀₀ are parameters. A similar model was independently developed by Letovsky and Kasif [49]. However, the two studies used different computational approaches for protein function inference. In the following, we briefly describe the method used in Deng et al. [48].

It was shown that

where N₁(i) and N₀(i) are the numbers of direct neighbors of protein i having the function and not having the function, respectively, and X_[-i] = (X₁, … , X_i-1, X_i+1, … , X_n+m). A pseudo-likelihood approach was used to estimate the parameters a, b and c based on the annotated proteins. A Markov Chain Monte Carlo (MCMC) method was developed by Deng et al. [48] to estimate the posterior probabilities of X_i = 1 given the network and the labels of annotated proteins (X_n+1, X_n+2, … , X_n+m). The approach was later used to predict gene ontology (GO) functions [50] and extended to include multiple networks [50]. It should be noted that the model does not specify the signs of b and c, and they are estimated based on the annotations of proteins with known functions. Thus, the model does not assume that interacting proteins are more likely to have similar functions. Thus, this model can equally be applied to situations that interacting proteins may tend to have different functions. However, we observed that b < 0 and c > 0 for protein physical interaction networks and function categories containing ≥10 proteins [48]. The results indicate that the assumption that interacting proteins are more likely to have similar functions is generally true for protein physical interaction network. For other networks such as genetic interaction networks, this assumption may not hold. In general, we suggest to check the relationships of the functions of interacting proteins before the guilty-by-association principle is applied.

Lanckriet et al. [51] took a different approach to predict protein functions based on protein interaction networks. Instead of using the MRF model as in Deng et al. [48], a support vector machine (SVM) with the LED kernel over the protein interaction network was used to predict protein functions. The SVM with LED kernel was shown to outperform MRF for protein function prediction [51]. Combining the ideas from Deng et al. [48] and Lanckriet et al. [51], Lee et al. [52] subsequently proposed a LED kernel-based logistic regression approach to better model the neighborhood information to predict protein functions. Instead of using the direct neighbors only, the probability of the annotations of the proteins over the network is modeled to be proportional to

where

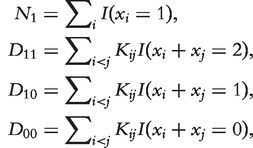and K_ij is defined in the LED kernel 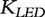. It was shown that

(8)

where K₀(i) = ∑_j≠i K_ij (1 − x_j) and K₁(i) = ∑_j≠i K_ij x_j. The MRF model of Deng et al. [48] is a special case of this new model. This method was called kernel logistic regression (KLR).

The performance of a protein function prediction method is usually evaluated using k-fold cross-validation. For a given function of interest, a set of proteins having the function of interest is chosen as the gold standard positive sample and a set of proteins not having the function is chosen as gold standard negative sample. Both the positive and negative samples are divided into k subsamples of roughly equal size. Each pair of positive and negative subsamples is used as test samples, and the remaining subsamples are used as training samples. Based on the trained model using the training samples, the functions of the test samples are predicted, and the predicted functions of the proteins are compared with the known annotations. Thus, receiver operating characteristic curves (ROC) can be plotted, and the area under the ROC curve (AUC) can be calculated. The average AUC score can be used to evaluate the performance of the function prediction method. Higher AUC score indicates better performance of a prediction method.

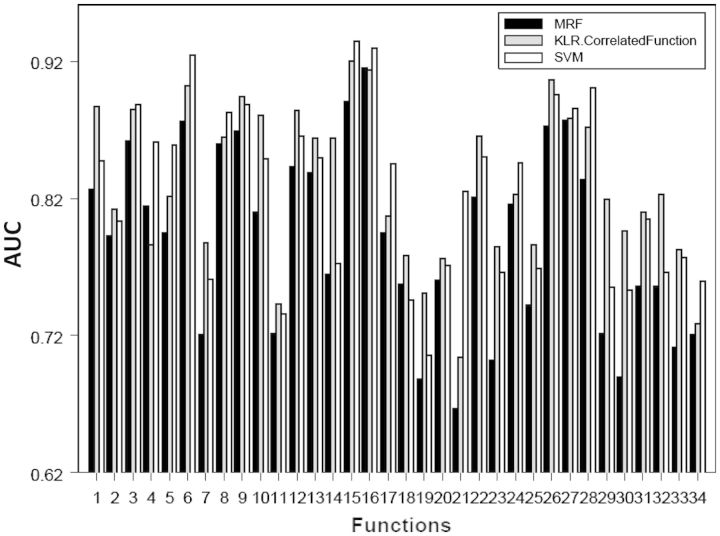
Extensive comparisons of the different protein function prediction methods showed that the performance of the LED kernel-based logistic regression model of Lee et al. [52] is similar to that of SVM with LED kernel as a similarity metric, and both methods out-performed the original MRF method of Deng et al. [48]. Figure 2 shows the AUC scores of the different protein function prediction methods using leave-one-out cross-validation for 34 functional categories. This result indicates that the LED kernel is effective in capturing extra information encoded in the protein interaction network.

Figure 2:

The areas under the receiver operating characteristic curves (AUC) for the prediction of 34 functions using Markov random field (MRF), support vector machine (SVM) and kernel logistic regression (KLR) based on the LED kernel; reprinted from Lee et al. [52] with permission. The 34 function categories are given in Lee et al. [52].

Several recent studies further reinforced results from previous studies. Kourmpetis et al. [53] developed a Bayesian approach for protein function prediction based on the model of Deng et al. [48]. In this approach, the parameters in the MRF model are assumed to be random variables with some prior distributions. Then Markov Chain Monte-Carlo approaches were used to jointly estimate the posterior distributions of the parameters and the annotation of the proteins. The Bayesian approach simultaneously estimates the parameters and the functions of the proteins, thereby overcoming the potential problem in Deng et al. [48] that the parameters in the MRF model were estimated using only the functions of the known proteins based on a pseudo-likelihood approach, which may lead to potentially inaccurate or biased estimation of the parameters. The results in Kourmpetis et al. [53] indicate that the Bayesian approach performed better than the original method of Deng et al. [48], but not as well as the KLR approach of Lee et al. [51]. Ching et al. [54] compared the performance of protein function prediction based on protein interaction networks using SVM with different kernels, including the LED kernel defined in Equation (1) and the Laplacian kernel defined in Equation (3). It was shown that the performance of the LED kernel is similar to that of the Laplacian kernel. Mondal and Hu [55] used KLR to predict protein localization and showed that KLR performs much better than classification algorithms based on protein features, such as amino acid content, hydrophobicity, side-chain mass and domain composition.

The performance of the protein function prediction methods depends on the interaction networks used. For example, Lee et al. [52] showed that RNA co-expression network is useful for the prediction of functions related to transcription to RNA, but not useful for other functional categories. This is reasonable as RNA expression profiles contain transcription information from DNA to RNA and do not contain translation information from RNA to proteins. Mondal and Hu [55] studied the performance of KLR for predicting protein localizations using four networks: protein physical interactions (PPPI), genetic interactions (GPPI), mixture of both physical and genetic interactions (MPPI) and co-expression network (COEXP). For this particular application, KLR coupled with the physical interaction performs better than using other networks. This study also showed that mixing networks into one network is not recommended for protein localization prediction in general. Even for one type of networks, e.g. physical interactions, the percentage of true interactions within the observed protein interaction network and the numbers of proteins and interactions that the network contains can all significantly affect the performance of the prediction methods. In fact, the performance of the prediction methods decreases as the noise level of the observed protein interaction increases and the size of the network decreases [52].

Integrative approaches for protein function prediction using protein interaction networks, gene expression profiles, sequence similarity and phylogenetic information are well-studied topics. Because this review focuses on the applications of diffusion kernels over networks in computational biology, we refer readers to the reviews in [33–36] for other works on integrative approaches for protein function prediction.

Application 2: prioritizing genes related to complex phenotypes

A typical problem in biological and biomedical studies involves the identification of genes related to certain phenotypes, such as disease status and certain quantitative traits including height, blood pressure and cholesterol level. Traditionally, linkage and association studies are powerful tools to identify loci associated with the phenotypes. These studies usually found large genomic regions containing tens to hundreds of candidate genes [56, 57]. Therefore, follow-up studies to identify the true underlying genes related to the phenotype of interest are needed. A good prioritization method to rank the candidate genes according to their potential impact on the phenotype will help plan follow-up studies for the identification of true underlying genes. However, the number of genes known to be related to a phenotype is usually small, and many other related genes have not yet been identified. Thus, the prioritization of genes related to a phenotype can be regarded as a one-class-learning problem with only positive training data [58]. Here, we focus on a successful application of random walks on networks by Kohler et al. [59] who proposed to prioritize genes by integrating protein interaction networks and seed genes known to be related to the phenotype.

Kohler et al. [59] reasoned that genes whose mutations render the host susceptible to a phenotype d should be close to each other within the protein interaction network. Therefore, they first mapped all the candidate genes to the protein interaction network, and then defined a similarity measure between proteins in the network using the LED kernel. Suppose a set of genes [seeds denoted as 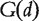] is known to be related to phenotype d. Each candidate gene j is scored using the formula

where S_ij is the similarity score between protein i and protein j in the protein interaction network. The method is based on the idea that the closer a gene j is to the seed genes, the more likely that gene j is related to the phenotype. Note that this score is the same as 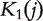in Equation (8). As the set of genes not related to the phenotype is not clearly known, the values of were not used for ranking the candidate genes.

Kohler et al. [59] also used a random-walk-with-restart (RWR) approach to rank candidate genes. Let p^t be the probability vector for the walker to be at different nodes at time t and be the initial probability vector, where 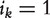if gene k is related to phenotype d and 0 otherwise, and |G(d)| is the total number of genes in gene set G(d). Consider the following iterative equation

(9)

that is, at a certain time t and a node 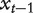, with probability β the walker moves to one of the neighbors of 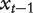with equal probability and with probability 1−β the walker restarts at the initial probability distribution. The steady-state probability of finding the walker over the network exists and is denoted as 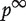. It can be shown that 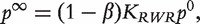where 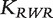is the RWR similarity matrix defined in Equation (7). Finally, the genes are ranked according to the values of the components of 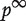. The authors also compared the aforementioned methods with gene prioritization methods based on direct neighbors or shortest path distance. For direct neighbors, a gene is predicted to be related to the phenotype if it interacts with one of the seed genes. For shortest path distance, the genes are ranked based on the shortest path distance to any of the seed genes.

The leave-one-out cross-validation is usually used to evaluate the performance of the different methods for gene prioritization related to a phenotype. For a given phenotype, each gene related to the phenotype, referred as the target gene, is mixed with a set of genes not related to the phenotype. These genes can either be chosen as those closest to the target gene according to their genomic locations or randomly chosen from all the genes. A gene prioritization method is used to rank all the genes. Several different criteria have been used in the literature to evaluate the performance of the prioritization method. The first criterion is the average rank of all the target genes. The second criterion is the fraction of target genes ranked above a certain percentage of all the genes, e.g. top 10 or 20%. The third criterion is through the ROC analysis and the AUC score as in Application 1. In this application, a gene is predicted as a phenotype-related gene if its rank is above a threshold. By changing the threshold, the ROC curve can be plotted, and the AUC score can be calculated.

Using the evaluation methods described earlier in the text, Kohler et al. [59] showed that the AUC scores based on the LED kernel, RWR, shortest path distance and directed neighbors were 90.8, 91.2, 84.1 and 73.2 based on 110 disease-gene families studied in the article, respectively, indicating superior performance of the LED kernel and RWR over the direct neighbor and shortest path approaches, whereas the performances with the LED kernel and RWR were similar.

The network-based gene prioritization methods developed in Kohler et al. [59] can only be applied to phenotypes with known seed genes. When seed genes are not available for a phenotype, the relationship between genes and other phenotypes closely related to the phenotype of interest can be used. In recent years, databases documenting genes for many phenotypes such as OMIM [19] and the Catalog of Published Genome-Wide Association Studies [60] are now available. Intuitively, closely related phenotypes should result from abnormalities of genes involved in similar functional pathways. This idea was first explored by Wu et al. [61] who prioritized genes for phenotypes with no seed genes and several extensions are now available. Here, we review the work of Zhang et al. [62] who made efficient use of the LED kernel to prioritize genes related to phenotypes.

Let be the similarity between phenotypes 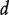and d’, and 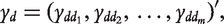where m is the total number of phenotypes of interest. Let 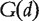be the set of all genes known to be related to phenotype d. The association score between gene g and phenotype d is defined by

i.e. the similarity between gene g and all known genes for phenotype d. Let 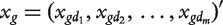. Suppose that there are p candidate genes Define 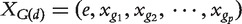, with all the elements of e being 1. Zhang et al. [62] modeled phenotype similarities by the similarity between the candidate genes and the phenotypes using linear model

(9)

where ε is the residual vector 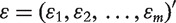modeling random noise and β is a p + 1 dimensional vector of coefficients.

To evaluate whether the set of candidate genes is associated with the phenotype of interest, we test the hypothesis 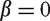. Zhang et al. [62] used Bayes Factor (BF) [63] as a scoring function to test this hypothesis. Several similarity measures between genes within the networks, including the LED kernel, direct neighbors and shortest path distance, were studied, and the LED kernel was shown to perform the best. Therefore, Zhang et al. [62] used the LED kernel in their studies. The model can be easily extended to multiple networks. This result again indicated the usefulness of the LED kernel in summarizing similarity information over networks.

Zhang et al. [62] also studied the performance of their method based on different protein interaction networks: HPRD, BioGRID, BIND, IntAct and MINT, with HPRD containing the largest numbers of proteins (9470), protein interactions (36 634) and seed genes (1440). As expected, the performance of their method based on HPRD is better than the performance based on other protein interaction networks because of its high coverage as well as high accuracy of the HPRD protein interaction network. The authors also integrated the different networks and showed that the performance is significantly increased by integrating multiple networks.

Application 3: prioritizing genes related to phenotypes by integrating expression profiles and protein interaction networks

With the development of high-throughput technologies, such as microarray and next-generation sequencing, researchers can obtain the expression levels of all genes across many disease/treatment conditions in a single study. Typically, genes whose expression level varies with disease/treatment conditions can be identified on the gene-by-gene basis. However, such individual gene-based methods are sensitive to noise, which is typical in high-throughput experiments. Thus, the identification of truly differentially expressed genes related to certain phenotypes by integrating gene expression profiles and networks is gaining increasing attention and several methods have been developed [64–66]. We focus here on one method called prioritizing genes by combining gene expression and protein interaction data (CGI) reported in Ma et al. [64] that effectively used LED kernel for integrating gene expression profiles and protein interaction networks. Intuitively, if the expression levels of a gene and its neighbors are all associated with the phenotype, then the gene is most likely to be related to the phenotype. For quantitative phenotypes, the method can be briefly described as follows.

First, let be the correlation between the expression profile of the ith gene and the phenotype measured by either the Pearson or the Spearman correlation coefficients. Ma et al. [64] also suggested using the Fisher’s transformation

so that is approximately normally distributed. Second, several similarity measures between genes based on the network were studied in Ma et al. [64], including (i) direct neighbor where the similarity matrix S is the same as the adjacency matrix A; (ii) shortest path distance where and is the shortest path distance between genes i and j; and (iii) the LED kernel . Third, they defined an integrated measure R_i by integrating the gene expression profiles and the network to rank genes associated with the phenotype

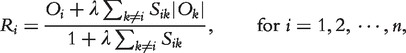where 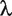is a constant.

Another method of ranking genes related to a phenotype integrating gene expression profiles and a network is GeneRank [65] that used the ideas from Google PageRank for webpage ranking. The algorithm is essentially the same as in Equation (9) except that the ith component of the initial probability distribution 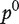is set to equal .

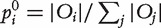To validate the methods, Ma et al. [64] used the expression level of a gene, termed target gene, as a special phenotype and prioritized other genes using the aforementioned approaches. For each target gene, a P-value is defined by testing whether genes within the same gene ontology functional category as the target gene are ranked higher than genes not within the same category as the target gene. Considering all the genes, the histogram of all the P-values can be obtained. Intuitively, if a ranking method is meaningful, the P-values will be close to 0. Therefore, they used the area under the cumulative distribution function (AUCD) of the resulting P-values as a metric to summarize the overall performance of a ranking method:

where G(p) is the cumulative distribution function of the P-values. The range of AUCD is between 0 and 1. If a ranking method is not meaningful, the AUCD is <0.5. A higher AUCD value indicates better ranking method.

Three different large-scale expression datasets, cell cycle [67, 68], knockout [69] and stress response [70], were used to evaluate and compare different ranking methods. Protein interaction data from MIPS [71] was used, as it was considered to be the most reliable at the time of the study. Figure 3 shows the AUCD values of CGI using direct neighbors, LED kernel and GeneRank [65], for all the three datasets. As it turned out, CGI with the LED kernel outperforms the direct neighbor and the shortest path distance similarity metrics, suggesting the advantage of diffusion kernel in measuring similarity between nodes in a network. CGI with the LED kernel was also shown to outperform GeneRank [65].

Figure 3:

The area under the cummulative distribution (AUCD) of the P-values of gene prioritization methods: CGI with direct neighbor (CGI + Direct Neighbor), GeneRank and CGI with the LED diffusion kernel (CGI + Diff Kernel) based on three gene expression data sets: cell cycle [67, 68], stress response [70] and gene knockout [69]. Higher AUCD value indicates better performance of the prioritization method. CGI with diffusion kernel outperforms CGI with direct neighbor and GeneRank [65].

Recently, Winter et al. [66] studied several computational methods to select biomarkers prognostic of survival time of pancreatic tumor patients. The methods include those based on individual genes such as (i) fold change defined by the ratio of mean expression level in cases over that in controls, (ii) the t-statistic comparing the mean expression level in cases versus that in controls, (iii) Spearman correlation between the expression levels and the survival time and (iv) a network approach similar as GeneRank [65]. The authors used three networks: the gene regulatory network in TRANFAC specifying the regulatory relationships of the transcription factors and their target genes, protein interaction network from HPRD and gene co-expression network. For each method, a given number of 5–10 genes are selected. SVM was used to train a model to predict patient survival using a set of 30 patients. The trained model was further used to predict the survival of 412 independent pancreatic cancer patients as testing samples. The prediction accuracy was defined as the fraction of correct predictions among the testing samples. It was shown that the accuracy of GeneRank using the TRANSFAC network is the highest indicating the usefulness of TRANSFAC network for selecting biomarkers.

Nitsch et al. [72] compared several gene prioritization methods, including kernel ridge regression [72], heat kernel diffusion [42] and Arnoldi Diffusion [73], integrating gene expression profiles and protein interaction networks. Let Y be a vector with the ith component being a measure of differential expression values of the ith gene. For a given (semi-) positive definite kernel K over a network, the kernel ridge regression approach tries to predict Y by 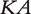where A is a column vector with regularization. That is, for a given parameter 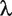, we find the minimum of

Let 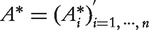be the solution to the aforementioned minimization problem. For a new point x, its updated value is given by 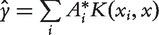. The updated values of the genes are used for ranking. The heat kernel diffusion approach ranks genes based on the component values of 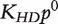, where 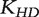is the head kernel diffusion matrix defined in Equation (6) and 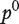is the initial preferential vector for the genes and its ith component is proportional to the absolute value of 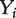. The detail of Arnoldi diffusion approach is complicated and is omitted here. Nitsch et al. [72] also considered three different normalization methods for gene expression data, MAS5, RMA and GCRMA and different statistical methods to summarize the difference of gene expression between two conditions for each gene. A total of 40 mouse knockout gene expression data were used as testing examples to evaluate the different methods. It was shown that the combination of t-statistics to evaluate the importance of each gene, together with the heat diffusion kernel defined in Equation (6) to integrate network data, gives the best performance. However, the relative performance of the heat diffusion kernel approach and CGI was not studied. Overall, these studies showed the importance of using diffusion kernels to prioritize genes related to a phenotype by integrating gene expression profiles and network data.

The authors also considered different mouse interaction networks including versions 7.1 and 8.2 of STRING [18] and BioGRID (version 2.0.61) [17] with version 8.2 of STRING having the highest number of proteins and highest number of interactions. It was shown that the performance of the heat diffusion kernel-based approach using version 8.2 of STRING is the best because of its high coverage of the proteins and the protein interactions.

Application 4: identification of false positives and false negatives in RNAi experiments

Functions of a gene can be studied by inhibiting its expression, for example, during messenger RNA translation. In the past few years, genome-wide RNA interference (RNAi) screenings have been conducted in several species, such as worm [74], fly [75, 76] and mammals [77]. As a high-throughput technology, RNAi results may contain many false positives (FP) and false negatives (FN). For example, a target gene may not be effectively knocked down so that no clear phenotype is observed leading to a false negative. On the other hand, the designed small interfering RNA (siRNA) may actually target hundreds of genes by the tolerance of mismatches and gaps during base pairing with target genes, leading to a phenotype that may not actually come from the desired target genes. This is called off-target effects and is believed to be the main reason for FPs. Thus, computational identification of FPs and FNs can greatly facilitate the efforts of investigators in elucidating gene functions using RNAi.

Guest et al. [78] used protein interaction network to guide RNAi screening of cell cycle related genes in Drosophila. Using a set of potential cell cycle-related genes identified through previous RNAi experiments and genes annotated as cell cycle related in gene ontology as seed genes, the authors identified 1843 other genes directly interacting with the seed genes. These genes were experimentally shown through RNAi experiments to be significantly enriched for cell cycle-related genes thus effectively filtered out FNs from previous RNAi experiments. The method is based on the idea that genes in the same pathway tend to be targeted by the same RNA. Several groups developed computational methods to integrate RNAi experimental results with protein interaction networks to efficiently identify FPs and FNs [79–82]. In RNAi experiments, a score is usually associated with each RNAi hit with higher score, indicating more important roles of the hit to the pathway or function of interest. However, a threshold separating pathway related hits from noise is hard to be determined based on the scores from the RNAi experiments. Realizing that pathway-related hits tend to cluster together in protein interaction networks, Kaplow et al. [80] used protein interaction networks to set a reasonable threshold for the RNAi scores to separate true RNAi hits from noise. For the k top-scored RNAi hits, the hypothesis is that they are highly connected in the network than random. The corresponding P-value, 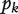, is the probability that the k genes have at least the observed number of interactions for random networks having the same degree distribution as the observed network. The 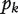as a function of k usually first decreases and then increases to form a V shape. The global minimum of this function is suggested as a threshold for the RNAi scores to separate pathway-related genes from noise.

Wang et al. [82] proposed to integrate RNAi screening results with protein interaction networks to identify putative FPs and FNs. The basic idea is that inhibition of genes in the same functional pathway is likely to lead to similar phenotypes. As interacting proteins, in contrast to other protein pairs, are more likely to be in the same functional pathway, it is reasonable to expect that interacting pairs in the protein interaction network would have similar RNAi phenotype. Consistent with this notion, Wang et al. [82] first demonstrated that RNAi hits are more likely to interact with each other than random gene pairs using 24 published genome-wide RNAi screens in Drosophila and protein interaction data from STRING [18], the largest Drosophila interaction network at the time of the study in 2009.

To efficiently integrate RNAi screening results with protein interaction data, Wang et al. [82] studied how to best use information encoded in the network by different similarity measures among the proteins, including direct neighbor, shortest path distance and the LED kernel. For each gene j, a network RNAi phenotype (NePhe) score indicating the potential for the gene to be a real RNAi hit is given by

where 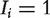if protein is observed as a RNAi hit and 0 otherwise. The first score, NePhe1, predicts the outcome for protein j based on the similarity scores of protein j with the observed hits. The second score, NePhe2, is similar to NePhe1 except it takes the weighted average hit values of the neighbors weighted by the similarity between protein j and other proteins. The third score, NePhe3, explicitly models the different contributions of hits (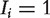) and non-hits (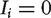). The parameters α and β can be estimated by the linear regression model based on the RNAi results

The authors used the following procedures to evaluate whether a NePhe scoring function can be used to identify FNs: (i) put each RNAi hit together with the non-hits as if it is a non-hit (simulated FN), (ii) calculate the NePhe scores for all the non-hits including the simulated FN, (iii) rank all the non-hits in descending order according to the NePhe scores and (iv) calculate the relative rank (RR) of the simulated FN. The procedures were repeated for every RNAi hit, and the average RR for all the hits was finally calculated. If the average RR for the hits is high, the NePhe score function will be able to identify the FNs in RNAi experiments. Similar procedures were used to evaluate whether a NePhe scoring function can be used to identify FPs by changing the roles of hits and non-hits. If the average RR for the non-hits is low, the NePhe score function will be able to identify the FPs in RNAi experiments. The authors used 24 RNAi experiments and the protein interaction network in STRING [18] to show that the NePhe3 scoring function combined with the LED kernel has the highest average RR for the hits and the lowest average RR for the non-hits. Thus, NePhe3 combined with the LED kernel can best identify FPs and FNs in RNAi experiments.

Realizing that observed RNAi hits can be noisy, DasGupta et al. [83] carried out follow-up RNAi experiments for the hedgehog (Hh) and Wnt signaling pathways to filter out potential FPs in previous studies. First, Wang et al. [82] showed that the reproducibility rate of the hits correlates strongly with the NePhe score indicating the usefulness of the NePhe score to filter out false positives. Second, it was shown that the NePhe scores of some known regulators of Hh/Wnt pathways are high, although these regulators failed to be confirmed by experimental validation. This observation indicates that the NePhe score function can be an even more powerful tool to filter out FPs than experimental validations. Third, NePhe scores correlate with sequence-based off-target effect prediction for FPs, although the NePhe score does not use any sequence information, indicating the usefulness of NePhe scoring function for the identification of FPs. This study clearly showed the usefulness of using protein interaction networks for the identification of FPs and FNs in RNAi experiments.

DISCUSSION AND CONCLUSIONS

Many biological relationships, such as physical interactions, genetic interactions, gene regulation and co-expression can be represented as networks. Efficient integration of network data with experimental results for individual genes such as protein functions, genes related to complex phenotypes, differential expression and RNAi hits, can help us obtain a more complete understanding of the biological system. One key issue in integrating network data with experimental results for individual genes is the definition of similarity between genes or their protein products within the networks. Many different ways of defining similarities of nodes over networks are available including direct neighbors, shortest path distance and various diffusion kernels. For a given similarity measure, various integration methods for network data and experimental results for individual genes can be used to efficiently answer biological questions, such as protein function prediction, gene prioritization based on seed genes and/or gene expression profiles for individuals of different phenotypes and identification of FPs and FNs in RNAi experiments. The results from several research groups clearly showed the advantages of using various diffusion kernels over other similarity measures such as direct neighbors and shortest path distance for data integration. On the other hand, a limited number of studies showed that different versions of diffusion kernels, in particular, the LED kernel [23], heat diffusion kernel [42], random-walk-with-restart (RWR) similarity matrix [30, 31], seem to perform similarly. More studies are needed to compare the performance of different diffusion kernels to solve various biological problems.

In this review, we compared the performance of different similarity measures over a network. In practice, the choice of the network is also important. The performance of the integration methods increases with the fraction of true interactions (reliability) in the network as well as its coverage of the proteins and their interactions. Our experiences showed that protein interaction networks in STRING [18] and HPRD [19] have a good balance between reliability and coverage. Thus, we suggest the use those networks in integrative studies. Further, networks from the various databases complement each other, and efficient combination of the various networks can further improve the performance of the integration methods as shown in Zhang et al. [62]. In addition, the choices of functional annotation of known genes, seed genes for phenotypes, gene expression profiles and the RNAi hits are all essential for optimally solving the corresponding problems we review here.

In conclusion, integration of molecular networks with experimental results of individual genes is a powerful approach for a more complete understanding of biological systems. For integration methods involving similarities among the molecules in networks, similarities defined based on various diffusion kernels and random walks have been shown to outperform other similarity measures such as direct neighbors and shortest path distance leading to the suggestion of using diffusion kernels in such studies. However, the relative performances of the integration methods using various diffusion kernels such as the Laplacian, Laplacian exponential and heat diffusion kernels and the random-walk-with-restart similarity matrix are not clear and more studies are needed to see their power and limitations.

Key Points.

• Integrating molecular networks and intrinsic properties of molecules significantly increases the understanding of biological systems.

• Integrating molecular networks with annotated proteins, genes related to complex phenotypes and RNAi hits allows more accurate predictions of protein functions, genes related to complex phenotypes and RNA targets.

• Diffusion kernels over networks have been consistently shown to have superior performance compared with other similarity measures over networks such as direct neighbors and shortest path distance.

• Explorations of diffusion kernels over networks to other biological problems promise to provide more in depth knowledge about the biological processes of interest.

Biographies

Xiaotu Ma, is currently a staff scientist in the Department of Molecular and Cell Biology, Center for Systems Biology, The University of Texas at Dallas. His research interests include protein interaction networks, gene expression and gene regulatory network analysis.

Ting Chen, is a full professor of Molecular and Computational Biology Program, University of Southern California. He has >18 years of research experiences in computational biology and has contributed significantly to the development of algorithms for proteomics, protein interaction networks and next-generation sequencing.

Fengzhu Sun, is a full professor of Molecular and Computational Biology Program, University of Southern California. He has >20 years of research experiences in computational biology and has contributed significantly to develop statistical approaches for the analysis of genomics and proteomics data. He is an elected fellow of AAAS and an elected member of ISI.

FUNDING

US National Institute of Health NHGRI (P50HG002790) and NHLBI MAPGen (1 U01HL108634).