Background: How voltage and temperature sensors are coupled to channel opening in transient receptor potential melastatin 8 (TRPM8) is still under debate.
Results: Temperature alone can open TRPM8 channels, and deactivation is described by two temperature-dependent closing steps.
Conclusion: A three-tiered allosteric model describes best the gating of TRPM8.
Significance: Temperature and voltage sensors are allosterically coupled to pore gates.
Keywords: Allosteric Regulation, Calcium Channel, Gating, Ion Channel, Thermodynamics, TRPM8, Allosteric Model, Deactivation Processes, Temperature Coefficient
Abstract
Expressed in somatosensory neurons of the dorsal root and trigeminal ganglion, the transient receptor potential melastatin 8 (TRPM8) channel is a Ca2+-permeable cation channel activated by cold, voltage, phosphatidylinositol 4,5-bisphosphate, and menthol. Although TRPM8 channel gating has been characterized at the single channel and macroscopic current levels, there is currently no consensus regarding the extent to which temperature and voltage sensors couple to the conduction gate. In this study, we extended the range of voltages where TRPM8-induced ionic currents were measured and made careful measurements of the maximum open probability the channel can attain at different temperatures by means of fluctuation analysis. The first direct measurements of TRPM8 channel temperature-driven conformational rearrangements provided here suggest that temperature alone is able to open the channel and that the opening reaction is voltage-independent. Voltage is a partial activator of TRPM8 channels, because absolute open probability values measured with fully activated voltage sensors are less than 1, and they decrease as temperature rises. By unveiling the fast temperature-dependent deactivation process, we show that TRPM8 channel deactivation is well described by a double exponential time course. The fast and slow deactivation processes are temperature-dependent with enthalpy changes of 27.2 and 30.8 kcal mol−1. The overall Q10 for the closing reaction is about 33. A three-tiered allosteric model containing four voltage sensors and four temperature sensors can account for the complex deactivation kinetics and coupling between voltage and temperature sensor activation and channel opening.
Introduction
The transient receptor potential melastatin 8 (TRPM8)5 is a cold-activated channel that behaves as a polymodal receptor, which is also activated by depolarizing voltages and by compounds such as menthol, icilin, and phosphatidylinositol 4,5-bisphosphate (1–8). TRPM8 channel gating, as well as that for the TRPV1 heat receptor, has been well studied, and there is a consensus that temperature sensitivity in these channels results from large negative enthalpy change (ΔHC→O) occurring during gating. This is compensated for by a large entropic change that leads the free energy change associated with closing/opening to proximate zero at the temperature range where TRPV1 or TRPM8 act as thermally activated channels (2, 9–11). Under the assumption that different structures in the channel-forming protein play the role of temperature and voltage sensors coupled to pore opening, allosteric models were used to explain the gating behavior of TRPV1, TRPM8, and TRPA1 (2, 12–15). Temperature and voltage drive transitions between resting and active states in these sensors. It is important to mention here that we cannot currently discard the possibility that temperature dependence in thermoTRP channels resides in the nature of the coupling constants that define the allosteric model (16). For example, it is possible to assume that the allosteric factor describing the interaction between temperature-sensor activation and pore opening in the allosteric model would be the temperature-dependent parameter. At present, neither the temperature nor the voltage sensor has been unequivocally identified, but there is evidence that they reside in different channel molecular structures. C-terminal deletion mutants of TRPV1 (17) and C-terminal chimeric constructs between TRPV1 and TRPM8 (2) have shown that it is possible to completely obliterate channel temperature dependence without affecting voltage dependence (18). However, it has been found that point mutations in the vicinity of the pore region greatly decreased TRPV1 temperature sensitivity without affecting its activation by depolarizing voltages. The molecular determinants of temperature sensing in TRPV1 have also been located in the N-terminal domain (19) and in the pore turret (20). When TRPV1 amino acid residues from the pore turret are replaced with an artificial sequence, temperature response is suppressed. This replacement, however, has not been observed to modify channel activation by capsaicin or depolarizing voltages (12, 20). These results support the idea that temperature activation in thermoTRPs depends on temperature sensors, which can be thought to be discrete structural modules within the channel structure.
Previous experiments have shown that voltage is a partial activator of TRPM8 and that the half-activation voltage (V0.5) saturates at extreme temperatures, which suggests a lack of strict coupling between TRPM8 voltage and temperature activation (2, 13, 14). These results have been explained on the basis of an allosteric model with separate voltage and temperature sensors, which upon activation promote the opening of the pore domain independently from one another. However, this type of model has been criticized (10) in terms of the following: (a) inaccuracy in determining the maximum open probability (Po, max); (b) very rapid TPRM8 channel deactivation at negative voltages, leading to an underestimation of the open probability (Po) from tail currents; and (c) voltage clamp errors. All these problems have been addressed in this study by carefully determining the Po, max through noise analysis (21, 22), measuring tail current at positive voltages, and extending the voltage range up to 500 mV to ensure saturation of the Po(V) curves. In agreement with the allosteric model prediction, we found that the lnPo(V) curve slope decreases at very large negative voltages and becomes voltage-independent at the limit of very large negative voltages. Our results indicate the following: (a) the channel can open when all voltage and temperature sensors are in the resting state; (b) temperature alone can activate TPM8 channels. Po increases 14-fold at −200 mV in response to a temperature drop from 25 to 15 °C, strongly suggesting that temperature affects channel opening through a pathway that does not involve voltage sensor activation. (c) Voltage behaves as a partial activator of TRPM8 channels at very high temperatures thus confirming the voltage independence of the close-open transition. The Po(V) curve obtained at 30 °C saturates at a Po, max = 0.55. (d) We show here that voltage-dependent transitions between closed states have very small temperature dependence. These results rule out the possibility that both temperature and voltage sensors move as a single molecular entity.
EXPERIMENTAL PROCEDURES
Molecular Biology
cDNA coding for rat TRPM8 (provided by David Julius, University of California at San Francisco; GenBankTM accession number NM_134371) was used. TRPM8-cDNA was subcloned into a pBSTA vector using the restriction enzymes NotI and KpnI (New England Biolabs) and was introduced into DH5α-competent cells. One μg of cDNA linearized with NotI was placed in a standard in vitro transcription reaction by using a T7 mMessagemMachine kit (Ambion, Austin, TX). The quantity and purity of the extracted RNA were determined by measuring absorbance at 260 nm. The integrity and size range of total purified RNA were checked by denaturing agarose gel electrophoresis (0.7%) and ethidium bromide staining.
Electrophysiology
Xenopus laevis oocytes were injected with 50 nl of water (control) or 50 nl of mRNA (0.05 ng/nl) and were then maintained at 18 °C in ND96 medium, which ensured 90% survival. Currents elicited by TRPM8 channels were recorded using the patch clamp technique on the cell-attached configuration (23) with an Axopatch 200B amplifier (Axon Instruments, Foster City, CA) 2–5 days after mRNA injection and after manual removal of the vitelline membrane. Patch pipettes were pulled in a horizontal pipette puller (Sutter Instruments) from borosilicate glass capillaries (World Precision Instruments, Sarasota, FL), and pipette tips were fire-polished by a heating filament under a microscope to promote high resistance seal formation. TRPM8 was recorded in cell-attached macropatches of oocyte membranes (0.4–1 megohm pipette resistance and 10–20-μm tip diameter) (24), which enabled us to obtain low noise levels and fast clamp patch recordings of many channels that could not be obtained by using other expression systems. Macroscopic current was filtered with an 8-pole low pass Bessel filter (900C9L8L, Frequency Devices, Haverhill, MA) at 20 or 40 kHz and digitized at a rate of 200 kHz by an NI-PCI-6014 Card (National Instruments). Data analysis was performed with the analysis application program (25), which was kindly provided by Dr. Francisco Bezanilla (University of Chicago) and the Clampfit 9 software (Axon Instruments). Curve fitting was made using either Solver complement of Microsoft Excel 2010 or Regression Wizard of SigmaPlot 10.
Temperature Control
The recording chamber consisted of a glazed aluminum block, which was located above a Peltier element. In turn, a heat sink made of bronze was located under this element, which was cooled or heated by water circulation. Temperature feedback signal was obtained by using a miniature thermistor located in the recording chamber, allowing us to measure the temperature of the bath. This temperature reading was compared with the set temperature, so that the proportional-integral-differential controller would deliver or remove heat to and from the system. Temperature was maintained at the set value ±0.2 °C. Temperature was settled in less than 1 min for 2 °C temperature jumps. The control system was built around the Arduino digital platform.
Macroscopic TRPM8 Currents
Pulse protocols used a holding potential of −60 mV for macroscopic current relaxation experiments, followed by a test pulse to different voltage steps from −160 to 300 or 500 mV in 10- or 20-mV increments, separated by intervals of 2 s, and ending with a voltage pulse of 100 mV. The duration of each episode was variable, due to the need to find a steady state current at each voltage. Consequently, when the voltage increased, the duration of episode diminished. The tail current, Itail(V), amplitude was determined by fitting each trace of the current obtained at +100 mV to a double exponential function and extrapolating to time 0. It was normalized by making the ratio between Itail(V) and the maximum tail current obtained at a given temperature, Imax(T). The resulting Itail(V)/Imax(T) versus voltage data were fitted to a isothermal Boltzmann function as shown in Equation 1,
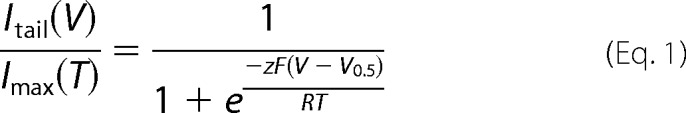 |
where z is the apparent number of gating charges, and F, R, and T have their usual meanings.
Nonstationary Noise Analysis
To determine the absolute Po(V) curves at different temperatures, we needed to determine the absolute open probability at a given voltage so as to scale the entire Itail(V)/Imax(t) plot obtained as described above. We used a nonstationary fluctuation analysis (21, 22) by calculating the average and variance of isochrones from 200 current relaxation traces in response to a 260-mV voltage pulse. The single channel current (i) and the number of channels (N) in the patch were established by nonlinear curve fitting to the current variance, σ2, versus average current 〈I〉 with the following Equation 2,
 |
The maximum absolute Po (Po, max) at 260 mV was calculated from the maximum mean current recorded (〈I〉max) divided by the mean current expected if all the channels present in the patch were open as shown in Equation 3,
 |
Current variance and means were calculated with the analysis software, which corrects for current rundown during the experiments (26, 27).
Limiting Slope
For limiting slope experiments, macropatches containing hundreds of channels were used. The number of channels, N, in the patch and the unitary current, i, were measured through a nonstationary noise analysis of current recorded in response to 100 pulses of 260 mV from −50 mV holding potential. After channel counting, membrane current was acquired for 2–10 s at Vm values ranging from +80 to −250 mV. This procedure was repeated for the different temperatures tested. To determine the open channel probability, we generated all-point histograms of the number of times a given current was observed. The ordinate values of the histogram were divided by the integral over the membrane current axis, I, so as to obtain the probability density function, PDF. Assuming that a maximum of nine channels can be open simultaneously, the theoretical PDF was constructed as a sum of 10 normal distributions over the current axis shown in Equation 4,
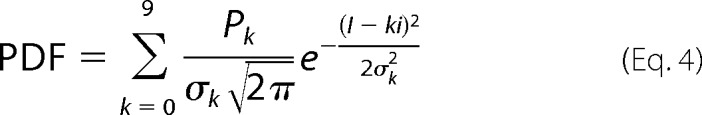 |
where k is the number of simultaneous open channels, and i is the unitary current. Therefore, each normal distribution was centered at the expected current level, ki, with a variance σk2. The variance of each current level had to account for instrumental noise and noise from open channels. The overall variance for the level with k open channels was taken as (σc + kσo)2, where σc2 is the variance of the closed level, and σo2 is the variance of one open channel noise value. Pk is the relative weight of each current level and was calculated by using the expected probability of finding simultaneous k open channels in a membrane containing N channels and with an open probability (Po) as described by Poisson distribution in Equation 5,
 |
Po was established by fitting the theoretical PDF to the experimental PDF and by fixing the number of channels, N, obtained by nonstationary noise analysis with the Solver complement of MS-Excel. Adjustable parameters were Po, σc2, σo2, and the single channel current, i. The data acquisition analog filter introduces asymmetric smearing between zero and the first open level distributions (28–30). To improve the fit, we replaced the normal distribution corresponding to the zero current level with a skewed normal distribution (31, 32) defined by parameters μ, σ, α, as shown in Equation 6,
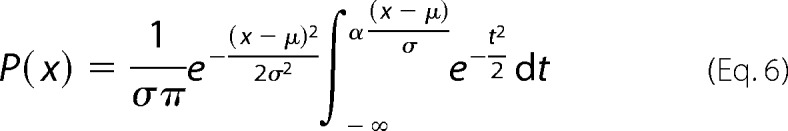 |
The introduction of the skewed normal distribution resulted in a better overall fit and linear voltage dependence of the calculated single channel current.
Relaxation Kinetics
The deactivation process was characterized over a wide range of voltage and temperature. One of the problems with previous TRPM8 channel deactivation analyses was that the time course of deactivation was too fast to be adequately followed when current signals were filtered at 2 kHz (2). In this study, we have overcome this limitation by using the macropatch technique and by filtering within the 20–40-kHz range. Fig. 1 shows that the time course of the deactivation current (black current trace) can be distinguished reasonably well from the capacitive transient (red current trace) even at the highest temperature used (i.e. 30 °C) and at very negative voltages (−260 mV). The time constant that described the time course of the capacitive current was, in this case, about six times faster than the time constant of the TRPM8 deactivation current exponential decay (32 μs).
FIGURE 1.
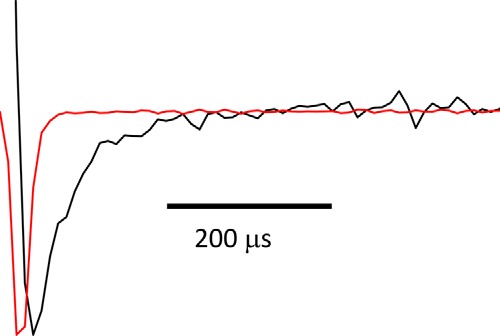
Patch clamp speed. Peak-normalized current traces for the fast deactivation of TRPM8 at 30 °C, −260 mV (black), and the capacitive current in response to a −5 mV voltage step (red) are shown. It can be seen that there is substantial TRMP8 current when the capacitive current has vanished, allowing for a reliable measure of fast deactivation kinetics. Time constants for the fast component of TRPM8 deactivation currents and capacitive transient were 32 and 5.1 μs, respectively. Current signal was low-pass filtered at 40 kHz and sampled at 5 μs per point (200 kHz).
Cole-Moore Shift Analysis
The initial lag of the ionic currents reflects the early transitions of the activation pathway. A large hyperpolarizing prepulse would populate closed states further removed from the open state, which would result in a longer lag in activation. Thus, under this principle, we applied the classical Cole-Moore protocol (33). The cell membrane was hyperpolarized to various potentials (from −200 to −40 mV) for 100 ms, and immediately thereafter, the current record was tested with a 12-ms depolarizing pulse to 260 mV. Time delay was evaluated by fitting each curve to the following Equation 7,
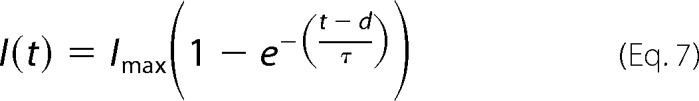 |
where Imax is the maximum current obtained in the experiment; t is time; d is the delay; and τ is the activation time constant. The fit is performed for t > 3d. This procedure was repeated at different temperatures.
RESULTS
Voltage and Temperature Dependence of Steady State Activation
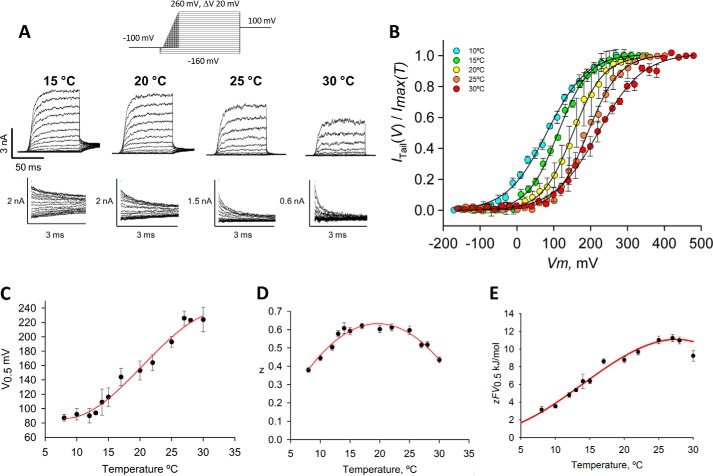
To determine the extent of coupling between temperature and voltage activation in TRPM8, we first measured the tail current-voltage Itail(V) relationships within a wide range of voltage. One of the problems with previous tail current measurements was the very fast TRPM8 channel deactivation at negative voltages, which made the determination of Itail(V) curves at high temperatures uncertain (2). We addressed this problem by measuring tail currents at 100 mV to ensure that the tail currents were reliably recorded (Fig. 2A). We also extended the voltage range up to 500 mV to reach the maximum tail current at each of the temperatures tested (Imax(T)). Fig. 2B shows a family of Itail(V)/Imax(T) curves taken within the 10–30 °C range fitted to isothermal Boltzmann functions (see Equation 1 under “Experimental Procedures”). Lowering the temperature caused the Itail(V)/Imax(T) relationship to shift to the left along the voltage axis. In the temperature range studied, the half-activation voltage, V0.5, varied from 92 mV at 10 °C to 220 mV at 30 °C. What is apparent is that V0.5 saturates at temperatures lower than 12 °C and higher than 27 °C (Fig. 2C). The observation that V0.5 saturates at low and high temperatures is incompatible with gating models in which the temperature sensor is strictly coupled to the pore opening (10, 13). In addition, we noted that z is also a function of temperature, decreasing for both high and low temperatures with a maximum being at about 17 °C (z = 0.62 ± 0.01; n = 12) (Fig. 2D). This is a characteristic of the allosteric models, as observed previously on the BK channel where z depends on calcium concentration, decreasing at low and high calcium concentration (34, 35). A shift to the left of the Itail(V)/Imax(T) relationship with decreasing temperature implies that the TRPM8 channel opening reaction produces a negative entropy change (36). This entropy can be calculated from the slope of the rectilinear part of ΔG0 = zFV0.5 versus T plot, which would be −122 cal mol−1 K−1 (Fig. 2E).
FIGURE 2.
Voltage and cold activation of TRPM8. A, macroscopic currents of TRPM8 recorded in cell-attached oocyte membranes at 15, 20, 25, and 30 °C. Below each current trace family, tail currents measured at 100 mV for each temperature are shown in an expanded time scale. Applied voltages were in the −160 to 260 mV range in 20-mV increments. Holding potential was −100 mV. Pulse duration was set to the minimum possible, to ensure current steady state conditions. B, Itail(V)/Imax(T) curves. For the sake of clarity, only 5 of the 13 different temperatures tested are shown. Error bars are standard deviations of the mean (n = 8). Solid lines are isothermal Boltzmann fits (Equation 1). C and D, V0.5 and z versus temperature, obtained from the Boltzmann fits for all the temperatures tested. Error bars are standard deviations of V0.5 or z as reported by the SigmaPlot 10 nonlinear curve fit procedure. Red line in C is a third order polynomial function and in D it is a second order polynomial function. E, zFV0.5 = ΔG0 versus temperature obtained from data in C and D. Solid red line is a third order polynomial function. From linear regression to data in the temperature interval 10 °C ≤ T ≤ 25 °C, ΔS and ΔH values were calculated as −117 cal mol−1 K−1 and −32.0 kcal mol−1, respectively.
Voltage Is a Partial Activator of TRPM8
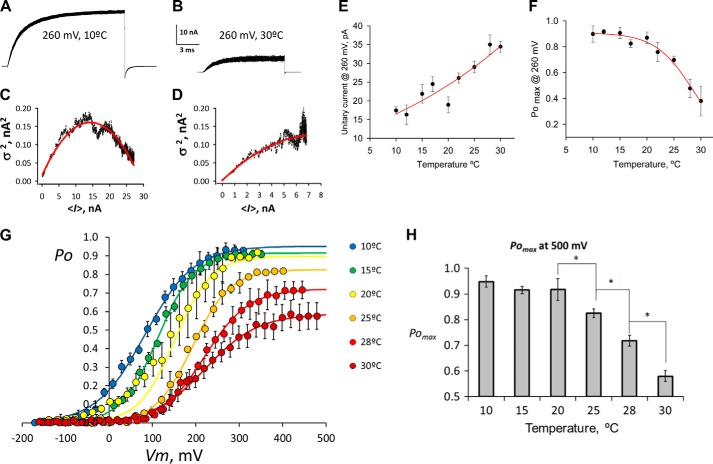
To determine the absolute Po(V) curves at each of the temperatures tested, we first carried out nonstationary noise analysis of the TRPM8 current fluctuations. Fig. 3, A and B, shows 200 superimposed current records obtained by applying a 260-mV pulse at 10 and 30 °C. Fig. 3, C and D, display the variance (σ2) as a function of the mean current (〈I〉) calculated from the current records shown in Fig. 3, A and B. Single channel current (i), number of channels in the patch (N), and absolute Po at 260 mV were obtained from nonlinear curve fitting by using Equations 2 and 3 (see “Experimental Procedures”). The parabolas described by red lines in Fig. 3, C and D, were drawn according to Equation 2. At 260 mV and 10 °C, i = 20 pA, N = 1431 channels, and Po, max is 0.91 (Fig. 3C). However, at 260 mV and 30 °C, i = 30 pA, N = 1452 channels, and Po, max = 0.41 (Fig. 3D). As expected, it was possible to observe that the unitary current increases and the Po, max value decreases as temperatures rise. Single channel current measured at 260 mV was essentially linear over temperatures from 10 to 30 °C (Fig. 3E). A fit of unitary current to the Arrhenius equation gave an enthalpy change of 6.3 ± 1.0 kcal mol−1, and in the temperature range tested the Q10 was 1.4. This value is close to that obtained for the Na+ channel (37) (Q10 = 1.35) or Kv channels (38) (Q10 = 1.44). The Po, max value determined for each temperature at 260 mV by nonstationary noise analysis is plotted in Fig. 3F. A family of absolute Po(V) curves at different temperatures was obtained by scaling Itail(V)/Imax(T) data to the Po, max determined at 260 mV for each temperature through the nonstationary noise analysis (Fig. 3G). Simple inspection of this figure shows that voltage is a partial activator of TRPM8, showing that Po, max is only 0.55 at high temperatures (30 °C) (Fig. 3H). Partial activation of the TRPM8 channel by voltage would be expected if the opening reaction is voltage-independent (see below).
FIGURE 3.
Voltage is a partial activator of TRPM8. A, 200 superimposed current traces in response to 260-mV pulses from a holding potential of −60 mV, recorded at 10 °C. B, same patch heated up to 30 °C and a slightly shorter 260-mV voltage pulse was repeated 200 times. C and D, variance versus mean current plot from isochronal sampling of the current traces shown in A and B, respectively. Red solid lines correspond to the best fit to each plot using Equation 2. Results from fit were as follows: i = 20 pA, n = 1431, Po, max = 0.91 in C, and i = 30 pA, n = 1452, Po, max = 0.41 in D. E, estimation of unitary current at 260 mV from variance analysis over a wide range of temperatures. Values are average ± S.E. for a set of 3–12 different patches. The red line corresponds to the expected current calculated from the Arrhenius plot with activation energy of 6.3 kcal mol−1. F, Po, max at 260 mV versus temperature. Po, max was obtained from the noise analysis data fitted by using Equation 2. Values are average ± S.E. for a set of 3–12 different patches. G, absolute probability of opening (Po) versus voltage curve. Each curve corresponds to a Itail(V)/Imax(T) versus voltage of A scaled by using the Po, max measured at 260 mV. Error bars are S.E. (3 < n < 12). Lines drawn over the points are Boltzmann functions scaled according to the open channel probability at 260 mV for each temperature displayed on F. H, column graph shows Po, max for 500 mV at different temperatures predicted by the Boltzmann fits of G. Error bars are the 95% confidence limits as reported by the nonlinear curve fitting procedure of SigmaPlot 10. Asterisks indicate nonoverlapping 95% confidence limits of Po, max.
Temperature Alone Is Able to Open TRPM8 Channels
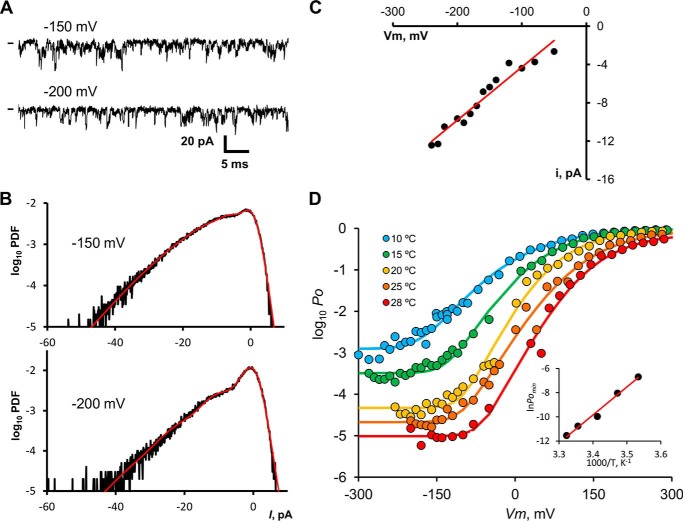
Voltage sensors should be in their resting configuration at a large enough negative voltage, even at low temperatures. The allosteric model predicts that under this extreme condition, TRPM8 channels can open in a temperature-dependent manner through direct interaction between temperature sensors and channel gate. To test this prediction, we quantified open channel probability at very negative voltages. Because open probability at negative voltages is expected to be low, we used patches that contain several hundreds of channels and analyzed stationary noise. Fig. 4A shows the current recorded at 15 °C for −150 and −200 mV from a patch containing 504 channels. Few simultaneous opening events caused the current trace to fluctuate downward from zero current level marked with a short dash on the left of Fig. 4A. We computed the PDF of the current from all-point histograms of current traces. The computed PDF did not show individual channel opening events due to the very fast kinetics of TRPM8 channels at negative potentials and to the cutoff frequency of the data acquisition low pass analog filter (10 kHz). Nevertheless, the PDF was skewed toward negative current, revealing the presence of open channels. To obtain the open probability of TRPM8 channels under these conditions, we described each discrete current level as bell-shaped distributions, and we scaled the expected contribution to the PDF according to the Poisson distribution (see under “Experimental Procedures”), which is only a function of the parameter NPo (Fig. 4B) (35, 39). By means of a nonlinear fit to Equation 4 to the all-point histogram, absolute Po was calculated at the different applied voltages from NPo taken from the histogram analysis, and the number of channels in the patch was determined by means of a nonstationary noise analysis. Single channel currents were also obtained from current histogram analysis. Fig. 4C shows that single channel current is a linear function of voltage and that single channel conductance results in 55 ± 3.9 pS. This conductance is lower than the 75 pS expected from the single channel currents measured at 260 mV (Fig. 3E).
FIGURE 4.
Limiting slope of logPo − V curve. A, samples of current recorded from a patch containing ∼500 TRPM8 channels at −150 and −200 mV at 15 °C. Channel openings are seen as brief downward deflections. Current data stream analogically filtered with a 8-pole Bessel filter tuned for a −3 db attenuation at 10 kHz, and it was digitized at a rate of 5 μs per point. B, normalized all-point histograms of current records taken at −150 and −200 mV lasting 2 s are shown in semi-log plots. Red lines drawn over the histograms are fits to the Poisson convolved with a Gaussian distribution (see “Experimental Procedures”), which allows us to retrieve the NPo value for each holding voltage. C, unitary current obtained from the Gaussian-convolved Poisson fit to the all-point histograms shown in B. Unitary conductance for this particular experiment (15 °C) was equal to 55 ± 3.9 pS from linear regression (solid line). D, absolute Po versus voltage curves for five temperatures, compiled for a set of 3–5 patches at each temperature. For log10Po < −2, Po was calculated from NPo determined using stationary current noise analysis, and N was calculated from nonstationary noise analysis. Data for log10Po > −2 were obtained from instantaneous tail currents and corrected for the maximum Po measured at 260 mV through nonstationary noise analysis. Solid lines are fits to a modified Boltzmann function: Po = Pmin + (Pmax − Pmin)/(1 +exp(−zF(V − V0)/RT)4. Pmin values are 1.1 × 10−3 at 10 °C, 3.1 × 10−4 at 15 °C, 4.3 × 10−5 at 20 °C, 2.6 × 10−5 at 25 °C, and 9.3 × 10−6 at 28 °C. Inset, ln(Po, min) versus 1/T. Because Po, min ≪1, we can approximate Keq ≈ Po, min. Red straight line corresponds to ΔH = −45.9 kcal mol−1 for the opening reaction only through temperature sensor activation.
Several single channel recordings and macroscopic recordings were averaged to construct the logPo(V) plots shown in Fig. 4D. The important conclusion of this analysis is that Po becomes voltage-independent at extreme negative voltages. We recall here that in voltage-dependent channels like, for example, Kv or Nav, the logPo(V) relationship becomes linear and reaches a maximum slope (limiting slope) at very low probabilities (40, 41). This is the type of behavior expected for any kinetic model in which the voltage-dependent step(s) are prior to the closed-open transition and from models of any number of open states, if there is no charge movement between them (42, 43). In such cases the limiting slope is given by Equation 8,
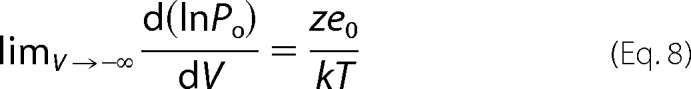 |
where ze0 is the voltage sensor charge effectively coupled to channel activation, and k is the Boltzmann constant. The TRPM8 channel departs from this behavior; it reaches a maximum slope of about 0.65 at Po ∼0.1, but at 25 °C and when Po is lower than 10−4, for example, Po becomes essentially voltage-independent (Fig. 4D). This limiting slope behavior (albeit at different Po values) is similar at other temperatures tested. This observation further supports an allosteric mechanism for the voltage-dependent activation of the TRPM8 channel. Allosteric models of the type we propose here have been shown to explain most of the behavior of the voltage- and Ca2+-activated channel of large conductance (BK). However, the data shown in Fig. 4D are clear evidence that, unlike the BK channel, the TRPM8 opening is essentially voltage-independent. The allosteric model also predicts that, under these extreme negative voltage conditions, TRPM8 channels can open in a temperature-dependent manner only through direct interaction between temperature sensors and channel gate. Fig. 4D shows that at negative voltage Po is highly sensitive to temperature (Po increases from 4.3 × 10−5 at 20 °C to 1.1 × 10−3 at 10 °C) with a Q10 of 25. This result indicates that low temperature alone has a strong effect on channel opening, even with all voltage sensors in their resting state. We note here that at voltages in which all voltage sensors are at rest, a plot of lnPo versus 1/T allows us to calculate the enthalpy change that controls channel opening. The inset of Fig. 4D shows that the lnPo is a linear function of 1/T with a ΔH = −46 kcal mol−1. More importantly, the data indicate that ΔH is independent of temperature.
Voltage and Temperature Dependence of the Delay in Ionic Current Activation
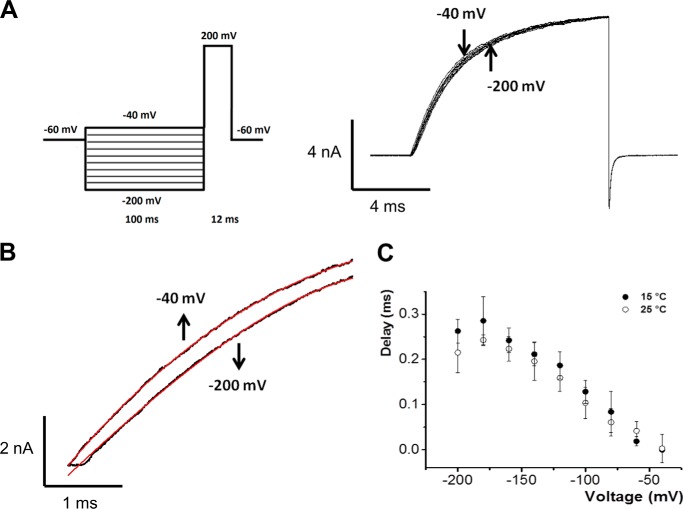
Fig. 5A shows TRPM8 ionic currents (Ii) evoked in response to a 10-ms pulse to 200 mV and elicited from 100-ms prepulse potentials from −200 to −40 mV at 20 °C. The time course of activation is well fit by an exponential function (Fig. 5A). A similar exponential kinetics was observed over a wide range of voltages and temperatures (2, 8). However, closer inspection of the results revealed that exponential activation of the ionic currents was preceded by a brief delay (Fig. 5B). Fig. 5B shows the initial time course of the ionic current activation in response to a voltage pulse of 200 mV, when the prepulses are −40 and −200 mV on an expanded time scale. As in HEK cells (13), when the holding voltage is −200 mV, Ii in Xenopus oocytes shows a delay of about 200 μs before the current begins to increase and achieve an exponential time course. Although this delay is brief compared with the subsequent relaxation of Ii, it is inconsistent with the two-state gating scheme and suggests that TRPM8 channels undergo several transitions among closed states before opening. The onset of TRPM8 Ii can be delayed by hyperpolarizing prepulses (cf. −200 and −40-mV prepulses in Fig. 5, B and C), suggesting that hyperpolarization brings the channel to deeper voltage-dependent closed states (the Cole-Moore shift (33)). Fig. 5C shows that current delay is a decreasing monotonic function of voltage and that it has weak temperature dependence. The slight temperature dependence observed for the initial delay of Ii (Q10 = 1.2) indicates that the reactions governing early voltage-dependent transitions have a very weak temperature dependence. Furthermore, given the relatively large change in Po at 200 mV between 25 and 15 °C (Fig. 3G), this result strongly suggests that these voltage-dependent reactions are temperature-independent, which is incompatible with models where the voltage and temperature sensors are strictly coupled.
FIGURE 5.
Kinetics of early transitions of the activation pathway. A, macroscopic ionic currents of TRPM8 elicited in response to conditioning prepulses shown in the pulse protocol (left). B, two current records obtained using 100-ms prepulses of −40 and −200 mV are shown in an expanded time scale, detailing the observed delay before current achieves an exponential time course (red solid line). C, delay duration is plotted versus prepulse voltage for two temperatures, 15 and 25 °C.
Voltage and Temperature Dependence of Ii Relaxation
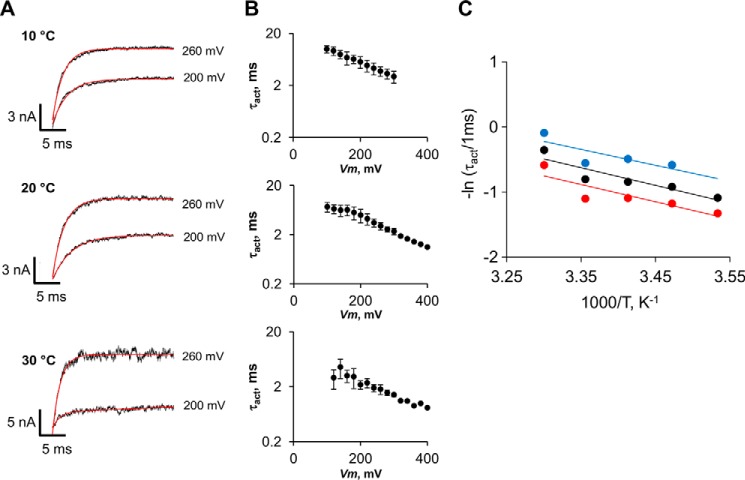
In response to a voltage step, Ii activates with an exponential time course after a brief delay (Fig. 5B). We have characterized the rate-limiting step of TRPM8 channel activation kinetics by fitting the Ii time course in response to a voltage step with a single exponential function (Fig. 6A) within a wide range of voltages and at different temperatures (Fig. 6B). Because the activation process appears to be limited by one main step, activation rates were estimated from the inverse of τa (Ii), and Arrhenius plots were constructed by plotting 1/τa (Ii) versus 1/T and fitted with Equation 9 (Fig. 6C),
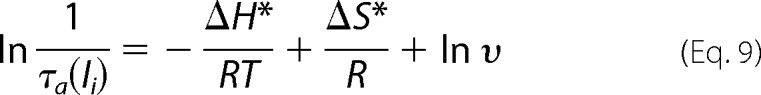 |
where ΔH* is the activation enthalpy; ΔS* the activation entropy, and υ is the pre-exponential frequency factor of the rate (106 s−1) (44). In line with previous data (2, 8), we found that ΔH* = 5.2 kcal mol−1, which is a value corresponding to Q10 = 1.3. Also in agreement with previous results (2, 8), this value indicates that the activation kinetics has a slight temperature dependence and that the high temperature dependence of Po does not reside in the rate-limiting step that controls channel activation. In addition, ΔH* was found to be voltage-independent in the voltage range of 240–340 mV, and in the temperature range from 10 to 30 °C (Fig. 6C).
FIGURE 6.
Voltage and temperature dependence of activation time constants. A, TRPM8 current traces in response to 200- and 260-mV pulses from a holding potential of −60 mV, acquired at 10, 20, and 30 °C. Activation time constants (τact) were determined by a mono-exponential fit (solid red line). B, corresponding τact versus voltage relationships for each temperature are shown in A. Vertical error bars are S.E. (n = 7). C, Arrhenius plot of activation time constants measured at 260 mV (red), 300 mV (black), and 340 mV (blue). Activation energies of 5.3, 5.4, and 4.8 kcal mol−1 for 260, 300, and 340 mV, respectively, were calculated from the slopes of the linear regressions (straight lines).
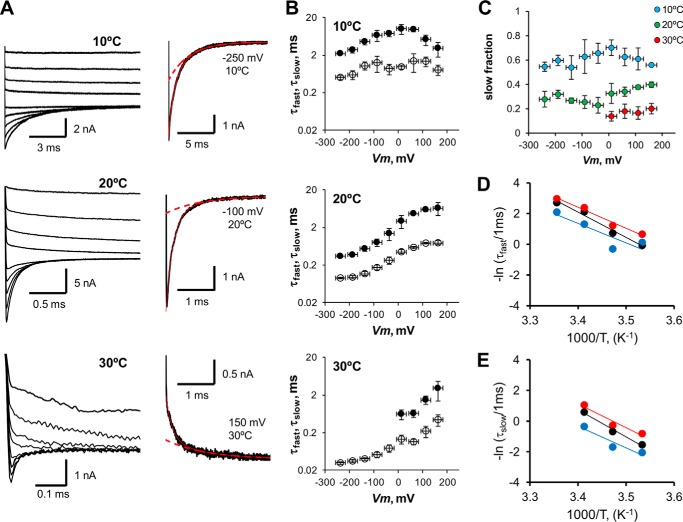
The deactivation process was also studied within a wide range of voltages and temperatures (Fig. 7A). At most voltages and temperatures tested here, we found that a bi-exponential function is needed to describe the deactivation process. However, at 30 °C, the time course of the deactivation process was well described by using two exponentials only at positive voltages; the amplitude of the slow component was too small to be measured at V <50 mV (Fig. 7C). The time constant of the slow component was 5–10 times longer than the fast time constant for all voltages and temperatures tested. Fig. 7B shows that both components of the deactivation current relaxation were voltage-dependent and that the peak of the τd (Ii) − V curves was shifted to the left along the voltage axis as temperature decreased. The leftward shift reached about 80 mV when the temperature fell from 20 to 10 °C, which resembles the leftward shift of the Itail(V)/Imax(T) curve when temperature decreases by 10 °C in the same temperature range (Fig. 2, B and C).
FIGURE 7.
Voltage and temperature dependence of TRPM8 deactivation. A, TRPM8 current traces in response to different voltage pulses (from −250 to 200 mV in 50-mV increments), after a prepulse of 260 mV acquired at 10, 20, and 30 °C. A bi-exponential decay (solid red line) is needed to properly fit the deactivation time course for the majority of voltages tested. Dashed red line corresponds to the slow component of the relaxation. B, fast (τfast, open circles) and slow (τslow, filled circles) time constant versus voltage at 10, 20, and 30 °C. The slow component is absent for negative voltages at 30 °C. Data were averaged in 50-mV bins for clarity. Error bars are S.E. (n = 5). C, plot of relative slow component amplitude as a function of voltage, calculated for 10, 20, and 30 °C. D, Arrhenius plot of fast deactivation time constant. Red, black, and blue circles correspond to deactivation rates at −240, −140, and −40 mV. From the slope of linear regression, the activation energies are 27.2, 32.6, and 25.0 kcal mol−1, respectively. E, Arrhenius plot of slow time constant. Red, black, and blue circles correspond to the same voltages as in D. Activation energies from the slope of linear regressions are 30.8, 35.2, and 27.8 kcal mol−1, respectively.
Regarding the slow component, these data are consistent with those reported previously (2). However, in the case of Voets et al. (8), the fast component was not detected. Probably because Brauchi et al. (2) filtered the current records at 2 kHz, they concluded that the fast deactivation component was voltage- and temperature-independent. Another feature of these data that is important to mention here is that ln(1/τ) versus 1/T plots are parallel for high negative voltages, thus implying a lack of voltage dependence for the activation enthalpies in both activation and deactivation processes (see Fig. 7, D and E, and under “Discussion”). Activation enthalpy for the fast and slow components of TRPM8 deactivation at −240 mV were 27.2 and 30.8 kcal mol−1, respectively, as calculated from the Arrhenius plots, within the 10–20 °C temperature range (Fig. 7, D and E). These enthalpies correspond to Q10 values of 5.2 and 6.4, respectively, thereby indicating that temperature sensitivity of the TRPM8 channels resides in the deactivation process. A double exponential time course for the deactivation is predicted in a C-C-O kinetic scheme, in which the forward rate in the C-O transition is different from zero (45). We can quantitatively demonstrate that TRPM8 temperature dependence completely resides in the deactivation process by assuming that the closed-open transition corresponds to fast relaxation and that the close-close transition is related to a slow relaxation of the deactivation time course shown in Scheme 1.
SCHEME 1.
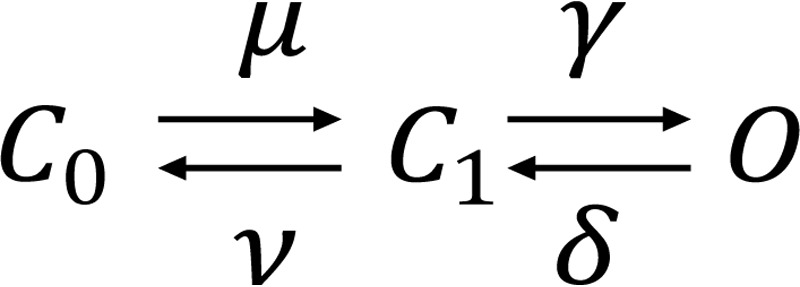
For this type of model, it can be shown that the Q10 of the TRPM8 deactivation process Q10(deact) is given by Equation 10 (see Appendices A and B and Equation B11),
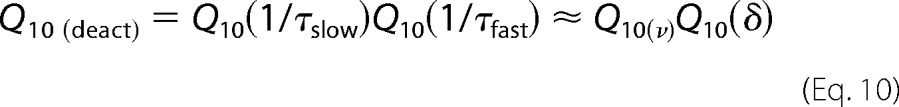 |
Considering the Q10 of the slow and fast deactivation processes given above, the total Q10 of the deactivation currents is 5.2 × 6.4 = 33.3. Because the Q10 for the activation process is 1.3, then the Q10 of the overall equilibrium (see Appendix A and Equation B11) is 33.3/1.3 = 25.6. Single channel Q10 is 1.4 (Fig. 2E), but the single channel current increases as temperatures increase. Therefore, the current temperature coefficient of the current carried by TRPM8 is 25.6/1.4 = 18.2, which is close to the Q10 = 23.8 value that was determined from current-temperature plots (2). The justification for using this simple kinetic scheme in terms of complex allosteric models is provided under “Discussion.”
DISCUSSION
The fact that TRPM8 knock-out animals show a near-complete loss of cold sensitivity underscores the importance of this channel in both innocuous and noxious cold sensation in vivo (46, 47). Besides temperature and voltage, TRPM8 is activated by phosphatidylinositol 4,5-bisphosphate and a variety of the so-called cooling agents, such as menthol, because of their property of inducing a cold sensation (5–7, 48, 49). Because of its physiological importance, the gating of this channel has been studied in some detail, but there are still some divergences regarding how temperature, voltage, and agonist effects are coupled to the channel gate (2, 8, 10, 13, 14, 50, 51). One of the main problems that have prevented us from reaching an agreement in this regard has been the goodness of the data reported before (2). We note here that the present data do not have the previous experimental caveats (2), which were criticized by Voets et al. (10). Moreover, even for the most demanding experimental conditions (e.g. high temperatures and negative voltages), we were able to determine the relaxation time constants free of artifacts due to the fast voltage clamp speed enabled by the low resistance pipettes used to make the macropatches (Fig. 1).
Analysis of single channel gating kinetics indicates that TRPM8 enters a minimum of at least five closed states and two open states (52). A seven-state kinetic model was able to account for TRPM8 channel voltage dependence at two different temperatures. Those result led the authors to conclude that depolarization and cooling accelerate forward transitions between the same set of two adjacent closed states. This model is at odds with the results presented here, which show that temperature can activate the channel when all voltage sensors are at rest, that voltage-dependent transitions are weakly sensitive to temperature, and that voltage is a partial activator of TRPM8.
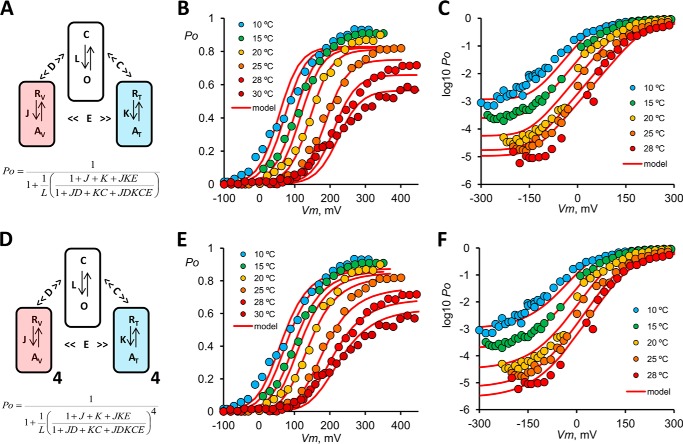
Our data indicate that an allosteric model (2, 13, 14, 34, 39) would be more appropriate to explain TRPM8 gating kinetics. This kind of model is based on the idea that voltage and temperature sensors are structurally different modules that can act independently from one another. The results that best support this idea for TRPM8 gating are the saturation of V0.5 at extreme low and high temperatures (Fig. 2C) and the voltage-independent transitions observed at extreme negative and positive voltages (Figs. 3, G and H, and 4E). In particular, these results rule out kinetic models in which temperature and/or voltage activation is strictly coupled to the pore opening. This includes linear models with many open and closed states and Monod-Wyman-Changeaux with voltage- or temperature-dependent central transitions. In this context, Brauchi et al. (2) as well as Matta and Ahern (14) made the simplifying assumption that there would only be one voltage sensor and one temperature sensor giving rise to a dual allosteric coupling model (Fig. 8A). In particular, the dual allosteric coupling model proved to be most helpful in explaining the experimental results with the proviso that temperature sensors activate in an orchestrated manner, although there is a lack of a detailed knowledge regarding the number temperature sensors. However, this model is incompatible with the following: (a) single channel data suggesting the existence of a minimum of five closed states and two open states (52); (b) voltage-dependent delay of Ii activation (Fig. 5); and (c) double exponential time course of the channel deactivation process (Fig. 7). Additionally this model failed to give an adequate fit to the Po(V) (Fig. 8, B and C).
FIGURE 8.
Allosteric models. A, dual allosteric coupling model. The pore has two conformations, closed (C) and open (O). The equilibrium constant for the closed to open reaction is L, defined for resting voltage and temperature sensors. L is voltage- and temperature-independent. The voltage sensor equilibrium between resting (RV) and active (AV) conformations is governed by the constant J = exp(zJ(Vm − V0)F/RT), defined for closed pore and resting temperature sensor. The temperature sensor resting (RT) to active (AT) reaction is controlled by equilibrium constant K = exp(−(ΔH − TΔS)/RT), defined for closed pore and resting voltage sensor. When the voltage sensor is active, the pore opening reaction is favored by the allosteric factor D and the equilibrium constant becomes LD. In the same way, when temperature sensor is active, the pore opening reaction is favored by the allosteric factor C. When both sensors are active, the pore opening equilibrium constant is LCD. Factor E accounts for the interaction between voltage and temperature sensors. The equation for Po is shown in terms of equilibrium constants and allosteric factors. B and C, global fit to steady state data using the model in A. Parameters of the fit are as follows: zJ = 0.80; V0 = 260 mV; L = 6.2 × 10−6; ΔH = −53 kcal mol−1; ΔS = −193 cal mol−1 K−1 (T0 = 3.0 °C); C = 2253; D = 346; E = 2062. The sum of the squared residual was 3.1. D, two-tiered allosteric model. This model has the same number of free parameters as the dual allosteric coupling model but considers the existence of four voltage and four temperature sensors that can be activated independently, and each voltage sensor contributes with equal amounts of energy to displace the closed to open equilibrium. For instance, when the four voltage sensors are in the active state, the closed to open equilibrium constant becomes LD4. Likewise, when the four temperature sensors are in the active conformation, the closed to open equilibrium constant is now LC4. E and F, global fit to steady state data using the model in D. Parameters of the fit are as follows: zJ = 0.37; V0 = 234 mV; L = 4.3 × 10−8; ΔH = −19 kcal mol−1; ΔS = −70 cal mol−1 K−1 (T0 = −1.6 °C); C = 52.3; D = 2.3; E = 60. The sum of squared residual was 2.1.
Based on the tetrameric organization of TRPM8 channels, the observation that positive charges in the fourth transmembrane domain (S4) and in the S4-S5 linker are involved in sensing changes in the electric field and that there is a large number of closed states at 30 °C (51–54), it is possible to hypothesize that there are four voltage sensors and four temperature sensors. This type of model is based on the two-tiered allosteric model (also known as the H-A model) proposed for the Ca2+- and voltage-activated K+ (BK) channel (Fig. 8D) (39, 55, 56). Despite the fact that steady state description of these two models has eight free parameters, the squared sum of residuals is less for the H-A model, supporting the hypothesis of having four independent voltage and temperature sensors (Fig. 8, A–C).
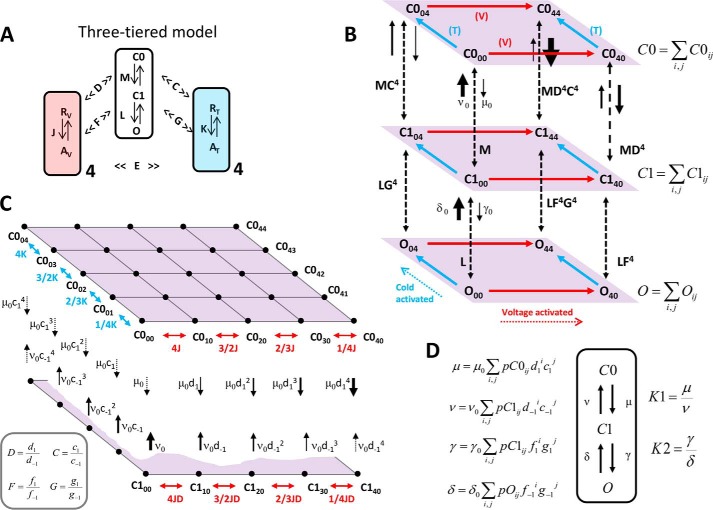
However, the two-tiered allosteric model considers that the opening reaction proceeds in a single step, which predicts a single-exponential relaxation of Ii (39, 55). The temperature-dependent double exponential decay of the TRPM8 channel deactivation that we report on here forced us to modify the two-tiered model so as to include an intermediate tier of closed states, which makes the opening reaction a two-step process (Fig. 9A). The resulting allosteric model accounts for all the experimental data presented here, including the double exponential time course of the Ii deactivation. By grouping each of the three different tiers into one state, the complex model can be transformed into a C-C-O scheme (Fig. 9; see also Appendix A). This transformation is only acceptable for the limit in which the transition among states within the same tier is very fast and is considered to be in equilibrium with respect to the inter-tier transitions. This assumption is the same as what was predicted for the monoexponential relaxation of the two-tiered allosteric model. For the three-tiered allosteric model in Fig. 9, the open probability (Po) is given by Equation 11,
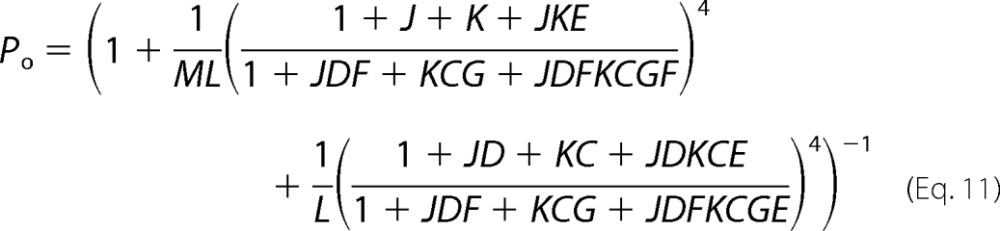 |
FIGURE 9.
Three-tiered allosteric model. A, simplified scheme shows the central opening reaction proceeding in two steps as follows: a transition between two closed states C0-C1, and a transition representing channel opening C1-O. In the absence of voltage and cold stimuli, these transitions are governed by the equilibrium constant M = C1/C0 and L = O/C1, respectively. Four voltage sensors (light red) and four temperature sensors (light blue) are governed by the voltage-dependent and temperature-sensitive equilibrium constants J = exp(zJ(Vm − V0)F/RT) and K = exp(−(ΔH − TΔS)/RT), respectively. Activation of these sensors by their respective stimuli, multiplies the M and L equilibrium constants to different extents due to allosteric interactions. Each voltage sensor activation shifts M and L equilibria toward the open state by allosteric factors D and F, respectively. Each temperature sensor activation shifts M and L equilibria toward the open state by allosteric factors C and G, respectively. E is an allosteric factor describing the interaction factor between the voltage sensor and temperature sensor. B, pore conformations C1, C2, and O consist of a set of sub-states grouped in three levels (tiers). Sub-states of each level are labeled with two indexes i and j (for example C0ij), which represent the possible combination of activated sensors, being i and j the number (0, 1, 2, 3, 4) of active voltage and temperature sensors, respectively. For clarity, only extreme sub-states are shown. Red and cyan arrows parallel to each level represent the direction of voltage- and cold-driven activation, respectively. Vertical dashed arrows represent the different transition pathways between corresponding sub-states of each tier. For instance, in the absence of active sensors, the opposing rate constants μ0 and ν0 determine the equilibrium constant M, whereas γ0 and δ0 are the corresponding rate constants for L. Active voltage and temperature sensors shift the C0-C1 and C1-O equilibria by increasing the forward reaction and by decreasing the backward reaction. This is depicted with solid arrows of different widths representing the magnitude of each rate constant for the C0-C1 transitions. The same principle applies to the C1-O transitions (not shown for clarity). C, detailed view of the C0 level emphasizing all the combinations of active voltage and temperature sensors (black dots). Double pointing red arrows are voltage-dependent equilibrium constants between states with no active temperature sensors. Conversely, double-pointing cyan arrows are temperature-dependent equilibrium constants between states with no active voltage sensors. Assuming that voltage sensors move independently, the equilibrium constants for the successive steps are 4J, 3/2J, 2/3J, and 1/4J. The same progression applies for the four temperature sensors. Each sub-state of the C0 level has an associated rate for transit to the corresponding sub-state in the C1 level, and vice versa, which are represented by downward and upward black arrows. The magnitude of each rate depends on the number of active voltage and temperature sensors. Allosteric factors applied to the equilibrium constants have to be split into two allosteric factors to be applied to the corresponding rate constants (e.g. D is split into d1 and d−1). The four relations enclosed within the gray box (bottom left) are required to enforce the principle of detailed balance. In particular, for any ij combination of voltage and temperature sensors, the downward rate constant is μ0 multiplied by d1ic1j. The equilibrium and rate constants for the remaining sub-states are omitted for clarity. D, assuming equilibrium within each level (C0, C1, O), one can condense the whole tier in one state giving rise to a simple C0-C1-O three-state model. Four voltage- and temperature-dependent rate constants μ, ν, γ, and δ can be calculated as the weighted contribution of every sub-state in each tier, according to their corresponding probability, pC0ij, pC1ij, and pOij (see “Appendix A”). The corresponding voltage- and temperature-dependent equilibrium constants K1 and K2 derived from the condensed scheme C0-C1-O are determined by the rate constants as noted in the figure.
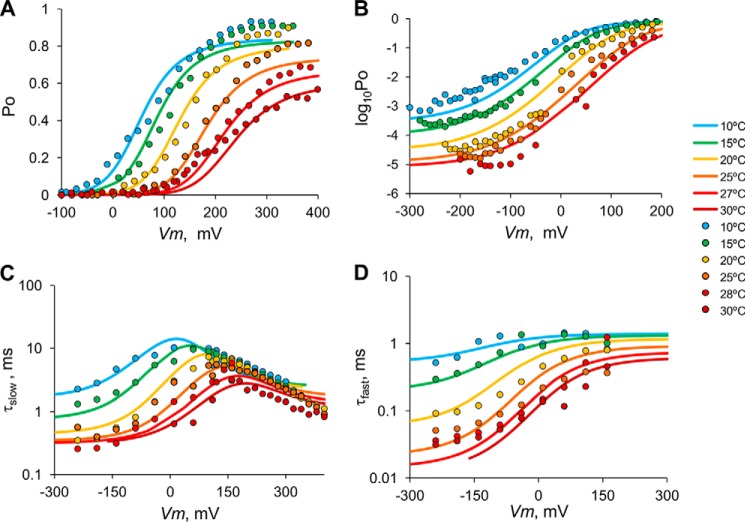
We performed a global fit to the steady state and kinetic data using the equations derived for the three-tiered allosteric model (Fig. 10; see also Appendix A). In Fig. 10, A and B, we can appreciate that the model accounts for the experimental observation that voltage cannot fully activate TRPM8 and that temperature alone activates TRPM8 at high negative voltages. The three-tiered allosteric model can also account for Po behavior at all the temperatures tested within the whole range of applied voltages, and it can fit the kinetic data reasonably well (Fig. 10, C and D). The similar shapes of the τd(Ii) − V relationships at low or high temperatures are also predicted by the allosteric model.
FIGURE 10.
Global fit of the data to the three-tiered allosteric model. A and B, Po versus voltage. C, τslow versus voltage, obtained from activation and deactivation kinetics. D, τfast versus voltage, obtained from deactivation kinetics only. Parameters: opening reaction, μ0 = 9.0 × 10−4 ms−1, ν0 = 3.6 ms−1 (M = 2.5 × 10−4), γ0 = 2.4 ms−1, δ0 = 157.2 ms−1 (L = 1.5 × 10−2); voltage sensor, V0 = 267 mV, z?J = 0.35; temperature sensor, ΔH = −29.8 kcal mol−1, ΔS = −104 cal mol−1 K−1 (To = 13.2 °C), voltage-coupled allosteric factors d1 = 6.6, d−1 = 0.86 (D = 7.7), f1 = 1.1, f−1 = 0.77 (F = 1.36); temperature-coupled allosteric factors c1 = 0.66, c−1 = 0.63 (C = 1.1), g1 = 0.68, g−1 = 0.18 (G = 3.8); interaction factor between voltage- and temperature- sensors, E = 29.6.
The allosteric model presently used considers, as it has been previously, that both ΔH and ΔS are independent of temperature. This assumption has been challenged by Clapham and Miller (57), who hypothesized that, in general, thermoTRP channel gating may be accompanied by large changes in molar heat capacity (ΔCp). However, there is at present no evidence that thermoTRP channel gating involves large changes in ΔCp. On the contrary, the behavior of the lnPo(1/T) (see inset Fig. 4D) rather suggests that ΔH and ΔS are independent of temperature within the temperature range we have explored. Moreover, there is no experimental evidence that thermoTRP channels can normally switch from cold receptors to heat receptors or vice versa (there is a lack of parabolic van't Hoff plots for channel activation) despite the fact they have been tested in a wide temperature range (2, 8, 9, 14, 19, 58). More recently, Chowdhury et al. (59) by introducing amino acid residues of different polarities at sites undergoing state-dependent changes were able to confer temperature sensitivity to a voltage-dependent channel. These results were interpreted on the same basis as those proposed by Clapham and Miller (57). However, without a direct demonstration of Cp changes, these results can be also explained by large negative or positive enthalpy changes.
It is interesting to note that the effect of temperature on the deactivation time constants (Fig. 6) is predicted by the three-tiered allosteric model as an indirect effect of temperature on the pore opening transitions. In this context, the activation of temperature sensors upon cooling results in the redistribution of populations of states within the different levels toward the subset of states that are more likely to lead to the open pore conformation due to the allosteric factors C and G (Fig. 7). The way in which allosteric factors C and G alter the C0-C1 and C1-0 equilibria can either be by increasing the forward rate or by decreasing the backward rate in those transitions. The increase in both relaxation time constants with cold temperatures (Fig. 6) indicates that the main effect of allosteric factors C and G is to decrease the backward rates (Fig. 9, legend).
Although we do not currently have a detailed structure for the TRPM8 channel, it is tempting to suggest that the gating mechanisms in different thermoTRP channels are similar and that allosteric models of the type we propose here can be used to explain the gating mechanisms of other polymodal receptors such as TRPV1 or TRPA1. Moreover, it is appealing to hypothesize that the fact that TRPM8 opening proceeds in two steps (C-C-O) may indicate the presence of two gates controlled by stimuli, as revealed by the recently resolved structure of the TRPV1 channel (60).
We must account for the detection of cold by the TRPM8 channel on free nerve endings on the skin. Assuming a resting potential of −60 mV and an input resistance of 50 megohms, it takes a current of 200 pA to depolarize the terminal to −50 mV, activate voltage-dependent Na+ channels, and fire action potentials. Because the single channel conductance of TRPM8 is 55 pS, the single channel current at −60 mV would be 3.3 pA, and therefore, 60 open TRPM8 channels are needed to depolarize the terminal. According to our results, a temperature change from 30 to 10 °C raises the TRPM8 open channel probability from ∼10−5 to ∼10−2. Consequently, to have 60 open channels, the free nerve ending must have ∼600 TRPM8 channels. This is a reasonable channel number based on TRPM8 activation on Xenopus oocyte membranes. Given that V0.5 is shifted to the right in these membranes, as compared with mammalian cells (2), the number of TRPM8 channels needed to detect cold may be less.
Acknowledgment
We thank Luisa Soto for excellent technical assistance.
APPENDIX A
The model we have developed is an extension of the two-tiered allosteric model (34, 55), and it is illustrated in Fig. 9. The equilibrium constants of the two opening steps L and M are assumed to be temperature-independent, and equilibria are affected by allosteric interactions between the four voltage sensors and four temperature sensors. Each sensor has two states (i.e. resting and active). Therefore, there are 25 different combinations of active voltage and temperature sensor for each pore configuration (C0, C1, O). For instance in the C0 level, the sub-state C0ij has “i” active voltage sensors and “j” active temperature sensors, where i,j = 0, 1, 2, 3, 4. In the same way, closed state C1 and open state O also have 25 different configurations.
The equilibrium constant governing one individual voltage sensor, J(V), is a function of membrane potential, V, which is defined as shown in Equation A1,
where z is the valence of the gating charge; F is the Faraday constant; R is the universal gas constant, and T is the absolute temperature. J(V) = 1 for V = V0. J(V) is > 1 for V > V0. The voltage sensor activates on membrane depolarization.
In the same way, the equilibrium constant for one individual temperature sensor, K(T), being only a function of temperature is defined as shown in Equation A2,
 |
where ΔH is enthalpy change associated with sensor activation; R is the universal gas constant, and T is the absolute temperature. If ΔH < 0, K(T) = 1 for T = T0. K(T) is > 1 for T < T0. The temperature sensor activates when temperature is lower than T0, thus being a cold sensor.
The easiest way to describe the probability distribution of sub-states within a level is by using the corresponding partition function. By using C000 as the reference state, the partition function for the C0 level can be expressed as shown in Equation A3,
Following the same reasoning line, the partition functions for the C1 and O levels are shown in Equations A4 and A5, respectively,
The probability distribution of the sub-states within C1 and O levels is calculated as done for the C0 level. These distributions are used to calculate the rate constants governing the inter-level transitions, assuming rapid equilibrium among sub-states within each level.
Considering that C0 and C1 partition functions are referred to as the C000 and C100 sub-states, respectively, and recalling that L represents the ratio C100/C100, the ratio between C1 and C0 populations can then be defined shown in Equation A6,
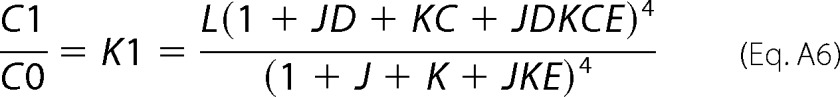 |
and similarly,
 |
The last two equations are equivalent expressions to equilibrium constants for the condensed model in Fig. 9. Even though the K1 and K2 ratios are complex functions of voltage and temperature due to J(V) and K(T), it is easy to show that for extreme cases with full active or full resting voltage sensors (J ≫ 1 or J ≪ 1, respectively) and full active or full resting temperature sensors (K ≫ 1 or K ≪ 1, respectively), K1 and K2 become voltage- and temperature-independent.
Kinetic Equations
To model the kinetics of the C0-C1-O process, we assumed that the C0-C1 and C1-O transitions are slow compared with the distribution of states within each level of the three-tiered scheme in Fig. 9, B and C. This assumption allows us to condense the complete model into Scheme 1, defined above (Fig. 9). Following Cox et al. (55), the rate constant for the transition from the C0 level to the C1 level is the sum of the rate constant of every transition of one sub-state in the C0 level to the corresponding sub-state in the C1 level, each weighed by their probability with regards to the C0 level. This is shown in Equation A8,
 |
The equilibrium constant L has to be split into two rate constants as follows: a rate constant μ0 for the forward reaction and a rate constant ν0 for the backward reaction, such that L = μ0/ν0. In addition, the allosteric constants that modify L (i.e. C and D) must also be split into two parts. This can be done by defining kinetic allosteric factors, one for multiplying the forward rate μ0 and one for multiplying the backward rate ν0 as shown in Equation A9,
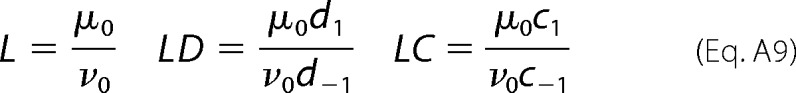 |
This way, the rate constant defining the C0-C1 transition of a channel with i active voltage sensors and j active temperature sensors is shown in Equation A10,
Combining Equations A8 and A10 we obtain for an ensemble of channels Equation A11,
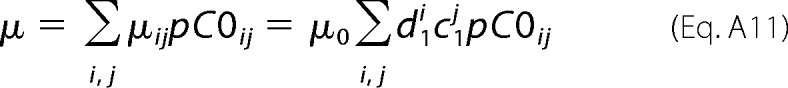 |
Each term in the expanded expression of Equation A3 represents the population ratio of any C0 sub-state (C0ij) with respect to the C000 sub-state. For instance, the first term (“1”) in the partition function of the C0 level represents the population ratio of C000, and therefore, the probability of this state with respect to the C0 level (i.e. pC000) is calculated as Equation A12,
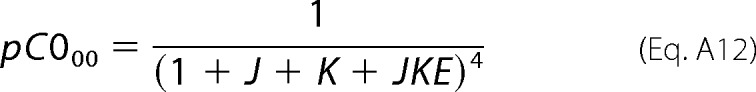 |
For the sake of clarity, the last term in the expanded expression of Equation A4 (i.e. J4K4E4) corresponds to the C044 sub-state, and therefore we get Equation A13,
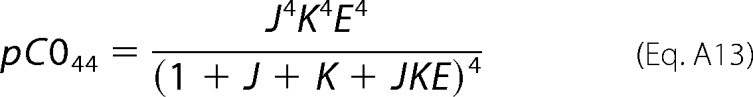 |
It can be shown that the full expression for Equation A11 can be reduced to Equation A14,
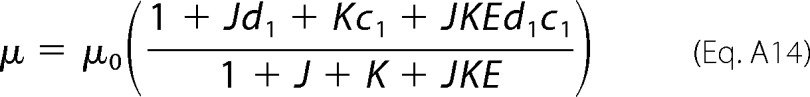 |
By following the same line of reasoning, the other three rate constants are calculated as shown in Equations A15 to A17.
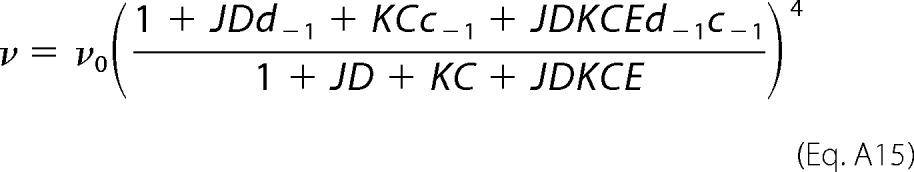 |
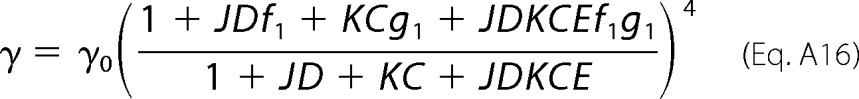 |
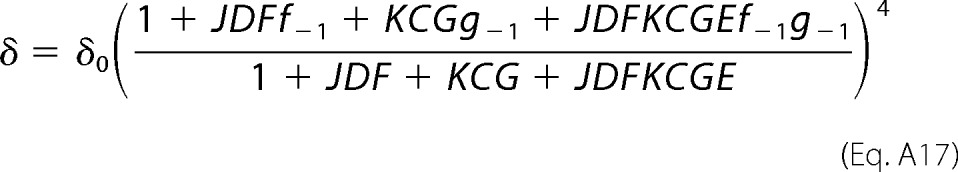 |
We note here that the above description is under the assumption that there are four independent voltage sensors and four independent temperature sensors. For instance, the above equations can be derived for the general case in which the number of voltage and temperature sensors (i and j, respectively) are both equal to n. In that case, the only difference is that the fourth power in Equations A3 to A17, must be replaced by the nth power. It is also necessary to note that the model assumes that temperature and voltage sensors can only interact through interaction factor E for temperature and voltage sensors belonging to the same subunit (34).
APPENDIX B
Temperature Coefficient for the TRPM8 Macroscopic Current
As we have already discussed, the three-tiered model can be reduced to Scheme 1. For this kinetic scheme, the open probability as a function of temperature and at a constant voltage, P0(T), is given in terms of the equilibrium constants defined in Equations A6 and A7, by Equation B1,
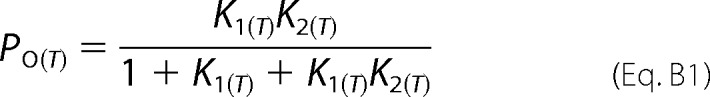 |
Po(T) is very low at large negative voltages (<10−3), indicating that equilibrium is displaced toward C0, K1 ≪ 1. Therefore, Equation B1 can be approximated to Equation B2,
Recalling that (Equation B3),
where I(T) is the temperature-dependent macroscopic ionic current; i(T) is the single-channel current, and N is the number of channels. The temperature coefficient of the macroscopic current (Q10(I)) combines the temperature coefficient of the single channel current Q10(i) and the temperature-dependent open channel probability, and it can be defined as shown in Equation B4,
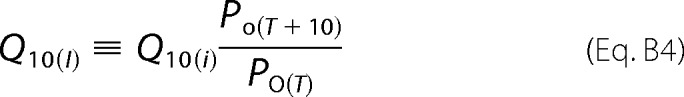 |
By combining Equations B2 and B4 we have the temperature coefficient for the limit of very low open channel probability as shown in Equation B5,
Temperature Coefficient of the Time Constants
Experimental observations indicate that the deactivation process can be described using a double exponential function with time constants τfast and τslow. Deactivation drives the equilibrium from state O to state C1 and eventually to state C0 in Scheme 1. Assuming that τfast ≪ τslow, the probability C0 can be taken as a constant during the initial times of relaxation. Therefore, the fast relaxation time constant is shown in Equation B6,
Equation B6 allows us to define a Q10 for the fast process as the temperature coefficient of the deactivation rate, which is the reciprocal value of the measured time constants shown in Equation B7,
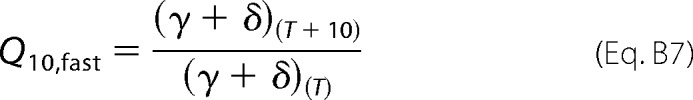 |
However, during the slow deactivation process we can assume that the transition C1-O in Scheme 1 is in equilibrium with respect to the C0-C1 transition. Therefore, the slow time constant of open state decay will be equal to the time constant of the C0 state buildup. The differential equation describing this process is shown in Equation B8,
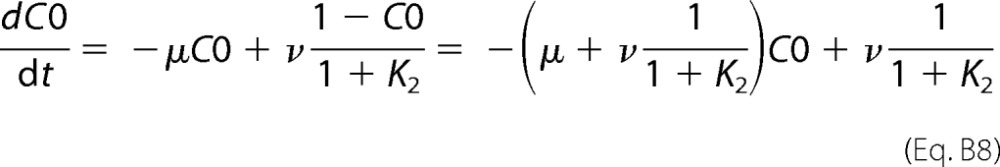 |
If Po is very low at the end of the relaxation, one can assume that μ ≪ ν. The time constant of the slow relaxation time is therefore shown in Equation B9,
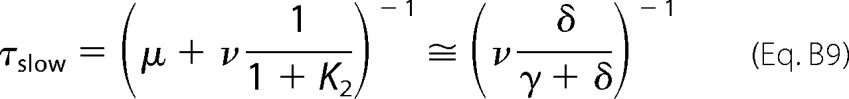 |
Defining the Q10 for kslow is shown in Equation B10
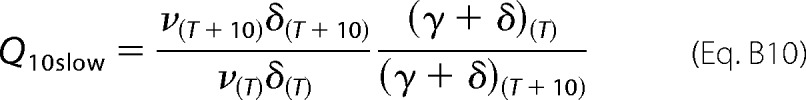 |
By combining Equations B7 and B10, we have Equation B11,
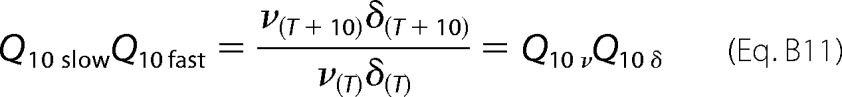 |
Equation B11 shows that the product of the Q10 of the deactivation rates (the reciprocal value of the measured time constants) is the product of the Q10 of the backward rate constants ν and δ.
Equation B5 can be rewritten in terms of the temperature coefficients of the rate constants shown in Equation B12,
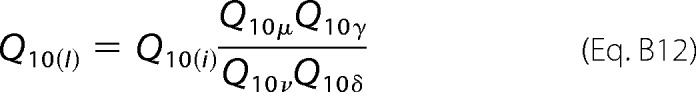 |
This work was supported by Grants FONDECYT 1110430 (to R. L.) and 1120802 (to C. G.) and Anillo ACT-1104 (to C. G.). The Centro Interdisciplinario de Neurociencia de Valparaíso is a Millennium Institute supported by the Millennium Scientific Initiative of the Ministerio de Economía, Fomento y Turismo (Chilean Government).
This article was selected as a Paper of the Week.
- TRPM8
- transient receptor potential melastatin 8
- thermoTRP
- thermo-transient receptor potential
- probability density function
- pS
- picosiemens.
REFERENCES
- 1. Bödding M., Wissenbach U., Flockerzi V. (2007) Characterisation of TRPM8 as a pharmacophore receptor. Cell Calcium 42, 618–628 [DOI] [PubMed] [Google Scholar]
- 2. Brauchi S., Orio P., Latorre R. (2004) Clues to understanding cold sensation: thermodynamics and electrophysiological analysis of the cold receptor TRPM8. Proc. Natl. Acad. Sci. U.S.A. 101, 15494–15499 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Chuang H. H., Neuhausser W. M., Julius D. (2004) The super-cooling agent icilin reveals a mechanism of coincidence detection by a temperature-sensitive TRP channel. Neuron 43, 859–869 [DOI] [PubMed] [Google Scholar]
- 4. Liu B., Qin F. (2005) Functional control of cold- and menthol-sensitive TRPM8 ion channels by phosphatidylinositol 4,5-bisphosphate. J. Neurosci. 25, 1674–1681 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. McKemy D. D., Neuhausser W. M., Julius D. (2002) Identification of a cold receptor reveals a general role for TRP channels in thermosensation. Nature 416, 52–58 [DOI] [PubMed] [Google Scholar]
- 6. Peier A. M., Moqrich A., Hergarden A. C., Reeve A. J., Andersson D. A., Story G. M., Earley T. J., Dragoni I., McIntyre P., Bevan S., Patapoutian A. (2002) A TRP channel that senses cold stimuli and menthol. Cell 108, 705–715 [DOI] [PubMed] [Google Scholar]
- 7. Rohács T., Lopes C. M., Michailidis I., Logothetis D. E. (2005) PI(4,5)P2 regulates the activation and desensitization of TRPM8 channels through the TRP domain. Nat. Neurosci. 8, 626–634 [DOI] [PubMed] [Google Scholar]
- 8. Voets T., Droogmans G., Wissenbach U., Janssens A., Flockerzi V., Nilius B. (2004) The principle of temperature-dependent gating in cold- and heat-sensitive TRP channels. Nature 430, 748–754 [DOI] [PubMed] [Google Scholar]
- 9. Liu B., Hui K., Qin F. (2003) Thermodynamics of heat activation of single capsaicin ion channels VR1. Biophys. J. 85, 2988–3006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Voets T. (2012) Quantifying and modeling the temperature-dependent gating of TRP channels. Rev. Physiol. Biochem. Pharmacol. 162, 91–119 [DOI] [PubMed] [Google Scholar]
- 11. Zakharian E., Cao C., Rohacs T. (2010) Gating of transient receptor potential melastatin 8 (TRPM8) channels activated by cold and chemical agonists in planar lipid bilayers. J. Neurosci. 30, 12526–12534 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Cui Y., Yang F., Cao X., Yarov-Yarovoy V., Wang K., Zheng J. (2012) Selective disruption of high sensitivity heat activation but not capsaicin activation of TRPV1 channels by pore turret mutations. J. Gen. Physiol. 139, 273–283 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Latorre R., Brauchi S., Orta G., Zaelzer C., Vargas G. (2007) ThermoTRP channels as modular proteins with allosteric gating. Cell Calcium 42, 427–438 [DOI] [PubMed] [Google Scholar]
- 14. Matta J. A., Ahern G. P. (2007) Voltage is a partial activator of rat thermosensitive TRP channels. J. Physiol. 585, 469–482 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Salazar M., Moldenhauer H., Baez-Nieto D. (2011) Could an allosteric gating model explain the role of TRPA1 in cold hypersensitivity? J. Neurosci. 31, 5554–5556 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Jara-Oseguera A., Islas L. D. (2013) The role of allosteric coupling on thermal activation of thermo-TRP channels. Biophys. J. 104, 2160–2169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Vlachová V., Teisinger J., Susánková K., Lyfenko A., Ettrich R., Vyklický L. (2003) Functional role of C-terminal cytoplasmic tail of rat vanilloid receptor 1. J. Neurosci. 23, 1340–1350 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Grandl J., Kim S. E., Uzzell V., Bursulaya B., Petrus M., Bandell M., Patapoutian A. (2010) Temperature-induced opening of TRPV1 ion channel is stabilized by the pore domain. Nat. Neurosci. 13, 708–714 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Yao J., Liu B., Qin F. (2011) Modular thermal sensors in temperature-gated transient receptor potential (TRP) channels. Proc. Natl. Acad. Sci. U.S.A. 108, 11109–11114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Yang F., Cui Y., Wang K., Zheng J. (2010) Thermosensitive TRP channel pore turret is part of the temperature activation pathway. Proc. Natl. Acad. Sci. U.S.A. 107, 7083–7088 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Alvarez O., Gonzalez C., Latorre R. (2002) Counting channels: a tutorial guide on ion channel fluctuation analysis. Adv. Physiol. Educ. 26, 327–341 [DOI] [PubMed] [Google Scholar]
- 22. Sigworth F. J. (1980) The variance of sodium current fluctuations at the node of Ranvier. J. Physiol. 307, 97–129 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Hamill O. P., Marty A., Neher E., Sakmann B., Sigworth F. J. (1981) Improved patch clamp techniques for high-resolution current recording from cells and cell-free membrane patches. Pflugers Arch. 391, 85–100 [DOI] [PubMed] [Google Scholar]
- 24. Stühmer W., Methfessel C., Sakmann B., Noda M., Numa S. (1987) Patch clamp characterization of sodium channels expressed from rat brain cDNA. Eur. Biophys. J. 14, 131–138 [DOI] [PubMed] [Google Scholar]
- 25. Starace D. M., Bezanilla F. (2004) A proton pore in a potassium channel voltage sensor reveals a focused electric field. Nature 427, 548–553 [DOI] [PubMed] [Google Scholar]
- 26. Heinemann S. H., Conti F. (1992) Nonstationary noise analysis and application to patch clamp recordings. Methods Enzymol. 207, 131–148 [DOI] [PubMed] [Google Scholar]
- 27. Sigg D., Stefani E., Bezanilla F. (1994) Gating current noise produced by elementary transitions in Shaker potassium channels. Science 264, 578–582 [DOI] [PubMed] [Google Scholar]
- 28. Villarroel A., Alvarez O., Oberhauser A., Latorre R. (1988) Probing a Ca2+-activated K+ channel with quaternary ammonium ions. Pflugers Arch. 413, 118–126 [DOI] [PubMed] [Google Scholar]
- 29. Yellen G. (1984) Relief of Na+ block of Ca2+-activated K+ channels by external cations. J. Gen. Physiol. 84, 187–199 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. FitzHugh R. (1983) Statistical properties of the asymmetric random telegraph signal with applications to single channel analysis. Math. Biosci. 64, 75–89 [Google Scholar]
- 31. Azzalini A. (1985) A class of distributions which includes the normal ones. Scand. J. Stat. 12, 171–178 [Google Scholar]
- 32. Ashour S. K., Mahmood A. A. (2010) Approximate skew normal distribution. J. Adv. Res. 1, 341–350 [Google Scholar]
- 33. Cole K. S., Moore J. W. (1960) Potassium ion current in the squid giant axon: dynamic characteristic. Biophys. J. 1, 1–14 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Horrigan F. T., Aldrich R. W. (2002) Coupling between voltage sensor activation, Ca2+ binding and channel opening in large conductance (BK) potassium channels. J. Gen. Physiol. 120, 267–305 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Orio P., Latorre R. (2005) Differential effects of β1 and β2 subunits on BK channel activity. J. Gen. Physiol. 125, 395–411 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Correa A. M., Bezanilla F., Latorre R. (1992) Gating kinetics of batrachotoxin-modified Na+ channels in the squid giant axon. Voltage and temperature effects. Biophys. J. 61, 1332–1352 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Horn R., Vandenberg C. A., Lange K. (1984) Statistical analysis of single sodium channels. Effects of N-bromoacetamide. Biophys. J. 45, 323–335 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Rodríguez B. M., Sigg D., Bezanilla F. (1998) Voltage gating of Shaker K+ channels. The effect of temperature on ionic and gating currents. J. Gen. Physiol. 112, 223–242 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Horrigan F. T., Cui J., Aldrich R. W. (1999) Allosteric voltage gating of potassium channels I. Mslo ionic currents in the absence of Ca2+. J. Gen. Physiol. 114, 277–304 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Schoppa N. E., McCormack K., Tanouye M. A., Sigworth F. J. (1992) The size of gating charge in wild-type and mutant Shaker potassium channels. Science 255, 1712–1715 [DOI] [PubMed] [Google Scholar]
- 41. Hirschberg B., Rovner A., Lieberman M., Patlak J. (1995) Transfer of twelve charges is needed to open skeletal muscle Na+ channels. J. Gen. Physiol. 106, 1053–1068 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Almers W. (1978) Gating currents and charge movements in excitable membranes. Rev. Physiol. Biochem. Pharmacol. 82, 96–190 [DOI] [PubMed] [Google Scholar]
- 43. Sigg D., Bezanilla F. (1997) Total charge movement per channel. The relation between gating charge displacement and the voltage sensitivity of activation. J. Gen. Physiol. 109, 27–39 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Yang W. Y., Gruebele M. (2003) Folding at the speed limit. Nature 423, 193–197 [DOI] [PubMed] [Google Scholar]
- 45. Goldman L. (1991) On the extraction of kinetic rate constants from experimental data. Biophys. J. 60, 519–523 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Bautista D. M., Siemens J., Glazer J. M., Tsuruda P. R., Basbaum A. I., Stucky C. L., Jordt S. E., Julius D. (2007) The menthol receptor TRPM8 is the principal detector of environmental cold. Nature 448, 204–208 [DOI] [PubMed] [Google Scholar]
- 47. Dhaka A., Murray A. N., Mathur J., Earley T. J., Petrus M. J., Patapoutian A. (2007) TRPM8 is required for cold sensation in mice. Neuron 54, 371–378 [DOI] [PubMed] [Google Scholar]
- 48. McKemy D. D. (2013) The molecular and cellular basis of cold sensation. ACS Chem. Neurosci. 4, 238–247 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Yudin Y., Rohacs T. (2012) Regulation of TRPM8 channel activity. Mol. Cell. Endocrinol. 353, 68–74 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Nieto-Posadas A., Jara-Oseguera A., Rosenbaum T. (2011) TRP channel gating physiology. Curr. Top. Med. Chem. 11, 2131–2150 [DOI] [PubMed] [Google Scholar]
- 51. Voets T., Owsianik G., Janssens A., Talavera K., Nilius B. (2007) TRPM8 voltage sensor mutants reveal a mechanism for integrating thermal and chemical stimuli. Nat. Chem. Biol. 3, 174–182 [DOI] [PubMed] [Google Scholar]
- 52. Fernández J. A., Skryma R., Bidaux G., Magleby K. L., Scholfield C. N., McGeown J. G., Prevarskaya N., Zholos A. V. (2011) Voltage- and cold-dependent gating of single TRPM8 ion channels. J. Gen. Physiol. 137, 173–195 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Phelps C. B., Gaudet R. (2007) The role of the N terminus and transmembrane domain of TRPM8 in channel localization and tetramerization. J. Biol. Chem. 282, 36474–36480 [DOI] [PubMed] [Google Scholar]
- 54. Stewart A. P., Egressy K., Lim A., Edwardson J. M. (2010) AFM imaging reveals the tetrameric structure of the TRPM8 channel. Biochem. Biophys. Res. Commun. 394, 383–386 [DOI] [PubMed] [Google Scholar]
- 55. Cox D. H., Cui J., Aldrich R. W. (1997) Allosteric gating of a large conductance Ca-activated K+ channel. J. Gen. Physiol. 110, 257–281 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Rothberg B. S., Magleby K. L. (2000) Voltage and Ca2+ activation of single large-conductance Ca2+-activated K+ channels described by a two-tiered allosteric gating mechanism. J. Gen. Physiol. 116, 75–99 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Clapham D. E., Miller C. (2011) A thermodynamic framework for understanding temperature sensing by transient receptor potential (TRP) channels. Proc. Natl. Acad. Sci. U.S.A. 108, 19492–19497 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Yao J., Liu B., Qin F. (2010) Pore turret of thermal TRP channels is not essential for temperature sensing. Proc. Natl. Acad. Sci. U.S.A. 107, E125–E127 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Chowdhury S., Jarecki B. W., Chanda B. (2014) A molecular framework for temperature-dependent gating of ion channels. Cell 158, 1148–1158 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Cao E., Liao M., Cheng Y., Julius D. (2013) TRPV1 structures in distinct conformations reveal activation mechanisms. Nature 504, 113–118 [DOI] [PMC free article] [PubMed] [Google Scholar]