Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Dec 19;4:7565. doi: 10.1038/srep07565

Dimensionality-dependent charge transport in close-packed nanoparticle arrays: from 2D to 3D

Ying Wang 1,2, Chao Duan 1, Lianmao Peng 1, Jianhui Liao 1,a
PMCID: PMC4271260  PMID: 25523836

Abstract

Charge transport properties in close-packed nanoparticle arrays with thickness crossing over from two dimensions to three dimensions have been studied. The dimensionality transition of nanoparticle arrays was realized by continually printing spatially well-defined nanoparticle monolayers on top of the device in situ. The evolution of charge transport properties depending on the dimensionality has been investigated in both the Efros-Shaklovskii variable-range-hopping (ES-VRH) (low temperature) regime and the sequential hopping (SH) (medium temperature) regime. We find that the energy barriers to transport decrease when the thickness of nanoparticle arrays increases from monolayer to multilayers, but start to level off at the thickness of 4–5 monolayers. The energy barriers are characterized by the coefficient βD at ES-VRH regime and the activation energy Ea at SH regime. Moreover, a turning point for the temperature coefficient of conductance was observed in multilayer nanoparticle arrays at high temperature, which is attributed to the increasing mobility with decreasing temperature of hopping transport in three dimensions.

Nanoparticle arrays are composed of close-packed monolayer-encapsulated metallic or semiconductor nanoparticles arranged into one- (1D)1,2,3, two- (2D)4,5, and three- (3D) dimensions6,7,8,9,10. The controllability of parameters of nanoparticle arrays11 makes them appropriate for investigating physical properties of granular electronic systems12,13,14,15. It has been found that the collective properties of nanoparticle arrays are determined not only by the properties of individual nanoparticles, but also by the coupling between each other16,17,18,19,20,21,22. Particularly, extensive effort has been devoted to study the charge transport in nanoparticle assembles and composite films12,14,16,23,24,25,26,27. In these studies, the Coulomb charging energy is one of the most important energy scales in determining the charge transport behavior11,28,29.

On the other hand, dimensionality is critically important in determining the electronic structure and properties of materials30. As a typical example, although graphite, graphene, and carbon nanotube are composed of the same carbon atoms, they have entirely different electronic structure and properties due to their different dimensions31. In the field of nanoscience, one important and interesting issue is to study and understand the evolution of material properties during the crossover of dimensions32,33,34,35. For nanoparticle arrays, various techniques have been developed to fabricate 1D, 2D, and 3D nanoparticle arrays so that their physical properties can be investigated14,36,37,38. Particularly, Heath and his coworkers have made an impressive progress33 in the study of dimensionality transition of nanoparticle assemblies. They fabricated nanoparticle arrays that continuously crossover from 2D to 1D. The transport properties of these nanoparticle arrays were investigated and some unexpected behaviors were found solely in 1D nanoparticle arrays. Despite this exciting progress, it remains a great challenge to fabricate nanoparticle arrays that can crossover from 2D to 3D continuously39. As a consequence, the evolution of the transport properties of nanoparticle array during the transition of the dimensionality from 2D to 3D is unclear up to now. In this paper, we overcame the difficulty of preparing nanoparticle arrays continuously crossing over from 2D to 3D. The thickness of the nanoparticle array under test could be increased monolayer by monolayer in situ. This enables us to investigate the evolution of the charge transport properties of nanoparticne arrays during dimensionality transition.

Figure 1 illustrates the sample preparation method used in this paper, with which we can fabricate spatially well-defined nanoparticle arrays and increase their thickness layer by layer. The method is based on the technique to fabricate patterned nanoparticle arrays developed by our group previously40. In brief, 2D nanoparticle monolayers were self-assembled at the air/water interface by spreading several drops of solution containing octanethiol-capped 13 nm gold nanoparticles (Fig. 1a) on the water surface. After evaporation of the solvent (chloroform), the gold nanoparticles self-assembled into 2D monolayers (Fig. 1b). Then, protrusion of SiO2 connected by electrodes (5 nm Ti + 20 nm Au) fabricated lithographically was covered by the monolayer of nanoparticles using the micro-contact printing technique (Fig. 1c). To increase the thickness of the nanoparticle array under test, the micro-contact printing technique was repeated on the device in situ (Fig. 1d). After each printing of nanoparticle monolayer, the current-voltage curves were measured at various temperatures ranging from 4 K to 310 K. The key issue in our preparation method is the predefined protrusion region of the SiO2 between electrodes, which guarantees the uniformity of the position and morphology of the printed nanoparticle monolayers. In this way, our method enables us to change the dimensionality of the nanoparticle arrays under test from 2D to 3D continuously.

Figure 1. Schematic diagram of fabrication of two-dimensional to three-dimensional patterned close-packed nanoparticle arrays and SEM characterization of one measured device.

Figure 1

Open in a new tab

(a), Several drops of chloroformic solution containing octanethiol-capped gold nanoparticles were cast onto a slightly convex deionized water surface in a Teflon container. (b), With the evaporation of the solvent, nanoparticles self-assembled into an ordered compact 2D monolayer at the air/water interface, as shown in the top inset. (c), A flat PDMS stamp was used to transfer the nanoparticle sheet from the air/water interface onto the substrate surface with designed electrodes prepared using lithographic techniques. (d), Schematic of the device with one nanoparticle superlattice. By simply repeating the same transferring process, devices with a continuous change of the number of monolayers were obtained. (e), SEM image of a typical device used for the electrical measurements, which contains 15 identical nanoparticle monolayers. Magnified SEM image of the area framed by the rectangle in (e) is shown in (g). (f), Titled SEM image of the device shown in (e). Magnified SEM image of the area framed by the rectangle in (f) is shown in (h).

To avoid the influence of the e-beam exposure, devices were characterized by scanning electron microscopy (SEM) after all electronic measurements. Figure 1e shows the SEM image of the top view of one typical measured device after printing 15 nanoparticle monolayers. The nanoparticle array between two electrodes is 2 μm in length and 60 μm in width. The closer image of the nanoparticle arrays under test is shown in Fig. 1g, corresponding to the region indicated by the rectangular frame in Fig. 1e. One can see that nanoparticles in the array stay separately without sintering on the top. The side view of the device is shown in Fig. 1f, taken by a SEM with a tilted angle of 30°. It is clear that the substrate is covered by the nanoparticle multilayer. The framed region is magnified and shown in Fig. 1h. The image shows the cross-sectional view of the printed multilayer formed by stacking monolayers. The measured thickness from the SEM image was comparable to that of 15 times of the monolayer thickness, ~150 nm. Moreover, the nanoparticles can be distinguished individually, indicating that there is no sintering inside the nanoparticle array.

The device was electronically characterized in a cryostat. After each printing of nanoparticle monolayer over the device up to 9 layers, the current-voltage curves of the device were measured at various temperatures ranging from 4 K to 310 K. From the ninth layers, we did the electronic measurements every 3 monolayers printing up to 15 layers. For current-voltage curves of nanoparticle arrays with different thickness, the similar behavior is that the nonlinearity is getting more obvious with lowering the temperature due to the Coulomb interaction (see Supporting Information). To investigate the transport mechanism, we extract the zero-voltage conductance (G0) by linearly fitting the current-voltage curves at low voltage range (−0.1 V–0.1 V). The data suggest that there are three transport regimes. At low temperature, the G0 data can be nicely described by the Efros-Shaklovskii variable-range-hopping model (ES-VRH). When the temperature is increased into the medium range, the charge transport mechanism transmitted to the thermally activated sequential hopping. However, new transport phenomenon, i.e., increasing conductivity with decreasing temperature, appears for nanoparticle multilayers at high temperature, which is attributed to exponentially activated hopping with lower activation energy in three dimensions. In the following, we study the dimensionality-dependent transport behavior of nanoparticle arrays in these three regimes.

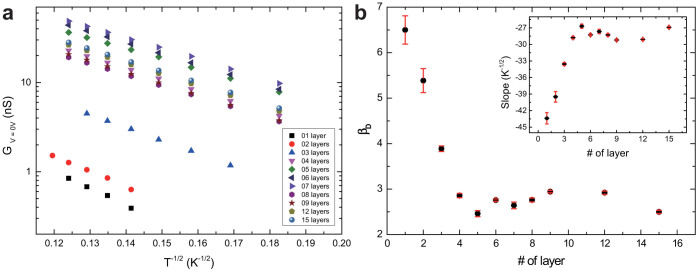
Figure 2a shows the zero-voltage conductance of nanoparticle arrays with different thickness as a function of T−1/2 in the temperature range from 30 K to 70 K. The data show that the logarithm of the zero-voltage conductance is linearly proportional to T−1/2 regardless of the thickness of the arrays at low temperature. Another feature of the data sets is that the conductance increases obviously from monolayer to few multilayers, but starts to level off after stacking 4–5 monolayers. For fewer multilayers, the zero-voltage conductance is beyond the limit of our measurement system at low temperature. This explains that there are fewer data points for thinner multilayers.

Figure 2. Dimensionality-dependent charge transport properties of nanoparticle arrays with different number of monolayers at low temperature.

Figure 2

Open in a new tab

(a), Temperature-dependent conductance at low voltage bias in a semi-log scale. The logarithm of the zero-voltage conductance of all nanoparticle arrays is linearly proportional to the T−1/2 at low temperature regardless of the layers of the nanoparticle arrays. (b), The coefficient βD in ES-VRH model, which is supposed to depend on the system dimensionality D, as a function of the number of nanoparticle monolayers. Inset: Slopes of the ln(G)-T−1/2 curves shown in (a) plotted as a function of number of nanoparticle monolayers.

The linear relationship between lnG0 and T−1/2 indicates the charge transport mechanism at low temperature. Two theoretic models have predicted similar results: the ES-VRH model41 and the elastic/inelastic cotunneling model42,43. Here, we choose ES-VRH model to interpret our data. The ES-VRH model was developed to explain the hopping transport in weakly doped semiconductors with taking account of the Coulomb interactions44. Now, this model has been widely applied in artificial solids made from metallic42,43,45,46 or semiconductor nanoparticles47. According to the ES-VRH model, the zero-voltage conductance and the temperature follow the formula:

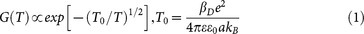graphic file with name srep07565-m1.jpg

where βD is the coefficient depending on the system dimensionality D, and a is the localization length of carriers33,42,43,44.

The slopes of the data set shown in Fig. 2a were extracted and shown in the inset of Fig. 2b with respect to the number of printed nanoparticle monolayers. In weakly coupled nanoparticle arrays, the localization length is estimated by the diameter of the nanoparticle, which is ~13 nm in our system. Considering that the coefficient βD is 6.5 in 2D systems suggested by theory and simulations48,49, an effective dielectric constant ε = 4.8 for octanethiol-capped gold nanoparticle arrays has to be assumed. Based on this assumption, the coefficient βD can be obtained as a function of the thickness of nanoparticle arrays. Intuitively, βD is expected to decrease with increasing the dimensionality from 2D to 3D by printing more and more nanoparticle monolayers. However, to our surprise, the coefficient βD decreases deeply in the first 4–5 nanoparticle layers, and starts to fluctuate in thicker arrays. In detail, the coefficient is 6.5 for the 2D array and decreases to 2.8 for the tetralayer array, which is nicely consistent with that suggested by theory and simulations for 3D systems48. When the number of layers is more than 4, the coefficient fluctuates between 2.4 and 3.0 up to 15 layers.

Note that although the specific value of the coefficient βD depends on the effective dielectric constant that we use, the ratio between coefficients does not change. The dimensionality-dependent coefficient characterizes the energy barrier for conductance by establishing percolating hopping paths through the arrays. The transition of the coefficient suggests that the energy barrier for arrays with 4–5 nanoparticle layers is similar to that of 3D nanoparticle arrays. The data indicates that the energy barrier decreases very fast for the first few layers and levels off for more layers. The crossover from 2D to 3D happening in a few monolayers analogies to that from 1D to 2D, which happens in a few lines of nanoparticles33.

To characterize the transition of the energy barrier during the change of the dimensionality, we turn our eyes to the transport properties in the medium temperature range. Our data suggest that the zero-voltage conductance between 75 K and 130 K follows Arrhenius behavior, as shown in the inset of Fig. 3a (also see Supporting Information). In the VRH model, this happens when the nearest neighbor hopping is most favored50,51. According to the thermally activated Arrhenius model, the zero-voltage conductance and the temperature follow the formula:

graphic file with name srep07565-m2.jpg

where Ea is the activation energy, which is supposed to be a good estimation of the Coulomb charging energy in metallic nanoparticle arrays40. The activation energies determined by data fitting are shown in Fig. 3a as a function of the number of printed monolayers. Our data show that the activation energy decreases deeply with increasing the thickness of the nanoparticle array for the first four layers from 15.1 meV to 10.1 meV. Afterward, the activation energy fluctuates between 9 meV and 10 meV with increasing more nanoparticle monolayers.

Figure 3. Dimensionality-dependent Coulomb charging energy in nanoparticle arrays at medium temperature.

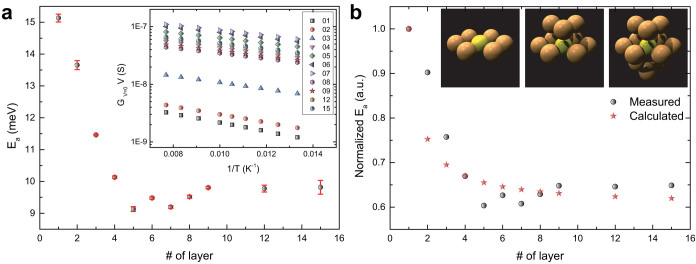
Figure 3

Open in a new tab

(a), The Coulomb charging energy of nanoparticle arrays with different number of monolayers. Inset: The zero-voltage conductance of nanoparticle arrays with different thickness as a function of inverse temperature at medium temperature ranging from 75 K to 130 K. (b), The normalized measured and calculated Coulomb charging energy of nanoparticle arrays as a function of number of nanoparticle monolayers. The normalized calculated Coulomb charging energy are relay on the assumption of the self-capacitance and mutual capacitance of nanoparticles. Inset: Schematics of the nearest-neighbor-number of an individual nanoparticle in monolayer arrangement (left), bilayer arrangement (middle), and trilayer arrangement (right).

The change trend of the activation energy reminds us to compare it with that of the coefficient βD presented in Fig. 2b. Interestingly, both of them have similar change trend, i.e., decreasing rapidly with increasing the first four monolayers and leveling off for printed more monolayers. The reason for the similarity might be attributed to the physical meaning of these two parameters. On one hand, the coefficient βD is dimensionality-dependent and should increase with decreasing the dimensionality, meaning that the energy barrier for conductance is higher to percolate through the system with reducing the dimensions. On the other hand, the activation energy Ea is used to estimate the Coulomb charging energy of nanoparticles, which is the energy needed to add an extra electron onto an electronically neutral nanoparticle. The similar change trend of βD and Ea indicates that both of them characterize the same energy barrier in the system, but at different temperature ranges. In other words, the energy barrier for conductance in weakly coupled nanoparticle arrays stems from the Coulomb charging energy.

For an individual nanoparticle, the Coulomb charging energy might be influenced by several parameters, including the size of the nanoparticle, the inter-particle distance, the dielectric constant of the surroundings, and the nearest-neighbor-number (N)11. In our case, the nanoparticles are from the same batch, indicating the same average size. The capping ligands are octanethiols, suggesting the similar inter-particle distance and the same dielectric constant of the surroundings. The only dramatically changed parameter is the dimensionality of the system, by which we expect to change N. For a nanoparticle in a 2D array, N is approximately 6. However, it increases to 9 in a bilayer and 12 in a multilayer. The inset in Fig. 3b schematically shows the change of N in a monolayer (left), bilayer (middle), and multilayer (right). The relation between the Coulomb charging energy Ea and N is bridged by the capacitance Ctotal of the nanoparticle.

graphic file with name srep07565-m3.jpg

where Cself is the self-capacitance and Cmutual is the capacitance between two neighboring nanoparticles. From the measured activation values for monolayer and tetralayer, the ratio of Cself to Cmutual can be determined, Cself = 3.13Cmutual. The measured and calculated normalized activation energies are shown in Fig. 3b. The same change trend and good satisfaction between measured data and calculated data infer that our model is reasonable. The increase of the dimensionality lowers the activation energy, therefore the energy barrier for conduction, by changing the mutual capacitance of nanoparticle through N.

In the high temperature region, new feature appears in the relationship between the zero-voltage conductance and the temperature. As shown in the shaded box in Fig. 4a, the temperature coefficient of conductance turns from positive to negative for multilayer arrays thicker than 4 or 5 monolayers. In the literature, similar transition of the temperature coefficient of conductance has been reported for 2D or 3D nanoparticle arrays52,53,54,55,56,57. The mechanism of the transition has not been clearly understood, although Mott-Hubbard metal-to-insulator transition52,54,55,56, polaron transport53, and thermal expansion of the substrates57 have been proposed. However, our data can be understood in the frame of hopping transport instead of mentioned mechanisms above.

Figure 4. The turning point of the temperature coefficient of conductance at high temperatures in 3D nanoparticle arrays.

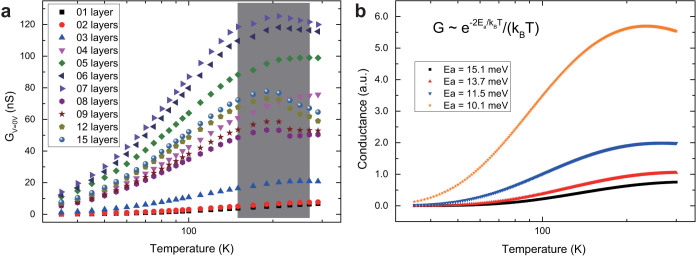
Figure 4

Open in a new tab

(a), The zero-voltage conductance of nanoparticle arrays with different thickness is plotted as a function of temperature. To see the turning point more clearly, a semi-log scale is used. The shaded box indicates the temperature region where the turning point appears when the thickness of nanoparticles is more than 4–5 nanoparticle monolayers. (b), Curves plotted according to the relationship between the conductance and temperature shown in the inset. Here, the conductance is not in real unit, but in arbitrary unit (a.u.). To make the curves more readable, the blue, red, and black curves have been divided by 10, 8, and 5, respectively. The activation energy Ea is treated as a variable. 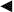Curves plotted with different activation energy are using different symbols: 15.1 meV (Inline graphic), 13.7 meV (Inline graphic), 11.5 meV (Inline graphic), and 10.1 meV (Inline graphic).

Generally, the relation between mobility and diffusion in three dimensions can be described by Einstein's equation:

graphic file with name srep07565-m4.jpg

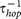where Inline graphic is the effective hopping rate. Suppose hopping is a thermally activated process,

graphic file with name srep07565-m5.jpg

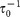where Inline graphic is the attempt frequency of hopping47. The number of carrier in nanoparticle arrays is also thermally activated, which gives 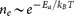Inline graphic. Consequently, the conductivity of the system can be expressed as: 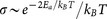Inline graphic Based on this relation, we expect that the conductivity, therefore the conductance, increases with decreasing temperature up to T = 2Ea/kB. Figure 4b shows four curves plotted according to the above relationship between conductance and temperature. The activation energy values for these four curves correspond to that of nanoparticle arrays from monolayer to tetralayer. The transition point in the curve with the smallest activation energy (10.1 meV) is at the temperature of 234 K. From the measured Ea values presented in Fig. 2a, the transition temperature is estimated to be in the range from 208 K to 232 K, considering the fluctuation of the activation energy between 9 meV and 10 meV. In fact, Fig. 4a shows that the transition temperature is 190 ± 20 K, which satisfactorily agrees with the estimation value and the analytical value.

In summary, charge transport properties of nanoparticle arrays were measured when the dimensionality was continuously changed from 2D to 3D. The evolution of the transport properties has been studied and can be attributed to the change of the energy barrier due to the change of the dimensionality. The dimensionality effect indicates the variability of the gap thus the barrier between neighboring nanoparticles. All transport behaviors can be understood in a consistent frame of hopping transport mechanism at different temperature regions.

Methods

Self-assembly of two-dimensional nanoparticle arrays at the air/water interface

Octanethiol-capped gold nanoparticles (~13 nm in diameter) were prepared and dispersed in chloroform using the colloidal method described in the literature58. Firstly, a homemade Teflon container was cleaned carefully using the tube brush and washed several times with deionized water to remove the ion. Then, the container was filled with ~20 ml deionized water, and a slightly convex water surface was produced. The self-assembly process was performed, when ~400 μl nanoparticle solution was cast onto the water surface. After 10 minutes, the chloroform evaporated, leading to the formation of ordered 2D naoparticle arrays.

Micro-contact printing of 2D nanoparticle arrays

Flat PDMS Stamps were prepared using clean silicon chips in accordance with the procedure described in the literature58. After the PDMS was peeled off the template, a scalpel was used to cut it into suitable size. Then, one of such PDMS stamps was cleaned ultrasonically in ethanol and dried by nitrogen gas. As it described in the Langmuir-Schaefer technique, the cleaned stamp was brought to contact the nanoparticle film for 10 s and lifted carefully away from the film. A piece of clean soft paper was used to absorb away the water drops at the edge of the PDMS stamp. After that, the inked stamp was gently placed on the pre-fabricated substrates and lifted slightly from one end to another ten seconds later. The close-packed 2D nanoparticle array was printed on the substrate.

Device fabrication on a SiO2/Si substrate

Devices with designed structures on a SiO2/Si substrate were fabricated using micro-nanofabrication techniques. At the very beginning, the gap between two electrodes was defined by photolithography (SÜSS MicroTec, MJB4). Metals of 5 nm Ti, 20 nm Au, and 50 nm Cr were deposited by an electron beam evaporator (Kurt J. Leaker AXXIS). After the liftoff process in acetone, another photolithography was done to define the width of trenches of devices, followed by the deposition of 70 nm Cr. After liftoff, dry etching was performed by an inductively coupled plasma machine (TRION). Removal of Cr layers was carried out by wet etching in Chromium etchant (pursed from ALDRICH).

Characterization and charge transport measurements

Structures and devices were mainly characterized by SEM (FEI Quanta 600). The charge transport properties of devices were measured with a homemade electronic measurement system. The main component of the station was a cycling refrigerator (CRYOMECH) with helium as the refrigerant to lower ambient temperature of the device down to 4 K. The I-V curves were collected using a data acquisition card. A current amplifier (Keithley 428) was used to amplify the current. The temperature of the devices was controlled by a temperature controller (Lake Shore, Model 332).

Author Contributions

Y.W. and J.L. designed the research; J.L. supervised the project; Y.W. and C.D. performed electronic measurements; Y.W. carried out all experiments; Y.W. and J.L. analyzed data and wrote the main manuscript text. L.P. analyzed data. All authors reviewed the manuscript.

Supplementary Material

Supplementary Information

Supporting Information

srep07565-s1.pdf (643.6KB, pdf)

Acknowledgments

This work was financially supported by the Ministry of Science and Technology of the People's Republic of China (No. 2011CB933001, 2012CB932702) and the National Natural Science Foundation of China (no. 60971001).

References

  1. Tang Z. Y. & Kotov N. A. One-dimensional assemblies of nanoparticles: Preparation, properties, and promise. Adv. Mater. 17, 951–962 (2005). [Google Scholar]
  2. Jiang L., Wang W. C., Fuchs H. & Chi L. F. One-Dimensional Arrangement of Gold Nanoparticles with Tunable Interparticle Distance. Small 5, 2819–2822 (2009). [DOI] [PubMed] [Google Scholar]
  3. Jiang X. et al. Using micro to manipulate nano. Small 10, 258–264 (2014). [DOI] [PubMed] [Google Scholar]
  4. Bigioni T. P. et al. Kinetically driven self assembly of highly ordered nanoparticle monolayers. Nat. Mater. 5, 265–270 (2006). [DOI] [PubMed] [Google Scholar]
  5. van der Stam W. et al. Self-assembly of colloidal hexagonal bipyramid- and bifrustum-shaped ZnS nanocrystals into two-dimensional superstructures. Nano Lett. 14, 1032–1037 (2014). [DOI] [PubMed] [Google Scholar]
  6. Nykypanchuk D., Maye M. M., van der Lelie D. & Gang O. DNA-guided crystallization of colloidal nanoparticles. Nature 451, 549–552 (2008). [DOI] [PubMed] [Google Scholar]
  7. Macfarlane R. J. et al. Nanoparticle superlattice engineering with DNA. Science 334, 204–208 (2011). [DOI] [PubMed] [Google Scholar]
  8. Goubet N. et al. Modulating physical properties of isolated and self-assembled nanocrystals through change in nanocrystallinity. Nano Lett. 13, 504–508 (2013). [DOI] [PubMed] [Google Scholar]
  9. Ye X. et al. Shape alloys of nanorods and nanospheres from self-assembly. Nano. Lett. 13, 4980–4988 (2013). [DOI] [PubMed] [Google Scholar]
  10. Auyeung E. et al. DNA-mediated nanoparticle crystallization into Wulff polyhedra. Nature 505, 73–77 (2014). [DOI] [PubMed] [Google Scholar]
  11. Duan C. et al. Controllability of the Coulomb charging energy in close-packed nanoparticle arrays. Nanoscale 5, 10258–10266 (2013). [DOI] [PubMed] [Google Scholar]
  12. Beloborodov I. S., Lopatin A. V., Vinokur V. M. & Efetov K. B. Granular electronic systems. Rev. Mod. Phys. 79, 469–518 (2007). [Google Scholar]
  13. Pileni M. P. Supracrystals of inorganic nanocrystals: an open challenge for new physcial properties. Acc. Chem. Res. 41, 1799–1809 (2008). [DOI] [PubMed] [Google Scholar]
  14. Zabet-Khosousi A. & Dhirani A. A. Charge transport in nanoparticle assemblies. Chem. Rev. 108, 4072–4124 (2008). [DOI] [PubMed] [Google Scholar]
  15. Gong J., Li G. & Tang Z. Self-assembly of noble metal nanocrystals: fabrication, optical property, and application. Nano Today 7, 564–585 (2012). [Google Scholar]
  16. Middleton A. A. & Wingreen N. S. Collective transport in arrays of small metallic dots. Phys. Rev. Lett. 71, 3198–3201 (1993). [DOI] [PubMed] [Google Scholar]
  17. Urban J. J., Talapin D. V., Shevchenko E. V., Kagan C. R. & Murray C. B. Synergis-min binary nanocrystal superlattices leads to enhanced p-type conductivity in self-assembled PbTe/Ag2 Te thin films. Nat. Mater. 6, 115–121 (2007). [DOI] [PubMed] [Google Scholar]
  18. Talapin D. V., Shevchenko E. V., Murray C. B., Titov A. V. & Kral P. Dipole-diple interactions in nanoparticle superlattices. Nano Lett. 7, 1213–1219 (2007). [DOI] [PubMed] [Google Scholar]
  19. Podsiadlo P. et al. The role of order, nanocrystal size, and capping ligands in the collective mechanical response of three-dimensional nanocrystal solids. J. Am. Chem. Soc. 132, 8953–8960 (2010). [DOI] [PubMed] [Google Scholar]
  20. Chen J. et al. Collective dipolar interactions in self-assembled magnetic binary nanocrystal superlattice membranes. Nano Lett. 10, 5103–5108 (2010). [DOI] [PubMed] [Google Scholar]
  21. Kuzyk A. et al. DNA-based self-assembly of chiral plasmonic nanostructures with tailored optical response. Nature 483, 311–314 (2012). [DOI] [PubMed] [Google Scholar]
  22. Lisiecki I. et al. Coherent longitudinal acoustic phonons in three-dimensional supracrystals of cobalt nanocrystals. Nano Lett. 13, 4914–4919 (2013). [DOI] [PubMed] [Google Scholar]
  23. Blom P. W. M., Schoo H. F. M. & Matters M. Electrical characterization of electroluminescent polymer nanoparticle composite devices. Appl. Phys. Lett. 73, 3914–3916 (1998). [Google Scholar]
  24. Simon U. Charge transport in nanoparticle arrangements. Adv. Mater. 10, 1487–1492 (1998). [Google Scholar]
  25. McConnell W. P. et al. Electronic and optical properties of chemically modified metal nanoparticles and molecularly bridged nanoparticle arrays. J. Phys. Chem. B 104, 8925–8930 (2000). [Google Scholar]
  26. Wessels J. M. et al. Optical and electrical properties of three-dimensional interlinked gold nanoparticle assemblies. J. Am. Chem. Soc. 126, 3349–3356 (2004). [DOI] [PubMed] [Google Scholar]
  27. Krasteva N. et al. Vapor sorption and electrical response of Au-nanoparticle-dendrimer composites. Adv. Funct. Mater. 17, 881–888 (2007). [Google Scholar]
  28. Herrmann J., Bray D. J., Muller K. H., Wei G. & Lindoy L. F. Tuning the Coulomb charging energy in cross-linked nanoparticle films. Phys. Rev. B 76, 212201 (2007). [Google Scholar]
  29. Mangold M. A., Calame M., Mayor M. & Holleitner A. W. Negative Differential Photo-conductance in Gold Nanoparticle Arrays in the Coulomb Blockade Regime. ACS Nano 6, 4181–4189 (2012). [DOI] [PubMed] [Google Scholar]
  30. Alivisatos A. P. Semiconductor clusters, nanocrystals, and quantum dots. Science 271, 933–937 (1996). [Google Scholar]
  31. Tanaka K. & Iijima S. Carbon nanotubes and graphene, Elsevier, 2nd edition, 2014. [Google Scholar]
  32. Roncali J., Leriche P. & Cravino A. From one- to three-dimensional organic semiconductors: In search of the organic silicon. Adv. Mater. 19, 2045–2060 (2007). [Google Scholar]
  33. Xu K., Qin L. D. & Heath J. R. The crossover from two dimensions to one dimension in granular electronic materials. Nature Nanotech. 4, 368–372 (2009). [DOI] [PubMed] [Google Scholar]
  34. Ghosh S. et al. Dimensional crossover of thermal transport in few-layer graphene. Nat. Mater. 9, 555–558 (2010). [DOI] [PubMed] [Google Scholar]
  35. Faure B. et al. 2D to 3D crossover of the magnetic properties in ordered arrays of iron oxide nanocrystals. Nanoscale 5, 953–960 (2013). [DOI] [PubMed] [Google Scholar]
  36. Schmid G. & Simon U. Gold nanoparticles: assembly and electrical properties in 1-3 dimensions. Chem. Comm. 6, 697–710 (2005). [DOI] [PubMed] [Google Scholar]
  37. Talapin D. V., Lee J. S., Kovalenko M. V. & Shevchenko E. V. Prospects of colloidal nanocrystals for electronic and optoelectronic applications. Chem. Rev. 110, 389–458 (2010). [DOI] [PubMed] [Google Scholar]
  38. Kane J., Ong J. & Saraf R. F. Chemistry, physics, and engineering of electrically percolating arrays of nanoparticles: a mini review. J. Mater. Chem. 21, 16846–16858 (2011). [Google Scholar]
  39. Noguchi Y., Terui T., Katayama T., Matsushita M. M. & Sugawara T. Charge transport in various dimensions of small networks composed of gold nanoparticles and terthiophene wire-molecules. Appl. Phys. Lett. 98, 263114 (2011). [Google Scholar]
  40. Liao J. H. et al. Patterned Close-Packed Nanoparticle Arrays with Controllable Dimensions and Precise Locations. Small 8, 991–996 (2012). [DOI] [PubMed] [Google Scholar]
  41. Efros A. L. & Shklovskii B. I. Coulomb gap and low temperature conductivity of disordered systems. J. Phys. C 8, L49–L51 (1975). [Google Scholar]
  42. Tran T. B. et al. Multiple cotunneling in large quantum dot arrays. Phys. Rev. Lett. 95, 076806 (2005). [DOI] [PubMed] [Google Scholar]
  43. Tran T. B. et al. Sequential tunneling and inelastic cotunneling in nanoparticle arrays. Phys. Rev. B 78, 075437 (2008). [Google Scholar]
  44. Shklovskii B. I. & Efros A. L. Electronic Properties of Doped Semiconductors, Springer, 1984. [Google Scholar]
  45. Moreira H. et al. Electron cotunneling transport in gold nanocrystal arrays. Phys. Rev. Lett. 107, 176803 (2011). [DOI] [PubMed] [Google Scholar]
  46. Dayen J. F. et al. Enhancing the Molecular Signature in Molecule-Nanoparticle Networks Via Inelastic Cotunneling. Adv. Mater. 25, 400–404 (2013). [DOI] [PubMed] [Google Scholar]
  47. Guyot-Sionnest P. Electrical Transport in Colloidal Quantum Dot Films. J. Phys. Chem. Lett. 3, 1169–1175 (2012). [DOI] [PubMed] [Google Scholar]
  48. Levin E. I., Nguen V. L., Shklovskii B. I. & Efros A. L. Coulomb gap and hopping electric conduction. Computer simulation. Sov. Rhys. JETP 65, 842–848 (1987). [Google Scholar]
  49. Nguyen V. D., Nguyen V. L. & Dang D. T. Variable range hopping in the Coulomb gap and gate screening in two dimensions. Phys. Lett. A 349, 404–410 (2006). [Google Scholar]
  50. Neugebauer C. A. & Webb M. B. Electrical conduction mechanism in ultrathin, evaporated metal films. J. Appl. Phys. 33, 74–81 (1962). [Google Scholar]
  51. Yu D., Bang C., Wehrenberg B. L. & Guyot-Sionnest P. Variable range hopping conduction in semiconductor nanocrystal solids. Phys. Rev. Lett. 92, 216802 (2004). [DOI] [PubMed] [Google Scholar]
  52. Collier C. P., Saykally R. J., Shiang J. J., Henrichs S. E. & Heath J. R. Reversible tuning of silver quantum dot monolayers through the metal-insulator transition. Science 277, 1978–1981 (1997). [Google Scholar]
  53. Doty R. C., Yu H. B., Shih C. K. & Korgel B. A. Temperature-dependent electron transport through silver nanocrystal superlattices. J. Phys. Chem. B 105, 8291–8296 (2001). [Google Scholar]
  54. Sampaio J. F., Beverly K. C. & Heath J. R. DC transport in self-assembled 2D layers of Ag nanoparticles. J. Phys. Chem. B 105, 8797–8800 (2001). [Google Scholar]
  55. Beecher P., Quinn A. J., Shevchenko E. V., Weller H. & Redmond G. Insulator-to-metal transition in nanocrystal assemblies driven by in sity mild thermal annealing. Nano Lett. 4, 1289–1293 (2004). [Google Scholar]
  56. Zabet-Khosousi A., Trudeau P. E., Suganuma Y. & Dhirani A. A. Metal to insulator transition in films of molecularly linked gold nanoparticles. Phys. Rev. Lett. 96, 156403 (2006). [DOI] [PubMed] [Google Scholar]
  57. Muller K. H., Herrmann J., Wei G., Raguse B. & Wieczorek L. Temperature dependence of electrical resistance in films of gold nanoparticles linked by organic molecules. J. Phys. Chem. C 113, 18027–18031 (2009). [Google Scholar]
  58. Liao J., Bernard L., Langer M., Schonenberger C. & Calame M. Reversible formation of molecular junctions in 2D nanoparticle arrays. Adv. Mater. 18, 2444–2447 (2006). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supporting Information

srep07565-s1.pdf (643.6KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES