Skip to main content
PMC home page
Molecular Biology and Evolution logoLink to Molecular Biology and Evolution
. 2014 Nov 3;32(1):268–274. doi: 10.1093/molbev/msu300

IQ-TREE: A Fast and Effective Stochastic Algorithm for Estimating Maximum-Likelihood Phylogenies

Lam-Tung Nguyen 1,2, Heiko A Schmidt 1, Arndt von Haeseler 1,2, Bui Quang Minh 1,*
PMCID: PMC4271533  EMSID: EMS61526  PMID: 25371430

Abstract

Large phylogenomics data sets require fast tree inference methods, especially for maximum-likelihood (ML) phylogenies. Fast programs exist, but due to inherent heuristics to find optimal trees, it is not clear whether the best tree is found. Thus, there is need for additional approaches that employ different search strategies to find ML trees and that are at the same time as fast as currently available ML programs. We show that a combination of hill-climbing approaches and a stochastic perturbation method can be time-efficiently implemented. If we allow the same CPU time as RAxML and PhyML, then our software IQ-TREE found higher likelihoods between 62.2% and 87.1% of the studied alignments, thus efficiently exploring the tree-space. If we use the IQ-TREE stopping rule, RAxML and PhyML are faster in 75.7% and 47.1% of the DNA alignments and 42.2% and 100% of the protein alignments, respectively. However, the range of obtaining higher likelihoods with IQ-TREE improves to 73.3–97.1%. IQ-TREE is freely available at http://www.cibiv.at/software/iqtree.

Keywords: phylogenetic inference, phylogeny, maximum likelihood, stochastic algorithm

Introduction

Phylogenetic inference by maximum likelihood (ML) is widely used in molecular systematics (Felsenstein 1981, 2004). It involves the estimation of substitution model parameters, branch lengths and tree topology. These parameters are usually estimated one after another with the tree topology being the main parameter of interest. While efficient numerical methods for estimating substitution model parameters and branch lengths on a fixed tree exist (Yang 2000), finding the optimal tree topology is an NP-hard combinatorial optimization problem (Chor and Tuller 2005). Therefore, one has to rely on search heuristics to find the “best” tree.

ML tree searches apply inter alia local tree rearrangements such as nearest neighbor interchange (NNI), subtree pruning and regrafting (SPR), or tree bisection and reconnection (TBR) to improve the current tree (Guindon and Gascuel 2003; Swofford 2003; Stamatakis 2006). Here, only modifications that increase the tree likelihood (“uphill” moves) are allowed. Such approaches are prone to be stuck in local optima (e.g., Swofford and Olsen 1990). The problem becomes more severe if the local tree rearrangement method can only generate a small number of trees in neighborhood of the current tree. As a result, SPR algorithms often find trees with higher likelihoods than those that are based on NNI (Morrison 2007; Whelan and Money 2010; Money and Whelan 2012). TBR is not often used due to its high computational demand.

Stochastic algorithms were developed to overcome the problem of local optima encountered by hill-climbing algorithms. Current ML implementations of stochastic algorithms allow “downhill” moves (Salter and Pearl 2001; Vos 2003; Vinh and von Haeseler 2004) or maintain a population of candidate trees (Lewis 1998; Zwickl 2006; Helaers and Milinkovitch 2010) to avoid local optima. However, in terms of both likelihood maximization and computation time such implementations have been found not to perform as well as SPR-based hill-climbing algorithms (Stamatakis 2006; Morrison 2007). The large variety of techniques makes it difficult to combine them into effective and efficient stochastic algorithms. While the possibilities to enhance a hill-climbing algorithm are limited, the potential to improve the effectiveness and efficiency of stochastic algorithms is not yet fully explored.

New Approaches

This article presents a fast and effective stochastic algorithm for finding ML trees. The core idea is to perform an efficient sampling of local optima in the tree space. Here, the best local optimum found represents the reported ML tree. To this end, we combine elements of hill-climbing algorithms, random perturbation of current best trees, and a broad sampling of initial starting trees. Comparative analyses for many large DNA and amino acid (AA) multiple sequence alignments retrieved from TreeBASE (Sanderson et al. 1994) showed that our new search strategy often achieves higher likelihoods compared with RAxML (Stamatakis 2006) and PhyML (Guindon et al. 2010).

Results

Benchmark Setup

Here, we compared the performance of our approach (implemented in IQ-TREE 1.0) with the default tree searches implemented in PhyML 3.1 and RAxML 7.3.5. To that end, we downloaded multiple sequence alignments from TreeBASE (Sanderson et al. 1994; accessed December 1, 2012) fulfilling the following criteria. First, the number of sequences must be between 200 and 800 for DNA and between 50 and 600 for AA alignments. Second, the alignment length must be at least four (or two) times the number of sequences in DNA (or AA) alignments. Third, the proportion of gaps/unknown characters must be less or equal than 70%. Identical sequences were discarded from the alignments keeping only one. We obtained 70 DNA and 45 AA alignments (see supplementary tables S1 and S2, Supplementary Material online). The DNA alignment lengths range from 976 to 61,199 sites. The AA alignment lengths were between 126 and 22,426 sites.

For all programs, we used GTR (general time reversible; Lanave et al. 1984) and WAG (Whelan and Goldman 2001) models for DNA and AA alignments, respectively. Rate heterogeneity followed the discrete Γ model (Yang 1994) with four rate categories, where relative rates are computed as the mean of the portion of the Γ distribution falling in the respective category. To avoid numerical discrepancies between different likelihood implementations, we used PhyML to compute the log-likelihoods of the final trees based on parameters produced by each program. We note that, for 92% of the trees the differences in log-likelihoods recomputed by IQ-TREE and PhyML are smaller than 0.01 and the maximal difference is 0.05 (supplementary fig S0, Supplementary Material online). All analyses were performed on the Vienna Scientific Cluster (VSC-2, vsc.ac.at).

Comparison with Equal Running Times

As RAxML and PhyML are considered as the two high-performance ML tree-inference programs, we first benchmarked IQ-TREE by restricting the running time of IQ-TREE to that required by each RAxML and PhyML run. This is done to study how efficiently IQ-TREE uses its search time compared with the other programs. For each alignment, we ran RAxML ten times and PhyML once (because the default tree search in PhyML is deterministic). Subsequently, we ran IQ-TREE ten times for each alignment with restricted CPU time. Then, we compared for each alignment the average log-likelihood of trees produced by IQ-TREE with those by the other two programs.

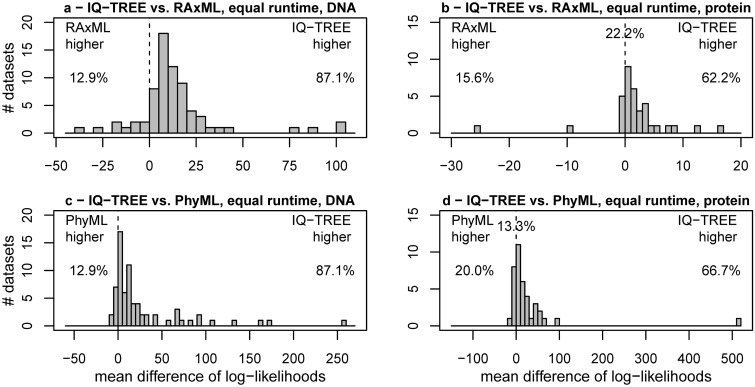
Figure 1 (and supplementary fig. S1, Supplementary Material online) displays the pairwise log-likelihood difference distributions for IQ-TREE versus RAxML (fig. 1a and b) and PhyML (fig. 1c and d). Trees inferred with IQ-TREE for DNA alignments had in 87.1% of the instances a higher likelihood than RAxML-trees or PhyML-trees (fig. 1a and c). Although these percentages are identical, the alignments for which IQ-TREE found better trees if compared with RAxML or PhyML are not the same (see supplementary fig. S1, Supplementary Material online). For 12.9% of the alignments, RAxML or PhyML found better trees.

Fig. 1.

Fig. 1.

Open in a new tab

Performance of IQ-TREE for fixed CPU times: (a, b) Display frequencies of log-likelihood differences for IQ-TREE minus RAxML for 70 DNA (a) and 45 AA (b) alignments. (c) and (d) show the same if IQ-TREE is compared with PhyML. IQ-TREE’s CPU times were limited to those required by RAxML and PhyML, respectively. The percentages on the dashed line in (b) and (d) represent the fraction of alignments where log-likelihood differences are smaller than 0.01.

For the AA alignments, IQ-TREE found higher likelihoods in 62.2% if compared with RAxML (fig. 1b) and in 66.7% if compared with PhyML (fig. 1d). Contrary to DNA we observed 22.2% of the alignments where RAxML and IQ-TREE found trees with negligible log-likelihood differences (<0.01). This number is 13.3% when comparing PhyML with IQ-TREE. In only 15.6% and 20% of the AA alignments, RAxML and PhyML performed better (with respect to tree log-likelihoods) than IQ-TREE, respectively.

We note that the distributions in figure 1a, c, and d are skewed to the right. Thus, our tree search strategy sometimes leads to substantially better likelihoods.

In summary, based on the analysis of a large collection of alignments, we demonstrate that IQ-TREE shows higher likelihoods in approximately three-quarters of the analyzed data. The improvement is almost the same compared with RAxML or PhyML. Because we fixed IQ-TREE’s running time to the time the other programs needed, we conclude that the employed search strategy explores tree-space more efficiently.

Comparison with Different Running Time

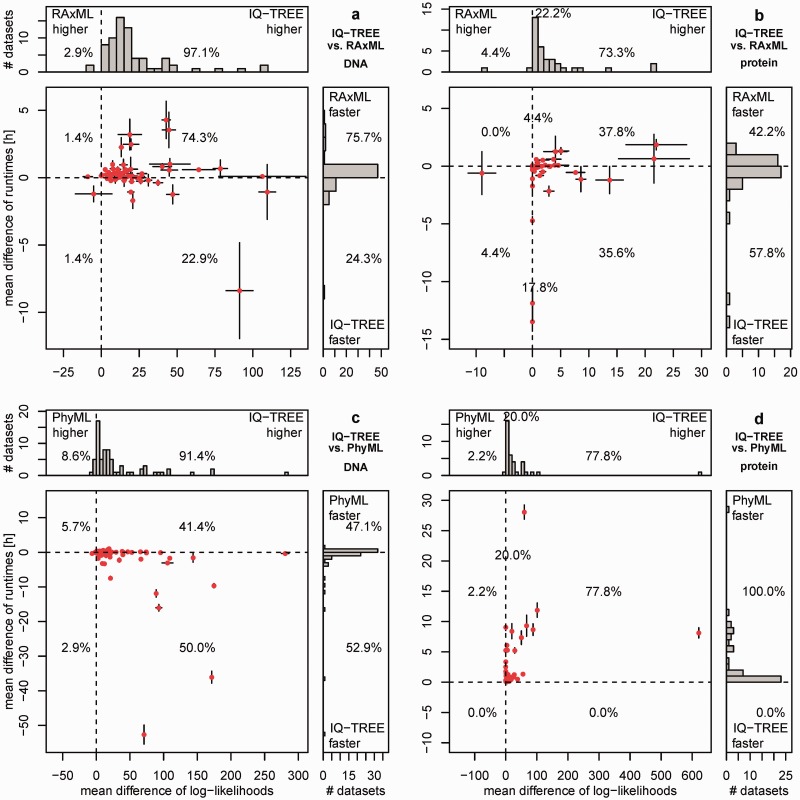
We now discuss the performance of IQ-TREE if the CPU time is not determined by RAxML or PhyML but rather by the default stopping rule (see Materials and Methods). Thus, we compared the differences in CPU times and the differences in log-likelihoods (fig. 2 and supplementary fig. S2, Supplementary Material online). Again, the analyses were based on average of ten independent IQ-TREE and RAxML runs. Figure 2 is organized like figure 1 (RAxML vs. IQ-TREE results in the first row, PhyML vs. IQ-TREE results in the second row, DNA alignments left column, and AA alignments right column).

Fig. 2.

Fig. 2.

Open in a new tab

Performance of IQ-TREE for variable CPU times: The upper plots (a, b) show the performance of IQ-TREE against RAxML using the 70 DNA (a) and 45 AA (b) alignments. The lower plots (c, d) show the same against PhyML. Each dot in the main diagrams represents for one alignment the mean differences of the CPU times (y axis) and of the mean differences of log-likelihoods (x axis) of the reconstructed trees by the programs compared. The whiskers at each point show the standard errors of the differences. The histograms at the top and the side present the marginal frequencies. Dots to the right of the vertical dashed line represent alignments where IQ-TREE found a higher likelihood. If a dot is below the horizontal dashed line, the reconstruction by IQ-TREE was faster. Percentages in the quadrants of histograms denote the fraction of alignments in that region. Percentages on the dashed line reflect the number of alignments where log-likelihood differences are smaller than 0.01 (see [b] and [d]).

By allowing variable CPU time, the number of the alignments for which IQ-TREE found higher-likelihood trees than RAxML or PhyML increases. For 97.1% of the DNA alignments, the likelihood is improved compared with RAxML (fig. 2a) with the maximal average log-likelihood difference of 109.5 (TreeBASE ID: M7964). For two DNA alignments, IQ-TREE obtained trees with lower likelihoods than RAxML with log-likelihood differences up to −8.9 (M2534).

This success in finding higher likelihoods comes at a cost; IQ-TREE required longer CPU times than RAxML for 75.7% of the DNA alignments. However, the situation is complicated; the differences in average CPU times are highly variable, and for some alignments, one program is much faster than the other. For example, for the alignment M7024 IQ-TREE needed 4.2 h more than RAxML to finish, whereas RAxML required 8.3 h more to find an optimal tree for M14582. To finish all ten repetitions for the 70 DNA alignments, IQ-TREE needed 2,020 CPU hours (∼87 CPU days), whereas RAxML needed 1,870 CPU hours (∼78 CPU days). This is an average CPU time difference of less than 13 min per run.

Figure 2b displays the results for the 45 AA alignments. For ten AA alignments (22.2%, cf. supplementary fig. S2b, Supplementary Material online), IQ-TREE and RAxML inferred trees with likelihood differences smaller than 0.01 for all ten runs. For 73.3% of the AA alignments, IQ-TREE obtained higher likelihoods than RAxML with a maximal log-likelihood difference of 21.9 (M11012). And for only 4.4% of the AA alignments, the results were in favor of RAxML, with a maximum log-likelihood difference of −8.9 (M3114). In terms of computing time, IQ-TREE obtained the result faster than RAxML in 57.8% of the AA alignments, whereas RAxML was faster in 42.2%. In total, IQ-TREE needed 2,042 CPU hours to complete all 450 runs, whereas RAxML required 2,380 CPU hours. This is an excess of 16.6% compared with the CPU time of IQ-TREE. Thus, on average RAxML needed 45 CPU minutes more per run. The runtime ratios between IQ-TREE and RAxML range from 0.6 to 3.2 for DNA and from 0.5 to 1.9 for protein alignments.

Finally, figure 2c and d displays the results of IQ-TREE and PhyML for the DNA and AA alignments, respectively. IQ-TREE obtained higher likelihoods than PhyML for 91.4% of the DNA and 77.8% of the AA alignments. PhyML obtained higher likelihoods in 8.6% and 2.2% for DNA and AA, respectively. Notably, the maximal log-likelihood differences in favor of IQ-TREE were 280.5 (M4794) and 621.1 (M8630) for DNA and AA, respectively. The maximal differences in favor of PhyML were −6.3 (M9143) and −0.27 (M8175) for DNA and AA, respectively.

With respect to computing times, PhyML was faster in 47.1% of the DNA and for all AA alignments, whereas IQ-TREE was faster in 52.9% of the DNA alignments. PhyML spent 357 and 61 CPU hours for all DNA and AA alignments, respectively, compared with the average CPU times for IQ-TREE of 202 and 204 h for all DNA and AA alignments, respectively. However, in the shorter runtime PhyML produced lower likelihoods for 77.8% of the AA alignments. The runtime ratios between IQ-TREE and PhyML range from 0.3 to 2.5 (DNA) and from 2 to 7.5 (protein).

In addition, we ran PhyML ten times per alignment using a random starting tree and SPR search strategy. Supplementary figure S3, Supplementary Material online, shows the results. In terms of computing time, PhyML ran slower than IQ-TREE for 98.6% DNA alignments but faster than IQ-TREE for 100% AA alignments. With respect to log-likelihoods, IQ-TREE produced higher likelihoods than PhyML for 88.6% DNA and 93.3% AA alignments (an increase by 2.8% for PhyML on DNA, but a decrease by 15.5% on AA). Hence, IQ-TREE performed better than PhyML under both the default and random starting tree options.

Discussion

We have combined well-known phylogenetic and combinatorial optimization techniques into a fast and effective tree search algorithm. The success of IQ-TREE results from two factors: The new tree search strategy helps to escape local optima and, thus, leads to trees with high likelihood and the phylogenetic likelihood library (Flouri et al. 2014) reduces the time for the likelihood computation. Given the same amount of computing time, the efficient IQ-TREE implementation of hill-climbing and stochastic NNI operations (see Materials and Methods) computed trees with higher likelihood than RAxML or PhyML in the majority of cases (up to 87.1% of the benchmark data). This improvement is further boosted if the internal stopping rule was used (up to 97.1%). The success of IQ-TREE in finding trees with higher likelihoods is somehow at odds with the discussion in the literature about the effectiveness of NNI compared with SPR (Hordijk and Gascuel 2005; Guindon et al. 2010; Whelan and Money 2010). One explanation for the very good performance of IQ-TREE is possibly the introduction of the stochastic NNI. This random perturbation of locally optimal trees helps to escape local optima. The perturbed trees are then optimized by hill-climbing NNI, thus allowing for the possibility to find new and higher local optima. The combination of random and deterministic elements for ML searches has been previously proposed in Vos (2003) and Vinh and von Haeseler (2004).

In addition, we employed some elements of evolution strategies (Rechenberg 1973) to allow for a broader exploration of the tree space. To this end, we maintain a small population (candidate tree set) of locally optimal trees initially generated from a large number of maximum parsimony (MP) trees. Throughout the ML tree search, we continuously update the candidate tree set with better trees. This extension of the tree-search also contributes to the performance of IQ-TREE.

It would be interesting to evaluate the relative importance of all these heuristic optimization techniques implemented in IQ-TREE, but this is beyond the scope of this article and will be discussed in forthcoming technical publications.

We also observed that the improvement in log-likelihood differences is positively skewed for all comparative analyses with the exception of the time constrained IQ-TREE versus RAxML for AA data (fig. 1b). Thus, not only the average log-likelihood improved with IQ-TREE but also for some alignments, the improvement is substantial. It would be interesting to find out the characteristics of such alignments to further improve ML tree reconstruction methods. Moreover, by using many large alignments we show that the very good performance of our search strategy is not limited to a few alignments. Based on our benchmark results, we are confident that IQ-TREE will generally work very well.

We would like to point out that it is not enough to run phylogenetic programs with a stochastic component only once. RAxML and IQ-TREE showed some variation in the log-likelihoods, if they were run several times (here ten times) on the same alignment (fig. 2 and supplementary fig. S2, Supplementary Material online). This observation implies that both programs still finish sometimes in local optima and one should rerun the programs as many times as possible. In addition, we also offer the possibility to run IQ-TREE longer by adjusting the corresponding parameter of the stopping rule or by applying the statistical stopping rule suggested by Vinh and von Haeseler (2004). Compared with other programs, our results show that with the standard setting of the stopping rule IQ-TREE can produce very good results, with a moderate increase in running time.

The proposed tree search in IQ-TREE also improves the accuracy of the recently introduced ultrafast bootstrap approximation approach (Minh et al. 2013). To further facilitate large phylogenetic analyses, we also consider future development of IQ-TREE for distributed computing platforms. The highly independent components of our stochastic search algorithm would allow us to implement an efficient parallelization strategy (cf. Minh et al. 2005) with near-optimal speedup. Thus, the running time of very large phylogenetic analyses would then be greatly reduced.

In conclusion, IQ-TREE is a time and search efficient ML-tree reconstruction program. It complements the collection of available ML-programs and shows a better performance with respect to the ML search than RAxML or PhyML. However, as IQ-TREE is not always better than the other programs, we recommend using all three programs.

Materials and Methods

In the following, we describe the ingredients of the fast tree reconstruction method that are implemented in IQ-TREE. We used the phylogenetic likelihood library (Flouri et al. 2014) for likelihood and parsimony computations. We first describe our fast hill-climbing NNI algorithm that is repeatedly used throughout the tree search. Subsequently, we will explain the initial tree generation and the stochastic NNI process.

Hill-Climbing NNI

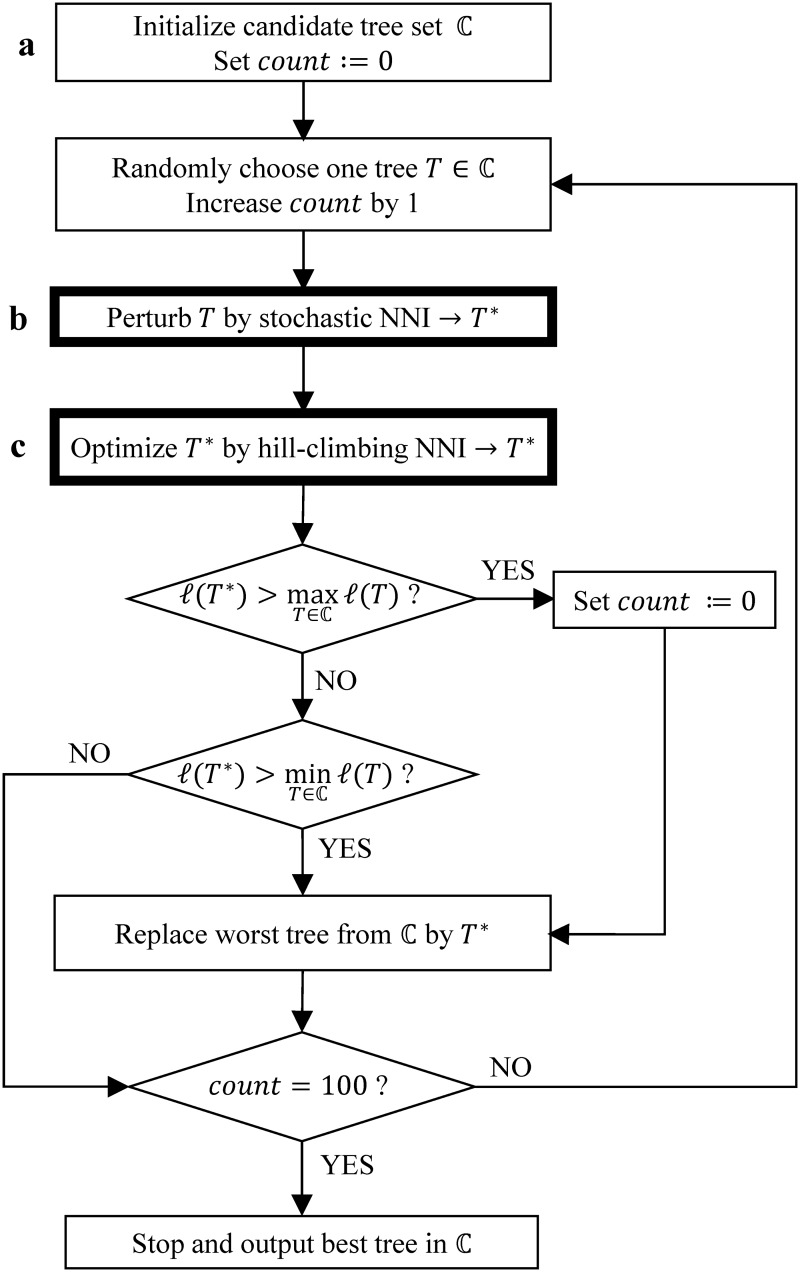
For the determination of locally optimal trees, we implemented a fast hill-climbing NNI search. Our approach is based on the work of Guindon and Gascuel (2003) where they applied several NNIs simultaneously. The hill-climbing NNI is a central element of the search strategy (fig. 3 box c).

Fig. 3.

Fig. 3.

Open in a new tab

Flowchart for the stochastic search algorithm. The variable count counts the number of random perturbations (box b and box c) as a new best tree was found.

NNI is a local tree rearrangement operation that swaps two subtrees across an internal branch. Each inner branch defines two distinct NNIs. Thus, for an unrooted bifurcating tree with n taxa, there are 2(n-3) NNI-trees in the NNI-neighborhood of that tree.

For a given tree (current tree), we first compute the approximate likelihoods of each NNI-tree by optimizing the respective inner branch and the four adjacent branches. In the following, we only consider NNIs that increase the tree likelihood compared with the current tree. We then create a list of nonconflicting NNIs. Two NNIs are considered conflicting if they operate on the same inner branch or adjacent branches. The list is initialized with the best NNI. We then add the next best NNI to the list if it does not conflict with any existing NNI in the list otherwise we discard it. We repeat this procedure until all NNIs have been processed.

Afterwards, we simultaneously apply all NNIs in the list to the current tree and compute the likelihood of the resulting tree by doing one tree traversal of ML branch length optimization. If the likelihood of the resulting tree is worse than the likelihood of the best NNI-tree, we discard all topological modifications except that of the best NNI in the list. Thus, if the list is not empty, a new tree with higher likelihood will be found. This tree will replace the current tree. Furthermore, we tag the inner branches on the new current tree on which NNIs were applied and perform the remaining procedure as follows.

Instead of computing the full NNI-neighborhood we conduct a reduced NNI search on the new current tree, applying the following heuristic to find a locally optimal tree. We only compute the NNI-trees on inner branches that are at most two branches away from the tagged branches. For such admissible branches, we compute the list as described. If the list is empty, a locally optimal tree has been found and the hill-climbing search is finished. Otherwise, we continue the reduced NNI search with the better tree as described above.

Initial Tree Generation

Tree search heuristics typically start with a quickly built initial tree that is subsequently improved. For example, PhyML starts with a BIONJ tree (Gascuel 1997) whereas RAxML starts with a stepwise addition tree (Farris 1970) using MP (Fitch 1971) where the MP tree is further optimized with lazy subtree rearrangement (Stamatakis 2006). To get a representative sample of plausible initial trees, we generate 100 parsimony trees using the same strategy as RAxML. From the 100 trees, we collect all unique topologies and compute their approximate likelihoods by doing one tree traversal of ML branch length optimization. From the ranked list of ML values, we select the top 20 trees and perform hill-climbing NNI on each tree to obtain the locally optimal ML trees. We then retain the top five topologies with highest likelihood in the so-called candidate tree set ℂ for further optimization (fig. 3 box a).

A Stochastic NNI Step

The locally optimal trees in the candidate set ℂ are randomly perturbed to allow the escape from local optima. To this end, we introduce a so-called stochastic NNI step (fig. 3 box b). Here, we perform 0.5(n − 3) random NNIs on a tree T randomly drawn from ℂ, where n − 3 is the number of inner branches. Then, we apply hill-climbing NNI to the perturbed tree to obtain a new locally optimal tree T* (fig. 3 box c).

If T* has a higher likelihood than the best tree in ℂ, we replace that tree by T*. Moreover, the stochastic NNI successfully found a better tree, thus the number (count) of perturbations after a new better tree was found is set to zero. If T*’s likelihood is higher than the likelihood for the worst tree in ℂ, then that tree is replaced by T*. Finally, ℂ does not change if the likelihood of T* is smaller than the smallest likelihood for the trees in ℂ. In the last two cases, the tree with the highest likelihood did not change and count is increased by one.

The tree search stops, if the current best tree has not changed for count = 100 random perturbations. The flowchart of our stochastic tree search is summarized in figure 3.

Supplementary Material

Supplementary figures S0–S3 and tables S1 and S2 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).

Supplementary Data
supp_32_1_268__index.html (1.1KB, html)

Acknowledgments

The authors thank Tomas Flouri, Fernando Izquierdo-Carrasco, and Alexandros Stamatakis for help with the phylogenetic likelihood library, Pablo A. Goloboff and an anonymous reviewer for helpful comments on the manuscript. The computational results presented have been achieved using the Vienna Scientific Cluster (VSC-2). This work was supported by the Austrian Science Fund—FWF (grant number I760-B17) to B.Q.M. and A.v.H., and the University of Vienna (Initiativkolleg I059-N) to L.-T.N. and A.v.H.

References

  1. Chor B, Tuller T. Maximum likelihood of evolutionary trees is hard. Lect Notes Comput Sci. 2005;3500:296–310. [Google Scholar]
  2. Farris JS. Methods for computing Wagner trees. Syst Zool. 1970;19:83–92. [Google Scholar]
  3. Felsenstein J. Evolutionary trees from DNA sequences: a maximum likelihood approach. J Mol Evol. 1981;17:368–376. doi: 10.1007/BF01734359. [DOI] [PubMed] [Google Scholar]
  4. Felsenstein J. Inferring phylogenies. Sunderland (MA): Sinauer Associates; 2004. [Google Scholar]
  5. Fitch WM. Toward defining course of evolution—minimum change for a specific tree topology. Syst Zool. 1971;20:406–416. [Google Scholar]
  6. Flouri T, Izquierdo-Carrasco F, Darriba D, Aberer AJ, Nguyen L-T, Minh BQ, von Haeseler A, Stamatakis A. The phylogenetic likelihood library. Syst Biol. 2014 doi: 10.1093/sysbio/syu084. Advance Access published October 30, 2014, doi:10.1093/sysbio/syu084. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Gascuel O. BIONJ: an improved version of the NJ algorithm based on a simple model of sequence data. Mol Biol Evol. 1997;14:685–695. doi: 10.1093/oxfordjournals.molbev.a025808. [DOI] [PubMed] [Google Scholar]
  8. Guindon S, Dufayard JF, Lefort V, Anisimova M, Hordijk W, Gascuel O. New algorithms and methods to estimate maximum-likelihood phylogenies: assessing the performance of PhyML 3.0. Syst Biol. 2010;59:307–321. doi: 10.1093/sysbio/syq010. [DOI] [PubMed] [Google Scholar]
  9. Guindon S, Gascuel O. A simple, fast, and accurate algorithm to estimate large phylogenies by maximum likelihood. Syst Biol. 2003;52:696–704. doi: 10.1080/10635150390235520. [DOI] [PubMed] [Google Scholar]
  10. Helaers R, Milinkovitch MC. MetaPIGA v2.0: maximum likelihood large phylogeny estimation using the metapopulation genetic algorithm and other stochastic heuristics. BMC Bioinformatics. 2010;11:379. doi: 10.1186/1471-2105-11-379. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Hordijk W, Gascuel O. Improving the efficiency of SPR moves in phylogenetic tree search methods based on maximum likelihood. Bioinformatics. 2005;21:4338–4347. doi: 10.1093/bioinformatics/bti713. [DOI] [PubMed] [Google Scholar]
  12. Lanave C, Preparata G, Saccone C, Serio G. A new method for calculating evolutionary substitution rates. J Mol Evol. 1984;20:86–93. doi: 10.1007/BF02101990. [DOI] [PubMed] [Google Scholar]
  13. Lewis PO. A genetic algorithm for maximum-likelihood phylogeny inference using nucleotide sequence data. Mol Biol Evol. 1998;15:277–283. doi: 10.1093/oxfordjournals.molbev.a025924. [DOI] [PubMed] [Google Scholar]
  14. Minh BQ, Nguyen MA, von Haeseler A. Ultrafast approximation for phylogenetic bootstrap. Mol Biol Evol. 2013;30:1188–1195. doi: 10.1093/molbev/mst024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Minh BQ, Vinh LS, von Haeseler A, Schmidt HA. pIQPNNI: parallel reconstruction of large maximum likelihood phylogenies. Bioinformatics. 2005;21:3794–3796. doi: 10.1093/bioinformatics/bti594. [DOI] [PubMed] [Google Scholar]
  16. Money D, Whelan S. Characterizing the phylogenetic tree-search problem. Syst Biol. 2012;61:228–239. doi: 10.1093/sysbio/syr097. [DOI] [PubMed] [Google Scholar]
  17. Morrison DA. Increasing the efficiency of searches for the maximum likelihood tree in a phylogenetic analysis of up to 150 nucleotide sequences. Syst Biol. 2007;56:988–1010. doi: 10.1080/10635150701779808. [DOI] [PubMed] [Google Scholar]
  18. Rechenberg I. Evolutionsstrategie—optimierung technischer systeme nach prinzipien der biologischen evolution. Stuttgart (Germany): Frommann-Holzboog Verlag; 1973. [Google Scholar]
  19. Salter LA, Pearl DK. Stochastic search strategy for estimation of maximum likelihood phylogenetic trees. Syst Biol. 2001;50:7–17. [PubMed] [Google Scholar]
  20. Sanderson MJ, Donoghue MJ, Piel W, Eriksson T. TreeBASE: a prototype database of phylogenetic analyses and an interactive tool for browsing the phylogeny of life. Am J Bot. 1994;81:183. [Google Scholar]
  21. Stamatakis A. RAxML-VI-HPC: maximum likelihood-based phylogenetic analyses with thousands of taxa and mixed models. Bioinformatics. 2006;22:2688–2690. doi: 10.1093/bioinformatics/btl446. [DOI] [PubMed] [Google Scholar]
  22. Swofford DL. 2003. PAUP*. Phylogenetic analysis using parsimony (* and other methods) Version 4. Sunderland (MA): Sinauer Associates. [Google Scholar]
  23. Swofford DL, Olsen GJ. Phylogeny reconstruction. In: Hillis DM, Moritz C, editors. Molecular systematics. Sinauer Associates: Sunderland (MA); 1990. pp. 411–501. [Google Scholar]
  24. Vinh LS, von Haeseler A. IQPNNI: moving fast through tree space and stopping in time. Mol Biol Evol. 2004;21:1565–1571. doi: 10.1093/molbev/msh176. [DOI] [PubMed] [Google Scholar]
  25. Vos RA. Accelerated likelihood surface exploration: the likelihood ratchet. Syst Biol. 2003;52:368–373. doi: 10.1080/10635150390196993. [DOI] [PubMed] [Google Scholar]
  26. Whelan S, Goldman N. A general empirical model of protein evolution derived from multiple protein families using a maximum-likelihood approach. Mol Biol Evol. 2001;18:691–699. doi: 10.1093/oxfordjournals.molbev.a003851. [DOI] [PubMed] [Google Scholar]
  27. Whelan S, Money D. The prevalence of multifurcations in tree-space and their implications for tree-search. Mol Biol Evol. 2010;27:2674–2677. doi: 10.1093/molbev/msq163. [DOI] [PubMed] [Google Scholar]
  28. Yang Z. Maximum likelihood phylogenetic estimation from DNA sequences with variable rates over sites: approximate methods. J Mol Evol. 1994;39:306–314. doi: 10.1007/BF00160154. [DOI] [PubMed] [Google Scholar]
  29. Yang Z. Maximum likelihood estimation on large phylogenies and analysis of adaptive evolution in human influenza virus A. J Mol Evol. 2000;51:423–432. doi: 10.1007/s002390010105. [DOI] [PubMed] [Google Scholar]
  30. Zwickl DJ. 2006. Genetic algorithm approaches for the phylogenetic analysis of large biological sequence data sets under the maximum likelihood criterion. [Ph.D. dissertation]. Austin (TX): The University of Texas at Austin. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_32_1_268__index.html (1.1KB, html)
supp_msu300_SupplementaryFigures.pdf (49.9KB, pdf)
supp_msu300_SupplementaryTables.pdf (582.4KB, pdf)

Articles from Molecular Biology and Evolution are provided here courtesy of Oxford University Press

RESOURCES