Computerized Liver Volumetry on MRI by Using 3D Geodesic Active Contour Segmentation

Abstract

OBJECTIVE

Our purpose was to develop an accurate automated 3D liver segmentation scheme for measuring liver volumes on MRI.

SUBJECTS AND METHODS

Our scheme for MRI liver volumetry consisted of three main stages. First, the preprocessing stage was applied to T1-weighted MRI of the liver in the portal venous phase to reduce noise and produce the boundary-enhanced image. This boundary-enhanced image was used as a speed function for a 3D fast-marching algorithm to generate an initial surface that roughly approximated the shape of the liver. A 3D geodesic-active-contour segmentation algorithm refined the initial surface to precisely determine the liver boundaries. The liver volumes determined by our scheme were compared with those manually traced by a radiologist, used as the reference standard.

RESULTS

The two volumetric methods reached excellent agreement (intraclass correlation coefficient, 0.98) without statistical significance (p = 0.42). The average (± SD) accuracy was 99.4% ± 0.14%, and the average Dice overlap coefficient was 93.6% ± 1.7%. The mean processing time for our automated scheme was 1.03 ± 0.13 minutes, whereas that for manual volumetry was 24.0 ± 4.4 minutes (p < 0.001).

CONCLUSION

The MRI liver volumetry based on our automated scheme agreed excellently with reference-standard volumetry, and it required substantially less completion time.

Medical and surgical advances have brought about a global success of liver transplantation with increasing survival rates after transplantation over the past decades. One of the important assessments contributing to the success of a transplantation procedure is the estimation of total and segmental liver volumes. This is a major factor in predicting the safe outcome for both donor and recipient. Hence, an accurate estimation of liver volumes is crucial for planning liver transplantation [1, 2]. Although the manual tracing method can give accurate results, it is subjective, tedious, and time consuming. In addition, relatively large intraobserver and interobserver variations still occur with the manual method. To address this issue, automated liver segmentation is being developed with image analysis techniques and has become an important research topic.

Several approaches to computerized liver segmentation on CT images have been published, including image-processing techniques [3–5], feature analysis [6], and level-set segmentation [7–9]. In comparison with CT-based schemes, there are few publications on an automated liver segmentation scheme for MRI, even though MRI carries no risk related to ionizing radiation, probably because it is thought that MRI liver volumetry has more variations and is more difficult than CT. Karlo et al. [10] compared the CT- and MRI-based volumetry of resected liver specimens with intraoperative volume and weight measurements to calculate conversion factors. A semiautomated dual-space clustering segmentation method was proposed by Farraher et al. [11]. Their semiautomated method required, first, manual drawing of a small region of interest on the liver; then it iteratively evaluated temporal liver segmentations with repeated adjustment of parameters to obtain the final liver segmentation result. They evaluated the performance of their method on 18 normal and nine abnormal cases. Ruskó and Bekes [12] proposed a partitioned probabilistic model to represent the liver. In this model, the liver was partitioned into multiple regions, and different intensity statistical models were applied to these regions. The scheme was tested on two normal and six abnormal cases. Gloger et al. [13] developed a three-step segmentation method based on a region-growing approach, linear discriminant analysis, and probability maps. Their method was evaluated with 20 normal cases and 10 fatty cases.

Although those studies showed promise, there is still room for improvement in accuracy, especially for diseased cases, and in the execution time of the computerized liver segmentation in MRI to make it suitable for routine clinical use. In this study, we developed an automated liver segmentation scheme for MRI based on a geodesic active contour model and a fast-marching algorithm. The performance of our scheme was evaluated on 23 patients with cancer, and a comparison between the computerized volumetry and reference standard manual volumetry was performed.

Subjects and Methods

Liver MRI Datasets

This study was approved by the institutional review board of the University of Chicago Medical Center and was compliant with the HIPAA. Informed consent was obtained from all patients. Twenty-three patients (14 men and nine women; age range, 46–84 years) were scanned in the supine position with 1.5-T MRI scanners (Signa HDx/HDxt, GE Healthcare; and Achieva, Philips Healthcare) at the University of Chicago Medical Center. IV gadolinium contrast-based agent (8–20 mL; mean [± SD], 15.3 ± 4.2 mL) was administrated. Contrast-enhanced MRI was performed by use of T1-weighted liver acquisition with volume acceleration or T1-weighted high-resolution isotropic volume examination sequence (flip angle, 10°; TR/TE, 3.48–3.92/1.64–1.84). The scanning parameters included a slice thickness of 5 mm (for the GE system) or 4 mm (for the Philips Health-care system) and reconstruction intervals of 2.5 mm (for the GE system) or 2 mm (for the Philips Healthcare system). Each MRI slice had a matrix size of 256 × 256, 384 × 384, or 512 × 512 pixels with an in-plane pixel size ranging from 1.17 to 1.72 mm. The 23 cases in our database had liver diseases (hepatocellular carcinoma in 11 cases and metastasis in 12 cases).

The manual liver contours were traced carefully by a board-certified abdominal radiologist on each slice containing the liver. The number of slices in each case ranged from 88 to 120 (average, 97.9 slices). The liver volume was calculated by multiplying the areas of the manually traced regions in each slice by the reconstruction interval. Note that the slice thickness was different from the reconstruction interval, and consecutive slices overlapped. The total liver volume in each case was obtained from summation of the volumes in all slices. We also recorded the time required for the completion of the manual contour tracing. The performance of our computerized liver volumetry scheme was evaluated by using manual liver volume, which is considered as the reference standard.

Computerized Measurement Scheme for MRI Liver Volumes

A computerized scheme using level-set algorithms coupled with geodesic active contour segmentation was proposed by our group for CT liver segmentation. In this study, we developed a scheme for the automated liver segmentation on MRI, based on the knowledge and techniques acquired in the development of our CT liver segmentation scheme. Our MRI liver segmentation scheme applied to the portal venous phase images in T1-weighted sequences consists of three main stages: preprocessing, rough estimation of the liver shape, and segmentation of the liver. The details of our scheme are presented in Appendix 1. In the first stage, a 3D MRI volume, I(x,y,z), consisting of portal venous phase images was processed to reduce noise, enhance liver boundaries, and produce the edge potential image. This edge potential image was used as a speed function for level-set segmentation and fast-marching algorithms. The output of the fast-marching algorithm in the next stage was a time-crossing map indicating the time traveling to each point. It forms a rough shape of the liver on MRI. Finally, we used a 3D geodesic active contour algorithm [14] to refine the initial surface determined by the time-crossing map to obtain the liver boundaries more precisely. The liver regions segmented by the geodesic active contour algorithm were used to calculate the liver volume.

Evaluation Criteria

The liver volumes obtained by using our computerized scheme were compared with the reference-standard manual volumes determined by a radiologist. We determined true-positive (TP), false-positive (FP), true-negative (TN), and false-negative (FN) segmentation for detailed analysis (see Appendix 2 for their definitions). We calculated the accuracy of the segmentation as follows:

$$\mathit{Accuracy}=(\mid TP\mid +\mid TN\mid )/\mid I\mid ,$$ (1)

where I is the entire image. The Dice measurement representing the fraction of the overlapping volume and the volume of two segmentation methods is given by the following equation:

$$\mathit{Dice}=\frac{2\mid TP\mid }{2\mid TP\mid +\mid FP\mid +\mid FN\mid }.$$ (2)

We also determined the percentage volume error (E) for each computerized volume (V_c) and the reference-standard manual volume (V_m) as follows:

$$E=\mid (V_c-V_m)/V_m\mid .$$ (3)

The association between the computerized volumetry and the manual volumetry was measured by the Pearson product-moment correlation coefficient (r). The significance of the correlation coefficient was evaluated by using the Student t test. An agreement between the two measurements was assessed by using the intraclass correlation coefficient (ICC) [15, 16]. The two-way random single measure model, ICC(2,1), was used because we assumed that the cases were chosen randomly and each case was measured by two volumetric methods. The ICC(2,1) was defined by the following equation:

$$\mathit{ICC}(\mathit{2},\mathit{1})=\frac{\mathit{BMS}-\mathit{EMS}}{\mathit{BMS}+(k-1)+k(\mathit{RMS}-\mathit{EMS})/n},$$ (4)

where n is the number of cases, k is the number of raters (i.e., volumetric methods), BMS is the between-cases mean square, EMS is the error mean square, and RMS is the between-raters mean square. The statistical significance was obtained by analysis of variance. We performed a posthoc power analysis with the Walter-Eliasziw-Donner model [17] for ICC-based reliability studies to determine the statistical power in this study. As done by Suzuki et al. [7], we assumed a type 1 error (α) of 0.05 and a type 2 error (β) of 0.20 in this analysis. An additional agreement analysis for two measurements was performed by the Bland-Altman method [18] based on the mean difference (bias) and the SD of the difference. The limits of agreement, which are given by bias ± 1.96 × SD, were used to consider the degree of agreement.

Results

The intermediate results of our scheme for an example case are illustrated in Figure 1. The original MRI (Fig. 1A) was processed by the anisotropic diffusion filter to reduce noise while preserving the major liver structures, such as the portal vein and liver boundaries (Fig. 1B). The edge potential image was generated from the noise-reduced image by using a 3D gradient magnitude filter, and a sigmoid gray-scale converter was applied to the fast-marching algorithm to generate the initial contour (Fig. 1C). Finally, the liver was segmented more precisely by using the geodesic active contour algorithm (Fig. 1D). The liver volume was computed from the segmented regions.

Fig. 1. 67-year-old man with liver cancer. Intermediate results of our scheme for sample case are shown.

A, Original axial T1-weighted MRI of liver in portal venous phase.

B, Three-dimensional anisotropic diffusion noise reduction. Noise in image is reduced substantially, whereas major structures in liver, such as major vessels and liver boundaries, are maintained. Retained structures inside liver are smoothed out, because they are structural noise in liver segmentation.

C, Three-dimensional fast-marching algorithm. Time-crossing map indicates traveling time to each voxel. Most vessels inside liver are excluded at this stage.

D, Three-dimensional geodesic active contour segmentation.

A comparison of the liver volume between the two measurements is shown in Table 1. The mean reference standard manual volume was 1710 ± 401 cm³ (range, 1013–2529 cm³), whereas the mean volume of our computerized scheme was 1697 ± 400 cm³ (range, 1120–2418 cm³). The mean absolute difference and the percentage volume error (E) were 56 cm³ and 3.6%, respectively. The overall mean of the Dice coefficients was calculated as 93.6 ± 1.7, and the accuracy of liver segmentation was 99.4% ± 1.4%. The relationship between the computerized volumetry and the manual volumetry is shown in Figure 2. The Pearson correlation coefficient was 0.98 at a level that was statistically significant (p < 0.0001). Table 2 presents the results from the ICC analysis. The two volumetric methods achieved excellent agreement, with an ICC of 0.98 and no statistically significant difference (p = 0.42). The statistical power in the study was evaluated by using the posthoc power analysis based on the Walter-Eliasziw-Donner model [17]. The lowest ICC between the computer-based volumetry and the manual volumetry that we should have been able to detect with the 23 cases was 0.95, and this study had the power to detect a bias of 0.03 in the ICC. The Bland-Altman plot for assessing agreement is also presented in Figure 3. Here, the mean difference was −13.2cm³. The limits of agreement with the 95% CI were −163.3 to 136.9 cm³, which were small enough to show a good agreement between the two volumetric methods.

TABLE 1.

Comparison Between Computer-Based Volumetry and Reference-Standard Manual Volumetry

Volume	Average	SD
Computer (cm3)	1697	400
Manual (cm3)	1710	401

Fig. 2.

Relationship between computer-based volumes and reference-standard manual volumes. Two volumetric methods reached excellent agreement (intraclass correlation coefficient, 0.98).

TABLE 2.

Analysis of Variance Table From Intraclass Correlation Coefficient Analysis

Comparison	Degrees of Freedom	Sum of Squares	Mean Squares	F Statistic Value
Between raters	1	2008	2008	0.69
Between cases	22	6,999,296	318,150	108.5
Within cases	23	66,496	2891
Residual	22	64,488	2931
Total	45	7,065,792

Fig. 3.

Bland-Altman plot for agreement between computer and manual volumetry. Bias was −13.2 cm³; 95% limits of agreement were −163.3 and 136.9 cm³.

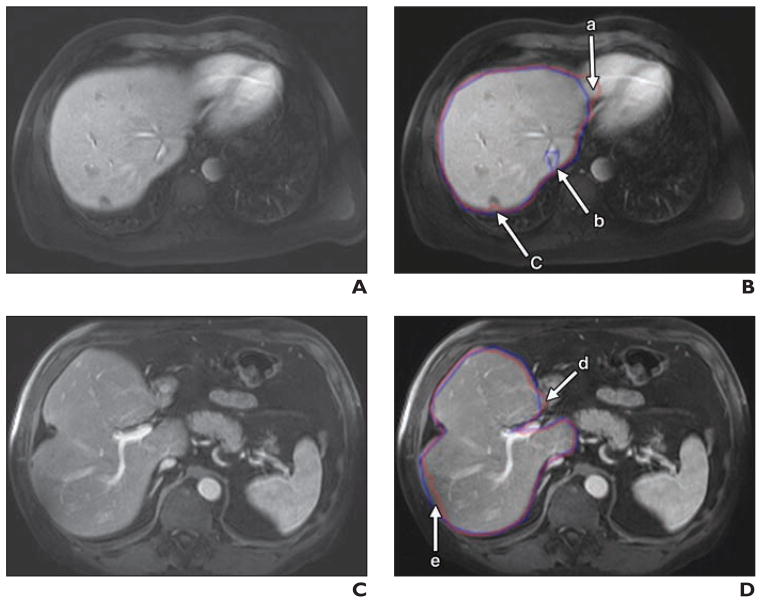
Figure 4 illustrates the computerized liver segmentation and manual liver segmentation for a case with a high accuracy (99.7%). The computerized segmentation agreed almost perfectly with the reference-standard manual segmentation for slices through the superior portion of the liver (Figs. 4B and 4D). Two other cases with more typical results, which had accuracies close to the average accuracy, are presented in Figure 5. Overall, the computerized method was able to segment the livers very accurately. However, occasionally there was over- and undersegmentation in the segmented livers. Major FP and FN segmentation sources are illustrated in Figure 6. The major FN sources included a lesion attached to the liver boundaries, low-contrast liver boundaries, and inhomogeneous density due to focal fat and noise. The major FP sources included the heart, kidney, vena cava, and stomach, which abut the liver. They also were from artifact due to the partial volume effects. Other under- and oversegmentation sources were convex and concave boundary parts with high curvatures.

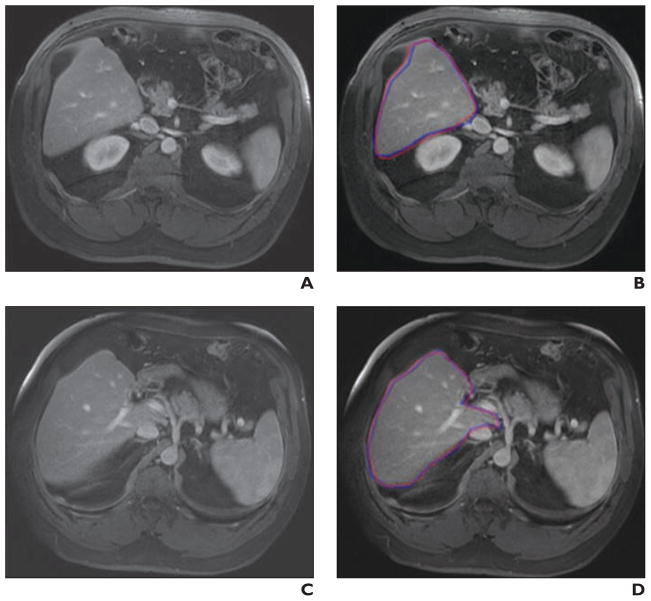
Fig. 4. 54-year-old man with liver cancer. Comparisons are shown of computer-based liver segmentation with reference-standard manual liver segmentation for case with high accuracy (99.7%).

A, Original axial MRI from case.

B, Computer-based liver segmentation (red contour) and reference-standard manual liver segmentation (blue contour) are shown.

C, Original axial MRI (different slice) from same case.

D, Computer-based liver segmentation (red contour) and reference-standard manual liver segmentation (blue contour) are shown.

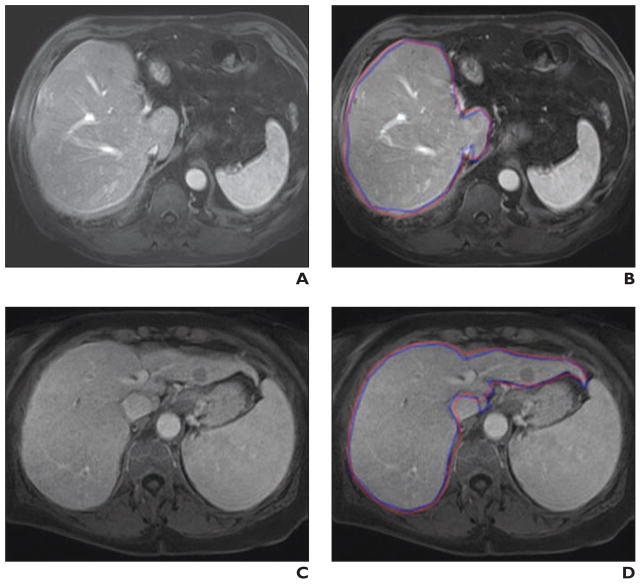
Fig. 5. Comparisons of computer-based liver segmentation with reference-standard manual liver segmentation for two cases with accuracies (99.5% for first case; 99.2% for second case) close to average accuracy (99.4%).

A and B, 68-year-old man with liver cancer. Shown are original axial MRI (A) and corresponding image (B) showing computer-based liver segmentation (red contour, B) and reference-standard manual liver segmentation (blue contour, B).

C and D, 70-year-old woman with liver cancer. Shown are original axial MRI (C) and corresponding image (D) showing computer-based liver segmentation (red contour, D) and reference-standard manual liver segmentation (blue contour, D).

Fig. 6. Illustrations of major false-positive (FP) and false-negative (FN) sources.

A and B, 54-year-old man with liver cancer. Shown are original axial MRI scan (A) and corresponding image (B) showing computer-based liver segmentation (red contour, B) and reference-standard manual liver segmentation (blue contour, B). In panel B, there is FP due to heart (a), FN due to vein (b), and FN due to lesion on liver boundary (c).

C and D, 68-year-old man with liver cancer. Shown are original axial MRI scan (C) and corresponding image (D) showing computer-based liver segmentation (red contour, D) and reference-standard manual liver segmentation (blue contour, D). In panel D, there is FP due to duodenum (d) and FN due to low-intensity region (e).

The average processing time of our scheme for liver segmentation was 1.03 ± 0.13 minutes per case (range, 0.9–1.5 min/case) on a PC (CPU: Intel, Xeon, 2.66 GHz), whereas that for the manual method was 24.0 ± 4.4 minutes per case (range, 18–30 min/case). The difference was statistically significant (p < 0.001).

Discussion

Liver volumetry is performed for hepatectomy to treat patients with liver tumors. Because the liver volume is reduced after hepatectomy, it must be ensured that the remaining liver volume is sufficient to maintain the liver function. A minimum of 40% of the standard liver mass is required by the recipient, whereas 30–40% of the original volume must remain for the donor to survive [19]. In the case of complicated treatment, such as that for chronic liver disease, a larger remaining liver volume is required [20]. Many researchers have tried to estimate the liver volume accurately on the basis of CT images, such as by use of virtual hepatectomy [21]. However, fewer researchers have reported liver volumetry on MRI, probably because it is thought that MRI liver volumetry has more variations and that manual liver volumetry with MRI is more difficult than with CT. Furthermore, manual liver volumetry is very time consuming and not cost effective. Therefore, it is crucial to investigate the potential of a computerized volumetry for liver MRI. We think that computerized MRI liver volumetry has the potential to be very useful.

Although our computerized liver volumetry had excellent agreement with the reference-standard manual liver volumetry (ICC, 0.98), there were still occasional FNs and FPs that were mainly caused by the similar density of other organs abutting the liver. The liver segmentation accuracy was also interfered with by the partial volume effects and the liver intensity variation among different studies and patients, because the intensity depends on acquisition timing and on the characteristics of the contrast material.

Although the volumes obtained by using our computerized method had a strong correlation to those by the reference-standard manual tracing method (Pearson product-moment correlation coefficient, 0.98), it still does not reach the minimal variation obtained in CT volumetry between expert radiologists, which was reported as 0.997 [22]. (Although we could not find a study reporting the variation for MRI volumetry, we expect that it would be larger than that for CT.) One can increase the overall accuracy by correcting FP and FN segmentations manually. This can be accomplished rapidly with routine manipulations. The substantial amount of time saved by using the computerized method may justify the small error rate (average percentage volume error, 3.6%) compared with the manual tracing method, for which the average processing time was 24 minutes per case.

Direct comparisons of our method with existing methods in literature are not easy because different databases and quality measurements were used. Nakayama et al. [6] obtained a correlation coefficient between their method and the manual tracing method of 0.883 for CT liver volumetry. Freiman et al. [23] achieved volume errors of 5.36% and 2.36% for CT volumetry of their database and a publicly available database (SLIVER07), respectively. Florin et al. [24] obtained a volume error of 10.72% in CT volumetry. For evaluation of liver MRI segmentation, Gloger et al. [13] obtained volume errors of 8.3% for normal livers and 11.8% for fatty livers, with run times of 11.2 and 15.4 minutes, respectively. Besides volume errors, some researchers used the shape alignment measurement to evaluate the segmentation performance. A robust measurement based on the shape alignment is the modified Hausdorff distance, which overcomes the noise and outlier sensitivity of the original Hausdorff distance. The modified Hausdorff distance (MHD) is defined by the following equations:

$$\mathit{MHD}=max\{d_H(X,Y),d_H(Y,X)\},$$ (5)

$$d_H(X,Y)=\frac{1}{\mathit{card}(X)}\sum _{\mathbf{x}\in X}\underset{\mathbf{y}\in Y}{min}\Vert \mathbf{x}-\mathbf{y}\Vert ,$$ (6)

where X and Y are two sets of boundary positions of the liver segmented by a manual method and a computerized method, respectively. Our scheme achieved an average modified Hausdorff distance of 12.8 ± 2.24 mm for livers with diseases, whereas the average original Hausdorff distance reported by Gloger et al. [13] was 20.35 ± 8.66 mm for fatty livers. Note that a modified Hausdorff distance was not provided by Okamoto et al. [20].

The 95% limits of agreement between our computerized volumes and the reference standard manual volumes were −163.3 and 136.9 cm³. These limits are smaller than the results reported by Nakayama et al. [6]: the limits between automated and manual volumes were −230.3 and 327.9 cm³, and those between automated and measured liver volumes were −309.3 and 412 cm³. In addition, these 95% limits of agreement were smaller than those in our previous work on CT images [7], which were −211 and 278 cm³ for agreement between the automated and manual CT volumes. Note that these comparisons were not direct comparisons because different databases were used.

There are several parameters to be adjusted in our scheme. They were determined by empirical analysis. Because the intensity on liver MRI varies significantly among patients, we used two sets of parameters: one for lower average intensity images (below 700) and one for higher average intensity images (greater than or equal to 700). Note that this strategy does not disturb automation, because the average intensity is measured automatically from images.

Different protocols and MRI scanners can result in different image sizes, which would affect the stability or robustness of our scheme. To reduce this effect, the images of different sizes were resampled so that the size of image slices became 256 × 256 pixels. Note that this strategy did not affect the precision of volume calculation, because the volume obtained by multiplying the number of voxels by the voxel size was unchanged.

One of the limitations of this study was that the evaluation was performed with the reference-standard manual volumes determined by a single expert radiologist. Ideally, the reference-standard volumes are determined by multiple radiologists who are experts in liver diagnosis. However, such an ideal evaluation would not be available at all institutions because not many institutions have a number of such radiologists who are sufficiently experienced in liver diagnosis. Many publications reported the evaluation based on the reference-standard manual volumes; however, none of them used reference-standard volumes estimated by multiple radiologists, probably for the aforementioned reason. Furthermore, it was shown that the correlation between two manual volumes by radiologists was 0.997 [22], which may imply that the interobserver variation is small and that the differences among manual volumes determined by multiple radiologists and those by a single radiologist are not significant. We used the manual volumes determined by an experienced radiologist as the reference standard. We thought that the manual volumes obtained by multiple inexperienced radiologists or a mixture of inexperienced radiologists and experienced radiologists may be less reliable, compared with volumes determined by an experienced radiologist who traces liver boundaries very carefully.

Another limitation of this study is the relatively small number of cases. We evaluated our scheme on 23 cases, whereas other studies evaluated four cases [4], eight cases [12], 30 cases (20 normal cases and 10 fatty liver cases) [13], 27 cases (18 normal cases and nine abnormal cases) [11], 20 cases [25], nine cases [26], 10 cases [3], and 15 cases [8]. In general, a small number of cases limits the variations among cases. In the future, we will need to increase the number of cases used for evaluation.

In conclusion, the increasing use of liver MRI as a single examination for liver resection and transplantation leads to imperative demands for investigative research in automatic MRI liver volumetry. However, few studies have been reported for this challenging task. In this study, we developed an automatic scheme for liver volumetry on MRI by using the fast-marching algorithm combined with geodesic active contour segmentation. MRI liver volumes obtained by our scheme agreed excellently with those determined by the current reference-standard manual tracing method. With our computerized volumetry, the time required for volumetry was reduced significantly from 24 minutes to 1 minute per case. Therefore, our computerized scheme would be useful for radiologists in liver volumetric analysis on MRI.

APPENDIX 1: Computerized Measurement Scheme for MRI Liver Volumes

The computerized measurement scheme for MRI liver volumes is shown in Figure 7. First, a 3D MRI volume, I(x,y,z), must be processed to reduce noise and enhance liver structures by using an anisotropic diffusion algorithm, which is based on the modified curvature diffusion equation given by the following:

$$\frac{\partial I}{\partial t}=\mid \nabla I\mid \nabla ·c(\mid \nabla I\mid )\frac{\nabla I}{\nabla I},$$ (7)

where c(·) is the diffusion coefficient controlling the sensitivity of edge contrast. This algorithm smoothes noise in the image while preserving the major liver structures, such as major vessels and the liver boundaries. The noise-reduced image was then passed through a Gaussian gradient magnitude filter to enhance the boundaries. The final step in this preprocessing stage was to produce the edge potential image from the gradient magnitude image by using a sigmoid function defined by the following equation:

$$f(x)=\frac{1}{1+e^{-(x-\beta )/\mathrm{\alpha }}},$$ (8)

where x is an intensity in the gradient magnitude image, and α and β are parameters specifying the range and center, respectively, of the intensity to be enhanced. They were set to −2.5 and 8.0 in our scheme. The normalized output image of the sigmoid gray-scale converter was used as a speed function for the level-set segmentation and fast-marching algorithms.

Fig. 7.

Overview of our computerized MRI liver volumetry scheme.

In the next stage, the shape of the liver was estimated roughly by using a fast-marching algorithm. This algorithm was initially proposed as a fast numerical solution of the eikonal equation, represented as follows:

$$\mid \nabla T\mid F=1,$$ (9)

where F is a speed function and T is an arrival time function. The algorithm requires 5–8 initial seed points. From the initial location (T = 0), the algorithm propagates the information in one way from smaller values of T to larger values based on the first-order scheme. This algorithm consists of two main processes. First, all grid points generated from the entire region were divided into three categories: seed points corresponding to the initial location were categorized as Known; the neighbors of Known points were categorized into Trial with the computed arrival time; and all other points were categorized into Far that the arrival time was set to infinity. An iterative process served points in the Trial and Far list. The Trial point p with the smallest T value was chosen and moved to the Known. The arrival time of neighbors of p was recomputed on the basis of the first-order scheme, and the Far points that are neighbors of p were moved to the Trial. This iterative process was terminated when the maximum number of iterations was reached. The salient point of this algorithm is to use a heap data structure that can rapidly locate points with the smallest T value. The output of the fast-marching algorithm is a time-crossing map indicating the time traveling to each point. It forms a rough shape of the liver on MRI.

A 3D geodesic active contour algorithm [14] was used to refine the initial surface determined by the time-crossing map to determine the liver boundaries more precisely. This algorithm is based on the relation between active contours and the computation of geodesic or minimal distance curves, which allows stable boundary detection with large variations of gradients, including gaps. Let ψ(p, t) be a level-set function with the initial surface corresponding to ψ(p, t = 0). This level-set function is then evolved to fit the form of the liver following the partial differential equation:

$$\frac{d\psi }{dt}=\mathrm{\alpha }\mathbf{A}(\mathbf{p})·\nabla \psi -\beta F(\mathbf{p})\mid \nabla \psi \mid +\gamma Z(\mathbf{p})\kappa \mid \nabla \psi \mid ,$$ (10)

where A(·) is an advection vector function, F(·) is a propagation (or expansion) function, and Z(·) is a spatial modifier function for the mean curvature κ. The scalar constants α, β, and γ allow trading off among three terms: advection, propagation, and curvature. The algorithm requires an initial zero level set containing an initial surface that roughly approximates the liver boundaries. The initial surface was propagated with speed and direction (outward, inward) controlled by the propagation function. The spatial modifier term controls the smoothness of the surface where regions of high curvature are smoothed out. The level-set evolution was terminated when the convergence criterion or the maximum number of iterations was reached. The convergence criterion was defined in terms of the root mean squared change in the level-set function. The evolution was considered to be converged if the root mean squared change is below a predefined threshold.

APPENDIX 2: Definitions Used in Evaluation of Computerized Liver Segmentation

The definitions used in evaluation of a computerized liver segmentation compared with the reference standard manual liver segmentation are shown in Figure 8. True-positive (TP) segmentation was defined as an overlapping region (gray color) between the computerized liver segmentation (indicated by a red contour), C, and a reference standard manual segmentation (indicated by a blue contour), G (i.e., TP = G ∩ C). False-positive (FP) segmentation (red region) was defined by FP = C − TP. False-negative (FN) segmentation (blue region) was defined by FN = G − TP. Finally, true-negative (TN) segmentation was defined by TN = I − G ∪ C, where I is the entire image.

Fig. 8.

67-year-old man with liver cancer. Image illustrates definitions of true-positive (TP) (gray region), false-positive (FP) (red region), and false-negative (FN) segmentation (blue region) in evaluation of computerized liver segmentation (red contour) compared with reference-standard manual segmentation (blue contour).