Network Ecology and Adolescent Social Structure

Abstract

Adolescent societies—whether arising from weak, short-term classroom friendships or from close, long-term friendships—exhibit various levels of network clustering, segregation, and hierarchy. Some are rank-ordered caste systems and others are flat, cliquish worlds. Explaining the source of such structural variation remains a challenge, however, because global network features are generally treated as the agglomeration of micro-level tie-formation mechanisms, namely balance, homophily, and dominance. How do the same micro-mechanisms generate significant variation in global network structures? To answer this question we propose and test a network ecological theory that specifies the ways features of organizational environments moderate the expression of tie-formation processes, thereby generating variability in global network structures across settings. We develop this argument using longitudinal friendship data on schools (Add Health study) and classrooms (Classroom Engagement study), and by extending exponential random graph models to the study of multiple societies over time.

Studies of tie formation in social networks point to the salience and seeming ubiquity of several generative micro-level mechanisms: homophily, balance, and status (Gould 2002; Heider 1946; McPherson, Smith-Lovin, and Cook 2001). The story differs, however, when we focus our analytic lens on the structure of the entire network. The image of similarity in micro-mechanisms gives way to one of significant variation in global-level network features like graph segregation, clustering, and hierarchy. This difference points to the central question of this article: how can the same generative micro-mechanisms lead to significant variation in global-level network structures? We answer this question with a theory of network ecology that specifies how elements of the social context combine to moderate the expression of relational preferences and thereby generate different global network structures.

An ecological approach to social networks examines how features of the social environment shape network structures by affecting the nature of interactions and relationships, and how those relations, in turn, affect the social environment. In general, ecological theories in the social sciences are the primary alternative to individualist and emergentist accounts (Abbott 2005; McPherson 1983). Rather than pit individual and contextual explanations against each other, ecological work articulates how they operate through one another (Blau 1960). Ecological approaches in social psychology, for example, examine how emotion, cognition, and action are shaped by the social environment (Oishi and Graham 2010). Much of this work draws directly on behavioral ecology, which attempts to understand how variation in features of natural habitats leads to divergent behaviors and interactions among different populations. Notably, behavioral ecology is increasingly drawing on network analysis to answer its core questions (Krause, Croft, and James 2007). Among social network scholars, however, the role of the ecological setting in shaping interactional patterns has not been the subject of systematic formalization (Pattison and Robins 2002). Instead, tie-formation processes are treated as largely context invariant and endogenous to the network.

In the first part of this article, we lay out the core components of our theory of network ecology using the specific case of adolescent friendship networks in high schools and their classrooms. We then empirically identify social mechanisms consistently associated with adolescent friendship formation across both classroom and school contexts and assess whether their significance differs across settings and through time. We then demonstrate the presence of significant variation in global-level features of these same networks in terms of graph segregation, clustering, and hierarchy. Finally, we examine the ecological features that moderate the relationship between tie-formation processes and network structures.

SCHOOLS, CLASSROOMS, AND A THEORY OF NETWORK ECOLOGY

Several common, if somewhat contradictory, images persist of social life in typical U.S. middle and high schools. Adolescent networks are often seen as highly segregated by race and ethnicity (Hallinan 1982; Moody 2001), social class (Eckert 1989), and, among middle school students, gender (Cotterell 2007). They are also thought to frequently display hierarchies, with vertical differentiation between high- and low-status individuals and groups (Coleman 1961; Gordon 1957). Finally, adolescent societies are typically described as highly clustered into largely non-overlapping classes, castes, or cliques of close friends (Giordano 1995; McFarland 2001). While we can imagine fully segregated, hierarchical, or clustered networks, such ideal forms are never found in empirical reality (Martin 2009).

How can we explain global variation if networks are generated by the same tie-formation mechanisms? Non-ecological network approaches have difficulty answering this question because they treat global network features as the agglomeration of individual-level tie preferences and the network itself as the most important social context. The implication is that particular micro-mechanisms are natural and should generate the same macro-structure regardless of context (e.g., Barabási and Albert 1999; Simmel 1950). Here network theory reflects a logic similar to evolutionary psychology, concentrating on species-wide and trans-situational social drives. As we will show, however, there is nothing inevitable about the expression of tie-formation preferences, even when, as with adolescents, they seem to have a central developmental tendency (Cairns et al. 1995; Gest et al. 2007).

To account for this variability, we need to augment our standard evolutionary view of network formation processes with an ecological perspective that explains how the expressions of trans-situational relational drives are differentially shaped by features of the proximal social environment. In doing so, we transpose one of the central issues of behavioral ecology to the social field in a novel way, namely how differences in habitat lead to structural variation in the networks of different populations of the same species (Krause et al. 2007). Answering this question requires that we identify contextually ubiquitous mechanisms of tie formation as well as features of the proximal social habitat that moderate their expression. In terms of the first category, we focus on the relational drives for familiarity (homophily), conformity (clustering), and distinction and status (hierarchy). There may be ambivalence between these drives, however, either because of limited emotional energy and resources or because they may contradict each other in particular contexts (Gould 2002). The particular (shifting) balance struck across them will vary depending on the confluence of contextual factors within particular social environments, leading to variation in global-level network structures.

Relationships and interactions often shape the social environment through a feedback process, but the process here differs from natural ecology in two ways.¹ First, animals are distinct from their natural habitat, whereas humans create and continually reproduce their social and cultural ecology. The continued existence of the social environment is thus itself evidence of an ongoing feedback process. Second, when we do see change in the institutional or demographic environment, it is not because the social habitat is directly responding to human action, but because people have changed their own behavior or social action has been mobilized to change institutional structures, practices, or rules.² We would thus expect this type of feedback, in the form of institutional, relational, or demographic change, to happen over longer periods of time than the scope covered in this article.

In recent years, research and theory has increasingly emphasized not only the psychological but also the ecological contexts within which adolescent development occurs (Steinberg and Morris 2001). A theory of network ecology applied to schools and classrooms needs to incorporate adolescents’ developmentally driven relational practices, as well as the systematically varying elements of the context that differentially shape how those relational practices are expressed. While our broad interest is in developing a framework for studying how institutional ecologies moderate ubiquitous tie-formation processes across settings, in the following sections we also discuss how such processes interact specifically with adolescence as a unique developmental period.

Tie-Formation Mechanisms

We can usefully characterize adolescent networks based on their global-level features of clustering, hierarchy, and segregation.³ Current research attempts to explain these network structures in terms of particular micro-mechanisms (Mouw and Entwisle 2006; Wimmer and Lewis 2010).⁴ Unlike the current study, however, this work lacks a theory of network ecology and as such cannot explain variation across settings. As the first step in elaborating such a theory, we discuss three tie-formation mechanisms seen as ubiquitous in studies of network generation and in the literature on adolescent relationships: balance, dominance, and homophily.

Adolescents, like all humans, seek security and solidarity in their social relationships (Coleman 1961; Homans 1950). During adolescence, primary attachments shift from parents and family to peers, with schools serving as an important context for this change (Allen and Land 1999). In comparison to childhood, dyadic relations become more intimate and supportive and cliquing increases during adolescence (Cotterell 2007; Erwin 1998). At the dyadic level there is increased pressure toward mutuality in relations and the tendency to reciprocate interactions over time (Gouldner 1960). At the triadic level, balance leads to closure, which is the pressure for friends of friends to also become friends and for enemies of friends to stay enemies (Cartwright and Harary 1956).

Social status, in contrast, is built by pursuing control and dominance over interactional partners (Gould 2002; Ridgeway and Diekema 1989). The key to hierarchical relations is comparability on some feature that makes ranking possible. For adolescents, this occurs globally and along distinct dimensions like appearance, academics, and moral conduct (Masten et al. 1995). Some work also suggests that for developmental reasons, adolescents are more concerned with their positioning in social hierarchy than are children or adults (Eder 1985; LaFontana and Cillessen 2010), particularly as the importance of peers eclipses parents in adolescents’ self-image (Adler and Adler 2003). In response, adolescents secure status by employing interactional strategies such as gossip and teasing (Eder and Enke 1991) or by adopting adult-like behaviors (Moody et al. 2011).

Homophily, or assortative mixing, is the preference for forming relationships with individuals who share similar attributes, behaviors, or attitudes (Goodreau, Kitts, and Morris 2009). The fulfillment of this preference results in individuals disproportionally interacting with similar alters. While some work suggests that homophily is partly the result of structural segregation (Blau 1977; Feld 1981), assortative mixing also occurs because of attraction to similar others (Byrne 1971), ease of communication (Rogers and Bhowmik 1970), and reduction in interactional uncertainty (Prisbell and Andersen 1980). For close friendships among adolescents, the salient features for homophily are typically age, race, socioeconomic background, and gender (Smetana, Campione-Barr, and Metzger 2006).⁵

Features of School and Classroom Ecology

A long empirical tradition demonstrates the ubiquity of these three tie-formation mechanisms, but their expression varies across social contexts. The next step in laying out a network ecological theory is to identify the environmental features of schools and classrooms that previous research suggests systematically vary in ways that might shape generative network processes. From an ecological standpoint, certain features of an ecosystem will establish conditions of survival and feedback: for example, the size of the population being carried in a naturally bounded area, the different species composing it, their differentiated patterns of using the environment, and the degree to which their interactions might create a climate of stress. The schooling literature describes comparable features. For example, Crosnoe, Johnson, and Elder (2004) identify three important features of schools that vary across settings in ways that shape student outcomes and experiences: demographic composition, structure of instruction, and educational climate.⁶ We regard the population’s size as a fourth feature, because of its structural impact on network processes (Mayhew and Levinger 1976) and its importance in contemporary policy and research debates at the school (Leithwood and Jantzi 2009) and classroom levels (Wobmann and West 2006). All four of these features have been identified as central to relational processes in schools (Eccles and Roeser 2010; McNeely, Nonnemaker, and Blum 2002), but only with recent advances in network methodology can we study their moderating roles simultaneously. Table 1 summarizes our expectations for how ecological features moderate micro-mechanisms.

Table 1.

Ecological Moderators and Their Influence on Micro-Mechanisms

		Ecological Moderators
Network Outcome	Micro-Mechanism	Size Small ← → Large	Differentiation Selective ← → Elective	Composition Homog. ← → Heterog.	Climate Positive ← → Negative
Clustering	Reciprocity and social balance. Desire for security and solidarity; people prefer mutually recognized friendships and group boundaries. There is a tendency for a friend of a friend to be a friend.	Larger size creates more strangers and pressure toward security.	Electivity enables feedback and reproduction of clusters.	Heterogeneity creates insecurity and amplifies concern about trust and group boundaries.	In positive climates, trust is enhanced and issues of security are less salient.
Hierarchy	Social dominance. Desire for status compared to others; people prefer some asymmetry and rank ordering in their relations. There is tendency to form a “pecking order.”	Larger size increases uncertainty and status recognition.	Electivity affords access and status-seeking opportunities.	Heterogeneity creates status classes and bases of ranking.	In positive climates, there is generalized cohesion that flattens hierarchy.
Segregation	Choice homophily. Desire for familiarity; people prefer friends who are similar to themselves. There is a tendency for “birds of a feather to flock together.”	Larger size entails more variance and choice.	Electivity allows for greater self-selection on traits.	Heterogeneity highlights dissimilarity and encourages self-selection.	In positive climates, shared opinions eclipse selection on ascribed characteristics.

We begin with network size. Size affects both the mathematics of constraint as well as the perception of interactional possibilities (Rytina and Morgan 1982). As groups grow in size, they freedom and uncertainty (Simmel 1950). In terms of freedom, being exposed to a larger number of persons makes it simpler to fulfill homophilous preferences and match alters across multiple dimensions (Blau 1977). Uncertainty, in contrast, arises from coming into contact with numerous unknown others without possessing knowledge of whether they can be trusted. For example, prior work finds that in larger settings like high schools, youth are exposed to a wider circle of friends and acquaintances who judge peers on stereotypical grounds of status and appearance. In these settings, youth rely heavily on their close, intimate cliques for more supportive interactions that can offset and correct such negative, stereotyped judgments (Giordano 1995). Taken together, we expect the freedom and uncertainty that come from increases in network size to amplify all three of our tie-formation mechanisms.

Next, we consider the structure of instruction in terms of organizational differentiation, or how students are divided into subgroups for instruction. We distinguish here between selective and elective modes of differentiation (Sørensen 1970). When differentiation is selective, sorting of students is involuntary and engineered by the school, as when tracking divides students by age and ability. When differentiation is elective, assignment to groups is driven by adolescent preferences through the availability of extracurricular and elective coursework. Most work on selective and elective differentiation is limited to the school level (Oakes, Gamoran, and Page 1992), but we extend this distinction to the classroom in terms of the extent to which interaction is centralized and controlled by the teacher (selective) or open and decentralized among students (elective), and whether seating is assigned (selective) by the teacher or chosen (elective) by the students (Doyle 2006; Stodolsky 1988).

At both the school and classroom levels, selectivity will sort students on organizationally selected grounds (e.g., achievement levels), electivity will allow students the opportunity to sort themselves according to external identities (e.g., shared attributes [Sorenson 1970]). Both lead to network segregation, but through different mechanisms—electivity through student self-selection and selectivity through the correspondence of attributes with tracks (Oakes et al. 1992). We expect the opportunity to choose partners and repeatedly interact with them will increase reciprocity and closure. By allowing for greater access and status-seeking opportunities, we also expect electivity to encourage status contests and more developed hierarchal arrangements (Milner 1994).

A third important feature of network ecology is demographic composition. First, compositional heterogeneity of potential partners moderates tie-formation mechanisms, because the quantity of a particular attribute in the population is important for both interactional opportunity and salience. In terms of opportunity, a group’s relative size influences individuals’ ability to satisfy their preference for homophily (Blau 1977). Similarly, while the distribution of many such categories is exogenous, the social salience of any particular category is likely related to its distribution in the network (Frank et al. 2008). The more universally an attribute is shared, the less likely it will become an important basis of sorting. For both these reasons, we expect that as network composition becomes more heterogeneous, we will see more segregation at the network level.

We also expect compositional heterogeneity to create an uncertain context that amplifies concerns for trust and group boundaries (Stolle et al. 2007). For this reason, we expect greater heterogeneity to be associated with interpersonal solidarity formed via greater mutuality and clustering. Network composition also moderates the concern for hierarchy and advantageous social positioning (Blau 1977). As a population loses variance on a status characteristic (e.g., race), there are fewer categorical bases for ranking and clustering. We thus expect to see more hierarchy as heterogeneity—and perceptions of dissimilarity—increase.

The final ecological feature we examine is schools’ educational climate (Crosnoe, Johnson, and Elder 2004).⁷ Previous work demonstrates that prevailing or average adolescent attitudes and behaviors form a comparative context that shapes what students perceive and experience as normative. This educational climate includes average parental education (Crosnoe, Mistry, and Elder 2002), average alcohol use (Crosnoe, Muller, and Frank 2004), average body mass index, and average romantic activity (Crosnoe and Muller 2004). In this article, we focus on schools’ and classrooms’ educational climates in terms of average levels of academic orientation and school attachment (Johnson, Crosnoe, and Elder 2001).

High average levels of academic achievement and school attachment render school identity a point of focus (in contrast to more informal, exogenously based identities), which then heightens the salience of the school’s boundary and renders it a less permeable membrane with the external environment. As such, attention is directed more inward than usual (Coleman 1994); institutional bases of association are considered more legitimate; and exogenous, informal bases of association become less relevant. When students are academically oriented or attached to the school, they share interests and a collective identity that renders them more familiar, equal, and secure with one another. Conversely, when the student identity is poorly received, youth find other informal bases of association more relevant.

These four ecological factors of population size, differentiation, composition, and climate, all interrelate to amplify or impede general mechanisms of network formation. Clearly, reality entails complex ecologies that are different combinations of these environmental factors, but for the sake of explication, we can identify and discuss two ideal-type network ecologies located on the ends of a spectrum between external identity inclusion and external identity exclusion. External identity inclusion arises in open settings where there are few constraints on interaction. In these settings, external identities and informal inclinations of interpersonal association are amplified. Such contexts have little formal organization coupled with high levels of uncertainty, heterogeneity, and choice—for example, large, detracked, heterogeneous schools with many electives. In such an ideal-type setting, we would expect the large size and elective coursework to offer many more contacts to choose from and less monitoring of group norms; the detracking to prevent most pre-selection of persons into settings; and the heterogeneity to afford youth more variety. In these uncertain conditions of broad choice and opportunity, the salience of all tie-formation mechanisms is amplified so as to create segregated and hierarchically clustered networks of relations. An adolescent society emerges that is highly differentiated into rank-ordered social crowds (Milner 2004).

Under the opposite ideal-type condition of external identity exclusion, the system is closed and constrained; the usual tie-formation mechanisms are thus inhibited and prescribed modes of association endogenous to the organization become more relevant (e.g., achievement). In effect, closed and socially controlled contexts bind actors to the metaphorical “mast” (like Ulysses), establishing greater relevance for formal organizational designs. We see this level of certainty when formal organization and minimal heterogeneity dominate, as observed in small, tracked, homogeneous contexts. In such settings, we expect the small size to force contacts, tracking to pre-select persons into settings, and homogeneity of the population to diminish choice. In these environments, the bases of relation formation are defined by the organization, so the usual mechanisms of informal relational definition are dampened. In such conditions, we would expect to see a dense, undifferentiated network with a (perhaps weak) core-periphery structure. While discussion of these two ideal types helps us understand theoretically how tie-formation processes hang together differently depending on the context, we now turn to a series of empirical cases to more fully illuminate our ecological model using real world networks.

RESEARCH DESIGN AND DATA

Our basic research design involves first identifying the micro-mechanisms generating network structure using the exponential random graph model (ERGM) framework; we then examine variability in the model coefficients by setting, using a multilevel framework to identify ecological moderation (for similar approaches, see Lubbers and Snijders 2007; Snijders, van de Bunt, and Steglich 2010; Zijlstra, van Duijn, and Snijders 2006). We collected our data from two larger projects that include friendship networks in classrooms or schools and contain information on friendship selection and change over a single school year. We believe the comparison of classroom and school networks is important because it highlights distinct ranges of ecological factors that have different effects on relational mechanisms.

Classroom Friendship Network Data

For the data on classroom friendships, we use a sample previously collected and made public by McFarland (2001). To the best of our knowledge, it is the single largest dataset for longitudinal networks within high school classrooms (including interaction networks). This dataset affords cross-sectional, first-semester information on 35 classes, 566 persons, and 2,628 ties, as well as longitudinal information on 25 classes, 391 students, and 2,598 semester-two ties. The classrooms selected for study vary on several dimensions: they are composed of either 10th- or 12th-grade students, concern various core subjects (i.e., English, math, history, and science), and span tracks specific to each school.

The two schools are quite distinct. One school is a traditional, tracked high school (grades 9 through 12) of around 1,600 students located in a small Midwestern town. Almost all residents are white; racial minorities comprise only 3 percent of the population. The second school is a magnet high school of around 900 students (grades 8 through 12) located in a distressed neighborhood of a large city. The school’s student body is racially and economically heterogeneous, but the population is admitted via test scores, so it is homogeneous in achievement.

We use several data sources, including classroom surveys, observations, and school records. The focus here is on friendships, so the key variables are drawn from two waves of classroom-specific sociometric surveys (95 percent response rate) asking students to nominate classmates that they “hung around” with as friends. This classroom survey was administered in late November and again in late April, affording some notion of network change.

Each classroom was also observed an average of 12 class days. During these visits, an observer recorded the use of different activities (Stodolsky 1988), seating assignments, and enumerated the exchanges among classroom participants. Exchanges were recorded as student-initiated interaction turns directed toward someone else. We supplement this sociometric and observational information with school records from transcripts and yearbooks to code students’ course grades, current grade-level, and race and gender demographic information.

Whole-School Friendship Network Data

To study friendships that move beyond a particular classroom and span an entire school, we use the National Longitudinal Study of Adolescent Health (Add Health), a nationally representative study of youth in grades 7 through 12 (Bearman, Jones, and Udry 1997; Crosnoe et al. 2004). Add Health’s social network information was initially collected in the 1994 to 1995 school year by a school-based survey administered to all students in attendance at 144 middle and high schools, amounting to 90,118 respondents. The survey covers a wide-ranging number of topics and includes a series of items asking respondents to list up to five of their closest male and female friends (i.e., up to ten friends total). For a subset of these schools, respondents were interviewed repeatedly, making it possible to measure social network change. Information was also collected about students’ academic careers and attitudes, as well as characteristics of the entire school, including size, composition, and organizational structure.

In cross-sectional models, we follow prior Add Health studies (Haas, Schaefer, and Kornienko 2010) and use schools with a friendship survey response rate greater than 50 percent. This reduces the dataset to 129 schools, 75,122 students, and 311,216 semester-one ties. In longitudinal models, we use saturated schools that were repeatedly surveyed and allowed for 10 friendship nominations.⁸ This reduces the dataset to nine schools, 2,225 students, and 4,683 semester-two ties.

Dependent Variable

Our primary concern rests with modeling adolescent friendship networks. For the classroom study, tie selection is bounded by the classroom setting and this narrower choice range often entails weak friendships. For the school study, tie selection is bounded by the school setting and this broader choice range enables youth to choose closer ties.⁹ While network boundaries and the strength of ties differ across samples, the unit of time and modeling of longitudinal effects are the same. Our longitudinal models lag prior friendship choices and use them as predictors of current nominations (see also Robins and Pattison 2001).

Network Mechanisms

The network mechanisms mirror our hypothesized tie-formation processes (reciprocity and closure, hierarchy, and homophily) as well as propinquity (see Table A1 in the Appendix). First, dyad mutuality and triadic closure represent tendencies to form clustered, symmetrically connected networks. The mutuality measure captures the number of dyads where there is a tie from i to j and j to i. Next, clustering is the endogenous network tendency toward triadic closure. This measure captures the extent to which a friend of a friend is a friend. In directed networks such as these, transitivity is traditionally measured as the proportion of two-step paths (a→b, b→c) that are also one-step paths (a→c). In tight closed-network settings, such as complete cliques, every possible triple will be transitive.

While useful for some purposes, recent network modeling suggests that a simple transitivity parameter often leads to “degenerate” models that imply incorrect model specification. These degenerate model specifications stem, in part, from the cascading tendencies implied by the transitivity term (closing one triad will often open another triad involving adjacent nodes in an infinite regress [Handcock 2003]). To counter this effect, network statisticians recommend using the GWESP, or “geometrically weighted edgewise shared partner” parameter (Hunter et al. 2008). The GWESP term adds one network statistic to the model equal to the (geometrically weighted) edgewise shared partner distribution. This term captures the distribution for the number of times each connected pair shares ties with a common third. Compared to the (more intuitive) transitivity term, this specification implies a decreasing marginal return to each additional shared partner that would create a transitive triad. Together, processes of reciprocity and local closure reveal a complementary tendency of forging horizontally differentiated clusters in networks.

We also construct a term to capture processes that lead to hierarchical (vertical) differentiation based on triad patterns. In the simplest sense, a hierarchy exists when pairs of nodes similarly nominate third parties “up” the hierarchy. This implies an over-representation of “up” pointing triads; building on prior research, we can summarize this distribution with a tau statistic. The tau statistic weights triad types and counts their occurrence compared to a specified random network (Wasserman and Faust 1994). Because our interest is in hierarchy, we regard 021D: , 021U: , 030T: , 120D: , and 120U: as the most relevant triadic configurations, which we build into the “hierarchical triad tau score.”¹⁰ This choice is built from the ranked-clustering weighting scheme (Davis and Leinhardt 1972).¹¹ For 021D, person A thinks persons B and C are both high status (i.e., are worth a friendship nomination), and B and C agree that person A is not high status, and so forth. By contrast, we regard 021C: as an antithetical case, because the lack of a nomination from the first to the third creates a potential inconsistency in the status ordering, so it receives a negative weight.¹² The common occurrence (greater than random) of these types of directed triads (and lack of 021C) suggests a tendency toward hierarchy in the overall network.¹³ Therefore, in the ERGM model, our network statistic parameter for hierarchy is the tau statistic based on a rank-cluster distribution of triads.¹⁴

Our third class of micro-mechanisms is homophily, which leads to potential network segregation by student characteristics. In this study we include homophily by gender, race, and grade level. We also include family socioeconomic status (SES)¹⁵ and student academic grades. We treat gender, race, and grade level categorically as same/different, but we leverage the continuous nature of SES and GPA with absolute difference scores.¹⁶

We also test whether other forms of contact are salient to tie formation. In the classroom data, we have information on interaction, or the rate of observed interaction turns between pairs per hour before each wave of sociometric survey. In the Add Health data, we use extracurricular co-affiliation (club ties), or an indicator for pairs sharing three or more clubs in common.¹⁷ Co-affiliation in clubs represents voluntary associations from which youth maintain old ties and develop new ones, often centered on a shared identity. In both instances, we believe these other forms of contact—whether direct interaction or shared affiliations—will generate more friendship nominations.

We also include control variables for individual- and network-level differences in sociability. At the individual level, we constrain all models on the number of inward and outward tie selections. All models include a baseline edges parameter to account for network density. The edges variable, along with constraining on outdegree, helps offset artificial issues arising from changes in our sociometric survey’s format.¹⁸ In the longitudinal models, we use a lagged version of the dependent variable as a predictor (prior friendships). Prior friendships are obviously associated with future friendships, but it is an empirical question as to how much inertia prior ties have when new ties are being formed.

Measures of Ecological Moderators of Tie Formation

Size is a simple measure of the number of students in a school or classroom. Selective organizational differentiation is measured at the school level by the degree of tracking (extent to which multiple tracks are present in a school) and at the classroom level by the degree to which task control rests with the teacher (prevalence of teacher-centered tasks). Elective differentiation is measured at the school level as the number of offered extracurricular clubs and at the classroom level by the presence or absence of elective seating. We measure the demographic composition of school and classroom populations in terms of race, age, and gender. Finally, as measures of education climate, we include average self-reported school attachment and GPA at the school level, and average student-reported liking of the class and honors class labeling at the classroom level. Table A1 in the Appendix provides a description of these variables and their summary statistics.

METHODS

We use a two-step procedure to identify social mechanisms and moderating features of network ecology associated with friendship tie formation across multiple classroom and school networks. We first model network formation specific to each setting. Next, we take these results (coefficients and standard errors) and assess whether they differ significantly across settings and whether contextual factors moderate tie-formation mechanisms.

Modeling Networks with Exponential Random Graph Models

We use exponential random graph models (ERGM) to model the network in each setting as a function of individual, dyadic, group, and network substructure (e.g., triads and cycles) parameters (Robins et al. 2007; Wasserman and Pattison 1996).

The ERG model formulates the conditional probability of observing a network as follows:

$$\mathrm{P}(\mathrm{Y}=\mathrm{y}|\mathrm{X})=\text{exp}[{\mathrm{\theta }}^{\mathrm{T}}\mathrm{g}(\mathrm{y},\mathrm{X})]/\mathrm{\kappa }(\mathrm{\theta })$$ (1)

This is the probability that a random network Y (of a given size) has a particular realization y conditional on the matrix of covariates X. On the right side of the equation, g(y,X) is a vector of network statistics, θ is a vector of coefficients, and κ(θ) is a normalizing constant (Wasserman and Pattison 1996). The details of this modeling framework are well specified in the recent statistical literature (for an overview of the ERG framework and software, see Handcock et al. 2008; Hunter et al. 2008).¹⁹

We use multiple specifications of recent extensions of ERGMs to nested and longitudinal data structures in a way that allows us to identify the ecological moderators of micro-network formation. We begin with a general cross-sectional ERGM:

$$\mathrm{P}(\mathrm{Y}=\mathrm{y}|\mathrm{X})={\mathrm{\beta }}_{0\mathrm{c}}({\text{Edges}}_{\text{ij}})+{\mathrm{\beta }}_{1\mathrm{c}}({\text{Mutuality}}_{\text{ij}})+{\mathrm{\beta }}_{2\mathrm{c}}({\text{Closure GWESP}}_{\text{ij}})+{\mathrm{\beta }}_{3\mathrm{c}}({\text{Tau Hierarchy}}_{\text{ij}})+{\mathrm{\beta }}_{4\mathrm{c}}({\text{Prior Contact}}_{\text{ij}})+{\mathrm{\beta }}_{5\mathrm{c}}({\text{Same Age}}_{\text{ij}})+{\mathrm{\beta }}_{6\mathrm{c}}({\text{Same Gender}}_{\text{ij}})+{\mathrm{\beta }}_{7\mathrm{c}}({\text{Same Race}}_{\text{ij}})+{\mathrm{\beta }}_{8\mathrm{c}}({\text{GPA Difference}}_{\text{ij}})+{\mathrm{\beta }}_{9\mathrm{c}}(\text{SES}{\text{Difference}}_{\text{ij}})$$

In this model, each coefficient illustrates the log-odds of observing an entire network with the number of X tie configurations (e.g., mutual ties or transitive), conditional on everything else. This can practically be interpreted as the effect on the log-odds of a friendship tie between i and j. We can extend this model to be longitudinal by incorporating the preceding friendship network as a control variable.

Multiple Network Analysis via Meta-Analysis of ERGM Estimates

We next look at how the identified mechanisms vary across settings and whether certain contextual factors moderate their magnitude. Multilevel analysis assists us in weighting for measurement error and in performing meta-analysis of ERGM results (Raudenbush and Bryk 2002). In a standard multilevel model, the higher-level models can be thought of as predicting the coefficients from the lower-level models. In the implementation of meta-analysis, the first-level models have already been run (in this case, our ERGMs for each classroom and school accomplished that), and the meta-analyst has access to the estimates and standard errors for the variables in these models (because single equation methods do not exist). A simple meta-analysis of these results would predict the estimates weighted by the variance of each result (variance = 1 / [standard error × standard error]).

If we stop here, we remove measurement error in the ERGM estimates for each school and afford a better overall estimate of population effects than by simply averaging the estimates across settings. The drawback to doing this, however, is that we are likely making an incorrect assumption that the estimates behave independently of one another and have equal variance. In the case of our ERGMs, this is incorrect as the variables often have a patterned interrelation (e.g., reciprocity is correlated with triadic closure) within each setting that should be taken into account to generate the most unbiased estimates possible (for correlations, see Table A2 in the Appendix).

Multilevel modeling allows us to posit different underlying covariance structures that can remove such bias from estimates. By approaching this as a problem of repeated measures, we can take into account the fact that multiple measures are done on the same setting and thus have some interrelation that depends on the setting’s characteristics. This means the mixed procedure iteratively arrives at a covariance matrix of the estimates that best fit the sample of settings (a posteriori). In our smaller samples of classrooms and longitudinal network data, we lack the statistical power to use an unstructured covariance structure, so we revert to simpler ones that converge and best fit the data (Littell et al. 2006:379).²⁰ A key benefit of multilevel models is their ability to test cross-level interactions—the effects of group or setting characteristics on ERG estimates. This allows us to evaluate our key question: whether, and to what degree, characteristics of classrooms and schools moderate mechanisms of tie formation.

The following equations represent the basic cross-sectional model and procedure discussed. The level-1 equation consists of the ERGM models above. Multilevel meta-analyses take the level-1 coefficients as exogenously given, simply assuming Y = β + ε. At the second level, the equations are as follows:

$$\text{Level}2(\text{predicting ERGM coefficients across models}):{\mathrm{\beta }}_{1\mathrm{c}}={\mathrm{\gamma }}_{10}+{\mathrm{\mu }}_{1\mathrm{c}}\text{Level}2(\text{with a level-2 variable interaction}):{\mathrm{\beta }}_{1\mathrm{c}}={\mathrm{\gamma }}_{10}+{\mathrm{\gamma }}_{11}(\text{Class size})+{\mathrm{\mu }}_{1\mathrm{c}}$$

Here, γ₁₀ is the fixed-effect intercept that captures the effect of the level-1 variable across level-2 units (classrooms or schools); γ₁₁ is the fixed-effect interaction of the level-2 variable on the level-1 variable in question; and µ_1c is the random effect, the variance across groups. Many of the ERGM coefficients are strongly related to network size (for both technical and substantive reasons), and this can make interpreting bivariate correlations at the second level difficult.²¹ We thus emphasize the multilevel models that control for network size.

RESULTS

We next present three sets of analyses. First, we demonstrate that the tie-formation micro-mechanisms are consistent across settings. Second, we show that sufficient variability in macro-structures can be generated by change in the micro-mechanism weights to warrant an ecological model. Finally, we present models demonstrating the moderating effect of organizational features on the micro-processes of tie formation.

Micro-Mechanisms of Tie Formation

Our first set of results identifies the micro-mechanisms that generate adolescent social networks. We present effects separately for school and classroom networks, and we show cross-sectional (e.g., baseline results) and longitudinal models of friendship formation (e.g., predictions of future ties controlling for prior ties). For each, we present the null model likelihood test showing how much the model improves with the inclusion of variables and the deviance statistic for model fitness.²² We report significance levels to the p < .10 level because of the relatively small sample sizes of schools and especially classrooms.

Results for Whole-School Networks

Table 2 shows that our three endogenous network processes of interest are significant factors in network structure. We find a much-greater-than-chance effect of reciprocity (odds ratio of 29.767), indicating the networks are characterized by significantly more mutual ties than would be expected at random. The clustering term (GWESP) similarly shows that the network has a statistically significant tendency toward local clustering.²³ Finally, the triad-vector term associated with the ordered asymmetric triads suggests the networks exhibit a clear tendency toward hierarchy. Combined, these three terms suggest settings that, net of attributes or propinquity, exhibit clustered hierarchy.

Table 2.

Mechanisms of Friendship Formation across Groups: Results of Multilevel Models with Measurement Error Correction

	School Networks
	Cross Sectional			Longitudinal
	Odds	Log-Odds	t	Odds	Log-Odds	t
Edges	.001	−6.689	−128.88 ***	.001	−6.615	−12.76 ***
Mutuality	29.767	3.393	71.51 ***	21.802	3.082	8.60 ***
Closure	2.595	.954	111.07 ***	2.372	.864	15.43 ***
Hierarchy	1.131	.123	64.34 ***	1.177	.163	11.54 ***
Club Ties	1.508	.411	28.21 ***	1.664	.509	5.68 ***
Prior Year				26.552	3.279	13.12 ***
Same Race	1.647	.499	20.05 ***	3.221	1.170	6.96 ***
Same Gender	1.202	.184	25.50 ***	1.492	.400	7.38 ***
Same Age	3.425	1.231	37.16 ***	2.035	.710	7.22 ***
GPA Diff.	.813	−.207	−35.13 ***	.828	−.188	−5.56 ***
SES Diff.	.966	−.035	−19.32 ***	1.001	.001	.04 ns
Null Model Likelihood Ratio Test
χ-square			1256.9 ***			100.3 ***
Model Fit
Deviance			−1302.4			69.5
	Classroom Networks
	Cross Sectional			Longitudinal
	Odds	Log-Odds	t	Odds	Log-Odds	t
Edges	.018	−3.996	−49.21 ***	.013	−4.366	−50.03 ***
Mutuality	15.044	2.711	27.08 ***	12.290	2.509	23.20 ***
Closure	1.673	.515	15.17 ***	1.692	.526	15.57 ***
Hierarchy	1.279	.246	15.22 ***	1.285	.250	21.18 ***
Interaction	1.162	.150	11.42 ***	1.182	.167	9.93 ***
Prior Friendships				6.344	1.848	17.71 ***
Same Race	1.599	.469	13.04 ***	1.115	.109	1.56
Same Gender	1.470	.385	9.55 ***	1.130	.122	1.78 ~
Same Age	1.658	.506	7.47 ***	1.355	.304	4.42 ***
GPA Diff.	.899	−.106	−4.50 ***	.941	−.060	−2.56 *
Null Model Likelihood Ratio Test
χ-square			98.6 ***			38.7 **
Model Fit
Deviance			−81.2			6.8

Source: Add Health and McFarland Classroom Study.

Note: For Add Health data, we used unstructured covariance structure in cross-sectional models and FA(1) in longitudinal models. For McFarland data, we used the TOEPH covariance structure.

^*p < .05

^**p < .01

^***p < .001

^~for small samples p < .10.

As expected, features of the population and setting that cluster students together drive relationship formation. We find, for example, that propinquity in extracurricular clubs predicts tie formation, and that for every three clubs adolescents share, the odds of friendship increase by 50 percent. The network is similarly clustered by attributes, with ties overrepresented among same-sex, same-race, and similar-age students, and among students who are close with respect to GPA and SES.

Whereas the cross-sectional model shows baseline associations, the longitudinal model for school networks illustrates structural effects on new friendship formation over the course of the school year. Not surprisingly, past friendships strongly predict future friends in the next school year (odds ratio: 26.552). But even net of past relations, the same three micro-mechanisms are clearly active in the formation of new ties. The magnitude of mutuality diminishes in the longitudinal model, but the significance of the other endogenous network processes remains high. Similarly, effects of club membership and GPA remain basically the same.

The shift to new ties highlights the differential effects of race and SES. The effects of same-race status on new tie formation increase from 1.65 in the cross-section to 3.2 in the longitudinal models, suggesting that race homophily is a key feature in the formation of new ties (and the maintenance of old ones). Net of past ties, SES is no longer significant. These results confirm findings that cross-race ties are particularly fragile (Hallinan 1982) and suggest that SES may work largely through setting selection embedded in prior relations.

Classroom Networks

Next, we turn to classroom friendship ties and find similar results to the whole-school models described earlier. Again, the three micro-mechanisms of reciprocity, clustering, and hierarchy are all significant predictors of relationship formation in both the cross-sectional and longitudinal models. Mutual ties are 15.044 times more likely than expected by chance. Triad closure is similarly more likely than would be found at random. While both terms are significant, it is worth noting that the classroom coefficients for mutuality and closure are only half the magnitude of the corresponding school-level coefficients, suggesting that strong ties of intra-classroom friendships rely more on balance than do the weaker, more contingent ties formed in classrooms. There is a similar over-representation of hierarchical triads, net of individual popularities, suggesting students are coordinating asymmetric nominations along a hierarchical status order.

Propinquity and homophily effects are similar. For every additional interaction per hour between two students, there is a 1.162 odds increase in the likelihood of being friends. Homophily, too, has the expected associations, with same race, gender, and age students more likely to form ties among each other. Furthermore, as the level of academic achievement between two students becomes more similar, the odds of forming a friendship tie increase significantly.

Holding constant past ties and focusing on changes, the longitudinal models show the consistent effect of endogenous network mechanisms over time. The exception again is mutuality, which is associated with 12.29 greater odds of identifying a new tie. This is a strong result, but smaller than in the baseline model. The coefficients for closure, hierarchy, and interaction, in contrast, remain virtually the same. The biggest change in the longitudinal models is that homophily terms decrease in magnitude and tend toward nonsignificance across the board. Being the same race is not a significant basis for tie change, and being the same sex and having a similar GPA have only mild associations (+13 and +6 percent, respectively). Being the same age remains significant, but at a diminished level. Taken together, these results suggest classrooms are constrained contexts. Classrooms contain a limited pool of potential alters who are brought into close proximity and frequent interaction with one another. This means endogenous network processes remain important over time, but classmates frequently form relationships with whomever is present, including students who possess different attributes.

In general, results in Table 2 confirm our hypotheses concerning micro-processes of tie formation. In both schools and classrooms, in the cross-section and over time, we see local choices being driven by the micro-processes of balance, hierarchy, homophily, and propinquity.

Demonstrating Macro-Structural Variation

The preceding section’s results indicate that adolescent societies in schools and classrooms are formed through the same generative mechanisms. Nonetheless, our intuition is that these societies vary in macro-structural form. This raises the question: can small changes in the extent of closure, homophily, and status inequality really generate different macro-structural network patterns?

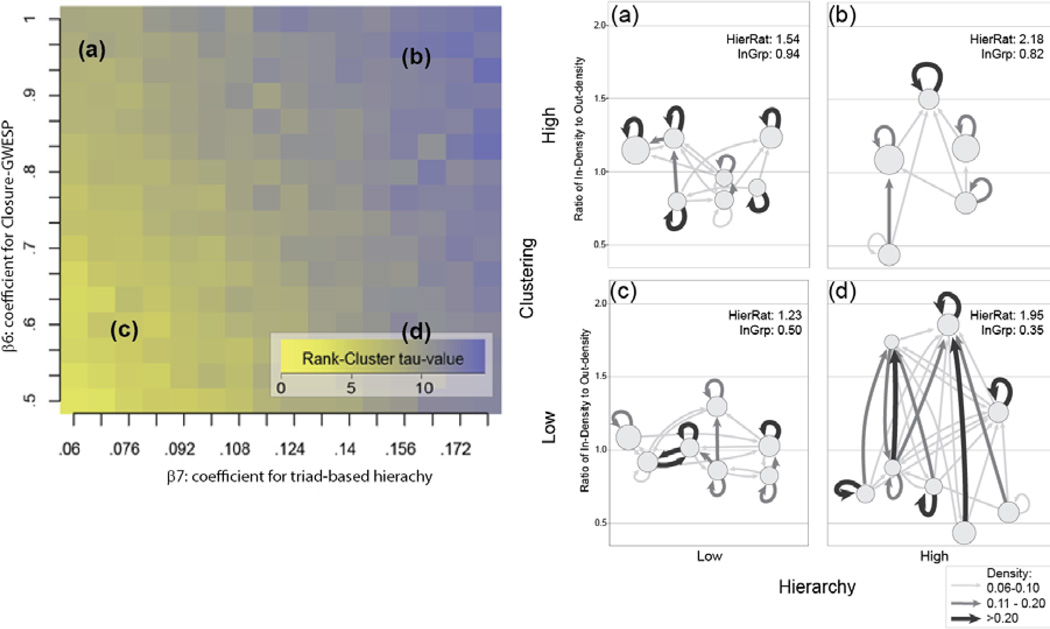
Figure 1 illustrates this potential with a model-based example. Here, we simulate networks from a simplified micro-process, encapsulated in the ERGM equation:

$$\mathrm{P}(\mathrm{Y}=\mathrm{y}|\times )=\mathrm{-}5.12+{\mathrm{\beta }}_2\times \text{Mutuality}+1.34\mathrm{x}\text{Same Age}+.32\times \text{Same Gender}+.6\times \text{Club Ties}+{\mathrm{\beta }}_6\times \text{Closure}+{\mathrm{\beta }}_7\mathrm{x}\text{Hierarchy}\mathrm{.}$$

Figure 1.

Variability in Hierarchical Macro-Structure Resulting from Variability in Micro-structural Parameters with Detailed Blockmodels from Selected Regions (based on ERGM simulations from observed parameter estimate ranges)

Note: Heat map measures the rank-cluster tau score for simulated networks from the example equation on p. 26, using coefficient values reflecting the range of our observed models. To better explain the implication of these scores, we draw four examples from the extreme regions of our space and blockmodel the resulting networks. We use a modularity maximization routine to identify the number of positions in each network, a mean density cuttoff for drawing arcs in the image network (no cuttoff used for calculating hierarchy position), and array positions vertically according to the ratio of density received over density sent. Respondents with a ratio of one have equal ties sent and received, greater than one receive more than they send, and less than one send more than they receive.

We use this equation to generate networks of size 100 while varying the coefficients on clustering and hierarchy (β₆ and β₇) and maintaining constant realized reciprocity (β₂) across the simulations within the observed Add Health school range.²⁴ We measure the change in macro-structure with a ranked-clustered tau statistic (Johnsen 1985). Because our interest in the tau at this point is merely to demonstrate variability in the links between micro and macro models, we use the rank-cluster model, which compares the observed network to a hypothesized structure of asymmetrically ordered complete cliques. Larger values of tau imply a network characterized by hierarchically arranged groups, and smaller values imply no ordered hierarchy beyond random. In short, the axes capture micro tendencies toward clustering or hierarchy, and the z-axis (shade) captures the resulting group-based hierarchy at the macro level. We find a plane lying diagonally over this space that increases monotonically as local tendencies for clustering and asymmetric triads increase.

Because Tau is an abstract summary of the concrete macro-structure within the network, we flesh out the meaning of this pattern by selecting exemplar cases from the four quadrants of the micro-parameter space to model in detail with blockmodels.²⁵ In the first column (networks a and c), we see compressed status structures, with hierarchy ratios between .8 and 1.3 and high group-level reciprocity. These two networks differ most strongly in the strength of in-group ties, with 94 percent of ties falling within-position for network a compared to 50 percent for network b. In contrast, the high hierarchy column (networks b and d) has clearly ordered image networks with wider hierarchy ratios, ranging from .47 to 1.86. Without clustering (network d) the network is really a smooth ordering, with many positions and high between-group volume (only 35 percent of ties fall within-position). When both clustering and hierarchy are high, we get a smaller number of clearly ordered self-recognized groups (82 percent of ties within-group). These results suggest that different combinations of local closure and hierarchy will give rise to very different macro network features within the observed parameter range found in our empirical sample.

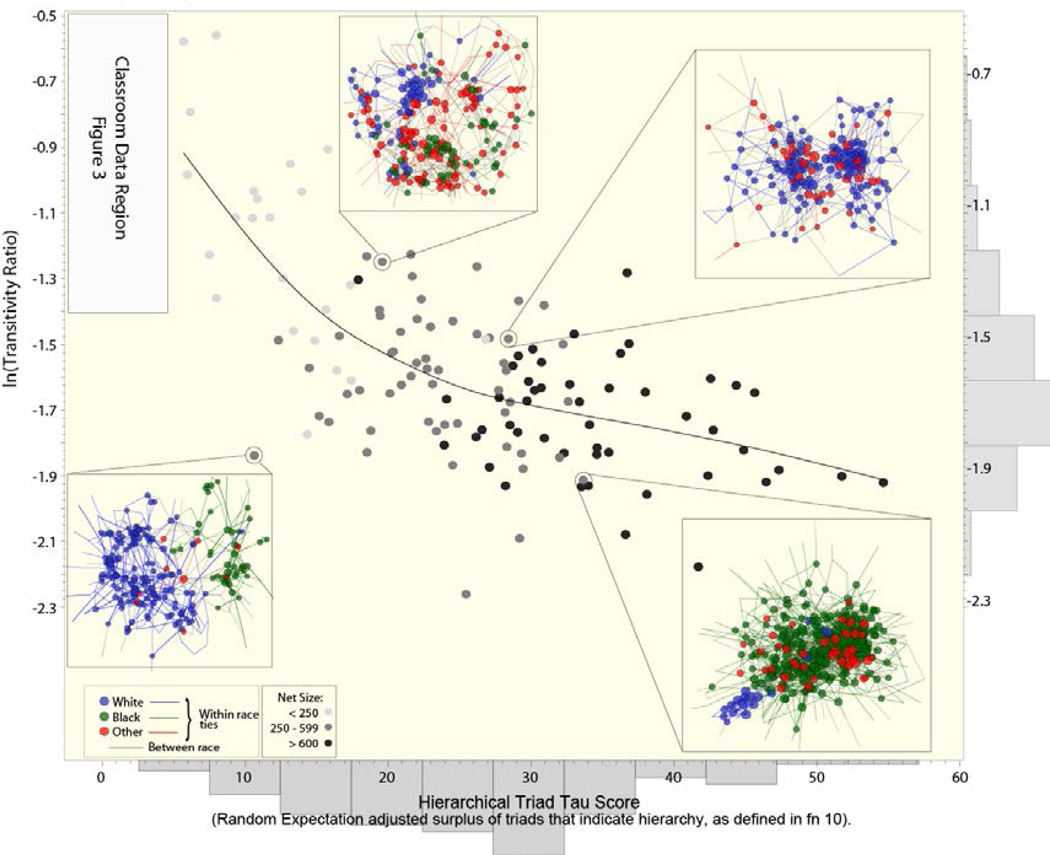
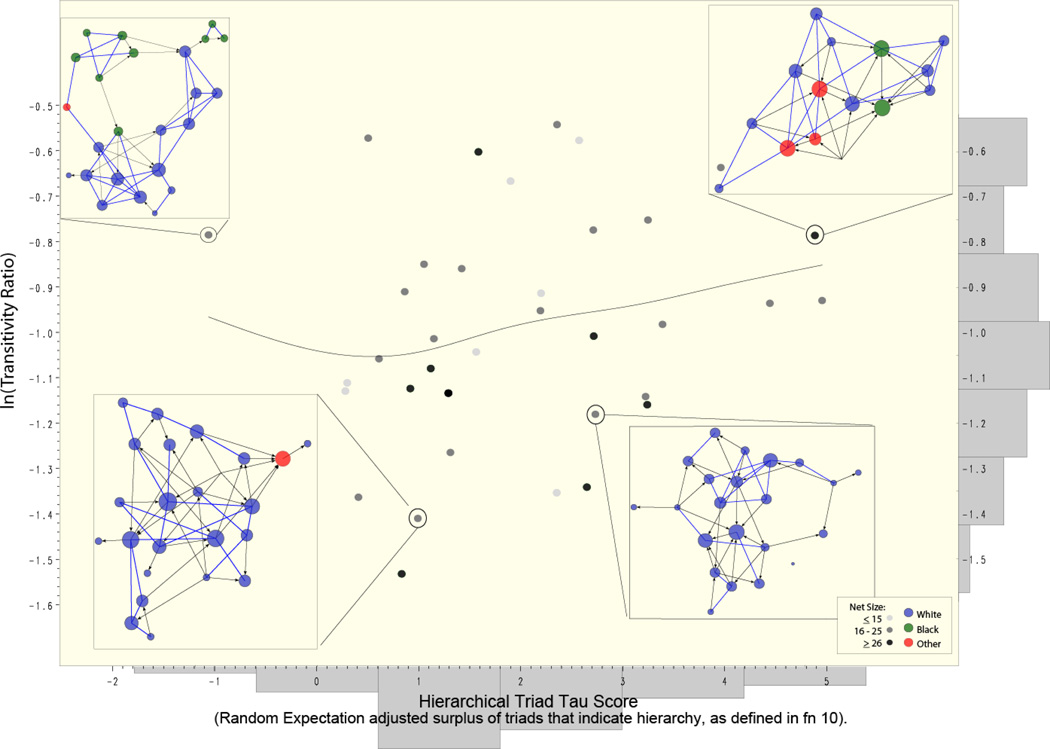
Figures 2 and 3 provide a picture of how the Add Health data and the classroom data correspond substantively to the network space implied by the models in Figure 1 by plotting the log of observed transitivity levels, which capture clustering, in a network against the observed hierarchy score.²⁶ In the Add Health sample (Figure 2), which includes a wider range in network size, we see a generally negative correlation between clustering and hierarchy and a much wider variability in hierarchy. In the smaller, higher-reciprocity classroom networks (Figure 3), we find a smaller variability in hierarchy and generally high local clustering (the space represented in Figure 3 is the shaded inset of Figure 2).

Figure 2.

Distribution of a Network Field; Add Health Networks Arranged by Transitivity, Hierarchy, and Size, with Exemplars

Figure 3.

Distribution of a Network Field; Classroom Networks Arranged by Transitivity, Hierarchy, and Size, with Exemplars

We highlight four networks from different regions of the space, and include an inset sociogram of each, to give a sense of the variability in macro-structures. Variation in clustering and segregation is readily visible. Variation in hierarchy is shown through the differences in node sizes within each sociogram. Results illustrate how distinct macro-structures arise when our micro-mechanisms are amplified or dampened. In the following section, we relate our specific findings on micro-mechanisms and how the moderating effects of organizational features forge distinct macro-structures.

Moderating Features of Network Ecology

Having shown there is significant variation at the global level of network properties in schools and classrooms, we again return to our central question: how can the same processes of tie formation lead to macro-structural variation? The simplest answer is that the ecology of organizational features in the setting moderates the baseline micro-mechanisms—amplifying in some settings and dampening in others—to generate different macro features in the network.

Tables 3, 4, and 5 present results of models where contextual factors are allowed to act as moderators for the tie-formation mechanisms.²⁷ Table 3 presents changes in model fitness due to the inclusion of moderators. It also shows results of a type-3 test of fixed effects, which examines if our moderators are significantly associated with the variation of all micro-mechanism coefficients. Given our smaller sample size of schools and classrooms, we first introduce the moderators in bivariate form. Then in the second model, for the school data, we assess the association for all moderators simultaneously. For the classroom data, our sample is limited, so we assess the association for class size with each of the other moderators in pairs.

Table 3.

Model Fitness and Moderator Fixed Effects

School Networks	Bivariate Models		Full Model
Model Fitness	Deviance	Δ Dev	Deviance	Δ Dev
Unconditional Model	−1302.4		1465.8	163.4 ***
School Size	−1412.4	110.0 ***
Tracking	−1300.7	−1.7 ns
Number of Clubs Offered	−1316.6	14.2 ns
High School	−1371.6	69.2 ***
Race Heterogeneity	−1343.1	40.7 ***
Gender Heterogeneity	−1345.3	42.9 ***
Age Heterogeneity	−1347.0	44.6 ***
Average GPA	−1322.2	19.8 *
Attachment to School	−1237.6	−64.8 ns
	Bivariate Models		Full Model
Type-3 Test of Fixed Effects	F-value		F-value
School Size	68.81 ***		59.41 ***
Tracking	5.60 ***		2.31 *
Number of Clubs Offered	13.63 ***		9.68 ***
High School	20.60 ***		12.90 ***
Race Het	11.66 ***		10.14 ***
Gender Het	5.10 ***		5.00 ***
Age Het	8.68 ***		8.71 ***
Average GPA	8.64 ***		6.28 ***
School Attachment	5.82 ***		1.25 ns
Classroom Networks	Bivariate Models		Bivar. + Size
Model Fitness	Deviance	Δ Dev	Deviance	Δ Dev
Unconditional Model	−81.2
Size	−41.3	−39.9 ns
Task Control	−65.6	−15.6 ns	−25.4	−55.8 ns
Elective Seating	−65.9	−15.3 ns	−23.3	−57.9 ns
Race Het	−87.4	6.2 ns	−48.4	−32.8 ns
Gender Het	−99.8	18.6 *	−58.3	−22.9 ns
Age Het	−77.3	−3.9 ns	−32.7	−48.5 ns
Honors Class	−59.0	−22.2 ns	−20.1	−61.1 ns
Liking of Class	−70.0	−11.2 ns	−27.0	−54.2 ns
	Bivariate Models		Bivar. + Size
Type-3 Test of Fixed Effects	F-value		F-value
Size	4.33 ***
Task Control	1.82 ~		1.97 *
Elective Seating	2.87 **		2.82 **
Race Het	4.40 ***		5.09 ***
Gender Het	1.08 ns		.93 ns
Age Het	1.74 ~		1.62 ns
Honors Class	1.50 ns		1.93 *
Liking of Class	2.86 **		2.42 *

Note: N coefficients for schools = 1,230, N coefficients for classrooms = 272. Δ Dev denotes change in deviance statistic.

^*p < .05

^**p < .01

^***p < .001

^~for small samples p < .10.

Table 4.

Moderator Results: How Organization Size, Differentiation, Composition, and Climate Influence Tie-Formation Mechanisms (log-odds)

		Development		Size		Differentiation
		High School (vs. Middle School)		Larger		Tracking (selectivity)		Number of Clubs Offered (electivity)
Schools	Main	Bivar.	Full	Bivar.	Full	Bivar.	Full	Bivar.	Full
Edges	−6.689 ***	−.135 *	.248 **	−.524 ***	−.504 ***	.059	.106 **	−.891 ***	−.386 ***
Mutuality	3.393 ***	.282 ***	.294 ***	.630 ***	.529 ***	.176 ***	.013	.612 ***	.188 **
Closure	.954 ***	.023 *	.016	.090 ***	.074 ***	.012	−.010	.105 ***	.044 **
Hierarchy	.123 ***	.008 ***	.010 **	.010 ***	.006 **	−.004 ~	−.006 **	.006	−.005
Club Ties	.411 ***	.127 ***	.158 ***	.141 ***	.087 ***	.047 **	.009	.069 *	−.056 *
Same Race	.499 ***	.064 *	.059	.099 ***	.045 ~	.044 ~	.048 *	.073	−.048
Same Gender	.184 ***	−.037 ***	−.059 ***	−.005	.021 **	−.021 **	−.008	−.037 *	−.054 ***
Same Age	1.231 ***	−.056	−.351 ***	.079 *	.116 ***	−.177 ***	−.116 **	.205 **	.159 *
GPA Diff.	−.207 ***	.010	.006	.002	−.010	−.002	−.009	−.008	−.010
SES Diff.	−.035 ***	.001	−.005	−.004 *	−.001	−.001	−.004	−.010 *	−.007

		Development		Size		Organizational Differentiation
		High School (vs. Middle School)		Larger		Task Control (selectivity)		Elective Seating (electivity)
Classrooms	Main	Bivar.	w/Size	Bivar.	w/Size	Bivar.	w/Size	Bivar.	w/Size
Edges	−3.996 ***	NA	NA	−.282 ***	NA	−.154 ~	−.157 ~	−.109	−.090
Mutuality	2.711 ***			.260 *		−.112	−.116	.372 ~	.345 ~
Closure	.515 ***			.028		.011	.012	−.019	−.014
Hierarchy	.246 ***			−.014		−.007	−.005	.001	.008
Interaction	.150 ***			.038 *		.043 **	.042 **	.010	.011
Same Race	.469 ***			.032		.062	.067 ~	.113 ~	.099
Same Gender	.385 ***			−.012		.007	.014	.042	.050
Same Age	.506 ***			.175 **		.013	.009	−.159	−.055
GPA Diff.	−.106 ***			.005		.018	.016	.034	.024

	Composition						Climate
	Racial Heterogeneity		Gender Heterogeneity		Age Heterogeneity		Average GPA		Attachment to School
Schools	Bivar.	Full	Bivar.	Full	Bivar.	Full	Bivar.	Full	Bivar.	Full
Edges	−.328 ***	−.129 **	−.055	.052	−.138 *	−.140 ~	.027	.005	.127 *	−.023
Mutuality	.120 *	−.049	−.059	−.035	.154 **	−.383 ***	−.190 ***	−.105 **	−.260 ***	−.051 ~
Closure	.036 ***	.004	.020	.000	.011	−.031 *	−.030 **	−.019 *	−.037 ***	−.006
Hierarchy	.010 ***	.009 ***	−.007 *	−.007 **	.006 **	−.004	−.005 *	−.006 **	−.004 ~	.000
Club Ties	.009	.028 *	−.033 **	−.020 *	.093 ***	−.075 **	−.043 **	−.018	−.037 *	.007
Same Race	.157 ***	.190 ***	.008	−.012	.054 *	−.001	−.078 **	−.037	−.046 ~	.026
Same Gender	.036 ***	.018 *	.113 *	.051	−.030 ***	.021	−.012	−.021 **	.000	−.001
Same Age	.064 ~	.008	−.109 **	−.078 **	.050	.343 ***	.141 ***	.115 ***	.049	.021
GPA Diff.	.005	.009	−.006	−.008	.013 ~	.019	−.020 **	−.015 *	−.011 ~	−.009
SES Diff.	−.003 ~	−.004 ~	−.001	−.001	.003	.011 *	−.003 ~	−.006 **	.004 *	.003

	Composition						Climate
	Racial Heterogeneity		Gender Heterogeneity		Age Heterogeneity		Honors Class		Liking of Class
Classrooms	Bivar.	w/Size	Bivar.	w/Size	Bivar.	w/Size	Bivar.	w/Size	Bivar.	w/Size
Edges	−.016	−.085	−.015	−.020	−.108	−.055	−.057	−.032	.079	.013
Mutuality	−.139	−.080	−.135	−.130	.074	.023	.059	.034	−.003	.063
Closure	.038	.044	−.012	−.013	.006	.003	−.052	−.054	.036	.045
Hierarchy	.007	.003	.010	.009	.003	.009	−.019	−.016	−.008	−.016
Interaction	−.005	.008	−.005	−.006	.013	.005	.086 **	.089 ***	−.011	.000
Same Race	−.291 ***	−.317 ***	.028	.038	.067	.073 ~	.013	−.003	−.067 ~	−.069
Same Gender	−.089 *	−.095 **	.074 ~	.078 ~	.032	.039	−.016	−.011	−.056	−.068
Same Age	−.085	.004	.194	−.009	.387 *	.224	.100	.110	−.158 **	−.121 **
GPA Diff.	.010	.013	−.014	−.013	−.017	−.020	.039	.034	.020	.023

Note: Moderators measured as continuous variables reflect the change in network mechanism due to one standard deviation shift (elective seating and honors are left as raw dummy variables). Table A1 in the Appendix illustrates that, due to lack of variance in some settings (e.g., on SES), the N varies for bivariate school results from 94 to 129 depending on the focal level-2 variable. For the full school models, the N is 94. For classroom models, the N varies from 15 to 35 classes depending on the focal level-2 variable (e.g., there is no racial or age homophily in some classrooms).

^*p < .05

^**p < .01

^***p < .001

^~p < .10

Table 5.

Summary Table of Moderator Effect Patterns on Key Mechanisms of Macro-Structural Variation

	Ecological Features
	Development	(1) Size	(2) Differentiation		(3) Composition			(4) Climate
Micro-Mechanism	High School	Larger	Selectivity	Electivity	Race Het	Age Het	Gender Het	Achieve	Attachment
School Friends
Clustering
Mutuality	+	+	+	+	+	−		−	−
Closure	+	+		+	+	−		−	−
Hierarchy
Tau Asymm. Triads	+	+	−		+	+	−	−	−
Segregation
Race Homophily	+	+	+		+	+		−	−
Age Homophily	−	+	−	+	+	+	−	+
Gender Homophily	−	+	−	−	+	−	+	−
Classroom Friends
Clustering
Mutuality	NA	+		+
Closure	NA
Hierarchy
Tau Asymm. Triads	NA
Segregation
Race Homophily	NA			+	−				−
Age Homophily	NA	+				+			−
Gender Homophily	NA				−		+

Note: + denotes a significant positive relation; – denotes a significant negative relation. Bold font denotes significance in models entailing all ecological features (schools) or at least controls for class size. Normal font indicates bivariate relation.

Results for schools reveal that all the moderators increase model fitness (see Δ deviance), but some increase model fitness more than others. The full model, however, is robust (Δ deviance = 120.9). Looking to the fixed effects, we find all the moderators (particularly school size) significantly change the variance in coefficient sizes for our micro-mechanisms.

We have less straightforward results for classrooms, mostly due to reasons of statistical power. Here, model fitness is only significantly improved from the baseline by the inclusion of gender heterogeneity, but this drops when we include class size as a level-2 characteristic. In spite of our limited statistical power, the fixed effects show that certain moderators are more strongly associated with the salience of micro-mechanisms than are other moderators: for example, class size, elective seating (electivity), racial heterogeneity (composition), and class liking (climate).

Developmental shifts

Table 4 provides a description of the relation between structural moderators and the identified micro-mechanisms, and Table 5 presents these results in a more readable summary format. The first moderator we examine is the developmental shift between middle school and high school settings. We find that high schools entail more reciprocated, closed sets of relations, rank-ordered relations, and increased racial segregation. However, as youth grow older, they form more dating ties that span age and gender, as reflected in these negative estimates. This is consistent with Dunphy’s (1963) and Cotterell’s (2007) accounts of adolescent network development. In the full model, these effects are net of other moderators, and therefore likely reflect either that our models do not capture all cultural and ecological features of adolescent settings that change with their development, or that older youth are more skilled and experienced at social sorting and ranking.

Ecological moderators size.²⁸

As the size of a school increases, we expect the importance of all endogenous processes to increase as well, and we find that our measures of clustering and hierarchy increase with network size.²⁹ We also see an increase in the magnitude of homophily across age, race, and SES and the importance of shared extracurricular ties. Looking at classrooms, we see that as class size increases, so too do the odds of age homophilous preferences, tie reciprocation, and repeated interactions leading to tie formation. These effects are expected, as small schools and classrooms lack the range of potential targets necessary for clear social differentiation. Thus, we find the most pronounced hierarchy and attribute sorting in large settings where uncertainty and unfamiliarity are common.

In general, the cost of excluding others changes with the size of the setting. In small settings, acts of exclusion bring high costs so persons avoid such behavior. This means the mechanisms leading to clustering are dampened and there are more cross-cutting social circles. It also means the boundaries between high- and low-status students are blurred, so dominance hierarchies are lessened. By contrast, in large settings, the cost of exclusion is less because there are greater degrees of freedom for forming homogeneous peer groups of less-contested status. Therefore, we observe a greater tendency toward clustering and ranking in larger settings.

Ecological moderators: organizational differentiation

We next include aspects of organizational differentiation that moderate tie-formation mechanisms by shaping opportunities for mixing. First, students in tracked schools have more ties, less hierarchy, more racial segregation, and more age-heterophilous relations. In these schools, students are selected into courses on the basis of their achieved grades and test scores. This tends to correlate with race and therefore amplifies racial homophily. However, it also creates pools of students with similar academic orientations. This creates a sense of shared fate and trust, and this diminishes the felt need to cluster and rank-order relations.

Whereas tracks reflect selectivity, the number of clubs at a school reflects electivity. As the number of clubs increases (net of population size), so too does reciprocity and closure because students have more identity-related groups to choose from. However, counter to our expectations, electivity and selectivity have no effect on hierarchy (Milner 2004). As such, hierarchy may be more a function of variation than of choice. Other results follow our intuitions. As the number of clubs increases and becomes an available means of differentiation, club ties become more important for friendship tie formation. More clubs are also associated with an increase in age and SES homophily, but a decrease in preference for same-gender friends. This follows because clubs are often age-segmented (e.g., 9th grade, junior varsity, and varsity) and correlated with SES groupings (e.g., orchestra versus basketball) but cross genders (e.g., theater).

Moving to classroom results, we look first at the moderating effect of task control as a measure of organizational selectivity. Task structures chosen by teachers shape the amount and type of classroom interaction students have with one another. In general, differences in task structures are less strongly associated with network forms than are other classroom features, but, the more closed the structure, the more important social interaction is to friendship formation. In teacher-centered lessons, peer interaction is a risky endeavor and rare. In such settings, peer interactions are used more sparingly and become more heavily valued and meaningfully regarded.

Furthermore, we find only a weak moderating effect for elective seating. Specifically, when students choose where they sit, we find slight increases in mutuality and racial homophily. These results reflect the general effect of elective differentiation because students’ seating choices reinforce the security mechanisms characterized by sharing ties with similar partners. In summary, school and classroom features reflective of organizational differentiation either select for students their various groupings and render certain mechanisms more or less salient, or they open up choice and the possibilities for self-selection and homophily.

Ecological moderators: composition

As schools become more racially heterogeneous, their friendship networks are not only more clustered and hierarchical but are also sparser (i.e., we find a decrease in the total number of ties as measured by the edges variable). In addition, school racial heterogeneity is associated with amplification of race as a selection attribute (and, to a lesser extent, gender and age homophily). These results support the idea that students avail themselves of the greater freedom to select similar friends and create more tightly clustered, homophilous networks. Moreover, we see that this selection will arise on the dimension of greatest variability.

Our other models of school composition afford a more complex story of attribute selection. On the one hand, we find evidence that gender heterogeneity is associated with gender homophily—further evidence that an attribute’s variance determines its salience for real preferences. On the other hand, gender heterogeneity diminishes the relevance of control and hierarchy in tie formation. Even more complex are the results for age heterogeneity. The coefficients flip in sign as we go from bivariate to full model inclusion, suggesting age is correlated with other factors like tracking and club affiliations. Net of these organizational affiliation structures, age heterogeneity is associated with less cliquishness and increases in hierarchy (age differentiation) and cross-gender association (dating). Supplemental models suggest dating relationships break down structural differentiation by spanning same-sex, age-similar cliques, but such complex relations between types of composition warrant further detailed study of their own.

In contrast, classroom ties have fewer forms of attribute homophily than do (stronger) school ties. Gender homophily is slightly more likely to arise in gender-heterogeneous classes, as is age homophily in age-heterogeneous contexts. In contrast, racially heterogeneous classrooms experience a significant decrease in both gender and racial homophily (Plank 2000). This is exactly the inverse of what we see in the whole-school networks. One likely reason for this is that classrooms are small group contexts where face-to-face contact is unavoidable and scope conditions of status selection are broken over time. But why does this occur only for racial heterogeneity, whereas age and gender heterogeneity have the expected effects? We are uncertain and think it is worth further attention in future studies.

Ecological moderators: organizational climate

Finally, we look at the moderating effect of organizational climate. We find that increasing academic orientation (measured as average GPA) is associated with weaker effects of all three of our endogenous network processes of interest as well as those for shared club ties. Furthermore, while a climate of high achievement correlates with preferences for alters of similar ages, GPAs, and SES backgrounds, it corresponds with lower rates of racial homophily. We see a very similar set of results when looking at average school attachment, with one important distinction being that the preference for similar SES backgrounds diminishes. This suggests that when there is a culture of high achievement or attachment to the school, preferences for tie formations are different, with similarity in academic orientations trumping other features (Stark 2011). In many regards, this reflects the sort of positive academic climate Coleman had in mind when he wrote the Adolescent Society (1961). In these settings, status is conferred through achievement, and thus ascribed characteristics become less significant.

The moderating effects of classroom climate are weak but similar to those of school climate. In classrooms students report liking, we see a decrease in age (p < .01) and race (p < .10) homophily. This is much the same for school attachment where, in both cases, we see that students’ emotional satisfaction is related to decreases in various forms of homophily. As such, positive climates are the cultural analogue to our notion of external identity exclusion. Positive climates make the system membrane more salient, and this excludes external concerns. Conversely, as participants detach from the group, the system membrane lessens and external identities are imported as a basis for friendship formation.

CONCLUSIONS

This article can be seen as a response to recent calls for a network analysis that more systematically takes social context into account (Entwisle et al. 2007). Here we do so by examining how features of network ecology moderate the relationship between micro-mechanisms of tie formation and global features of social structures. Specifically, we find that as settings become more open and free they include externalities and amplify naturally present bases of association as defined by mechanisms of homophily, closure, and status ranking. Conversely, as settings become more closed and socially controlled, they exclude externalities and dampen natural modes of association, enabling organizationally defined and more random bases of association to take hold. In other words, as settings become more marked by external identity inclusion—that is, as schools become larger, less organizationally differentiated, and more racially heterogeneous—the prevalence of clustering, hierarchy, and segregation increases. In contrast, as contexts become more marked by external identity exclusion—that is, as schools become smaller and characterized more by structured interaction—they have more random and egalitarian mixing among students. Moreover, when students share school attachment and achievement norms, balance, hierarchy, and racial homophily all decrease.

While our design limits strong causal statements and warrants cautious interpretation, the consistency between results and theory could have important implications for schools. For example, the most direct implication of these results is that one can infer what sort of adolescent society will emerge in various ecological settings. The literature on schools proposes a variety of organizational reforms, such as detracking (Oakes et al. 1992), desegregation (Plank 2000), curricular choice (Powell, Farrar, and Cohen 1985), small schools (Watt 2003), and even changes in school climate (Bryk, Lee, and Holland 1993). Our results suggest that all these prescriptions probably have repercussions on adolescent society: school desegregation increases informal bases of hierarchy and leads to school-wide homophily but classroom heterophily; curricular choice exacerbates self-selection; small schools encourage more random mixing; and schools with positive academic climates encourage dense, random associations.

But what are desirable macro-structural arrangements for youth? Sociologists have not studied the effects of macro-structural variation on educational and developmental outcomes. We have folk theories about which network arrangement is best, but we lack systematic empirical evidence. Is it better to develop in an unstructured environment or a structured one, and for what type of child? Prior work on individual educational outcomes consistently finds within-school variation is greater than between-school variation (Raudenbush and Bryk 2002), so we suspect that individual positioning within social networks may be more important than school-level network properties. Hence, the greatest returns to policy may arise from considering how movement across positions in different adolescent social structures can result in developmental gains. What structural and setting changes have the greatest returns on a youth’s educational and social development?

The features of network ecology we discuss were all drawn from existing school research, but several other components might prove fruitful for future work. One such area is the inclusion of additional aspects of school and classroom culture, like the strength or prevalence of common belief in, or commitment to, a shared group or institution as well as differences in the perception of shared identity (Brint 2001). Future research could also incorporate additional aspects of the physical environment (besides seating) that contribute to opportunity and choice constraints, such as building design and classroom setup.

Future work could explore changes in the context itself, which we treated here as a set of static variables, because our analysis looked only at small windows of time. However, if we were to follow schools over a longer time period, we might see compositional changes as certain groups move in and out of the communities from which schools draw their students (perhaps even in response to perceived qualities of the school itself). The shifting culture of, and attachment to, these contexts may help reveal how youth differentially invest themselves, thereby amplifying and dampening the salience of certain settings and their ties (Phelan, Davidson, and Cao 1991). Moreover, we know that mobile populations have different relationships with their local institutions like schools (Sampson, Morenoff, and Gannon-Rowley 2002). Perhaps even more interestingly, longer-term studies could examine the type of feedback processes we alluded to earlier, in which some ecological features may co-evolve with networks themselves. We might study, for instance, whether evolution in network structures shapes the nature of shared identity or the degree of group commitment and vice versa, or how it leads to mobilization processes aimed at changing institutional structures and rules. Such extensions will represent an exciting next step in the study of the interrelation of networks and social settings.

Biographies

Daniel A. McFarland is a Professor of Education, Sociology, and Organizational Behavior at Stanford University. He specializes in the study of social dynamics and is currently engaged in several projects concerning the coevolution of social networks and cultural systems. He received a PhD in sociology at the University of Chicago and teaches graduate courses in social networks, organizations, sociology of knowledge, and microsociology.

James Moody has published extensively in the field of social networks, methods, and social theory. His work has focused theoretically on the network foundations of social cohesion and diffusion, with a particular emphasis on building tools and methods for understanding dynamic social networks. He has used network models to help understand school racial segregation, adolescent health, disease spread, economic development, and the development of scientific disciplines.

David Diehl is an Assistant Professor of Human and Organizational Development at Vanderbilt University. His research examines how institutional structures, practices, and logics shape, and are in turn shaped by, organizational actors’ social networks and relationships. He is especially interested in how these dynamics play out during institutional change efforts in schools and other educational organizations as reformers and policymakers attempt to instantiate contested moral ideals about how teachers and students ought to live and learn together.

Jeffrey A. Smith is an Assistant Professor of Sociology at the University of Nebraska-Lincoln. His research interests include social networks, quantitative methodology, and stratification. He has done methodological work on network sampling, simulation, and missing data, and more substantive work on homophily, social distance, status, and the relational meaning of demographic categories.

Reuben J. Thomas is Assistant Professor of Sociology at the University of New Mexico. He studies interpersonal social networks, particularly their reproduction and segregation. His research has looked at the endogamous consequences of how romantic couples meet, how ego network disruptions alter friendship segregation, the civic and political outcomes of adolescent affiliations, and the prehistoric emergence of inherited social inequality.

APPENDIX

Table A1.

Descriptive Statistics

	School			Classroom
	Mean	SD	N	Mean	SD	N	Variable Description
Cross-Sectional Estimates
Edges	−6.435	.941	129	−4.113	.602	35	Number of ties
Reciprocity	3.210	.709	129	2.757	.755	35	Number of mutual relationships
Closure	.945	.132	129	.539	.172	35	Number of closed triads
Hierarchy	.131	.033	129	.240	.143	35	Number of hierarchical triads
Race Homophily	.406	.325	123	.485	.187	16	Proportion racially homophilous ties
Gender Homophily	.196	.131	129	.375	.282	35	Proportion gender-homophilous ties
Age Homophily	1.350	.478	127	.482	.332	15	Proportion age-homophilous ties
GPA Diff.	−.199	.086	94	−.080	.174	33	Difference in GPA
SES Diff.	−.031	.027	112				Difference in parents’ highest education
Club Ties	.421	.207	129				Number of club ties
Interaction				.226	.135	33	Rate of interaction an hour per dyad
Moderators
Racial Heterogeneity	.473	.174	129	.305	.228	35	Heterogeneity = 1 – (Σ squared proportions for each race)
Gender Heterogeneity	.493	.043	129	.460	.049	35	Heterogeneity = 1 – (Σ squared proportions for each gender)
Age Heterogeneity	.732	.082	129	.248	.234	35	Heterogeneity = 1 – (Σ squared proportions for each grade level)
Size	634.092	494.507	129	22.722	4.227	35	Number of students in the school or classroom
Tracking	.306	.271	129				1 – Herfindahl index (product of administrator-reported proportions of students in each track)
Number of Clubs	31.057	4.072	129				Number of clubs at school
Task Control				.162	.435	35	Task control = teacher centered – student centered – (.5)individual work
Elective Seating				.528	.506	35	Dummy for elective seating versus assigned (1,0)
Average GPA	2.846	.253	129				Average GPA
Honors				.389	.494	35	Dummy for honors versus other class (1,0)
School Attachment	−11.255	1.126	129				Attachment to school: composite of how often you get along with the teacher, pay attention, get along with other students, how close you feel to others at school, and how much you felt like you are a part of the school (Attachment = [h1ed15 + h1ed16 + h1ed18 + (h1ed19 − 5) + (h1ed20 − 5)] x−1), Cronbach’s alpha = .65).
Liking of Class				3.020	.465	35	Liking of class 1 = dislike, 4 = like very much.
High School vs. Middle	.613	.489	129				High school = 1, middle school = 0.
Longitudinal Estimates
Edges	−5.583	1.394	9	−4.503	.596	25	Same as above
Reciprocity	2.114	1.288	9	2.394	.618	25	Same as above
Closure	.824	.210	9	.566	.223	25	Same as above
Hierarchy	.152	.115	9	.266	.062	25	Same as above
Prior Friends	2.534	1.013	9	2.047	.603	25	Same as above
Race Homophily	.512	.615	4	.093	.301	13	Same as above
Gender Homophily	.351	.234	9	.163	.440	25	Same as above
Age Homophily	1.233	.682	9	.223	.218	10	Same as above
GPA Diff.	−.322	.159	9	−.067	.166	23	Same as above
SES Diff.	−.019	.082	9				Same as above
Club Ties	.233	.512	9				Same as above
Interaction (semester 1)				.210	.140	25	Same as above
Prior Friends	2.534	1.013	9	2.047	.603	25	Prior friendship (1,0)

Table A2.

Correlation Table of Estimates Revealing Covariance Patterns Exist

		1	2	3	4	5	6	7	8	9	10
1.	Edges	1.000	−.627	−.289	−.507	−.581	−.359	−.270	−.564	−.060	.112
Network Mechanisms
2.	Mutuality	−.627	1.000	.340	.364	.582	.160	.044	.146	.046	−.149
3.	GWESP	−.289	.340	1.000	.459	.501	.217	−.263	−.057	.273	−.093
4.	Hierarchy	−.507	.364	.459	1.000	.367	.198	.317	.306	.208	.111
5.	Club Ties	−.581	.582	.501	.367	1.000	.202	−.108	.026	.088	−.112
Homophily
6.	Race Homophily	−.359	.160	.217	.198	.202	1.000	.123	−.224	.074	−.287
7.	Gender Homophily	−.270	.044	−.263	.317	−.108	.123	1.000	.229	−.115	.141
8.	Age Homophily	−.564	.146	−.057	.306	.026	−.224	.229	1.000	−.062	.124
9.	GPA Difference	−.060	.046	.273	.208	.088	.074	−.115	−.062	1.000	.158
10.	SES Difference	.112	−.149	−.093	.111	−.112	−.287	.141	.124	.158	1.000

Findings: Network variables are correlated, indicating the need for more complex covariance structures.