Demonstrating frequency-dependent transmission of sarcoptic mange in red foxes

Abstract

Understanding the relationship between disease transmission and host density is essential for predicting disease spread and control. Using long-term data on sarcoptic mange in a red fox Vulpes vulpes population, we tested long-held assumptions of density- and frequency-dependent direct disease transmission. We also assessed the role of indirect transmission. Contrary to assumptions typical of epidemiological models, mange dynamics are better explained by frequency-dependent disease transmission than by density-dependent transmission in this canid. We found no support for indirect transmission. We present the first estimates of R₀ and age-specific transmission coefficients for mange in foxes. These parameters are important for managing this poorly understood but highly contagious and economically damaging disease.

1. Introduction

Rates of disease transmission are typically assumed to increase with host density for most directly transmitted infections but to be unrelated to density for sexually and indirectly transmitted diseases [1]. Increasingly, studies are challenging this assumption, suggesting that behaviours mediating contact rates do not always show simple relationships with host density [2]. Many diseases are also transmitted indirectly through contact with contaminated substances known as fomites, a pathway only recently incorporated into wildlife disease models [3,4]. Insight into pathogen spread is informative for controlling disease: nonlinear dynamics can result in ineffective culling [5]; disease-induced extinction risk increases when transmission is density-independent [6]; and indirect transmission can promote disease persistence [3]. Given the threat of emerging infectious diseases, the possibility of domestic–wildlife cross-infection and the cost of disease control [7,8], understanding transmission mechanisms is clearly important.

Sarcoptic mange, caused by the highly contagious mite Sarcoptes scabiei, affects over 100 domestic and wild mammalian species [9]. Mange is a potential emerging disease [7], posing a risk for endangered species and domestic–wildlife infection [8]. The economic costs of controlling mange are substantial [10]. Despite its importance, fundamental aspects of mange epidemiology, including genetic resistance and transmission dynamics in wild populations, are poorly understood [9]. Further, mange occurs in a range of species exhibiting different levels of sociality [11–14].

Mange epizootics have caused significant declines in red fox Vulpes vulpes populations worldwide [11,15,16]. Previous mange models have only considered direct, density-dependent transmission [12,17] but off-host mite survival [9] and low inter-group contact in foxes [18] suggest that indirect transmission is likely. Moreover, the social nature of foxes suggests that the traditional assumptions of density- and frequency-dependent disease transmission might be complicated [19]. We developed a model of mange spread and fitted it to a long-term dataset. This model allowed us to (i) estimate epidemiological parameters; (ii) explore whether transmission is frequency- or density-dependent and (iii) assess the potential role of indirect transmission.

2. Material and methods

An urban fox population in Bristol, UK, experienced a mange epizootic [20], followed by an enzootic phase [11], during a four-decade long study (1977 to present). Pre-epizootic spring population density (adults and juveniles) was exceptionally high (58.3 individuals km⁻²) and post-epizootic density was reduced by more than 95% [20]. Monthly mange prevalence was determined for juveniles (younger than one year) and adults (older than one year), given observed age-related patterns (see the electronic supplementary material for full details).

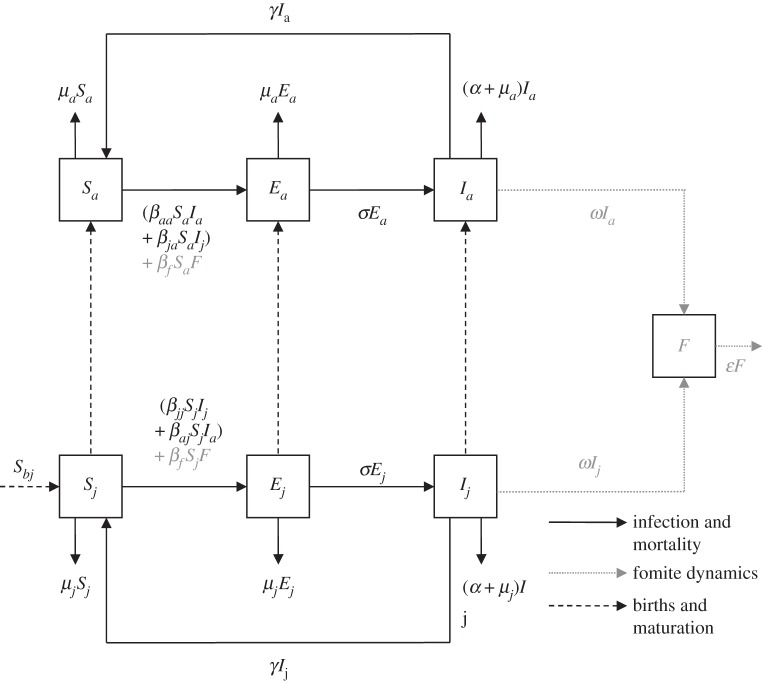
Using an age-structured susceptible–exposed–infected (SEI) model, we tested two forms of direct transmission: density- and frequency-dependent transmission (M_D and M_F, respectively, figure 1; see the electronic supplementary material for full model details). Two epidemiological parameters, the transmission coefficient, β, and infectious period, γ, were estimated by fitting the models to data. To account for potential age-specific variation in prevalence between juveniles (j) and adults (a), the SEI model included age-specific transmission, denoted by the coefficients β_jj and β_aa. The exposed class was included to incorporate the time taken between foxes becoming exposed to the mites and becoming infectious, typically 30 days (table 1). Mean time to disease-induced mortality (α) is estimated to be 100 days (table 1) which, with a life-expectancy without the disease of two years, translates to a sevenfold increase in mortality rate due to mange. Recovered individuals were assumed to return directly to the susceptible class because re-infection of individuals was observed (S. Harris 1977–2014, unpublished data). Host demography was modelled assuming a fixed background per capita mortality rate (table 1) and an annual birth pulse. The total population density (N) was reset annually to an observed post-breeding density (N_k) to simulate the birth pulse, with susceptible juveniles (S_bj) introduced into the population each year, t (i.e. S_bj = N_k(t) − N).

Figure 1.

SEI compartment model diagram illustrating age-specific density-dependent direct transmission with host demography (M_D). Indirect transmission and fomite dynamics are indicated in grey (M_DI). Transmission terms in brackets are replaced with (β′_aa S_a I_a + β′_ja S_a I_j)/N and (β′_jj S_j I_j + β′_aj S_j I_a)/N for frequency-dependent models (M_F and M_FI) (table 1 provides parameter definitions).

Table 1.

Definition of fitted and fixed parameters used in SEI models.

parameter	definition	fixed or fitted* parameter
βjj, βaa	age-specific density-dependent transmission (day−1)	a
β′jj, β′aa	age-specific frequency-dependent transmission (individual−1 day−1)	a
βf	indirect transmission (day−1 per unit of fomite) (age-invariant)	a
γ	infectious period = 1/γ (day−1)	a
σ	latent period = 1/σ (day−1)	30 days
α	disease-induced mortality rate = 1/α (day−1)	100 days
μj	juvenile per capita mortality probability (year−1)	0.3b
μa	adult per capita mortality probability (year−1)	0.5b
ω	per capita reproductive rate of mite on infected individuals (day−1)	a
ɛ	rate of loss of the pathogen in environment = 1/ɛ (day−1)	10 days
S0j	initial density of susceptible juveniles (km−2)	21
S0a	initial density of susceptible adults (km−2)	36
I0j	initial density of infected juveniles (km−2)	0.01
I0a	initial density of infected adults (km−2)	0.01
F0	initial density of fomites (normalized)	1

^aFitted parameter.

^bAnnual probabilities were converted to daily rates by –ln(μ)/360.

In models M_DI and M_FI, indirect transmission was combined with direct transmission (figure 1), given that indirect pathways are unlikely to be the sole transmission mechanism. An additional compartment (F) followed mite density on fomites and the transmission coefficient, β_f, described infection through the contact of susceptible individuals with free-living mites on infected substrates. Owing to paucity of data, the rate at which mites are released into the environment, ω, was a fitted parameter, assumed to depend on the reproductive rate of the mites and individual parasite loads.

Parameter estimates were determined using maximum likelihood (see the electronic supplementary material for full methods) in R v. 3.1.0 (www.r-project.org). Where possible, initial parameter values were estimated from the literature [11,20,21] (table 1). To determine the performance of the disease transmission models, predicted dynamics were compared with a null model with time-invariant disease prevalence. Evidence for inter-annual variation in post-breeding density, density- versus frequency-dependent transmission and the role of indirect transmission were assessed by performing model selection using Akaike's Information Criterion (AIC) [22]. The basic reproductive number, R₀, determining the probability of disease invasion, was calculated for the best AIC model using a ‘next generation matrix’ [23] (see the electronic supplementary material).

3. Results

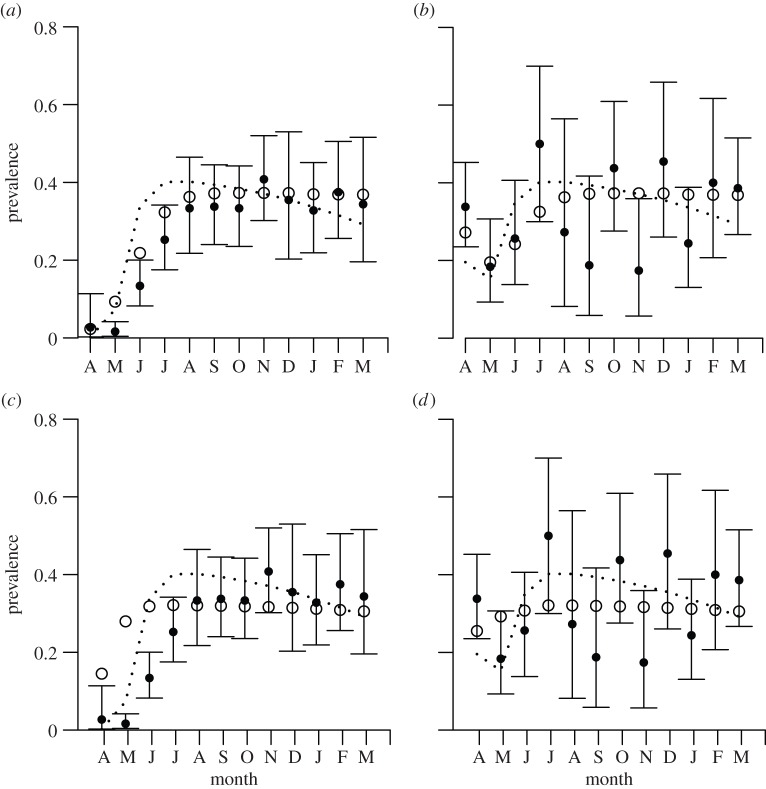
Age-related patterns in the monthly prevalence of mange (electronic supplementary material, figure S2) suggest some seasonality, particularly in juveniles. Prevalence data were overdispersed with respect to the binomial distribution (variance inflation factor, ṽ = 2.79) and, therefore, all model likelihoods were calculated using the beta-binomial distribution [22]. SEI models consistently outperformed the null model (electronic supplementary material, table S1). AIC values for the null and all eight time-varying disease models are presented in electronic supplementary material, table S1. The most parsimonious models (M_F and M_FI) indicated strong support for frequency-dependent mange transmission in the Bristol fox population. The frequency-dependent model incorporating indirect transmission (M_FI) performed well but model comparison showed that the extra parameters did not justify the increased complexity relative to model M_F (figure 2a,b) [22]. M_F captured observed prevalence patterns in both juveniles (figure 2a) and adults (figure 2b); the discrepancy between empirical and observed juvenile prevalence from May to July is probably due to the window of offspring birth being rather wider in reality than in our model. Density-dependent models did not perform well (figure 2c,d), overestimating juvenile prevalence from April to June.

Figure 2.

The predicted probability of infection (open circles) for (a,b) the frequency-dependent model (M_F) and for (c,d) the density-dependent model (M_D), for juveniles (a,c) and adults (b,d), against the observed prevalence data (closed circles). Dotted lines indicate the predicted probability of infection for models including indirect transmission (M_FI and M_DI, respectively); 95% confidence intervals (CIs) were calculated from likelihood profiles.

The 95% confidence intervals (CIs) of R₀ are all above one, consistent with mange persistence in the population (table 2). The best estimate of β′_jj was ten times higher than β′_aa, with no overlap between CIs (table 2), suggesting a key role of juveniles for mange transmission. The wide CIs and the discrepancy between the best model estimate of γ (table 2, corresponding to 30 days) and the estimate from the literature [21], may reflect trade-offs between γ and unknown parameters.

Table 2.

Estimated parameter values for the best-fitting model (95% CIs in parentheses estimated by bootstrapping 10 000 replicates, see the electronic supplementary material). See table 1 for parameter descriptions.

model	β′jj	β′aa	γ	φa	R0
MF, frequency-dependent	0.340 (0.164–0.705)	0.030 (0.006–0.151)	0.039 (0.029–0.111)	0.247 (0.156–0.392)	2.67 (1.54–5.12)

^aDispersion parameter, φ, indicating that data are overdispersed. See table 1 for epidemiological parameter descriptions.

4. Discussion

This study presents the first published model of mange transmission dynamics in foxes. The estimate of R₀ is consistent with mange invading the Bristol fox population and is similar in magnitude to that estimated for mange in chamois Rupicapra rupicapra (R₀ = 4.8–5.1) [12].

In other fox populations, the relationship between mange and density is unclear [11,15,24]. However, contrary to expectation, frequency-dependent transmission of mange appears most probable in the Bristol fox population, implying that the per capita rate of infectious contact remains constant despite increases in densities of infected individuals. This is consistent with fox behaviour, as opportunities for infectious contact may be limited due to low inter- and intra-group encounters [18,25]. Density-dependent models particularly overestimated juvenile disease prevalence post-birth, when movement is limited. The minimal effect of density on mange is supported by the observation that mange persists at low fox densities [20], because frequency-dependent diseases can be sustained at lower host densities than density-dependent diseases [26]. The contrast between our results and those of assessments of mange transmission in chamois, a species that does not show complex group structuring, and for which density-dependent transmission of mange was well supported [12], emphasizes the role of sociality in mediating disease dynamics within a population [1,2,5,19]. Further work is needed to examine how transmission mechanisms vary across different species affected by the same disease.

We found no support for indirect transmission. This could reflect the limited role of this pathway between social groups in the study area: although inter-group den sharing promoted mange transmission in a Russian fox population [16], this behaviour may be less frequent in the Bristol population. Poor support for indirect transmission also suggests poor support for the importance of alternative hosts. In single host–single pathogen models, alternative hosts may appear to play a role equivalent to indirect transmission, especially where the vectors are host generalists (as in the case of mange mites). However, in Bristol, there was only evidence of mange transmission from foxes to dogs during the initial epizootic phase, and no evidence of transmission from dogs to foxes (S. Harris, unpublished data). Thus, consistent with our findings on indirect transmission, the role of alternative hosts is likely to be negligible. These findings should recognize, however, that population-level SEI models do not discriminate between inter- and intra-group encounter rates and, thus, could overestimate the importance of direct transmission between individuals of the focal species. Simulations of individual-level behaviour may provide further insight into the relative importance of transmission mechanisms.

The predicted age-specific prevalence may reflect the restricted post-birth movement of juveniles [27] and the subsequent pulse of infection driven by the naive source of susceptible juveniles. The high predicted age-specific transmission rate suggests either that juveniles are more prone to infection given contact (owing to less effective immune systems and increased nutritional stress from independent foraging) and/or that they encounter infected individuals more often than adults (owing to life-stage-specific movement patterns); however, combining data on all individuals younger than one year may mask underlying mechanisms. Mange is probably maintained by older individuals since adults have a longer time to become infected compared to the short disease duration in younger individuals. Such insight into age-specific transmission is important for disease control.

This study provides the first estimates of stage-dependent transmission rates and R₀ for mange in foxes and suggests that the dominant transmission mechanism is frequency-dependent. These results indicate the importance of sociality in mange transmission and highlight the need to test long-standing assumptions of disease transmission.

Funding statement

We thank Durham University and the Dulverton Trust for financial support.