Quantitative prediction of radio frequency induced local heating derived from measured magnetic field maps in magnetic resonance imaging: A phantom validation at 7 T

Abstract

Electrical Properties Tomography (EPT) technique utilizes measurable radio frequency (RF) coil induced magnetic fields (B1 fields) in a Magnetic Resonance Imaging (MRI) system to quantitatively reconstruct the local electrical properties (EP) of biological tissues. Information derived from the same data set, e.g., complex numbers of B1 distribution towards electric field calculation, can be used to estimate, on a subject-specific basis, local Specific Absorption Rate (SAR). SAR plays a significant role in RF pulse design for high-field MRI applications, where maximum local tissue heating remains one of the most constraining limits. The purpose of the present work is to investigate the feasibility of such B1-based local SAR estimation, expanding on previously proposed EPT approaches. To this end, B1 calibration was obtained in a gelatin phantom at 7 T with a multi-channel transmit coil, under a particular multi-channel B1-shim setting (B1-shim I). Using this unique set of B1 calibration, local SAR distribution was subsequently predicted for B1-shim I, as well as for another B1-shim setting (B1-shim II), considering a specific set of parameter for a heating MRI protocol consisting of RF pulses plaid at 1% duty cycle. Local SAR results, which could not be directly measured with MRI, were subsequently converted into temperature change which in turn were validated against temperature changes measured by MRI Thermometry based on the proton chemical shift.

Very-high field (VHF) and ultra-high field (UHF) Magnetic Resonance Imaging (MRI) systems (operating at 3 T and above, or 7 T and above, respectively) have been pursued with increasing interest.¹ Their main advantages include higher signal-to-noise ratio (SNR) enabling higher spatial resolution, and increased sensitivity for intrinsic contrast mechanisms such as blood oxygenation level-dependent (BOLD) contrast.^2,3 However, higher magnetic field scanners operate at a higher Radio Frequency (RF), resulting in higher energy deposition in tissues, essentially in the form of heat (the required RF power for a given excitation flip angle increases approximately with the square of the operating frequency). Safety concerns relating with these thermal effects are one of the main challenges faced with VHF and UHF MRI systems, a situation seriously complicated by concomitant larger spatial heterogeneity in magnetic (B) and electric (E) fields. Inhomogeneous coil-induced magnetic fields (B1 fields) result in inhomogeneous contrast in MRI images, whereas inhomogeneous E fields may yield localized increases in RF energy deposition and subsequent local tissue heating. These “hot spots” of energy deposition, for a given RF coil and MRI protocol can substantially vary in shape, localization, and magnitude between subjects, as well as between different positions inside the RF coil for a given subject. Although increases in absolute temperature represent the actual sources of risk, monitoring temperature at high precision with MRI sequences in real time during a clinical MRI session is not doable with state-of-the-art technology. As a result, predictive computation of the Specific Absorption Rate (SAR), representing the RF power absorbed in tissues and expressed in W/kg, is used as a proxy by regulatory agencies (International Standard IEC 60 601-2-33 2010). In these guidelines, maximum SAR limits are defined (based on previously documented relationship between SAR and in-vivo biological tissue heating) at a global and local level, considering SAR averaged over the entire body and over 10 g of tissue (10 g average), respectively.⁴ It should be noted that VHF and UHF MRI applications are significantly impacted by safety regulations,^5,6 with local 10 g average SAR, most of the time, reaching maximum upper limits before global SAR does.

Several issues, however, are currently involved with guidelines based only on SAR: (1) Heat propagation in tissues (bio-heat transfer) is complex, involving thermal conductivity, metabolic heat production, and blood perfusion, with different functional regimes for different ranges of absolute temperature,^7–9 whereas by definition, SAR computation ignores these tissue- and space-specific relationships with actual temperature variation; (2) SAR by nature is linked with relative temperature changes rather than absolute temperature levels; and (3) estimating local SAR for human MRI experiments typically relies on highly time-consuming computational electromagnetic (EM) simulations, based on generic numerical models of EM properties of the human body^7,10 derived from MRI scans obtained in only a few individuals (male, female, children, etc.) and subsequently segmented in about 25 to 30 tissue categories¹¹ that cannot reflect variations in body geometry, body positioning, or tissue composition encountered between actual subjects undergoing a scan.^12,13 Recently, developed parallel transmission (pTX) RF technologies, using multiple transmission RF channels,^14,15 play a crucial role on these issues from two different perspectives: on one hand, using pTX resources may result in even higher maximum 10 g average SAR than conventional single-channel RF coils, while on the other hand pTX RF pulse design allows for controlling and dramatically mitigating global and local SAR.¹⁶ Naturally, accurately exercising such control upon 10 g average SAR ideally requires direct knowledge of EP and E fields on a per-subject basis, whereas current SAR computations are typically based on aforementioned generic models.

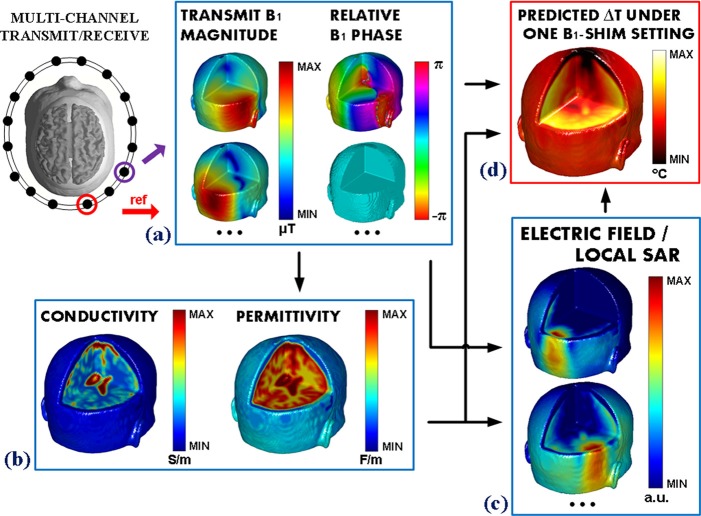
As summarized in Fig. 1, these considerations provide strong rationales especially for VHF and UHF MRI systems so as to: (1) develop methods to determine subject-specific and RF coil-specific EP and E fields derived from measured B1 maps, and (2) validate with temperature measurement the final impact of RF deposition, in order to ultimately determine a real-time, subject specific RF safety procedure with optimized pTX RF pulse design.

FIG. 1.

Conceptual framework of the experimental design in heat quantification utilizing a B1-based technique.

Although establishing this full framework will require multiple methodological developments, the current study demonstrates in a phantom at 7 T that using an approach based on MRI measurements (derived from Electrical Property Tomography (EPT)), accurate spatial distribution of SAR and local temperature increase can effectively be predicted. EPT utilizes measurable RF-coil-induced magnetic fields (B1 fields) in an MRI system to quantitatively reconstruct the local EPs of biological tissues. Proposed using different RF coil designs (e.g., birdcage quadrature, multi-channel transmit array) and at different main static magnetic fields (1.5 T–7 T), EPT methods start with the acquisition of B1 maps^17–22 followed by tissue EPs reconstruction based on a variety of dedicated algorithms,^23–25 while also providing E maps. Based on the latter, pTX RF pulse can then be designed on a subject-specific basis in order to mitigate local SAR in VHF and UHF MRI applications. The present work investigates experimentally the feasibility of B1-based local SAR estimation, expanding on previously proposed EPT approaches^13,26 in a modified formalism²⁷ where local SAR can be assessed based on measured B1 maps without explicitly reconstructing EP values, a step non-required as long as the latter are known from another source (bench measurement in the present case). This can be formalized as follows:

$$\mathit{\text{SA}}R=\sigma /2\rho ({\mu }^2{\omega }^2{(\epsilon -i\sigma /\omega )}^2)\parallel \nabla \times \mathbf{B}{\parallel }^2,$$ (1)

where tissue-related variables are σ (conductivity), ε (permittivity), and ρ (mass density), while μ (permeability) is assumed equal to free space; angular frequency ω and RF coil induced magnetic field vector B are determined by coil sensitivity profile and RF pulse. As previously mentioned, SAR is not accessible to direct MRI measurement, thus MRI thermometry will be used to monitor and compare temperature changes experimentally imposed with RF pulses in a dedicated MRI sequence against temperature changes predicted from SAR computation. Conducted on a system equipped with pTX resources, this work will also verify that B1 calibration obtained under a particular B1-shim setting can be used to predict SAR under a different B1-shim setting. B1 shim setting usually consists of 16 relative complex coefficients (magnitude and phase) applied to the 16 transmit RF channels driving the 16-channel RF coil; however, in the current study, no magnitude changes are utilized, thus, different B1-shim settings differ from the other by different relative phase transmit B1 values. In practice, due to complex interference spatial distribution, when the 16 channels are pulsing together, different B1-shim setting may result in large variations in magnitude and phase pattern of the resulting B1 spatial pattern.²⁸

For this study, a single-compartment cylinder phantom (12 cm in radius and 20 cm in height), consisting of H₂O, NaCl, Cu₂SO₄·5H2O, and Gelatin (mass ratio 100:0.27:0.1:3) was constructed with mass density of 1033 kg/m³. Bench measurements of EP were conducted with an Agilent 85070E dielectric probe kit and an Agilent E5061B network analyzer (Agilent, Santa Clara, CA, USA) at 298 MHz (conductivity: 0.56 S/m, relative permittivity 75.7), and the heat capacity (C_phantom = 3.7 kJ/kg/°C) was measured with a KD2 Pro probe (Pullman, WA, USA). Three cylinder phantoms (1 cm in radius and 6 cm in height) of mineral oil were attached to the cylinder phantom and evenly distributed to the surface of the phantom, providing a reference for phase drift corrections.²⁹ The phantom was imaged in a 7 T scanner (Magnetom 7 T, Siemens, Erlangen, Germany) equipped with an elliptical 16-channel head transceiver coil³⁰ after being placed in the bore overnight to achieve thermal equilibrium. Twelve contiguous transverse slices were sampled at a spatial resolution of 1.5 × 1.5 × 3 mm³. Two B1 phase shim settings were employed sequentially, approximating two different Circularly Polarized (CP) modes: (I) with stronger B1 in the periphery (CP2+ mode-like), and (II) with stronger B1 in the center (standard CP mode-like).

RF-heating was achieved using a sequence of 2 ms square-shaped RF pulses applied at Larmor frequency every 200 ms for a total duration of 3 min. No encoding gradients were switched during the sequence, while local temperature change for the same heating sequence will be recorded using the MRI Thermometry technique based on the proton chemical shift (PRF),³¹ denoted as ΔT_PRF. The entire experiment consisted of eight identical heating sequences that were interleaved by nine PRF temperature measurements (experiment started/ended with temperature measurements) using phase maps acquired with a 3D GRE sequence (TE = 10 ms, TR = 15 ms, acquisition time 30 s with 1 average and accelerated with a GRAPPA factor of 2 (Ref. 32)). These phase images were then converted into temperature maps according to literature^29,31 with a PRF shift coefficient of −0.01 ppm/ °C as for water. Note that RF pulses in MRI sequences typically range between about 0.5 ms and 10 ms; the corresponding bandwidth, not exceeding a few kHz, is too narrow to result in any significant variation of EP values at operating MRI frequencies.³³

For local SAR estimation through B1 mapping, a series of 16 small flip angle GRE images were acquired with each individual channel transmitting at a time while receiving all together, as described in literature.^28,34 A 3D map of the excitation flip angle was obtained utilizing the AFI technique.¹⁸ Based on both data sets, transmit B1 magnitude maps for each coil element, and the relative phase maps between each other were acquired. Then the absolute phase of spatial transmit B1 distribution of all channels can be estimated.²⁶ Finally, the voxel-wise local SAR for the shimmed excitation can be estimated using complex transmit B1 and probe-measured EP under the assumption of a dominant z-component of electric fields compared to their transverse components as described previously,^13,35 and averaged into a regional SAR value in 10 g of tissue (10 gSAR). Given the limited period of time t (up to several minutes) after starting RF-heating, thermal conduction was negligible, and the temperature increase ΔT within the non-perfused gelatin solution over time t can be treated as proportional to the induced local SAR as ΔT = t·SAR/C_phantom.²⁹ Therefore, B1-based temperature change, defined as ΔT_B1, can be calculated directly from estimated local SAR values.

The two B1-shim settings (shim I: CP mode; shim II: CP2 + mode) were applied separately in two experiments to obtain ΔT_PRF for shim I (termed ΔT_PRF,shimI) as well as ΔT_PRF for shim II (termed ΔT_PRF,shimII), and the same shim setting was used during each experiment for heating and PRF measurements, respectively. For the SAR based temperature change estimation, however, B1 maps were only obtained using shim I, and the resultant B1 map using shim II can be deduced knowing the altered B1 phase of individual channels. Based on this acquisition, ΔT_B1 was first predicted for B1-shim setting I (termed ΔT_B1,shimI), then ΔT for B1-shim setting II (termed ΔT_B1,shimII) was predicted based on the same measurement but taking the phase alteration from shim I to II into account during the SAR calculation step.

Under B1-shim setting I, ΔT_PRF maps on slice #6 measured before, during, and after RF-heating are shown in Fig. 2. The ΔT_PRF,shimI map converted from the phase image acquired before heating showed an overall mean of −0.01 °C with a standard deviation of 0.03 °C. Fig. 2 illustrates two dramatically different types of temperature-change time-courses, corresponding to locations with high temperature changes (“hot spot” H1 and H2, in the periphery) and locations with low temperature changes (“cold spot” C1 and C2, close to the center). Consistent with findings documented previously,²⁹ (1) in the hot spots, where RF energy deposition is expected to be the dominant source of local temperature alteration, ΔT_PRF,shimI changed by +0.14 °C/min on average observed during RF-heating and by −0.04 °C/min on average after RF heating with a sharp curve discontinuity in the between; (2) on the contrary, in cold spots where RF energy absorption is expected to be minimal but thermal conduction being the dominant source of temperature variation, the temperature increased at a much slower pace (+0.03 °C/min) during RF-heating and kept increasing even after RF heating was turned off, slowly tending to reach a plateau within the total duration of the experiment. In order to compare the predicted ΔT_B1,shimI through estimating 10g SAR versus temperature increase measured by PRF, only the ΔT_PRF,shimI measurement obtained for the first heating cycle (3 min) was considered in order to minimize thermal conduction contribution (considered to be negligible during this period of time).

FIG. 2.

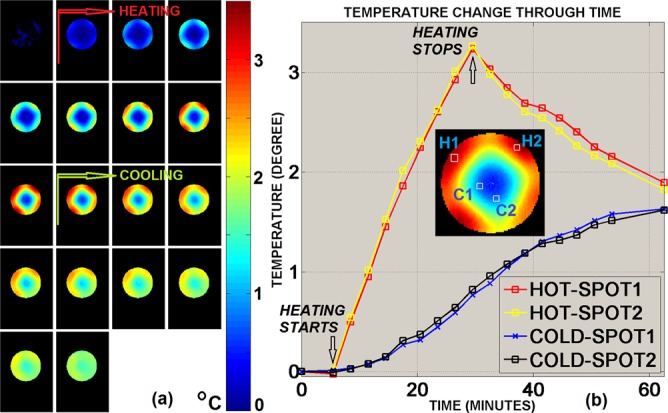
(a) Under B1-shim I, measured temperature change using MRI Thermometry; the first phase image acquired before heating was used as the reference. (b) Time course of measured temperature change at four local “hot” and “cold” spots.

Under B1-shim setting I, measured flip angle map, measured ΔT_PRF,shimI map (for the 1st heating cycle) and predicted temperature change ΔT_B1,shimI are shown in Fig. 3, on the slice of interest (slice #6). A similarity can be observed between ΔT_PRF,shimI and ΔT_B1,shimI maps, including four regional hot spots relatively symmetrically distributed in the periphery and a diamond-shaped colder center region. Taking ΔT_PRF,shimI as the reference, for regions with measured ΔT_PRF,shimI larger than 0.1 °C (arbitrarily chosen for a higher sensitivity in MRI thermometry), ΔT_B1,shimI exhibits a highly correlated distribution with a correlation coefficient of 0.941 and mean relative error of −1.2% ± 14.8% as defined previously.¹³ Within the four regional hot spots in the periphery located at 2, 5, 8, and 10 o'clock, the maximum values in ΔT_PRF,shimI measurement were 0.64 °C, 0.54 °C, 0.68 °C, and 0.55 °C, versus the corresponding predicted values at the same locations in ΔT_B1,shimI measurement of 0.51 °C, 0.41 °C, 0.46 °C, and 0.46 °C, respectively, which are overall lower than measured values at hot spots. We speculate that two major reasons may result in this underestimation: (1) the PRF shift coefficient of −0.01 ppm/ °C was used in this study as it was suggested for both water-based phantom and aqueous tissues,^29,36 whereas a value of −0.013 ppm/ °C was rigorously measured and used for agar-gel solutions³⁷—the slight discrepancy between materials suggests adding gelatin may change the chemical shift coefficient and lead to a lower ΔT_PRF,shimI measurement values which deserves further investigation; (2) the z-component of electric fields is assumed dominant in this study when calculating local SAR values; thus, eliminating the transverse components of electric fields may result in a residual deviation towards an lower temperature prediction.

FIG. 3.

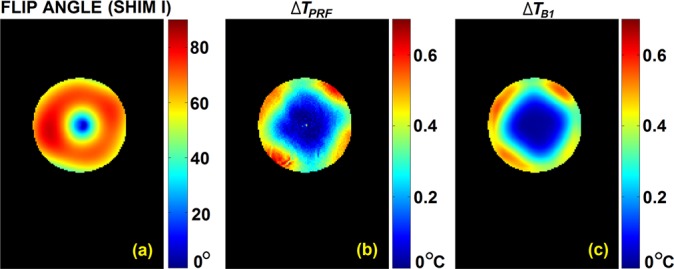
Under B1-shim I, (a) measured actual flip angle, (b) measured temperature change by PRF, and (c) predicted temperature increase calculated from B1 measured under B1-shim I.

Fig. 4 shows, on the slice of interest (slice #6), measured flip angle distribution and ΔT_PRF,shimII map (for the 1st heating cycle) under B1-shim setting II, and predicted temperature change ΔT_B1,shimII. A noticeable level of noise is observed in ΔT_PRF,shimII measurement. In addition to some regions where transmit B1 amplitude was very weak in this setting, resulting in very low flip angle values (see regions in the periphery located at 4 and 12 o'clock) with less reliable measurement, limited sensitivity of PRF measurement to much lower temperature increases under B1-shim II yielded less reliable local temperature measurement: compared to B1-shim I (CP2 + mode-like), the power dissipated into the object using B1-shim II (standard CP mode-like) was significantly less,³⁸ i.e., roughly 0.13 °C (B1-shim II) vs. 0.27 °C (B1-shim I) as average temperature increase in the corresponding ΔT_PRF maps during the first heating cycle. Less absorbed RF energy resulted in a lower sensitivity in capturing MRI phase difference that was partially corrupted by system noise and thus became less accurate in MRI thermometry result. Nevertheless, predicted ΔT_B1,shimII preserves an overall similar spatial pattern with a prediction of high (maximum value of 0.35 °C) and low SAR regions as compared to those in ΔT_PRF,shimII, showing a correlation coefficient of 0.820 and mean relative error of 43.2% ± 23.8%.

FIG. 4.

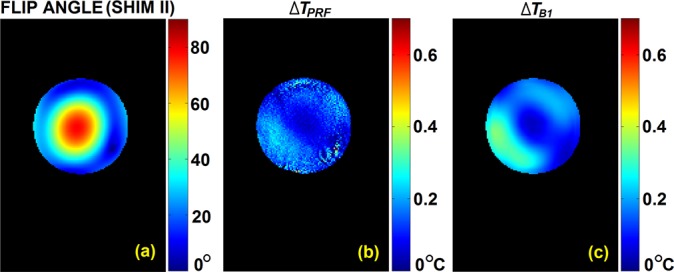
Under B1-shim II, (a) measured actual flip angle, (b) measured temperature change by PRF, and (c) predicted temperature increase calculated from B1 measured under B1-shim I.

Current widely accepted guidelines in MRI provide regulations for upper limits on global SAR as well as on maximum local SAR averaged through 10 g of tissue. While the measurement of global SAR is relatively straightforward—either by measurement of the temperature rise in a thermally isolated phantom (calorimetric method) or by monitoring the forward and reflected RF power (pulse energy method),³⁹ the B1-based approach suggests an alternative practical means for subject-specific local SAR estimation. The main purpose of this study was to demonstrate the feasibility of B1-based reconstruction in estimating local SAR distributions in VHF- and UHF-MRI applications, and measurable local temperature change due to RF-heating was chosen as the metric for validation. A non-perfused physical gelatin phantom experiment has been designed with a short period (3 min) of RF-heating so that the effect of thermal conduction can be neglected, and estimated local SAR values can be linearly correlated and converted into predicted local temperature change. Real temperature increase has been measured with well-established MRI thermometry technique as the reference. As seen in Fig. 3 as a validation, B1-based local SAR estimation can predict temperature increase distribution in good agreement with PRF measurement; moreover, results in Fig. 4 indicate that B1 calibration obtained under a particular B1 shim setting can be used to predict local SAR under a different B1 shim setting, suggesting the B1-based approach may ultimately be practiced to determine a real-time, subject specific RF safety procedure with optimized pTX RF pulse design.

Note that temperature measurement and prediction were performed on the central slice #6, based on two considerations. First, 10 g averaged SAR in a voxel is ideally computed in a cube of 10 g mass centered on this voxel; with a voxel size of 1.5 × 1.5 × 3 mm³, this corresponds approximately to a 12 × 12 × 12 voxels cube which could be built only for voxels on the center slice given our B1 mapping data collected over 12 contiguous transverse slices. Second, as documented in our previous simulation study,¹³ the largest local SAR values (that define safety constraints on RF pulse design and MRI protocols) are typically found on the central transverse slice with the RF coil used in this study. We also verified that the spatial pattern of un-averaged voxel-wise local SAR, computed on each of the 12 transverse slices, was fairly similar through all slices, with an overall trend towards decreasing values when moving away from the central slice along the z direction, consistent with previous reports.¹³

Ultimately, the full implementation of subject-specific local SAR prediction would require knowing EP values specifically for each subject, a concern which is especially relevant in the case of pathological alteration of tissues where literature based EP may not be reliable. As of today, however, most EPT techniques are fairly sensitive to boundary conditions in heterogeneous samples, with associated Laplacian operation inherently amplifying experimental noise, potentially resulting in excessively long MRI acquisition duration to reach higher SNR. Recent studies, on the other hand, indicate that new algorithms such as an effective gradient-based method (demonstrated with a microtrip array coil in the brain) may address this issue by providing the necessary robustness to achieve satisfactory subject-specific EP maps in vivo.⁴⁰ In parallel to these efforts, a new concept for robust B1-based local SAR prediction in vivo has also been proposed, avoiding the needs for explicitly reconstructing EP distribution, thereby providing great simplification of the problem and increasing the degrees of freedom to find optimum tradeoffs between speed, robustness and patient safety.²⁷ The present study is deliberately focusing on demonstrating that reliable SAR prediction can be obtained based on measured B1 + maps, which is a necessary methodological component for both the aforementioned promising developments. Note that another simplification in the present study derives from the fact that no perfusion occurs in a gelatin phantom, whereas in-vivo implementation of these methods will require including bio-heat equations in the models to take into account the impact of blood flow upon local temperature.⁸ Encouraged by the present validation results, the establishment of B1-based local SAR quantification may ultimately lead to comprehensive development and use of VHF- and UHF-MRI in human subjects.