Abstract
Purpose:
Theoretical dose–response models offer the possibility to assess second cancer induction risks after external beam therapy. The parameters used in these models are determined with limited data from epidemiological studies. Risk estimations are thus associated with considerable uncertainties. This study aims at illustrating uncertainties when predicting the risk for organ-specific second cancers in the primary radiation field illustrated by choosing selected treatment plans for brain cancer patients.
Methods:
A widely used risk model was considered in this study. The uncertainties of the model parameters were estimated with reported data of second cancer incidences for various organs. Standard error propagation was then subsequently applied to assess the uncertainty in the risk model. Next, second cancer risks of five pediatric patients treated for cancer in the head and neck regions were calculated. For each case, treatment plans for proton and photon therapy were designed to estimate the uncertainties (a) in the lifetime attributable risk (LAR) for a given treatment modality and (b) when comparing risks of two different treatment modalities.
Results:
Uncertainties in excess of 100% of the risk were found for almost all organs considered. When applied to treatment plans, the calculated LAR values have uncertainties of the same magnitude. A comparison between cancer risks of different treatment modalities, however, does allow statistically significant conclusions. In the studied cases, the patient averaged LAR ratio of proton and photon treatments was 0.35, 0.56, and 0.59 for brain carcinoma, brain sarcoma, and bone sarcoma, respectively. Their corresponding uncertainties were estimated to be potentially below 5%, depending on uncertainties in dosimetry.
Conclusions:
The uncertainty in the dose–response curve in cancer risk models makes it currently impractical to predict the risk for an individual external beam treatment. On the other hand, the ratio of absolute risks between two modalities is less sensitive to the uncertainties in the risk model and can provide statistically significant estimates.
Keywords: radiation induced cancer, risk modeling
1. INTRODUCTION
Advances in radiation therapy and more conformal treatments have resulted in fewer side effects and an overall higher life expectancy of cancer survivors. Understanding late effects has thus become more important, in particular, for pediatric patients undergoing radiation therapy. The potential long term benefits of new innovative treatment technologies become apparent only after years or decades of follow-up. Prospective risk assessments to expose possible health benefits are, therefore, needed. Theoretical dose–response models provide estimates with respect to potential outcomes of a treatment. One long term side effect of concern particularly for pediatric patients is the development of a second cancer.1
Dose–response relationships for cancer risk prediction are usually obtained by analyzing retrospective cohort studies. At present, the largest amount of data available comes from the survivors of the atomic bomb incident in Japan. Studies on this cohort have found that the risk of developing a radiation-induced second solid tumor is linear with the dose in the range between ∼0.1 and ∼2.5 Gy.3–5
At low doses, some of the published models recommend extrapolating the linear dose–response to 0 Gy (linear no-threshold or LNT).3–5 There are indications that this extrapolation should be reconsidered because of complex mechanisms such as adaptive dose response.6 Studies on the potential risk to develop a second cancer from scattered radiation in radiation therapy outside of the main radiation field, i.e., in the dose range below ∼2.5 Gy, have been reviewed previously.7
The majority of second cancers from radiation therapy occur in the volume irradiated by the primary radiation field at doses in excess of ∼2.5 Gy. The frequency of second cancer incidences in radiation therapy is relatively low, which hampers an accurate description of dose–response relationship for organs at risk.2 Furthermore, most epidemiological studies are very specific to the primary and secondary cancers evaluated. Understanding the dose–response relationships in this dose region is important for second cancer risk assessments after radiation therapy. Dose–response relationships might become nonlinear because cell survival may counteract cell mutation. Further, repopulation plays a significant role. So far, a nonlinear dose response has only been found for thyroid cancer as shown in a study by Bhatti et al.8 based on the childhood cancer survivor study (CCSS), which most likely reflects the fact of limited repopulation for thyroid. Thus, for other sites, the nonlinearity at higher doses may not be valid.2 Many epidemiological studies on second cancer induction after radiation therapy focus on a typically narrow dose range, making the transfer of the reported risk to other doses difficult. In addition, treatments, which have occurred decades ago, do often not provide complete dosimetric information leading to high and unknown uncertainties in retrospective risk assessment studies. A reconstruction of the dosimetry is often not feasible. Modern radiation therapy is highly conformal resulting in heterogeneous dose distributions in organs at risk thus hindering the correlation of a second tumor with a local dose.
Phenomenological risk models are frequently applied to estimate the risk of radiation-induced cancers at doses in excess of 2.5 Gy, i.e., for organs inside the primary radiation field. The underlying model parameters, however, are determined with limited data. Consequently, uncertainties will impact the model predictions.
Our study assesses the uncertainty in risk prediction by empirically estimating the uncertainties in the parameters of a widely used risk model for various organs. First, we performed an extensive literature review on second cancer studies. We then compared the collected data with the prediction of the model using published parameters and determined a new set of parameters by fitting the model. This new parameter set was subsequently applied to estimate the uncertainties of the published parameters.
The significance of the deduced uncertainties was tested using treatment plans of five representative pediatric patients with primary brain tumors. Second cancer risks in the primary radiation field for different proton and photon treatment modalities were evaluated with respect to modeling uncertainties.
2. MATERIALS AND METHODS
2.A. Prediction of cancer risks for doses above 2.5 Gy
As the dose increases to values not covered by the atomic bomb survivor cohort, potential relations between radiation-induced cell sterilization, cell proliferation, and repopulation may cause a deviation from a linear dose response. Furthermore, dose–response models describing cancer incidence in this dose region do have to consider that organ doses are typically heterogeneous. Various theoretical models have been developed with model parameters fitted to clinical data. 9–11 Recent studies (e.g., Ref. 12) have applied a model developed by Schneider et al.13 to estimate the outcome of different treatment modalities. We refer to this model as “S-model.” Based on assumptions on cell repopulation/repair, mutation, and sterilization, this model gives a dose dependent formulation for the excess absolute risk (EAR). The EAR is expressed by a dose dependent function with an initial slope βinit, the risk equivalent dose (RED) describing the local (e.g., in a CT voxel) change in EAR with dose, and the function μ(e, a), which describes the change in EAR with age at exposure (e) and attainted age (a) [Eqs. (1) and (2)] using age related parameters are γe and γa4
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
The S-model provides parameters for two types of cancers, namely, carcinoma [Eqs. (3) and (4)] and sarcoma [Eq. (5)]. The parameters used are a repopulation/repair parameter R (values between 0 and 1), the dose per voxel D, the prescribed total target dose DT, the prescribed target dose per fraction dT, and the parameters of the linear quadratic dose–response model α and β [Eq. (6)].
To consider heterogeneous organ doses, the organ equivalent dose (OED) as the volume averaged RED in the region of interest is applied.14 The EAR is linearly proportional to OED and depends on the dose distribution as shown in Eqs. (7) and (8) (with the total volume VT being divided into i voxels with dose Di)
| (7) |
| (8) |
We define as the “reference model” the S-model using the published organ-specific parameters listed in Table I (reference parameters). All parameters with the exception of thyroid were published in a study by Schneider et al.15 The parameters for thyroid cancer were taken from a study by Mihai et al.16 For organs described by the sarcoma model, R was arbitrarily set to 0.5 because no clear tendency to a specific value has been established.15 Note that many of the parameters in Table I were published without specifying their uncertainties.
TABLE I.
Organ parameters used for the S-model as published by Schneider et al. (Ref. 15) and Mihai et al. (Ref. 16) for either the sarcomaa or the carcinomab model (* indicates that the uncertainty has not been published).
| Organ | βinit | γe | γa | α | R |
|---|---|---|---|---|---|
| Bonea | 0.2* | −0.013 | −0.56 | 0.067* | 0.5* |
| Brainb | 0.7 | −0.024 | 2.38 | 0.018* | 0.93* |
| Breastb | 8.2 | −0.037 | 1.7 | 0.044* | 0.15* |
| Lungb | 8 | 0.002 | 4.23 | 0.042* | 0.83* |
| Soft tissuea | 0.6* | −0.013 | −0.56 | 0.06* | 0.5* |
| Thyroidb | 2.14* | −0.046 | 0.6 | 0.031* | 1* |
An often used parameter for quantifying the cancer incidence risk is the lifetime attributable risk (LAR) as given in Eq. (9) 17
| (9) |
It describes the total cancer risk between age at exposure e and an attained age of a. L is the latency time, which was set to 5 yr in our study. S(a)/S(e) is the probability of surviving from age e to age a, while the quantity S(x) itself describes the amount of survivors at age x out of 100 000 newly born. Values for the U.S. population were obtained from the newest U.S. life table published by the National Center of Health Statistics.18
2.B. Review of epidemiological studies
In order to judge the quality of the model predictions, we performed a comprehensive review of published studies on radiation-induced cancer incidences in clinically irradiated cohorts. Risks in these studies were reported as either relative risks (RR), odds ratios (OR), or signal incidence ratios (SIR). Their definitions are based on RE (risk of disease in exposed group), RU [risk of disease in unexposed group (baseline risk)], O (number of disease cases observed), and E (number of disease cases expected) as shown in Eqs. (10) and (11)
| (10) |
| (11) |
To calculate the EAR, we use the definitions for EAR shown in Eq. (12) and combined them with the expressions in Eqs. (10) and (11) 19
| (12a) |
| (12b) |
where PY denotes person-years.
Table II summarizes all reviewed studies with the number of data points considered for the present study. A total of 103 cancer incidence data points for various doses and organs were collected. Sixty-three of those were reported relative to the lowest dose category in the corresponding study (marked accordingly in the table). A recalculation of the cancer risk relative to an unexposed population i.e., the baseline risk was therefore necessary. For this purpose, a baseline risk model with site specific parameters published by Shuryak et al.11 was used. The published parameters are based on the surveillance, epidemiology, and end results (SEER) database (http://seer.cancer.gov). No model parameters were reported for bone cancer. For this case, the baseline risk was taken from the SEER-13 data set, which includes cancer incidences from 1992 to 2010.20
TABLE II.
List of reviewed studies and organs/structures with cancer risk data at clinical relevant doses.
| Organ/structure | Data source reference | # Data points | Baseline cancer risk calculated?a | Doseb |
|---|---|---|---|---|
| Bone | Ref. 21 | 1 | n | Mean1 |
| Ref. 22 | 4 | y, SEER | Mean2 | |
| Ref. 23 | 5 | n | Mean1 | |
| Ref. 24 | 1 | n | Mean1 | |
| Ref. 25 | 1 | n | Mean1 | |
| Ref. 26 | 1 | n | Mean1 | |
| Ref. 27 | 1 | n | Mean1 | |
| Ref. 28 | 1 | n | Mean1 | |
| Ref. 29 | 3 | n | Mean1 | |
| Brain | Ref. 22 | 4 | y∗ | Mean2 |
| Ref. 30 | 6 | n | Mean1 | |
| Ref. 31 | 6 | y∗ | Mean1 | |
| Breast | Ref. 22 | 5 | y∗ | Mean2 |
| Ref. 32 | 4 | y∗ | Mean1 | |
| Ref. 33 | 6 | y∗ | Mean1 | |
| Ref. 34 | 1 | y∗ | Mean1 | |
| Ref. 35 | 7c | n | Median | |
| Ref. 36 | 4 | y∗ | Median | |
| Ref. 37 | 1 | n | Mean1 | |
| Lung | Ref. 38 | 3 | y∗ | Mean1 |
| Ref. 39 | 5d | y∗ | Mean1 | |
| Soft tissue | Ref. 27 | 5 | y∗ | Median |
| Ref. 29 | 3 | y∗ | Mean1 | |
| Thyroid | Ref. 4 | 1e | n | Mean1 |
| Ref. 8 | 10e | n | Mean1 | |
| Ref. 22 | 4 | y∗ | Mean2 | |
| Ref. 40 | 5 | y∗ | Mean1 | |
| Ref. 41 | 4 | y∗ | Mean1 | |
| Ref. 42 | 1e | n | OED |
Indication whether a calculation of the baseline cancer risk was calculated (y) or not (n). The baseline risk was taken from Shuryak et al. (Ref. 11) (∗) or from the SEER database (Ref. 20).
Dose related to second cancer. Mean1: the mean dose was reported in the respective study. Mean2: no mean dose was reported and the dose was assessed using the mean value of the published dose range. Median: the median dose was reported by the respective study. OED: organ equivalent dose.
EAR values given elsewhere (Ref. 43).
EAR values given elsewhere (Ref. 44).
EAR values given elsewhere (Ref. 16).
The reported risks were initially given for different ages at exposure and attained ages. An additional normalization was therefore necessary to represent them at a chosen age. Previous S-model predictions were presented for an age at exposure and attained age of 30 and 70.15 Consequently, we chose the same values for the present study and transferred the risk by applying Eq. (2).
2.C. Uncertainty estimation for the dose–response model
The uncertainty in the S-model was estimated using error propagation according to Eq. (13) as follows:
| (13) |
For a given set of model parameters of an organ, we assume that all parameters in this set are independent. This will eliminate the covariance term given in Eq. (13). The uncertainties in γe, γa were estimated using the maximum difference in the 95% confidence interval (CI) published in the atomic bomb survivor study.4 For βinit, the 95% CI was taken from the study by Schneider et al.15 To estimate the uncertainties in R and α, the parameters were determined by fitting the model to the data given in Table II. Discrepancies between the fitted parameters and the reference parameters were used as uncertainty estimations. Exceptions were used for thyroid, bone, and soft tissue where βinit was determined in the fitting procedure because the 95% CI was not published for the reference parameters. Only the study on thyroid reported a value for R, which was approximately 0 (Table IV in Ref. 16), so that Eq. (4) could be applied.
This procedure has its limitations but seems to be the only one feasible given that parameter uncertainties for the S–model based on limited data are not reported but expected to be substantial.
2.D. Application to clinical cases
For the application of the reference model with its estimated uncertainties, five pediatric cases of primary brain tumor have been chosen from a previous study.45 Those cases were selected from a database of pediatric patients treated at the Massachusetts General Hospital. All patients received a 4 field passive scattered proton beam treatment (PPT). The patients were selected as a representative group of pediatric head and neck tumors with different ages and genders and with different tumor sizes as well as patients who could be planned with two different field numbers for protons and IMRT. The patient characteristics are summarized in Table III. For each patient, five additional treatment plans for different treatment modalities were prepared: two IMRT plans with five and seven fields and one VMAT plan using Raystation (RaySearch laboratories); one PPT with three fields using XiO (Elekta); one proton beam scanning (PBS) plan with an average spot size, σ, of 10 mm at isocenter using Astroid. All treatment plans met the prescribed target coverage and OAR dose constraints. The main planning objective, as required by the clinical protocol, was to avoid the occurrence of hot spots (larger dose than prescribed) within the optic nerves, chiasm, and brainstem. The values for mean dose to soft tissue and skull for all patients are listed elsewhere.45
TABLE III.
Characteristics of patients used in this study. DT denotes the prescribed dose and dT the dose per fraction in Gy.
| Age at treatment | Gender | DT | dT | Tumor histology | CTV volume (cm3) |
|---|---|---|---|---|---|
| 4 | F | 54 | 1.8 | Ependymoma | 74.1 |
| 6 | F | 52.2 | 1.8 | Craniopharyngioma | 19.55 |
| 11 | F | 50.4 | 1.8 | Craniopharyngioma | 11.3 |
| 13 | M | 52.2 | 1.8 | Craniopharyngioma | 30.37 |
| 15 | F | 50.4 | 1.8 | Astrocytoma | 23.39 |
The patient analysis did focus on the risks for brain carcinoma, brain sarcoma, and bone sarcoma. The dose–volume histograms for all relevant areas within the primary radiation field were extracted and the corresponding LARs were calculated. The attained age was set to 78 in accordance with the average lifetime of a U.S. citizen.46 For the comparison of second cancer risks of two individual treatment modalities, a new quantity was defined which is the ratio of both LARs. It will be noted in this study as the ratio of risk (ROR). The uncertainty of the ROR was calculated using the assessed LAR uncertainties and standard error propagation.
The results for IMRT with five and seven fields and VMAT were averaged over all patients to represent the second cancer risk after a treatment with photons. As for protons, we averaged the results of PPT with 3/4 fields and PBS.
3. RESULTS
3.A. Comparison of published data with model predictions
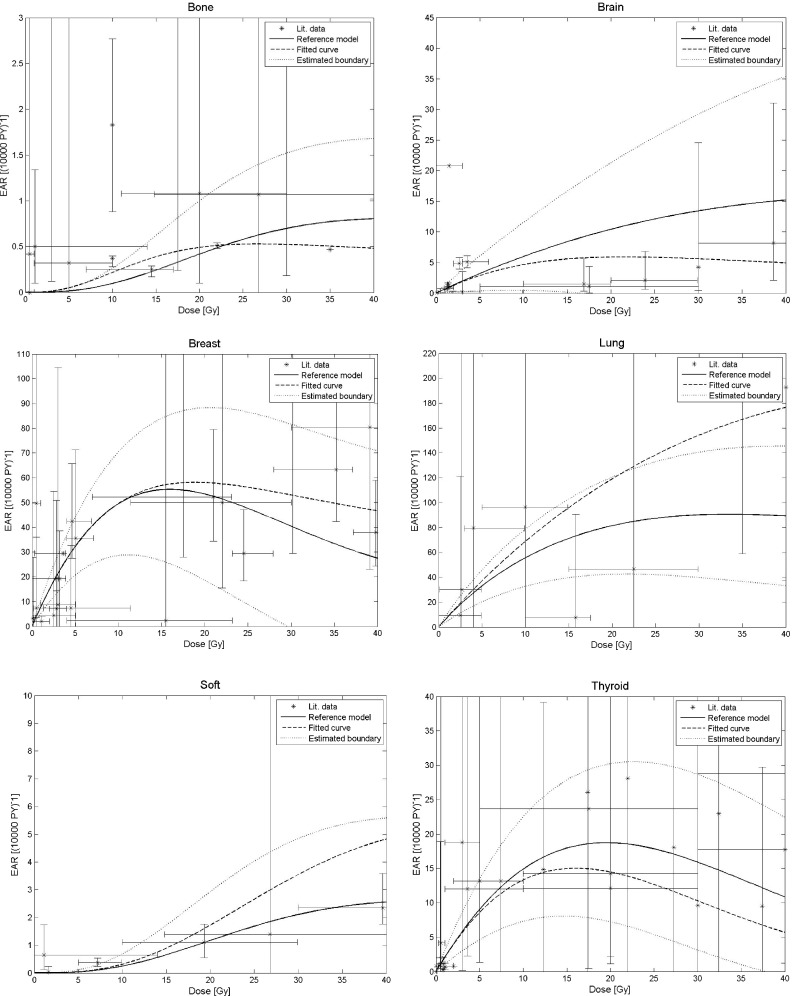
The predictions of the reference model for the collected data in Table II are shown in Fig. 1. There are several potential reasons for the considerable difference between data and prediction. In the original work by Schneider et al.,15 the parameters (Table I) for the model were determined using data from the atomic bomb survivors as well as clinical data from Hodgkin’s disease patients. Those data as well as the clinical data surveyed for this study contain no information on the dose at the region where the second cancer originated. This is, in particular, problematic for organs that received heterogeneous dose distributions during treatment. Further, the model predicts solely sarcoma and carcinoma, whereas most reported studies refer to second cancers in general. Moreover, the assumed population independence of the collected data is in general not valid. Many factors including lifestyle of the population, environmental, or genetic predisposition may have influenced cancer induction. For example, the reported baseline risk for stomach cancer in the Netherlands was reported to be five times lower than in a Japanese cohort.47 Thus, proper population transfer techniques are necessary to relate observed cancer rates from one population to another.5
FIG. 1.
Comparison of the reported second cancer incidence data shown in Table II and the prediction of the reference model as a function of dose. The black dotted lines show the estimated uncertainty when applying the reference model (solid line) using Tables I and V and Eq. (13). Also shown is a fit of the S-model using the data listed in Table II (dashed line). Age at exposure and attained age were set to 30 and 70, respectively.
3.B. Estimated model uncertainties
Table IV summarizes the resulting parameters when fitting the S-model to the data from Table II. The fit did not converge for bone and soft tissue. We therefore fixed R to 0.5 and assumed the highest uncertainty, i.e., ΔR = 0.5. The estimated uncertainties for all parameters in Table I are summarized in Table V using the procedure described in Sec. 2.C. The fit results and the uncertainties of the reference model are shown in Figs. 1. Deviations in excess of 100% can be found for all organs considered. The magnitude of the uncertainty strongly depends on the prescribed doses DT, dT, and chosen ages e and a. The relative uncertainties for breast carcinoma, for example, are below 100% up to a dose of ∼30 Gy for the parameters: DT = 40 Gy, dT = 2 Gy, e = 30 y, and a = 70 y.15 Because of the dose dependency, the uncertainty assessment using Eq. (13) depends on the fractionation regimen.
TABLE IV.
Model parameters obtained by fitting the S-model to the reviewed data.
| Organ | βinit,fit | αfit | Rfit |
|---|---|---|---|
| Bone | 0.197 | 0.093 | 0.5 |
| Brain | — | 0.051 | 0.455 |
| Breast | — | 0.066 | 0.635 |
| Lung | — | 0.017 | 0.864 |
| Soft tissue | 0.874 | 0.062 | 0.5 |
| Thyroid | 1.109 | 0.017 | — |
TABLE V.
Estimated absolute uncertainties for the reference parameters given in Table I.
| Organ | Δβinit | Δγe | Δγa | Δα | ΔR |
|---|---|---|---|---|---|
| Bone | 0.124 | 0.093 | 2.24 | 0.013 | 0.5 |
| Brain | 0.61 | 0.008 | 0.48 | 0.033 | 0.475 |
| Breast | 2.8 | 0.013 | 0.8 | 0.022 | 0.485 |
| Lung | 3 | 0.026 | 1.47 | 0.025 | 0.034 |
| Soft tissue | 0.364 | 0.093 | 2.24 | 0.035 | 0.5 |
| Thyroid | 0.307 | 0.03 | 1.2 | 0.004 | — |
3.C. Estimated uncertainties when predicting cancer incidence risks for clinical cases
The patient averaged LAR for all treatment plans as well as the uncertainties using the results in Table V are given in Table VI. For instance, the patient averaged LAR for brain carcinoma was estimated as 1.9 ± 1.9% for the 4 field PPT plan and 2.8 ± 2.8% for the 7 field IMRT plan. The patient averaged LAR for a treatment with photon and protons was found to be 2.8 ± 2.9% and 1.7 ± 1.7%, respectively.
TABLE VI.
Patient averaged LAR values for an attained age of 78 yr.
| Bone sarcoma | Brain carcinoma | Brain sarcoma | ||||
|---|---|---|---|---|---|---|
| Modality | LAR (%) | ΔLAR (%) | LAR (%) | ΔLAR (%) | LAR (%) | ΔLAR (%) |
| IMRT 5 field | 0.1 | 0.2 | 2.8 | 2.9 | 0.8 | 2.3 |
| IMRT 7 field | 0.1 | 0.2 | 2.8 | 2.8 | 0.7 | 2.2 |
| VMAT | 0.1 | 0.2 | 2.8 | 2.9 | 0.7 | 2.2 |
| PPT 3 field | <0.1 | 0.1 | 1.7 | 1.7 | 0.5 | 1.5 |
| PPT 4 field | <0.1 | 0.1 | 1.9 | 1.9 | 0.5 | 1.4 |
| PBS, σ = 10 mm | <0.1 | 0.1 | 1.4 | 1.5 | 0.4 | 1.2 |
| Photon | 0.1 | 0.2 | 2.8 | 2.9 | 0.8 | 2.3 |
| Proton | <0.1 | 0.1 | 1.7 | 1.7 | 0.5 | 1.4 |
The large uncertainty demonstrates that it may generally not be feasible to reliably predict absolute cancer risks for radiation therapy patients solely based on treatment plan information. It is apparent that the uncertainties associated with model predictions do not allow a reasonable estimation of second cancer risks in radiation therapy to within at least a factor of 2. The exception may be the thyroid [Fig. 1] where the risk model uncertainties due to available data are lower for certain age groups and prescribed doses.
For the estimation of brain sarcoma risk, we applied the parameters for soft tissue in Table I as has been done in a previous study.48 This approximation had to be made because for the most frequent form of brain cancer, i.e., meningioma, dose–response relationships, and specific model parameters are not available.
3.D. Estimated uncertainties when comparing cancer incidence risks for different modalities
The patient averaged ROR as well as the calculated uncertainties is given in Table VII. For instance, for brain carcinoma, we find a patient averaged ROR between the 7 field IMRT plan and the 4 field PPT plan of 1.59 with an uncertainty of just ∼1%. The ROR for brain carcinoma between the considered proton and photon plans was estimated as 0.56 with an uncertainty of 1.7%.
TABLE VII.
Patient averaged ROR values using LAR values relative to PPT with four fields. PPT: passive proton beam therapy; PBS: proton beam scanning; PvP: risk after a proton treatment divided by the risk after a photon treatment.
| Bone sarcoma | Brain carcinoma | Brain sarcoma | ||||
|---|---|---|---|---|---|---|
| Modality | ROR | ΔROR/ROR (%) | ROR | ΔROR/ROR (%) | ROR | ΔROR/ROR (%) |
| IMRT, 5 field | 3.84 | 9.6 | 1.58 | 1.1 | 1.71 | 0.7 |
| IMRT, 7 field | 3.62 | 8.7 | 1.59 | 1 | 1.69 | 0.8 |
| VMAT | 3.18 | 8.2 | 1.61 | 1.2 | 1.68 | 0.8 |
| PPT, 3 field | 1.21 | 4.6 | 0.89 | 3.1 | 1.09 | 0.9 |
| PPT, 4 field | 1 | — | 1 | — | 1 | — |
| PBS, 3 field, 10 mm | 0.86 | 5 | 0.76 | 2.2 | 0.88 | 1.5 |
| PvP | 0.35 | 5.1 | 0.56 | 1.7 | 0.59 | 1.4 |
In comparison to the results in Table VI, the uncertainties in the actual dose–response curve do not contribute significantly to uncertainties in the ROR. This is due to large covariance terms appearing in the standard error propagation procedure, because the same dose–response model is used for all treatment modalities. Thus, the uncertainties in the dose–response curves largely cancel out in these relative estimations, so that the main difference in risk between modalities is due to differences in the dose distribution. For example, would the dose–response curve be perfectly linear, the uncertainty in the ROR would be reduced to the uncertainty of the dose predictions. Note that the S-model does consider the inhomogeneous organ dose distributions via the OED.
4. DISCUSSION AND CONCLUSIONS
This study did focus on the in-field region of the dose distribution because second solid tumors are mostly found within or close to the primary cancer treatment field.49 Not included are the contributions from scattered radiation (e.g., neutrons in proton therapy) which can be neglected inside the primary radiation field.45
In the first part of this study, we estimated the uncertainties of dose–response curves predicted by the S-model for various organs. They were determined by estimating the uncertainties of a recently published set of site specific parameters for the model (Table I). The uncertainties in the dose–response curves were found to exceed 100% of the predicted second cancer risk. There are various factors that might have caused the substantial uncertainties. As mentioned in Sec. 2.C, for the majority of the model parameters, the uncertainty was estimated using the maximum difference in the 95% CI. This procedure assumes that the uncertainty for each parameter is symmetric and could lead to an overestimation of the lower boundary in the dose–response curve. On the other hand, various properties in the data, e.g., gender, genetic predisposition, or lifestyle could have influenced the published model parameters. We decided to consider a rather broad estimation of the model parameters for each organ.
Several aspects impacting the risks are not considered in the S-model formalism. For instance, genetic factors that may play a role when applying risk parameters from the general population to cancer patients who may have a genetic predisposition toward radiogenic secondary malignancies. These uncertainties will affect LAR values considerably, while the effect on ROR can be expected to be much smaller.
The model uncertainties depend on the prescription doses. One would expect that the uncertainties decrease with decreasing dose, because of the increase in linearity of the dose–response. This holds for the absolute uncertainties as well as for the uncertainties when comparing modalities. Furthermore, the second cancer risk for one organ might be correlated to the second cancer risk of another organ. Such correlations are generally not known.
Our applied formalism does not include a dose and dose rate effectiveness factor (DDREF) to take into account fractionation when using dosimetric data for risk analysis for solid tumors. Several DDREF values, typically between 1.5 and 3, have been suggested by regulatory bodies (see discussion in Ref. 5). These values were recommended for linear dose–response relationships and for low doses, i.e., doses much lower than typical doses in-field. The uncertainty of risk estimations due to uncertainties in DDREF is unclear.
In the second part of this study, we tested the model with its uncertainties using treatment plans for brain cancer. The large uncertainties in the model lead to uncertainties of the same magnitude for the calculated LAR. However, these uncertainties are significantly reduced when comparing individual treatment plans or different treatment modalities as demonstrated by the ROR. This is because relative risks are mainly determined by the difference in dose and are less affected by uncertainties in the actual dose–response curve. Uncertainties in the organ dose prediction by the planning system and the dose delivery could result in an additional uncertainty of ∼3%, which was not considered.
This study shows that absolute risks are by far less reliable than relative risks. Treatment decision, in particular for pediatric patients, typically involves the question whether to refer the patient to a proton facility or treat with photons (considering that the achievable target conformality is more or less comparable). This study demonstrates that risk models can indeed offer guidance with respect to the risk for second malignancies.
ACKNOWLEDGMENT
The project was supported by the Federal Share of program income earned by Massachusetts General Hospital on C06 CA059267, Proton Therapy Research, and Treatment Center.
REFERENCES
- 1.Henderson T. O., Whitton J., Stovall M., Mertens A. C., Mitby P., Friedman D., Strong L. C., Hammond S., Neglia J. P., Meadows A. T., Robison L., and Diller L., “Secondary sarcomas in childhood cancer survivors: A report from the childhood cancer survivor study,” JNCI, J. Natl. Cancer Inst. 99(4), 300–308 (2007). 10.1093/jnci/djk052 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Suit H., Goldberg S., Niemierko A., Ancukiewicz M., Hall E., Goitein M., Wong W., and Paganetti H., “Secondary carcinogenesis in radiation treated patients. A review of data on radiation induced cancers in human, non human primate, canine and rodent subjects,” Radiat. Res. 167, 12–42 (2007). 10.1667/RR0527.1 [DOI] [PubMed] [Google Scholar]
- 3.BEIR, Health Risks from Exposure to Low Levels of Ionizing Radiation, BEIR VII, Phase 2 (National Research Council, National Academy of Science, Washington, DC, 2006). [PubMed] [Google Scholar]
- 4.Preston L., Ron E., Tokuoka S., Funamoto S., Nishi N., Soda M., Mabuchi K., and Kodama K., “Solid cancer incidence in atomic bomb survivors: 1958-1998,” Radiat. Res. 168, 1–64 (2007). 10.1667/RR0763.1 [DOI] [PubMed] [Google Scholar]
- 5.United Nations Scientific Committee on the Effects of Atomic Radiation, in Effects of Ionizing Radiation: United Nations Scientific Committee on the Effects of Atomic Radiation: UNSCEAR 2006 Report, Volume 1—Report to the General Assembly, with Scientific Annexes A and B (United Nations Publications, Vienna, 2008). [Google Scholar]
- 6.Newhauser W. D. and Durante M., “Assessing the risk of second malignancies after modern radiotherapy,” Nat. Rev. Cancer 11(2), 438–448 (2011). 10.1038/nrc3069 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Xu X. G., Bednarz B., and Paganetti H., “A review of dosimetry studies on external-beam radiation treatment with respect to second cancer induction,” Phys. Med. Biol. 53(13), R193–R241 (2008). 10.1088/0031-9155/53/13/R01 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bhatti P., Veiga L. H., Ronckers C. M., Sigurdson A. J., Stovall M., Smith S. A., Weathers R., Leisenring W., Mertens A. C., Hammond S., Friedman D. L., Neglia J. P., Meadows A. T., Donaldson S. S., Sklar C. A., Robison L. L., and Inskip P. D., “Risk of second primary thyroid cancer after radiotherapy for a childhood cancer in a large cohort study: An update from the childhood cancer survivor study,” Radiat. Res. 174, 741–752 (2010). 10.1667/RR2240.1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lindsay K. A., Wheldon E. G., Deehan C., and Wheldon T. E., “Radiation carcinogenesis modelling for risk of treatment-related second tumours following radiotherapy,” Br. J. Radiol. 74(882), 529–536 (2001). 10.1259/bjr.74.882.740529 [DOI] [PubMed] [Google Scholar]
- 10.Shuryak I., Hahnfeldt P., Hlatky L., Sachs R. K., and Brenner D. J., “A new view of radiation-induced cancer: Integrating short- and long-term processes. Part I: Approach,” Radiat. Environ. Biophys. 48(2), 263–274 (2009). 10.1007/s00411-009-0230-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Shuryak I., Hahnfeldt P., Hlatky L., Sachs R. K., and Brenner D. J., “A new view of radiation-induced cancer: Integrating short- and long-term processes. Part II: Second cancer risk estimation,” Radiat. Environ. Biophys. 48(3), 275–286 (2009). 10.1007/s00411-009-0231-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Schneider U., “Mechanistic model of radiation-induced cancer after fractionated radiotherapy using the linear-quadratic formula,” Med. Phys. 36(4), 1138–1143 (2009). 10.1118/1.3089792 [DOI] [PubMed] [Google Scholar]
- 13.Fuji H.et al. , “Assessment of organ dose reduction and secondary cancer risk associated with the use of proton beam therapy and intensity modulated radiation therapy in treatment of neuroblastomas,” Radiat. Oncol. 8(255) (2013). 10.1186/1748-717X-8-255 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Schneider U., Zwahlen D., Ross D., and Kaser-Hotz B., “Estimation of radiation-induced cancer from three-dimensional dose distributions: Concept of organ equivalent dose,” Int. J. Radiat. Oncol., Biol., Phys. 61(5), 1510–1515 (2005). 10.1016/j.ijrobp.2004.12.040 [DOI] [PubMed] [Google Scholar]
- 15.Schneider U., Sumila M., and Robotka J., “Site-specific dose–response relationships for cancer induction from the combined Japanese a-bomb and Hodgkin cohorts for doses relevant to radiotherapy,” Theor. Biol. Med. Modell. 8(27) (2011). 10.1186/1742-4682-8-27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tomozeiu M. M., “Modeling a dose–response relationship for thyroid cancer at radiotherapy dose levels,” M.Sc. thesis (ETH Zurich, 2012. ). [Google Scholar]
- 17.Walsh L. and Schneider U., “A method for determining weights for excess relative risk and excess absolute risk when applied in the calculation of lifetime risk of cancer from radiation exposure,” Radiat. Environ. Biophys. 52, 135–145 (2012). 10.1007/s00411-012-0441-x [DOI] [PubMed] [Google Scholar]
- 18.Arias E., Curtin L. R., Wei R. W., and Anderson R. N., “U.S. decennial life tables for 1999–2001,” United States Life Tables, National Vital Statistics Reports (National Center for Health Statistics, Hyattsville, Maryland: ), Vol. 57(1). [Google Scholar]
- 19.Travis L. B.et al. , “Second primary cancers and cardiovascular disease after radiation therapy,” Report No. 170 (NCRP, Bethesda, MD, 2012). [DOI] [PubMed] [Google Scholar]
- 20.National Cancer Institute, SEER Incidence Data 1992-2011 with Other Software (downloaded from SEER website).
- 21.Hawkins M. M., Wilson L. M., Burton H. S., Potok M. H., Winter D. L., Marsden H. B., and Stovall M. A., “Radiotherapy, alkylating agents, and risk of bone cancer after childhood cancer,” JNCI, J. Natl. Cancer Inst. 88, 270–278 (1996). 10.1093/jnci/88.5.270 [DOI] [PubMed] [Google Scholar]
- 22.Svahn-Tapper G., Garwicz S., Anderson H., Shamsaldin A., De Vathaire F., Olsen J. H., Døllner H., Hertz H., Jonmundsson G., Langmark F., Lanning M., Sankila R., Tulinius H., and Möller T., “Radiation dose and relapse are predictors for development of second malignant solid tumors after cancer in childhood and adolescence: A population-based case-control study in the five nordic countries,” Acta. Oncol. 45, 438–448 (2006). 10.1080/02841860600658633 [DOI] [PubMed] [Google Scholar]
- 23.Le Vu B., de Vathaire F., Shamsaldin A., Hawkins M. M., Grimaud E., Hardiman C., Diallo I., Vassal G., Bessa E., Campbell S., Panis X., Daly-Schveitzer N., Lagrange J. L., Zucker J. M., Eschwège F., Chavaudra J., and Lemerle J., “Radiation dose, chemotherapy and risk of osteosarcoma after solid tumours during childhood,” Int. J. Cancer 77, 370–377 (1998). [DOI] [PubMed] [Google Scholar]
- 24.Rizzo J. D., Curtis R. E., Socié G., Sobocinski K. A., Gilbert E., Landgren O., Travis L. B., Travis W. D., Flowers M. E. D., Friedman D. L., Horowitz M. M., Wingard J. R., and Deeg H. J., “Solid cancers after allogeneic hematopoietic cell transplantation,” Blood 113, 1175–1183 (2009). 10.1182/blood-2008-05-158782 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Chaturvedi A. K., Engels E. A., Gilbert E. S., Chen B. E., Storm H., Lynch C. F., Hall P., Langmark F., Pukkala E., Kaijser M., Andersson M., Fosså S. D., Joensuu H., Boice J. D., Kleinerman R. A., and Travis L. B., “Second cancers among 104,760 survivors of cervical cancer: Evaluation of long-term risk,” JNCI, J. Natl. Cancer Inst. 99, 1634–1643 (2007). 10.1093/jnci/djm201 [DOI] [PubMed] [Google Scholar]
- 26.Kleinerman R. A., J. D. Boice, Jr., Storm H. H., Sparen P., Andersen A., Pukkala E., Lynch C. F., Hankey B. F., and Flannery J. T., “Second primary cancer after treatment for cervical cancer. An international cancer registries study,” Cancer 76, 442–452 (1995). [DOI] [PubMed] [Google Scholar]
- 27.Wong F. L., J. D. Boice, Jr., Abramson D. H., Tarone R. E., Kleinerman R. A., Stovall M., Goldman M. B., Seddon J. M., Tarbell N., J. F. Fraumeni, Jr., and Li F.P., “Cancer incidence after retinoblastoma. Radiation dose and sarcoma risk,” JAMA, J. Am. Med. Assoc. 278, 1262–1267 (1997). 10.1001/jama.1997.03550150066037 [DOI] [PubMed] [Google Scholar]
- 28.Cote T. R., Dores G. M., and Travis L. B., “New malignancies following hodgkin lymphoma, non-hodgkin lymphoma, and myeloma,” in New Malignancies Among Cancer Survivors: SEER Cancer Registries 1973–2000 (National Cancer Institute, Bethesda, MD, 2006), pp. 397–435. [Google Scholar]
- 29.Rubino C., Shamsaldin A., Lê M. G., Labbé M., Guinebretière J.-M., Chavaudra J., and de Vathaire F., “Radiation dose and risk of soft tissue and bone sarcoma after breast cancer treatment,” Breast Cancer Res. Treat. 89, 277–288 (2005). 10.1007/s10549-004-2472-8 [DOI] [PubMed] [Google Scholar]
- 30.Ron E., Modan B., J. D. Boice, Jr., Alfandary E., Stovall M., Chetrit A., and Katz L., “Tumors of the brain and nervous system after radiotherapy in childhood,” N. Engl. J. Med. 319, 1033–1039 (1988). 10.1056/NEJM198810203191601 [DOI] [PubMed] [Google Scholar]
- 31.Neglia J. P., Robison L. L., Stovall M., Liu Y., Packer R. J., Hammond S., Yasui Y., Kasper C. E., Mertens A. C., Donaldson S. S., Meadows A. T., and Inskip P. D., “New primary neoplasms of the central nervous system in survivors of childhood cancer: A report from the childhood cancer survivor study,” JNCI, J. Natl. Cancer Inst. 98, 1528–1537 (2006). 10.1093/jnci/djj411 [DOI] [PubMed] [Google Scholar]
- 32.J. D. Boice, Jr., Harvey E. B., Blettner M., Stovall M., and Flannery J. T., “Cancer in the contralateral breast after radiotherapy for breast cancer,” N. Engl. J. Med. 326(12), 781–785 (1992). 10.1056/NEJM199203193261201 [DOI] [PubMed] [Google Scholar]
- 33.Inskip P. D., Robison L. L., Stovall M., Smith S. A., Hammond S., Mertens A. C., Whitton J. A., Diller L., Kenney L., Donaldson S. S., Meadows A. T., and Neglia J. P., “Radiation dose and breast cancer risk in the childhood cancer survivor study,” J. Clin. Oncol. 27, 3901–3907 (2009). 10.1200/JCO.2008.20.7738 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Storm H. H., Andersson M., J. D. Boice, Jr., Blettner M., Stovall M., Mouridsen H. T., Dombernowsky P., Rose C., Jacobsen A., and Pedersen M., “Adjuvant radiotherapy and risk of contralateral breast cancer,” JNCI, J. Natl. Cancer Inst. 84, 1245–1250 (1992). 10.1093/jnci/84.16.1245 [DOI] [PubMed] [Google Scholar]
- 35.Travis L. B., Hill D. A., Dores G. M., Gospodarowicz M., van Leeuwen F. E., Holowaty E., Glimelius B., Andersson M., Wiklund T., Lynch C. F., Van’t Veer M. B., Glimelius I., Storm H., Pukkala E., Stovall M., Curtis R., J. D. Boice, Jr., and Gilbert E., “Breast cancer following radiotherapy and chemotherapy among young women with Hodgkin disease,” JAMA, J. Am. Med. Assoc. 290, 465–475 (2003). 10.1001/jama.290.4.465 [DOI] [PubMed] [Google Scholar]
- 36.van Leeuwen F. E., Klokman W. J., Stovall M., Dahler E. C., van’t Veer M. B., Noordijk E. M., Crommelin M. A., Aleman B. M. P., Broeks A., Gospodarowicz M., Travis L. B., and Russell N. S., “Roles of radiation dose, chemotherapy, and hormonal factors in breast cancer following Hodgkin’s disease,” JNCI, J. Natl. Cancer Inst. 95, 971–980 (2003). 10.1093/jnci/95.13.971 [DOI] [PubMed] [Google Scholar]
- 37.Guibout C., Adjadj E., Rubino C., Shamsaldin A., Grimaud E., Hawkins M., Mathieu M.-C., Oberlin O., Zucker J.-M., Panis X., Lagrange J.-L., Daly-Schveitzer N., Chavaudra J., and de Vathaire F., “Malignant breast tumors after radiotherapy for a first cancer during childhood,” J. Clin. Oncol. 23, 197–204 (2005). 10.1200/JCO.2005.06.225 [DOI] [PubMed] [Google Scholar]
- 38.Inskip P. D., Stovall M., and Flannery J. T., “Lung cancer risk and radiation dose among women treated for breast cancer,” JNCI, J. Natl. Cancer Inst. 86(13), 983–988 (1994). 10.1093/jnci/86.13.983 [DOI] [PubMed] [Google Scholar]
- 39.Travis L. B., Curtis R. E., Hankey B. F., and J. F. Fraumeni, Jr., “Second cancers in patients with chronic lymphocytic leukemia,” JNCI, J. Natl. Cancer Inst. 84(18), 1422–1427 (1992). 10.1093/jnci/84.18.1422 [DOI] [PubMed] [Google Scholar]
- 40.de Vathaire F., Hardiman C., Shamsaldin A., Campbell S., Grimaud E., Hawkins M., Raquin M., Oberlin O., Diallo I., Zucker J. M., Panis X., Lagrange J. L., Daly-Schveitzer N., Lemerle J., Chavaudra J., Schlumberger M., and Bonaïti C., “Thyroid carcinomas after irradiation for a first cancer during childhood,” Arch. Intern. Med. 159, 2713–2719 (1999). 10.1001/archinte.159.22.2713 [DOI] [PubMed] [Google Scholar]
- 41.Tucker M. A., Jones P. H., J. D. Boice, Jr., Robison L. L., Stone B. J., Stovall M., Jenkin R. D., Lubin J. H., Baum E. S., and Siegel S. E., “Therapeutic radiation at a young age is linked to secondary thyroid cancer. The late effects study group,” Cancer Res. 51, 2885–2888 (1991). [PubMed] [Google Scholar]
- 42.Dores G. M., Metayer C., Curtis R. E., Lynch C. F., Clarke E. A., Glimelius B., Storm H., Pukkala E., van Leeuwen F. E., Holowaty E. J., Andersson M., Wiklund T., Joensuu T., Veer M. B., Stovall M., Gospodarowicz M., and Travis L. B., “Second malignant neoplasms among long-term survivors of Hodgkin’s disease: A population-based evaluation over 25 years,” J. Clin. Oncol. 20, 3484–3494 (2002). 10.1200/JCO.2002.09.038 [DOI] [PubMed] [Google Scholar]
- 43.Schneider U., Sumila M., Robotka J., Gruber G., Mack A., and Besserer J., “Dose-response relationship for breast cancer induction at radiotherapy dose,” Radiat. Oncol. 6(67) (2011). 10.1186/1748-717X-6-67 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Schneider U., Stipper A., and Besserer J., “Dose–response relationship for lung cancer induction at radiotherapy dose,” Z. Med. Phys. 20(3), 206–214 (2010). 10.1016/j.zemedi.2010.03.008 [DOI] [PubMed] [Google Scholar]
- 45.Moteabbed M., Yock T. I., and Paganetti H., “The risk of radiation-induced second cancers in the high to medium dose region: A comparison between passive and scanned proton therapy, IMRT and VMAT for pediatric patients with brain tumors,” Phys. Med. Biol. 59, 2883–2899 (2014). 10.1088/0031-9155/59/12/2883 [DOI] [PubMed] [Google Scholar]
- 46.World population prospects, The 2012 revision, United Nations, New York, 2012.
- 47.van den belt-Dusebout A. W., Aleman B. M., Besseling G., Bruin M.L.de., Hauptmann M., van Veer M. B., de Wit R., Ribot J. G., Noordijk E. M., Kerst J. M., Gietema J. A., and van Leeuwen F. E., “Roles of radiation dose and chemotherapy in the etiology of stomach cancer as a second malignancy,” Int. J. Radiat. Oncol., Biol., Phys. 75, 1420–1429 (2009). 10.1016/j.ijrobp.2009.01.073 [DOI] [PubMed] [Google Scholar]
- 48.Paganetti H., Athar B. S., Moteabbed M., Adams J. A., Schneider U., and Yock T. I., “Assessment of radiation-induced second cancer risks in proton therapy and IMRT for organs inside the primary radiation field,” Phys. Med. Biol. 57(19), 6047–6061 (2012). 10.1088/0031-9155/57/19/6047 [DOI] [PubMed] [Google Scholar]
- 49.Diallo I.et al. , “Frequency distribution of second solid cancer locations in relation to the irradiated volume among 115 patients treated for childhood cancer,” Int. J. Radiat. Oncol., Biol., Phys. 74(3), 876–883 (2009). 10.1016/j.ijrobp.2009.01.040 [DOI] [PubMed] [Google Scholar]