Abstract
Simulating the evolution of a chemically reacting system using the bimolecular propensity function, as is done by the stochastic simulation algorithm and its reaction-diffusion extension, entails making statistically inspired guesses as to where the reactant molecules are at any given time. Those guesses will be physically justified if the system is dilute and well-mixed in the reactant molecules. Otherwise, an accurate simulation will require the extra effort and expense of keeping track of the positions of the reactant molecules as the system evolves. One molecule-tracking algorithm that pays careful attention to the physics of molecular diffusion is the enhanced Green's function reaction dynamics (eGFRD) of Takahashi, Tănase-Nicola, and ten Wolde [Proc. Natl. Acad. Sci. U.S.A. 141, 2473 (2010)]. We introduce here a molecule-tracking algorithm that has the same theoretical underpinnings and strategic aims as eGFRD, but a different implementation procedure. Called the small-voxel tracking algorithm (SVTA), it combines the well known voxel-hopping method for simulating molecular diffusion with a novel procedure for rectifying the unphysical predictions of the diffusion equation on the small spatiotemporal scale of molecular collisions. Indications are that the SVTA might be more computationally efficient than eGFRD for the problematic class of non-dilute systems. A widely applicable, user-friendly software implementation of the SVTA has yet to be developed, but we exhibit some simple examples which show that the algorithm is computationally feasible and gives plausible results.
I. INTRODUCTION
Chemically reacting systems at the cellular level, where the molecular population of one or more reactant species can be relatively low, are often analyzed using the chemical master equation (CME) or the logically equivalent stochastic simulation algorithm (SSA). But the CME and SSA require some rather restrictive conditions to be satisfied. The best known of those is the requirement that the reactant molecules be well-mixed throughout the system volume Ω. However, it has recently been argued1 that a more critical requirement is that the reactant molecules be dilute in Ω. Here, dilute means that the average separation between the reactant molecules is very large compared to their diameters, or equivalently, that the reactant molecules occlude only a negligibly small fraction of Ω.2 Two observations support the view that diluteness is a necessary (but not sufficient) condition for using the CME and the SSA: First, the derivation from molecular physics of the bimolecular propensity function, which plays a key role in both the CME and the SSA, requires that the reactant molecules be not only well-mixed but also dilute in Ω;1 e.g., analyzing a bimolecular reaction as though it involves only two molecules, without the complications of a third molecule, will be justified in the CME and SSA only if the system is so dilute that three co-located molecules will be a rarity. Second, only if the reactant molecules are dilute in Ω can ordinary diffusion keep them well-mixed.3 The underlying reason for that is easy to understand: only if the reactant molecules are separated by distances comfortably larger than their diameters will they be able to wander around without colliding with each other for a long enough time to become well-mixed between collisions. It follows that diluteness is also a prerequisite for using the ordinary differential equations of traditional chemical kinetics, since those equations arise as an approximation of the CME/SSA when the molecular populations of the species and the system volume are all very large.
Diluteness is also a necessary (but not sufficient) condition for the reaction-diffusion CME/SSA. That formalism seeks to circumvent the globally well-mixed requirement of the CME and the SSA by subdividing the system into imaginary subvolumes or voxels which individually are well-mixed—a condition that generally requires the voxels to be “small.” Chemical reactions are assumed to occur inside individual voxels, and reactant molecules are moved from voxel to voxel by special “hopping reactions” that replicate the diffusion equation when the voxels are, again, “small.” But we cannot legitimately use a bimolecular propensity function inside a voxel unless the reactant molecules are dilute in that voxel. That requires, at a minimum, that the voxel volume be much larger than the volume occluded by two reactant molecules, and that requirement might not always be compatible with the requirement that the voxels be “small.”
Overcoming the diluteness limitation of the SSA and its voxel extension would seem to require a simulation strategy that tracks the positions of the reactant molecules, thereby obviating unwarranted assumptions about where those molecules are and are not. The gold standard of such strategies is molecular dynamics. It tracks both the positions and the velocities of not only all the reactant (solute) molecules, but also all the more numerous solvent molecules. That approach, however, is rarely feasible. A much less ambitious, somewhat less accurate, but still computationally challenging approach is to track only the positions of only the solute molecules. An algorithm of that kind which pays careful attention to the physics of diffusion is the enhanced Green's function reaction dynamics (eGFRD) of Takahashi, Tănase-Nicola, and ten Wolde.4 An important feature of eGFRD is its use of imaginary absorbing surfaces to segregate or corral the reactant molecules into small groups, a strategy originally devised by Opplestrup et al.5 The time evolutions of the molecules inside individual corrals are then simulated independently and in parallel until the absorption of some molecule at a corral boundary signals that a corral has been breached. When such a breach occurs, the simulations are temporarily halted to allow any necessary adjustments to be made to the corrals, and any necessary synchronizations to be made in the corral times.
Of the several tasks that comprise the eGFRD simulation strategy, we will be concerned here only with the task of accurately simulating the time evolution of the reactant molecules inside a single corral until either a chemical reaction or a breach of the corral occurs. Such “halting events” are simulated in the current formulation of eGFRD by using analytical Green's function techniques to compute the times of those events and the locations of the reactant molecules at those times.4 Here we will present another way of performing those tasks, which we have dubbed the small-voxel tracking algorithm (SVTA), which might offer some computational advantages in certain situations. The implementation procedure of the SVTA is quite different from that of eGFRD, but as we will show, the SVTA and eGFRD share the same theoretical underpinnings. We will not address in this paper the problem of determining the best way to lay out the corrals, nor the problem of how to most efficiently coordinate and synchronize their local times when a halting event occurs.
After reviewing in Sec. II some results in the theory of diffusion and diffusion-induced chemical reactions that we will need later, we introduce the SVTA in Sec. III in the context of carrying out the core calculations for “single particle events” as defined in eGFRD.4 We illustrate that with a simple numerical example in Sec. IV. In Sec. V we develop the SVTA's procedure for carrying out the core calculations in eGFRD's “two particle events.” After showing in Sec. VI that the SVTA and eGFRD share the same theoretical foundation, we give in Sec. VII some simple numerical examples of two-molecule events which show that the SVTA is computationally feasible and gives plausible results. In Sec. VIII we show how the SVTA can deal with three-molecule events, and in Sec. IX we show how it can take account of forces between reactant molecules when such forces are prescribed. We conclude in Sec. X with a summary of our work and a forward-looking assessment of the SVTA.
II. BACKGROUND THEORY
In this section, we will review some results in the theory of diffusion and diffusion-induced chemical reactions which we will need later to derive the SVTA, and also to make clear its relation to other simulation strategies such as the SSA, the reaction-diffusion SSA, and eGFRD. Derivations of most of these results can be found in Ref. 6.
A. Modeling assumptions
We begin by stating the physical assumptions that underlie our analysis. All reactant molecules are assumed to be solute molecules that are in solution with very many, much smaller, chemically inert solvent molecules. All molecules are confined to a region Ω whose boundary ∂Ω is perfectly reflecting, and kept at absolute temperature T. Reactant molecule i is assumed to be a hard sphere with diameter σi, mass mi, diffusion coefficient Di, and unimolecular reaction constant ki; the last is defined so that kidt is the probability that molecule i will so react in the next infinitesimal time dt. And finally, two molecules i and j will react bimolecularly only if they collide, and then only with probability qij, where 0 ⩽ qij ⩽ 1. The collision-conditioned reaction probability qij can, at least in principle, be calculated from a detailed knowledge of the physical properties of the two molecules; e.g., if the reaction occurs only if the two molecules have a collisional kinetic energy above some threshold value Ethr, then qij will be the Arhhenius factor exp (−Ethr/kBT), where kB is Boltzmann's constant.
B. Molecular diffusion and its simulation
On sufficiently large space and time scales, the position R(t) of the center of a diffusing reactant molecule at time t can be regarded as a random variable whose probability density function (PDF) p(r, t | r0, t0), conditioned on R(t0) = r0 for t0 ⩽ t, obeys the Einstein diffusion equation,
| (1) |
The Einstein diffusion equation differs from the traditional diffusion equation in that the latter's solution is the average density of many non-interacting solute molecules, instead of the PDF of a single solute molecule. The restriction of Eq. (1) to “sufficiently large space and time scales” can be spelled out quantitatively as follows:6 Equation (1) accurately describes the physical motion of a diffusing solute molecule only if the time scale on which that motion is being observed is large enough that the time
| (2) |
is infinitesimally small, and only if the length scale on which that motion is being observed is large enough that the length
| (3) |
is infinitesimally small. If instead we observe the solute molecule on scales where τ or λ is very large, then the motion of the solute molecule will appear to be ballistic, as in an ideal gas. That is because during such small times and over such small distances, the solute molecule will not experience enough collisions with the much smaller and lighter solvent molecules to noticeably alter its velocity. Constant velocity motion is ballistic motion, and ballistic motion cannot be described by Eq. (1). Indeed, on very small space-time scales the motion described by Eqs. (1) is not merely inaccurate; it is bizarrely unphysical.6
A mathematically exact way of simulating the unrestricted motion of a molecule that moves according to Eq. (1) is provided by the Einstein stepping formulas, which allow us to compute the location of the center of the molecule at time t + Δt in terms of its location at earlier time t:
| (4) |
Here nx, ny, and nz are independent samples of the normal random variable with mean 0 and variance 1. Equation (4) is exact with respect to Eq. (1) for all Δt ⩾ 0. But since Eq. (1) itself is physically accurate only on time scales much larger than τ, formulas (4) will be physically accurate only if Δt ≫ τ. A generalization of formulas (4) in which Δt is not subject to the restriction Δt ≫ τ exists,7 but we will not be needing it in this paper. But even in the great majority of situations in which Eq. (4) is accurate, they have a serious drawback from a simulation standpoint: they cannot tell us where the molecule went between times t and t + Δt.
A way of simulating the movement prescribed by the diffusion equation which does not have this drawback, and which is asymptotically exact, is the voxel-hopping algorithm used in the reaction-diffusion CME and SSA. With space subdivided into cubic voxels of edge length h, so that each interior voxel shares a voxel face with its six adjacent voxels, this algorithm requires the center of the diffusing molecule to hop according to the following rule:
| (5) |
Voxels that are not accessible to the center of the molecule are those whose occupancy would put some part of the molecule either outside the system volume or inside another reactant molecule.
Rule (5) is “asymptotically exact” with respect to the diffusion equation (1) in the following sense: The master equation which describes the stochastic time evolution of a random walker that hops from voxel to voxel according to rule (5) becomes Eq. (1) in the limit h → 0.8 We know of no other rule for jumping on a lattice that models the diffusion equation with such clearly established mathematical fidelity, provided the lattice spacing h is “small.” However, since the physical validity of rule (5) is contingent on Eq. (1) being physically accurate on the scale of an individual voxel, then the limitation of Eq. (1) to lengths much larger than λ in Eq. (3) implies that rule (5) will be physically accurate only if h is large enough that
| (6) |
Detailed studies9 have shown that the voxel-hopping rule (5) most accurately describes the first-passage of the molecule's center from a point that is randomly uniform inside its current voxel to a point that is randomly uniform inside its destination voxel. This result is corroborated by the observation that if the center of the molecule were more likely closer to one voxel face than another, then the hopping rule (5) would be incorrect in treating the six adjacent voxels as equally likely destinations for the next jump. We conclude that the voxel-hopping strategy (5) carries the additional implication that between hops, the center of the molecule will be randomly and uniformly distributed inside its current voxel. This result will be critical to our derivation of the SVTA.
C. Diffusion-induced chemical reactions in a dilute, well-mixed system
If the system is dilute and well-mixed—a circumstance that is not assumed by the SVTA—then two molecules in Ω chosen at random, call them molecules 1 and 2, will undergo a bimolecular reaction in the next infinitesimally small time dt with probability k|Ω|−1·dt, where |Ω| is the volume of Ω and10
| (7) |
In formula (7),
| (8) |
| (9) |
and
| (10) |
is the average speed of either molecule relative to the other if they were in thermal equilibrium in a dilute gas, with m12 ≡ m1m2/(m1 + m2) being the so-called reduced mass of the two molecules. The derivation of Eq. (7) is summarized in Appendix A; we will be needing some intermediate results of that derivation later in this paper.
If molecules 1 and 2 are of different species, and if there are x1 molecules of species 1 and x2 molecules of species 2, all dilute and well-mixed inside Ω, then k|Ω|−1x1x2 is called the propensity function of the reaction in question. Its product with dt gives the probability that a bimolecular reaction between some species 1 molecule and some species 2 molecule will occur somewhere inside Ω in the next dt. If molecules 1 and 2 are of the same species, then the propensity function will instead be . The existence of a propensity function for a bimolecular reaction— i.e., the existence of some function whose product with dt gives the probability that the reaction will occur in the next infinitesimal time dt—is essential for the system to be described by a CME and simulated by the SSA.
Two important limiting cases of formula (7) are
| (11a) |
and
| (11b) |
The regime defined by the condition in (11a) is called the ballistic regime, because the formula for the reaction probability kbal|Ω|−1dt implied by Eq. (11a) is exactly what one obtains using simple kinetic theory arguments when the two molecules are moving ballistically, as in an ideal gas.11,1 The regime defined by the condition in (11b) is called the diffusion-limited regime; it is the regime that characterizes most cellular reactions.
A better understanding of what diffusion-limited means can be gained by noting that the formulas for kbal and kdif in Eqs. (11a) and (11b) allow us to rewrite Eq. (7) as
| (12) |
Since k is a measure of how quickly the reaction occurs, then 1/k is a measure of how slowly the reaction occurs. In an electrical circuit analogy, k is the “conductance” of the reaction, while 1/k is the “resistance” of the reaction. Equation (12) evidently expresses the resistance of the reaction as a sum of a “diffusional resistance” and a “ballistic resistance.” That way of combining these resistances implies that they are “connected in series,” and that mirrors rather well the actual physical situation: In order for the reaction to occur, molecules 1 and 2 must first overcome the diffusional resistance associated with their approach to each other via classical diffusion over a relatively large distance. Then they must overcome the ballistic resistance associated with their approach to each other immediately before they collide. If kdif ≪ kbal, so that the diffusional resistance 1/kdif is much greater than the ballistic resistance 1/kbal, then it is diffusion that is the bottleneck to the reaction: the ballistic resistance term in Eq. (12) will then be negligibly small, and we will have k ≈ kdif.
There are several surprises in Eqs. (11a) and (11b). First, in spite of the fact that the exact equation (7) shows that k → 0 as q12 → 0, the diffusion-limited regime's approximation for k in Eq. (11b) has k independent of q12. What that means is that if q12, whose value is confined to the interval 0 ⩽ q12 ⩽ 1, is non-zero enough that the condition is satisfied, then k will be insensitive to the exact value of q12. But notice that even if q12 were equal to 1, so that every collision produced a reaction, it would not necessarily follow that the reaction will be diffusion-limited; in order for that to be so it would also have to be true that . At the other extreme, we can always imagine q12 to be small enough (yet not zero) that condition (11a) will be satisfied; in that case the reaction will be in the ballistic regime and we would have k ≈ kbal, even though the system is obviously a solution and not a gas.
D. Connection with some other approaches
If the numerator and denominator on the right of Eq. (7) are multiplied by πσ12, that formula becomes, after invoking the definition in (11a),
| (13) |
The form on the right appears in earlier literature more frequently than the form on the left, although with kbal usually denoted differently—for example, as ka by Takahashi et al.,4 or as kr by Hellander et al.12—and referred to as either the “intrinsic” rate constant or the “microscopic” rate constant. In either guise, kbal in Eq. (13) is usually regarded as an independent parameter, with no reference made to the formula for it in Eq. (11a) in terms of σ12, , and q12. Indeed, the parameter q12 rarely appears in existing works on chemical reaction simulation, although it is a well established parameter in chemical kinetics more generally. If kbal is considered to be the given quantity instead of q12, then q12 can easily be deduced from Eq. (11a) as
| (14) |
When this expression for q12 is substituted into Eq. (11b), the condition for being diffusion-limited becomes 4πσ12D12 ≪ kbal.
III. SVTA’S ONE-MOLECULE CORRAL
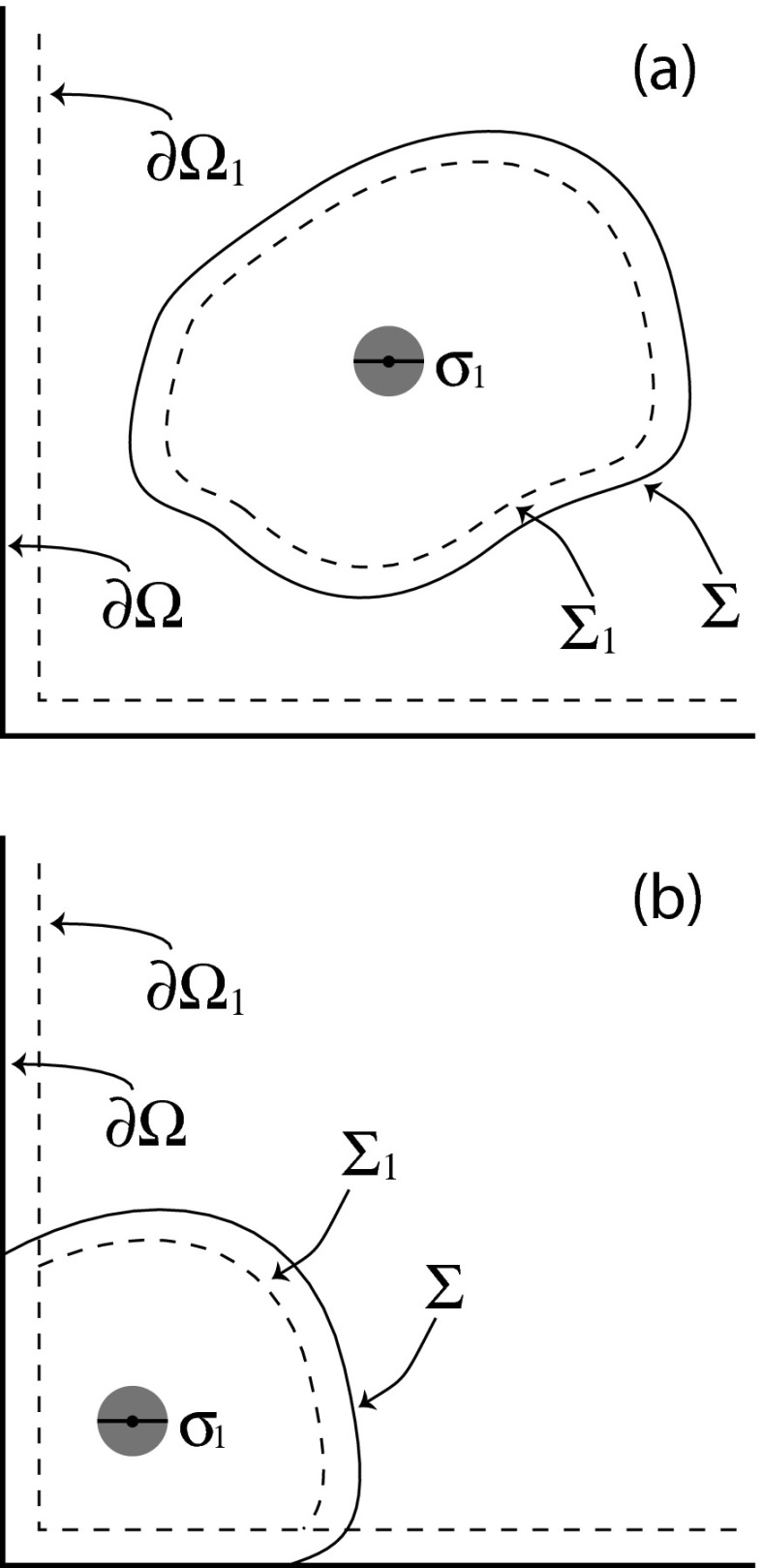
eGFRD4 considers two different corralling scenarios: one molecule in a corral, and two molecules in a corral. We will first describe how the SVTA deals with the simpler one-molecule corral. That situation is illustrated (in two dimensions) in Fig. 1: molecule 1 at initial time t0 is cordoned off from the other molecules in Ω by an imaginary absorbing surface Σ, either all by itself as in Fig. 1(a), or with the help of part of the system boundary ∂Ω as in Fig. 1(b). The surfaces Σ and ∂Ω corral the entire molecule, but we will be locating the molecule by its center. So we introduce the two surfaces Σ1 and ∂Ω1 (dashed lines in Fig. 1) which are set in from the respective surfaces Σ and ∂Ω by the radius σ1/2 of the molecule; Σ1 and ∂Ω1 corral the center of molecule 1. If the center of molecule 1 comes into contact with ∂Ω1, the molecule will be reflected. If the center of molecule 1 comes into contact with Σ1, we will halt the simulation because of a corral breach. This one-molecule scenario is a little more general than the single particle event scenario in eGFRD;4 there the corralling surface is assumed to be a sphere that is centered on the initial location of molecule 1 and lies completely inside Ω.
FIG. 1.
A single solute molecule of diameter σ1, one of the possibly many solute molecules inside a containing region Ω, is at time t0 separated from the other molecules by an imaginary surface Σ. That surface “corrals” molecule 1, either entirely as in (a), or with the help of the system boundary ∂Ω as in (b). In the 2-dimensional representation of these figures, the surfaces Σ and ∂Ω are shown as solid lines. The surfaces Σ1 and ∂Ω1 (dashed lines) are formed by tracing the position of the molecule's center when the molecule is rolled around on the insides of Σ and ∂Ω, respectively. So if the center of molecule 1 contacts any point on Σ1 or ∂Ω1, then molecule 1 will be in contact with the boundary of its corral.
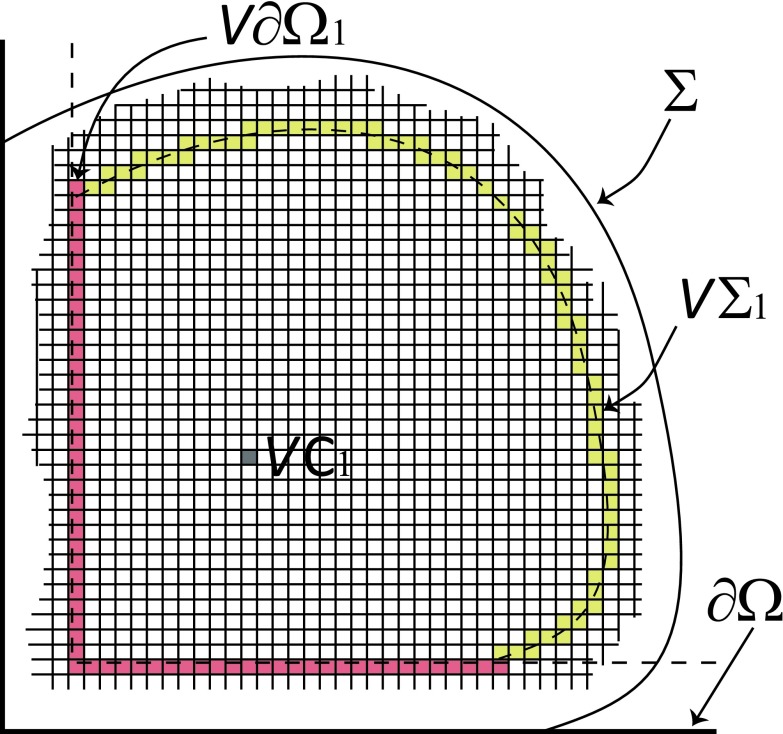
The SVTA will simulate the diffusional motion of molecule 1 using the voxel-hopping rule (5). That requires us to partition the space accessible to the center of molecule 1 into voxels in the form of cubes of edge length h. This “voxelation” of space transforms the situation illustrated in Fig. 1(b) to that illustrated in Fig. 2. The voxel containing the center of molecule 2 is designated VC1. In Fig. 2 we have colored that voxel a uniform gray to emphasize the fact, discussed at the end of Sec. II B, that between hops the center of molecule 1 is distributed randomly and uniformly inside VC1. When molecule 1 hops to an adjacent voxel, it is VC1 that does the hopping. Also, we replace the dashed line surfaces Σ1 and ∂Ω1 in Fig. 1(b) with the sets of voxels VΣ1 and V∂Ω1 which those respective surfaces intersect. We will not allow VC1 to hop into any voxel belonging to V∂Ω1 (the red voxel set in Fig. 2) because that would place some part of molecule 1 outside of Ω. We will allow VC1 to hop into any voxel belonging to VΣ1 (the yellow voxel set in Fig. 2), but that will constitute a corral breach which halts the simulation.
FIG. 2.
The configuration in Fig. 1(b) as represented by the SVTA. The corralling region for the molecule's center, namely the region enclosed by Σ1 and portions of ∂Ω1, has been subdivided into cubic voxels of edge length h < σ1. In this voxelated space, the center of molecule 1 is assumed to be distributed randomly and uniformly inside the particular voxel VC1 that contains that point. The corralling surfaces Σ1 and ∂Ω1 have been replaced by the respective sets of voxels that those surfaces intersect; those “voxelated surfaces” VΣ1 and V∂Ω1 are shown in yellow and red, respectively. If voxel VC1 were to coincide with any voxel belonging to VΣ1 or V∂Ω1, then some part of molecule 1 would lie outside the corralling region formed by Σ and Ω. So VC1 will not be allowed to jump to a voxel belonging to V∂Ω1. VC1 will be allowed to jump to a voxel belonging to VΣ1, but that will immediately suspend the simulation.
At any instant t during the simulation, two potential “events” compete with each other to occur first: a unimolecular reaction, and a hop. The definition of the unimolecular reaction rate constant k1 (see Sec. II A) can be shown to imply that the time until that reaction fires is the exponential random variable (k1) with decay constant k1 (and mean ). Therefore, if a corral breach does not occur earlier, molecule 1 will undergo its unimolecular reaction at time
| (15a) |
where
| (15b) |
The right side of Eq. (15b) may be read “a sample value of (k1).”
Competing with the unimolecular reaction event is a hop of VC1 to one of its accessible adjacent voxels. In the one-molecule scenario, the only voxels that are not accessible to VC1 are voxels belonging to V∂Ω1. For example, if Ω were a cube, then could be as large as 6 if VC1 were well inside Ω, or as small as 3 if VC1 were in a corner of Ω. In any case, by applying the addition law of probability to (5) we may infer that the probability that VC1 will hop in the next dt to any one of its accessible adjacent voxels is . That implies that the time to the next hop will be an exponential random variable with decay constant . So at the current time t, unless molecule 1 reacts unimolecularly earlier, VC1 will hop to an adjacent voxel at time
| (16a) |
where
| (16b) |
The particular voxel to which VC1 hops at this time is obtained by selecting one of the accessible adjacent voxels “at random.” If those voxels are indexed in any order from 1 to , then the index kdest of the destination voxel can be computed as
| (17) |
where [x] denotes “the greatest integer in x” and (0, 1) denotes a sample value of the uniform random variable in the unit interval.
The SVTA imposes some stringent bounds on the voxel edge length h. Since a minimal requirement for a molecule tracking algorithm is that the resolution of the tracking should be smaller than the molecule, the SVTA imposes the upper bound h < σ1. Thus, a voxel cannot contain the center of more than one molecule, and one molecule generally occludes many voxels. The SVTA also imposes a lower bound on h. For reasons explained in connection with Eq. (3), the diffusion equation (1), and hence also the voxel-hopping rule (5), will be physically accurate on the scale of a voxel only if . Thus, in the SVTA the voxel edge length h must satisfy
| (18) |
To get some idea of what condition (18) implies for a typical cellular molecule, let us put in some order-of-magnitude values for its parameters. If our spherical molecule 1 has the same mass (m1 = 1.66 × 10−19g) and density (1.37 g/cm3) as a typical protein molecule,13 then simple geometry gives for its diameter σ1 = 6.1 × 10−7 cm. If this molecule is diffusing in water (viscosity η = 0.001 kgm−1 s−1) at room temperature (T = 293 K), then the Stokes formula γ1 = 3πησ1 for the molecule's drag coefficient γ1, together with the Einstein relation D1γ1 = kBT, imply a diffusion coefficient of D1 = 0.7 × 10−10 m2/s. That value for D1 is probably an overestimate;14 nevertheless, with all these values, condition (18) becomes
| (19) |
Since the right side of (19) is over 400 times larger than the left side, and since also the figure on the left side is probably an overestimate, we conclude that condition (18) on h should be feasible for cellular systems.
The SVTA's strategy for simulating a single-molecule corral is quite straightforward: It hops VC1over the voxels repeatedly until either t exceeds tuni, or VC1 arrives in a voxel belonging to VΣ1. The following steps describe in more detail how this strategy is actually carried out.
-
1.
Divide the space accessible to the center of molecule 1 into cubic voxels of edge length h which satisfies condition (18). Label each voxel with three (signed) integers ix, iy, iz, so that the center of voxel (ix, iy, iz) is at point (x, y, z) = (ixh, iyh, izh).
-
2.
Identify the voxels that belong to the voxelated corralling surface VΣ1, and also the voxels that belong to the voxelated boundary V∂Ω1.
-
3.
Set the current time t to the given initial time t0. Take voxel VC1 ≡ (i1x, i1y, i1z) to be the voxel that contains the given initial location of the center of molecule 1.
-
4.
Using Eqs. (15a) and (15b), compute the tentative time tuni at which molecule 1 will undergo its unimolecular reaction. If no unimolecular reaction is possible, set tuni = ∞.
-
5.
(Begin simulation loop) If VC1 is a voxel belonging to VΣ1, set thalt = t and halt.
-
6.
Determine which if any of the six voxels adjacent to VC1—namely voxels , and —belong to V∂Ω1, and hence are not accessible to VC1 on its next jump. Number the remaining accessible adjacent voxels with the index . Then compute the tentative time thop of the next jump of VC1 using Eqs. (16a) and (16b).
-
7.Branch on which of the two times thop and tuni is the earlier:15
-
(a)If thop < tuni: Set t = thop. Compute the index k = kdest of the destination voxel using Eq. (17). Execute the hop by moving VC1 ≡ (i1x, i1y, i1z) to that destination voxel. Then return to 5.
-
(b)If tuni ⩽ thop: Set thalt = tuni. Execute the unimolecular reaction, and then halt.
-
(a)
The foregoing procedure is totally focused on what is happening inside this one corral, and is oblivious to what is happening inside other corrals in Ω. If it is subsequently determined that a solute molecule from outside this corral has diffused to Σ at a time tencroach that is earlier than the time thalt determined above, then tencroach becomes the actual halting time for our corral. We will then have to backtrack the simulation, and restore molecule 1 to its voxel location at time tencroach. The voxel-hopping procedure makes that relatively easy to do: we need only keep a log of the times and the destinations of each hop. More specifically, if the journey of molecule 1 from its initial voxel v0 at time t0 to time thalt contained a total of J jumps, then we will keep a record of the time tj of the jth jump, and the voxel vj which molecule 1 jumped to on that jump, for all j = 1, …, J. Since during each time interval [ti − 1, ti) molecule 1 was always in voxel vi − 1, the two data sets {t0, t1, …, tJ} and {v0, v1, …, vJ} allow us to immediately determine where molecule 1 was at any time t ′ ∈ [t0, thalt). These two data sets can be discarded once it is certain that no encroachment occurred prior to time thalt.
IV. EXAMPLE SIMULATION OF A ONE-MOLECULE CORRAL EVENT USING THE SVTA
We will illustrate the SVTA's single-molecule simulation procedure with an example that will show that the voxel-hopping rule (5) is indeed a very accurate way to simulate the diffusion equation if we take h “sufficiently small.” To that end, we take the corralling surface Σ to be a sphere that is wholly inside ∂Ω and centered on the center of molecule 1 at time 0. And we set k1 = 0 so that the halting event will always be the arrival of molecule 1 at the surface of Σ. The halting time will therefore be a first-passage time random variable, which we will denote by T. We take D1 = 1, and we let the radius of Σ be equal to 100 units of length plus the radius of molecule 1; thus, the sphere Σ1, which corrals the center of molecule 1, is a sphere of radius 100 length units.
To generate a sample value of T using the SVTA, we use the procedure described in Eqs. (16) and (17) with to hop VC1 from its initial location at the center of Σ1 until it enters a voxel whose center is ⩾100 length units from the center of Σ1. The final value of t is then the desired sample of T. We carried out this procedure for five values of h ranging from 1 to 20. For each value of h we made 106 runs, and from the 106 sample values of T thus obtained we constructed a normalized frequency histogram by plotting the number of sample values that fell into time bin j divided by the product of the bin width (180) times 106. We then compared these histograms not only with each other, but also with a plot of the theoretically predicted PDF of T, PT(t), which we computed using essentially the same theory used by eGFRD;4 for details of how we computed PT(t), see Ref. 16. Our results are shown in Fig. 3. The dashed black curve is the theoretically predicted PDF, and the five colored curves are the normalized frequency histograms for h = 1, 2, 4, 10, and 20. Each histogram curve is a smooth interpolation of the values found in 50 bins over the time range shown in the figure. The large number (106) of sample values of T that we used for each h-value had the salutary effect of making the one-standard deviation uncertainty range for each bin-value approximately equal to the line width of the curves in the figure.
FIG. 3.
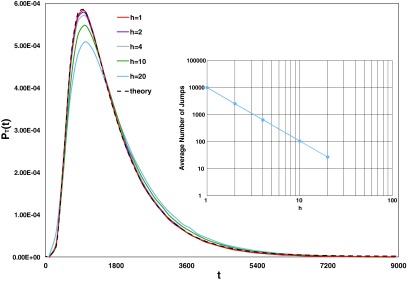
Example of a first-passage time calculation in the single-molecule SVTA. The dashed black curve is the theoretically predicted PDF PT(t) of the first passage time T for the case in which the corralling surface is a sphere of radius 100 around the initial location of the center of a molecule with diffusion coefficient 1. The colored curves are the normalized frequency histograms provided by SVTA for five h values, h = 1, 2, 4, 10, and 20. The theoretical PDF was computed as described in the supplemental material.16 It can be seen that as h → 0, the SVTA histograms converge to PT(t). The excellent agreement for the three smallest h values indicates that the SVTA is an accurate algorithm for simulating molecular diffusion. The inset shows a log-log plot of the average number of jumps per run as a function of h. The slope of the fitted linear curve is −1.97 ≈ −2, which shows that the average number of jumps is proportional to h−2. Since halving h increases the number of jumps by a factor of 4, the computation time will increase accordingly. Thus, there is a tradeoff between accuracy and computation time.
The expected convergence of the histograms to PT(t) as h → 0 is clear from the figure. The h = 1 and h = 2 curves are excellent approximations to the theoretically predicted curve, and the h = 4 curve is arguably “good enough.” Accuracy drops off as h is increased to 10 and then 20. But since for h = 20 the radius of Σ1 is only 5 voxels, it is perhaps more surprising that the h = 20 histogram is as good as it is. The inset figure shows that the average number of jumps per run decreases with increasing h in proportion to h−2, falling from 10 066 jumps per run at h = 1 to 27.3 jumps per run at h = 20. Since the simulation time is roughly proportional to the number of jumps per run, this implies that the average simulation time for a run also increases with decreasing h in proportion to h−2. The trade-off between accuracy and computational effort is illustrated by the findings here that the “excellent” h = 2 curve requires on average 2533 jumps for a first passage, and the “very good” h = 4 curve requires on average 639 jumps for a first passage. The implication seems to be that on the order of a thousand hops need to be made in order for the voxel-hopping method (5) to give an accurate modeling of diffusion.
This example should not be construed as suggesting that the usual goal of the SVTA is to estimate the form of the PDF PT(t) of the first-passage time T. However, estimating PT(t) is the goal of the first step of eGFRD,4 because eGFRD uses that function in its second step to compute a sample value of T. The third step of eGFRD is to compute the molecule's arrival point on Σ1. That task is easy when Σ1 is a sphere, but not if Σ1 has some other shape, or if ∂Ω1 forms part of the corral. In contrast, the SVTA accomplishes all of these tasks at the end of a single run. But of course, that single SVTA run usually entails very many hops.
V. SVTA'S TWO-MOLECULE CORRAL
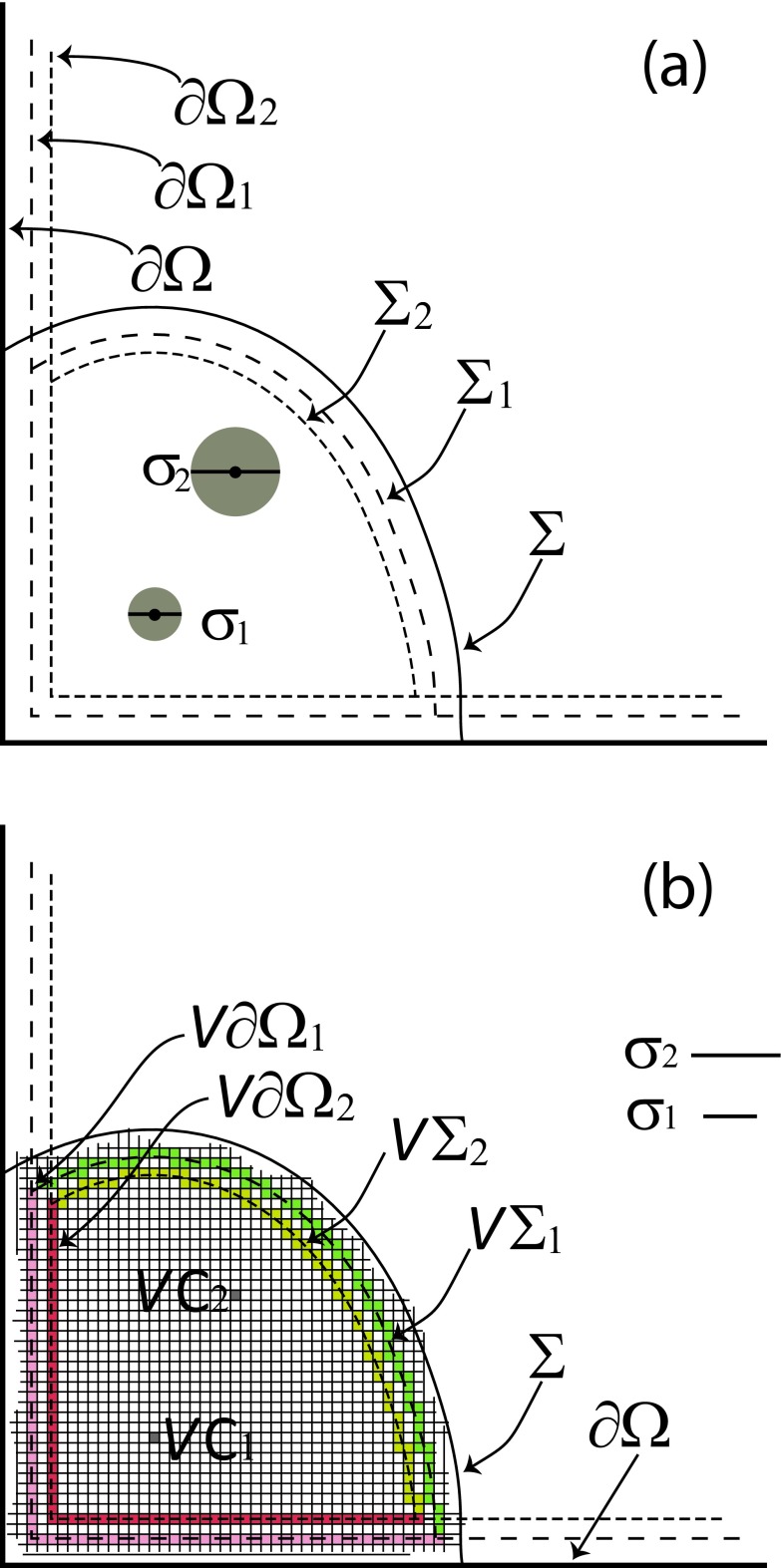
Next we consider two solute molecules 1 and 2 inside a corral. As in the one-molecule case just discussed, these molecules will usually be part of a larger collection of reactant molecules that are all contained within a common boundary ∂Ω. But we assume that at an initial time t0 molecules 1 and 2 have been cordoned off from the other molecules by an imaginary absorbing surface Σ. We define the four surfaces Σj and ∂Ωj (j = 1, 2) as the surfaces generated by the center of molecule j when molecule j is rolled around on the insides of Σ and ∂Ω, respectively. See Fig. 4(a). In eGFRD4 the specification of Σ for two molecules is more complicated: it involves two spheres associated with two auxiliary variables which are linear transforms of the position variables of the centers of the two molecules, and no provision is made for portions of ∂Ω to form a part of the corral for the molecules.
FIG. 4.
(a) Two solute molecules of diameters σ1 and σ2, part of a larger system of solute molecules enclosed in some containing region Ω, are at time t0 separated from the other molecules in Ω by an imaginary surface Σ and possibly a portion of the system boundary ∂Ω. The surfaces Σ1 and ∂Ω1 (dashed lines) are formed by tracing the positions of the center of molecule 1 when that molecule is rolled around on the insides of Σ and ∂Ω, respectively. The surfaces Σ2 and ∂Ω2 are formed in a similar way by the center of molecule 2. (b) After subdividing the corralling region enclosed by the larger of the Σ1 and Σ2 surfaces (Σ1 in this case) into cubic voxels of edge length h < min (σ1, σ2), the SVTA assumes that the centers of molecules 1 and 2 are distributed randomly and uniformly inside the particular voxels in which they respectively reside; those two voxels are shown here in gray, and are labeled VC1 and VC2, respectively. The surfaces Σ1, ∂Ω1, Σ2, and ∂Ω2 are replaced by their voxelated counterparts VΣ1 (in green), V∂Ω1 (in pink), VΣ2 (in yellow), and V∂Ω2 (in red). Although in this pictorial representation VΣ1 and VΣ2 do not have any voxels in common, they will if σ1 ≈ σ2, and in fact they will be identical if σ1 = σ2. Likewise for V∂Ω1 and V∂Ω2.
We subdivide the region accessible to the centers of the molecules into cubic voxels of edge length h, and we denote by VC1 and VC2 the voxels that currently contain the centers of molecules 1 and 2, respectively. See Fig. 4(b). A hop by molecule j will be implemented as a hop by the voxel VCj. Between hops, the center of molecule j is distributed randomly and uniformly inside VCj. We replace the surfaces Σ1, Σ2, ∂Ω1, and ∂Ω2 by the sets of all voxels which those surfaces intersect, denoting those respective voxel sets by VΣ1, VΣ2, V∂Ω1, and V∂Ω2. If VCj hops into a voxel belonging to VΣj we will halt the simulation. We will not allow VCj to hop into a voxel belonging to V∂Ωj since that would put some part of molecule j physically outside of Ω.
In a straightforward generalization of (18), the SVTA for a two-molecule corral imposes the following conditions on the voxel size h:
| (20) |
Notice that the upper bound on h here contradicts the requirement h ≫ (σ1, σ2) that is imposed by the reaction-diffusion SSA (RD-SSA) on its voxels. The latter requirement arises because the RD-SSA simulates bimolecular reactions inside individual voxels using the bimolecular propensity function, and that will not be physically justified unless the two reacting molecules occlude no more than a negligibly small fraction of a voxel. This difference has two important consequences. First, the SVTA cannot use the bimolecular propensity function to model bimolecular reactions. Second, the much smaller h values that are used in the SVTA make the simulation of diffusion using the voxel-hopping rule (5) much more accurate in the SVTA than in the RD-SSA. These observations should make it clear that, even though the SVTA and the RD-SSA both use the voxel-hopping strategy (5), they are really very different algorithms: the RD-SSA requires its voxels to be large enough that many reactant molecules can fit inside a single voxel, whereas the SVTA requires its voxels to be so small that they cannot contain the center of more than one molecule at a time; the RD-SSA uses the bimolecular propensity function, whereas the SVTA does not; and the SVTA tracks individual reactant molecules, whereas the RD-SSA does not.
The plan of the SVTA for a two-molecule corral is to hop VC1 and VC2 repeatedly, using the hopping rule (5), until either molecule 1 or molecule 2 reacts unimolecularly, or VC1 hops into a voxel belonging to VΣ1 or VC2 hops into a voxel belonging to VΣ2, or molecules 1 and 2 react bimolecularly. The task of determining the tentative time until either molecule reacts unimolecularly is a straightforward generalization of what was done in the one-molecule corral simulation. But hopping VC1 and VC2 is more complicated, because now we have to take care that a hop does not result in the molecules overlapping each other. And determining the tentative time when the molecules react bimolecularly is even more complicated; because, in the SVTA two molecules will react with each other only if they collide, and collisions occur on the smallest of space-time scales where the diffusion equation (1), and hence also the voxel-hopping rule (5), do not accurately describe the motion of the molecules. We will now describe in turn how the SVTA accomplishes the foregoing three tasks.
A. Simulating a unimolecular reaction
For the unimolecular reactions, it follows from the definition of ki (see Sec. II A) and the addition law of probability that the probability that either molecule will react unimolecularly in the next dt is
So, barring interfering eventualities, the time to the next unimolecular reaction will be exponentially distributed with decay constant k1 + k2. The tentative time to a unimolecular reaction can therefore be computed as
| (21a) |
where
| (21b) |
The molecule that reacts at this time will be
| (22) |
B. Simulating a hop
A new challenge in the two-molecule corral is that we must make sure that a hop by VC1 or VC2 does not result in the two molecules overlapping each other. This is another significant difference between the SVTA and the RD-SSA: The latter never checks to see if the destination voxel in a hop actually has room for the hopping molecule; the tacit assumption that there always is room can be justified, at least approximately, only if the system is dilute in the reactant molecules. Thus, the RD-SSA does not model molecular crowding, whereas the SVTA does.
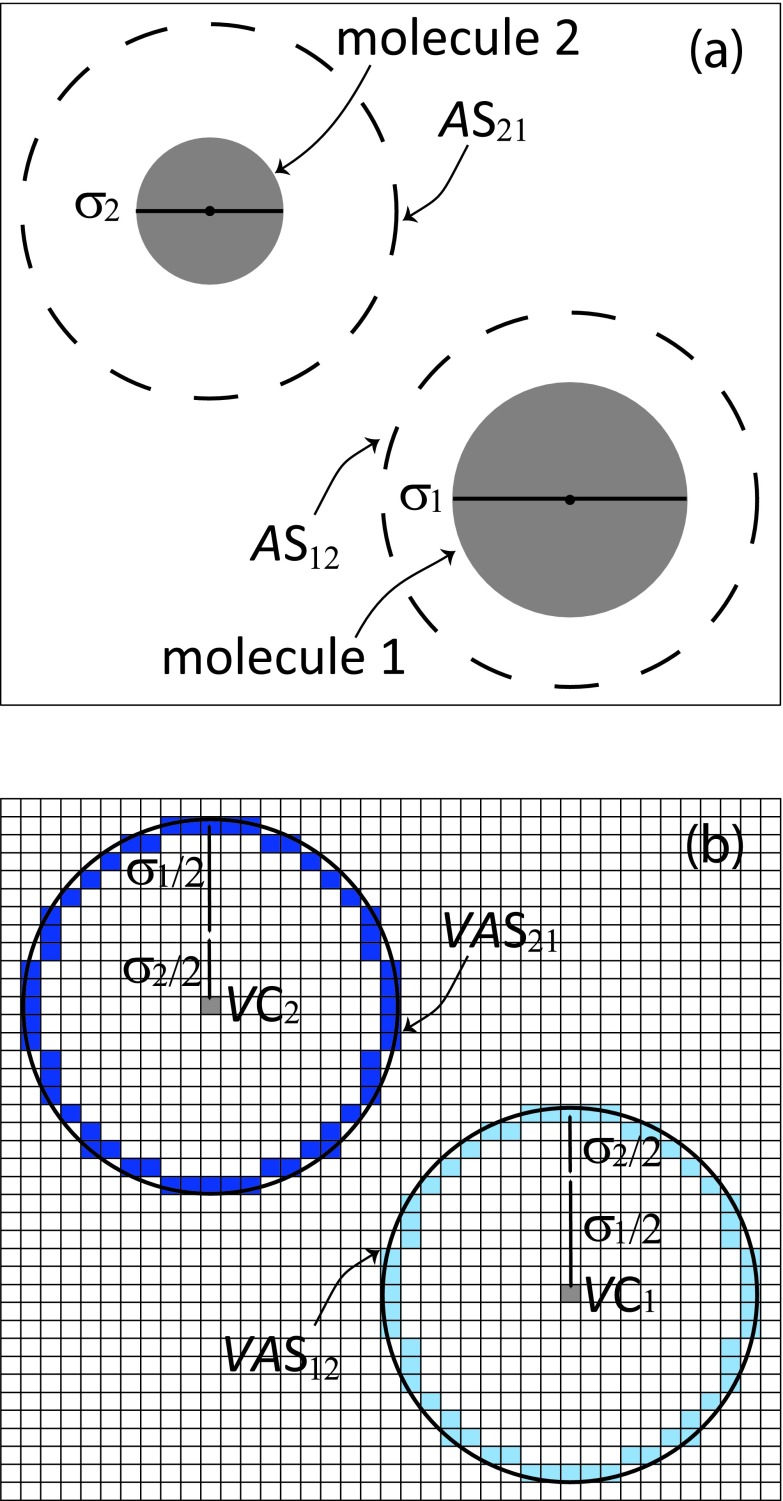
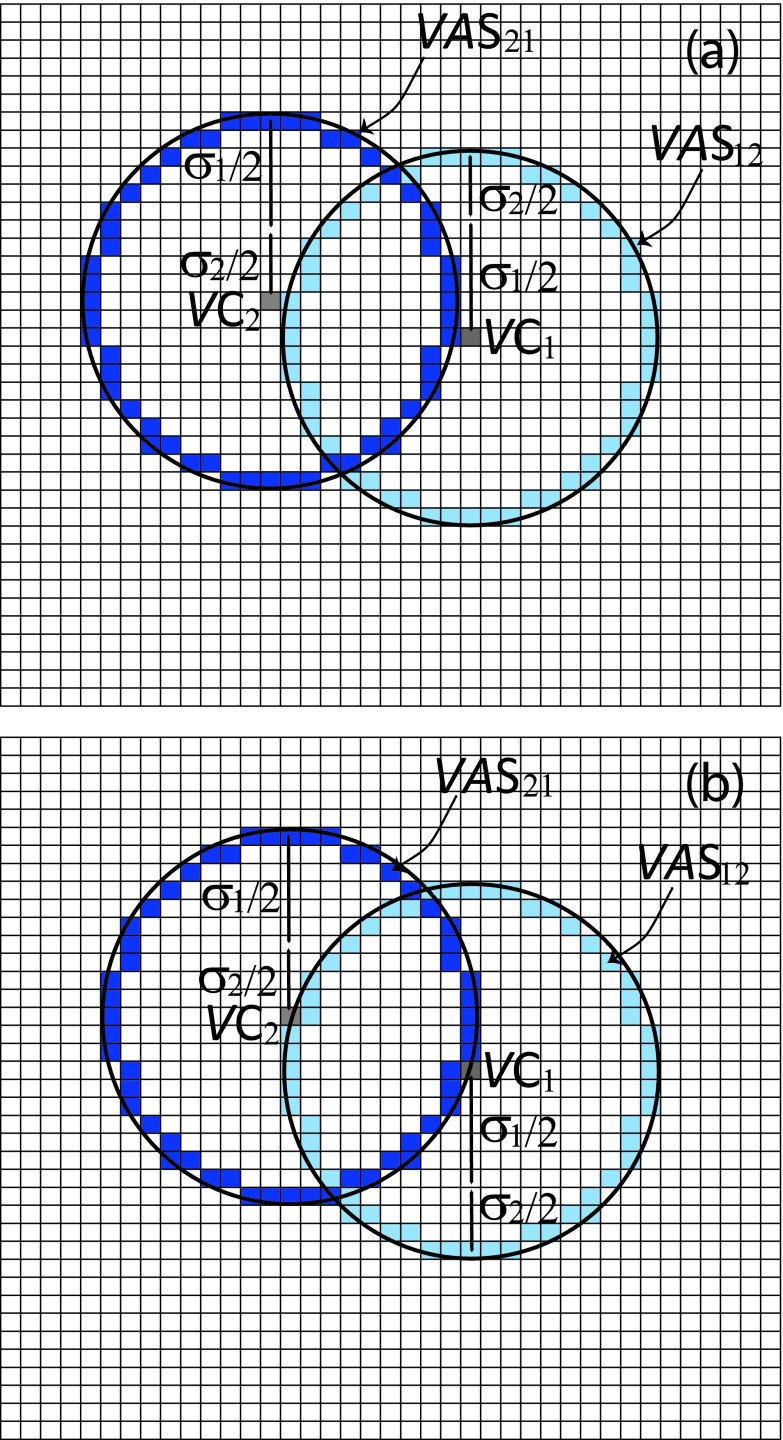
The SVTA's procedure for doing this is based on the simple rule that molecules 1 and 2 will be in collisional contact with each other if and only if the center of each lies on an imaginary sphere of radius σ12 that is concentric about the other. These spheres are called “action spheres.” To adapt this condition for collisional contact to our voxelated space, we must construct voxel approximations of the action spheres: VASij (i ≠ j) will denote the set of voxels that approximates the action sphere about molecule i relative to molecule j. One way to define VASij would be as the set of all voxels that are intersected by a sphere of radius σ12 which is centered on voxel VCi. But analytically determining if a voxel is intersected by a sphere is complicated. So we adopt instead the following nearly equivalent but more computationally convenient definition: VASij is the set of all voxels whose centers are a distance ⩽σ12 from the center of voxel VCi and which have at least one adjacent voxel whose center is a distance >σ12 from the center of VCi. Appendix B describes a computer-oriented procedure for constructing the set of voxels VASij according to this definition for given values of h and σ12.
Figure 5 attempts to clarify our definition of the voxelated action spheres in a simpler two-dimensional context. Figure 5(a) reminds us what molecules 1 and 2 are assumed to look like in the “real” world; the dashed circles are the imaginary action spheres around each molecule. Figure 5(b) shows molecules 1 and 2 in a voxelated world. Here the voxels VC1 and VC2 that contain the centers of the respective molecules are colored flat gray to emphasize that the center of each molecule is uniformly distributed inside its voxel. Spheres of radius σ12 are shown ascribed about the centers of voxels VC1 and VC2. The voxels colored dark blue have their centers inside the sphere about VC2, and also have at least one adjacent voxel whose center is not inside that sphere; they comprise the voxelated action sphere VAS21. The voxels colored light blue similarly comprise the voxelated action sphere VAS12. The two voxelated action spheres are of course identical structures. VAS21 surrounds and hops with VC2, and VAS12 surrounds and hops with VC1.
FIG. 5.
(a) Molecules 1 and 2 with their respective diameters σ1 and σ2. We imagine each molecule to be concentrically surrounded by an “action sphere” of radius . When the two molecules collide, the center of each molecule will be in contact with the action sphere about the other molecule. (b) In the SVTA, the centers of molecules 1 and 2 are assumed to be distributed randomly and uniformly inside voxels VC1 and VC2, respectively. The action sphere about molecule j is now represented by the set of all voxels whose centers are ⩽σ12 from the center of voxel VCj and which have at least one adjacent voxel that does not satisfy that condition. Here the voxelated action sphere VAS21 about molecule 2 relative to molecule 1 is the set of dark blue voxels, and the voxelated action sphere VAS12 about molecule 1 relative to molecule 2 is the set of light blue voxels. In the SVTA, the two molecules collide with each other whenever the center of either molecule comes into contact with the boundary of the voxelated action sphere about the other molecule. That will be possible only if either VC1 has hopped to a voxel that is adjacent to VAS21, or VC2 has hopped to a voxel that is adjacent to VAS12. VAS12 hops rigidly with VC1, and VAS21 hops rigidly with VC2; however, in an actual simulation we do not need to explicitly execute the hops of either voxelated action sphere.
Molecular crowding is modeled in the SVTA simply by making the voxels comprising VASij inaccessible to VCj, in the same sense that the voxels comprising V∂Ωj are inaccessible to VCj; i.e., VCj will not be allowed to hop into any voxel that belongs to VASij. This means that before each hop of VCj, we must determine which if any of its six adjacent voxels belong to VASij. Since voxelated action spheres may contain hundreds or even thousand of voxels, this task can be very time consuming in two ways: (i) many voxel comparisons have to be made prior to each hop of VCj, and (ii) the voxels that belong to VASij, unlike the voxels that belong to V∂Ωj, move every time VCi hops.
Although we have not found a way to alleviate problem (i), we have find a way to alleviate problem (ii): we can determine which adjacent voxels to VCj belong to VASij without having to explicitly hop VASij every time VCi hops. This is accomplished with the help of the virtual voxelated action sphere vVASij, which is a copy of VASij that is centered on the origin. Unlike VASij, vVASij does not hop with VCi, and it does not inhibit the motion of VCj. The utility of vVASij owes to the following lemma.
Lemma 1: The ±x-adjacent voxel to VCj will belong to VASij if and only if the voxel obtained by subtracting from the coordinates of that voxel the coordinates of VCi belongs to vVASij; and likewise for the ±y-adjacent voxel to VCj and the ±z-adjacent voxel to VCj.
Lemma 1 allows us to determine all the voxels adjacent to VCj that belong to VASij without directly consulting VASij. Once that is done, the next lemma allows us to immediately determine which voxels adjacent to VCi belong to VASji.
Lemma 2: If the ±x-face of VCj abuts VASij, then the ∓x-face of VCi will abut VASji; likewise for the ±y-faces and the ±z-faces of VCj.
The foregoing is the procedure that the SVTA uses before each hop by either VC1 or VC2 to determine the number of voxels adjacent to VC1 that belong to VAS21—a number that is also equal to the number of voxels adjacent to VC2 that belong to VAS12. The number of adjacent voxels to VCj that are accessible to VCj on its next jump will then be 6 minus minus the number of voxels adjacent to VCj that belong to V∂Ωj. (The latter number might not be the same for j = 1 and 2, so will not always be equal to .) Since all this information is obtained without ever explicitly referencing the two ever-moving voxelated action spheres VAS21 and VAS12, a hop will always involve explicitly relocating only one voxel—namely VC1 or VC2.
Using the foregoing procedure to determine before each hop which voxels adjacent to VC1 and VC2 are open, the procedure for executing the next hop is a fairly straightforward extension of the procedure used in the one-molecule corral. Applying the addition law of probability to the hopping rule (5), we see that the probability that either molecule will hop in the next dt is
This implies that if t is the current time, then the tentative time of the next hop is
| (23a) |
where
| (23b) |
Since is the probability that it will be molecule j that hops at this time, then the molecule that makes the hop can be computed as
| (24) |
The destination of the hopping molecule j* is then obtained by selecting one of that molecule's accessible adjacent voxels “at random.” One way to do that is to number those voxels in any order from 1 to and then take the number of the destination voxel to be
| (25) |
where [x] denotes “the greatest integer in x.” We implement the hop by moving accordingly.
C. Simulating a collision
The third and final part of the SVTA's two-molecule corral plan is to determine the tentative time when molecules 1 and 2 will react bimolecularly. But here we face a problem: molecules 1 and 2 will react with each other only if they collide, and collisions occur on small space-time scales where neither the diffusion equation (1) nor the voxel-hopping rule (5) is physically valid. In devising a rule for when two molecules collide in voxelated space, we cannot just make something up; we must be guided by the physics that describes the motion of solute molecules. To that end, we turn to a result that is used in the derivation of the bimolecular propensity function (which ironically is not used by the SVTA). As stated in Appendix A, the fact that solute molecules move ballistically on small space-time scales implies the result (A4). That result says that if the PDF of a solute molecule near a small surface element of area a has the value p0, then the probability that the molecule will impinge on or collide with that surface element in the next infinitesimal time dt will be equal to , where is the average speed the molecule would have if it were in an ideal gas at the same temperature. As a preliminary test of this result in a voxel context, let us use it to calculate the probability that the center of our molecule 1, which is uniformly distributed inside voxel VC1, will impinge on (or collide with) a particular one of VC1's six faces. The value of the constant PDF of the center of molecule 1 inside VC1 must be equal to the reciprocal of the voxel volume h3 for normalization, and the area of a voxel face is h2. So, according to (A4), the probability that the center of molecule 1 will impinge on a given face of VC1 in the next dt is
| (26) |
Here, is the average speed of molecule 1 in a dilute gas at temperature T. Is this result plausible? It evidently implies that the reciprocal of the coefficient of dt on the right of Eq. (26) is the average time to the impingement. Physically, we expect that {the average time until the center of molecule 1 impinges on a voxel face} should be much smaller than {the average time until the center of molecule 1 hops across that voxel face and uniformly populates the voxel on the other side}. The latter time is of course the reciprocal of the hopping probability rate D1/h2. It is not hard to show that the requirement in (20) implies exactly the expected result:
| (27) |
So we conclude that the result (26) is indeed plausible, and hence that (A4) should enable us to correctly describe a collision between two molecules in voxelated space.
Returning to that problem, we note that the two “adjacency” situations depicted in Figs. 6(a) and 6(b) could have come about as a result of several possible hops. In Fig. 6(a), for example, VC1 and VAS12 could have just jumped one voxel up or down or left; or VC2 and VAS21 could have just jumped one voxel down or up or right. Regardless of which of these six hops led to the situation depicted in Fig. 6(a), molecules 1 and 2 have not yet collided. But a collision is now possible: molecules 1 and 2 will collide whenever the center of either molecule impinges on a voxel face that is shared with the voxelated action sphere about the other molecule. However, when we work on the small length scale of an impingement, we must abandon some voxel-inspired approximations that were acceptable on larger length scales: On small length scales, the action sphere about each molecule can no longer be regarded as a stationary structure that is centered on the voxel containing the molecule's center; it must instead be regarded as a structure that is centered on, and rigidly moving with, the molecule which it surrounds. That implies that the average speed of the impingment will be the average relative speed of the two molecules. It also implies that an impingement of the center of molecule 1 on the action sphere about molecule 2 will always be accompanied by the impingement of the center of molecule 2 on the action sphere about molecule 1; i.e., although molecules 1 and 2 hop independently, they collide together. Therefore, a collision between molecules 1 and 2 is the impingement of the center of molecule 1 on any face of its containing voxel VC1 that is shared with VAS21, and the impingement occurs at the average relative speed of the two molecules.
FIG. 6.
(a) VC1 shares one voxel face with VAS21, and VC2 shares one voxel face with VAS12. (b) Two voxel faces are being shared; the number of shared faces will always be the same. A collision between molecules 1 and 2 requires either the center of molecule 1, which is uniformly distributed inside voxel VC1, to impinge on the face of a voxel that belongs to VAS21, or the center of molecule 2, which is uniformly distributed inside voxel VC2, to impinge on the face of a voxel that belongs to VAS12. But on the small spatiotemporal scale of a collision, those two events will always occur together; also, since the action sphere about molecule j is really centered on molecule j rather than voxel VCj, then each voxelated action sphere will see the center of the other molecule moving with the relative speed of the two molecules.
With this perspective, we can now use (A4) to compute the probability of a collision between molecules 1 and 2 in the next dt when VC1 shares faces with VAS21 (in which case VC2 will share faces with VAS12). Since the PDF of the center of molecule 1 everywhere inside VC1 is p0 = h−3, and since the total surface area shared by VC1 and VAS21 is , then the impingement probability formula yields
| (28) |
where is given by Eq. (10). Therefore, defining
| (29) |
we conclude that
| (30) |
This result implies that if, at the current time t, VC1 shares faces with VAS21, then unless a unimolecular reaction or a hop occurs first, molecules 1 and 2 will collide at time
| (31a) |
where
| (31b) |
D. Simulating a bimolecular reaction
The collision time τcol would not be needed if q12 = 0, because then it would not matter when or even if molecules 1 and 2 collide. All that is needed when q12 = 0 is the rule that VCj is not allowed to hop into any voxel belonging to VASij. But if q12 > 0, we need the result (31) to determine if and when a reaction between the two molecules occurs. We do that as follows: Let ncol be the number of collisions between molecules 1 and 2 that are required to initiate a reaction. Since q12 is the probability that one collision will produce a reaction, then
| (32) |
This functional form implies that ncol is the geometric random variable with mean 1/q12:
| (33) |
So, at the initial time t0, we generate a random value for ncol according to Eq. (33). Then at each subsequent collision between molecules 1 and 2 we reduce ncol by 1, and we execute the bimolecular reaction when ncol reaches zero.17 Note that the collisions might be interspersed with hops, and thus be distributed over several separate VC1-VAS21 adjacencies, whose values for β12 cannot be predicted in advance.
To summarize: In a two-molecule corral, the next event will always be either a unimolecular reaction of either molecule, or a diffusional hop by either molecule, or a collision between the two molecules. We have computed in Eqs. (21), (23), and (31) the tentative times tuni, thop, and tcol for these possible next events. If tcol < min (thop, tuni), we will execute the collision by advancing t to tcol and simultaneously decrementing ncol (which was generated according to Eq. (33) at time t0) by 1. If that decrement makes ncol = 0, we execute the bimolecular reaction and halt. Otherwise, since the collision did not change the voxel location of either molecule, we will generate a new tentative time of the next collision according to Eqs. (31a) and (31b) and continue the simulation. But if instead tcol ⩾ min (thop, tuni), we will proceed as follows: if thop < tuni, we will advance t to thop, execute a hop, and then continue the simulation; otherwise, we will advance t to tuni, execute a unimolecular reaction, and halt. The full simulation procedure for the two-molecule SVTA is outlined in Fig. 7.
FIG. 7.
Outline of the two-molecule SVTA procedure.
VI. EQUIVALENCE OF THE SVTA AND eGFRD
We will now show that the SVTA and eGFRD4 are equivalent, in that they can be derived from the same line of reasoning. That line of reasoning is the derivation in Appendix A of the bimolecular propensity function and its rate constant k in Eq. (7), but with one important difference: the bimolecular propensity function requires the system to be dilute in the solute molecules, but the SVTA and eGFRD do not. This difference arises because any analysis of the interaction between two molecules makes the tacit assumption that their relative motion will not be affected by the presence of a third reactant molecule. The SVTA and eGFRD satisfy that assumption by putting a corral around the two molecules. But the bimolecular propensity function, which underlies both the CME and the SSA, does not know where any of the reactant molecules really are, so the only way it can satisfy the assumption is to require the reactant molecules be so dilute in Ω that clusterings of three or more molecules will be so infrequent that they can be ignored. We will now show that, except for this difference, the SVTA and eGFRD follow from the same reasoning used to derive Eq. (7).
As noted in Appendix A, the derivation of Eq. (7) proceeds in two phases. The first phase uses the Einstein diffusion equation (1) to derive Eq. (A3). The second phase takes account of the fact that on the small length scales where molecular collisions occur, the physical motion of a solute molecule is actually ballistic, and hence not described by the diffusion equation. The second phase combines the ballistic motion result (A4) with the definition of q12 to obtain Eq. (A6). When Eq. (A6) is combined with Eq. (A3) from the first phase of the derivation, the result is the explicit formula for k in Eq. (7).
That the SVTA's procedure for simulating a bimolecular reaction follows this same line of reasoning can be seen as follows. Just as the first phase of the derivation of k used the diffusion equation in the region outside the action sphere around molecule 2 to derive Eq. (A3), the SVTA begins by using the voxel-hopping procedure (5) to bring molecules 1 and 2 to within almost contact distance of each other. The smallness of h demanded by the SVTA ensures that the voxel-hopping procedure will give an accurate rendering of the motion prescribed by the diffusion equation.8 Next, just as the second phase of the derivation of k combined the ballistic result (A4) with the definition of q12 to obtain Eq. (A6), the SVTA uses the ballistic result (A4) to obtain Eqs. (29) through (31), and then invokes the definition of q12 to obtain Eqs. (32) and (33). Thus we see that the SVTA's procedure for simulating a bimolecular reaction emerges from the same logic that gave us the bimolecular reaction rate constant k in Eq. (7), although without the latter's requirement that the system be dilute in the reactant molecules.
To show that eGFRD's procedure for simulating a bimolecular reaction likewise finds its justification in the derivation of Eq. (7), we begin by noting that both that derivation and eGFRD use the Einstein diffusion equation (1), with D replaced by D12 ≡ D1 + D2, to describe the motion of molecule 1 relative to molecule 2 in the region outside the action sphere around molecule 2. Indeed, in Appendix A, the PDF p1(r, t | r0, t0) of the position of the center of molecule 1 relative to the center of molecule 2 is none other than the “Green's function” of eGFRD. But let us focus now on Eqs. (A1) and (A5) in Appendix A. In both of those equations, da is an infinitesimal area element on the surface of the action sphere at point . Equation (A1) encapsulates the first phase of the derivation of k: it describes the initial diffusional approach of the two molecules over center-separation distances that are large compared to σ12. Equation (A5) encapsulates the second phase of the derivation of k; it describes the final ballistic approach of the two molecules when the distance between their centers is nearly equal to σ12. But since the right sides of Eqs. (A1) and (A5) describe the same probability, then their left sides must be equal:
Simplifying this gives
| (34a) |
Equation (34a) says that the gradient of p1 at any point on the action sphere must at all times be equal to a certain constant times the value of p1 at that point. Equation (34a) can therefore be used as a boundary condition for the diffusion equation at the action sphere; indeed, it is a kind of boundary condition that is known generically as a “radiation” boundary condition. Since the derivation we just gave of Eq. (34a) made use of the ballistic relation (A4), then solving the diffusion equation subject to boundary condition (34a) should yield a solution that takes proper account of the ballistic motion of molecule 1 relative to molecule 2 in the immediate vicinity of the action sphere. And that is exactly what eGFRD4 does, although it eliminates the parameter q12 in Eq. (34a) in favor of the parameter kbal via Eq. (14) to obtain the equivalent formula
| (34b) |
Equation (34b) is eGFRD's radiation boundary condition as written in Eq. (S20) of Ref. 4, allowing for the fact, mentioned earlier in connection with Eq. (13), that the “intrinsic rate constant” ka in Ref. 4 is the same as our kbal. (We note as an aside that Eq. (A7) is a more explicit rendering of the radiation boundary condition when the system is dilute and well-mixed.) The fact that eGFRD's radiation boundary condition (34b) can be derived from the same physics that underlies the SVTA establishes the logical equivalence of these two simulation procedures.
Those who have long known, e.g., from the work of Bicout et al.,18 that imposing the radiation boundary condition (34b) on the diffusion equation yields a physically correct modeling of a bimolecular reaction, might choose to adopt the following perspective: the SVTA's procedures at Eqs. (29)–(33) amount to a way of imposing the radiation boundary condition on the voxel-hopping method of simulating the diffusion equation.
VII. EXAMPLE SIMULATIONS WITH THE TWO-MOLECULE SVTA
We will illustrate the two-molecule SVTA simulation procedure of Sec. V by using a simplified version of it in which molecules 1 and 2 are the only reactant molecules in Ω, there is no corralling surface Σ, and the molecules cannot react unimolecularly. Thus, the only halting event will be the reaction of the two molecules with each other. We will assume that molecules 1 and 2 have the same diameters, so that the surfaces ∂Ω1 and ∂Ω2 which confine their centers will coincide. To lend some element of realism to our example, we will assign values to the physical parameters that are roughly typical of real cellular systems [see the discussion leading to Eq. (19)]:
With T = 293K, Eq. (10) gives for the average relative speed of the two molecules
| (35d) |
Lacking guidance for a realistic choice for the collision-conditioned reaction probability q12, we will arbitrarily take
| (35e) |
so that on average 5 collisions will be needed to induce a reaction. Finally, we will take the containing volume Ω to be a cube of edge length H. For our first three examples, we will assign H the value
| (36) |
which is slightly over 21 times larger than the diameter of each molecule. And for the voxel edge length h, we will choose the value
| (37) |
so that there are exactly 201 voxels that are accessible to VC1 and VC2 along each axis of the cube Ω. The value of the left side of condition (20) in this case is 0.014 × 10−9 m, so the lower bound condition on h is well satisfied.
In our first example, molecules 1 and 2 are initially placed near the middle of the cube Ω, with their edges separated by five molecular diameters. This initial condition is depicted in the inset to Fig. 8, in which the sizes of the molecules and Ω are drawn to scale. With this initial condition, we made 105 runs of the STVA. A normalized frequency histogram of the times to reaction thus obtained is shown in Fig. 8. The vertical bar over each histogram bin shows the one-standard deviation uncertainty limits for that bin. The dashed vertical line locates the mean of the data. The open-circle curve shows what the histogram would look like if the data were exponentially distributed with that mean. We see that while the match between that exponential distribution and the histogram is good above the mean, it is not good below the mean; in particular, the large spike in the first bin makes it clear that these reaction times are not exponentially distributed. That fact has an interesting consequence: there is no reaction rate constant which characterizes these reaction times; i.e., there is no constant c such that c·dt gives the probability that molecules 1 and 2 will react with each other in the next infinitesimal time dt.
FIG. 8.
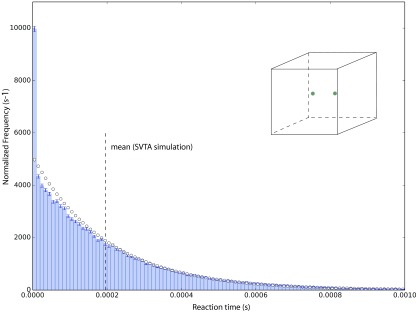
A normalized frequency histogram of 105 times to reaction of two molecules in a cubic container, as simulated by the SVTA. The parameter values are as given in Eqs. (35)–(37). The inset figure shows the size of the two molecules in relation to the size of Ω, as well as the initial positions of the centers of the two molecules at points (−3σ12, 0, 0) and (3σ12, 0, 0). The vertical bar around each histogram bin level denotes the one-standard deviation statistical uncertainty interval for that bin. The vertical dashed line is the mean of the data, and the open-circle curve is the exponential distribution corresponding to that mean. Owing to the discrepancies between the histogram and the open-circle curve below the mean, especially in the first histogram bin, the distribution of the time to reaction is not exponential. That implies that these reactions times cannot be characterized by a reaction rate constant; i.e., there is no constant c such that c·dt gives the probability that molecules 1 and 2 will react with each other in the next infinitesimal time dt.
Our second example is the same system but with a different initial condition. Now we start with molecules 1 and 2 in opposite corners of Ω, as shown in the inset to Fig. 9. The accompanying histogram is of the reaction times obtained in 105 runs of the STVA for this initial condition. Compared to the histogram in Fig. 8, the mean here is 18% larger, and the spike in the first bin in Fig. 8 has been replaced by a deep valley. But once again, the histogram is not exponential, so there is no reaction rate constant.
FIG. 9.
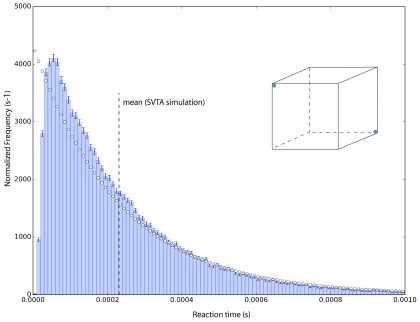
A repeat of Fig. 8, but now with molecules 1 and 2 initially located in opposite corners of Ω, as illustrated in the inset. Again the time to reaction is not exponentially distributed. The implication of Figs. 8 and 9 is that the PDF of the time to reaction for a delta-function initial condition will generally be non-exponential, and moreover will be different for different initial positions of the two molecules. As a consequence, the notion of a “reaction rate” loses practical utility. But this poses no problem for the SVTA.
The results in Figs. 8 and 9 are not surprising: it is perfectly reasonable that if the molecules are initially close together their time to reaction will tend to be smaller than if they were initially far apart. But the result that neither case can be described by a reaction rate constant may come as a surprise to many. Some might counter that this simply means that the reaction rate in these cases is not a constant, but rather a function of time. However, the facts that (i) the form of that function of time apparently can be deduced only through a post hoc analysis, and (ii) there will be a different reaction rate function for every different initial condition, seem rather to suggest that the concept of “reaction rate” is simply not useful when the initial positions of the molecules are sharply specified. Although that might be a problem if one were intent on describing these reactions with a differential equation, it is not a problem for the SVTA, nor for eGFRD either.
The foregoing results naturally make one wonder how the SVTA connects with situations in which reaction rates do exist. Those situations are described by the bimolecular propensity function. As discussed in Sec. II C and Appendix A, for a system containing two reactant molecules the bimolecular propensity function is the constant k|Ω|−1, where k is given by Eq. (7). By definition, k|Ω|−1dt is the probability that molecules 1 and 2 will react with each other in the next infinitesimal time dt. That implies that the time to reaction will be the exponential random variable with decay constant k/|Ω| and mean |Ω|/k. However, all this requires the system to be dilute and well-mixed. Satisfying those two conditions turns out to be more complicated than one might imagine.
Diluteness in this case requires σ12 to be small enough, or Ω to be large enough, that the volume occluded by molecules 1 and 2 is negligibly small compare to |Ω|. That means that diluteness is a limiting ideal that cannot be attained by any finite system; any finite system can be, at best, only approximately dilute. However, there is one aspect of the small occluded volume requirement that we can fold into the theory, at least approximately, rather easily: An inspection of the derivation of the bimolecular propensity function10 reveals that |Ω| in the formula k/|Ω| for the bimolecular propensity function is actually supposed to be the volume that is accessible to the center of molecule 1. For a truly dilute system in which σ12/H ≈ 0, that volume would be, to a satisfactory approximation, H3. But if σ12/H is not infinitesimally small, we should recognize that the center of molecule 2 actually has access only to a cube whose walls are set in from those of Ω by σ12/2, and whose edge length is therefore H − σ12. Furthermore, for most (but not all) of the time, the action sphere around molecule 2 will occlude an additional volume . It should therefore be more accurate to take the bimolecular propensity function to be
| (38) |
This expression obviously reduces to k/H3 in the dilute limit σ12/H → 0. In the system depicted in the insets to Figs. 8 and 9, a system which at first sight might seem to be “reasonably dilute,” this correction to the bimolecular propensity function amounts to a surprisingly large 16% increase in the value of the bimolecular propensity function.
As for the propensity function's well-mixed requirement, one might think that it could be satisfied simply by choosing the initial positions r1 and r2 of the centers of molecules 1 and 2 in a randomly uniform way inside the cube , discarding pairs for which |r1 − r2| < σ12. However, doing that would not establish the initial distribution that is actually assumed in the physics derivation of the bimolecular propensity function and its constant k in Eq. (7). As is shown in Appendix A, that derivation assumes that the PDF of the initial vector r1 − r2 ≡ r is the solution of the steady-state, isotropic diffusion equation
| (39) |
which satisfies the two boundary conditions
| (40a) |
and
| (40b) |
If molecules 1 and 2 were non-reacting, so that q12 = 0, then the boundary condition (40b) on the action sphere would be the same as the far-field boundary condition (40a), and the solution to Eq. (39) would then be P1(r) = |Ω|−1 for all accessible r; that is the distribution that would be generated by the uniform seeding procedure just described. But in the present case we have q12 = 0.2, and the prefactor in Eq. (40b) is 0.04 instead of 1. In Ref. 16, we derive a Monte Carlo procedure for generating the initial positions r1 and r2 of the centers of molecules 1 and 2 in such a way that r will distributed according to the solution of Eq. (39) for the boundary conditions (40a) and (40b) for any value of q12 in [0,1].
Using this special random seeding procedure to generate the initial positions of molecules 1 and 2, we again made 105 runs of the system in Figs. 8 and 9. The histogram of the reaction times thus obtained is shown in Fig. 10. Again the vertical dashed black line locates the mean of the data, and the open-circle curve is the exponential distribution corresponding to that mean. We see that except for a very slight excess of events in the first histogram bin, the reaction times can now be considered exponentially distributed. So now we have a reaction rate constant, namely, the reciprocal of the data average. The red vertical line in Fig. 10 locates the average reaction time corresponding to the “corrected” bimolecular propensity function (38)—i.e., the reciprocal of the right side of (38)—and the red curve shows the exponential distribution corresponding to that average. There is evidently a noticeable difference between the SVTA simulation results and the predictions of the (corrected) bimolecular propensity function theory: the mean reaction time of the data is 15% larger than the mean reaction time predicted by the theory underlying the bimolecular propensity function.
FIG. 10.
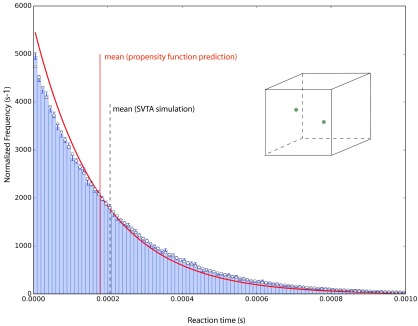
As in Figs. 8 and 9, but now the initial positions of the molecules are not as shown in the inset figure; instead, the initial positions were generated from the probability distribution that is assumed in the derivation of the bimolecular propensity function (see text). The histogram of the generated reaction times now approximates very closely the exponential curve (open-circles) corresponding to the data mean (vertical dashed black line); there is only a small discrepancy in the very first bin. Therefore, to a very good approximation, the reaction times for this distribution of initial positions can be described by a reaction rate constant—namely, the reciprocal of the data mean. The solid vertical red line locates the mean reaction time predicted by the bimolecular propensity function in formula (38), which takes account of the fact that its derivation considers |Ω| to be the volume that is actually accessible to the center of either molecule. The solid red curve is the exponential distribution corresponding to that mean. A perspective on the mismatch between the propensity function prediction and the SVTA data can be gained by comparing with the results in Fig. 11.
Any attempt to understand the apparent discrepancy in Fig. 10 must begin by noting that, if we had not made the correction to the propensity function formula in (38), which reduced the mean predicted by the bimolecular propensity function by 16%, we would be looking here at only a 1% discrepancy, and we might be feeling quite satisfied. However, the logic motivating the correction in (38) is very compelling; moreover, the results obtained in an additional simulation suggest that correction is in fact warranted. That additional simulation is of the same two molecules as in the preceding three simulations, but now enclosed in a smaller cube whose edge length, H = 32.177 × 10−9 m, is one-fourth of the value in Eq. (36). The relative sizes of the two molecules and their new Ω are illustrated to scale in the inset to Fig. 11. In simulating this system, we reduced the voxel edge length to h = 0.1297 × 10−9 m in order to maintain the condition that there will be exactly 201 voxels accessible to VC1 and VC2 along each axis of Ω. With the initial locations of the two molecules again chosen according to the probability distribution assumed in deriving the bimolecular propensity function (see Ref. 16), we made another series of 105 SVTA simulations. The histogram of the reaction times thus obtained is shown in Fig. 11.
FIG. 11.
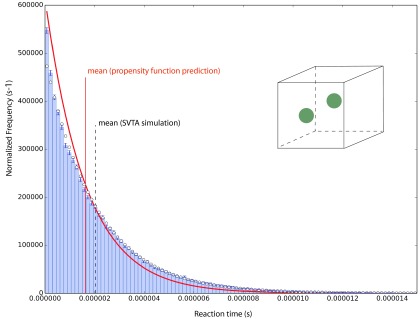
A re-do of the run in Fig. 10 after reducing the edge length H of Ω by a factor of one-fourth, and making a corresponding reduction in h. Again, the inset figure illustrates only the relative sizes of the molecules and Ω; the initial positions of the molecules were generated from the probability distribution that is assumed in the derivation of the bimolecular propensity function. Notice that the time scale on the horizontal axis here is nearly two orders of magnitude smaller than in Fig. 10. In contemplating the differences between the SVTA results and the bimolecular propensity function predictions in Figs. 10 and 11, several points should be kept in mind: (i) the SVTA never takes notice of the bimolecular propensity function's rate constant k in Eq. (7), which determines the locations of the red lines in these figures; (ii) neither of these systems is perfectly dilute, as is assumed by the bimolecular propensity function; and (iii) the predictions of the bimolecular propensity function may not be exact, because its derivation (see Appendix A) makes approximating assumptions. What these two figures do show is that the differences between the SVTA results and the predictions of the bimolecular propensity function are smaller in the more dilute system of Fig. 10 that in the less dilute system of Fig. 11, as theory predicts.
A careful comparison of Figs. 10 and 11 reveals two significant facts. First, exponential distribution that corresponds to the mean of the data (the open-circle curve) fits the histogram of the data better in Fig. 10 than in Fig. 11; this can be seen by comparing the fits in the first two histogram bins of each figure. Second, the fractional difference between the mean of the data (vertical dashed black line) and the mean predicted by the bimolecular propensity function theory (vertical red line) is smaller in Fig. 10 (15%) than in Fig. 11 (25%). Qualitatively, these results are just what we expect: neither system is perfectly dilute, as is required by the derivation of the bimolecular propensity function, but the system that is more dilute (Fig. 10) agrees with the prediction of the bimolecular propensity function better than the less dilute system (Fig. 11). On top of all that is the fact that we really have no warrant for regarding the theory underlying the bimolecular propensity function as being exact. That is because the derivation of formula (7) for k (see Appendix A) made some assumptions: it assumed a steady-state, isotropic initial condition, which provided us with Eq. (39); and it assumed a large reservoir at infinity, in order to sustain the outer boundary condition (40a) in the presence of the lower inner boundary condition (40b). Although those assumptions are physically reasonable for a system that is dilute and well-mixed, they ultimately amount to approximations. Therefore, their consequences cannot be presumed to be exact. For example, formula (7) for the bimolecular propensity function is completely independent of the shape of Ω, yet it is easy to imagine extreme shapes that would invalidate that formula. So the red lines in Figs. 10 and 11 cannot confidently be regarded as exact benchmarks. Indeed, it might turn out that the approximations made in deriving the SVTA are more accurate than the approximations that were made in deriving the bimolecular propensity function, in which case Figs. 10 and 11 would be revealing errors in the propensity function theory. Finally, in further defense of the excluded volume correction (38), the highly plausible similarity of Figs. 10 and 11 would be spoiled without that correction.
With all this in mind, and also taking into account that (i) the time scales on the horizontal axes in Figs. 10 and 11 differ by nearly two orders of magnitude, and (ii) the SVTA never takes notice of the propensity function's formula (7) for k or its formula (38), it could be argued that the level of agreement between the SVTA results and the bimolecular propensity function theory in Figs. 10 and 11 is actually rather good. We conclude that the simulations in Figs. 10 and 11 show that the SVTA gives results that appear to be as compatible with the bimolecular propensity function as we are presently entitled to expect.
VIII. THREE-MOLECULE EVENTS IN THE SVTA
Situations will often arise in which three solute molecules will be situated so equitably relative to each other that putting an absorbing surface Σ around two of them and a second absorbing surface Σ′ around the third would seem arbitrary. While doing so anyway would certainly not be incorrect, it might be more efficient to put a single absorbing surface Σ around all three molecules. This would appear to be difficult to do using the current method for implementing eGFRD.4 But the SVTA can treat the three-molecule case by making straightforward extensions of the two-molecule procedure described in Sec. V. Here we outline those extensions in just enough detail that the interested reader should be able to generalize the two-molecule procedure in Fig. 7 to the three-molecule case.
The voxel VCj containing the center of molecule j for j = 1, 2, 3, and the voxelated corralling surfaces VΣj and V∂Ωj for those centers, are all defined in the same way as in a two-molecule corral. The bounds on h are the obvious generalization of those in (20). There will now be six voxelated action spheres: VAS12 and VAS13 surround and hop with VC1; VAS21 and VAS23 surround and hop with VC2; and VAS31 and VAS32 surround and hop with VC3. They are defined in the same way as in the two-molecule case (see Appendix B). But as discussed in Sec. V, we will not need to explicitly track any of them. We need only construct one virtual voxelated action sphere for each pair—e.g., vVAS12, vVAS23, and vVAS31—each of which will remain centered on voxel (0, 0, 0) throughout the simulation.
The tentative time of a unimolecular reaction will be [cf. Eqs. (21a) and (21b)]
| (41) |
The molecule that so reacts at that time will be molecule j with probability ; thus, the index of the reacting molecule can be generated by an obvious extension of Eq. (22).
In order to determine the tentative times to the next hop and the next collision, we must first determine the status of the six voxels adjacent to each of VC1, VC2, and VC3. This is done in the same way as in the two-molecule case. In that way we learn the value of , the number of voxels adjacent to VC1 which do not belong to V∂Ω1 or VAS21 or VAS31, and similarly the values of and . We also learn the values of , the number of voxels adjacent to VCj that belong to (which is the same as the number of voxels adjacent to that belong to ) for all j′ ≠ j.
The tentative time of the next hop will be [cf. Eqs. (23a) and (23b)]
| (42) |
where t is the current time. The molecule that hops at that time will be molecule j with probability ; thus, the index of the hopping molecule can be generated by an obvious extension of Eq. (24).
As for bimolecular reactions, if none or only one of the qjj′'s are >0, the simulation procedure will be an obvious extension of the two-molecule case. To illustrate what happens if more than one pair of molecules can react bimolecularly, let us consider the case in which pairs (1, 2) and (2, 3) can react, but the pair (3, 1) cannot:
| (43a) |
Before entering the main simulation loop, we will generate, for each pair that can react, the number of collisions that will produce a reaction of that pair [cf. Eqs. (32) and (33)]:
| (43b) |
Then in the main simulation loop, as part of the decision process to determine whether the next event will be a unimolecular reaction or a hop or a collision between two reactable molecules, we will generate a tentative time of the last as [cf. Eqs. (29) and (31)]
| (43c) |
where t is the current time and
| (43d) |
Note that we do not care when or even if the non-reactable pair (3, 1) collides, because that collision has no consequence other than the blocked hopping destinations of molecules 1 and 3, and those we account for simply by obeying the blocks. If tcol ⩽ min (tuni, thop), we will select the pair that actually collides by generating u = (0, 1) and then choosing
| (43e) |
We will then execute the collision of the chosen pair (j, j′) by reducing by 1. If that reduction brings to zero, we will immediately execute the reaction of that pair.
The three-molecule SVTA procedure can obviously be extended to more molecules, and indeed, at least in principle, to all the molecules in the system without any corralling surfaces. However, the increasing combinatorial complexity associated with checking to see which molecular pairs are imminently colliding, coupled with the concomitant loss of the computational parallelism that is provided by the corrals, will inevitably result in some optimal (and probably small) number of molecules to corral. This is a matter that requires future investigation.
IX. ACCOMMODATING NON-COLLISIONAL FORCES BETWEEN REACTANT MOLECULES
Practically all reactant molecules in a cell are electrically neutral, in that they contain the same number of protons and electrons. But those positive and negative charges are distributed differently over the molecules, and that gives rise to electrical forces between the molecules. Such forces will generally be of much shorter range than the 1/r2 force between two point charges. Examples of such forces in cell biology are the van der Waals interactions that hold together the nonpolar regions of fat molecules to form the lipid bilayer in cells, and the forces between proteins as they fold and bind with each other to form bigger structures (e.g., red blood cells).19,20
When a solute molecule i is subject to a force F that does not arise from collisions with the surrounding solvent molecules, the motion of the molecule on sufficiently large spatial and temporal scales is described by the Smoluchowski equation:21
| (44) |
The Smoluchowski equation reduces to the standard diffusion equation (1) when F ≡ 0. It turns out that the voxel-hopping procedure (5) for simulating the motion of a molecule according to the diffusion equation (1) can be extended to the Smoluchowski equation (44), once again in a way that becomes exact in the limit h → 0, by a fairly simple modification of the hopping probability rate Di/h2.22 This allows the SVTA to take account of forces of attraction or repulsion between reactant molecules. We will now describe how this is procedurally implemented.
For definiteness, let us suppose that two solute molecules 1 and 2 attract each other with a force whose magnitude F depends only on the distance between their centers, and whose direction is along their line of centers. To adapt this situation to the voxelated space of the SVTA, we let r1 and r2 be the position vectors, relative to some fixed point O, of the centers of the voxels VC1 and VC2 that contain the respective molecules. Then with r21 ≡ r2 − r1, r21 ≡ |r21|, and , molecule 1 feels a force due to molecule 2, and molecule 2 feels a force due to molecule 1. With the point O as origin, we set up a Cartesian reference frame in the space of the voxel mesh with the mutually orthogonal unit vectors , , and aligned with the edges of the voxels. Then we have
| (45a) |
and
| (45b) |
We resolve the force exerted on molecule 1 by molecule 2 into its Cartesian components by invoking the definition and Eq. (45b):
| (46) |
We call the voxel whose center is at relative to the center of voxel VC1 “adjacent voxel x±,” and we similarly define adjacent voxels y±, and z±. Then it can be shown (see Ref. 16) that the jump probability rate for molecule 1 will be
| (47) |
and similarly for hops to adjacent voxels y± and z±. This result of course assumes that the adjacent voxel in question is accessible to molecule 1. It also assumes that h is “small,” and in particular small enough that all of the jump probability rates are non-negative.
If we label the six adjacent voxels to VC2 in the same way (i.e., x±, y±, z±), then the jump probability rates for molecule 2 will be given by Eq. (47) except that the “±” signs inside the large parentheses must be replaced by “∓.” That same sign replacement must be made to both molecule jump probability rates if the force is repulsive instead of attractive.
X. SUMMARY AND CONCLUSIONS
This paper has introduced the small-voxel tracking algorithm (SVTA) for simulating chemical reactions among diffusing hard-sphere molecules. At first sight, the SVTA might seem to be merely a modified version of the reaction-diffusion SSA (RD-SSA), since both use the voxel-hopping procedure (5) to move molecules around on a discrete spatial lattice in continuous time. But the differences between the two algorithms run much deeper than those similarities. The fact that the SVTA requires its voxels to be smaller than the reactant molecules while the RD-SSA requires its voxels to be much larger than the reactant molecules has major ramifications: First, it means that voxel-hopping in the SVTA simulates the diffusion equation more accurately than does voxel-hopping in the RD-SSA, since (5) is exact only in the limit h → 0. Second, it enables the SVTA to track individual reactant molecules (at least to resolution h), which the RD-SSA does not do. Third, it enables the SVTA to prevent a molecule from hopping into a voxel that is occluded by another molecule, and to thereby model the effects of molecular crowding. The RD-SSA does not do that either, because it allows a molecule to hop into a voxel without checking to see whether the voxel actually has room for the molecule. Many of the limitations of the RD-SSA can be traced to the fact that it requires the system to be dilute in the reactant (solute) molecules. That requirement stems from the fact that non-diluteness invalidates the physics derivation of the bimolecular propensity function, which is central to the RD-SSA. But the SVTA does not use the bimolecular propensity function. And more importantly, the SVTA does not require the system to be dilute in the reactant molecules.
The real inspiration for the SVTA is eGFRD.2 The SVTA and eGFRD have the same strategic aims, but very different implementation procedures. Nevertheless, we showed in Sec. VI that the SVTA and eGFRD are equivalent in that both find their theoretical justification in the same physical theory, namely, the theory used to derive the bimolecular propensity function (see Appendix A). This equivalence reflects yet another significant difference between the SVTA and the RD-SSA: In addition to using the probability (5) for hopping to an adjacent voxel, the SVTA also uses the probability (26) for impinging on a voxel face. More specifically, the SVTA supplements the hopping probability rule (5) with the collision probability rule (30); when the latter is combined with the collision-condition reaction probability q12, the result is a modeling of a collision-induced reaction that is equivalent to what eGFRD obtains when it supplements the standard diffusion equation with the radiation boundary condition (34b).
Both the SVTA and eGFRD need additional research to determine (i) an efficient strategy for erecting the corrals, (ii) the optimal number of solute molecules to enclose in a corral, (iii) the best way to synchronize the corrals when a breach occurs, and (iv) how to place multiple product molecules of a reaction in relation to the prior location of the parent molecule(s). None of these important issues has been addressed in this paper. In addition, the SVTA needs additional research on how to optimally choose h.23
In closing, we list what we perceive to be the strengths and weaknesses of the SVTA.
Weaknesses of the SVTA:
-
(a)
It requires us to impose a voxel mesh on the region enclosed by the corralling surface Σ, and to identify the voxels belonging to VΣi and V∂Ωi for each corralled molecule. In multi-molecule scenarios, we also have to stay continually aware of all abutments between the voxel containing a molecule's center and the associated voxelated action spheres around the other molecules.
-
(b)
Since h is “small” there will be many voxels inside Σ, so many hops will usually have to be executed before something interesting happens. And the more dilute the system is, the more acute this problem will be.
-
(c)
We must determine an optimal value for h; i.e., we must find the best compromise between the greater accuracy that comes with smaller values of h, subject to condition (20), and the faster simulation speed that comes with larger values of h.
Strengths of the SVTA:
-
(a)
Like eGFRD, it has a carefully considered basis in molecular physics.
-
(b)
It works for non-dilute systems.
-
(c)
It easily models the effects of molecular crowding, simply by not allowing a molecule to hop into a voxel that is barred by the presence of another molecule or the system boundary.
-
(d)
It does not require solving any partial differential equations.
-
(e)
It allows arbitrary shapes and positions for the corralling surface Σ.
-
(f)
It is straightforwardly extendable to a three-molecule corral.
-
(g)
It can accommodate non-collisional forces between reactant molecules.
-
(h)
Once a reaction or a corral breach occurs, we immediately know what happened, when it happened, and where the molecules were.
-
(i)
By logging the times and destinations of the hops, we can straightforwardly backtrack if an outside molecule breaches Σ before the computed halting time.
-
(j)
Specific areas on the boundary ∂Ω, which we have thus far assumed to be reflecting, could easily be changed to reaction sites or absorption sites.
-
(k)
Active transport of reactant molecules along physically confined pathways, which is often very important in cellular systems, could be modeled as non-diffusional hops along connected voxel strings.
Finally, we note that the fact that the SVTA appears to be more efficient for less dilute systems, while eGFRD appears to be more efficient for more dilute systems, suggests that it would be fruitful to explore the possibility of an eGFRD-SVTA hybrid algorithm.
ACKNOWLEDGMENTS
The authors thank Linda Petzold and her group at UCSB, especially Brian Drawert, Andreas Hellander, and Stefan Hellander, for several enlightening and helpful discussions. D.G. was funded by the University of California, Santa Barbara under Professional Services Agreement No. 130401A40, pursuant to NIH under Award No. R01-EB014877-01. The content of this paper is solely the responsibility of the authors and does not necessarily represent the official views of these agencies.
APPENDIX A: OUTLINE OF THE DERIVATION OF EQ. (7)
The derivation of Eq. (7) as given in Ref. 9 proceeds in two phases. The first phase is based solely on the Einstein diffusion equation (1). Working in the rest frame of molecule 2, we take the center of that molecule to be the origin of coordinates for the position vector R(t) ≡ R1(t) − R2(t) of the center of molecule 1 relative to the center of molecule 2. It can be shown that the conditional PDF p1(r, t | r0, t0) of R(t) obeys Eq. (1) with D replaced by D12. In that equation, the hard sphere assumption restricts the variable r to the region outside the “action sphere” of radius σ12 about the origin. If the center of molecule 1 lies anywhere on the action sphere, then the two molecules will be colliding with each other. In contrast, a reaction between the two molecules is mathematically represented as the absorption of the center of molecule 1 on the action sphere. From the fact that the right side of Eq. (1) can be written as minus the divergence of −D12∇rp1(r, t | r0, t0), it follows that the latter is the probability flux for the position of the center of molecule 1 relative to molecule 2. That implies in particular that, if da is an infinitesimal area element on the action sphere at point , where the circumflex denotes a unit vector, then
| (A1) |
Therefore, the probability that molecules 1 and 2 will react in the next dt, which by definition is k|Ω|−1·dt, can be computed as the sum of the absorption probabilities (A1) over all the infinitesimal area elements da on the action sphere:
| (A2) |
To evaluate Eq. (A2), we must first solve Eq. (1) for p1 subject to physically appropriate initial and boundary conditions. The physically appropriate initial condition for p1 is taken to be neither the function δ(r − r0) that is suggested by the conditioning on p1 in Eq. (A2), nor the uniform distribution inside Ω, but rather the steady state solution of the diffusion equation for spherically symmetric boundary conditions. The function p1 therefore does not vary with time, and it depends only on the magnitude r of r. The physically appropriate “outer” boundary condition is taken to be p1 = 1/|Ω| everywhere on and outside a sphere centered on the origin whose radius ρ satisfies σ12 ≪ ρ ≪ |Ω|1/3. The physically appropriate “inner” boundary condition is taken to be some as yet unspecified value p1(σ12). When the stationary solution to Eq. (1) which satisfies all these conditions is computed and then substituted into Eq. (A2), the integration is straightforwardly performed and yields
| (A3) |
The result (A3) is a formula for k that is incomplete since it involves the as yet unknown value of p1(σ12). The fact that the Einstein model of diffusion is unable to specify the value of p1(σ12) is a consequence of the fact that the collision between the two molecules which initiates the reaction takes place on a vanishingly small length scale where Eq. (1) is not physically valid. The resolution of this difficulty is to recognize that on very small length scales, a solute molecule moves ballistically, as in an ideal gas. That brings us to the second phase of the derivation.
A well known result in the kinetic theory of the ideal gas is that if ρ is the average number of gas molecules per unit volume and is the average speed of those molecules, then the average number of collisions of the molecules with the boundary of Ω, per unit area and per unit time, is .24 A stochastic reformulation of the derivation of this result focusing on the small-scale motion of a single solute molecule establishes the following general result: If p0 is the value of the PDF of the solute molecule in the immediate neighborhood of an infinitesimally small stationary area element da, then25
| (A4) |
Here, is the average speed of the solute molecule if it were in a dilute gas at the system temperature T. Applying (A4) to our present problem, where the diffusing molecule is molecule 1 and da is an infinitesimal area element on the action sphere at point r′, and noting that multiplying a collision probability by the collision-conditioned reaction probability q12 gives us a reaction probability, we obtain
| (A5) |
Since in our problem p1(r′, t | r0, t0) = p(σ12) everywhere on the action sphere, then summing (integrating) the probability (A5) over all area elements da on the action sphere just replaces da with . Thus we obtain the following formula for the probability that molecules 1 and 2 will react in the next dt:
| (A6) |
In Eqs. (A6) and (A3), we evidently have two formulas for the two unknowns k and p1(σ12). Formula (A3) was derived from the Einstein diffusion equation, and formula (A6) was derived from the equations for ballistic motion. Upon solving Eqs. (A6) and (A3) simultaneously, we obtain for k the formula in Eq. (7), and also the result
| (A7) |
APPENDIX B: THE VOXELATED ACTION SPHERE
We consider space to be subdivided into cubic voxels whose edges, of length h, are aligned with a Cartesian reference frame. We label each voxel with three signed integers ix, iy, and iz, and we define the voxel (ix, iy, iz) to be the voxel whose center is at the Cartesian point (x, y, z) = (ixh, iyh, izh). Here we describe a computer-oriented procedure for identifying all the voxels belonging to the virtual voxelated action sphere vVAS21 for given values of the action sphere radius σ12 and h. vVAS21 is just VAS21, except it is centered on voxel (0,0,0) instead of on voxel VC2.
We begin by defining Sball to be the set of all voxels whose centers are located on or inside a sphere of radius σ12 about the center of voxel (0,0,0). Then we define vVAS21 to be the set of all voxels belonging to Sball that have at least one adjacent voxel that does not belong to Sball; i.e., vVAS21 consists of all the exterior boundary voxels of Sball.
The number of voxels belonging to the set Sball that have their centers on the positive x-axis is
| (B1) |
where [a] denotes “the greatest integer in a.” It follows that the set of voxels
| (B2) |
comprises a cube which contains the voxel set Sball as a subset. We now construct the voxel set vVAS21 by carrying out the following two steps:
Step 1. Select from the set Scube all voxels whose centers are a distance ⩽σ12 from the origin. These selected voxels comprise the set Sball.
Step 2. Select from the set Sball all voxels (ix, iy, iz) for which at least one of its adjacent voxels , , does not belong to Sball.
The final set of selected voxels is vVAS21.
What the SVTA requires is the list of the indices (ix, iy, iz) of the voxels that make up vVAS21. It is fortunate that only the computer, and not the human modeler, needs to interact with that list, because the number of voxels that comprise vVAS21 increases rapidly with increasing σ12/h, and visualizing the structure of vVAS21 is extremely difficult for all but the smallest values of σ12/h. Two examples illustrate this point: In the simplest (and least accurate) case where h is taken to be as large as possible, so that σ12/h is slightly larger than 1, vVAS21 consists of the 6 voxels that are adjacent to VC2: ( ± 1, 0, 0), (0, ±1, 0), and (0, 0, ±1). In this obviously crude approximation to a sphere, there are a total of 18 voxels exteriorly adjacent to vVAS21, of which 6 share one voxel face with vVAS21 and 12 share two. In the more accurate case in which σ12/h = 10, which is the case illustrated in 2D in Figs. 5 and 6, vVAS21 consists of 978 voxels; those voxels have a total of 1118 exteriorly adjacent voxels, of which 558 share one face with vVAS21, 336 share two faces, and 224 share three faces.
There is one artifact of the voxelated action sphere that deserves mentioning. As h is taken smaller and smaller, the voxelated action sphere provides an increasingly better approximation to the true action sphere as regards the latter's diameter, but not as regards its surface area. Whereas the minimum and maximum diameters of vVAS21 both converge to 2σ12 as h → 0, the ratio of the exterior surface area of vVAS21 to fluctuates around 1.5, with no indication of approaching 1 as h → 0. Is this a problem? We do not think so. We suspect that this increase in the surface area of a voxelated action sphere over the area of the true action sphere compensates for the restriction in the hopping rule (5) to six mutually orthogonal hopping directions. And it seems clear, not only from theory6 but also from the simulation results in Fig. 3, that the hopping rule (5) does simulate the diffusion equation more and more accurately as h → 0.
REFERENCES
- 1.Gillespie D., Petzold L., and Seitaridou E., J. Chem. Phys. 140, 054111 (2014). 10.1063/1.4863990 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. By this definition of diluteness, a collection of molecules at any given concentration (number of molecules per unit volume) could be dilute if the molecules are sufficiently small, and not dilute if the molecules are sufficiently large. Diluteness therefore cannot be quantified solely by the concentration; account must also be taken of the sizes of the molecules. We are unaware of any widely accepted measure of diluteness, but candidates might be (a) the ratio of {the average separation distance between the reactant molecules} to {the average size of those molecules}, or (b) the ratio of |Ω| to {the volume occluded by the reactant molecules}, or (c) the logarithm of either (a) or (b).
- 3. This result was derived analytically in Sec. III of Ref. 1 where, unforturnately, the section title incorrectly asserted that diluteness is a necessary and sufficient condition for the system to stay well-mixed. In fact, the analysis there demonstrates only necessity, not sufficiency; i.e., the molecules must be dilute to stay well-mixed, but being dilute does not guarantee that they will at all times be well-mixed. For example, the close proximity of the two product molecules of a reaction immediately after the reaction occurs will temporarily violate the well-mixed condition, even if the system is “on average” well-mixed. That such a temporary small-scale violation of the well-mixed condition can cause qualitative changes in the behavior of a cellular system, even if the system is dilute, has been demonstrated in the paper by Takahashi et al. which is cited in Ref. 4.
- 4.Takahashi K., Tănase-Nicola S. and ten Wolde P. R., Proc. Natl. Acad. Sci. U.S.A. 107, 2473 (2010); 10.1073/pnas.0906885107 [DOI] [PMC free article] [PubMed] [Google Scholar]; see especially the supplementary material for that paper. The enhancement in eGFRD consists of major modifications prompted by Ref. 5 that resolve several shortcomings of the original GFRD of van Zon J. S. and ten Wolde P. R., J. Chem. Phys. 123, 234910 (2005). 10.1063/1.2137716 [DOI] [PubMed] [Google Scholar]
- 5.Opplestrup T., Bulatov W., Gilmer G., Kalos M., and Sadigh B., Phys. Rev. Lett. 97, 230602 (2006). 10.1103/PhysRevLett.97.230602 [DOI] [PubMed] [Google Scholar]
- 6.Gillespie D. and Seitaridou E., Simple Brownian Diffusion: An Introduction to the Standard Theories (Oxford University Press, 2012). A down-loadable Errata for this book, which features a heavily revised Section 5.6, is available at http://ukcatalogue.oup.com/product/9780199664504.do#. [Google Scholar]
- 7. The transition of a solute molecule's motion from diffusional to ballistic as the spatiotemporal scale is decreased below the values in Eqs. (2) and (3) is clear in Langevin's theory of molecular diffusion, which is more comprehensive than Einstein's theory. The transition is especially vivid in the Langevin counterpart of the Einstein stepping formulas (4), in which not only the position but also the velocity of a diffusing molecule gets updated. Unencumbered by any restrictions on the size of Δt, the Langevin stepping formulas reduce smoothly to the Einstein formulas (4) for Δt ≫ τ, and to the equations of ballistic motion for Δt ≪ τ. For details, see Ref. 6, Chap. 9.
- 8. A concise proof of the fact that the hopping rule (5) becomes exactly equivalent to the diffusion equation (1) in the limit h → 0 can be found in the Appendix of Ref. 1 A version of that proof which gives the more general form of the hopping rule when an external force is acting on the diffusing molecule can be found in Ref. 16.
- 9. See Sections 11.7–11.9 of Ref. 6.
- 10.The original derivation of Eq. (7) was given in Gillespie D., J. Chem. Phys. 131, 164109 (2009). An improved derivation, which is the one summarized in Appendix A, is given in Ref. 6, Sections 3.7 and 4.8. 10.1063/1.3253798 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gillespie D., J. Comput. Phys. 22, 403 (1976). 10.1016/0021-9991(76)90041-3 [DOI] [Google Scholar]
- 12.Hellander S., Hellander A., and Petzold L., Phys. Rev. E 85, 042901 (2012). 10.1103/PhysRevE.85.042901 [DOI] [PubMed] [Google Scholar]
- 13.Erickson H. P., Biol. Proced. Online 11, 32 (2009). 10.1007/s12575-009-9008-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. As noted in Ref. 13, a real protein molecule is not a smooth sphere, and it carries around with it a hydrated layer of water molecules. Those complicating features increase the drag coefficient γ1 over the value given by the Stokes formula, and that in turn is expected to produce, through the Einstein relation, a smaller value for D1.
- 15. If two “events” E1 and E2 can occur in the next infinitesimal time interval dt with respective probabilities a1dt and a2dt, then the time to and identity of the next occurring event can be computed in either of two ways. The direct method is to take the time to the next event as τ = /article/back/ref-list/ref/mixed-citation/inline-formula (a1 + a2) and the index of the next event as 1 if a1 ⩾ (a1 + a2)·/article/back/ref-list/ref/mixed-citation/inline-formula (0, 1), else 2. The first reaction method is to compute two tentative reaction times τ1 = /article/back/ref-list/ref/mixed-citation/inline-formula (a1) and τ2 = /article/back/ref-list/ref/mixed-citation/inline-formula (a2), and then take τ = min (τ1, τ2), and the event as the one whose tentative time is smaller. That these two methods are equivalent is proved in Ref. 11, Section 5b. The SVTA employs both methods.
- 16. See supplementary material at http://dx.doi.org/10.1063/1.4903962E-JCPSA6-141-064447 for three additional appendices to this article.
- 17. If q12 ≪ 1, ncol in Eq. (33) might be so large that many successive VC1-VAS21 adjacencies will usually occur before a bimolecular reaction occurs. In that case, the following approximate procedure should be faster than the exact procedure described in the text: At each VC1-VAS21 adjacency, advance t by τ′ = min (τhop, τuni) and subtract from ncol a sample value of the Poisson random variable with mean β12tmin , viewing that sample as the number of collisions that occur during the current VC1-VAS21 adjacency. If that subtraction leaves ncol positive, continue the simulation by executing either the hop or the unimolecular reaction as is called for. But if the subtraction reduces ncol from a value nb > 0 to some value na ⩽ 0, then estimate the bimolecular reaction to have occured at time t + [na/(nb − na)]·τ′. The actual time of the bimolecular reaction will usually be some unknown time between t − τ′ and t, but the consequent relative error in the total time to the reaction will be small if many VC1-VAS21 adjacencies have occurred. Note that β12 will in general take different values in successive VC1-VAS21 adjacencies.
- 18.Bicout D., Berezhkovskii A., and Szabo A., J. Chem. Phys. 114, 2293 (2001); see in particular Sec. II A 10.1063/1.1332807 [DOI] [Google Scholar]
- 19.Dill K. A. and Bromberg S., Molecular Driving Forces: Statistical Thermodynamics in Chemistry and Biology (Garland Science, 2003). [Google Scholar]
- 20.Phillips R., Kondev J., Theriot J., and Garcia H., Physical Biology of the Cell (Garland Science, 2008). [Google Scholar]
- 21. Two different derivations of the Smoluchowski equation can be found in Chapter 10 of Ref. 6.
- 22. We do not know how widely known this generalized hopping result is, but we first learned of it from R. Erban, LMS/EPSRC Short Instructional Course: Stochastic Modelling in Biological Systems (March 18–23, Oxford University, 2012), lecture #5. A derivation of Erban's result from the perspective of the present paper is given in Ref. 16.
- 23. Future work on the SVTA should include a study of how best to choose the voxel size h The usual expectation, that smaller values of h give more accurate results, is nicely illustrated by our one-molecule simulations in Fig. 3 But it is not always true in the SVTA, because of the fuzzy lower bounds on h in conditions (18) and (20) A test made during our two-molecule simulations for Fig. 10 indicated that decreasing h by 50% resulted in a 3% increase in the mean time to reaction, but no other change in the character of the histogram. Since that decrease in h left h 21 times larger than the value on the left side of condition (20), its results probably were indeed 3% more accurate. But that decrease in h also caused the average run time to increase by 400%.
- 24.Present R., Kinetic Theory of Gases (McGraw-Hill, 1958). [Google Scholar]
- 25. For details of the derivation of Eq. (A4), see Secs. 4.6 and 4.7 of Ref. 6.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- See supplementary material at http://dx.doi.org/10.1063/1.4903962E-JCPSA6-141-064447 for three additional appendices to this article.