Abstract
AC Faradaic reactions have been reported as a mechanism inducing non-ideal phenomena such as flow reversal and cell deformation in electrokinetic microfluidic systems. Prior published work described experiments in parallel electrode arrays below the electrode charging frequency (fc), the frequency for electrical double layer charging at the electrode. However, 2D spatially non-uniform AC electric fields are required for applications such as in plane AC electroosmosis, AC electrothermal pumps, and dielectrophoresis. Many microscale experimental applications utilize AC frequencies around or above fc. In this work, a pH sensitive fluorescein sodium salt dye was used to detect [H+] as an indicator of Faradaic reactions in aqueous solutions within non-uniform AC electric fields. Comparison experiments with (a) parallel (2D uniform fields) electrodes and (b) organic media were employed to deduce the electrode charging mechanism at 5 kHz (1.5fc). Time dependency analysis illustrated that Faradaic reactions exist above the theoretically predicted electrode charging frequency. Spatial analysis showed [H+] varied spatially due to electric field non-uniformities and local pH changed at length scales greater than 50 μm away from the electrode surface. Thus, non-uniform AC fields yielded spatially varied pH gradients as a direct consequence of ion path length differences while uniform fields did not yield pH gradients; the latter is consistent with prior published data. Frequency dependence was examined from 5 kHz to 12 kHz at 5.5 Vpp potential, and voltage dependency was explored from 3.5 to 7.5 Vpp at 5 kHz. Results suggest that Faradaic reactions can still proceed within electrochemical systems in the absence of well-established electrical double layers. This work also illustrates that in microfluidic systems, spatial medium variations must be considered as a function of experiment time, initial medium conditions, electric signal potential, frequency, and spatial position.
I. INTRODUCTION
Electrokinetic microfluidics utilize interactions between (bio)particles or fluids and electric fields to achieve electroosmosis, dielectrophoresis (DEP), and other forms of electrophoresis. These phenomena have proven to be effective in multiple applications such as electroosmotic flow pumping1,2 and (bio)particle separation or concentration.3,4 Alternating current (AC) electric fields are widely used in those applications due to advantages of relatively stable medium conditions (pH, ionic concentration and ionic strength). Stability is based on the assumption that infinitely small Faradaic currents occur during AC electrokinetic processes.
Reaction kinetics and electrical double layer (EDL) processes play key roles in determining AC Faradaic reaction rates in microfluidics systems. Faradaic reactions are electrochemical reactions at electrode surfaces where ions are transferred into or out of electrolyte solutions thus causing oxidation or reduction.5
In addition to Faradaic reactions, EDLs establish at the interface between charged electrodes and electrolyte solutions as reviewed previously.5,6 For positively charged electrodes, the EDL includes a compacted layer of strongly absorbed anions adjacent to the electrode called the Stern layer. This layer is composed of both specifically adsorbed ions, governed by electrode material adsorption of the ions, and non-specifically adsorbed counterions, governed by Coulomb forces. Beyond the Stern layer is the diffuse layer, which includes both anions and cations freely transporting in the electrolyte solution via thermal motion and electrostatic interactions. In this model, the inner Helmholtz plane (IHP) is the distance equal to the radius of a non-specifically adsorbed anion from the charged electrode and the outer Helmholtz plane (OHP) is a distance from the electrode equal to the radius of a specifically adsorbed ion plus the solvent molecule diameter.
Grahame's review7 examined the relationship between electrode processes and EDL, and proved that ion reduction occurs within the EDL instead of the solution interior and the reaction rate-related concentration should be at the outer Helmholtz plane instead of in the bulk solution. Further, the EDL does not reach equilibrium instantaneously. Instead, it is established during a finite electrode charging time (inversely related to the characteristic angular velocity, ), which is given by the product of typical resistance of bulk electrolyte 8,9 and the typical capacitance of EDL,
| (1) |
where is characteristic time, and are the fluid permittivity and conductivity, and are the system's characteristic length and area, respectively, and is the Debye length, which for the monovalent electrolyte can be expressed as
| (2) |
where is gas constant, is temperature, is Faradaic constant, and is bulk molar concentration.
Thus, the significant period of the externally applied electric field should be regarded as a relative value to in Hertz. For example, the applied signal period relative to was reported as the determining factor for AC electroosmosis (ACEO) pumps,8 As a result, is the electrode characteristic charging frequency which is equal to the inverse charging time.
When the frequency of an applied electric potential is much less than the charging frequency, , EDL is well established and the Faradaic reaction progresses with ions from the EDL at rates close to DC conditions. On the opposite extreme, when , there is not enough time for EDLs to be established and the reaction rate is negligible. This can also be understood from a simplified electrode/electrolyte interface model, in which a capacitor, which represents the EDL, is connected in parallel with a resistor, which represents charge transfer across the interface. At higher frequencies, most of the current to the electrode charges the EDL when the EDL shows low impedance. Thus, most of the potential drop occurs within the bulk electrolyte instead of the EDL, which results in negligible Faradaic current before polarity reverses in the AC field.10
Within the bulk solution, the constant, uniform concentration assumption has been questioned. Garcia-Sanchez et al.11 and Studer et al.12 found that flow reversal occurred during experiments on ACEO pumps. Garcia-Sanchez et al.11 proposed and experimentally demonstrated in parallel electrode arrays below that such flow reversal was induced by an AC Faradaic reaction; this was subsequently verified by Ng et al.,13 by experimentally detecting pH in AC electrokinetic systems.
Faradaic reactions have previously been detected by examining solution pH changes: Garcia-Sanchez et al.11 detected significant pH change at 500 Hz using 0.1 mM KCl solution in 10 μm and 20 μm characteristic length systems, deducing . Ng et al.13 detected pH change at 100 Hz using 1 mS/m KCl solution in a characteristic length system of 80 μm, deducing . These previous experiments were conducted at frequencies around where the EDL is established and Faradaic reactions are expected and predicted by theory.
However, in microfluidic devices, many applied frequencies are close to or higher than . For ACEO pumps,2,9 maximum velocities are observed around and above . For a majority of (bio)particle DEP characterizations, operational and crossover frequencies are much greater than , and cellular changes attributed to ion non-uniformities have been quantified at frequencies around .14 Thus, to better understand solution behaviors and facilitate intelligent device designs, Faradaic reaction behaviors need to be examined at frequencies higher than .
Faradaic reactions in parallel electrode arrays generating spatially uniform pH gradients11,13 are fairly well explored, while spatially non-parallel electrode systems are unexplored to the authors' best knowledge. Many ACEO pumps and all DEP manipulations require spatially non-uniform electric fields. Thus, 2D non-uniform electric field Faradaic reaction behaviors must be characterized over a range of frequencies and electric field path lengths to discern variations in Faradaic reaction rates. In this work, 4 mM NaCl solutions (0.048 S/m, relative permittivity of 77.98) were explored within a microdevice with the smallest characteristic length of 100 μm; these conditions yield a maximum characteristic electrode charging frequency of ∼500 Hz.
For electrokinetic microfluidics, water electrolysis is often the most dominant Faradaic reaction15,16 as studied in previous works.17–19 pH changes are induced by water electrolysis according to the anode and cathode redox reactions
| (3) |
| (4) |
Thus, to remain consistent with prior Faradaic reaction measurements, we also detect pH changes in solutions. We first perform qualitative control experiments to detect the impact from electric field shape and solvent material to illustrate that water electrolysis dominates the Faradaic current. Then, we quantitatively detect pH change in 2D spatially non-uniform electric fields created by orthogonally positioned electrode pairs via time analysis. Finally, we detect pH change at frequencies from 6 to 24 to examine how Faradaic reaction performs around and above .
II. MATERIALS AND METHODS
A. Materials
Fluorescein sodium salt (460/515 nm), a pH dependent dye with detection range above pH = 4, was used to detect pH change in real time. Fluorescein sodium salt (Sigma-Aldrich, USA) was prepared to 10−5 M in both e-pure water (pH = 7) and methanol (MeOH, 99.99% Sigma-Aldrich, USA).
4 mM NaCl (>99% pure, Macron Chemicals, USA) aqueous solutions with pH was adjusted to 7.0 ± 0.1 with 1 M NaOH (Sigma Aldrich, USA) or 1 M HCl (Sigma Aldrich, USA). 4 mM NaCl MeOH solution was similarly prepared.
B. Microdevices design and fabrication
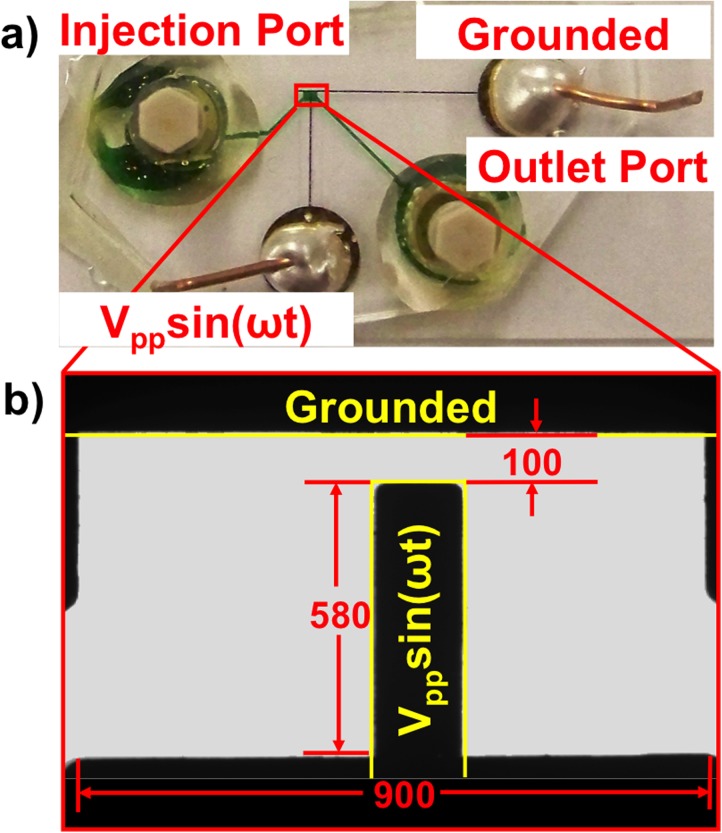
Orthogonally positioned Ti/Au (50/50 nm thickness) electrode pairs with 100 μm gap created 2D spatially non-uniform electric fields. Standard soft photolithography fabrication procedures were followed.14 Briefly, photoresist was spun, masked, and exposed to create the necessary electrode features. Next, a Ti/Au layer ∼200 nm thick was sputtering then remaining photoresist removed via acetone sonication. A PDMS (Polydimethylsiloxane) fluidic layer was molded over a silicon wafer prepared by spinning photoresist to 70 μM thick, masking and exposing to UV, baking, and then removing unpolymerized photoresist. The PDMS fluidic layer was adhered after air plasma bonding to the glass slide with electrode features. Figure 1 shows (a) an entire device photo and (b) 10× magnified view of experimental test chamber. AC signals were generated via an Agilent 33 250 A waveform generator across the vertical electrode (Vpp sin(ωt)) and horizontal electrode (grounded).
FIG. 1.
Microdevice design. (a) Photo of device with fluid channel filled with green dye. Ti/Au electrodes are microfabricated on the supporting glass slide and electrically connected via silver epoxy and copper leads. The working fluidic chamber is boxed in red. (b) Expanded 10× microscope of region in red box. Electrodes are outlined in yellow. All units are in micrometers.
C. Experiments
Fluorescein at 0.4 μM was calibrated from pH 4 to 8 in 4 mM NaCl adjusted with NaOH or HCl. All fluorescent imaging experiments were completed with a Zeiss Axiovert 200 m microscope. Videos were recorded with an AxioCam MRm camera and fixed exposure times between 250 and 290 ms. Fluorescein photobleaching was quantified by recording emission light intensity every 1 s under exposure to excitation light for 120 s.
Samples for pH change experiments were prepared with 4:96 Fluorescein and aqueous 4 mM NaCl solution; Control experiments utilized mixture of Fluorescein in MeOH phase and 4 mM NaCl also in MeOH at the ratio of 4:96. Experimental samples were injected via an input port shown in Figure 1(a) then sealed with One-Piece Fitting (LabSmith, USA) to prevent any net pressure driven flow. The device was mounted on the microscope stage. AC signals ranging in amplitude of 3.5 to 7.5 Vpp and frequency ranging from 3 to 12 kHz were applied. Microscope videos at 10× magnification were recorded at 1 fps for 120 s; no electric fields were applied in the first 5 frames to check system stability. Each experiment was repeated 5 times.
To demonstrate the difference in pH change behavior between 2D uniform and non-uniform electric fields, parallel electrode pairs were utilized to create uniform electric fields at 5 kHz, 5.5 Vpp in both aqueous and MeOH phases.
D. Data analysis methods
1. Intensity analysis
Both 2-D gray scale images and 3-D mesh images were utilized to demonstrate averaged data from 5 repeated experiments at each pixel. For time analysis and control experiments, recorded videos (121 frames for 0 to 120 s) were exported as individual images, then imported into MATLAB to generate gray scale matrixes ranging from 0 (dark) to 255 (bright). For each experiment, an average pixel value was obtained over 5 repeats and standard deviation was calculated by pixel. MATLAB output was either a 2-D reformed image of 5 superimposed repeats or a 3-D mesh plot with z-axis expressing emission intensity. Also, intensity/pH change was determined by subtracting intensity at 120 s from intensity at 8 s. Time = 8 s was chosen as a basis due transient higher emission intensity induced by fluorescein molecule enrichment as discussed in Sec. III C.
For peak-to-peak potential and frequency dependency analysis, centerline intensity was obtained between two electrodes (50 μm away from each electrode), then averaged intensity was calculated and normalized to range from 0 to 255. Similarly, each pixel was averaged from 5 repeats with standard deviation.
2. Converting intensity to pH
Obtained intensities were corrected with a derived photobleaching equation to exclude the intensity drop induced by FITC (fluorescein isothiocyanate) degradation with light. Then, pH values at each time and position were calculated from the corrected intensity via Figure 2(c) calibration.
FIG. 2.
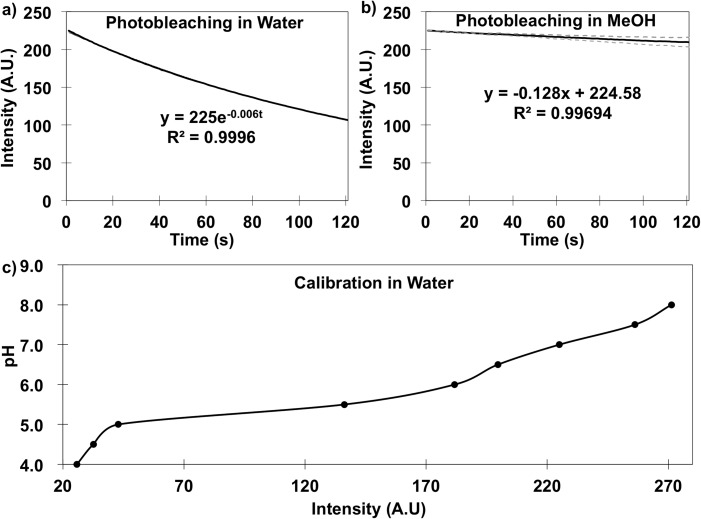
Dye properties controls. (a) In water, fluorescein photobleaching under fixed illumination conditions over 120 s. (b) In pure methanol, fluorescein photobleaching is less pronounced. Equation describing trend is shown for each. (c) Calibration plot for pH and fluorescein emission intensity conducted within the device in Figure 1.
III. RESULTS AND DISCUSSION
To capture the most dominant electrochemical reaction behavior and to be consistent with published data, pH was detected to track Faradaic reactions. pH sensitive fluorescein salts were utilized to quantify photobleaching effects and to obtain fluorescein emission intensity versus pH calibration curve. Comparison experiments were performed to exclude potential emission intensity side mechanisms including photobleaching, temperature changes, induced flows, or other phenomena induced by non-uniform electric fields. Intensity measurements were converted into pH correcting for photobleaching, then position distributions were mapped in the device. Finally, signal magnitude and frequency dependencies were quantified.
A. Fluorescein calibrations
The fluorescein [H+] ion indicator controls were completed to account for photobleaching, background, and intensity calibrations. First, photobleaching properties were examined by detecting emission intensity without electric fields in both aqueous solution (Figure 2(a)) and MeOH solution (Figure 2(b)). Photobleaching in each solution was quantified from 5 repeats; Figure 2 results illustrate the average value. The standard error was less than 5% in water while the upper and lower limits in MeOH were plotted. Fluorescein emission intensity decreased from 225 to ∼120 (arbitrary units (AU)) in aqueous solution over 120 s with no field, while in MeOH, the decrease was only from 225 to ∼210. Photobleaching behavior was fit into an exponential or linear function with R2 > 0.995 for water and MeOH, respectively. The photobleaching equations shown in Figure 2 were utilized to remove the photobleaching effect from all subsequent intensity measurements.
Second, manually pipetted and meter verified pH solutions were calibrated against emission intensity as shown in Figure 2(c). Fluorescein emission intensity reduced to zero at pH < 4. For pH > 4, emission intensity increased with pH. In our experiments, Faradaic currents primarily yielded emission intensity decreases, which correspond to pH decreases. Intensity data was first scaled from 0 to 255, then the calibration used to obtain the pH value.
B. Comparison experiments
Comparison experiments were conducted to elucidate other potential mechanisms impacting local [H+] and thus pH measurement accuracy. In contrast to uniform electric fields, 2D spatially non-uniform electric fields can potentially induce possible side effect depending on experimental parameters such as solution concentration, conductivity, applied potential, and frequency. Under the experimental conditions in this work, ACEO flow is the most probable induced phenomenon due to the low kHz applied frequencies. ACEO is caused by the applied electric fields exerting force on hydrated ions in the induced EDL thus generating flow movement. Such flow can change emission intensity via mass transfer induced changes in fluorescein concentration. Thus, to accurately quantify pH change in the system, ACEO effects were examined.
MeOH can be electrolyzed only in the presence of water,20 so this pure solvent was used for comparison experiments. A mixture of 4 mM NaCl in MeOH and 10−5 M fluorescein in MeOH was employed. Negligible Faradaic reaction products were detected in the MeOH system as illustrated in Figure 3. This enabled determination of any phenomena other than Faradaic reactions inducing intensity changes in the non-uniform electric fields.
FIG. 3.
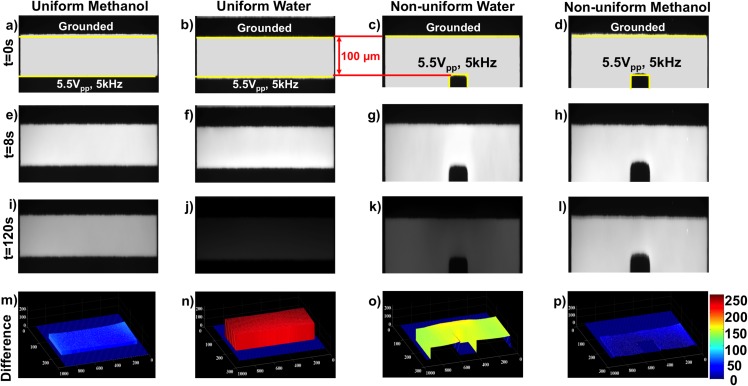
Field and medium comparison experiments at 5 kHz and 5.5 Vpp. Columns are organized by methanol and water in uniform and nonuniform DEP electric field configurations. Rows are organized by time with t = 0, 8, and 120 s and intensity difference obtained by MATLAB image analysis. Fluorescein intensity changes are apparent in water in both uniform and non-uniform DEP electric field configurations as emphasized in (n) and (o) while negligible changes were observed in methanol in (m) and (p).
To examine Faradaic reactions above the charging frequency ( > 500 Hz) in both 2D spatially uniform and non-uniform electric fields, both MeOH and aqueous solutions were observed under 5.5 Vpp and 5 kHz sinusoidal AC signals (relative frequency = 10 ). Figure 3 shows 5 repeated control experiment results already corrected for photobleaching. For all combinations of solvents and electric field shape, results at t = 0, 8, and 120 s are shown in Figures 3(a)–3(d), 3(e)–3(h), and 3(i)–3(l), respectively. Figures 3(m)–3(p) shows intensity differences between t = 8 s and t = 120 s. Time = 8 s was chosen as a basis due to fluorescein molecule enrichment as will be discussed in Sec. III C.
For MeOH in uniform electric fields generated via parallel electrode pairs (Figure 3(m)) and MeOH in non-uniform electric fields generated via perpendicular electrode pairs, no substantial intensity changes were observed. For the aqueous uniform electric field case (Figure 3(n)), intensity changes up to 200 AU were observed. For the aqueous non-uniform electric field case (Figure 3(o)), an intensity change of ∼150 AU was observed. These intensity changes were consistent with pH shifts generated by Faradaic reactions. The smaller intensity change in the nonuniform case is likely the result of the orthogonal effective electrode surface area being smaller than the parallel electrode surface area. Since the Faradaic reactions are electrode surface area-driven, this result is consistent with Faradaic pH products. For the MeOH non-uniform electric field case (Figure 3(p)), in which ACEO flow was possible, the emission intensity change was negligible. Figure 3(m) shows that in the MeOH phase, negligible intensity change—beyond the 8 s fluorescein molecule enrichment—was observed when compared to water phase results in Figure 3(n). Such observations are consistent with negligible Faradaic electrolysis reactions in water-free, yet ion rich MeOH. Further, other non-uniform electric field side effects in ionic solutions such as ACEO, thermal convection flows, or other solution property change are not evident.
These comparison experiments reveal that the observed intensity changes in Figure 3(o) can be confidently correlated with pH changes generated by Faradaic reactions and not fluid transport at frequencies greater than the electrode charging frequency in non-uniform electric fields. This, in combination with prior publications9 increases confidence in the fluorescently measured pH change accuracy and conclusion that Faradaic reactions drive the pH.
C. Time analysis of intensity change
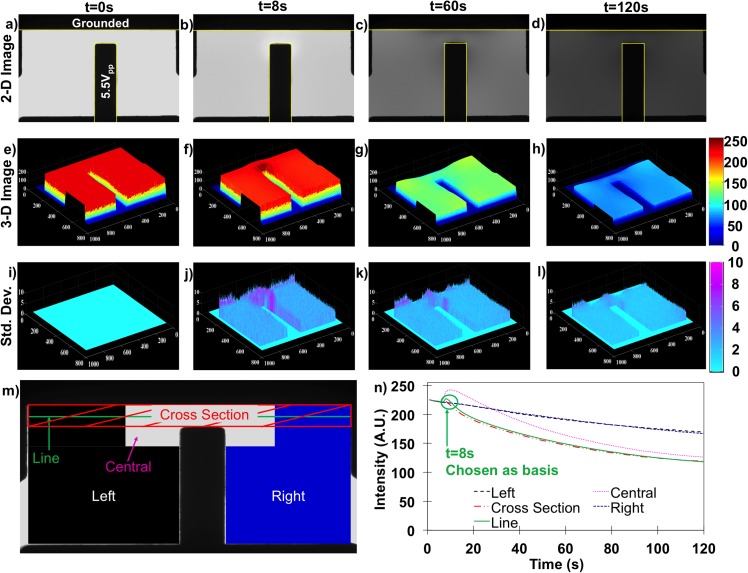
Since the intensity change can be directly correlated with Faradaic reactions, further analysis was conducted on time and spatial dependencies within the electric fields. Figure 4 shows time and spatial results at 5.5 Vpp and 5 kHz after photobleaching corrections revealing Faradaic reaction-induced intensity changes. Results are organized into columns correspond to experiment time: column 1 is for t = 0 s (a), (e), and (i), column 2 is for t = 8 s (b), (f), and (j), column 3 is for t = 60 s (c), (g), and (k), and the last column is t = 120 s (d), (h), and (l). The respective rows from top to bottom are: first row shows 2-D gray scale image averaged pixel by pixel from 5 experimental repeats (a)–(d), the second row is a 3-D mesh image where the z height corresponds to the intensity magnitude (e)–(h), and the third row is a 3-D mesh of the pixel by pixel standard deviation calculated from the 5 experiments (i)–(l).
FIG. 4.
(a)–(d) Gray-scale 2-D dye intensity plot at t = 0, 8, 80, and 120 s under 5.5 Vpp and 5 kHz. (e)–(h) 3-D MATLAB plot of the same data at the same time points. (i)–(l) Calculated standard deviations of 5 repeats of the data in the first two rows. (m) Diagram illustrating regions examined for intensity analysis. (n) Time dependencies of the regions in (m). Line intensity (solid green) was utilized for all subsequent analysis.
For the first column at t = 0, images illustrate the spatially uniform fluorescein emission intensity when no electric field was applied; for comparisons between runs, this initial intensity was always normalized to 225 AU. These baseline images represent the microdevice pH state without influence from Faradaic reactions or electric field effects (other mechanisms were negligible in Sec. III B).
To quantify the time dependence of [H+] concentrations by area, Figures 4(m) and 4(n) identify and compare spatial subareas including the left and right peripheral areas, central area, cross-sectional area, and a single line intensity profile within the nonuniform field case. Each subarea or line was tracked frame-by-frame in each separate experiment as shown in Figure 4(n), and then compiled into trend data for time dependence. Left and right area intensities were steady to 5 s, then once the electric field was applied, monotonically decrease from 225 to ∼180 by 120 s. Central and cross-sectional areas and line profile intensities also started from 225 and remained steady to 5 s. Upon electric field application, intensities reached a maximum at t = 8 s. Since trends were similar, the simpler line intensity was selected to sufficiently capture aggregate trends for all subsequent time, potential, and frequency dependencies. Since the measured intensity of the fluorescein directly correlates with pH as illustrated in Figure 2(c), this tool was used to track pH changes beyond the electrode charging frequency.
The field remained off until t = 5 s, but within 3 s of 5.5 Vpp and 5 kHz electric field application, a higher emission intensity was observed in the central area while intensity was unchanged elsewhere. This spatial variation was attributed to fluorescein molecular movement to this high electric field density region. Reasoning for this is threefold: (1) As shown in Figure 3, experiments completed in MeOH also demonstrated a small intensity increase after 3 s in the field, (2) In this MeOH system, no further intensity changes were observed after 8 s, and (3) In uniform electric field experiments, no spatial changes were discernable in either MeOH or water. These three clues suggest this 3 s increase is directly related to the electric field non-uniformity and not the result of any electrochemical reactions, since such reactions would progress with time. Although this non-Faradaic phenomenon is not a major focus of this work, it still impacts the intensity measurements necessary to quantify progression of the Faradaic reactions. Thus, the higher intensities at 8 s were used as a baseline to more accurately map the Faradaic reaction effects in the system and decouple the fluorescein concentration effects from pH change effects as shown in Figure 4(n).
Progressing up to t = 60 s, significant intensity decrease was observed throughout the entire observed device chamber; the most significant intensity decreases were observed in the central area. This intensity decrease was attributed to increasing [H+] per the calibration in Figure 2(c). The [H+] products indicate Faradaic reactions occurring at 5.5 Vpp and 5 kHz, beyond the electrode charging frequency. Also, spatially non-uniform intensities indicate that the reaction rate varies spatially; reaction rate is higher in the central area and lower in the peripheral areas as illustrated in Figure 3(g). This spatial variance of reaction rate is induced by the electric field non-uniformity and more specifically, by the non-uniformity of the characteristic length of the electric field lines. The voltage drop within the EDL thus depends on the distance between electrodes. The distance between electrodes in the central area is much shorter resulting in a larger potential drop within the EDL driving greater Faradaic reaction rates. In the peripheral areas, potential drop within the EDL is lower resulting in lower Faradaic reaction rates. Since 2D nonuniform electric fields have varying distances between electrodes, for any given applied signal frequency, potential drop within EDL that the solution experiences varies spatially due to this electric field non-uniformity, thus resulting in a spatially different Faradaic reaction rate.
Observations to 120 s (4th column in Figure 4) reveal further decreases in the emission intensity, which supports that continual Faradaic reaction products accumulate in the solution. Comparisons between the central area of shortest electric field path lines (Fig. 4(m)) and peripheral areas with longer electric field path lines reveal spatially non-uniform [H+] as a result of the spatially varied reaction rate.
D. 2-D mapping of pH change
Using the pH value obtained from Figure 2(c) calibration curve, pH was mapped as a function of time and position. Also, to increase accuracy, pH change (pH = pHt = 8 s − pHt) was demonstrated instead of an absolute pH value to further exclude molecular accumulation effects prior to t = 8 s. Absolute pH was then calculated from the difference from the starting neutral pH via pH = 7 − pH.
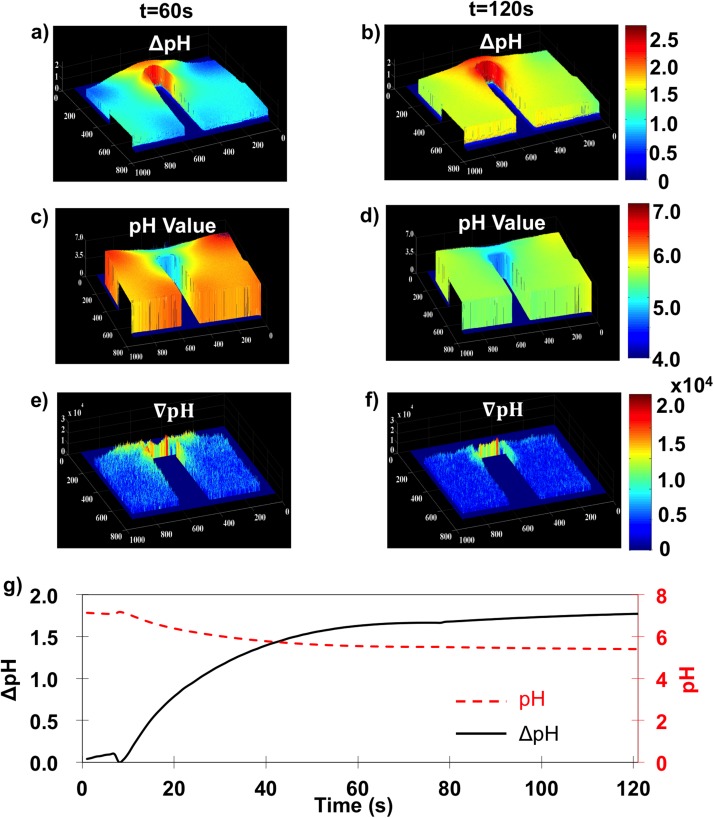
Figures 5(a) and 5(b) illustrate pH differences from 5.5 Vpp and 5 kHz between t = 8 and 60 s as well as t = 8 and 120 s, respectively. Figures 5(c) and 5(d) show pH values obtained from a uniform neutral pH everywhere at t = 0 s. Figures 5(e) and 5(f) show the geometric pH gradient (). Figure 5(g) shows both pH change (black solid line) and absolute pH (red dashed line) for the average line intensity (labeled in Figure 4(m)) with respect to time. Together, Figure 5 plots illustrate that spatial variations of pH change, pH value, and thus the pH gradient are more substantial than Figure 4 conveys. At t = 60 s, the pH change was >1.5 log (pH ≤ 5.5) in the central area, while pH changes were ∼1 in the peripheral areas. By t = 120 s, pH change increased to >2 (pH < 5) in the central area and ∼1.5 in the periphery.
FIG. 5.
For 5.5 Vpp and 5 kHz, spatially mapped pH change from 8 s for (a) 60 s and (b) 120 s. Absolute pH value obtained from controls in Figure 2 for (c) 60 s and (d) 120 s. pH gradient calculated at a per pixel resolution at 60 s (e) and 120 s (f). (g) Time dependence of the pH change (solid black line) and absolute pH value (dashed red line).
Figures 5(e) and 5(f) show the geometric pH gradient or spatial variance of pH change. At t = 60 s, the central area value was twice that in the surrounding area illustrating widespread spatial variations in pH. By t = 120 s, however, large pH gradients are only observed in the central area, indicating that solution pH became more uniform and reached equilibrium in peripheral regions. To better elucidate the time dependence, Figure 5(g) shows the time dependent averaged pH change and real pH value in bulk solution 50 μm from both electrodes. Bulk pH changes rapidly in the first 60 s suggesting Faradaic reaction rates are fastest initially, but slow as products accumulate. For 5.5 Vpp and 500 kHz, the [H+] change was 1.5 units by t = 60 s. From 60 to 120 s, the Faradaic reaction rate gradually decreased such that a pH change of only ∼0.25 took place between 60 and 120 s.
In summary, due to system geometry, the distance between electrode surfaces varies by position. For a given frequency, the potential drop within the EDL is smaller at longer electrode distances while the potential drop is larger at shorter electrode distances. A pH change of 1.5 units within the first 60 s gives a change in [H+] of ∼ in the first 60 s and ∼ by 120 s. This infers an average Faradaic reaction rate of for the first 60 s and for the entire 120 s experiment.
E. Potential and frequency dependency
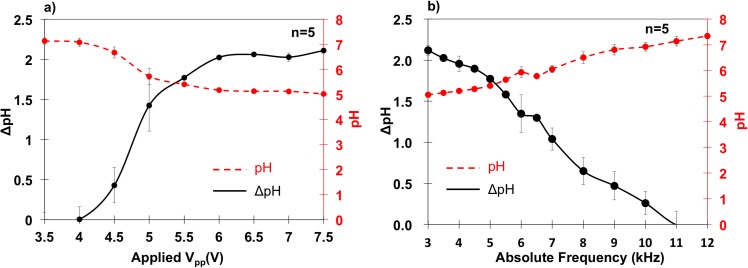
Peak-to-peak (Vpp) potential and frequency dependencies of pH changes were also quantified. Vpp ranged from 3.5 Vpp to 7.5 Vpp at a fixed frequency of 5 kHz, since negligible pH change was observed below 3.5 V and above 7.5 V severe electrode damage occurred. Next, frequencies from 3 to 12 kHz (relative frequency = 6 to 24) at a fixed applied potential of 5.5 Vpp were tested to examine Faradaic reaction behavior around and above the electrode charging frequency. The pH change between t = 8 s and 120 s was tracked with line intensity data (Figure 4(m)) as a function of position as shown in Figure 6. Each condition in Figures 6(a) and 6(b) contains 5 repeats with error bars representing standard deviations.
FIG. 6.
(a) Potential dependency of pH change (solid black) and absolute pH value (dashed red) at 5 kHz. (b) Frequency dependency of pH change (solid black) and absolute pH value (dashed red) at 5.5 Vpp. This infers that Faradaic reactions increased with peak-to-peak potential and decreased with frequency.
Vpp dependency results in Figure 6(a) showed that pH changes, and thus Faradaic reaction rate, increased with peak-to-peak potential. The reaction rate was negligible at 3.5 Vpp and started to increase at 4 Vpp. From 4 to 6 Vpp, the pH change increased rapidly from 0.1 to 2. At 6 Vpp, reaction rate slowed to negligible above 7.5 Vpp.
Frequency dependence results in Figure 6(b) showed that reaction rate decreased linearly with frequency. Faradaic reaction products were considerable at frequencies above the presumed 500 Hz electrode charging frequency. In fact, pH changes were observed up to ∼11 kHz at which products could no longer be fluorescently detected.
F. Discussion
Results from Figures 5(a) and 5(b) indicate that Faradaic reactions are more pronounced in the central area between the electrodes. This is attributed to differences in the ion transfer properties along the non-uniformed ion paths at different lengths represented by the differences in relative frequency () governed by the electrode charging frequency, which is inversely proportional to ion path lengths [Eq. (1)]. At a fixed applied frequency across spatially non-uniform electrodes, the potential drop within EDL is highest in regions with the smallest electrode spacing, resulting in greater Faradaic reaction rates. While in peripheral regions, the greater distance between electrodes results in lower EDL potential drops and thus lower Faradaic reaction rates.
Increases in relative frequency cause lower reaction rates, evidenced in this work by formation of pH gradients. Figures 5(e) and 5(f) illustrate the pH gradient becomes less pronounced at large time, because [H+] diffuses throughout (Figure 5(g)). However, pH gradient formation at short time scales provides interesting insights into the Faradaic reactions. It can be inferred from Figure 5(g) that the Faradaic reaction producing H+ becomes equilibrium limited, thus slowing the production of H+. Concurrently, H+ diffusion down the pH gradient occurs on an unchanging time scale (, D is diffusion coefficient, x is diffusion length). The pH gradient decrease can be understood via a relative ion rate ratio (Rr) between the driving reaction rate (Rrxn) and resulting diffusion rate (Rd) as Rr = Rrxn/Rd. At t < 60 s, Rrxn ≫ Rd in both the central and surrounding area, which leads to higher Rr and thus a pronounced pH gradient. In the peripheral areas, Rrxn and Rd are similar number of unit such that pH gradients are not apparent. From t = 60 to 120 s, Figure 5(f) suggests Rrxn decreases. In central areas with minimum characteristic length, Rrxn remains high, but in peripheral areas, Rrxn is reduced. However, Rd is a phenomenon responding to the pH (concentration) gradient such that when the pH gradient is large, the effective Rd is also high. As time progresses, the central pH is relatively constant, but the accumulation of H+ in the periphery increases, thus decreasing the pH gradient and effectively reducing Rd. Thus, Rr remains high in the central area, while Rr in the surrounding areas reduces. This combination results in a shrinkage of the high pH gradient footprint and a pH uniformity in the peripheral area.
Figure 6(a) showed how the peak-to-peak potential, at a fixed frequency of 5 kHz, impacted the Faradaic reaction rate and thus the resulting pH change. In this specific electrode configuration, the Faradaic reaction was initiated at 4 Vpp (2 V for each half period); this is the “AC onset potential” for 5 kHz. This AC onset potential is slightly higher than the reported 1.23 V theoretical standard electrode potential18 calculated based on reaction thermodynamics and consistent with a previously reported 2 V experimentally obtained onset potential for a similar gold electrode configuration under DC potential yielding water electrolysis.21 With increasing overpotential (applied potential—standard electrode potential), the Faradaic reaction rate increased significantly, evidenced by the pH change increasing from 0 to 2.5. Beyond 6 Vpp, the Faradaic reaction became mass transfer limited such that pH did not further increase with increasing overpotential.
Figure 6(b) showed the Faradaic reaction frequency dependence at a fixed applied potential of 5.5 Vpp. Frequencies examined were at 3 kHz and above the electrode charging frequency. The Faradaic reaction was highly pronounced at 3 kHz and steadily declined to negligible at 11 kHz. This trend illustrated that the Faradaic reaction persisted above the charging frequency of 500 Hz. This can be explained through an electrode-electrolyte interface model with a parallel capacitor and resistor.22 The capacitor represents the electric double layer (EDL) while the resistor represents electron transfer across the electrode-electrolyte interface, which generates the Faradaic reaction. Previous work was conducted23–27 at frequencies close to the electrode charging frequency, whereby the capacitor remains charged in each half period. The charged capacitor functions as a high impedance element preventing current passage, while the resistor facilitates electron transfer for the Faradaic reaction to progress. At frequencies above , which this work explored, the capacitor was not fully charged and the EDL was not fully established (electrode not fully polarized/screened). Thus, a similar impedance across the parallel resistor and capacitor results in current passing through both pathways yielding Faradaic reaction products, albeit at an attenuated rate compared to reactions below . With increases in frequency, the EDL capacitor charges less, favoring current passage through the capacitor over the parallel resistor. The increasing capacitor current thus increasingly bypasses the resistor effectively short circuiting the electrode-electrolyte interface to thus decrease and eliminate the Faradaic reaction rate.
IV. CONCLUSIONS
This work spatially and temporally examined Faradaic reactions in spatially non-uniform AC electric fields via spatial pH detection at frequencies higher than the theoretical electrode charging frequency.
Faradaic reaction products were observed across the entire microdevice chamber over the course of the 120 s experiment. The applied frequencies were higher than the theoretically predicted electrode charging frequency meaning that the electric double layer was not well charged. Despite this, pH changes up to 2.5 units were observed proving the existence of Faradaic reactions above the electrode charging frequency.
Further, spatial variances in the Faradaic reaction rate were observed and attributed to the varied electrode spacing resulting from the spatial non-uniformity of the electric fields. These spatially varying Faradaic reactions were tracked via observation of pH gradients reaching magnitudes of 2 104 unit/μm.
Finally, Faradaic reaction rate increases were observed with increasing potential and Faradaic reaction rate decreases were observed with increasing frequency. The reaction rate increased with potential due to increasing electron transport rate from electrode to electrolyte. Reaction rate decreased with frequency due to insufficient time to fully charge the electric double layer in accordance with the RC electrode-electrolyte behavior model.
This work demonstrates that Faradaic reactions influence the local pH above the electrode charging frequency. Further, these pH changes vary with time and position. The implications are that pH gradients may induce anomalous (bio)particle dielectrophoretic responses and hydrodynamic fluid behaviors. Further, the techniques utilized in this work to quantify pH gradients may be adapted to other microfluidic systems to ascertain the impact of Faradaic reactions on ACEO pumps or related hydrodynamic phenomena.
ACKNOWLEDGMENTS
This research was derived from work supported by the National Science Foundation Grant No. CBET 1041338. Additional financial support of Ran An came from Teaching Assistantships with the Chemical Engineering Department at Michigan Tech.
References
- 1.Ramos A., Morgan H., Green N. G., Gonzalez A., and Castellanos A., “ Pumping of liquids with traveling-wave electroosmosis,” J. Appl. Phys. 97(8), 084906 (2005). 10.1063/1.1873034 [DOI] [Google Scholar]
- 2.Garcia-Sanchez P., Ramos A., Green N. G., and Morgan H., “ Experiments on AC electrokinetic pumping of liquids using arrays of microelectrodes,” IEEE Trans. Dielectr. Electr. Insul. 13(3), 670–677 (2006). 10.1109/TDEI.2006.1657983 [DOI] [Google Scholar]
- 3.Minerick A. R., “ The rapidly growing field of micro and nanotechnology to measure living cells,” AIChE J. 54(9), 2230–2237 (2008). 10.1002/aic.11615 [DOI] [Google Scholar]
- 4.Minerick A. R., Zhou R. H., Takhistov P., and Chang H. C., “ Manipulation and characterization of red blood cells with alternating current fields in microdevices,” Electrophoresis 24(21), 3703–3717 (2003). 10.1002/elps.200305644 [DOI] [PubMed] [Google Scholar]
- 5.Bard A. J. and Faulkner L. R., Electrochemical Methods: Fundamentals and Applications ( Wiley, 2000). [Google Scholar]
- 6.Bruus H., Theoretical Microfluidics ( Oxford University Press, 2008). [Google Scholar]
- 7.Grahame D. C., “ Electrode processes and the electrical double layer,” Annu. Rev. Phys. Chem. 6, 337–358 (1956). [Google Scholar]
- 8.Gonzalez A., Ramos A., Garcia-Sanchez P., and Castellanos A., “ Effect of the combined action of Faradaic currents and mobility differences in AC electro-osmosis,” Phys. Rev. E 81(1), 016320 (2010). 10.1103/PhysRevE.81.016320 [DOI] [PubMed] [Google Scholar]
- 9.Garcia-Sanchez P., Ramos A., Green N. G., and Morgan H., “ Traveling-wave electrokinetic micropumps: Velocity, electrical current, and impedance measurements,” Langmuir 24(17), 9361–9369 (2008). 10.1021/la800423k [DOI] [PubMed] [Google Scholar]
- 10.Linkov V., Electrolysis ( InTech, 2012). [Google Scholar]
- 11.Garcia-Sanchez P., Ramos A., Gonzalez A., Green N. G., and Morgan H., “ Flow reversal in traveling-wave electrokinetics: An analysis of forces due to ionic concentration gradients,” Langmuir 25(9), 4988–4997 (2009). 10.1021/la803651e [DOI] [PubMed] [Google Scholar]
- 12.Studer V., Pepin A., Chen Y., and Ajdari A., “ An integrated AC electrokinetic pump in a microfluidic loop for fast and tunable flow control,” Analyst 129(10), 944–949 (2004). 10.1039/b408382m [DOI] [PubMed] [Google Scholar]
- 13.Ng W. Y., Lam Y. C., and Rodriguez I., “ Experimental verification of Faradaic charging in AC electrokinetics,” Biomicrofluidics 3(2), 022405 (2009). 10.1063/1.3120273 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.An R., Wipf D. O., and Minerick A. R., “ Spatially variant red blood cell crenation in alternating current non-uniform fields,” Biomicrofluidics 8(2), 021803 (2014). 10.1063/1.4867557 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Persat A., Chambers R. D., and Santiago J. G., “ Basic principles of electrolyte chemistry for microfluidic electrokinetics. Part I: acid-base equilibria and pH buffers,” Lab Chip 9(17), 2437–2453 (2009). 10.1039/b906465f [DOI] [PubMed] [Google Scholar]
- 16.Persat A., Suss M. E., and Santiago J. G., “ Basic principles of electrolyte chemistry for microfluidic electrokinetics. Part II: coupling between ion mobility, electrolysis, and acid-base equilibria,” Lab Chip 9(17), 2454–2469 (2009). 10.1039/b906468k [DOI] [PubMed] [Google Scholar]
- 17.Contento N. M. and Bohn P. W., “ Tunable electrochemical pH modulation in a microchannel monitored via the proton-coupled electro-oxidation of hydroquinone,” Biomicrofluidics 8(4), 044120 (2014). 10.1063/1.4894275 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cheng L. J. and Chang H. C., “ Switchable pH actuators and 3D integrated salt bridges as new strategies for reconfigurable microfluidic free-flow electrophoretic separation,” Lab Chip 14(5), 979–987 (2014). 10.1039/c3lc51023a [DOI] [PubMed] [Google Scholar]
- 19.Cheng L.-J. and Chang H.-C., “ Microscale pH regulation by splitting water,” Biomicrofluidics 5(4), 046502 (2011). 10.1063/1.3657928 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Xie C. G., Bostaph J., and Pavio J., “ Development of a 2 W direct methanol fuel cell power source,” J. Power Sources 136(1), 55–65 (2004). 10.1016/j.jpowsour.2004.05.025 [DOI] [Google Scholar]
- 21.Senftle F. E., Grant J. R., and Senftle F. P., “ Low-voltage DC/AC electrolysis of water using porous graphite electrodes,” Electrochim. Acta 55(18), 5148–5153 (2010). 10.1016/j.electacta.2010.04.022 [DOI] [Google Scholar]
- 22.O'M. Bockeris J. and Reddy A. K. N., Modern Electrochemistry 1: Ionics, 2nd ed. ( Springer, 1998). [Google Scholar]
- 23.Shipley J. W., “ The alternating current electrolysis of water,” Can. J. Res. 1(4), 305–358 (1929). 10.1139/cjr29-020 [DOI] [Google Scholar]
- 24.Shaw M. and Remick A. E., “ Studies on alternating current electrolysis: I. The nature of polarization capacity and polarization resistance,” J. Electrochem. Soc. 97(10), 324–334 (1950). 10.1149/1.2777889 [DOI] [Google Scholar]
- 25.Silverman J. and Remick A. E., “ Studies on alternating current electrolysis: II. Oscillographic studies,” J. Electrochem. Soc. 97(10), 335–345 (1950). 10.1149/1.2777890 [DOI] [Google Scholar]
- 26.Bump D. D. and Remick A. E., “ Studies on alternating current electrolysis: V. Double layer resistance and electrode area as factors in electrode kinetics,” J. Electrochem. Soc. 111(8), 981–988 (1964). 10.1149/1.2426304 [DOI] [Google Scholar]
- 27.Remick A. E. and Mccormick H. W., “ Studies on alternating current electrolysis: III. Effects of concentration on polarization capacity and polarization resistance,” J. Electrochem. Soc. 102(9), 534–544 (1955). 10.1149/1.2430142 [DOI] [Google Scholar]