Design and Demonstration of a Microbiaxial Optomechanical Device for Multiscale Characterization of Soft Biological Tissues with Two-Photon Microscopy

Abstract

The biomechanical response of tissues serves as a valuable marker in the prediction of disease and in understanding the related behavior of the body under various disease and age states. Alterations in the macroscopic biomechanical response of diseased tissues are well documented; however, a thorough understanding of the microstructural events that lead to these changes is poorly understood. In this article we introduce a novel microbiaxial optomechanical device that allows two-photon imaging techniques to be coupled with macromechanical stimulation in hydrated planar tissue specimens. This allows that the mechanical response of the microstructure can be quantified and related to the macroscopic response of the same tissue sample. This occurs without the need to fix tissue in strain states that could introduce a change in the microstructural configuration. We demonstrate the passive realignment of fibrous proteins under various types of loading, which demonstrates the ability of tissue microstructure to reinforce itself in periods of high stress. In addition, the collagen and elastin response of tissue during viscoelastic behavior is reported showing interstitial fluid movement and fiber realignment potentially responsible for the temporal behavior. We also demonstrate that nonhomogeneities in fiber strain exist over biaxial regions of assumed homogeneity.

Introduction

It has been shown that the mechanical properties of tissue change significantly with age and under different disease states (Halloran et al., 1995; Lipman et al., 2002; Okamoto et al., 2002; Vande Geest et al., 2004; Jani & Rajkumar, 2006; Haskett et al., 2010). Specifically, blood vessels have shown modified mechanical properties associated with advanced disease progression, as is the case in atherosclerosis and aneurysmal disease (Safar et al., 2000; Vande Geest et al., 2006). It is generally accepted that the identification of the mechanical properties of tissues on the macroscopic scale can be used in assessing the functionality of a soft tissue.

In addition, a blood vessel’s extracellular matrix (ECM) can be remodeled in response to mechanical stimuli (Fung, 1993; Fung & Liu, 1995; Zoumi et al., 2004). The primary underlying contributing microstructural components contributing to this behavior are the collagen and elastin found within the ECM (Zoumi et al., 2004). The ECM gives tissue its mechanical behavior, and quantifying relative amounts and orientations of the fibers within such tissues can give a better understanding of the effects of specific stimuli or disease states (Humphrey et al., 1987). Furthermore, understanding the underlying microstructure of tissue under mechanical stimuli is important because this microstructure is ultimately responsible for the macromechanical response. Obtaining microstructural behavior over a large spatial domain can also give insight into homogeneity in fiber strain during mechanical loading. These data can provide useful comprehension into areas of local weakness or strength and can give researchers guidance in the treatment of such areas. For these reasons we also believe that understanding these relationships will be critical when optimizing tissue engineering constructs in the future, as a functional tissue construct may require the microstructural response of native tissue.

Previous endeavors have been made into characterizing the relationship between tissue microstructure and function (Billiar & Sacks, 1997; Zoumi et al., 2004; Humphrey et al., 2008). The first studies of this kind were incapable of performing simultaneous mechanical stimulation while examining ECM architectures through the depth of the tissue. Many of these approaches utilized fixing or freezing tissue while in the deformed state. In addition, they used histology to examine the microstructure after fixing or freezing. With regard to examining the mechanical behavior under microscopy without the need for sectioning or fixing, some of these studies have provided novel investigations into the behavior of culture systems, collagen gels, and biomaterials under mechanical stimulation (Gleason et al., 2004; Humphrey et al., 2008). These experiments have identified structure-function relationships in tissues via simultaneously imparting mechanical stimulation while noninvasively recording collagen or other biological signals (Roeder et al., 2002; Voytik-Harbin et al., 2003; Hu et al., 2009). The characterization of this architecture provides critical information on the mechanical behavior of soft tissues.

Nonlinear optical microscopy techniques have provided a method by which researchers can examine microstructure without the need for staining the ECM or performing potentially destructive operations to the tissue (Zoumi et al., 2002; Cox et al., 2003). Researchers have already used these microscopy techniques to provide insight into arterial compositions. When these techniques are coupled to mechanical stimulation, further information regarding the behavior of tissues in configurations other than the stress-free state, typically investigated during microscopy, have been reported (Boulesteix et al., 2006; Timmins et al., 2010).

The purpose of this article is to demonstrate the design and use of a microbiaxial optomechanical device (MOD) that allows the simultaneous mechanical stimulation of fully hydrated tissue while performing multiphoton microscopy (collecting second harmonic generation and two-photon emission fluorescence signal). This device has been specifically designed for integration with the Advanced Intravital Microscope at the University of Arizona’s BIO5 Institute. Initial tests have been run on the behavior of planar porcine coronary artery under viscoelastic testing conditions and at different strain states. This device will provide a unique opportunity for studying disease-related alterations in the complex structure-function relationships of cardiovascular and other soft tissues. In addition, the MOD provides us with the unique capabilities to identify functional micro-structural changes of tissues in a nonhomogenous manner (i.e., which microstructural components are most responsible for the bulk response). The device and data presented here can begin to answer questions on the mechanisms of fiber remodeling and passive realignment in soft tissues.

Materials and Methods

Microbiaxial Optomechanical Device

The overall MOD consists of a tissue sample sitting in a temperature controlled (37°C) saline bath coupled to inline motion control and load measurement (up to 1 kg) systems to apply mechanical load. Optical systems record macroscopic and microscope behaviors. Motion is accomplished via stepper motors routed through a pulley scheme to allow for application of biaxial loads to the sample. The load is measured via load cells calibrated with precision hanging masses. Macroscopic strain is recorded automatically from underneath the sample during the test. ECM changes under macroscopic strain are imaged via multiphoton microscopy on the top surface of the sample. Macroscopic strain for planar samples is accomplished by examining markers on the samples (Humphrey et al., 1987).

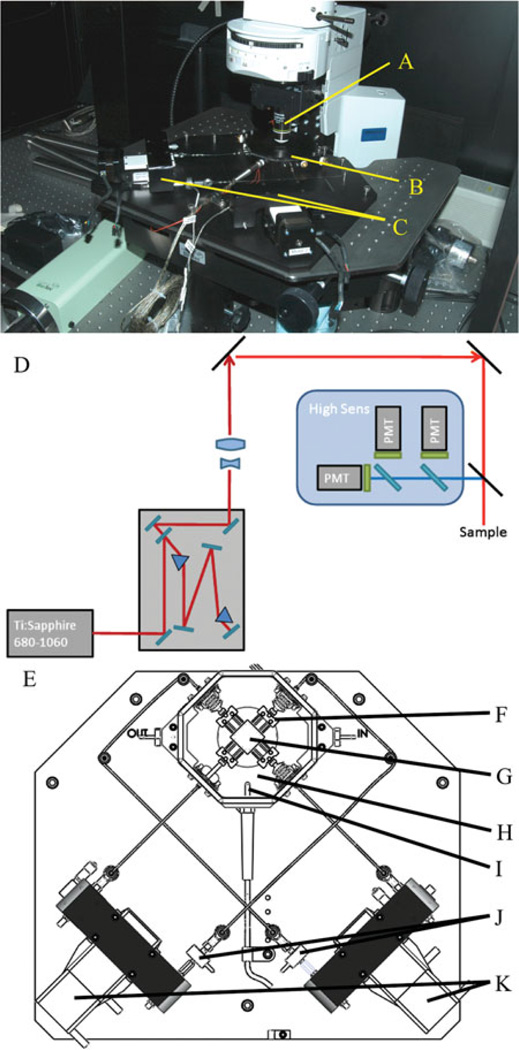
Imaging is done through multiphoton excitation with collagen recorded from second harmonic generation (SHG) with 780 nm illumination (Ti-Saph laser). SHG light is collected through a bandpass filter (377/50 Semrock). Fluorescence emission from elastin is collected through another bandpass filter (460/80 Semrock). Laser power on the sample for the purposes of this study was 29 mW. All imaging was performed via nonlinear microscopy (no confocal microscopy). Multiphoton imaging offers advantages in our situation (hydrated ex vivo tissues) over confocal microscopy in the ability to have superior image quality, deeper optical sectioning, reduced photo damage, and lack of a need for staining to visualize the extracellular matrix (Bell, 2008). Figure 1 shows the microscope set up in the laboratory with the device placed on the imaging stage along with the optical layout and a top down view of our device.

Figure 1.

Microscope set up. The MOD is placed on the x, y stage and positioned so the cover slip in the lid of the bath is placed beneath the objective lens (A). B: Testing bath with a sample inside. C: Motors of the MOD. D: The microscope optical layout used in this study. E: Arrangement of the pulling scheme for the MOD (top-down view). F: The spindle the sample is attached to (to allow free shear in the sample). G: A sample sutured in place. H: The bath. I: The thermocouple. J: The load cells attached to the rod end and the linear stages. K: The linear stages. Not shown are the heaters under the bath.

For planar biaxial tension, the second Piola Kirchhoff stress tensor and Green’s strain tensor are reported from the MOD’s computer via the following equations (Fung, 1993; Debes & Fung, 1995):

$$S_{11}=\frac{1}{{\mathbf{\lambda }}_1}\frac{F_{11}}{L_{2o}{h}_o},S_{22}=\frac{1}{{\mathbf{\lambda }}_2}\frac{F_{22}}{L_{1o}{h}_o},$$ (1)

$$\mathit{E}=0.5({\mathit{F}}^T\mathit{F}-\mathit{I}),$$ (2)

where S are the stresses, λ are the stretches, F are the forces, L is the sample width in either direction, h is the sample thickness, E is the Green’s strain tensor, and F is the deformation gradient tensor.

Testing Procedure

All experimental procedures were performed according to the approved protocols of the University of Arizona Institutional Animal Care and Use Committee. Porcine hearts were obtained from the University of Arizona Meat Sciences Laboratory. The ostium of the left coronary artery was located in the aorta and the coronary artery cut away from the myocardium (Fig. 2C). Fat and other extraneous tissue from the heart were cleaned from the vessel (Fig. 2A). The adventitia was carefully cut away so that the medial layer was not destroyed. Dissection occurred around 4°C. The entire vessel was kept in a Krebs-Ringer buffer solution (Sigma-Aldrich pH7.4) at 4°C until 1 h before the imaging session (maximum time of 12 h). An hour before the imaging session, a segment was excised, splayed (with orthogonal edges corresponding to the axial and circumferential directions respectively), sutured, and attached to the MOD. Attachment occurs through free rotating pieces that allow free shear and allow transfer of the applied load from the stepper motors. The axial and circumferential direction dimensions were measured separately and loaded to different forces but the same tension. The entire procedure occurs in a dish kept at 4°C while keeping the tissue moist with Krebs-Ringer solution. A notch was cut in one corner to denote orientation of the sample. Figure 2B shows an example of the excised coronary vessel after mounting in the device and with the lid on the MOD.

Figure 2.

C: Picture of an obtained porcine heart showing sample location. LV = left ventricle, RV = right ventricle. A: Excised specimen after cleaning. This segment is splayed open to a planar square section, sutured, then placed in the testing bath. B: Bath with the lid on when the sample has been put in place.

Visualization markers were then applied by mixing 40 µm ceramic microspheres (Zeeospheres Ceramics, LLC, Lockport, LA, USA) with cyanoacrylate and then placed via a needle onto the surface of the tissue. On the intima (microscope-facing side), a single marker was placed so the same area of the sample could be located in the microscope across load and time states. This allows for cross-image comparison (e.g., same sample but different strain/time states) from the microscope. On the adventitial side four markers were placed approximately in a square to allow monitoring of the macroscopic strain via the system’s incorporated vision-strain system. The sample was mounted in the bath, covered with the lid (Fig. 2B), and heated to 37°C.

The first tests run were to determine the macroscopic behavior of the samples. The outcome of this set of tests was to obtain the macroscopic tissue behavior of the planar porcine coronary arteries. With the porcine coronary arteries, creep, stress relaxation, and quasi-static loading data were performed. After the macroscopic test the same samples were tested with the same protocol as the macroscopic test, but under the microscope. The desired output of this test was collagen and elastin orientation and force data. More particularly we were interested in how orientations of the ECM changed under the same mechanical states in which macroscopic data were recorded.

For quasistatic loading, the tissue was tested under displacement controlled cyclic loading with discrete displacement steps. Discrete displacement steps to reach maximum tension were implemented as opposed to a constant displacement rate being applied because it takes 10 min to run a raster scan of an individual image stack at a given strain state. For viscoelastic testing, creep and stress relaxation tests were performed. These tests were done first to obtain macroscopic behavior (on the testing cart). For the macroscopic test, the system was turned on and put through a cyclic biaxial preconditioning sequence (15 cycles 70 g maximum load). The preconditioning value was based on the maximum physiological force (Law of LaPlace with 120 mm Hg of pressure) of the samples tested. The sample underwent a biaxial preload sequence after preconditioning to bring the sample to 20 g preload. The preload value was determined by examining the slack on the lines in the system and electrical noise experienced in the lab. After the sample was preloaded, the four markers were located with the strain vision system and selected to get the center of geometry of each marker for tracking. The specific testing protocol (stepped loading, creep, stress relaxation) was initiated after this, and the test commenced. The Law of LaPlace with dimensions taken from tested tissue and pressure taken to be 120 mm Hg (systolic pressure) provided the target wall tension for testing (Fung, 1993; Zhang et al., 2007). Coronary dimensions and tension details may be seen in Table 1. Individual samples were tested to the specific parameters corresponding to the individual vessel as opposed to the average from all samples.

Table 1.

Testing Parameters for Porcine Coronary Arteries (n = 10).^*

Circumference (mm)	9.96 ± 1.38
Thickness (mm)	0.25 ± 0.06
Wall tension (N/m)	250 ± 54.4

^*Data are reported as average ± standard deviation.

For planar biaxial testing, the samples were tested to the desired tension by providing displacement steps biaxially until the desired force was met. For the stress relaxation test, biaxial strain was held constant at 0.07 and forces monitored. This strain was chosen from the average strain at peak tension between the two directions in the quasi-static loading test. For the creep test, the force was held constant at 70 g biaxial load, and strain was monitored over time.

After each macroscopic test the system was placed on the microscope and imaged to get a baseline where images can be taken. For displacement controlled stepped loading, a baseline scan was done under the no load condition first then taken to subsequent strain states while keeping a marker in the field of view. Following the marker in the microscope field of view is necessary so the same section of the sample through image stacks at different strain states could be compared. Subsequently, the height of the sample (modified during loading) was kept in focus by changing the objective height to maintain focus on the sample. An image stack was then taken at the no load, preload, an intermediate strain, and full strain states keeping the marker in the field of view. The same displacement conditions were applied to the sample when on the microscope as when it was being tested for macroscopic properties to assure the macroscopic and microscopic results can be related. Image stack slices were separated by 5 µm and took 10 min with three line averages. Line averages are accomplished through multiple scans of the same region of the sample.

Thickness was monitored by performing microscopy scans on the naturally thin excised samples (less than ~250 µm). The thickness was originally measured with high-precision calipers (±10 µm). The thinner samples were exclusively used so the microscope could scan through the entire sample to allow for tracking thickness over time. Sample thicknesses were tracked by looking for the top and bottom of the image stacks obtained for signals from fibers. By knowing the individual slice thicknesses, the overall thickness could be computed to the resolution of the optical slice thickness. Thicknesses calculated via microscopy in the unstrained states were compared to caliper readings to assure accuracy in the thickness reading from the microscope. This is to reassure that attenuation through the sample was not preventing accurate measurement of the thickness via optical sectioning. For stress relaxation and creep, images were taken after 30 s and every 2 min afterward until the stress relaxation or creep behavior reached a steady-state value macroscopically. Raster scans took around 30 s with a 5 µm slice thickness.

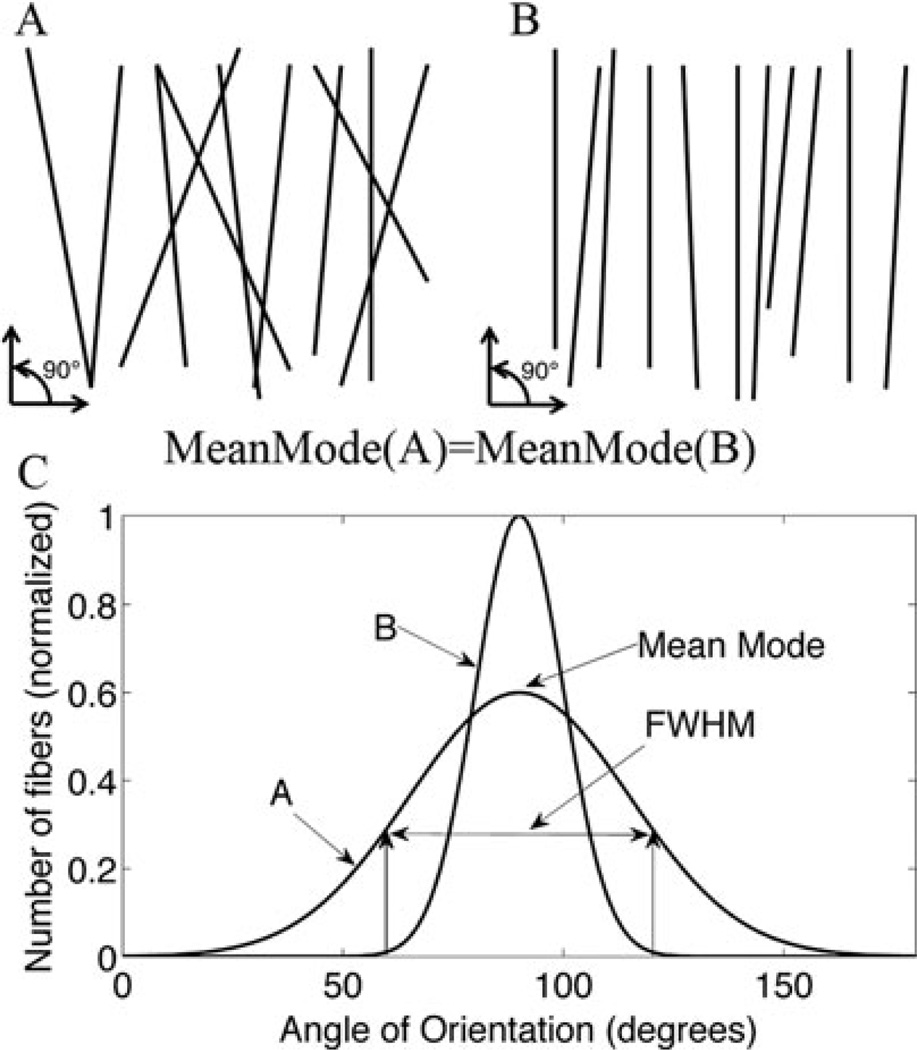
Fiber orientations were computed via a custom Matlab code to analyze orientation based on edge detection (Kirkpatrick et al., 2007). Fiber angles are put into a histogram with 50 angular bins. The mode of the histogram is a measure of the preferential alignment of the tissue. The mean mode is the average value of preferential alignment from several sample histograms. Quantifying the full-width at half-maximum (FWHM) of the histogram gives an indication of the degree of alignment about the preferential direction. Figure 3 shows a graphical representation of these measures. Each of the created pictures indicates the same mean mode (primary orientation), but Figure 3A shows a wider spread about the preferential alignment of the fibers.

Figure 3.

A: Line representative of fibers aligned primarily in the 90° (mean mode), but with a wider spread (FWHM) of fiber alignment than image B. B: Primarily aligned to 90° with a smaller spread of fiber alignment (more tightly aligned to 90°) than image A. C: Graphical representation of a histogram line graph showing differences in FHWM and mean mode in images A and B.

Digital image correlation (DIC) was used to quantify strain homogeneity (Gianola & Eberl, 2009). Eberl et al. (2006) provides an open source DIC Matlab program to the Mathworks, Inc. community. The downloaded program determines displacement of edge markers between images. Our group modified the program to calculate the deformation gradient tensor from displacements (u_i) and initial coordinates (X_j) [equation (3)] and calculate subsequent strains [equation (2)]. Principal strain was calculated via equation (4) and reported in a contour plot indicating local regions of strain (Mase & Mase, 1999). The z-projected images of the quasistatic test were analyzed via the DIC program.

$$F_{\mathit{\text{ij}}}={\delta }_{\mathit{\text{ij}}}+\frac{\partial u_i}{\partial X_j},$$ (3)

$$E_1=\frac{E_{11}+E_{22}}{2}+\sqrt{{\left(\frac{E_{11}-E_{22}}{2}\right)}^2+{\left(\frac{{\gamma }_{12}}{2}\right)}^2}.$$ (4)

Results

Biaxial Planar Displacement Controlled Stepped Loading

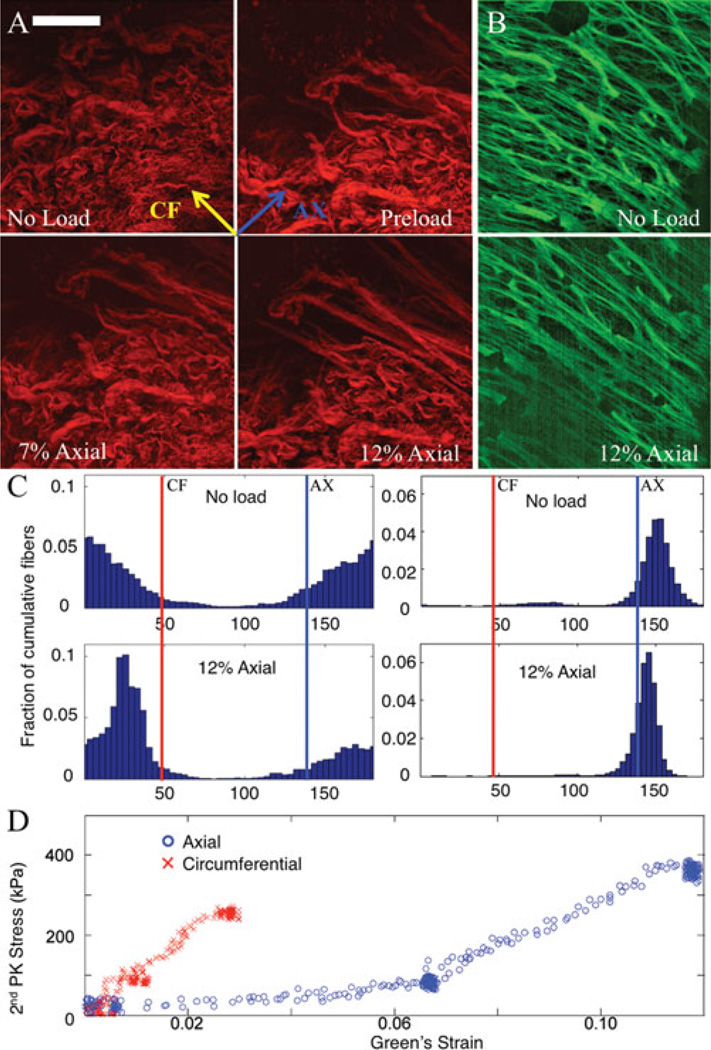
Stepped loading displayed noticeable collagen realignment at the higher strain states (E_ax = 0.12) with minor changes at smaller strains (E_ax = 0.07), as compared to the unloaded specimen. The circumferential strain at these two axial strain points was 0.02 and 0.05. See Figure 4A for a representative mosaic of collagen fibers in different load states (no load, preload, E_ax = 0.07, E_ax = 0.12). Figure 4B shows the elastin signal in the no load and 12% axial strain states (5% in the circumferential direction). The particular images shown in this manuscript are Z-projections of the entire data stack. This transforms three-dimensional data into representative two-dimensional images for publication. The projection is done weighted via the brightest pixel in a given (x, y) location in the image (ImageJ). The elastin data did not display much change over load states other than minor angular shifting toward the axial direction. Fewer elastin images are displayed as the collagen is the primary contributor to mechanical behavior at higher strains (Sokolis, 2008). Figure 4C shows the quantification of fiber orientation between load states with the collagen on the left and elastin on the right.

Figure 4.

(Color online): A Representative mosaic of fibers from porcine coronary artery in different load states. Scale bar is 100 µm. Top left of the red fibers (collagen) shows an unloaded state; top right shows a preloaded state; bottom left and bottom right show a 7% and 12% axial strain loading, respectively. B: Elastin signal is shown with the two images to the right (green) at 12% axial strain and preloaded states. C: Quantification of fiber orientation between load states. Left two histograms are of collagen, and right two are elastin. Top is with no load, and bottom is under 12% axial strain. D: Stress-strain plot of macroscopic data.

The data are split into 50 angular bins, and heights of the bars correspond to a higher percentage of the cumulative fibers (through all slices) appearing in a specific bin. Figure 4D shows the macroscopic stress-strain data for this particular test. Darker areas in the plot (with more data points) represent stationary points in the testing sequence. Images were taken at these points. The circumferential direction was noticeably more stiff displaying a stiffness of up to 5.4 times greater than the axial direction. Thickness of the unloaded to loaded specimen changed as well. The thickness decreased by 7 ± 2% as determined by optical sectioning. This was expected due to the Poisson effect under planar loading of the tissue.

Collagen fiber direction was quantified with the majority (mode) of the orientation appearing in the 4°–8° bin in the unloaded state. In the loaded state, the collagen fibers were primarily oriented in the 29°–33° bin. An angle of 45° corresponds to the circumferential direction, and an angle of 135° corresponds to the axial direction. Comparing the unloaded to loaded states for collagen orientation, we obtained a difference of 5.7° of the FWHM (97.6° for the unloaded state and 91.9° for the maximum strain state) indicating a change in the degree of orientation as shown by the spread of the data. The collagen fibers also showed noticeable qualitative straightening of collagen crimps. The elastin displayed a small shift from the unloaded to loaded states in the mode of orientation (144°–148° to 140°–144°). FWHM shifted from 18.0° to 10.8° indicating a tightening of the spread of elastin fiber distribution upon loading.

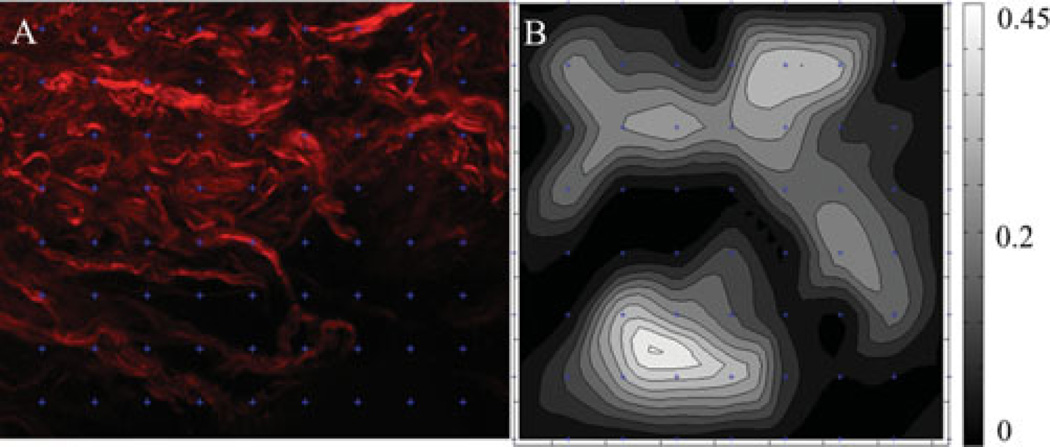
Qualitatively the tissue showed individual fiber bundle reorientation upon loading, with different fiber bundles showing different displacements in the same field of view. Upon quantitative analysis of the image via DIC, the sample showed variation in the strain field over the field of view. Figure 5 shows the image in the undeformed configuration with the marker grid used for tracking overlaid with the strain map. While macroscopic strain peaked at 0.12 in the sample, localized fiber strain peaked as high as 0.44 nonhomogenously through the field of view. These data demonstrate the nonhomogenous fiber strains in these tissues.

Figure 5.

A: Section of the undeformed collagen image in Figure 4 with an overlaid grid from DIC showing the location of the markers used for tracking. B: Strain map of the region. Strain is represented as first principal strain.

Planar Biaxial Viscoelasticity

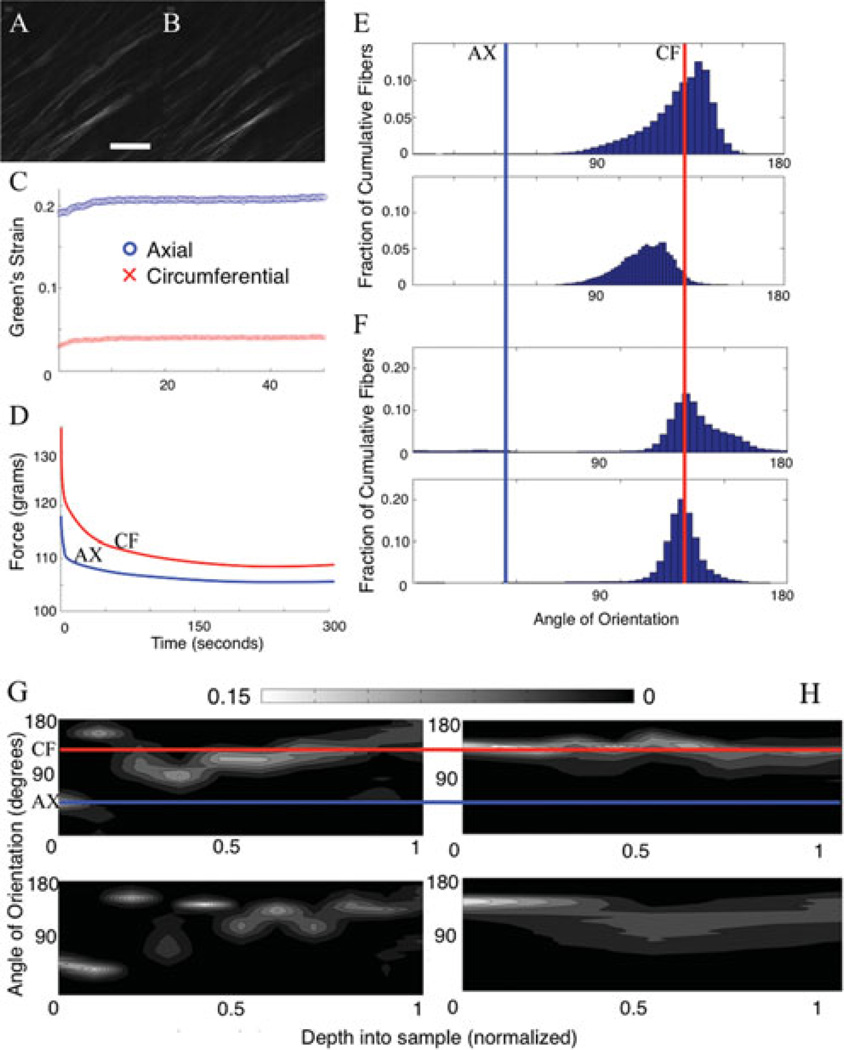
It was more difficult to qualitatively notice a change in fibers between time states under viscoelastic testing as compared to the stepped displacement testing. This could be due to the fact that tissue swelling could be a primary factor involved in the underlying response of viscoelastic behavior (Lillie & Gosline, 2007). To examine the behavior of the samples under the different time states, an orientation analysis was performed between load states. Figure 6A,B shows representations of collagen under different time states during creep at 80 µm deep.

Figure 6.

(Color online) A, B: Collagen from porcine coronary artery under different time states (30 s and 2 min, left and right) during a creep test. Scale bar is 100 µm. The fibers run along the circumferential direction. C, D: The macroscopic results from a creep and stress relaxation test, respectively. E: The fiber orientation analysis of a histogram cumulative through all the slices during creep. The top shows the fiber degree of orientation at time = 30 s, and the bottom shows time = 2 min. The circumferential direction corresponds to 135°. F: Fiber orientation analysis on the stress relaxation test data. The top shows orientation at time = 30 s, and the bottom shows orientation at time = 2 min. G, H: The fiber orientation at different depth in the image stack. The γ-axis shows the angle of orientation with the red line corresponding to the circumferential direction. The x-axis sample shows the location in depth of the sample. The z-axis (colorbar) shows the percent of fibers in a specific direction. Lighter colors indicate a preferential orientation (higher number of fibers in a given bin). G: Fiber orientation through the depth for stress relaxation from 30 s (top) to 2 min (bottom). H: Creep under the same temporal circumstances. Scale bar is 100 µm.

Upon loading the sample, the fibers were primarily orientated in the circumferential direction (as was similarly seen with the stepped displacement case) with no qualitative change to the fibers after time during stress relaxation or creep. Upon completing the fiber orientation analysis, some changes appeared evident. After full relaxation or creep, the fibers began to orient themselves more away from the circumferential direction indicated by a shift in the peak of the histogram. This did not occur at the intima but occurred only in the medial layer (Fig. 6G,H). It can be seen in the fiber orientation histograms that the angles also broadened over time in stress relaxation (smaller degree of orientation) and tightened over time during creep (higher degree of orientation) in Figure 6E,F. The summary of these data may be seen in Table 2.

Table 2.

Viscoelasticity Results Summary.

	Stress Relaxation
	Mode Range (°)	FWHM	FWHM Difference
Time = 30 s	134–137	28.76	8.37
Time = 2 m	118–124	37.13
	Creep
	Mode Range (°)	FWHM	FWHM Difference
Time = 30 s	129–132	66.72	− 42.57
Time = 2 m	129–132	24.16

Thickness was also monitored as viscoelasticity has been attributed to proteoglycans absorbing water in the tissue (Eshel & Lanir, 2001; DiSilvestro & Suh, 2002). Under stress relaxation the samples did not exhibit a change in thickness greater than 5 µm (chosen z-stack resolution of this particular scan). The sample’s starting thickness after stretching was 220 ± 5 µm as was the thickness after full stress relaxation. For creep, the sample did increase in thickness by 25 ± 5 µm over time. The thicknesses at t = 0 were 250 ± 20 µm. This equates to a change in thickness of roughly +10% over time.

Discussion

Summary

This study provides a description of a novel device that is capable of assessing structure-function relationships in soft tissues. We demonstrate that this device can be used to correlate the macroscopic biomechanical response of a tissue with its microstructure in a nondestructive manner. It can be used to study ECM alterations in both human and animal disease progression as well as probing the source of complex biomechanical phenomena (e.g., viscoleastic) present in soft tissues. While not demonstrated in this article, the MOD has also been designed to run longitudinal tissue culture experiments and tubular biaxial testing (e.g., mouse aorta). This novel capability allows researchers to investigate the micro-structure of tissue engineered constructs and microstruc-tural alterations of diseases in transgenic mice.

We present that tissue under mechanical loading is capable of realigning ECM fibers to the directions of loading. This passive ability of tissue is necessary for the strengthening of tissue in high-pressure conditions, as is the case in the circulatory system. In addition, we report that the temporal behavior of tissue can have multiple contributing factors such as fiber orientation modification and tissue swelling (interstitial fluid movement). We have also shown that homogeneity assumptions for biaxial testing may not be completely valid as the microstructure displays wide variance in strain behavior. The approach demonstrated here provides a unique opportunity to determine the mechanisms governing the macroscopic behavior of soft tissues.

A given drawback of this type of study though is the necessity of testing only thin tissues due to optical scattering. For thicker tissues, regions of the tissue not imaged could potentially confound the relationship between the microstructural and macromechanical response. Because the primary focus of this work was to describe this novel device and the types of questions it can answer, a small sample size was chosen. Therefore, the specific results and conclusions reported here should be interpreted carefully. The inability of the microscope to scan more than 400 µm square also presents problems as multiple 10 min scans need to be taken to capture the overall microstructural deformations within the macroscopic marker regions.

Biaxial Displacement Controlled Stepped Loading

It was expected that fiber bundles and collagen crimps would straighten over strain states, giving way to the increased stiffening during loading. It was also expected that fibers would align in the directions of the strain fields from the resting state (Driessen et al., 2003). While some literature has reported collagen remodeling under stressed configurations, we have reported a natural alignment tendency of vessel microstructure under stress while not looking at living tissue adaptation (Hariton et al., 2007a). It would be beneficial to examine the response of living tissue under longer time points as it may shed light on the remodeling of blood vessels under stress.

It can also be seen that the fibers preferentially align in the circumferential direction under stress in all tissue samples tested. This has physiological and pathological relevance, as the circumferential direction experiences a large amount of high-pressure cyclic loading. To maintain the artery wall’s integrity, vessels should have the reinforcing stiffness provided by collagen alignment in the circumferential direction during pulsatile flow (Hariton et al., 2007a, 2007b). Pathologically, an inability to adapt to pressure could cause vessel weakening via ECM degradation potentially leading to aneurysm, for example. This preferential circumferential alignment can also be expanded to the macroscopic data, as the circumferential direction was considerably stiffer.

These data could be expanded further to allow for the development of more accurate microstructurally-based constitutive models. This can be done for quasistatic and time-dependent loading cases. In addition, differences between healthy and diseased states can be quantified, and biological markers of the predisease states or progression of the disease states can be identified. The ability to collect microstructure during mechanical loading can also give valuable information in the modeling of porous tissues (blood vessels, sclera, cartilage, etc.) as void ratio changes during different loading conditions can be quantified.

While it was not demonstrated in this article, the device can also be used for tubular biaxial testing. This allows the testing of mouse aorta, which itself will allow investigation of disease progression. Many different types of transgenic mice exist for the investigation various cardiovascular ailments (Nishijo et al., 1998; Azhar et al., 2009). This device can provide beneficial information on the microstructural behavior of such transgenic mice, leading the way to knowledge of disease development, progression, and mechanical extracellular matrix properties.

Correspondingly, the quantification of the nonhomogenous strain of the sample allows for the novel investigation of the strain homogeneity assumptions in soft tissue mechanics. Tissue is assumed to behave in a homogenous manner within tracked markers in planar biaxial tensile testing (Stella et al., 2008; Sacks et al., 2009). Homogeneity testing can be done via the use of biaxial tensile testing coupled with multiphoton microscopy and followed by DIC analysis (Hepworth et al., 2001). The DIC analysis can provide details for local regions of fiber strain. We show that the strained region between tracked markers (which is assumed to be homogenous in mechanical testing) displays significant strain inhomogeneity. In addition, the DIC technique with the MOD can be useful to the scientific community to determine which regions of tissue microstructure specifically dominate in the contribution to the macroscopic mechanical properties. In blood vessels, local areas of strain could also be identified, providing insight to areas of local weakness that are potentially susceptible to damage.

A potential drawback to this study is the necessity of using stepped loading due to raster-scan times. To capture very small changes in microstructure, the device would need to take smaller steps and therefore require much longer imaging times. In addition, if loading rates are too fast, stress relaxation occurs upon reaching a given step. This could modify results as it has been shown in this article that small fiber realignment occurs during the viscoelastic response.

Biaxial Viscoelasticity

Several studies have suggested that tissue swelling via the response of the glycosaminoglycans contributes to the viscoelastic behavior of soft tissues (Bhatia & Vesely, 2005). We have reported that while swelling does occur over the course of a creep test, there exist some changes to the tissue microstructure as well. However, it cannot be discerned whether the change in the fiber orientation is a result of the swelling of the tissue. It is, however, an interesting effect that under the case of stress relaxation the degree of alignment became smaller (less fibers oriented in specific direction), whereas the degree of alignment became higher in the case of creep over time.

Identification of the underlying causes of the temporal behavior of tissues allows researchers to more accurately model these time-dependent effects. This could be especially important when modeling tissues in the dynamic domain (e.g., pulsatile loading). This study also identified the ability to quantify layer specific orientation between strain states. This insight allows for further identification of the role of layers in different tissues/disease states in the contribution to the overall response of the tissue (Humphrey, 2001).

A drawback of this viscoelastic study is that to quantify the behavior over a larger field of view, the sample would have to be loaded, unloaded, and reloaded several times as a single time-dependent scan occurs in a single field of view. To gather a larger idea of temporal behavior, the sample needs to be scanned until steady state after pulling to a strain (for stress relaxation), then subsequently unstrained then restrained to the same point. The difference in this second loading is that a different area would be scanned over time.

Disease states have shown modified viscoelastic properties (Labropoulos et al., 2000). Identifying the exact causes of viscoelastic changes under these states can offer further insight into these diseases. Further investigation within our laboratory is ongoing to investigate more thoroughly the causes behind the temporal response of tissue.

Conclusions

We have presented here a novel device that can examine the biomechanical behavior of tissue macroscopically and microscopically under several different conditions without the need for freezing, sectioning, or other destructive techniques that may cause physical realignment, swelling, tissue degradation, or other undesirable effects on the microstructure. In addition, the device is fit to test a variety of tissues under planar or tubular protocols and has also been designed to acquire macroscopic mechanical data on the same samples.

Initial investigations into the microstructural response of tissue in viscoelastic and quasistatic loading have been run and the results post-processed to provide the baselines for more extensive studies into the structure-function relationships of these tissues. We show the ability of tissue to passively align microstructural fibers to the directions of loading; in addition we show coupled influences of interstitial fluid movement and fiber realignment in the viscoelastic response. Finally, we present here nonhomogenous fiber straining in macroscopic mechanical testing via the use of nonlinear microscopy. Further studies will be required to provide a better understanding of the biomechanical response of tissue and for constitutive modeling, determination of disease progression, and tissue engineering. This device coupled with the software tools presented in this article provide the unique capabilities to perform such studies.