Abstract
Next-generation sequencing technology provides us with vast amounts of sequence data. It is efficient, and cheaper than previous sequencing technologies, but deep resequencing of entire samples is still expensive. Therefore, sensible strategies for choosing subsets of samples to sequence are required. Here we describe an algorithm for selection of a sub-sample of an existing sample if one has either of two possible goals in mind: maximizing the number of new polymorphic sites that are detected, or improving the efficiency with which the remaining unsequenced individuals can have their types imputed at newly discovered polymorphisms. We then describe a variation on our algorithm that is more focused on detecting rarer variants. We demonstrate the performance of our algorithm using simulated data and data from the 1000 Genomes Project.
Keywords: Imputation, SNP discovery, Coalescent
1 Introduction
As of the 2nd quarter of 2011 there were 1,449 published Genome-Wide Association Studies [GWAS] that reported finding a SNP associated with a human phenotype at a significance level of plt5×10-8 (NHGRI GWA Catalog: www.genome.gov/GWAStudies). These SNPs were associated with 237 traits in total. As such, the accumulation of knowledge that has resulted from GWAS represents both a great success and a tremendous potential for increasing our understand of the genetic causes of disease, and thereby leading to improved treatment for disease.
Despite this apparent success, one thing that remains beyond debate is that most of these SNPs are not located in genes, and for those that are in genes those genes generally have no known relationship with the phenotype of interest. Furthermore, the vast majority of phenotypic variation remains unexplained, even once such SNPs have been found. The canonical example of this is height in humans, for which a large number of associated SNPs have now been located, but for which only around 5–10% of variation is explained by most analyses (although see Yang et al. [2010]), even though around 80% of variation in height is thought to be heritable. This has led to the coining of the term “dark matter” to explain this missing connection between genetic and phenotypic variation. It remains to be seen to what degree this dark matter consists of rare variants, copy number variation, or complex interactions between multiple genes and/or environment, and to what degree it represents other “near misses”, in which the the associated SNP is linked to another nearby SNP that is actually causative.
A common strategy in following-up GWAS hits exploits so-called next generation sequencing [NGS] technology. A typical strategy is to take a subset of the parent cohort in which the GWAS hit was found and sequence those individuals in an attempt to detect other nearby variants. This strategy is often particularly focused on the detection of rare variants, since these are commonly excluded from the SNP array technologies that are used to interrogate the genome in the initial GWAS. Having identified the variant loci from the NGS data a common next step will be to attempt to impute genotype probabilities for the unsequenced members of the parent GWAS sample based on their available SNPs. This is essentially the same strategy as approaches that are widely used for imputation of untyped HapMap SNPs from GWAS data (e.g., MACH [Li et al., 2010], IMPUTE2 [Howie et al., 2009]), although we note that the imputation of rare variants harder than that of common SNPs because of weaker LD. Those imputed genotypes are then used as a basis for further tests of association, hoping to find stronger signals than in the original GWAS.
There are a rapidly growing number of papers that address aspects of this strategy, and develop appropriate statistical tests of association, particularly with respect to the hunt for associated rare variants (for example [Li and Leal, 2008; Madsen and Browning, 2009; Liu and Leal, 2010; Neale et al., 2011]). However, none of these papers address the following obvious question: given that one can typically only afford to sequence a subset of the parent GWAS cohort, which individuals should be sequenced? With this question in mind, we present methods for choosing a subset of the parent sample if one has either of two possible goals in mind: maximizing the number of new polymorphic sites that are detected, or improving the efficiency with which the remaining unsequenced individuals can have their types imputed at newly discovered polymorphisms. We then describe a variation on our algorithm that is more focused on detecting rarer variants.
2 Methods
We suppose the existence of a dataset, H, consisting of n haplotypes, over a target region with l observed SNPs. Our goal is to select a subset Hm ∈ H, consisting of m haplotypes, and sequence that subset using NGS technology in order to discover more new polymorphism in the target region and to allow improved imputation accuracy in the remaining Hu = H \ Hm unsampled haplotypes when imputation at newly-discovered SNPs relies upon using Hm as the reference population.
Let G and Gm denote the (unobserved) underlying genealogies for H and Hm, respectively. Further, let Sm denote the number of sites that are polymorphic in Hm; Sm will be positively correlated with the sum of total branch length (Bm) of Gm. The expected number of polymorphisms on a genealogical tree is the product of the length of the tree and the rate at which mutation occurs. Therefore, in order to attempt to maximize the number of polymorphisms we may discover by sequencing, we wish to choose a subsample Hm that has maximal tree length, i.e., such that Gm has a maximal Bm. The algorithm below attempts to do this while also attempting to increase the accuracy with which the remaining, unsequenced individuals will have their unobserved types imputed at newly-discovered polymorphisms.
Of course, since G and Gm are unobserved, we begin by constructing a tree,
 that approximates G. Having done this we employs an iterative procedure to choose the subset Hm. We now detail these steps.
that approximates G. Having done this we employs an iterative procedure to choose the subset Hm. We now detail these steps.
2.1 Construction of a tractable approximation to G
We begin by describing a computationally tractable scheme for constructing a tree
 that approximates the unobserved underlying genealogy G. We will do this using the UPGMA method Sokal and Michener [1958] after defining the a distance between each pair of haplotypes. G will, in all likelihood, contain recombination events and will therefore form an ancestral recombination graph (ARG) [Hudson, 1983; Griffiths and Marjoram, 1996]. The reconstruction of ARGs for large sample size (n ≫ 100) or long regions is computationally intractable. Instead, we propose to construct a single tree that captures, in some sense, the average behavior of G over the region of interest. We begin by measuring a ‘distance’ between any given pair of haplotypes. Griffiths and Tavaré [1998],Wiuf and Donnelly [1999], and Griffiths [2003] derived the expected time of occurrence of a mutation event given the number of mutant alleles (nm) under the coalescent and the diffusion models. For the diffusion model, Patterson [2005] derived the expected time of most recent common ancestor (MRCA) of the two copies of an allele. In this article, we extend Wiuf and Donnelly’s result [Wiuf and Donnelly, 1999] to compute the expected coalescent time in three cases: a pair of mutant alleles (which we denote by
) a pair of non-mutant alleles (
), and a pair consisting of one mutant and one non-mutant allele (
). (See Appendix for details.) Assuming we have l SNPs observed in the initial dataset in the region of interest, we define the distance between two haplotypes h1 and h2 as the average of the expected coalescence time for the two individuals across each of the l SNPs:
that approximates the unobserved underlying genealogy G. We will do this using the UPGMA method Sokal and Michener [1958] after defining the a distance between each pair of haplotypes. G will, in all likelihood, contain recombination events and will therefore form an ancestral recombination graph (ARG) [Hudson, 1983; Griffiths and Marjoram, 1996]. The reconstruction of ARGs for large sample size (n ≫ 100) or long regions is computationally intractable. Instead, we propose to construct a single tree that captures, in some sense, the average behavior of G over the region of interest. We begin by measuring a ‘distance’ between any given pair of haplotypes. Griffiths and Tavaré [1998],Wiuf and Donnelly [1999], and Griffiths [2003] derived the expected time of occurrence of a mutation event given the number of mutant alleles (nm) under the coalescent and the diffusion models. For the diffusion model, Patterson [2005] derived the expected time of most recent common ancestor (MRCA) of the two copies of an allele. In this article, we extend Wiuf and Donnelly’s result [Wiuf and Donnelly, 1999] to compute the expected coalescent time in three cases: a pair of mutant alleles (which we denote by
) a pair of non-mutant alleles (
), and a pair consisting of one mutant and one non-mutant allele (
). (See Appendix for details.) Assuming we have l SNPs observed in the initial dataset in the region of interest, we define the distance between two haplotypes h1 and h2 as the average of the expected coalescence time for the two individuals across each of the l SNPs:
where
is the number of mutant alleles at SNP x, and
and
are the type of the allele of haplotype h1 and h2 (respectively) at x. When doing so we will often be faced with situations in which we have multiple copies of identical haplotypes (particularly if the region is short, or the number of tagSNPs is low). During tree building, in such situations the UPGMA method constructs a tree in which, for such duplicate haplotypes, multiple nodes descend from a single internal node, forming a local star-like structure. Since, in fact, these haplotypes coalesce at a series of points in the past, and not a single point, we choose to break the star-like nodes into a subtree using the coalescent prior. This process is illustrated in figure 1. Specifically, suppose there is a node at time τ in
 , where the bottom of the tree is defined to occur at time τ = 0, and from which k identical haplotypes independently descend. Under the coalescent prior, the expected time at which the jth coalescence occurs in a sample of initial size k is given by
. We chose a random pair of the identical haplotypes and alter the tree to coalesce them at time τ × t1. We iterate this process, drawing a random pair from the set of un-paired haplotypes and the set of uncoalesced nodes on this subtree, and defining the ith such coalescence to occur at time τ × ti, for i = 1, …, k − 1. Under this construction the average distance between identical haplotypes on the new subtree is still τ.
, where the bottom of the tree is defined to occur at time τ = 0, and from which k identical haplotypes independently descend. Under the coalescent prior, the expected time at which the jth coalescence occurs in a sample of initial size k is given by
. We chose a random pair of the identical haplotypes and alter the tree to coalesce them at time τ × t1. We iterate this process, drawing a random pair from the set of un-paired haplotypes and the set of uncoalesced nodes on this subtree, and defining the ith such coalescence to occur at time τ × ti, for i = 1, …, k − 1. Under this construction the average distance between identical haplotypes on the new subtree is still τ.
Figure 1.
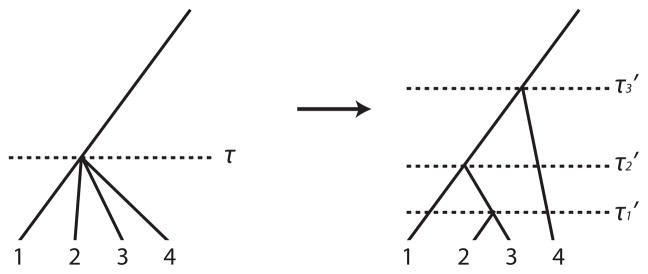
An illustration of the breaking up of a star-like node. A star-like node with 4 identical haplotypes at time τ is broken into 3 different nodes at and .
2.2 Choice of subsamples for sequencing
Haploid data
Our sampling method selects a subset of haplotypes Hm from the initial sample H, based on the tree
 constructed in the previous step. In order to aid intuition, we first describe how it proceeds when individuals are essentially haploids, such as with selfing plants for example. The process proceeds as follows:
constructed in the previous step. In order to aid intuition, we first describe how it proceeds when individuals are essentially haploids, such as with selfing plants for example. The process proceeds as follows:
Denote the set of sampled haplotypes by
 . Initially we set
. Initially we set
 = Ø. Let
= Ø. Let
 denote the subset of
denote the subset of
 that is ancestral to
that is ancestral to
 .
.For each of the two branches at the root node, sample a single haplotype from the haplotypes that descend from that branch. (We explain the details of how this choice is made below.) Add those haplotypes to
 and add the branches ancestral to those two haplotypes to
and add the branches ancestral to those two haplotypes to
 .
.Move to the next oldest node (i.e., move one node nearer to the bottom in the figure). Denote this node by η.
There are two branches that descend from η: b1 and b2, say. One will be contained in
 already. Without loss of generality we assume that b1 ∈
already. Without loss of generality we assume that b1 ∈
 . Sample a single haplotype from the haplotypes that descend from branch b2. (Again, we explain the details of how this choice is made below.) Add that haplotype to
. Sample a single haplotype from the haplotypes that descend from branch b2. (Again, we explain the details of how this choice is made below.) Add that haplotype to
 , and update
, and update
 to include all branches ancestral to
to include all branches ancestral to
 .
.Repeat steps 3. and 4. until m haplotypes are sampled.
The sub-tree
 will always has a maximal tree-length, and therefore maximizes the expected number of segregating sites in Hm (conditional on the UPGMA tree
will always has a maximal tree-length, and therefore maximizes the expected number of segregating sites in Hm (conditional on the UPGMA tree
 being a reasonable summary of G).
being a reasonable summary of G).
It remains to explain the details of how we choose the haplotype descendent from a given node during steps 2. and 4. Here, since we have already ensured maximal subtree length, the goal is to increase imputation accuracy. Heuristically, the imputation efficiency for unsampled individuals might be expected to be maximized when we minimize the distance between the most closely-related reference haplotype and the unsequenced individual for which data is being imputed. We define L to be the total sum of the branch lengths from each unsampled haplotype to
 , (i.e. the sum of the times at which all haplotypes currently not in
, (i.e. the sum of the times at which all haplotypes currently not in
 first coalesce with the current
first coalesce with the current
 ). When a haplotype is added to
). When a haplotype is added to
 at steps 2 and 4, we sample uniformly at random from among the haplotypes that satisfy the condition of that step and which will also minimize L once they are added to
at steps 2 and 4, we sample uniformly at random from among the haplotypes that satisfy the condition of that step and which will also minimize L once they are added to
 . This process is illustrated in figure 2.
. This process is illustrated in figure 2.
Figure 2.
An illustration of the sampling method. Based on a UPGMA tree for an initial dataset H containing 6 haplotypes, the sampling process begins at the root node, A. There are only two haplotypes (labeled 1 and 2) descendent from A using the left branch; one of those, haplotype 1, is chosen uniformly at random. Four haplotypes (3,4,5,6) descend from the right branch; We choose haplotype 6 (or 5) because it minimizes the total distance between each other haplotype descending from the right brach at node A and the sampled subset of the tree. The sampling process then moves to the next oldest node (node B). The right branch of the node B is already sampled so a haplotype under the left branch is selected. The sampling process moves to the next oldest node (node C), etc.
Diploid data
The sampling method for diploids is similar in spirit:
Denote the set of sampled haplotypes by
 . Initially we set
. Initially we set
 = Ø. Let
= Ø. Let
 denote the subset of
denote the subset of
 that is ancestral to
that is ancestral to
 . Haplotypes now come in pairs, defined by the diplotypes.
. Haplotypes now come in pairs, defined by the diplotypes.At the root node, sample a single individual (i.e., a pair of haplotypes), {h1, h2} say, uniformly at random from among those that minimizes L, the distance between all unsampled individuals and the tree that will result from adding {h1, h2} to
 . Set
. Set
 =
=
 ∪ {h1, h2}. Add the branches ancestral to those haplotypes to
∪ {h1, h2}. Add the branches ancestral to those haplotypes to
 . In the case that {h1, h2} descend from only one of two branches of the root node, we sample another diploid which has at least one haplotype descending from the unsampled branch and also minimizes L, and add those haplotypes to
. In the case that {h1, h2} descend from only one of two branches of the root node, we sample another diploid which has at least one haplotype descending from the unsampled branch and also minimizes L, and add those haplotypes to
 and the branches ancestral to those haplotypes to
and the branches ancestral to those haplotypes to
 as well.
as well.Move down the tree to the next oldest node. We denote this node by η.
There are two branches that descend from η: b1 and b2. By construction, at least one such branch will already be in
 . However, it is now possible that both b1 and b2 are included in
. However, it is now possible that both b1 and b2 are included in
 . If so, we move to next node without adding a sample. If not, suppose without loss of generality that b2 ∉
. If so, we move to next node without adding a sample. If not, suppose without loss of generality that b2 ∉
 . We sample a diploid pair of haplotypes from the set of pairs for which at least one component haplotype descends from branch b2, and which also minimizes L once that pair has been added to
. We sample a diploid pair of haplotypes from the set of pairs for which at least one component haplotype descends from branch b2, and which also minimizes L once that pair has been added to
 . Add this pair of haplotypes to
. Add this pair of haplotypes to
 .
.Repeat steps 3. and 4. until the required number of diploids are sampled.
Contrary to the haploid setting, our algorithm, being greedy in nature, is no longer guaranteed to produce a subtree of maximal total branch length. Nonetheless, the intent is that it will produce a subsample for which Hm is at, or near, the maximal length.
3 Results
We show results of applying our sampling method in a range of examples involving both simulated and real data. In each case we compare to an analysis in which an identical number of reference haplotypes is sampled uniformly at random from our initial data. In most cases, imputation results for haploid and diploid data were similar, in terms of relative performance of our sampling method and random sampling of haplotypes. Given this, for reasons of space we only show imputation results for diploids, since this is the harder, and more common case. We begin with an analysis of simulated data.
3.1 Simulation setting
We simulated 1000 haplotypes over a 500kb region, with mutation parameter 4Neμ = 100, and recombination parameter 4Ner = 50. We denote these haplotypes by H. We then constructed 500 diploid samples by random pairing of the haplotypes. We then randomly selected a set of σ SNPs from the set of all SNPs,
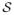 , such that each member of σ has minor allele frequency [MAF] > 5%, and ensuring that the selected SNPs were reasonably uniformly distributed over the region. This mimics the use of tag-SNPs in existing SNP-based array platforms. The unselected SNPs, ψ = S \ σ, were masked and treated as unobserved in H. For reasons of computational tractability, and since phasing is not the focus of this paper, we assumed phase information to be known. We then sampled a subset, Hm, of m/2 diploids using our sampling method, and modeled the sequencing step by simply reporting the previously unobserved information at the SNPs ψ in Hm. (Since the interest here is in the performance of our sampling method compared to random sampling, we choose not to model genotyping errors in the sequencing step.) In each case below, we compare results to those obtained when taking a random sample of the same size, where individuals are chosen uniformly at random.
, such that each member of σ has minor allele frequency [MAF] > 5%, and ensuring that the selected SNPs were reasonably uniformly distributed over the region. This mimics the use of tag-SNPs in existing SNP-based array platforms. The unselected SNPs, ψ = S \ σ, were masked and treated as unobserved in H. For reasons of computational tractability, and since phasing is not the focus of this paper, we assumed phase information to be known. We then sampled a subset, Hm, of m/2 diploids using our sampling method, and modeled the sequencing step by simply reporting the previously unobserved information at the SNPs ψ in Hm. (Since the interest here is in the performance of our sampling method compared to random sampling, we choose not to model genotyping errors in the sequencing step.) In each case below, we compare results to those obtained when taking a random sample of the same size, where individuals are chosen uniformly at random.
3.2 SNP discovery for diploid samples
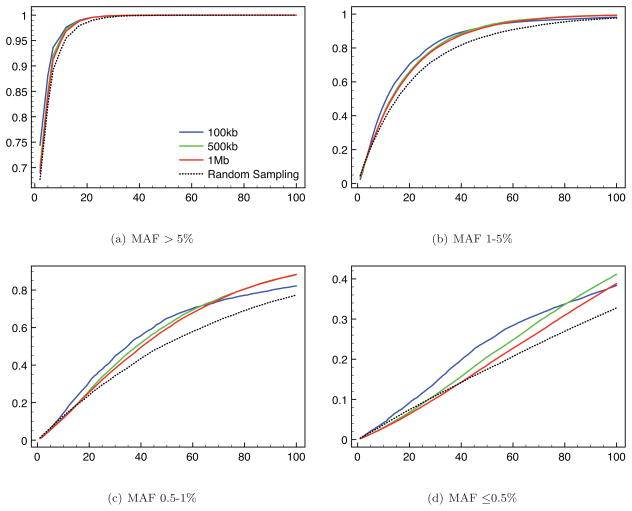
Figures 3 and 4 show a summary of the rate at which SNPs in the unobserved set ψ are discovered across 100 replicate analyses. Here, a SNP s ∈ ψ is considered ‘discovered’ if the sample Hm includes both alleles at that locus. We report results for a variety of sample sizes m/2, three tag-SNP densities (i.e., three densities of SNPs in the set σ), and various region lengths. In Figure 3 we show results according to the MAFs of the newly-discovered SNPs. We see that our sampling method results in increased SNP discovery rate in the sequenced individuals, particularly for loci with low to intermediate MAF. There is little dependency on tag-SNP density. However, we note a slight tendency for our sampling method to sample fewer very rare SNPs (MAF ≤ 0.5%) when applied to longer regions. This is a consequence of our desire to improve imputation accuracy by choosing haplotypes that share recent ancestry with other haplotypes in step 4 of our algorithm.
Figure 3.
SNP discovery rates for different tag-SNP densities (colored lines) over a 500kb region as a function of number of sampled diploids (x-axis).
Figure 4.
SNP discovery rates for different target region size (colored lines) as a function of number of sampled diploids (x-axis). Here tag-SNPs were chosen to have a density of roughly one tag-SNP per 5k. Results for random sampling are unaffected by region size, so only one such line is shown.
Figure 4 explores performance as a function of region size. Broadly speaking the performance of our sampling method is best for regions of short to intermediate length (up 500kb, say). This is because for wider regions the degree to which a single tree can summarize the behavior of the underlying ARG is clearly likely to be reduced. Over longer regions, performance begins to deteriorate, although it is still an improvement over random sampling for all but the rarest alleles (MAF ≤ 0.5%) at the smallest sample sizes (less than 30, say).
3.3 Imputation efficiency for diploids
Polymorphism discovery is not the sole function of sequencing studies of the type discussed here. Accuracy of imputation in the unsequenced sample is also of interest, where imputation occurs for newly-discovered polymorphic sites in ψ across individuals in H \ Hm. We now illustrate performance in this area. For computational tractability we again ignore phasing and sequencing errors error. We use IMPUTE2 [Howie et al., 2009] as the method of imputation (default options and parameter values were used). We report concordance between the imputed and true (but unobserved) genotypes for all ψ.
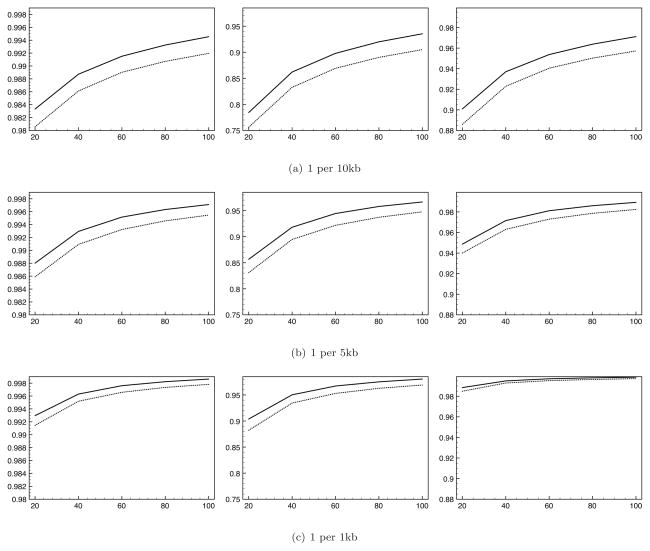
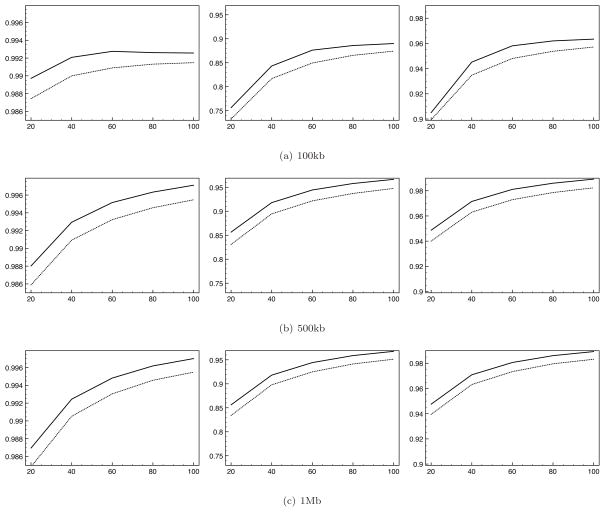
Figure 5 shows concordance as a function of minor allele frequency across 100 replicate analyses of 500 diploid individuals over a 500kb region. Here we used a tag-SNP density of one per 5kb. We show results as a function of the size of Hm and the MAF of the imputed SNP. We show results separately for each of the three possible genotypes: 0/0, 0/1, and 1/1, where 0 represents the wild-type allele and 1 represents the mutant allele. In all cases, imputation based upon samples chosen by our sampling method outperforms that based upon haplotypes sampled uniformly at random. Concordance is better for all genotypes, all MAFs, and all reference sample sizes, with the single exception of imputation of the genotype of homologous rare (< 1%) minor alleles using small (20) reference samples. In general, imputation with samples chosen using our sampling method shows the greatest improvement in performance when calling genotypes containing at least one copy of the mutant allele at sites with low MAF. In Figures 6 and 7 we show similar results, but this time allowing tag-SNP density (Figure 6) and region width (Figure 7) to vary. Again, in every case the concordance of imputed genotypes is improved by use of our sampling method.
Figure 5.
Concordance rates for imputed genotypes (y-axis) when based upon reference samples selected by our sampling method (blue columns) and uniform random sampling (red columns) as a function of MAF (x-axis). Left - concordances for 0/0 genotypes. Center - concordances for 0/1 genotypes. Right - concordances for 1/1 genotypes.
Figure 6.
Concordance rates for imputed genotypes (y-axis) when based upon reference samples selected by our sampling method (solid line) and uniform random sampling (dotted line) as a function of reference sample size (x-axis). Left - concordance for 0/0 genotypes. Center - concordance for 0/1 genotypes. Right -concordance 1/1 genotypes. We show results for three tag-SNP densities.
Figure 7.
Concordance rates for imputed genotypes (y-axis) when based upon reference samples selected by our sampling method (solid line) and uniform random sampling (dotted line) as a function off reference size (x-axis). Left - concordance for 0/0 genotypes. Center - concordance for 0/1 genotypes. Right - concordance 1/1 genotypes. We show results for three region widths.
3.4 Sampling method for rare SNP discovery
Individuals sampled by our method have more previously unobserved mutations on average, and result in better imputation accuracy, than results from random sampling of haplotypes. However, we observed a drop in performance for alleles with MAF ≤ 0.5% when fewer individuals were sampled. Here we propose a modification to our method that improves detection of such SNPs. Specifically, when applied to haploid data, we modify steps 2. and 4. of our algorithm. In each step, we now consider the set of haplotypes, Hb2, that descend from the branch (b2) that is not already in
 , assuming such a branch exists. For each haplotype h ∈ Hb2 we calculate the expected minor allele frequency for mutations that might appear in the subset of
, assuming such a branch exists. For each haplotype h ∈ Hb2 we calculate the expected minor allele frequency for mutations that might appear in the subset of
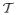 that descends from b2, and choose the haplotype for which this is minimized, adding that haplotype to
that descends from b2, and choose the haplotype for which this is minimized, adding that haplotype to
 . The diploid version proceeds in an analogous way.
. The diploid version proceeds in an analogous way.
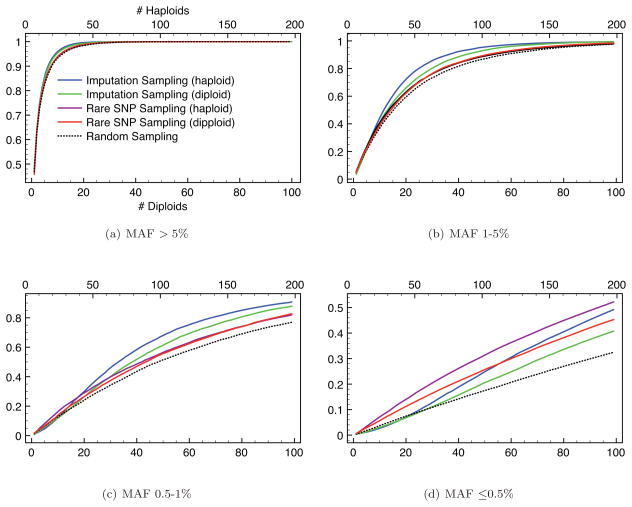
Figure 8 shows the SNP discovery rates of both our original sampling method (which we refer to as the “imputation sampllng method”) and of this modification designed to increase performance for rarer SNPs (which we call the “rare SNP sampling method”) on both diploid and haploid samples. As expected, there is no significant difference in the total number of SNPs discovered by the two methods [results not shown]. However, the SNP discovery rate does vary between the two methods as a function of MAF. The imputation sampling method results in better SNP discovery rates than the rare SNP method for SNPs with MAF > 0.5%. As intended, the rare SNP sampling method shows a better discovery rate for rarer SNPs. Both methods result in SNP discovery rates that are better than sampling uniformly at random. Results for haplotype data show better SNP discovery rates than those for diploid data, as would be expected given the compromises forced by the need to sample haplotypes in pairs in the latter. The price paid for this increased focus on discovering the rarest SNPs is that there is no substantial improvement in imputation efficiency on simulated data when using this method [results not shown].
Figure 8.
SNP discovery rates for haploid and diploid individuals resulting from our original sampling method (“Imputation Sampling”) and the variant of our method focused on rare SNP discovery (“Rare SNP Sampling”). 100 replicate sets of 1000 haplotypes (or 500 diploids) were simulated over 500kb region. We then selected 100 approximately uniformly-distributed tagSNPs. We show results as a function of reference sample size (x-axis) for differing MAFs. Results from uniform random sampling are shown for comparison
3.5 Applying to 1000 Genomes Project data
We close by applying our proposed method to data from the 1000 Genomes Project [1000 Genomes Project Consortium, 2010], as an example of application to non-simulated data. We used data from 162 exonic regions, each of which has been the target of deep resequencing using ~ 40× coverage and average region size = 90.2kb, across three populations: Yoruban (YRI, 76 individuals), CEPH (CEU, 78), Han Chinese from Beijing (CHB, 73). SNPs with sample MAF 5% are selected as tag-SNPs. There are an average of 272.6 (Yoruban), 194.4 (CEPH) and 179.0 (Chinese) tag-SNPs for each region. We masked all other SNPs from the data. (On average, each region then has 273.8 (Yoruban), 143.2 (CEPH) and 126.9 (Chinese) hidden SNPs.) We then applied both versions of our method to each region, and each population, separately. Data at masked SNPs was assumed to be read without error (corresponding to deep sequencing of the reference sample).
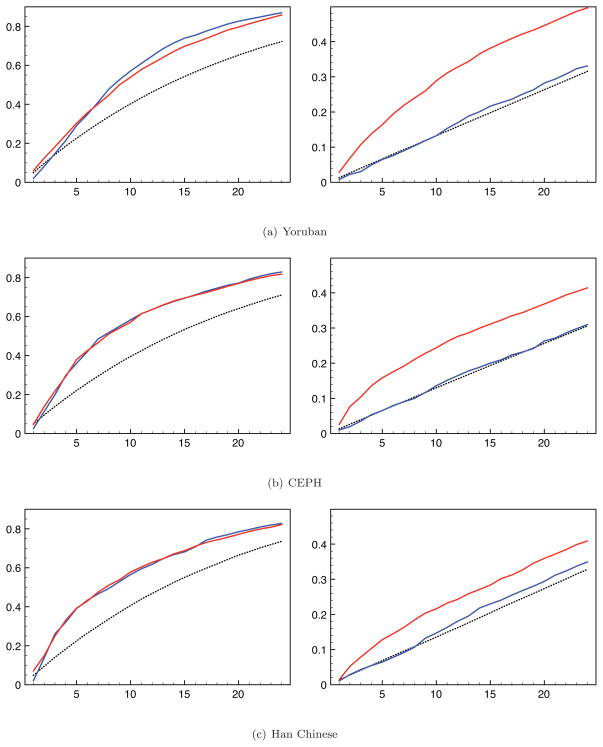
For SNPs with MAF 1%–5%, both versions of our method show similar SNP discovery rates (Figure 9 left column). However, the imputation sampling method shows similar discovery rates to sampling at random for SNPs with MAF ≤ 1% (which are singletons in this example) in all three populations. In contrast, the rare SNP sampling method shows a significantly better discovery rate for such singleton SNPs, particularly for the Yoruban population.
Figure 9.
The SNP discovery rates from the imputation sampling method (blue line) and the rare SNP sampling method (red line), as well as results from random sampling (dotted line) on 1000 Genomes Project data. Left - discovery rate for SNPs with MAF 1–5%. Right - discovery rate for SNPs with MAF ≤ 1%.
Figure 10 shows a summary of imputation results in each of the three populations. Here, we treated the masked allelic types reported in the 1000GP as the truth, and used the imputation sampling method. For all populations and all genotypes, the imputation accuracy resulting from the imputation sampling method is an improvement on that resulting from randomly selected reference haplotypes. When using the rare SNP sampling method, we still observe an improvement in imputation accuracy compared to sampling haplotypes uniformly at random, but the improvement is less than that shown in figure 10 [results not shown].
Figure 10.
The imputation results with the 1000 Genomes Project data in a function of reference sample size. Left - the concordances for 0/0 genotypes. Center - the concordances for 0/1 genotypes. Right - the concordances for 1/1 genotypes. The references were sampled by the imputation sampling method (solid line) or random sampling method (dotted line)
4 Discussion
Next generation sequencing technology enables us to generate sequence data on a large scale. Its cost is much lower than older sequencing technology and will continue to become cheaper, but full sequencing of larger samples is still economically challenging, particularly at deeper coverage levels. However, it remains the case that one of the primary hopes for this technology is that it will help explain some of the so-called dark matter that underlies the missing heritability in detected genotype/phenotype associations. A common strategy here will be to take samples from an existing GWAS, which will typically have large sample size, and sequence them to discover previously unobserved polymorphism. The next logical step will be to impute the types of unsequenced individuals at newly-discovered polymorphic sites (in the hope of improving power to detect association between such sites and phenotype - one potential explanation for the missing heritability.)
However, while the strategy we have outlined above is very appealing, cost constraints are, for the foreseeable future, going to mean that not all samples in the existing GWAS data can be sequenced. For this reason there is interest in approaches that sequence a subset of the existing sample. One is then faced with the following question: which samples should be sequenced? In this paper we present a method that improves upon sampling haplotypes at random, both in terms of the amount of polymorphism subsequently discovered, and in terms of the accuracy with which this newly discovered polymorphism can be imputed in the individuals that were not sequenced.
Our method is based upon ideas drawn from coalescent theory, and inference of the unobserved relationships between population-based samples. In particular, we exploit information from a UPGMA tree that approximates the underlying ARG. Such an approximation is necessary for tractability, but can be expected to less accurately capture the overall properties of the underlying ARG, this results in a slight degradation in performance as region length increases, although performance remains good for regions as long as 1Mb (likely to be longer than most regions sequenced in follow-up to a GWAS. The computational efficiency introduced by exploiting a tree rather than an ARG as the basis of our algorithm means that performance is good: we can build the phylogenetic tree for large sample sizes (~1000) over large regions (~1Mb) quickly (~1 minute for a typical desktop machine).
We show results for both simulated and observed data. Both version of our method performed well in all examples considered, resulting in significant improvements over approaches that simply sample haplotypes at random. We note two areas in which performance is less good. First, the improvement resulting from our method when applied to detection of common SNPs (MAF>5%) was smaller than for other SNPs, simply because, being common, such SNPs are likely to be included in the reference haplotypes under just about any sampling scheme. More importantly, we note a slight degradation of performance of our method for rarer SNPs. For this reason, if such SNPs are the focus of the study at hand, we also present results for a modified version of our algorithm, designed to better detect rarer SNPs.
There might be a concern that methods that lean on coalescent theory in its simplest form (e.g., we derive results for expected TMRCA based on a neutral, unstructured coalescent), or which exploit a UPGMA tree as an approximation to a more complex underlying ARG, might not work so well for longer regions, or if there is population structure or other real-life complications. Application to a range of simulated datasets suggest the former concern is not well-founded, while application to the 1000GP data suggest that our method works well in the ‘real world’.
Of course, there are numerous other questions associated with the design of a sequence-based follow-ups to an existing GWAS study. For example, which regions should we sequence and at what depth of coverage? And how far around a putative association should we sequence in order to be confident of discovering other associated loci (or aggregations of rare variants that might be associated with phenotype)? The design of follow-up to GWAS hits is an active area of research for many groups, including our own, and the literature related to this issue is going to grow rapidly over the immediate future. In this paper we focus on one specific aspect of such a design, how to choose the individuals for sequencing, but we would expect that an informed choice of exactly which haplotypes to sequence will positively impact the power of the resulting data with respect to each of the other, related questions.
Figure 11.
Illustration of notation used to derive TMRCAs. Blue lines indicates wild-type lineages. Red lines indicate mutant lineage. The green line indicates the lineage on which the mutant allele appeared. Here, γ = 2 and δ = 4.
Acknowledgments
The authors gratefully acknowledge funding from the NIH and NSF through awards MH084678 and HG005927.
6 Appendix
In this appendix we describe how the expected coalescent time of two alleles is computed. This generalizes a result of Wiuf and Donnelly [1999]. It requires substantial, and rather ugly notation, which we summarize in Table 1, maintaining consistency with their paper where possible.
Table 1.
The notation
| n | the number of haplotypes. (at the current time) | |
| nw | the number of wild-type haplotypes. (at the current time) | |
| nm | the number of mutant haplotypes. (at the current time) | |
| i | index of coalescent events. | |
| τi | time at the coalescent event with index i. (from the current time) | |
|
|
the number of wild-type lineages at the coalescent event with index i. | |
|
|
the number of mutant lineages at the coalescent event with index i. | |
| γ | the index of the MRCA of all mutant lineages. | |
| δ | the index of the coalescent event between the mutation lineage and the wild-type lineage. | |
|
|
a coalescent event that involves two mutant lineages at index i. | |
|
|
a coalescent event that involves two wild-type lineages at index i. | |
|
|
the coalescent time (TMRCA) of two randomly chosen mutant haplotypes given nm. (and similarly for mutant/wild-type and for wild-type/wild-type.) |
In a coalescent genealogy of n haplotypes at a locus of interest, x say, in which nm haplotypes carry the mutant allele at that locus, let i denote the index of the coalescent event node. Here we index events on the tree counting from the bottom, so the first coalescence has index 1, the second has index 2, etc. Now let τi be the time at which the node with index i appears (where τ = 0 at the bottom of the tree), be the number of the lineages that are of the mutant type at that locus at time τi, and be the number of lineages that are the wild-type at τi (so ). We then define γ to be the index of the coalescent event corresponding to the MRCA of all mutant lineages at x, and δ to be the index of the first coalescent event to involve the MRCA of the mutant lineages and some other non-mutant lineage (i.e., it is the immediately ancestor to the lineage on which the mutation event occurred at this locus - the mutation is assumed to occur only once).
Let be the coalescent time (TMRCA) of two randomly chosen mutant haplotypes given nm. Wiuf and Donnelly [Wiuf and Donnelly, 1999] derived the the probability that the next event was a coalescent event between mutant lineages given γ (Lemma 3 of their paper) and the distribution of as a function of i and nm (Corollary 4). They also derived the distribution of γ (equation (16) of their paper). Using those equations, we can compute the conditional probability of a coalescent event between mutant lineages at index i as:
where
And the expected value of can be derived as
where E(τi | n) is computed using the standard coalescent model. For more details, see Wiuf and Donnelly [1999].
We extend this work to compute the expected coalescence time of two wild-type haplotypes ( ) and one wild-type and one mutant lineage ( ). We being with the former.
After the MRCA of all mutant lineages is reached at index γ, there are n − γ − 1 wild-type lineages and one lineage from the MRCA of the mutant lineages, (we call this latter line the “mutation lineage” since it is where the mutation event happened). Let δ be the index of the coalescent event at which the mutation lineage coalesces with a wild-type lineage. The conditional probability of δ given γ and n is then computed as
We now compute the probability that the coalescent event at index i involves two wild-type lineages and results in there being remaining wild-type lineages, conditional on γ, n and nm:
We compute this separately for each of three cases, as follows:
- For i<γ (i.e., there are at least two surviving mutant lineages at index i):
- For γ< i < δ (i.e., the MRCA of the mutant alleles has already occurred but the mutation lineages has not yet coalesced with a wild-type lineage):
- For δ<i (i.e., There are only wild-type lineages after the coalescence of the mutation lineage):
The expected value of is then derived as
Last, we compute the expected coalescent time ( ) between one randomly chosen haplotype with the mutant allele and another with the wild-type allele. At index δ, there are n − δ wild-type lineages and no mutant lineages. We break this calculation into two cases.
-
For δ = n − 1:
Here, δ is the root of the tree, and it follows that all haplotypes with the mutant allele must coalesce with any wild-type alleles at the root. This corresponds to term (1) of the equation below.
-
For δ < n − 1:
The mutant lineage has a MRCA with one of the wild-type lineages at index δ, and will also have MRCAs with other wild-type lines at other indices between δ and n − 1. We break this into three sub-cases:
the MRCA between the wild-type lineage and the mutant lineage occurs at δ: This corresponds to term (2) below.
the MRCA between the wild-type lineage and the mutant lineage occurs at index δ < ε < n − 1. This corresponds to term (3) below.
the MRCA between the wild-type lineage and the mutant lineage occurs at index n − 1, the root of the tree. This corresponds to term (4) below.
For the subcase 2(b), the probability that one of the remaining wild-type lineages has a MRCA with the mutation lineage at index ε is
It then follows that the expected valued of is derived as follows:
| (1) |
| (2) |
| (3) |
| (4) |
Contributor Information
Chul Joo Kang, Dept. of Preventive Medicine, Keck School of Medicine, USC, Los Angeles, California 90089, USA.
Paul Marjoram, Dept. of Preventive Medicine, Keck School of Medicine, USC, Los Angeles, California 90089, USA.
References
- 1000 Genomes Project Consortium. A map of human genome variation from population-scale sequencing. Nature. 2010;467(7319):1061–73. doi: 10.1038/nature09534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffiths R. The frequency spectrum of a mutation, and its age, in a general diffusion model. Theor Popul Biol. 2003;64(2):241–251. doi: 10.1016/s0040-5809(03)00075-3. [DOI] [PubMed] [Google Scholar]
- Griffiths R, Marjoram P. Ancestral inference from samples of dna sequences with recombination. J Comput Biol. 1996;3(4):479–502. doi: 10.1089/cmb.1996.3.479. [DOI] [PubMed] [Google Scholar]
- Griffiths R, Tavaré S. The age of a mutation in a general coalescent tree. Stoch Models. 1998;14:273–295. [Google Scholar]
- Howie BN, Donnelly P, Marchini J. A exible and accurate genotype imputation method for the next generation of genome-wide association studies. PLoS Genet. 2009;5(6):e1000529. doi: 10.1371/journal.pgen.1000529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson R. Properties of a neutral allele model with intragenic recombination. Theor Popul Biol. 1983;2(23):183–201. doi: 10.1016/0040-5809(83)90013-8. [DOI] [PubMed] [Google Scholar]
- Li B, Leal SM. Methods for detecting associations with rare variants for common diseases: Application to analysis of sequence data. Am J Hum Genet. 2008;83(3):311–321. doi: 10.1016/j.ajhg.2008.06.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Willer CJ, Ding J, Scheet P, Abecasis GR. MaCH: using sequence and genotype data to estimate haplotypes and unobserved genotypes. Genet Epidemiol. 2010;34(8):816–834. doi: 10.1002/gepi.20533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu DJ, Leal SM. A novel adaptive method for the analysis of next-generation sequencing data to detect complex trait associations with rare variants due to gene main effects and interactions. PLoS Genet. 2010;6(10):e1001156. doi: 10.1371/journal.pgen.1001156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madsen BE, Browning SR. A groupwise association test for rare mutations using a weighted sum statistic. PLoS Genet. 2009;5(2):e1000384. doi: 10.1371/journal.pgen.1000384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neale BM, Rivas MA, Voight BF, Altshuler D, Devlin B, Orho-Melander M, Kathiresan S, Purcell SM, Roeder K, Daly MJ. Testing for an unusual distribution of rare variants. PLoS Genet. 2011;7(3):e1001322. doi: 10.1371/journal.pgen.1001322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson NJ. How old is the most recent ancestor of two copies of an allele? Genetics. 2005;169(2):1093–1104. doi: 10.1534/genetics.103.015768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sokal R, Michener C. A statistical method for evaluating systematic relationships. The University of Kansas Scientific Bulletin. 1958;38:1409–1438. [Google Scholar]
- Wiuf C, Donnelly P. Conditional genealogies and the age of a neutral mutant. Theor Pop Biol. 1999;(56):183–201. doi: 10.1006/tpbi.1998.1411. [DOI] [PubMed] [Google Scholar]
- Yang J, Benyamin B, McEvoy BP, Gordon S, Henders AK, Nyholt DR, Madden PA, Heath AC, Martin NG, Montgomery GW, Goddard ME, Visscher P. Common SNPs explain a large proportion of the heritability for human height. Nat Genet. 2010;42(7):565–569. doi: 10.1038/ng.608. [DOI] [PMC free article] [PubMed] [Google Scholar]