Abstract
Genomic footprinting has emerged as an unbiased discovery method for transcription factor (TF) occupancy at cognate DNA in vivo. A basic premise of footprinting is that sequence-specific TF-DNA interactions are associated with localized resistance to nucleases, leaving observable signatures of cleavage within accessible chromatin. This phenomenon is interpreted to imply protection of the critical nucleotides by the stably bound protein factor. However, this model conflicts with previous reports of many TFs exchanging with specific binding sites in living cells on a time scale of seconds. We show that TFs with short DNA residence times have no footprints at bound motif elements. Moreover, the nuclease cleavage profile within a footprint originates from the DNA sequence in the factor binding site, rather than from the protein occupying specific nucleotides. These findings suggest a revised understanding of TF footprinting, and reveal limitations in comprehensive reconstruction of the TF regulatory network using this approach.
Introduction
Site specific binding of transcription factors to regulatory elements forms the genetic basis for promoter activation and cell selective gene regulation. Direct recognition of primary DNA sequence elements is now an assumed property for most regulatory proteins. Early studies (Galas and Schmitz, 1978) found that the DNA elements to which these factor bind are selectively resistant to nuclease digestion, leading to the concept of a protein induced footprint on the DNA. This phenomenon was later extended to the identification of protein localization events in nuclei (Church et al., 1985; Jackson and Felsenfeld, 1985; Zinn and Maniatis, 1986), and whole cells (Becker et al., 1987), and has been frequently utilized to characterize factors acting at eukaryotic regulatory elements.
With the advent of deep sequencing methodology, the detection and characterization of nuclease resistant footprints becomes possible at an unparalleled level of sensitivity and resolution (Boyle et al., 2011; Hesselberth et al., 2009; Neph et al., 2012b; Henikoff et al., 2011). Digital genomic footprinting (DGF) is emerging as a major tool to identify proteins associated with specific enhancer or promoter structures. Throughout the evolution of this methodology, it has been assumed that the protein responsible for the footprint prevents nucleolytic attack on the protected nucleotides by simple steric blocking of the nuclease through stable DNA binding (Jackson and Felsenfeld, 1985). Furthermore, it is generally argued that the nuclease digestion pattern observed within the footprint results from differential protection of nucleotides contacted by the bound protein. Thus, the cleavage “signature” is thought to be induced at the binding site by the bound protein.
This interpretation of footprint profiles conflicts fundamentally with studies on the residence times for DNA binding proteins in living cells. Direct observation of site specific binding of a transcription factor to its response element in living cells led to the surprising discovery that the glucocorticoid receptor residence time on GRE’s is in the range of 10 sec. (McNally et al., 2000). Numerous other factors have been studied subsequently, with the general conclusion that many site-specific DNA binding proteins are moving rapidly on and off the template (Sprague et al., 2004; Bosisio et al., 2006; Stasevich et al., 2010; Gebhardt et al., 2013; Poorey et al., 2013) [see (Mazza et al., 2012) and (Voss and Hager, 2014) for review].
Resolving this conundrum is central to our understanding of transcription factor function. Genomic studies describe signals averaged across large cell populations, and by their nature mask complexity on molecular time scales. Real time analyses of factor-chromatin interactions, either in living cells (McNally et al., 2000), or through in vitro reconstitution approaches (McKnight et al., 2011; Nagaich et al., 2004; Kassabov et al., 2002), often reveal dynamic movement undetected in population-based experiments.
We have reexamined the issue regarding genome-wide nuclease cleavage patterns. Using a novel footprint detection algorithm, we find that the depth of protection conferred by a given factor is generally correlated with the published binding residence time of the factor. Factors with very short residence times have minimal, often undetectable, depth of protection, whereas factors with relatively long binding times produce extensive protection. Furthermore, there is often no correlation between extent of binding at a given site measured by ChIP-seq analysis, and the presence or absence of a detectable footprint at factor-specific sequence elements. Finally, we show that the selective digestion profiles associated with DNA footprints result not from protection by the bound protein, but rather from the molecular structure of the DNA itself. These cleavage signatures are invariably observed in digestion profiles either for total chromatin or for deproteinized DNA. These findings are consistent with the dynamic model of factor action that emerges from living cell studies, and provide a most plausible explanation of the site occupancy issue.
Results
Identification of localized nuclease resistant elements
We sought to evaluate the capacity of digital genomic footprinting (DGF) to predict individual transcription factor binding events for a mammalian genome. “Footprints” are classically defined as regions relatively protected from enzymatic cleavage within DNase I hypersensitive sites (DHSs). An accurate DGF analysis presents significant technical challenges. First, a highly enriched (low-background) DNase-seq sample must be sequenced at great depth to allow reliable detection of locally protected regions within a given DHS. Therefore, only deeply sequenced data sets were included for analyses here, as in previous studies (Neph et al., 2012b). Another limitation of DGF arises from inferring the relevant transcription factor based on the underlying DNA sequences and matches to known TF motifs. Such indirect determination is problematic for TFs with poorly characterized sequence motifs, or those in a large family of TFs sharing motif preferences. We avoided these complications by limiting our analyses mostly to TFs with well characterized sequence binding motifs, allowing unambiguous assignment of TFs based on DNA sequences at observed footprints. Moreover, we located genome wide occurrences of putative binding elements using high confidence position weight matrices generated from ChIP-seq peaks. Because of the binding motif-centric nature of footprinting, all DGF analyses in this study exclude indirect DNA binding of TF via binding to another TF, thus minimizing false negative cases in binding prediction. Finally, a major hurdle in DGF exists due to a dearth of fast and robust computational methods that can be used to search and find footprint candidates from DNase-seq data. DGF was originally applied to the yeast genome which allows a more accurate cleavage profile because of its small genome size (Hesselberth et al., 2009; Chen et al., 2010). Subsequently, computational detection of footprint candidates has been performed on the mitochondrial genome and the entire human genome (Mercer et al., 2011; Neph et al., 2012a; Neph et al., 2012b; Piper et al., 2013). However, the algorithms used in previous studies are either inefficient for mammalian genomes, or not publicly available, leaving the general community without proper computational tools.
To address this issue, we have developed DNase2TF, an efficient footprint detection program. It searches for relatively protected regions within DNase I hypersensitive sites and generates a set of footprint candidates at a preset FDR threshold (Supplemental Information, Figure 1 A and B; Figure S1). Starting with an empirical set of candidate regions based on raw cut counts, the algorithm proceeds by iterating two basic steps: I) assessing the significance of cut depletion for all regions in the current set and ii) deciding whether to merge two closest neighboring regions for improved significance of depletion (Supplemental Information, Figure 1B). DNase2TF provides a marked gain in computational speed, scanning DHSs in a mammalian genome for footprint candidates in minutes (Table S1). Long computation times would render analysis of multiple large-genome data sets difficult (Table S1). We achieved fast computation not only by software engineering to maximize efficiency of computation, but also by conceptual simplification of the search algorithm: empirical selection of seed regions and rapid successive merging based on rigorous statistic for local depletion. Interestingly, our simplification strategy results in comparable or even higher prediction accuracy relative to published algorithms (see below).
Poor prediction of TF binding by genomic footprinting
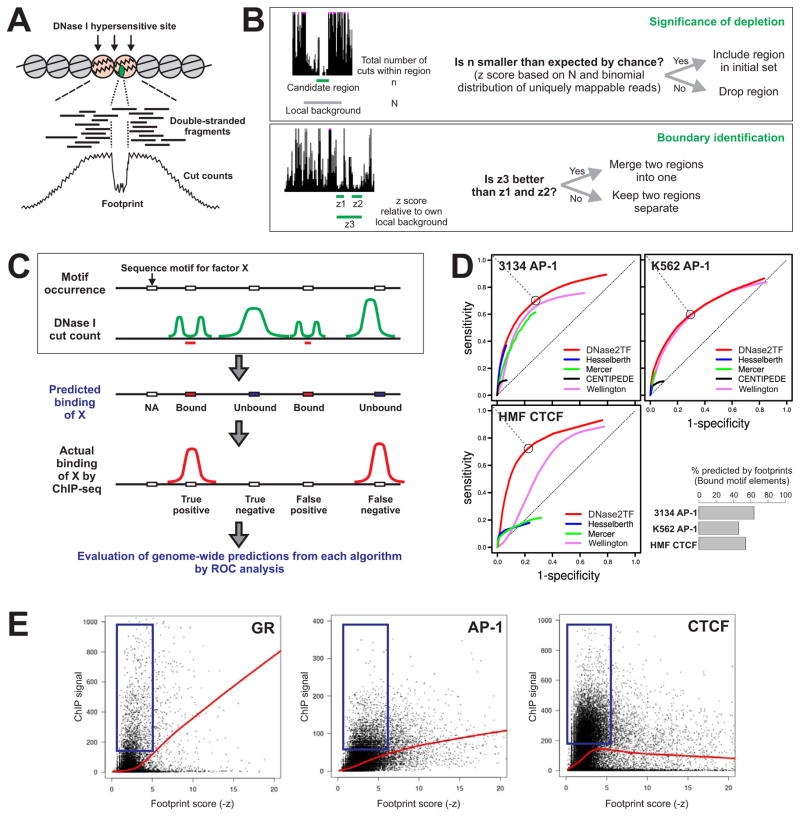
We used DNase-seq data sets from ENCODE (Thurman et al., 2012) and the 3134 mouse mammary cell line (John et al., 2011; Biddie et al., 2011) as reference data in a blind testing of footprint-based prediction of transcription factor binding. Such a test would directly examine the extent to which the presence of footprints over a cognate sequence motif is predictive of actual binding for a transcription factor. Figure 1C illustrates this validation framework: First, based on sequence occurrence for a given motif and DNase-seq data alone, prediction for binding is made for each sequence element. Those that have detectable footprints are predicted to bind and those without a footprint are predicted to be unbound by the factor. Then the outcome of predictions is measured against the binding regions from the ChIP-seq data for the particular transcription factor. The prediction accuracy across all possible footprint detection stringency is then assessed by ROC analysis. A high curve far above the diagonal indicates a successful predictor, whereas a random predictor produces a curve that is close to the diagonal.
Figure 1. Improved footprint detection by DNase2TF is still insufficient for accurate prediction of TF binding from computational scanning of DNase I hypersensitive sites for transcription factor footprints as regions of local protection from cleavage.
(A) Illustration of key procedures in genome-wide footprinting: DNase I digestion -> deep sequencing of released fragment ends -> nucleotide-level calculation of cut counts. (B) Basic steps of the DNase2TF footprint detection algorithm. Statistical significance of local cut count depletion is assessed by a binomial z score using a local background window centered at the candidate region. For boundary identification, the initial set of candidate regions goes through an iterative merging process to identify the regions that produce the most significantly cut-depleted regions. For a full description of the algorithm, see Methods. (C) Framework for transcription factor binding prediction and ROC analysis. For each algorithm, prediction about transcription factor binding is made based on the cut count profile for each binding motif occurrence that resides within a DNase I hypersensitive site. The bottom row illustrates how the ChIP-seq data is used only after the prediction step to evaluate the accuracy in terms of false positives, false negatives, etc. (D) ROC analysis results from DNase2TF and other methods. The prediction framework was applied to our algorithm and previously published algorithms using the DNase-seq and c-Jun (AP-1 subunit) ChIP-seq data from the mammary cell line 3134 (- Dex) (top left) or from ENCODE K562 (top right). Comparison was also performed using the DNase-seq and CTCF ChIP-seq data on HMF from ENCODE (bottom). The open circle on a DNase2TF ROC curve indicates the closest point from the upper left extreme, a trade-off between sensitivity and specificity, which is used in the bar plot on bottom right. Given a particular z score threshold, the percentage of bound motif elements (within ChIP peaks) predicted by footprinting is shown for each of the three data sets in the ROC plots. (E) The relationship between ChIP signal (maximum tag density over binding site) and the footprint score for all motif elements in mm9 identified as footprint candidates (FDR-unthresholded, z < 0). N: 12,742, 27,331, 32,732 for GR, AP-1, CTCF, respectively. The GR ChIP and DNase data set is from Dex-treated mouse mammary cell line 3134 (John et al., 2011). The AP-1 and CTCF ChIP and DNase data sets are from the unstimulated 3134 cells (Biddie et al., 2011). High footprint scores (-z) correspond to strong depletion of cleavage by DNase I. The red trend curves are from Lowess fitting of all the data points. The blue boxes indicate elements that do not conform to the trend curves. (See also Figures S1–S2)
We compared the prediction outcomes from our algorithm DNase2TF and three previously published footprint detection methods (Hesselberth et al., 2009; Mercer et al., 2011; Piper et al., 2013) using the reference data for TFs with well characterized sequence motifs and binding profiles. We also tested a transcription factor binding prediction program that utilizes information from motif sequences and conservation in addition to DNase-seq (Pique-Regi et al., 2011), Another method could not be evaluated in parallel due to lack of the software portability (Chen et al., 2010). Despite our simple search strategy, when predictive capacity was compared, the footprints detected by our algorithm were more successful in capturing binding events observed from ChIP-seq (Figure 1D; Figure S2B). In addition to the TFs used for the rigorous testing, we also performed a broad location analysis of DNase2TF-detected footprint candidates and found that they were highly enriched for known TF motif occurrences (Figure S2A). This indicates that more exhaustive search algorithms such as those included in our comparison do not necessarily yield more accurate predictions for actual binding events.
Unexpectedly, a major difficulty in predicting binding based on footprints was revealed by the incomplete ROC curves generated by all the algorithms tested. This is caused by the inability of the predictors to retrieve all bound elements even at the level of minimal specificity. That is, no matter how low the threshold for calling footprints is, the footprint-based prediction of binding does not capture all bound elements. Using the mammary data for example (Figure 1D), at the level of 90 % specificity (0.1 on the x axis), less than half of binding sites have footprints detected by DNase2TF (~0.44 on the y axis), while 56% of binding events are missed. Similar results were obtained using ENCODE DNase-seq and ChIP-seq data on K562 or HMF (Figure 1D; Figure S2B). Although some false positives (footprint but no ChIP peak) might be expected in our analysis (Schmiedeberg et al., 2009), it was actually the false negatives (ChIP peak but no footprint) that underlies the poor prediction of ChIP sites by footprinting. The false negatives cannot be explained by indirect binding of factors, because our framework begins with putative DNA elements for direct binding and does not attempt any prediction for sites without the sequence motif. Deeper sequencing may not significantly improve the prediction, since a 4-fold change in sequencing depth has only a marginal effect in detection sensitivity (Figure S2C). Nonetheless, DNase2TF performed best in all comparisons with maximal sensitivity (upper extremes of the curves) reaching up to 90%. This result prompted us to look more closely at the relationship between ChIP-seq signal intensity and footprint score. Surprisingly, we found little correlation between ChIP and extent of local depletion reported by the footprint score (Figure 1E). Although the trend curves were similar to those previously reported by ENCODE (Neph et al., 2012b), these plots indicate that presentation of curve fits only is highly misleading because it neglects a large fraction of bound sequence elements without footprints (Figure 1E, boxes).
Nuclease digestion signatures are present in the absence of the binding protein
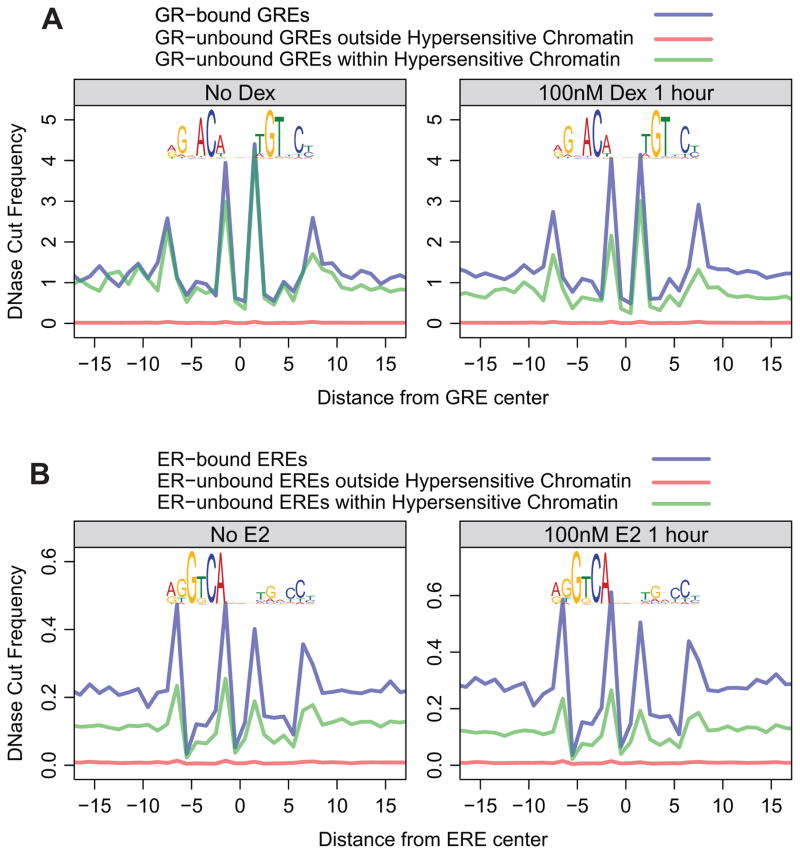
We next examined the cleavage patterns at bona fide direct binding sites to find additional characteristics accompanied by transcription factor binding. We chose the glucocorticoid (GR) and estrogen (ER) receptors because these factors bind to target elements only after hormone treatment and are thus ideal for distinguishing specific effects at the bound elements before and after binding. In fact, GR is mostly in the cytoplasm in the absence of the hormone dexamethasone. Both factors have distinct cut profiles over the nucleotide length of their sequence motif at binding sites observed in hormone-treated cells (Figure 2). However, nearly identical GR- and ER-associated profiles were also observed over GRE and ERE sequence elements at sites with no detectable binding. The similarity becomes more striking in the relative cut intensity scale normalized for the differential hypersensitivity to DNase I in bound versus unbound sites (Figure S3). It is possible that cut profiles over unbound sites might be contaminated by weakly bound sites that are undetected in ChIP-seq analysis. To obtain cleaner profiles at sites with no protein-DNA interactions, we assessed the cut profiles over these sites in untreated cells where the factors are either unbound (ER) or absent from the nucleus (GR). Surprisingly, we found that the same cut profiles exist even before hormone treatment, when the factors do not occupy these sites (Figure 2). These results demonstrate that the “DNA cut signature” over TF binding motif is not caused by the protein-DNA interaction, as interpreted previously. The signature is clearly detected in the absence of the binding protein.
Figure 2. DNase signatures precede nuclear receptor binding and do not result from protein-DNA interactions.
(A) GREs were classified into three classes: 1) overlapping with GR ChIP-seq peaks (transparent blue trace); 2) overlapping neither GR ChIP-seq peaks nor DNase hotspots (transparent red trace); 3) not overlapping with GR ChIP-seq peaks, but overlapping DNase hotspots (transparent green trace). The motif logos above the traces are composite GR binding motifs derived from ChIP-seq data. Each trace shows the average cut frequency at each position between nucleotides. The left panel shows that these signatures are present prior to GR binding to DNA; the right panel shows that these traces do not change upon GR-binding. ChIP-seq and DNase-seq data are from the mammary 3134 cell line. (B) The same analysis was performed for ER in the bottom panels. The MCF-7 ChIP-seq and DNase-seq data are from Guertin et al. (submitted) and ENCODE. (See also Figure S3)
DNA cut signatures are found in deproteinized DNA
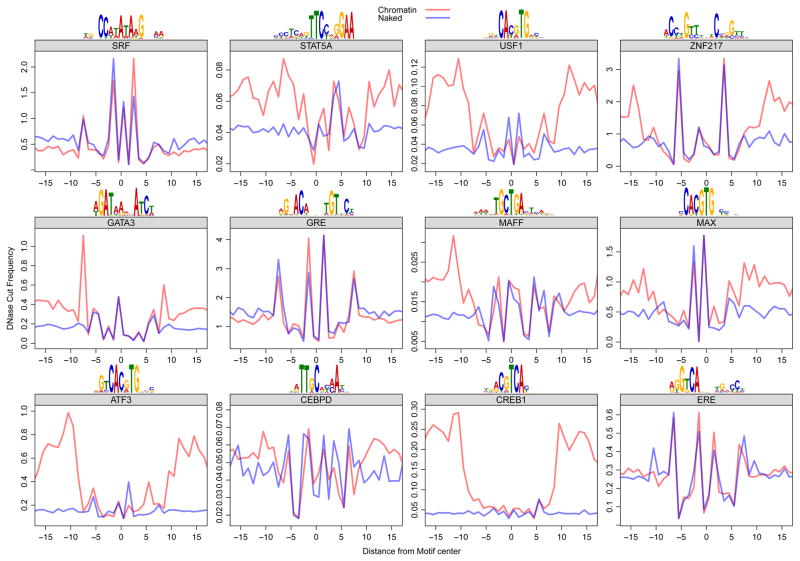
To test the hypothesis that the DNase signatures found at the site of TF binding were a result of DNase cut specificity and to rule out the possible involvement of other proteins, we analyzed DNase-seq data generated from cutting DNA that had been deproteinized (Lazarovici et al., 2013). For each TF motif, we compared the composite naked DNA cut frequency profile at sequence elements found genome wide to the in vivo profile at elements bound by their respective TF (using standard chromatin DNase-seq data). We found that the naked DNA composite cut profile is essentially identical to the chromatin cut profile of ChIP-seq validated binding sites (Figure 3). This is true for an array of TFs with distinct consensus binding motifs. The USF1 and SRF profiles match earlier generated profiles for these factors. However, previous investigators reported (Neph et al., 2012b) that the specific DNase signature profiles within the accessible regions of chromatin reflect the crystal structure of the protein-DNA complex, and concluded that the signatures result from direct protection by bound proteins. Notably, the composite profiles for chromatin versus naked DNA often display relatively increased cleavage in flanking regions outside the TF binding motif for many of the factors, albeit to a varying degree. This is consistent with a model wherein the footprint depth results directly from TF-DNA interactions, unlike the DNase signature that is found at the DNA motif. However, many factors (GR, ER, SRF, CEBPD) did not exhibit any signs of a footprint, despite the fact that the chromatin traces are composites from ChIP-seq-identified binding sites for each of the factors.
Figure 3. DNase digestion of deproteinized (naked) DNA and TF-bound chromatin reveals the same cut signatures at consensus binding sites.
For each factor, we used genomic ChIP-seq data (Gerstein et al., 2012) to identify the bound regions in the genome. We used the position weight matrix for each factor to infer the precise position of TF binding within the ChIP-seq peaks. The red trace shows the average DNase cut frequency at each position over all TF motif sites within ChIP-seq peaks for that particular TF. The blue trace shows the scaled (to equalize the maximum and minimum y values across profiles over each motif) average DNase cut frequency at all TF motif sites in the genome, noting that the DNase data was derived from naked DNA digestion. The traces flanking the motif are divergent, but the traces largely overlap within the consensus-binding site for each TF.
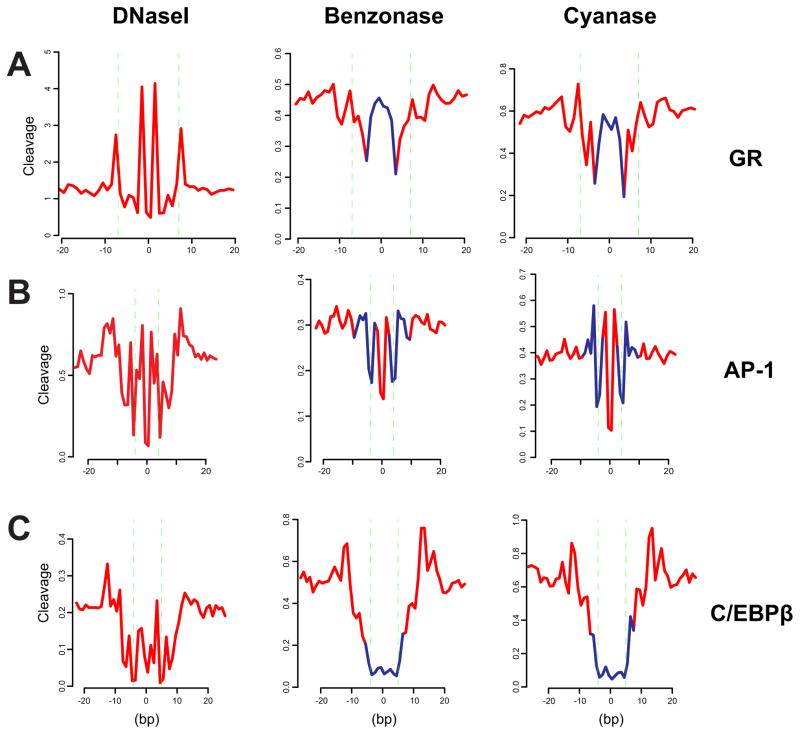
To further characterize the nature of DNA cut signatures, we examined the cleavage profiles generated with other nucleases. Genome wide chromatin accessibility has also been studied with benzonase and cyanase; nuclease hypersensitivity profiles obtained with these enzymes are quite similar to those produced with DNase I (Grontved et al., 2012). We found that the average cleavage profiles for these enzymes at bound motif elements are very different from those obtained by DNase I (Figure 4). This result is consistent with the model that the DNase signature reflects the DNA cleavage specificity for a given enzyme, rather than specific nucleotide protection by a bound protein.
Figure 4. The DNA cut signature depends on the cleaving enzyme.
Benzonase and Cyanase cleavage profiles at GR, AP-1, or C/EBPβ motifs were generated and compared next to the corresponding profile from DNase I. Benzonase and Cyanase data are from mouse liver (Grontved et al., 2012). (A) For GR, average cut profiles were computed over 6324 and 7670 bound motif sites from 3134 cells and liver cells, respectively. (B) Because AP-1 ChIP-seq data is not available for mouse liver, the comparison was instead made over AP-1 motif sites within hypersensitive sites (hotspots called in each sequencing data). The profile over hypersensitive sites is nearly identical in relative intensity to that over bound motif sites for 3134, where c-Jun ChIP-seq is available. For 3134 (-Dex), average cut profile was computed over 6708 unbound motif sites within DNase I hotspots. For Benzonase liver data, average profile was computed over 6300 motif sites within Benzonase hotspots. For Cyanase liver data, average profile was computed over 5745 motif sites within Cyanase hotspots. (C) For C/EBPβ, average DNase I cut profile was computed over 7964 bound motifs from 3T3-L1 cells 4 hr after induction (Siersbaek et al., 2011). For Benzonase and Cyanase liver data, average profiles were computed over 11133 bound motifs (-Dex) (Grontved et al., 2013). Blue segments in a Benzonase/Cyanase profile indicate deviations from the corresponding DNase I cleavage signature.
DNA cut signatures can be predicted from tetranucleotide frequency
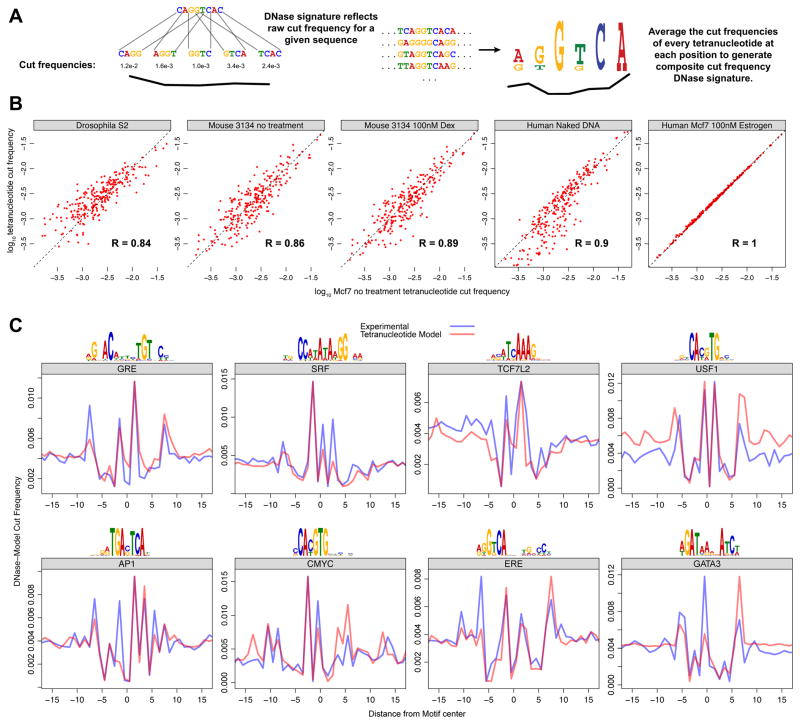
The identical appearance of naked DNA and chromatin cut profiles at TF binding sites suggests that sequence alone may be sufficient to derive the DNase signature. We posited that this DNase signature could be predicted directly from the sequence-specific cutting frequency of DNase for deproteinized DNA, for any set of DNA sequences (Figure 5A). To this end, we examined the DNase cleavage patterns for many experiments. We found that the tetranucleotide cut frequency, the two nucleotides that flank each side of the DNase cut, is highly correlated between experiments, treatments, and even organisms (Figure 5B). This measurement of DNase sequence preference indicated that the range of genome wide tetranucleotide cut frequency for a given experiment varies over two orders of magnitude (Figure 5B). Next we developed an algorithm (seqToSign - Figures S4 and S5) that predicts the DNase signature for a given TF motif from the sequence preference patterns of DNase I. In brief, the composite profile is generated by weighting the cut frequency of each tetranucleotide found in a given position by the number of occurrences of the tetranucleotides at that position (Figure S5). This model accurately predicts the jagged cut profile that would be present at each set of TF motif sites (Figure 5C). We also attempted to model the DNase signature using dinucleotide cut frequency and hexanucleotide cut frequency. The former was insufficient to model the DNase signature while the use of hexanucleotide cut frequency did not improve the model. This indicates that DNase cut specificity is largely determined by the four nucleotides that surround the cut site. Taken together, these findings further indicate that the DNA cut signatures that are observed at the sites of TF binding do not result from TF-DNA interactions.
Figure 5. DNase cut signatures of many TF motifs can be predicted from tetranucleotide preference for cleavage using seqToSign.
(A) For any given sequence, we expect that the relative DNase cut frequency at a particular site would directly reflect the genome wide experimental cut frequency for that particular tetranucleotide. For a set of sequences compiled to build a composite profile, the cut frequency for a given position is derived from the relative abundance of all the 256 possible tetranucleotides at that position. (B) Raw tetranucleotide cut frequency for DNase experiments are highly correlated, across diverse organisms and experimental treatments. The x-axis is the raw cut frequencies for all 256 tetranucleotides in Mcf7 cells. These correlate to the cut frequencies for DNase digestion of Drosophila S2 chromatin, 3134 mouse cell chromatin with and without dexamethasone treatment, naked DNA from IMR90 cells, and Mcf7 cells with the addition of Estrogen. (C) We compared the DNA cut signatures (model) predicted by seqToSign with the naked DNA (experimental) cut-profiles. As in Figure 4, we scaled the seqToSign traces such that each can be viewed relative to the experimental trace. (See also Figures S4–S5)
Footprint depth is related to the residence time of the binding factor
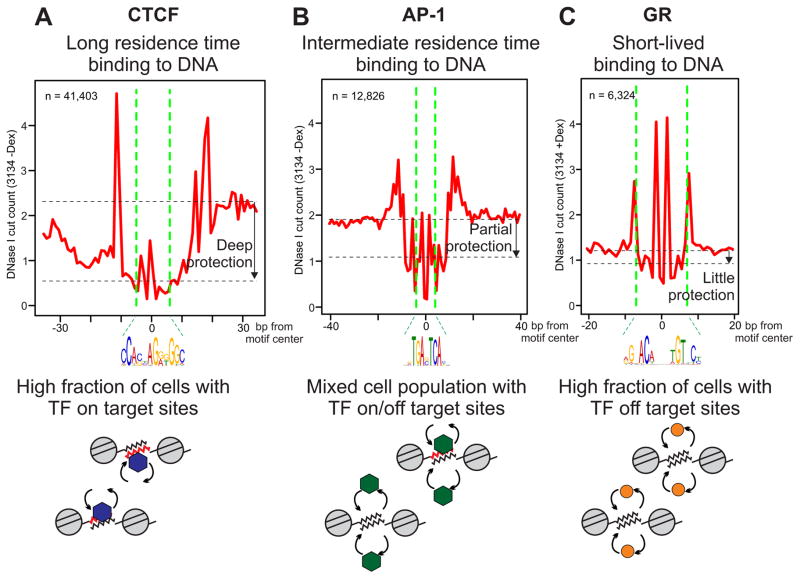
From surveying a large number of cleavage profiles for chromatin and naked DNA, it is evident that the central region of binding sites displays widely varying degrees of protection. In particular, GR and Sox2 manifest little or no protection (Figure 6C, Figure S6), which explains why DNase2TF, designed to detect significant protection from cleavage, fails to recover most of the bound motif elements that were observed in ChIP-seq. On the other hand, CTCF clearly conferred a pronounced protection on the bound DNA (Figure 6A), enabling de novo detection of a majority of directly bound sites by DNase2TF (e.g. 70% sensitivity at 80% specificity of prediction, Figure 1D). The yeast Rap1 also produces deep footprints at bound motif elements (Figure S6). Interestingly, these proteins have dramatically longer residence times on DNA than GR based on published binding kinetics measured in vivo. GR (McNally et al., 2000; Mazza et al., 2012) and Sox2 (Chen et al., 2014) bind to DNA transiently in living cells with a short residence time in the range of 6–12 seconds. Many other transcription factors share similar, or faster, binding kinetics compared to GR. These include NF-κB, p53, and ER, all of which exhibit rapid exchange dynamics with DNA (Bosisio et al., 2006; Sharp et al., 2006; Mazza et al., 2012). In contrast, CTCF behaves quite differently from most transcription factors due to the multitude of zinc finger domains that are utilized for stabilizing interactions with the target DNA. The binding kinetics of CTCF and Rap1 are two orders of magnitude slower than those of GR or NF-κB (Lickwar et al., 2012; Nakahashi et al., 2013). While GR and CTCF represent dramatically different mobilities, other factors fall between these two extremes. We observed that AP-1 binding motif elements tend to exhibit an intermediate level of protection (Figure 6B) that is readily detectable by DNase2TF. Similarly, CREB1 leaves noticeable footprints (Figure 3). The binding kinetics of AP-1 and CREB1 have been measured in living cells (Malnou et al., 2010; Mayr et al., 2005). Consistent with the intermediate level of footprinting, the binding kinetics of AP-1 and CREB1 were significantly slower than GR but faster than CTCF.
Figure 6. Depth of protection in TF footprints correlates with the residence time of binding.
The cut count profiles averaged over all bound motif elements (within ChIP peaks) for CTCF (A), AP-1 (B), and GR (C). n, the number of bound motif elements. Below each cut count profile, schematics show a mixture of chromatin templates from the population of cells that contribute to the DNase-seq experiment. The red DNA segment indicates TF-bound elements that are protected from cleavage by DNase I for the moment. CTCF exemplifies a TF with a long-lasting occupancy at cognate sequence elements, while GR is the opposite extreme known for its short residence time on target DNA in vivo. (See also Figure S6)
Discussion
The molecular mechanisms by which transcription factors bind to enhancers are central to our understanding of the regulation of gene expression (Guertin and Lis, 2013; Voss and Hager, 2014). In the past decade, genome-wide studies (primarily ChIP-seq) on cell populations and real time investigations (usually single cell approaches) have led to increasingly divergent models for factor-chromatin interactions. Population experiments are interpreted in terms of site specific factor binding over long time intervals, producing long range interactions that activate or repress promoters. Many living cell studies, however, suggest highly dynamic exchange events with very brief residence times. A primary line of argument supporting the “static” view of factor template interactions derives from classic footprinting experiments. It is argued that a footprint on the DNA requires a continuously bound protein to produce a nuclease resistant signature characteristic of the particular factor under study (Boyle et al., 2011; Bell et al., 2011; Neph et al., 2012b).
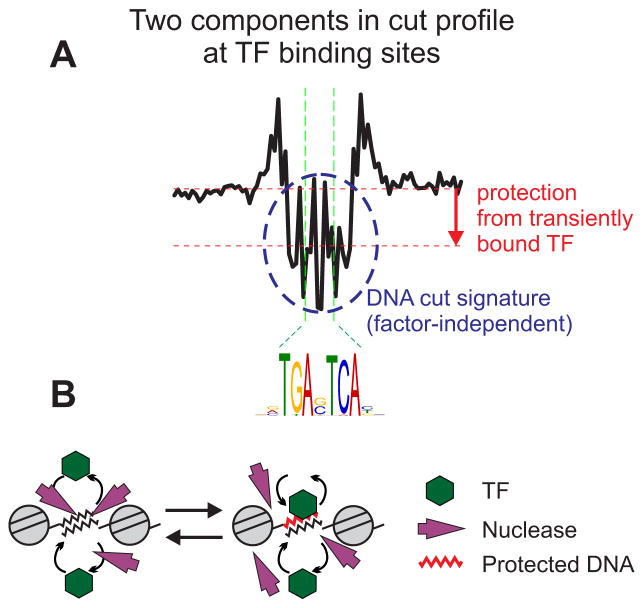
We propose a model which provides a potential resolution of this conundrum (Figure 7). We describe a general correlation between DNA binding kinetics and footprint depth (Figure 6; Figure S6). This phenomenon likely arises from competing events of dynamic factor binding and cleavage by DNase I. Any transcription factor binding reversibly to DNA with rapid on/off rates permits a time window for a nuclease to cleave the target DNA during the off period of the binding cycle. Furthermore, a DNase I treated sample comes from a heterogeneous population of unsynchronized cells, producing a snapshot of cleavage events at a given time. Therefore, observation of a deep protection from cleavage by a nuclease requires relatively stable binding of the transcription factor, such as with CTCF or Rap1, giving rise to a large fraction of the cells in a population with the factor occupying a target site at a given moment. However, in cases where the transcription factor has fast exchange kinetics with a short residence time on target DNA, a large fraction of cells in the captured sample must have the factor off a target DNA during a cycle of transient binding, thereby allowing DNase to cleave the site according to its sequence-inherent preference. Intermediate kinetics of binding results in a mixed population with a significant fraction of cells in which the factor occupies a target site while the remaining cells have the factor off the site at a given time. These findings prompt a re-interpretation of digital genomic footprinting results: a true factor-dependent “footprint” manifests in the protection depth, not in the nucleotide-level cut signatures, only for TFs with sufficiently long residence times on target DNA. Interestingly, adjusting the cut count profile for the observed tetramer bias did not significantly improve the prediction of TF binding (Figure S7), suggesting that the cut signatures and the footprint depth are two separable phenomena. We present a novel footprint search algorithm, implemented in DNase2TF, which allows efficient scanning of large genomes with comparable or better footprint detection accuracy in comparison to existing algorithms.
Figure 7. Revised model for the effect of TF binding in genomic footprinting.
(A) The AP-1 cut count profile is used to illustrate the two distinct components comprising a given DNase I cleavage profile. The local depletion relative to the flanking regions (downward arrow) signifies the protection conferred by TF binding whose dynamics may influence the depth of protection. The central DNA cut signature itself (dashed circle) is inherent to the DNA sequence and the enzyme chosen for the assay. (B) A model representing the competing actions of TFs and the nuclease which result in the two-component patterns detected in a genome-wide footprinting assay. The red DNA segment indicates a transiently protected motif element from dynamic TF binding. (See also Figure S7)
The second component of this dynamic view originates in the observation that the “DNA cut signatures” arise not from protection by a bound protein, but rather from the sequence preferences of the cleaving enzyme (Figures 3 – 5; Figures S4 and S5). Indeed, for nuclear receptors such as GR and ER, footprints with significant depth of protection are barely detectable in DNase-seq data, but the characteristic DNA cut signatures are quite pronounced (Figures 2 and 6). Furthermore, for all of the proteins we have examined, the cut signatures are clearly evident in deproteinized DNA. The algorithm described here, seqToSign, accurately models these signatures throughout the genome. These DNA elements are in fact the structures that site-specific DNA binding proteins recognize. This aspect of DNA structure has been recently reported as an artifact of DNase footprinting (He et al., 2014) but the dynamic basis of the footprint phenomenon was not elucidated.
We conclude that transcription factors manifest widely divergent interaction times with their recognition elements in chromatin. Protection against cleavage by nucleases results from the average time an exchanging protein is resident on the template. Several mechanisms have been advanced to explain the basis for these rapid exchange events, including chaperone action (Stavreva et al., 2004), proteasome degradation (Collins and Tansey, 2006; Kodadek et al., 2006), and factor mobility induced during ATP-dependent chromatin remodeling (Nagaich et al., 2004; Voss et al., 2011; Voss and Hager, 2014). An accurate model of transcription factor function will require an in depth understanding of the processes involved in these exchange phenomena.
Experimental Procedures
Receiver Operator Characteristic (ROC) analysis
Prediction for binding was made on motif occurrences within the initial search space (the set of FDR 1% DNase I hotspots), based on whether the element overlaps with a footprint candidate (with z score less than a threshold) by more than half the motif width. If an element coincides with a footprint this way and gets confirmed as factor-bound by ChIP-seq, then it is a true positive (TP). If a footprinted element does not overlap a ChIP-seq binding site, then it is a false positive (FP). If an element does not overlap a footprint but gets confirmed as factor-bound by ChIP-seq, then it is a false negative (FN). If it indeed lies outside of any ChIP-seq binding site, then it is a true negative (TN). The ROC curve displays prediction outcome over the entire spectrum of the sensitivity (= TP/(TP + FN)) and 1 – specificity (= FP/(FP + TN)) achieved by varying the prediction stringency. For DNase2TF, individual points on the ROC curve were generated by varying the z score threshold, starting with all the footprint candidates (without regards to FDR). For the other algorithms, p value threshold was varied from 0 to 1.
Enrichment analysis using known transcription factor binding motifs
We downloaded 213 motif matrices from the TRANSFAC (TRANSFAC® database 7.0 public 2005) database searched by the keyword ‘human’ and 76 matrices from JASPAR (http://jaspar.genereg.net/, core set downloaded on 2012-05-14). Downloaded frequency matrices were converted to a FIMO input format by the jaspar2meme (http://meme.nbcr.net/meme/doc/jaspar2meme.html) program with -pfm parameter. FIMO was run with the option --max-stored-scores 1000000 and motif occurrences were obtained at the default p value cutoff of 10−4 for each matrix. Performing this scan procedure for all 289 motif matrices resulted in 155,146,844 sites found by FIMO. By combining overlapping sites across the different motifs, we obtained 52,305,144 non-overlapping genomic regions (the union of motif occurrence sites from different matrices), referred to as ‘FIMO sites’. For each set of unthresholded footprint candidates from a detection method, we counted the number of footprint candidates overlapping a FIMO motif site by at least one nucleotide.
For a complete description of the algorithms, reference data sets, and analysis procedures, see Supplemental Experimental Procedures.
Supplementary Material
Figure S1 (related to Experimental Procedures). Cut count computation and DNase2TF algorithm. (A) Definition of cut count. The exact nucleotide position representing a DNase I cleavage event is defined consistently by assigning the 5′ base for a given dinucleotide encompassing a cut. The example shows two cleavage events observed by one read mapped on the reverse strand and by another mapped on the forward strand. The former results from a DNA fragment released at the dinucleotide GA, while the latter is from AG (both marked green, top track). The cut count track corresponds to the two events. (B) Flow diagram of DNase2TF. Necessary input information is shown at the top. The search space is the set of all DNase I hotspots pre-computed from the data. An alternative search space can be specified if desired. The dinucleotide bias is directly estimated from the data also, but could be generated from a different source.
Figure S2 (related to Figure 1). Performance of DNase2TF assessed by captured motif occurrences and dependence on sequencing depth. (A) Known transcription factor motifs are enriched in footprint candidates called by DNase2TF. Using the annotated human TF binding motif databases TRANSFAC and JASPAR, we assessed the overlap between putative footprints called using the ENCODE DNase-seq data on HMF or K562 by various methods and the genomic occurrences of all known motifs. DNase2TF without FDR thresholding captures more motif occurrences than the other methods (lower panels) with comparable enrichment levels as seen by proportions of footprints overlapping a motif occurrence (upper panels). (B) ROC analysis on additional TFs using ENCODE data. (C) The sequencing depth used is sufficient for evaluation of AP-1 binding prediction by ROC analysis. We performed a series of down-sampling of the full mammary 3134 DNase-seq dataset in Figure 1 and determined how the prediction accuracy is affected by the sequencing depth. Specifically, a random sample of given size was generated for each round of sub-sampling. From this sample, the set of DNase I hotspots was computed to define the initial search space for footprint detection. Note that, since footprint search is performed only on DHSs which themselves depend on sequencing depth, the total number of FDR-unthresholded footprint candidates decreases dramatically (from 2,791,566 for the full data of about 101 million reads to 334,956 for the 1 million-read sub-sampled data). DNase2TF was then applied and binding predictions were made based on footprints in the same manner as before. An ROC curve was generated for each sub-sampled data set. The resulting ROC curves show near-saturation of accuracy at the current depth of sequencing.
Figure S3 (related Figure 2). DNase signatures occur outside of chromatin. The same traces from Figure 2 are re-scaled to show that the DNase signature is present in each class of nuclear receptor motifs. The raw scales for each trace are shown to the left of the plot; the color of each scale corresponds to the color of the trace. Note that the traces are transparent so that the overlap can be visualized.
Figure S4 (related Figure 5). The tetranucleotide model outperforms dinucleotide and hexanucleotide models. A) We show the DNase signature traces of each model (di, tetra, and hexa) compared to experimental data. B) We compared the area between the DNase signatures derived from experimental data and either the tetranucleotide or hexanucleotide model. We used the Trapezoid Rule to integrate between the curves within the region that encompasses the motif sequence. Note that a smaller area indicates better performance. For each position within the motif, we compared the experimental and model-derived cut frequency by Pearson correlation coefficient. C) Comparison of all the models to experimental data, using the methods applied in panel B, shows that the tetranucleotide model performs best for each factor, with the exception of TCF7L2--the dinucleotide model performs best for TCF7L2.
Figure S5 (related Experimental Procedures). The seqToSign algorithm predicts DNase cut frequency from input sequences and tetranucleotide cut frequency. To generate the predicted cut frequency traces, sequences are first aligned on the TF motif. Next, a tetranucleotide DNase cut frequency table, with all 256 possible cut frequencies, is generated for each experiment. The frequency of each tetranucleotide is tallied for each position in the input DNA; this frequency is multiplied the corresponding genomic cut-frequency of that particular tetranucleotide. This value is averaged for all possible 256 tetranucleotides at this position. The process is repeated at each position along the x-axis.
Figure S6 (related to Figure 6). Additional TFs showing correlation between depth of TF footprints and the residence time of binding. The cut count pro les averaged over all bound motif elements (within ChIP peaks) for Rap1 (A) and Sox2 (B). n, the number of bound motif elements. (A) The yeast DNase data are from Hesselberth et al. 2009. The Rap1 binding sites are from Lickwar CR et al. Nature 2012. Rap1 motif sites were obtained using FIMO and the JASPAR PWM. (B) The mouse ES cell DNase-seq data are from ENCODE. Sox2 binding sites are from the ChIP-exo data in Chen J et al. Cell 2014. Sox2 motif sites were obtained using FIMO and a de novo discovered PWM from ChIP peaks.
Figure S7 (related to Figure 7). Adjusting the cut count for tetramer bias does not significantly improve prediction of TF binding. The cut count data were either left unadjusted, adjusted by the dimer bias (default setting of DNase2TF), or adjusted by the tetramer bias. The DNase and ChIP-seq data sets used are the same as in Figure 1, except for the additional GR ChIP-seq data for the 3134 cell line from John S. et al. Nature Genetics 2011.
Table S1 (related to Experimental Procedures). Computational speed of DNase2TF.
Table S2 (related to Experimental Procedures). Dinucleotide frequency of different nucleases.
Table S3 (related to Figure 1). ChIP-seq datasets used in the ROC analysis.
Acknowledgments
Extensive use was made of the NIH Biowulf cluster, a GNU/Linux parallel processing system for computational analysis; we acknowledge the NIH Helix Systems Staff for management of this system. This research was supported by the Intramural Research Program of the NIH, National Cancer Institute, Center for Cancer Research.
Footnotes
Author Contributions
The DNase2TF program was designed by M.H.S. and S.B. and implemented by S.B. The seqToSign program was designed and implemented by M.J.G. G.L.H. coordinated the project, and all authors interpreted the analysis results. M.H.S., M.J.G. and G.L.H. wrote the paper with contributions from S.B.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Becker PB, Ruppert S, Schutz G. Genomic footprinting reveals cell type-specific DNA binding of ubiquitous factors. Cell. 1987;51:435–443. doi: 10.1016/0092-8674(87)90639-8. [DOI] [PubMed] [Google Scholar]
- Bell O, Tiwari VK, Thoma NH, Schubeler D. Determinants and dynamics of genome accessibility. Nat Rev Genet. 2011;12:554–564. doi: 10.1038/nrg3017. [DOI] [PubMed] [Google Scholar]
- Biddie SC, John S, Sabo PJ, Thurman RE, Johnson TA, Schiltz RL, Miranda TB, Sung MH, Trump S, Lightman SL, Vinson C, Stamatoyannopoulos JA, Hager GL. Transcription factor AP1 potentiates chromatin accessibility and glucocorticoid receptor binding. Mol Cell. 2011;43:145–155. doi: 10.1016/j.molcel.2011.06.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bosisio D, Marazzi I, Agresti A, Shimizu N, Bianchi ME, Natoli G. A hyper-dynamic equilibrium between promoter-bound and nucleoplasmic dimers controls NF-kB-dependent gene activity. EMBO J. 2006;25:798–810. doi: 10.1038/sj.emboj.7600977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyle AP, Song L, Lee BK, London D, Keefe D, Birney E, Iyer VR, Crawford GE, Furey TS. High-resolution genome-wide in vivo footprinting of diverse transcription factors in human cells. Genome Res. 2011;21:456–464. doi: 10.1101/gr.112656.110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J, Zhang Z, Li L, Chen BC, Revyakin A, Hajj B, Legant W, Dahan M, Lionnet T, Betzig E, Tjian R, Liu Z. Single-molecule dynamics of enhanceosome assembly in embryonic stem cells. Cell. 2014;156:1274–1285. doi: 10.1016/j.cell.2014.01.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X, Hoffman MM, Bilmes JA, Hesselberth JR, Noble WS. A dynamic Bayesian network for identifying protein-binding footprints from single molecule-based sequencing data. Bioinformatics. 2010;26:i334–i342. doi: 10.1093/bioinformatics/btq175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Church GM, Ephrussi A, Gilbert W, Tonegawa S. Cell-type-specific contacts to immunoglobulin enhancers in nuclei. Nature. 1985;313:798–801. doi: 10.1038/313798a0. [DOI] [PubMed] [Google Scholar]
- Collins GA, Tansey WP. The proteasome: a utility tool for transcription? Curr. Opin Genet Dev. 2006;16:197–202. doi: 10.1016/j.gde.2006.02.009. [DOI] [PubMed] [Google Scholar]
- Galas DJ, Schmitz A. DNAse footprinting: a simple method for the detection of protein-DNA binding specificity. Nucleic Acids Res. 1978;5:3157–3170. doi: 10.1093/nar/5.9.3157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gebhardt JC, Suter DM, Roy R, Zhao ZW, Chapman AR, Basu S, Maniatis T, Xie XS. Single-molecule imaging of transcription factor binding to DNA in live mammalian cells. Nat Methods. 2013;10:421–426. doi: 10.1038/nmeth.2411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerstein MB, Kundaje A, Hariharan M, Landt SG, Yan KK, Cheng C, Mu XJ, Khurana E, Rozowsky J, Alexander R, Min R, Alves P, Abyzov A, Addleman N, Bhardwaj N, Boyle AP, Cayting P, Charos A, Chen DZ, Cheng Y, Clarke D, Eastman C, Euskirchen G, Frietze S, Fu Y, Gertz J, Grubert F, Harmanci A, Jain P, Kasowski M, Lacroute P, Leng J, Lian J, Monahan H, O’Geen H, Ouyang Z, Partridge EC, Patacsil D, Pauli F, Raha D, Ramirez L, Reddy TE, Reed B, Shi M, Slifer T, Wang J, Wu L, Yang X, Yip KY, Zilberman-Schapira G, Batzoglou S, Sidow A, Farnham PJ, Myers RM, Weissman SM, Snyder M. Architecture of the human regulatory network derived from ENCODE data. Nature. 2012;489:91–100. doi: 10.1038/nature11245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grontved L, Bandle R, John S, Baek S, Chung HJ, Liu Y, Aguilera G, Oberholtzer C, Hager GL, Levens D. Rapid genome-scale mapping of chromatin accessibility in tissue. Epigenetics Chromatin. 2012;5:1–12. doi: 10.1186/1756-8935-5-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grontved L, John S, Baek S, Liu Y, Buckley JR, Vinson C, Aguilera G, Hager GL. C/EBP maintains chromatin accessibility in liver and facilitates glucocorticoid receptor recruitment to steroid response elements. EMBO J. 2013;32:1568–1583. doi: 10.1038/emboj.2013.106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guertin MJ, Lis JT. Mechanisms by which transcription factors gain access to target sequence elements in chromatin. Curr Opin Genet Dev. 2013;23:116–123. doi: 10.1016/j.gde.2012.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He HH, Meyer CA, Hu SS, Chen MW, Zang C, Liu Y, Rao PK, Fei T, Xu H, Long H, Liu XS, Brown M. Refined DNase-seq protocol and data analysis reveals intrinsic bias in transcription factor footprint identification. Nat Methods. 2014;11:73–78. doi: 10.1038/nmeth.2762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henikoff JG, Belsky JA, Krassovsky K, MacAlpine DM, Henikoff S. Epigenome characterization at single base-pair resolution. Proc Natl Acad Sci U S A. 2011;108:18318–18323. doi: 10.1073/pnas.1110731108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hesselberth JR, Zhang Z, Sabo PJ, Chen X, Sandstrom R, Reynolds AP, Thurman RE, Neph S, Kuehn MS, Noble WS, Fields S, Stamatoyannopoulos JA. Global mapping of protein-DNA interactions in vivo by digital genomic footprinting. Nat Methods. 2009;6:283–289. doi: 10.1038/nmeth.1313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson PD, Felsenfeld G. A method for mapping intranuclear protein-DNA interactions and its application to a nuclease hypersensitive site. Proc Natl Acad Sci USA. 1985;82:2296–2300. doi: 10.1073/pnas.82.8.2296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- John S, Sabo PJ, Thurman RE, Sung MH, Biddie SC, Johnson TA, Hager GL, Stamatoyannopoulos JA. Chromatin accessibility pre-determines glucocorticoid receptor binding patterns. Nat Genet. 2011;43:264–268. doi: 10.1038/ng.759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kassabov SR, Henry NM, Zofall M, Tsukiyama T, Bartholomew B. High-resolution mapping of changes in histone-DNA contacts of nucleosomes remodeled by ISW2. Mol Cell Biol. 2002;22:7524–7534. doi: 10.1128/MCB.22.21.7524-7534.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kodadek T, Sikder D, Nalley K. Keeping transcriptional activators under control. Cell. 2006;127:261–264. doi: 10.1016/j.cell.2006.10.002. [DOI] [PubMed] [Google Scholar]
- Lazarovici A, Zhou T, Shafer A, Dantas-Machado AC, Riley TR, Sandstrom R, Sabo PJ, Lu Y, Rohs R, Stamatoyannopoulos JA, Bussemaker HJ. Probing DNA shape and methylation state on a genomic scale with DNase I. Proc Natl Acad Sci U S A. 2013;110:6376–6381. doi: 10.1073/pnas.1216822110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lickwar CR, Mueller F, Hanlon SE, McNally JG, Lieb JD. Genome-wide protein-DNA binding dynamics suggest a molecular clutch for transcription factor function. Nature. 2012;484:251–255. doi: 10.1038/nature10985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malnou CE, Brockly F, Favard C, Moquet-Torcy G, Piechaczyk M, Jariel-Encontre I. Heterodimerization with different Jun proteins controls c-Fos intranuclear dynamics and distribution. J Biol Chem. 2010;285:6552–6562. doi: 10.1074/jbc.M109.032680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayr BM, Guzman E, Montminy M. Glutamine rich and basic region/leucine zipper (bZIP) domains stabilize cAMP-response element-binding protein (CREB) binding to chromatin. J Biol Chem. 2005;280:15103–15110. doi: 10.1074/jbc.M414144200. [DOI] [PubMed] [Google Scholar]
- Mazza D, Abernathy A, Golob N, Morisaki T, McNally JG. A benchmark for chromatin binding measurements in live cells. Nucleic Acids Res. 2012;40:e119. doi: 10.1093/nar/gks701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKnight JN, Jenkins KR, Nodelman IM, Escobar T, Bowman GD. Extranucleosomal DNA Binding Directs Nucleosome Sliding By Chd1. Mol Cell Biol. 2011;31:4746–4759. doi: 10.1128/MCB.05735-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNally JG, Mueller WG, Walker D, Wolford RG, Hager GL. The glucocorticoid receptor: Rapid exchange with regulatory sites in living cells. Science. 2000;287:1262–1265. doi: 10.1126/science.287.5456.1262. [DOI] [PubMed] [Google Scholar]
- Mercer TR, Neph S, Dinger ME, Crawford J, Smith MA, Shearwood AM, Haugen E, Bracken CP, Rackham O, Stamatoyannopoulos JA, Filipovska A, Mattick JS. The human mitochondrial transcriptome. Cell. 2011;146:645–658. doi: 10.1016/j.cell.2011.06.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagaich AK, Walker DA, Wolford RG, Hager GL. Rapid periodic binding and displacement of the glucocorticoid receptor during chromatin remodeling. Mol Cell. 2004;14:163–174. doi: 10.1016/s1097-2765(04)00178-9. [DOI] [PubMed] [Google Scholar]
- Nakahashi H, Kwon KR, Resch W, Vian L, Dose M, Stavreva D, Hakim O, Pruett N, Nelson S, Yamane A, Qian J, Dubois W, Welsh S, Phair RD, Pugh BF, Lobanenkov V, Hager GL, Casellas R. A Genome-wide Map of CTCF Multivalency Redefines the CTCF Code. Cell Rep. 2013;3:1678–1689. doi: 10.1016/j.celrep.2013.04.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neph S, Stergachis AB, Reynolds A, Sandstrom R, Borenstein E, Stamatoyannopoulos JA. Circuitry and dynamics of human transcription factor regulatory networks. Cell. 2012a;150:1274–1286. doi: 10.1016/j.cell.2012.04.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neph S, Vierstra J, Stergachis AB, Reynolds AP, Haugen E, Vernot B, Thurman RE, John S, Sandstrom R, Johnson AK, Maurano MT, Humbert R, Rynes E, Wang H, Vong S, Lee K, Bates D, Diegel M, Roach V, Dunn D, Neri J, Schafer A, Hansen RS, Kutyavin T, Giste E, Weaver M, Canfield T, Sabo P, Zhang M, Balasundaram G, Byron R, MacCoss MJ, Akey JM, Bender MA, Groudine M, Kaul R, Stamatoyannopoulos JA. An expansive human regulatory lexicon encoded in transcription factor footprints. Nature. 2012b;489:83–90. doi: 10.1038/nature11212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piper J, Elze MC, Cauchy P, Cockerill PN, Bonifer C, Ott S. Wellington: a novel method for the accurate identification of digital genomic footprints from DNase-seq data. Nucleic Acids Res. 2013;41:e201. doi: 10.1093/nar/gkt850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pique-Regi R, Degner JF, Pai AA, Gaffney DJ, Gilad Y, Pritchard JK. Accurate inference of transcription factor binding from DNA sequence and chromatin accessibility data. Genome Res. 2011;21:447–455. doi: 10.1101/gr.112623.110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poorey K, Viswanathan R, Carver MN, Karpova TS, Cirimotich SM, McNally JG, Bekiranov S, Auble DT. Measuring chromatin interaction dynamics on the second time scale at single-copy genes. Science. 2013;342:369–372. doi: 10.1126/science.1242369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmiedeberg L, Skene P, Deaton A, Bird A. A temporal threshold for formaldehyde crosslinking and fixation. PLoS One. 2009;4:e4636. doi: 10.1371/journal.pone.0004636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp ZD, Mancini MG, Hinojos CA, Dai F, Berno V, Szafran AT, Smith KP, Lele TT, Ingber DE, Mancini MA. Estrogen-receptor-alpha exchange and chromatin dynamics are ligand- and domain-dependent. J Cell Sci. 2006;119:4101–4116. doi: 10.1242/jcs.03161. [DOI] [PubMed] [Google Scholar]
- Siersbaek R, Nielsen R, John S, Sung MH, Baek S, Loft A, Hager GL, Mandrup S. Extensive chromatin remodelling and establishment of transcription factor ‘hotspots’ during early adipogenesis. EMBO J. 2011;30:1459–1472. doi: 10.1038/emboj.2011.65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sprague BL, Pego RL, Stavreva DA, McNally JG. Analysis of binding reactions by fluorescence recovery after photobleaching. Biophys J. 2004;86:3473–3495. doi: 10.1529/biophysj.103.026765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stasevich TJ, Mueller F, Michelman-Ribeiro A, Rosales T, Knutson JR, McNally JG. Cross-validating FRAP and FCS to quantify the impact of photobleaching on in vivo binding estimates. Biophys J. 2010;99:3093–3101. doi: 10.1016/j.bpj.2010.08.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stavreva DA, Muller WG, Hager GL, Smith CL, McNally JG. Rapid glucocorticoid receptor exchange at a promoter is coupled to transcription and regulated by chaperones and proteasomes. Mol Cell Biol. 2004;24:2682–2697. doi: 10.1128/MCB.24.7.2682-2697.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thurman RE, Rynes E, Humbert R, Vierstra J, Maurano MT, Haugen E, Sheffield NC, Stergachis AB, Wang H, Vernot B, Garg K, John S, Sandstrom R, Bates D, Boatman L, Canfield TK, Diegel M, Dunn D, Ebersol AK, Frum T, Giste E, Johnson AK, Johnson EM, Kutyavin T, Lajoie B, Lee BK, Lee K, London D, Lotakis D, Neph S, Neri F, Nguyen ED, Qu H, Reynolds AP, Roach V, Safi A, Sanchez ME, Sanyal A, Shafer A, Simon JM, Song L, Vong S, Weaver M, Yan Y, Zhang Z, Zhang Z, Lenhard B, Tewari M, Dorschner MO, Hansen RS, Navas PA, Stamatoyannopoulos G, Iyer VR, Lieb JD, Sunyaev SR, Akey JM, Sabo PJ, Kaul R, Furey TS, Dekker J, Crawford GE, Stamatoyannopoulos JA. The accessible chromatin landscape of the human genome. Nature. 2012;489:75–82. doi: 10.1038/nature11232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voss TC, Hager GL. Dynamic regulation of transcriptional states by chromatin and transcription factors. Nat Rev Genet. 2014;15:69–81. doi: 10.1038/nrg3623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voss TC, Schiltz RL, Sung MH, Yen PM, Stamatoyannopoulos JA, Biddie SC, Johnson TA, Miranda TB, John S, Hager GL. Dynamic exchange at regulatory elements during chromatin remodeling underlies assisted loading mechanism. Cell. 2011;146:544–554. doi: 10.1016/j.cell.2011.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zinn K, Maniatis T. Detection of factors that interact with the human beta- interferon regulatory region in vivo by DNAase I footprinting. Cell. 1986;45:611–618. doi: 10.1016/0092-8674(86)90293-x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1 (related to Experimental Procedures). Cut count computation and DNase2TF algorithm. (A) Definition of cut count. The exact nucleotide position representing a DNase I cleavage event is defined consistently by assigning the 5′ base for a given dinucleotide encompassing a cut. The example shows two cleavage events observed by one read mapped on the reverse strand and by another mapped on the forward strand. The former results from a DNA fragment released at the dinucleotide GA, while the latter is from AG (both marked green, top track). The cut count track corresponds to the two events. (B) Flow diagram of DNase2TF. Necessary input information is shown at the top. The search space is the set of all DNase I hotspots pre-computed from the data. An alternative search space can be specified if desired. The dinucleotide bias is directly estimated from the data also, but could be generated from a different source.
Figure S2 (related to Figure 1). Performance of DNase2TF assessed by captured motif occurrences and dependence on sequencing depth. (A) Known transcription factor motifs are enriched in footprint candidates called by DNase2TF. Using the annotated human TF binding motif databases TRANSFAC and JASPAR, we assessed the overlap between putative footprints called using the ENCODE DNase-seq data on HMF or K562 by various methods and the genomic occurrences of all known motifs. DNase2TF without FDR thresholding captures more motif occurrences than the other methods (lower panels) with comparable enrichment levels as seen by proportions of footprints overlapping a motif occurrence (upper panels). (B) ROC analysis on additional TFs using ENCODE data. (C) The sequencing depth used is sufficient for evaluation of AP-1 binding prediction by ROC analysis. We performed a series of down-sampling of the full mammary 3134 DNase-seq dataset in Figure 1 and determined how the prediction accuracy is affected by the sequencing depth. Specifically, a random sample of given size was generated for each round of sub-sampling. From this sample, the set of DNase I hotspots was computed to define the initial search space for footprint detection. Note that, since footprint search is performed only on DHSs which themselves depend on sequencing depth, the total number of FDR-unthresholded footprint candidates decreases dramatically (from 2,791,566 for the full data of about 101 million reads to 334,956 for the 1 million-read sub-sampled data). DNase2TF was then applied and binding predictions were made based on footprints in the same manner as before. An ROC curve was generated for each sub-sampled data set. The resulting ROC curves show near-saturation of accuracy at the current depth of sequencing.
Figure S3 (related Figure 2). DNase signatures occur outside of chromatin. The same traces from Figure 2 are re-scaled to show that the DNase signature is present in each class of nuclear receptor motifs. The raw scales for each trace are shown to the left of the plot; the color of each scale corresponds to the color of the trace. Note that the traces are transparent so that the overlap can be visualized.
Figure S4 (related Figure 5). The tetranucleotide model outperforms dinucleotide and hexanucleotide models. A) We show the DNase signature traces of each model (di, tetra, and hexa) compared to experimental data. B) We compared the area between the DNase signatures derived from experimental data and either the tetranucleotide or hexanucleotide model. We used the Trapezoid Rule to integrate between the curves within the region that encompasses the motif sequence. Note that a smaller area indicates better performance. For each position within the motif, we compared the experimental and model-derived cut frequency by Pearson correlation coefficient. C) Comparison of all the models to experimental data, using the methods applied in panel B, shows that the tetranucleotide model performs best for each factor, with the exception of TCF7L2--the dinucleotide model performs best for TCF7L2.
Figure S5 (related Experimental Procedures). The seqToSign algorithm predicts DNase cut frequency from input sequences and tetranucleotide cut frequency. To generate the predicted cut frequency traces, sequences are first aligned on the TF motif. Next, a tetranucleotide DNase cut frequency table, with all 256 possible cut frequencies, is generated for each experiment. The frequency of each tetranucleotide is tallied for each position in the input DNA; this frequency is multiplied the corresponding genomic cut-frequency of that particular tetranucleotide. This value is averaged for all possible 256 tetranucleotides at this position. The process is repeated at each position along the x-axis.
Figure S6 (related to Figure 6). Additional TFs showing correlation between depth of TF footprints and the residence time of binding. The cut count pro les averaged over all bound motif elements (within ChIP peaks) for Rap1 (A) and Sox2 (B). n, the number of bound motif elements. (A) The yeast DNase data are from Hesselberth et al. 2009. The Rap1 binding sites are from Lickwar CR et al. Nature 2012. Rap1 motif sites were obtained using FIMO and the JASPAR PWM. (B) The mouse ES cell DNase-seq data are from ENCODE. Sox2 binding sites are from the ChIP-exo data in Chen J et al. Cell 2014. Sox2 motif sites were obtained using FIMO and a de novo discovered PWM from ChIP peaks.
Figure S7 (related to Figure 7). Adjusting the cut count for tetramer bias does not significantly improve prediction of TF binding. The cut count data were either left unadjusted, adjusted by the dimer bias (default setting of DNase2TF), or adjusted by the tetramer bias. The DNase and ChIP-seq data sets used are the same as in Figure 1, except for the additional GR ChIP-seq data for the 3134 cell line from John S. et al. Nature Genetics 2011.
Table S1 (related to Experimental Procedures). Computational speed of DNase2TF.
Table S2 (related to Experimental Procedures). Dinucleotide frequency of different nucleases.
Table S3 (related to Figure 1). ChIP-seq datasets used in the ROC analysis.