Abstract
Background
We have previously demonstrated reductions in cocaine choice produced by either continuous 14-day phendimetrazine and D-amphetamine treatment or removing cocaine availability under a cocaine vs. food choice procedure in rhesus monkeys. The aim of the present investigation was to apply the concatenated generalized matching law (GML) to cocaine vs. food choice dose-effect functions incorporating sensitivity to both the relative magnitude and price of each reinforcer. Our goal was to determine potential behavioral mechanisms underlying pharmacological treatment efficacy to decrease cocaine choice.
Methods
A multi-model comparison approach was used to characterize dose- and time-course effects of both pharmacological and environmental manipulations on sensitivity to reinforcement.
Results
GML models provided an excellent fit of the cocaine choice dose-effect functions in individual monkeys. Reductions in cocaine choice by both pharmacological and environmental manipulations were principally produced by systematic decreases in sensitivity to reinforcer price and non-systematic changes in sensitivity to reinforcer magnitude.
Conclusions
The modeling approach used provides a theoretical link between the experimental analysis of choice and pharmacological treatments being evaluated as candidate ‘agonist-based’ medications for cocaine addiction. The analysis suggests that monoamine releaser treatment efficacy to decrease cocaine choice was mediated by selectively increasing the relative price of cocaine. Overall, the net behavioral effect of these pharmacological treatments was to increase substitutability of food pellets, a nondrug reinforcer, for cocaine.
Keywords: Cocaine, Choice, Rhesus monkey, Monoamine releaser, Generalized matching law, Sensitivity to reinforcement
1. Introduction
Preclinical self-administration models provide a measure of abuse-related reinforcing drug effects and have been the most reliable predictor of medication efficacy in clinical settings (Mello and Negus, 1996; Haney and Spealman, 2008). In particular, drug self-administration procedures that involve the concurrent availability of an alternative nondrug reinforcer and determine treatment effects on behavior maintained by both drug and nondrug reinforcers may be especially predictive of medication effects (Banks and Negus, 2012). Important among these proposed advantages is the provision of a dependent variable, response allocation between two concurrently available reinforcers, which may be less sensitive to reinforcement-independent rate-altering effects and may more directly evince relative reinforcer value.
Previous studies have examined the determinants of drug reinforcement in choice procedures in which subjects choose between drug (e.g., cocaine) and an alternative nondrug reinforcer (e.g., food; for review, Banks and Negus, 2012). This literature body supports the general conclusion that choice between drug and food is sensitive to the magnitude (Nader and Woolverton, 1991), price (Banks et al., 2013a; Nader and Woolverton, 1992), frequency (Anderson et al., 2002; Anderson and Woolverton, 2000), and delay (Woolverton and Anderson, 2006; Maguire et al., 2013) dimensions of reinforcers. Although this research suggests that drug vs. food choice is sensitive to the relative value of drug reinforcement, relatively few studies have integrated these results with quantitative theories of operant choice.
The generalized matching law (GML) is a quantitative framework, which predicts that behavior will be allocated among different reinforcers in proportion to their relative value. Relative reinforcer value has been quantified most effectively by the concatenated GML (Baum and Rachlin, 1969; Killeen, 1972; Rachlin, 1971), which predicts that value is determined by a multiplicative combination of each reinforcer dimension listed above. A version of the GML suitable for drug vs. food choice may be written
| (1) |
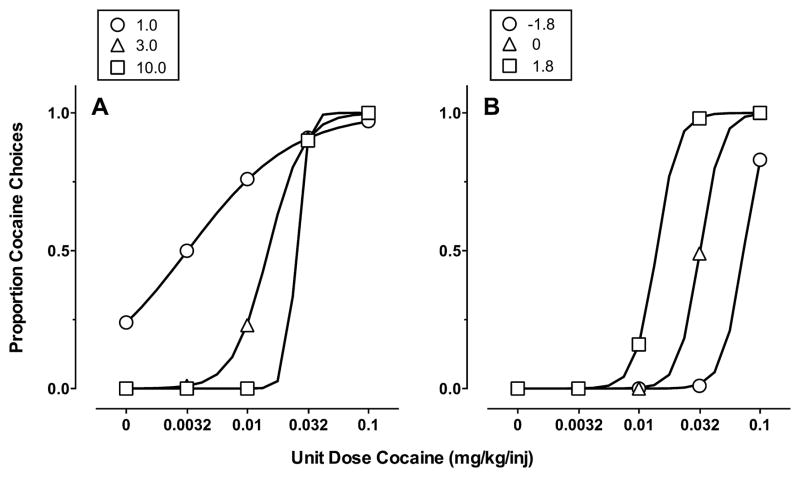
where B represents behavior allocated to cocaine (Bc) or food (Bf), M represents the magnitude dimension of each reinforcer, and P represents the price dimension (fixed-ratio schedule) of each reinforcer. For cocaine, Mc equals the unit dose (mg/kg/injection) and for food Mf equals the value of food scaled in dose units of cocaine (Mf ∝ Mc). On the basis of preliminary model simulations, the proportionality constant was set to 0.032 in the present study; consequently, the magnitude of a 1-g food pellet was set equal to a 0.032-mg/kg-cocaine injection. Furthermore, we have previously demonstrated comparable reinforcing effects of a 0.032-mg/kg cocaine injection and a 1-g food pellet in both progressive-ratio and choice procedures (Negus and Mello, 2003; Banks et al., 2013a). The present approach of fixing the scaling parameter at a single value is equivalent to previous applications of the GML using a bias parameter to account for choice between qualitatively different reinforcers (e.g., Hollard and Davison, 1971; Miller, 1976; Anderson et al., 2002). The free parameters sm (sensitivity to magnitude) and sp (sensitivity to price) capture the extent of changes in drug vs. food choice with changes in the relative magnitude and price of cocaine vs. food for an individual subject. For example, in the case of strict matching, sm = sp = 1, the proportion of responses allocated to the drug alternative is equal to the multiplicative combination of magnitude and price proportions. Fig. 1 shows cocaine choice dose-effect functions simulated by Eq. (1) with relative reinforcer magnitude and price equal to the values used in the present study. The main focus of these simulations is to demonstrate that the slope and horizontal position of the cocaine choice dose-effect functions are determined independently by sensitivity to reinforcer magnitude and reinforcer price, respectively.
Fig. 1.
Simulated cocaine vs. food choice dose-effect functions. (A) The effects of changing sensitivity to magnitude with sensitivity to price held constant at 1.0. (B) The effects of changing sensitivity to price with sensitivity to magnitude held constant at 5.0. Ordinates: proportion of cocaine choices. Abscissae: unit cocaine dose (mg/kg/injection).
The purpose of the present investigation was to determine monoamine releaser treatment effects in a cocaine vs. food choice procedure on sensitivity parameters of the GML. We reanalyzed data from Banks et al. (2013b) demonstrating reductions in cocaine vs. food choice produced by continuous 14-day D-amphetamine, phendimetrazine, and phenmetrazine treatment. A version of the concatenated GML incorporating the relative magnitude and price of cocaine and food reinforcers was fit to the cocaine choice dose-effect curves of individual monkeys. A multi-model comparison approach was used to evaluate competing hypotheses regarding dose- and time-course effects on sensitivity to reinforcement (Burnham and Anderson, 2002). For comparison, we also modeled 7-day effects of extinction on cocaine- or food-maintained responding during the choice procedure (Banks et al., 2011).
2. Methods
2.1. Study design and methods
The experimental methods have been previously described in detail in Banks et al. (2011, 2013b). Briefly, studies were conducted in four–six adult male rhesus monkeys (Macaca mulatta) surgically implanted with a double-lumen catheter inserted in a major vein. The catheter was connected to a fluid swivel attached to the top of each subject’s cage and was protected by a custom jacket and stainless steel tether. Animal research and maintenance were conducted according to the 8th edition of the Guide for the Care and Use of Laboratory Animals as adopted and promulgated by the National Institutes of Health (National Academies Press, 2011). Animal facilities were licensed by the United States Department of Agriculture and accredited by the Association for Assessment and Accreditation of Laboratory Animal Care. The Institutional Animal Care and Use Committee approved the research protocol. Monkeys had visual, auditory, and olfactory contact with other monkeys throughout the study. Operant procedures and foraging toys were provided for environmental manipulation and enrichment. Videos were played daily in animal housing rooms to provide additional environmental enrichment.
Experimental sessions were conducted in each monkey’s home cage. Monkeys responded in daily 2 h choice sessions (0900–1100 h) that consisted of a five-component concurrent schedule of food pellet and intravenous cocaine availability as described in detail previously (Negus and Mello, 2003). During each component, responses on the left key were reinforced with food (1-g banana-flavored pellets; Test Diets, Richmond, IN) according to a fixed-ratio (FR) 100 schedule, and responses on the right key were reinforced with intravenous cocaine (0–0.1 mg/kg/injection) according to an FR 10 schedule. A response on one key reset the ratio requirement on the alternative key. Each reinforcer delivery was followed by a 3-s timeout during which all stimulus lights were extinguished, and responding had no programmed consequences. During each component, the food key was transilluminated red. The stimulus lights for the cocaine key were flashed on and off in 3 s cycles, and longer flashes were associated with higher unit cocaine doses. Across components of the choice procedure, a different unit cocaine dose was available (0, 0.0032, 0.01, 0.032, and 0.1 mg/kg/injection during components 1–5, respectively) by manipulating the injection volume (0, 0.01, 0.03, 0.1, and 0.3 ml/injection, respectively) delivered via the ‘cocaine’ pump. Each component was in effect until 10 total reinforcers were earned or 20 min elapsed, whichever occurred first.
Once cocaine choice was stable, tests sessions were initiated. Subsequently, a 14-day treatment period was initiated during which a test solution was administered via the ‘treatment’ pump for 23 h/day. The treatment solutions and doses examined were D-amphetamine (0.032–0.1 mg/kg/h), (+)-phendimetrazine (0.32–1.0 mg/kg/h) or (+)-phenmetrazine (0.1–0.32 mg/kg/h). At the conclusion of each 14-day test period, a saline control treatment period was reinstated for at least 5 days and until cocaine choice returned to pretest levels. For the extinction studies, separate 7-day treatment periods were initiated where either cocaine was removed from the syringe or food pellets were removed from the dispenser. All other component-correlated stimuli were retained.
2.2. Modeling approach and dose-effect models
The dependent measure of interest was the proportion of cocaine choices (number of completed ratios on the cocaine-associated key/total completed ratios) for days 5–7 (7 days) and days 12–14 (14 days) of the continuous 14-day treatments or days 5–7 for the 7-day extinction condition. These data were then plotted as a function of unit cocaine dose. In the modeling presented below, the value of a single food pellet was held constant at 0.032 mg/kg/injection cocaine as in Fig. 1. Changes in response allocation produced by removal of cocaine or food availability were modeled using baseline reinforcer magnitudes. This approach allowed reinforcer sensitivity parameters to account for changes in response allocation and facilitated comparison with pharmacological manipulations. Parameters of Eq. (1) were estimated for individual monkeys by minimizing the residual sum of squares (RSS) using the Solver add-in of Microsoft Excel for Mac 2011. Model fitting was conducted separately for each manipulation. Data from a monkey were not included if (1) the monkey did not complete each dose of a treatment drug and (2) a choice proportion could not be calculated for two or more cocaine doses. The number of data points fit for individual monkeys are included in Table 1. Within a monkey and a treatment drug, a total RSS was computed by summing the RSS across each dose and treatment week. Therefore, if a monkey completed 14-day treatments for each test drug dose, the total RSS was computed from five cocaine choice dose-effect functions.
Table 1.
Multi-model comparison and selection for individual monkeys. The first column specifies the pharmacological or environmental manipulation. Each sub-column gives the AICc of the Null model and the ΔAICc of competing models. A ΔAICc > 4 is significantly better than the Null model. The best model (lowest AICc) is indicated in bold, n is the number of observations and R2 is the proportion of variance accounted for by the best model.
| Mean | M1452 | M1473 | M1504 | M1488 | M1478 | M1480 | M1412 | M1414 | |
|---|---|---|---|---|---|---|---|---|---|
| D-Amphetamine | |||||||||
| AICc (Null, H0) | −428.2 | −62.4 | −99.4 | −239.3 | −104.5 | −57.0 | −63.0 | ||
| Δ (Full, sm, sp) | 602.0 | 22.4 | 107.1 | −12.9 | 122.8 | 262.2 | 129.0 | ||
| Δ (Magnitude, sm) | −4.4 | 18.0 | −24.0 | −4.4 | 13.3 | 3.1 | −3.2 | ||
| Δ (Price sp) | 473.5 | 15.1 | 78.2 | −1.7 | 47.1 | 291.7 | 167.0 | ||
| n | 15 | 25 | 19 | 25 | 25 | 24 | |||
| R2 | 0.999 | 0.983 | 0.996 | 0.999 | 0.991 | 0.999 | 0.999 | ||
| (+)-Phendimetrazine | |||||||||
| AICc (Null, H0) | −276.7 | −67.6 | −50.8 | −136.8 | −70.3 | ||||
| Δ (Full, sm, sp) | 271.1 | 57.8 | 118.1 | 172.7 | 46.9 | ||||
| Δ (Magnitude, sm) | 63.5 | 0.2 | 131.0 | −1.1 | −3.3 | ||||
| Δ (Price sp) | 298.2 | 93.2 | 89.3 | 184.5 | 58.8 | ||||
| n | 20 | 23 | 25 | 25 | |||||
| R2 | 0.991 | 0.999 | 0.999 | 0.999 | 0.977 | ||||
| (+)-Phenmetrazine | |||||||||
| AICc (Null, H0) | −425.8 | −106.8 | −74.4 | −73.8 | −104.6 | −83.5 | |||
| Δ (Full, sm, sp) | 163.7 | 30.7 | 170.5 | 3.0 | 128.1 | 145.5 | |||
| Δ (Magnitude, sm) | 58.2 | 28.2 | 4.2 | 4.7 | −4.5 | 144.4 | |||
| Δ (Price sp) | 203.8 | 30.4 | 136.0 | 14.8 | 139.9 | 93.1 | |||
| n | 25 | 25 | 25 | 25 | 25 | ||||
| R2 | 0.997 | 0.982 | 0.999 | 0.999 | 0.999 | 0.997 | |||
| Extinction | |||||||||
| AICc (Null, H0) | −234.5 | −30.4 | −29.1 | −45.0 | −33.9 | ||||
| Δ (Full, sm, sp) | 235.6 | 150.1 | 83.2 | 226.4 | 21.3 | ||||
| Δ (Magnitude, sm) | 13.2 | −1.6 | −8.4 | 34.2 | 3.1 | ||||
| Δ (Price sp) | 239.1 | 157.3 | 90.5 | 238.0 | 18.4 | ||||
| n | 15 | 15 | 15 | 15 | |||||
| R2 | 0.996 | 0.999 | 0.999 | 0.999 | 0.900 | ||||
Multi-model comparison and selection for individual monkeys. The first column specifies the pharmacological or environmental manipulation. Each sub-column gives the AICc of the Null model and the ΔAICc of competing models. A ΔAICc > 4 is significantly better than the Null model. The best model (lowest AICc) is indicated in bold, n is the number of observations and R2 is the proportion of variance accounted for by the best model.
Different versions of Eq. (1) were fit to the data for days 5–7 (7 days) and days 12–14 (14 days) of each continuous 14-day pharmacological treatment to test different hypotheses regarding treatment effects on sensitivity to reinforcement. Thus, different combinations of the free parameters (k) were either allowed to vary or were constrained to determine whether dose had no effect on sensitivity to reinforcement (the Null model, H0), affected sensitivity to both reinforcer dimensions (Full model), or selectively affected sensitivity to a single reinforcer dimension. In the Null model, sensitivity to reinforcer magnitude and price (si) in Eq. (1) were constrained (e.g., k = 2; s(BL) = s(Dose 1) = s(Dose)). The Full model placed no restrictions on estimated sensitivity to reinforcement parameters (k = 10). The Magnitude model allowed sensitivity to reinforcer magnitude (sm(BL) ≠ / sm(Dose 1) ≠ / sm(Dose 2)) to vary across doses while sensitivity to reinforcer price (sp(BL) ≠ sp(Dose 1) ≠ sp(Dose 2)) was constrained (k = 6). The Price model constrained sensitivity to reinforcer magnitude (sm(BL) = sm(Dose 1) = sm(Dose 2)) while sensitivity to reinforcer price (sp(BL) ≠ / sp(Dose 1) ≠ / sp(Dose 2)) was allowed to vary across doses (k = 6).
The minimum corrected Akaike information criterion (AICc) score indicates the best model after correcting for the number of free parameters (see Supplement for further explanation). Multi-model comparison was used to characterize dose-effects of pharmacological treatments on sensitivity to reinforcement (Burnham and Anderson, 2002). The corrected Akaike information criterion (AICc) was used to compare different models and ΔAICc [i.e., ΔAICc (H0) − ΔAICc (H1) > 4.0] was used to select the best model for each monkey. The model-comparison approach is analogous to a significance test; therefore, the parameters of the selected model were treated as a significant effect of a specific experimental manipulation for an individual monkey. Because an alternative model was the selected model in 18/19 cases, we focused on the magnitude of systematic parameter changes below. Cocaine vs. food choice and sensitivity to reinforcement dose-effect curves were constructed by averaging the individual, best-fitting parameter estimates.
3. Results
A summary of the multi-model comparison for all treatment drugs and extinction is provided in Table 1 (see Supplemental Table S1 for raw AICc scores1). Overall, the null model was never the selected model for the group data and only for one experimental manipulation was this model selected for an individual monkey. These results indicate that in all but one instance, the treatment drug or extinction condition altered drug choice sufficiently to infer changes in reinforcer sensitivity. In addition, the selected model always fit the individual monkey and group data well, accounting for at least 97% of the variance.
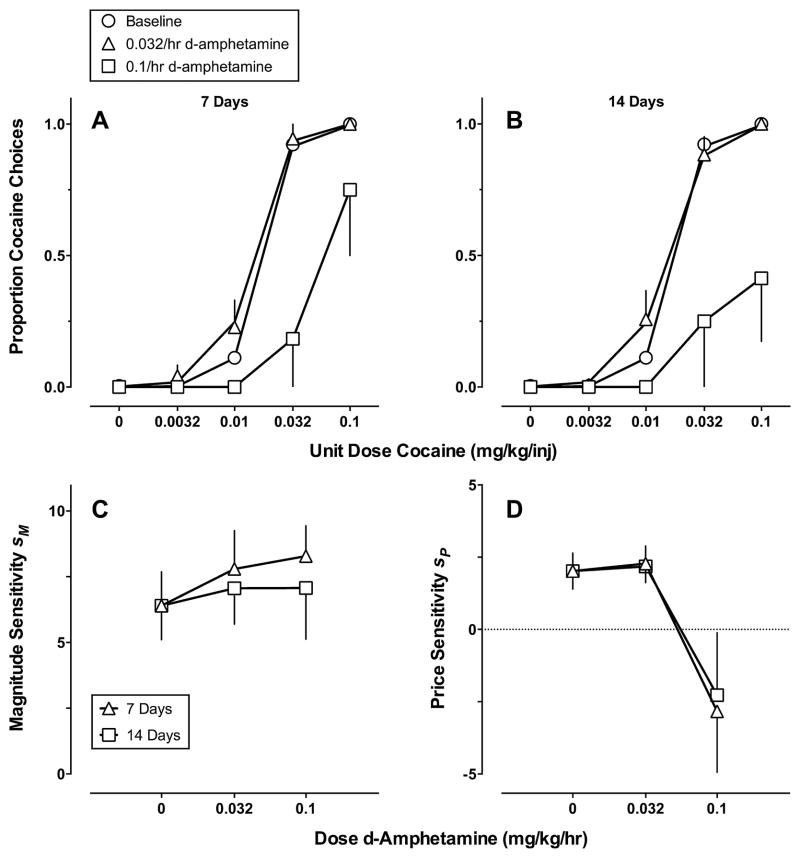
Fig. 2 shows continuous 14-day D-amphetamine treatment effects on (A) and (B) cocaine vs. food choice and (C) and (D) best-fitting parameter estimates of Eq. (1) plotted as a function of D-amphetamine dose. The GML model accurately described the cocaine choice dose-effect functions across each D-amphetamine dose and each treatment week (Table 1). The best-fit model for D-amphetamine effects differed somewhat between monkeys with the Full and Price models being selected. In 5/6 monkeys that were sensitive to pharmacological treatment, however, 0.1 mg/kg/h D-amphetamine produced an approximate 10-fold decrease in sensitivity to reinforcer price. Changes were less systematic across monkeys producing a 1.5-fold increase in sensitivity to reinforcer magnitude.
Fig. 2.
Continuous 14-day D-amphetamine treatment effects on (A) and (B) cocaine vs. food choice and (C) and (D) best-fitting parameter estimates of Eq. (1) plotted as a function of D-amphetamine dose. (A) and (B) Ordinates: obtained and predicted (solid curves) proportion cocaine choice. Abscissae: unit dose cocaine in mg/kg/injection (log scale). (C) and (D) Ordinates: sensitivity to reinforcer magnitude (sm) or price (sp). Abscissae: D-amphetamine dose in mg/kg/h. Model predictions (A) and (B) and parameter estimates (C) and (D) were derived from averaging the parameter estimates of the best-fitting model for individual monkeys. Note different ordinate scales in (C) and (D).
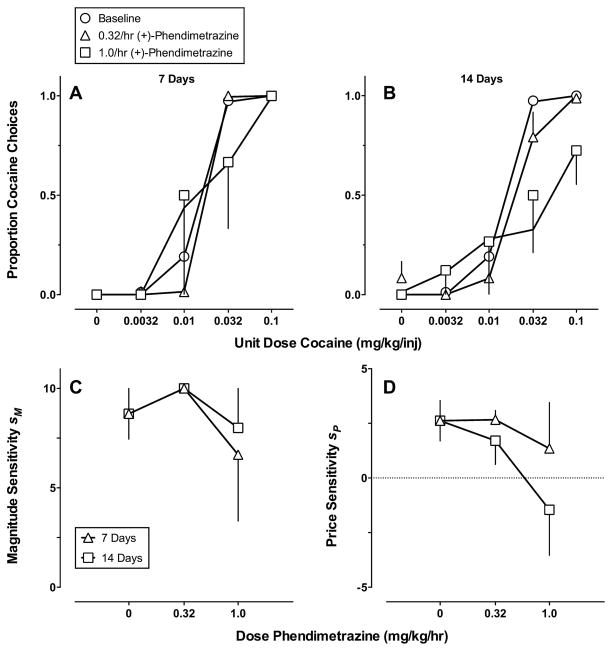
Fig. 3 shows continuous 14-day (+)-phendimetrazine treatment effects on (A) and (B) cocaine vs. food choice and (C) and (D) best-fitting parameter estimates of Eq. (1) plotted as a function of phendimetrazine dose. The GML model provided an accurate description of the cocaine choice dose-effect functions across each (+)-phendimetrazine dose and each treatment week (Table 1). The best-fit model was consistent for four of the five monkeys and indicated that (+)-phendimetrazine produced a selective decrease in sensitivity to reinforcer price. The best-fit model for the other monkey suggested (+)-phendimetrazine increased sensitivity to reinforcer magnitude during 0.32/mg/kg/h treatment and decreased sensitivity to reinforcer magnitude during 1.0/mg/kg/h treatment. The multi-model comparison suggested that sensitivity to reinforcer price decreased dose-dependently and these decreases were more pronounced after 14 days of treatment.
Fig. 3.
Continuous 14-day (+)-phendimetrazine treatment effects on (A) and (B) cocaine vs. food choice and (C) and (D) best-fitting parameter estimates of Eq. (1) plotted as a function of (+)-phendimetrazine dose. (A) and (B) Ordinates: obtained and predicted (solid curves) proportion cocaine choice. Abscissae: unit dose cocaine in mg/kg/injection (log scale). (C) and (D) Ordinates: sensitivity to reinforcer magnitude (sm) or price (sp). Abscissae: (+)-phendimetrazine dose in mg/kg/h. Model predictions (A) and (B) and parameter estimates (C) and (D) were derived from averaging the parameter estimates of the best-fitting model for individual monkeys. Note different ordinate scales in (C) and (D).
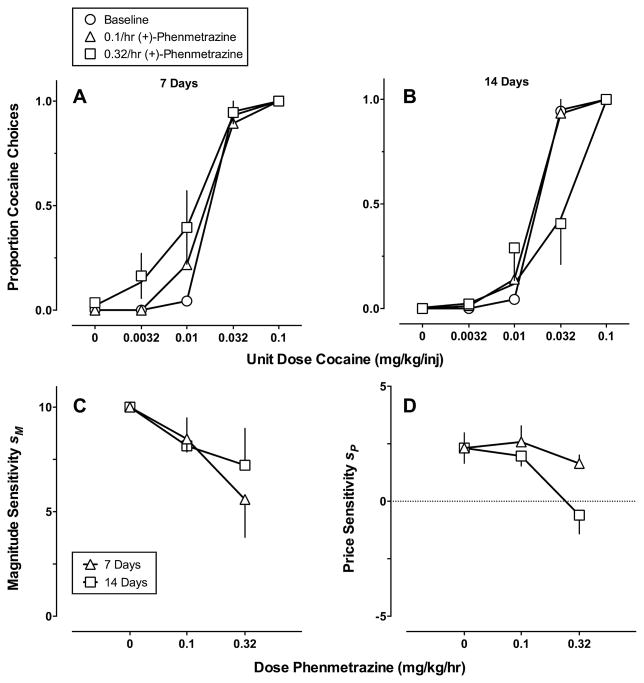
Fig. 4 shows continuous 14-day (+)-phenmetrazine treatment effects on (A) and (B) cocaine vs. food choice and (C) and (D) best-fitting parameter estimates of Eq. (1) plotted as a function of phenmetrazine dose The GML model provided an accurate description of the cocaine choice dose-effect functions across each (+)-phenmetrazine dose and each treatment week (Table 1). The best-fit model for three monkeys was the Full model and for the other three monkeys was the price sensitivity model. Decreases in sensitivity to reinforcer magnitude and price were apparent at 0.32 mg/kg/h (+)-phenmetrazine following 14 treatment days.
Fig. 4.
Continuous 14-day (+)-phenmetrazine treatment effects on (A) and (B) cocaine vs. food choice and (C) and (D) best-fitting parameter estimates of Eq. (1) plotted as a function of (+)-phenmetrazine dose. (A) and (B) Ordinates: obtained and predicted (solid curves) proportion cocaine choice. Abscissae: unit dose cocaine in mg/kg/injection (log scale). (C) and (D) Ordinates: sensitivity to reinforcer magnitude (sm) or price (sp). Abscissae: (+)-phenmetrazine dose in mg/kg/h. Model predictions (A) and (B) and parameter estimates (C) and (D) were derived from averaging the parameter estimates of the best-fitting model for individual monkeys. Note different ordinate scales in (C) and (D).
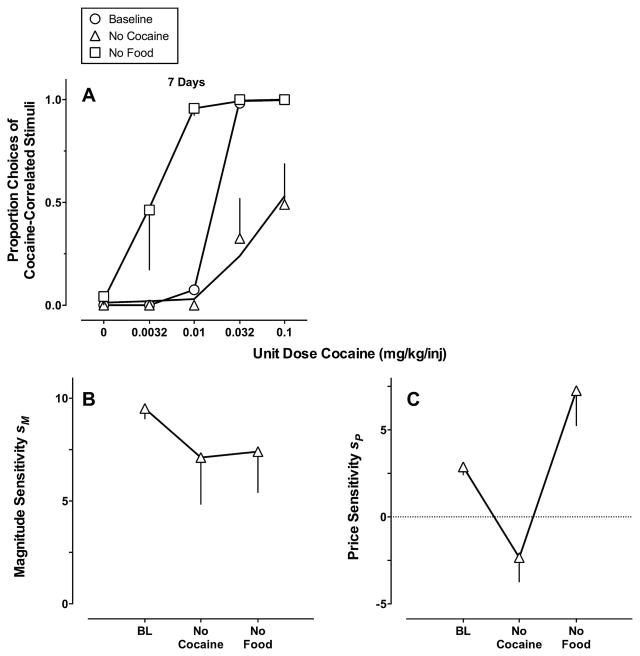
Fig. 5 shows the effects of extinguishing either cocaine- or food-maintained responding for 7 days on (A) and (B) cocaine vs. food choice and (C) and (D) best-fitting parameter estimates of Eq. (1). Substituting 0.001 for food or cocaine in the GML model during removal of each reinforcer provided an accurate description of the cocaine choice dose-effect functions (Table 1). The best-fit model was consistent between monkeys (note that the AICc values for full and price models are not significantly different for monkey M1414). Cocaine removal produced a greater than 8-fold decrease in sensitivity to reinforcer price, whereas food removal produced an approximately 2-fold increase in sensitivity to reinforcer price.
Fig. 5.
Effect of 7-day cocaine or food removal on (A) cocaine vs. food choice and (B) and (C) best-fitting parameter estimates of Eq. (1) plotted as a function of extinction manipulation. (A) Ordinate: obtained and predicted (solid curves) proportion cocaine choice. Abscissa: unit dose cocaine in mg/kg/injection (log scale). (B) and (C) Ordinates: sensitivity to reinforcer magnitude (sm) or price (sp). Abscissae: (+)-phenmetrazine dose in mg/kg/h. Model predictions (A) and parameter estimates (B) and (C) were derived from averaging the parameter estimates of the best-fitting model for individual monkeys. Note different ordinate scales in (B) and (C).
4. Discussion
The aim of the present investigation was to determine monoamine releaser treatment effects on sensitivity to reinforcement parameters of the GML. A multi-model comparison approach was used to evaluate competing hypotheses regarding dose- and time-course effects on sensitivity to relative reinforcer magnitude and price (Burnham and Anderson, 2002). There were two main findings. First, the GML models provided excellent fits to the cocaine choice dose-effect functions. In addition, in 18/19 fits to individual monkey data models assuming an effect of a manipulation on sensitivity to reinforcement were superior to the null hypothesis model justifying the use of additional model parameters. Second, pharmacological and environmental manipulations altered cocaine vs. food choice in 18/19 monkeys and did so by decreasing sensitivity to reinforcer price in 16/18 monkeys.
4.1. The generalized matching law model – comparison approach
Previous studies have employed the model comparison approach to determine the specificity of pharmacological and neurobiological manipulations on reinforcement-related processes (Avila et al., 2009; Peartree et al., 2012). The present study applied a well-known model of choice that incorporates various reinforcer dimensions to construct a relative value of the available reinforcers (Baum and Rachlin, 1969). Banks et al. (2013b) provided rhesus monkeys a choice between alternatives that differed in both reinforcer magnitude and price, and GML model comparison allowed us to determine which reinforcer dimension(s) were affected by pharmacological and environmental manipulations. Taken together, these studies suggest the model comparison provides a unique approach for testing competing hypotheses regarding the behavioral mechanisms of pharmacological and environmental manipulations.
The results of the present study are consistent with prior reports demonstrating GML framework applicability to drug choice procedures with rhesus monkeys (e.g., Woolverton, 1996). The estimates of sensitivity to reinforcer magnitude obtained in the present study, however, differ markedly from modal values of sensitivity to reinforcer rate established in earlier reviews (e.g., Baum, 1974; Myers and Myers, 1977). Sensitivity to reinforcer magnitude estimates displayed substantial overmatching, often 5–10-fold greater than in previous reports (cf., McLean and Blampied, 2001; Elliffe et al., 2008). There are at least two possible reasons for this difference. First, this study employed qualitatively different reinforcers, which may have enhanced discrimination of the choice alternatives (Baum, 1979; Davison and Jenkins, 1985). A previous study by Anderson et al. (2002), however, reported undermatching (s < 1.0) to reinforcer rate in a cocaine vs. food choice procedure employing concurrent variable interval schedules (see also, Heyman and Oldfather, 1992). Second, the present procedure employed ratio schedules of reinforcement and an additional reset contingency following changeover responses. Concurrent ratio schedules generally produce exclusive preference for the choice alternative associated with the lower ratio requirement (Herrnstein and Loveland, 1975; see also Galuska et al., 2006). In studies where choices are made between qualitatively different reinforcers, preference is determined by the relative magnitude and price of each reinforcer (Madden et al., 1999). The present findings are consistent with concurrent ratio schedules producing behavior allocation that maximizes relative reinforcer value (Rachlin et al., 1981).
Two potential limitations from the present GML analysis should be considered. One limitation is the scaling factor for the food reinforcer was held constant across all monkeys and, therefore, did not permit an assessment of individual differences. Although we chose the scaling factor based on previous studies, exploratory modeling with scaling factors of 0.032 ± 0.5 log units produced similar relative changes in parameter estimates, but provided a poorer fit to the data. A second limitation concerns the approach to modeling the effects of extinction. To model data from extinction and facilitate comparison to the pharmacological manipulations, we used non-zero values to predict the observed nonexclusive preference. Moreover, a single reinforcer magnitude (e.g., 0.001 mg/kg/injection for saline) could not predict the cocaine dose dependency still evident in the cocaine choice dose-effect function after 7 days of cocaine and food removal.
Therefore, while this ad hoc approach does not provide insight into the mechanisms by which the component-correlated stimuli maintained dose-dependent cocaine choice, model comparison suggests that the effects of extinction on price sensitivity were similar to the effects of pharmacological manipulations.
4.2. Effects of pharmacological treatments on sensitivity to reinforcement
Pharmacological manipulations that decreased cocaine vs. food preference did so mostly by decreasing sensitivity to reinforcer price. Changes in sensitivity to reinforcer magnitude were less consistent across monkeys compared to price changes. When changes in magnitude sensitivity did occur in individual monkeys, magnitude sensitivity decreased suggesting that total reinforcer consumption decreased (see below). Rachlin et al. (1980, 1981) proposed that the sensitivity parameter in the GML might serve as an index of economic substitutability between qualitatively different reinforcers (see also Green and Freed, 1993). The cocaine vs. food choice procedure employed in the present study systematically varied unit cocaine price (UP, fixed ratio/dose) by increasing the available cocaine dose and provided a measure of the own-price elasticity of cocaine demand and the cross-price elasticity of food demand. Therefore, changes in sensitivity to reinforcer price observed in the present study may be related to parameter values in behavioral economic models of choice (Hursh et al., 2013; Hursh and Roma, 2013).
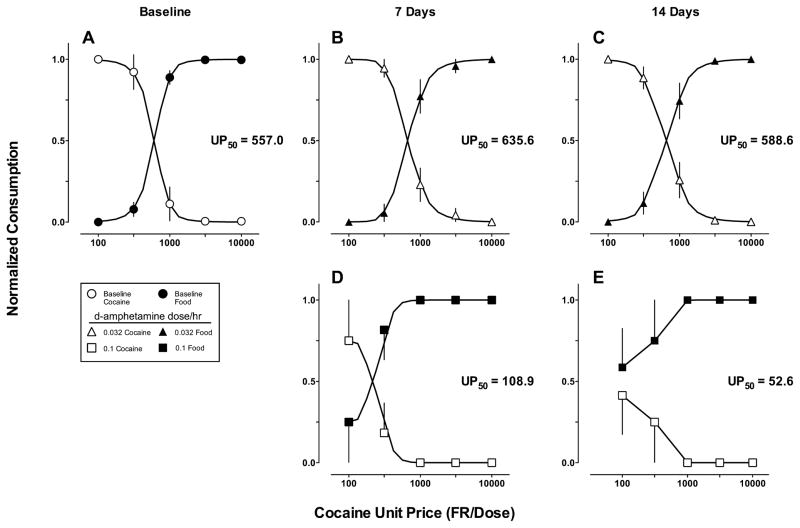
To examine the relationship between GML and economic approaches, choice data from each 7-day period of the continuous 14-day D-amphetamine (0.032–0.1 mg/kg/h) treatment are presented in Fig. 6 as demand curves; consumption is plotted as a function of the unit price of cocaine. The continuous curves are the predictions of the GML model and the interpolated unit cocaine price (UP50) at which cocaine and food consumption are predicted to be equal is given in each panel. Consistent with previous demand analyses of cocaine vs. food choice procedures, cocaine consumption was a decreasing function of UP of cocaine (Nader et al., 1993). At the end of the 14-day treatment, 0.1-mg/kg/h D-amphetamine produced a ten-fold decrease in UP50 and the GML model predicted an increase in cocaine elasticity and a corresponding decrease in food elasticity. Therefore, according to the substitutability interpretation of GML sensitivity to reinforcement, cocaine and food were imperfect economic substitutes under baseline conditions, and the effects of pharmacological and environmental manipulations increased the elasticity of cocaine preference.
Fig. 6.
Continuous 14-day D-amphetamine treatment effects on demand for cocaine and food. Model predictions were derived from averaging the parameter estimates of the best-fitting model for individual monkeys. Ordinates: normalized consumption (reinforcers earned/total reinforcers). Abscissae: unit price of cocaine (UP = FR/dose). The unit price at which cocaine and food consumption are predicted to be equal is indicated in the insets as UP50.
There was concordance among the effects of pharmacological treatment and extinction of cocaine-maintained behavior on sensitivity to reinforcer price. Consistent with previous studies, elasticity of demand for saline was greater than demand for drug (Banks et al., 2013b; Negus et al., 2008). Model comparison suggested that sensitivity to reinforcer magnitude was not altered over the 7 days of each extinction manipulation. This result is consistent with the dose-dependent increase in cocaine choice maintained by the component-correlated stimuli throughout extinction. Taken together, these findings suggest that pharmacological treatments and extinction may affect behavior allocation in the presence of cocaine-associated stimuli through a common behavioral mechanism.
Finally, the extension of the GML presented here is closely related to Shizgal and colleagues’ ‘reinforcement mountain’ model of brain stimulation reinforcement in intracranial self-stimulation (ICSS) procedures (Conover and Shizgal, 2005; Arvanitogiannis and Shizgal, 2008). Their approach employs a single-operant matching model along with generalized matching reinforcement sensitivity parameters (see also McDowell, 1986, 2013). An intriguing similarity between the present and Shizgal approaches is that matching law analyses suggest that pharmacological manipulations affecting dopaminergic neurotransmission selectively alter sensitivity to reinforcement (Hernandez et al., 2010; Trujillo-Pisanty et al., 2014). For example, Hernandez et al. (2010) reported that the cocaine-induced increases in low baseline rates of responding maintained by low frequencies of brain stimulation were consistent with a decreased sensitivity to the price of brain stimulation. Cocaine-induced facilitation of ICSS also correlates with self-administration procedures and has been interpreted as an abuse-related effect (Negus and Miller, 2014). In turn, the blunted expression of abuse-related cocaine effects on ICSS produced by chronic D-amphetamine treatment may also be attributable to altered reinforcer price sensitivity, consistent with the effects reported here on cocaine self-administration (Bauer et al., 2014).
4.3. Implications for preclinical behavioral studies assessing candidate anti-drug addiction medication efficacy
Cocaine addiction continues to present a significant public health problem, and the development of effective medications remains a priority of preclinical drug addiction research. The goal of ‘agonist-based’ medication research is to develop pharmacotherapies that decrease drug use by identifying compounds that share mechanisms of action with cocaine. In a recent review, Haney and Spealman concluded that preclinical self-administration procedures are the most reliable predictor of clinical medication outcomes (Haney and Spealman, 2008; see also Comer et al., 2008). This conclusion suggests the success of preclinical self-administration procedures to accurately predict medication efficacy in humans resides in the neuropharmacological and behavioral mechanisms of reinforcement. Model comparison results of the present study suggest that chronic D-amphetamine and phendimetrazine treatment may function as economic substitutes that selectively increase cocaine demand elasticity by increasing the effective price. Moreover, when a substitutable non-drug reinforcer is concurrently available during chronic D-amphetamine and phendimetrazine treatment, preference for an alternative therapeutic reinforcer will reciprocally increase.
Supplementary Material
Acknowledgments
Role of funding source
Research reported in this publication was supported by the National Institute on Drug Abuse of the National Institutes of Health under Award Numbers R01 DA026946 and T32 DA007027-38. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Appendix A. Supplementary data
Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.drugalcdep.2014.11.003.
Footnotes
Supplementary material can be found by accessing the online version of this paper at: http://dx.doi.org/10.1016/j.drugalcdep.2014.11.003.
Supplementary material can be found by accessing the online version of this paper at http://dx.doi.org/10.1016/j.drugalcdep.2014.11.003.
Contributors
Banks, Blough, and Negus designed the original study. Hutsell developed the modeling approach. Hutsell, Banks, and Negus wrote or contributed to the manuscript. All authors critically reviewed the content and approved the final version for publication.
Conflicts of interest
None of the authors have any conflict of interest to declare.
References
- Anderson KG, Velkey AJ, Woolverton WL. The generalized matching law as a predictor of choice between cocaine and food in rhesus monkeys. Psychopharmacology (Berl) 2002;163:319–326. doi: 10.1007/s00213-002-1012-7. [DOI] [PubMed] [Google Scholar]
- Anderson KG, Woolverton WL. Concurrent variable-interval drug self-administration and the generalized matching law: a drug-class comparison. Behav Pharmacol. 2000;11:413–420. doi: 10.1097/00008877-200008000-00007. [DOI] [PubMed] [Google Scholar]
- Arvanitogiannis A, Shizgal P. The reinforcement mountain: allocation of behavior as a function of the rate and intensity of rewarding brain stimulation. Behav Neurosci. 2008;122:1126. doi: 10.1037/a0012679. [DOI] [PubMed] [Google Scholar]
- Avila I, Reilly MP, Sanabria F, Posadas-Sánchez D, Chavez CL, Banerjee N, Killeen P, Castaneda E. Modeling operant behavior in the Parkinsonian rat. Behav Brain Res. 2009;198:298–305. doi: 10.1016/j.bbr.2008.11.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bauer CT, Banks ML, Negus SS. The effect of chronic amphetamine treatment on cocaine-induced facilitation of intracranial self-stimulation in rats. Psychopharmacology (Berl) 2014;231:2461–2470. doi: 10.1007/s00213-013-3405-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banks ML, Blough BE, Negus SS. Effects of monoamine releasers with varying selectivity for releasing dopamine/norepinephrine versus serotonin on choice between cocaine and food in rhesus monkeys. Behav Pharmacol. 2011;22:824–836. doi: 10.1097/FBP.0b013e32834d63ac. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banks ML, Negus SS. Preclinical determinants of drug choice under concurrent schedules of drug self-administration. Adv Pharmacol Sci. 2012 doi: 10.1155/2012/281768. http://dx.doi.org/10.1155/2012/281768. [DOI] [PMC free article] [PubMed]
- Banks ML, Blough BE, Negus SS. Interaction between behavioral and pharmacological treatment strategies to decrease cocaine choice in rhesus monkeys. Neuropsychopharmacology. 2013a;38:395–404. doi: 10.1038/npp.2012.193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banks ML, Blough BE, Negus SS. Effects of 14-day treatment with the schedule III anorectic phendimetrazine on choice between cocaine and food in rhesus monkeys. Drug Alcohol Depend. 2013b;131:204–213. doi: 10.1016/j.drugalcdep.2013.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baum WM. On two types of deviation from the matching law: bias and undermatching. J Exp Anal Behav. 1974;22:231–242. doi: 10.1901/jeab.1974.22-231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baum WM. Matching, undermatching, and overmatching in studies of choice. J Exp Anal Behav. 1979;32:269–281. doi: 10.1901/jeab.1979.32-269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baum WM, Rachlin HC. Choice as time allocation. J Exp Anal Behav. 1969;12:861–874. doi: 10.1901/jeab.1969.12-861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burnham KP, Anderson DR. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach. Springer-Verlag; New York: 2002. [Google Scholar]
- Comer SD, Ashworth JB, Foltin RW, Johanson CE, Zacny JP, Walsh SL. The role of human drug self-administration procedures in the development of medications. Drug Alcohol Depend. 2008;96:1–15. doi: 10.1016/j.drugalcdep.2008.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conover KL, Shizgal P. Employing labor-supply theory to measure the reward value of electrical brain stimulation. Game Econ Behav. 2005;52:283–304. [Google Scholar]
- Davison M, Jenkins PE. Stimulus discriminability, contingency discriminability, and schedule performance. Anim Learn Behav. 1985;13:77–84. [Google Scholar]
- Elliffe D, Davison M, Landon J. Relative reinforcer rates and magnitudes do not control concurrent choice independently. J Exp Anal Behav. 2008;90:169–185. doi: 10.1901/jeab.2008.90-169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galuska CM, Winger G, Hursh SR, Woods JH. Assessing unit-price related remifentanil choice in rhesus monkeys. J Exp Anal Behav. 2006;86:181–195. doi: 10.1901/jeab.2006.108.05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green L, Freed DE. The substitutability of reinforcers. J Exp Anal Behav. 1993;60:141–158. doi: 10.1901/jeab.1993.60-141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haney M, Spealman R. Controversies in translational research: drug self-administration. Psychopharmacology (Berl) 2008;199:403–419. doi: 10.1007/s00213-008-1079-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernandez G, Breton YA, Conover K, Shizgal P. At what stage of neural processing does cocaine act to boost pursuit of rewards? PLoS ONE. 2010;5:e15081. doi: 10.1371/journal.pone.0015081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrnstein RJ, Loveland DH. Maximizing and matching on concurrent ratio schedules. J Exp Anal Behav. 1975;24:107–116. doi: 10.1901/jeab.1975.24-107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heyman GM, Oldfather CM. Inelastic preference for ethanol in rats: an analysis of ethanol’s reinforcing effects. Psychol Sci. 1992;3:122–130. [Google Scholar]
- Hollard V, Davison MC. Preference for qualitatively different reinforcers. J Exp Anal Behav. 1971;16:375–380. doi: 10.1901/jeab.1971.16-375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hursh SR, Madden GJ, Spiga R, DeLeon IG, Francisco MT. The translational utility of behavioral economics: the experimental analysis of consumption and choice. In: Madden G, Dube WV, Hanley GP, Lattal KA, editors. APA Handbook of Behavior Analysis, Volume 2: Translating Principles Into Practice. American Psychological Association; Washington, DC: 2013. pp. 191–224. [Google Scholar]
- Hursh SR, Roma PG. Behavioral economics and empirical public policy. J Exp Anal Behav. 2013;99:98–124. doi: 10.1002/jeab.7. [DOI] [PubMed] [Google Scholar]
- Killeen P. The matching law. J Exp Anal Behav. 1972;17:489–495. doi: 10.1901/jeab.1972.17-489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madden GJ, Bickel WK, Jacobs EA. Three predictions of the economic concept of unit price. J Exp Anal Behav. 1999;73:45–64. doi: 10.1901/jeab.2000.73-45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maguire DR, Gerak LR, France CP. Delay discounting of food and remifentanil in rhesus monkeys. Psychopharmacology (Berl) 2013;229:323–330. doi: 10.1007/s00213-013-3121-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLean AP, Blampied NM. Sensitivity to relative reinforcer rate in concurrent schedules: independence from relative and absolute reinforcer duration. J Exp Anal Behav. 2001;75:25–42. doi: 10.1901/jeab.2001.75-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mello NK, Stevens Negus S. Preclinical evaluation of pharmacotherapies for treatment of cocaine and opioid abuse using drug self-administration procedures. Neuropsychopharmacology. 1996;14:375–424. doi: 10.1016/0893-133X(95)00274-H. [DOI] [PubMed] [Google Scholar]
- McDowell JJ. On the falsifiability of matching theory. J Exp Anal Behav. 1986;45:63–74. doi: 10.1901/jeab.1986.45-63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDowell JJ. On the theoretical and empirical status of the matching law and matching theory. Psychol Bull. 2013;139:1000. doi: 10.1037/a0029924. [DOI] [PubMed] [Google Scholar]
- Miller HL. Matching-based hedonic scaling in the pigeon. J Exp Anal Behav. 1976;26:335–347. doi: 10.1901/jeab.1976.26-335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers DL, Myers LE. Undermatching: a reappraisal of performance on concurrent variable-interval schedules of reinforcement. J Exp Anal Behav. 1977;27:203–214. doi: 10.1901/jeab.1977.27-203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nader MA, Hedeker D, Woolverton WL. Behavioral economics and drug choice: effects of unit price on cocaine self-administration by monkeys. Drug Alcohol Depend. 1993;33:193–199. doi: 10.1016/0376-8716(93)90060-4. [DOI] [PubMed] [Google Scholar]
- Nader MA, Woolverton WL. Effects of increasing the magnitude of an alternative reinforcer on drug choice in a discrete-trials choice procedure. Psychopharmacology (Berl) 1991;105:169–174. doi: 10.1007/BF02244304. [DOI] [PubMed] [Google Scholar]
- Nader MA, Woolverton WL. Effects of increasing response requirement on choice between cocaine and food in rhesus monkeys. Psychopharmacology (Berl) 1992;108:295–300. doi: 10.1007/BF02245115. [DOI] [PubMed] [Google Scholar]
- Negus SS, Mello NK. Effects of chronic D-amphetamine treatment on cocaine-and food-maintained responding under a progressive-ratio schedule in rhesus monkeys. Psychopharmacology (Berl) 2003;167:324–332. doi: 10.1007/s00213-003-1409-y. [DOI] [PubMed] [Google Scholar]
- Negus SS, Miller LL. Intracranial self-stimulation to evaluate abuse potential of drugs. Pharmacol Rev. 2014;66:869–917. doi: 10.1124/pr.112.007419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Negus SS, Schrode K, Stevenson GW. Mu/kappa opioid interactions in rhesus monkeys: implications for analgesia and abuse liability. Exp Clin Psychopharm. 2008;16:386. doi: 10.1037/a0013088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peartree NA, Sanabria F, Thiel KJ, Weber SM, Cheung TH, Neisewander JL. A new criterion for acquisition of nicotine self-administration in rats. Drug Alcohol Depend. 2012;124:63–69. doi: 10.1016/j.drugalcdep.2011.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rachlin H. On the tautology of the matching law. J Exp Anal Behav. 1971;15:249–251. doi: 10.1901/jeab.1971.15-249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rachlin H, Battalio R, Kagel J, Green L. Maximization theory in behavioral psychology. Behav Brain Sci. 1981;4:371–388. [Google Scholar]
- Rachlin H, Kagel JH, Battalio RC. Substitutability in time allocation. Psychol Rev. 1980;87:355. [Google Scholar]
- Trujillo-Pisanty I, Conover K, Shizgal P. A new view of the effect of dopamine receptor antagonism on operant performance for rewarding brain stimulation in the rat. Psychopharmacology (Berl) 2014;231:1351–1364. doi: 10.1007/s00213-013-3328-x. [DOI] [PubMed] [Google Scholar]
- Woolverton WL. Intravenous self-administration of cocaine under concurrent VI schedules of reinforcement. Psychopharmacology (Berl) 1996;127:195–203. [PubMed] [Google Scholar]
- Woolverton WL, Anderson KG. Effects of delay to reinforcement on the choice between cocaine and food in rhesus monkeys. Psychopharmacology (Berl) 2006;186:99–106. doi: 10.1007/s00213-006-0355-x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.