ON EDGE CHIPPING TESTING AND SOME PERSONAL PERSPECTIVES ON THE STATE OF THE ART OF MECHANICAL TESTING

Abstract

Objective

The edge chipping test is used to measure the fracture resistance of dental restoration ceramics and resin composites. This paper focuses on the progress of evaluating chipping resistance of these materials and also on the progress of standardization of this test method. This paper also makes observations about the state of the art of mechanical testing of ceramic and composite restorative materials in general. Interlaboratory comparative studies (“round robins”) are recommended.

Methods

An edge chipping machine was used to evaluate dozens of materials including porcelains, glass ceramics, aluminas, zirconias, filled resin-composites, new hybrid ceramic-resin composites, laminated composite ceramics, and even polymethyl methacrylate based denture materials. Force versus distance data were collected over a broad range with different indenters. Several chipping resistance parameters were quantified.

Results

Older restorative materials such as feldspathic porcelains and veneering materials had limited chipping resistance, but more modern ceramics and filled composites show significant improvements. A yttria-partially stabilized zirconia had the greatest resistance to chipping. Much of the early work on edge chipping resistance of brittle materials emphasized linear force versus distance trends obtained with relatively blunt Rockwell C indenters. More recently, trends for dental restorative materials with alternative sharper indenters have been nonlinear. A new phenomenological model with a simple quadratic function fits all data exceptionally well. It is loosely based on an energy balance between indenter work and fracture and deformation energies in the chipped material.

Significance

Although a direct comparison of our laboratory scale tests on idealized simple geometries to clinical outcomes has not yet been done, anecdotal evidence suggests the procedure does produce clinically relevant rankings and outcomes. Despite the variations in the trends and indenters, comparisons between materials can easily be made by chipping convenient block-shaped specimens with sharp conical 120°, Vickers, or Rockwell C indenters at a defined edge distance of 0.5 mm. Broad distance ranges are recommended for trend evaluation. This work has provided important information for standardization.

Introduction

The edge chipping test was originally developed in the late 1980s to study hard metal cutting tools at the National Physical Laboratory in London [1-4]. Chips are formed by advancing an indenter into a material near an edge as shown in the insert of Fig. 1. The force required for chip formation, F, increases with distance from the edge, d. The shape of the chip usually is independent of the material tested [1]. J. Quinn pioneered the application of this method to dental restorative materials in the mid-1990s to the time of her untimely death in 2008 [5-12]. This work has continued the ensuing years [13-17] including three papers in this Journal in 2014. Other groups are now using it for the evaluation of human teeth [18], dental restorative materials [19-24], and structural ceramics in general [25-30]. Clinical longevity studies have shown that chipping is a leading cause of restoration failure [e.g., 31-35]. In some cases it is possible to repair restorations, but in others a complete replacement is needed. Scherrer [36] showed eight clinical failures studies of which six were chipping of the veneer. Chipping in veneers has been specifically identified as a problem in modern zirconia restorations [37-39]. In other cases chipping can occur at a crown margin during manufacture [19,40,41] and can weaken the restoration dramatically. . Major cracks emanate from the margin starter chips and split a crown in half [42,43] due to hoop stresses. Unfortunately, the extent of the chipping and the type of chipping is often unreported in clinical studies. Ref. 44 is an interesting exception where six chipping modes were reported for twenty-two class IV restorations in a clinical study of 455 composite resin anterior restorations. Chipping in natural teeth was cited as a common problem associated with tongue piercing jewelry [45].

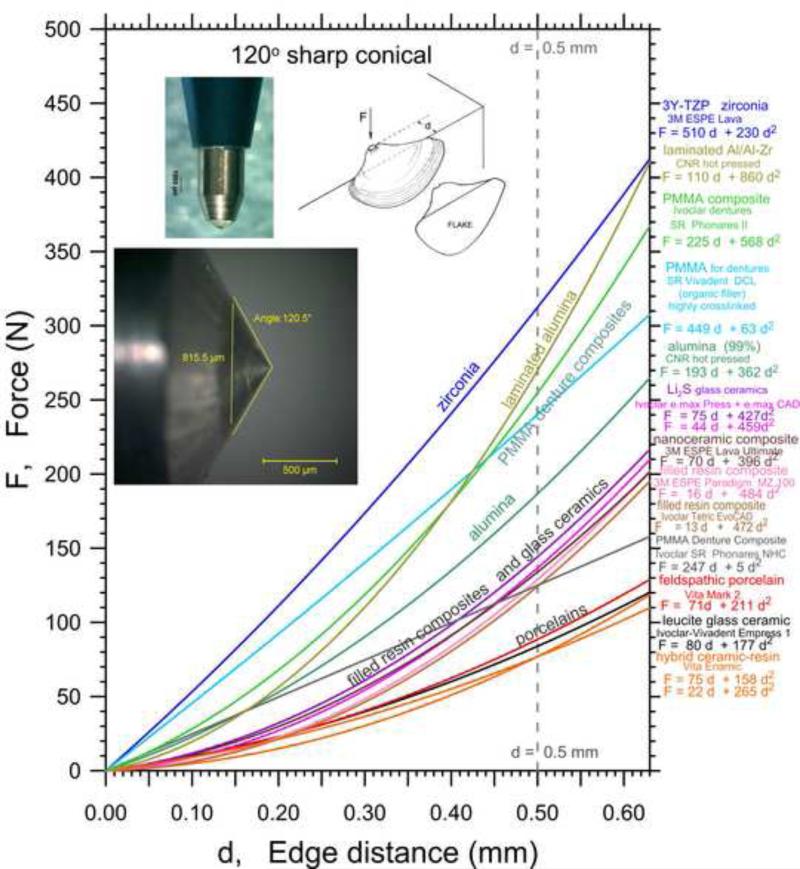
Fig. 1.

Edge chip results for fourteen materials obtained with the sharp conical 120° indenter.

Although the in-vitro edge chip tests use specific indenters on test blocks with carefully prepared edges, the chips physically resemble some types of in-vivo failures [36,41-44]. Our in vitro work [5-17] has focused on testing block-shaped specimens for the most part, but there is no reason that human [13,18] or artificial [14,24] teeth cannot be tested as shown in Fig. 2.

Fig. 2.

Edge chipping may be done on simple bocks or actual teeth as shown here. (a) and (b) show a sharp 120° conical indenter indenting into three teeth mounted side by side. Flats have been ground into the incisal and lingual faces to make a 90° edge. (c) shows a 5 mm alumina ball indenter about to indent three teeth with no flats.

A short review paper on the edge chipping test method as applied to dental materials was prepared in 2012 [12], but there has been substantial progress in the last 2 years [14-17]. Test procedures have been refined. The influence of indenter type has been clarified and it appears that material rankings do not change very much between indenter types. The actual force – distance trends do vary with indenter. Indenter sharpness was identified as a key factor in large part due to sideways wedging forces created during the chipping process [16]. It was shown that the Vickers indenter with face angles of 136° 30’ and edge angles of 148° was equivalent to a 140° sharp conical indenter. Unlike the early assumption that most materials follow linear trends, we now know that nonlinear behavior is common especially for dental restorative materials chipped with sharp indenters. Although a full characterization is best achieved by collecting data over a broad force and distance range, a simple comparison of materials can be made by measuring the “edge strength,” which is the force to make a chip at the arbitrary distance of 0.5 mm as done by Watts et al. [19,20,21]. Simple block shaped specimens that are at least 5 mm thick are adequate for most purposes. Comparative data taken on brittle denture materials showed that the data taken from flattened teeth matched the rectangular wear block data [14].

A new phenomenological model based on energy concepts was introduced in 2014 [16,17]. Indenter energy is converted into fracture and deformation energies in the chipped material. A simple quadratic equation that relates indenter force to edge chipping distance is an excellent match to the nonlinear outcomes measured on all materials tested.

This paper steps back from the details presented in the earlier papers and presents a broader view of the results and includes some fresh data. Nevertheless, the details (e.g., how well the specimen must be mounted, problems with “overchipping” and the post fracture determination of the distance) are important as this method is developed into a standard. There are two draft test method standards on the edge chipping resistance of brittle materials: one in the European committee for Standards [46] and one in ASTM International [47]. One goal of this study has been to recommend improvements or adaptations to the drafts so that the standards will be useful to the dental community.

Materials and Methods

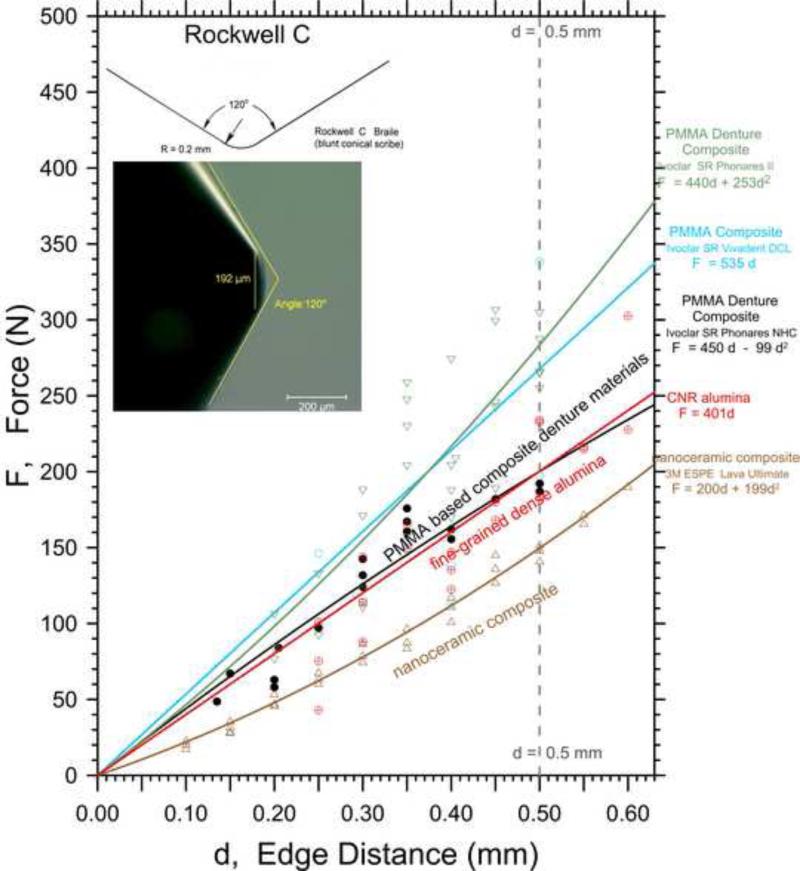
The thirty-two materials have been described previously.^a They include feldspathic porcelains [5,6,10,12,17], leucite porcelains [7,10,12,17], porcelain veneers [10,12], glass ceramics [5-7,15-17], dental and structural aluminas [5,6,9,12,17], dental and structural zirconias [5,6,15-17], filled resin-composites [11,12,17], a new resin nano-filled [17] composite, laminated composite alumina-zirconia ceramics [17,25], and even polymethyl methacrylate based denture materials [12,14]. Test specimens for the various materials varied in size and shape from 3 mm by 4 mm cross section sized bend bar fragments to larger square blocks of 10 mm to 20 mm length per side and 5- 6 mm thick. The most convenient shape was a wear test type rectangular block. Care is needed to grind the surfaces to make well-defined, reproducible edges. Additional details are in the original references. Several newer materials and data sets not included in the earlier publications are included. These include Ivoclar-Vivadent e.max press and e.max CAD lithium disilicate glass ceramics, and Ivoclar-Vivadent resin-filled composite Tetric EvoCAD. Also included are two batches of Vita Enamic, a “hybrid ceramic” made up of interconnected ceramic and polymer phases, that were obtained in March 2012 and in May 2013. New data on a high-purity structural alumina obtained with the Rockwell C indenter are included here for comparison to earlier sharp conical 120° indenter data [25].

A commercial edge chipping machine (Engineering Systems Model CK 10, Nottingham, UK) The 1000 N load cell readout resolution was 0.1 N. A reference mass with a certificate traceable to NIST standards was used to verify the accuracy of the load cell. The apparatus had a moveable head with the diamond indenter, a locating microscope, and an X-Y stage to position the test piece. The edge distance, d, was carefully set to a prescribed value prior to each chip test. All distances were from the specimen edge to the center of the point of load application. Most researchers use this convention especially since analytical fracture mechanics models that are relevant to the edge chipping problem usually are based on the axis of load application. The minimum edge distance was 0.10 mm. Usually twenty to thirty five-chips were made per material-indenter combination at distances from 0.10 mm to 0.60 mm. Force, F, was gradually applied in displacement control at 1 mm/min or 3 mm/min until fracture. For most of the materials, the chips popped off suddenly with an audible snap. All testing was done in laboratory ambient conditions. When a chip popped off, a sudden force drop off was detected by the break-load detection circuitry of the machine and the indenter extracted automatically and the peak load recorded. One problem detected in some of our early work, was “overchipping.” Since indenter extraction was not instantaneous, additional damage and a larger indentation was made in the test piece compared to the condition at the instant before the chip popped off. Overchipping severely affects measurements of the edge distances by posttest examination.

Although we favored the sharp tip (radius less than 5 μm) conical 120° indenter, we also experimented with 120° conical Rockwell C, Vickers, Knoop, and sharp conical indenters with 90° to 140° angles. The Rockwell C indenter may seem sharp, but it actually has a blunt rounded tip with a 200 μm radius and, at small forces, only the rounded tip contacts the test piece.

It is preferable to collected data over a broad range of distances and forces in order to ascertain the full trend. One goal has been to evaluate whether the force distance data was linear (as assumed in most of the early work), or if nonlinear, whether a power law or a new quadratic function was best. If the trend is linear, then:

$$F=T_{e}d$$ (1)

where F is the chipping force and d is the distance from the edge. The slope of the fitted line (usually in terms of force in Newtons per millimeter distance) has been defined as the edge toughness, M or T_e, (N/mm). T_e is numerically equivalent to the force necessary to create a chip at a distance of 1 mm. A power law is sometimes is used:

$$F=A{d}^n$$ (2)

Although this function fits much of the data, the significance of the constants A and n are problematic. The units of A (N/mmⁿ) are hard to rationalize. The physical significance of a non-integer exponent n is also hard to justify and our previous results have shown that exponents can vary from 1 to 2 [12,15,16]. An indentation mechanics model has been proposed [18], but only for the case of n = 1.5.

A better newer quadratic relationship based on a simple phenomenological model was derived in 2014 [16,17]:

$$F=a_{1}d+a_2{d}^2$$ (3)

where a₁ and a₂ are constants. Multiplying each side by d, gives:

$$Fd=a_1{d}^2+a_2{d}^3$$ (4)

This equation has units of energy. The term on the left can be related to the indenter energy, which is the integral of the applied force times distance penetrated during the chipping process. The a₁ terms represent a surface energy term related to fracture surface. The a₂ term is a volume energy term related to deformation volume. A quadratic equation of this form (with surface and volumetric energy terms) has previously been successfully applied as far back as 1941 [48,49,50] to brittle material hardness data, but with indentation load and indentation size as the variables. The quadratic is a much better fit and offers improved material insights and interpretation than the commonly used Meyer [51] law, which is a simple power law like eq. 2. Refs. 16 and 17 have a comprehensive exposition of eqs. 3 and 4 as applied to edge chipping.

Several other parameters to characterize edge chipping resistance have been devised. One is the edge strength, a term proposed by Watts et al. [19,20,21], which denotes the force necessary to create a chip at an arbitrary distance away from the edge. Edge strength with units of N may be represented by the symbol S_E(0.5) where the 0.5 denotes a distance of 0.5 mm, a clinically relevant distance. Alternative distances may be specified. The numerical value of the edge strength, S_E(0.5) with units of N is exactly one half the numerical value of the edge toughness, T_e, (eq. 1) which has units of N/mm, but only if the data fits a linear trend. The edge toughness, T_e is included in the two draft standards [46,47]. The power law Eq. 2, the quadratic Eq. 3, and the edge strength, S_E(0.5) are all included in the draft ASTM standard [47]. The CEN standard [46] also allows chipping measurements to be made at a prescribed distance, but specifies that the output should be reported as edge chip resistance, R_eA which is the ratio of force to distance with units of N/mm.

Results

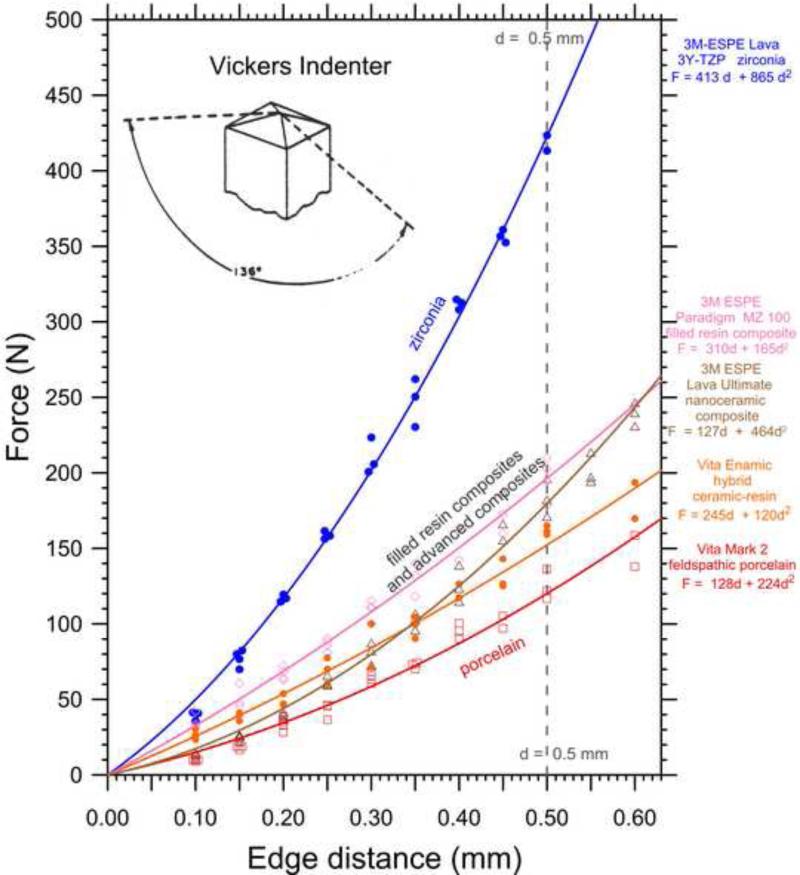
Figs. 1, 3 and 4 show the data trends for the sharp conical 120° (SC120), Vickers, and Rockwell C (RC) indenters, respectively. The best quadratic fit (eq. 3) is shown if the data were nonlinear. These new combined graphs provide an overview of all our findings on the same axes. The differences in edge chip resistance are as much as a factor of four depending upon the indenter type. The original references cited previously have individual data graphs with individual chip results, the data scatter, chip photographs, and uncertainty estimates for the various chipping parameters. Fig. 1 includes new sharp conical 120° indenter results on the Ivoclar-Vivadent e.max press and e.max CAD lithium disilicate glass ceramics, the Ivoclar-Vivadent resin-filled composite Tetric EvoCAD, and Vita Enamic materials. Fig. 3 has new Vickers data for Vita Enamic. (The individual curves for these materials are shown as Supplemental Figures S1 – S4 in the online version of this paper.) Fig. 4 has new Rockwell C data for the dense high-purity alumina (shown in Supplemental Fig. S5) that has not been published previously. The edge strength, S_E(0.5) for the materials can be judged by the vertical dashed lines in Figs. 1, 3 and 4. Two batches of Vita Enamic were evaluated and although, the data was very consistent, slightly different estimates of a₁ and a₂ resulted. Nevertheless, the edge strengths were identical: 77 N. This is very encouraging and suggests a simple approach for standardization. In another instance, results for the e.max press glass ceramic showed the precision of the edge chipping results was so good that edge chip variability with orientation was detected (Fig. S3). The variability was traced to a preferred orientation of the crystals in the pressed material. The e.max press curve shown in the summary Fig. 1 has data from both orientations combined.

Fig. 3.

Edge chip results for five materials obtained with the Vickers indenter.

Fig. 4.

Edge chip results for four materials obtained with the Rockwell C indenter. The data trends for this relatively blunt indenter are more linear than those from the Vickers and 120° sharp conical indenters.

Figs. 1 (SC120) and 3 (Vickers) reveal that the zirconia was the most chip resistant material. The laminated CNR alumina-zirconia composite material and several PMMA based denture materials were next as shown in Fig. 1. Figs. 1 and 4 show that the structural alumina had modest chipping resistance. Modern filled resin-composites and glass ceramics were next. The feldspathic and leucite porcelains and the Vita Enamic hybrid ceramic-resin material had the least chipping resistances.

The data trends for the Vickers and SC120 indenters were very nonlinear, with the exceptions of the SC120 zirconia data and two PMMA denture materials (Phonares NHC and SR Vivadent DCL) materials. All data for PMMA materials had very high scatter so the exact trends could not be ascertained. A linear fit was adequate. The Rockwell C trends in Fig. 4 were linear. More experiments with the Rockwell C indenter on the zirconia (the most chip resistant material) and the feldspathic porcelain (the least chip resistant) are planned to see if they behave linearly as well.

Discussion

The quadratic relationship eq. 3 is a good fit to all data. Depending upon the magnitudes of a₁ and a₂, the trend may either be essentially linear or nonlinear. Much of the data collected with the sharp conical 120° and Vickers indenters are nonlinear and have significant a₂ terms. In contrast, most of the blunter Rockwell C indenter data is practically linear and the a₁ term dominates. This indenter creates a primarily elastic contact impression. The deformation energy a₂ term is small and most of the indenter energy is converted to fracture. Even if the numerical values of a₁ and a₂ are comparable, the former dominates at d < 0.5, since the square of d (in the a₂d²) term is small. This term becomes more important as d approaches 1 mm.

The sharper Vickers and SC120 indenters create more permanent deformations, but at short distances from the edge (d << 1) only a small force is needed to cause fracture and the deformations are small. The nonlinear a₂ term begins to dominate as d approaches 1 mm. In the limit, far away from an edge, most of the indentation energy is expended in deformation and chip fracture does not occur. (Surface fracture energy is consumed by formation of indentation median, lateral, and radial cracks and shear faulting cracking around the indentation site, however that is a different problem from edge chipping.) The respective contributions of the fracture and deformation fracture terms can be simply understood by substituting d = 1 mm into eq. 3, so that F = a₁ + a₂.

More work needs to be done to directly correlate the a₁ and a₂ terms to hardness, H, elastic modulus, E, and fracture surface energies or fracture toughness, K_Ic. Our recent work has focused on collecting data with the newer dental restorative materials or with structural ceramics having a broader range of H, E, and K_Ic properties. New data are also being collected to compare the behavior of sharp versus blunt indenters. If the blunt RC indenter creates linear data trends, then good correlations between a₁, T_e and K_Ic are expected, much as shown in the early edge chipping work [3,4].

The good news is that the F – d curves usually do not cross over. This allows easy ranking of materials and a single edge chip resistance force at an arbitrary distance of 0.50 mm, as advocated by Watts et al.[19,20,21] and suggested in the CEN prestandard [46], is completely suitable for routine evaluations and comparative purposes. (The CEN prestandard does not report the outcome as the edge strength, but as the edge chip resistance, R_eA which is the ratio of force to the set distance with units of N/mm.)

The individual data curves shown in Supplemental figs S1 – S4 and in the earlier publications show very little scatter with the sharp conical and Vickers indenters (with the exception of the PMMA denture materials). It is important to collect data with at least 20 and preferably 30 or more chips over a broad range of d's for a trend line analysis. Even so, it appears that there can be some variability in the estimates of a₁ and a₂ as shown in Fig. S4 for the Vita Enamic ceramic resin composite for which we tested two batches a year apart. The two data sets (n = 38 and n = 44) could be added to create a larger n = 82 data set and improved estimates of a₁ and a₂. One way to obtain uncertainty estimates for the two constants would be to graph P/d versus d, (a simple transformation of eq. 3) so that the data could be regressed with a line having a slope of a₂ and an intercept (d = 0) of a₁. If the goal is to merely obtain a simple ranking number, the edge strength S_E(0.5) is perfectly suitable, and as few as five chips at d = 0.5 mm may be all that is needed no matter what the data trend may be!

Standardization opportunities for the edge chipping test

The two draft standards for edge chipping, prepared for other classes of brittle materials (structural ceramics and cutting tools) can be simply adapted to include dental materials. The CEN prestandard [46] was originally written with the expectation that F versus d trends were linear. That was quite reasonable and was due in large part to the fact that a lot of the early data was collected with the Rockwell C indenter. The prestandard specifies that edge chip resistance, R_eA be reported as the ratio of force, F, divided by distance, d. This ratio is computed for each and every chip and has units of N/mm. The overall edge chip resistance, $\overline{R_{eA}}$, is the average value of the individual results:

$${\overline{R}}_{eA}=\sum _{i=1}^N\frac{R_{eAi}}{N}$$ (3)

The edge chip resistance is very similar to, but not exactly the same as the edge toughness. Both have units of N/mm. T_e is the slope of a regressed line through many data points collected over many distances. $\overline{R_{eA}}$ is the average of all the individual F/d ratios. If the data are linear and are tightly clustered about the line, then edge toughness, T_e, and edge chip resistance, $\overline{R_{eA}}$, are about the same. The CEN prestandard [46] recommends that edge chips be made at a starting distance of 0.5 mm, but then other distances may be used as required depending upon the material. Although this distance is the same as advocated by Watts et al.,[19,20,21] the interpretations of the data are different. The edge chip resistance, $\overline{R_{eA}}$, is a force to distance ratio. The edge strength, S_E (0.5) is a force.

If the data are nonlinear, as with sharp indenters in the present study, then the edge chip resistance (an average F/d ratio) or the edge toughness, T_e, parameters are very problematic.

The draft ASTM standard [47] is more flexible. It allows sharp and blunt indenters and recognizes data may be nonlinear. If data are nonlinear, then either the trend itself can be reported, or more simply, the edge strength S_E(0.5). If the data are linear, then T_e, or $\overline{R_{eA}}$, or S_E(0.5) may be reported.

Eventually, an interlaboratory study (ILS, “round robin”) will be needed for this test method. There are not enough laboratories doing edge chipping at the present time to obtain a critical mass, however. So for example, ASTM International recommends no less than six laboratories (and preferably more) participate in order to obtain suitable repeatability and reproducibility uncertainty estimates [52]. Round robins can be very valuable but must be carefully planned and executed.

Observations about the state of the art of mechanical testing

Up to this point, the author has focused on one specific mechanical test method that is undergoing development. In a sense, this is a “case study” of how a test method evolves and matures into a rigorous consensus Standard. This process takes years. Round robins are an important step in this process. The author has considerable experience organizing and managing round robins over the course of thirty years. In the 1980s and 1990s, I conducted six successful round robins on flexural strength (1), fracture toughness (2), fractographic analysis (1), hardness (2) of advanced technical or structural ceramics and participated in many more. In my twenty years working full or part time in the dental materials field, I not have been aware of any ceramic or resin matrix composite mechanical property round robins. This is despite the fact that voices have been raised in the field about the validity, or lack thereof, of many of the testing procedures in use!

Kelly is to be commended for raising such concerns several times. His 2012 “Slippery Slope” paper [53] in this journal squarely identified the problems with shear bond tests, wear tests, and load-to-failure test of restorations that have little or no value because they are simply not clinically relevant. “Crunch the crown” tests often create fractures that bear no resemblance at all to actual fractures. Darvell rightly raised reservations about the validity of Brazilian disk (diametral compression) strength testing [54]. In nearly all instances, fracture occurs from contact cracks at the loading anvils and not from the middle as assumed in the usual analysis. In other words, most diametral compression data are wrong. Ruse [55] pointed out that no one noticed that people have been using a modulus of elasticity for periodontal ligaments for the last quarter of a century that was in error by a factor of one thousand.

There remain lingering questions about the validity of many of the flexural strength and fracture toughness procedures in use for ceramics and composites. The Academy of Dental Materials has occasionally published editorials and or papers calling attention to these matters, but little has changed. The Academy is to be commended for organizing the focused meeting in October 2009 in Oregon on “Adhesion in Dentistry –Analyzing Bond Strength Testing Methods” [56]. The articles in that 2010 special issue of Dental Materials were impressive and there were thoughtful discussions of testing issues for methods as controversial as the shear bond strength test. There was brief mention in Heintze's paper [57] about a round robin on adhesion by the notched-edge shear bond strength tests that was used to revise ISO standard 29022 [58]. The ADM conference organizers [56] quoted DeHoff: “....bond strength test may still provide useful information on procedural; changes although the actual bond strength value may have little meaning.” The organizers concluded: “... the field appears not to have moved significantly forward in terms of describing the true significance of bond strength testing . . ”

I have broached this matter of the quality of test data with a number of scientists and engineers in the field, and the consensus is that there problems, but there is little or no agreement on how to proceed. I believe this is in part due to pressure to publish, to write proposals to get funding, and to rapidly advance new products to the marketplace. Few have the time or inclination to delve into the details of the test methods or to optimize them. There is a lack of funding support and leadership for such work. A common refrain is: “we know there are weaknesses in the methods, but we only need the numbers for comparatives purposes.” The same argument was used 30 years ago before we set out to improve and standardize rigorous, valid test procedures for advanced structural ceramics. In this author's humble opinion, this is a lame excuse to justify faulty data.

All is not grim, however. Della Bona and colleagues have considered the use of documentary standards in international dental journals [59] and recommended that journal editors encourage authors to use standards more often. Additional cause for optimism arises from in vitro tests on simulated or actual restorations that mimic in vivo clinical fractures [e.g., 60,61,62,63,64].

The dental materials community should organize more ceramic and resin composite mechanical property round robins. For example, three common questions are: “How carefully should bend bars be prepared? Do little bend bars in three-point bending produce valid flexural strength results? How complex a fixture should be used?” The questions are of concern for ceramics, glass ceramics and resin-matrix composites and could be answered by a round robin with laboratories conducting tests on large and small bend bars on common materials. One possible venue is the Versailles Advanced Material and Standard (VAMAS) program [65]. VAMAS may be a good home for running such tests, but it will require some dental materials leaders to step forward and some agency or consortium of companies to provide some modest funding support.

VAMAS, a possible venue for prestandardization collaborations

VAMAS was launched in 1982 following an economic summit meeting held in Versailles by the G-7 Heads of State and representatives from the European Communities. Current members include Australia, Brazil, Canada, China, France, Germany, India, Italy, Japan, Mexico, South Africa, United Kingdom, and United States. VAMAS supports world trade in products dependent on advanced materials technologies, through international collaborative projects aimed at providing the technical basis for harmonized measurements, testing, specifications, and standards [65]. It does not provide funding, nor are there direct costs for participation. It is a neutral forum to coordinate prestandardization projects such as round robins. There are a number of Technical Working Areas (TWAs) devoted to different materials topics. TWA #3, Ceramics was an effective collaboration from 1990 to 2002 while I was its chairman. More than fifty laboratories and over 100 participants around the world ran a dozen full scale round robins with over 12,000 experiments on strength, hardness, grain size and porosity, elastic modulus, fracture toughness, and fractography [66]. TWA 3 conducted five full-scale round robins on fracture toughness with 4,500 experiments with forty participating laboratories [67]. A total of fourteen projects eventually were completed by TWA 3 [68] by 2004 when it finished its work. This work led directly to dozens of rigorous ASTM, European Community, Japanese Industrial Standards, ISO standards and even the world's first and only standard reference material for fracture toughness, K_Ic [69,70].

Round robins can be very valuable, but should not be undertaken lightly since they are a lot of work, they may raise more questions than they answer, and they may even backfire if one is not careful [66,67]. With good planning and management, round robins can accomplish a lot. They help:

1. Determine whether the procedure is sound

A round robin may determine whether a procedure can be done at all by other than expert laboratories. Equipment limitations, instruction problems, or practicality issues cannot be ignored. What are the pros and cons? What are the special tricks or secrets? What are the weak points? A round robin may determine the robustness and ruggedness of a procedure, since the participants inevitably make slight departures (intentional or unintentional) from the specified procedures. For example, several weaknesses in the single edged precracked beam (SEPB) method for fracture toughness were highlighted in a VAMAS round robin [67]. SEPB had been widely used in Japan. European laboratories had much greater difficulty due to precracking problems. These were traced to inadequate precracking fixtures. A high quality precracker with good alignment must be used.

2. Identify needs for future prestandardization research

For example, a round robin on instrumented indentation hardness identified severe problems with reproducibility of results from different laboratories. Despite glowing claims from equipment manufacturers, instrumented indentation and nanoindentation methods are notoriously inconsistent for hardness and even elastic modulus [71,72]. As another example, the SEPB ceramic fracture toughness round robins demonstrated that it is difficult to align a crack in a miniature three-point bend fixture [67]. Inflated fracture toughness values were obtained. This prompted one team to do new analytical work that refined the tolerances for precrack and fixture alignment. This work may prove useful for the dental materials community.

3. Furnish data for uncertainty statements in Standards. Are the results accurate and precise?

The strong precision and bias statement in the ASTM standard for ceramic fracture toughness [73] uses results from the VAMAS surface crack in flexure and SEPB round robins [67].

4. Identify needs for Reference Materials

The VAMAS projects on fracture toughness prompted NIST to prepare SRM 2100, the first reference material in the world for K_Ic.

5. Encourage laboratories to try new methods

6. Spread awareness of test methods favored in one country or group of countries

For example, the SEPB method which was popular in Japan was not widely used elsewhere due to perceptions about the difficulty of the method. These perceptions were dispelled after the VAMAS round robins. Participants were impressed with the quality of the results.

7. Expand scientific and technical knowledge

For example, the effects of stable crack growth on ceramic SEPB fracture toughness results were under appreciated until the first VAMAS fracture toughness round robin. One solitary laboratory with “outlier” results recognized the problem and brought it to the attention of all others [67]. The outlier laboratory was right! As another example, the razor-paste SEVNB round robin corroborated other research that showed the maximum allowable notch tip width for valid results can be directly related to the microstructure of the material [67]. The round robin showed that it is not possible to obtain valid, accurate results on yttria-stabilized zirconia materials with submicron grain sizes. That has not stopped ISO TC 106 from incorporating it in the latest drafts of ISO 6872 [74], much to this author's consternation.

8. Foster good communications between the standards researchers around the world

VAMAS projects enhanced “grass-roots” collaborations between scientists, engineers, industrialists, and standards writers in a neutral environment at a prestandardization level. Experts argue about technical details at an early stage, not in an ISO meeting. Our experiences with round robins paved the way for rapid standardization of over forty standards for structural ceramics in ISO Technical Committee 206, Fine, Advanced Ceramics. Additional information about particular round robins, and rounds robins in general, including my ten Rules of Thumb for round robins may be found in Refs. [66,67].

Overall utility of the edge chipping method

One criticism of the common lab scale edge chip tests is that they use sharp diamond indenters in very controlled conditions with specimens having nicely-defined 90° edges. People usually do not chew on sharp diamonds and teeth do not have flat surfaces with 90° corners. Would such tests provide useful comparisons? The answer is yes. One could apply the same reservations to classic fracture toughness (K_Ic) tests (e.g., compact tension specimens or single-edged precracked bend bars), but no one would deny that fracture toughness is a useful index for quantifying breakage resistance. The objective with the laboratory edge chip test is to measure chipping resistance under controlled conditions on convenient well-defined testing configurations. Future work could directly compare edge chip resistances measured with rectangular blocks and controlled indenters, to results obtained with large balls (Fig 2c), or even in vivo clinical outcomes.

The earliest work utilized conventional microindentation hardness machines or even universal strength testing machines adapted to collect chip data. It was very difficult to precisely align the indenter on the latter type machine. Edge distances had to be estimated with a separate microscope after a chip popped off, a difficult and problematic step. Chipping on conventional hardness type machines was not easy either. Although the built-in microscope could be used to precisely align an indenter a precise distance from the edge, such machines are designed to apply a constant peak force to a specimen (often by dead weights) and if a chip popped off they did not record the peak force. Maximum loads were 9.8 N (1 kgf) to 98 N (10 kgf), which are inadequate for most edge chipping work as may be seen by examining the vertical axes in Figs 1, 3, 4 of this paper. The limitations of such equipment designed for other purposes led several labs to construct dedicated edge chipping devices. The CK10 machine used in this study (and its predecessors) made by the Engineering Systems company in England are no longer available, due to the small demand for such machines in the late 2000s. As edge chipping is used by more laboratories and is encouraged by the existence of formal documentary standards, one can hope that commercial machines will become available again. Hopefully some improvements will be made to the microscope optics. The optics were adequate for metals and black opaque cutting tool materials, but were woefully inadequate for white translucent ceramics. The CK10 also has a troublesome loading lag at approximately 30 N – 40 N force, corresponding to the 3 kg – 4 kg mass of the upper crosshead which lifted on the crosshead drive screws during the displacement-controlled loading of the indenter.

Recent work by Tanaka and colleagues [23] has shown how a modern digital camera can be mounted on a universal strength teasing machine to facilitate the alignment of the indentation at a specified distance from the edge, prior to a test. Alternatively, some modern hardness machines have built-in load cells and rely on computer programing and closed loop feedback circuits to apply steadily increasing force to Vickers, Knoop or other indenters. They can presumably be programed to conduct edge chipping tests. Unfortunately some of these devices have woeful microscopes with crude optics, having no aperture or field diaphragms.

Conclusions

The edge chip resistances of thirty materials differ by as much as a factor of four. The Rockwell C indenter produces data trends that are approximately linear over the distance ranges used in this study. Scatter is somewhat greater with this indenter, but the edge strength, S_E(0.5), edge toughness, T_e, and edge chip resistances $\overline{R_{eA}}$ generate comparable material rankings. On the other hand, sharper indenters create more deformation at the contact site leading to nonlinear trends. The relative amounts of deformation and fracture energies vary with distance and force.

The edge chipping test is emerging as a new tool for researchers to use to characterize dental restorative materials and has great potential for standardization. A round robin should be done for edge chipping in the coming years. The dental community must find some way to begin round robin testing for mechanical properties of restorative materials in general. A number of very high quality test method standards were devised by the advanced, fine ceramic community in the 1990s, and it should not be too difficult to adapt these to dental materials. The dental materials community must find some way to organize more round robins to improve the state of the art of mechanical testing. The VAMAS collaboration is one possible venue.

Highlights.

Edge chipping tests with simple rectangular test blocks evaluate a materials resistance to chipping.

Materials may be ranked for their chipping resistance.

Force versus distance trends may be linear or nonlinear depending upon the sharpness of the indenter.

A new model of edge chipping resistance is presented.