Brain Microdialysis as a Tool To Explore the Ionic Profile of the Brain Extracellular Space in Neurocritical Patients: A Methodological Approach and Feasibility Study

Abstract

Our aim is to determine whether the ionic concentration in brain microdialysate enables calculations of the actual Na⁺, K⁺, and Cl⁻ concentrations in vitro and whether this method can be applied to determine the ionic concentrations in the brain extracellular fluid. We designed an experiment using CMA-71 probes (M Dialysis, Stockholm, Sweden) and the standard conditions used in a clinical setting. Nine CMA-71 probes were inserted in different matrices and perfused with mock cerebrospinal fluid containing 3% albumin at the standard infusion rate used in the clinical setting (0.3 μL/min). Microvials were replaced every 12 h, and the ionic concentrations, both in the dialysate and the matrix, were analyzed. For each ion, scatter plots were built, with [Na⁺], [K⁺], and [Cl⁻] in the dialysate as the predictor variables and the matrix concentrations as the outcome variables. A linear regression model allowed us to calculate the true ionic concentrations in the matrix. To demonstrate the feasibility of the method, we present the calculated ionic profile of one patient with a malignant infarction and a second with a severe traumatic brain injury. Our results confirm that the ionic concentration in microdialysate can be used to calculate the true concentrations of ions in a matrix and the actual concentrations in the extracellular fluid. Microdialysis offers the unique possibility of monitoring the dynamic changes of ions in the brain over time and opens a new avenue to explore the brain's ionic profile, its changes in brain edema, and how this profile can be modified with different therapies.

Introduction

Acute injury to the brain causes a variable disruption of ionic homeostasis and massive ionic fluxes with subsequent osmotic water movement across the cells and brain edema. Brain edema and the resulting increase in intracranial pressure (ICP) is a major cause of death and disability in patients with traumatic brain injury (TBI). Despite a much better understanding of its pathophysiology and molecular mechanisms, and an explosion in potential therapeutic targets, the translation of experimental findings into the clinical setting has not yet been successful, and the therapeutic options for managing brain edema are very limited thus far. The lack of translation is a result, in part, of the scarce availability of tools with which to monitor ionic shifts in the brain in the clinical setting, and this has restricted most of the relevant experiments of brain edema to animal models.

Microdialysis (MD) is a powerful tool that can monitor the composition of the interstitial spaces of any organ in vivo and allows for the quasi-continuous neurochemical sampling of the brain extracellular fluid (ECF) in neurocritical patients.^1,2 The tip of the MD probe is a porous semipermeable membrane that permits the diffusion of molecules in both directions until the ECF composition of the organ into which the probe is implanted equilibrates with the perfusate.³ Brain MD has been primarily used to study brain-energy metabolism, but it has rarely been used to study the ionic profile of the human brain.^4–7 Reinert and colleagues showed that 20% of patients with a severe TBI had increased K⁺ in the dialysate and that high levels of extracellular K⁺([K⁺]_ECF) were associated with increased ICP and poor outcomes.⁶ In different animal species, MD has also been used to study the ionic profile of uterine and nasal fluids.^8–11

A general principle in MD is that the dialysate does not reflect the actual concentration of the analyte of interest, but is only an estimate of the actual concentrations in the ECF.^10,12–15 Recovery is defined to be the proportion of compounds extracted in vitro from the medium surrounding the probe.¹⁶ The relative recovery (RR) is the efficiency of the probe in recovering a specific molecule and is primarily determined by the molecular weight cutoff and other properties of the MD probe. The recovery of an MD membrane is defined—and can be different—for each solute of interest, because despite their similar molecular weight and similar sizes of the pores in the membrane, the RR of different molecules can differ dramatically.¹⁷ In order to use MD to study the ionic profile of the brain ECF in a clinical setting, it is necessary to know the RRs of the ions of interest. To our knowledge, this information is not yet available, although it has been extrapolated from experimental studies, which have used various methods of calculation. Most frequently, the method of Bungay has been used to calculate the RR of the molecules of interest and correct the dialysate concentration.^3,18–20 Bungay's method uses a perfusate that does not contain the solute of interest, and thus in order to study ionic recovery, distilled and deionized water must be used. The main disadvantages of this method are that the ECF is diluted and that the fluid recovery is unstable as a result of the hypotonicity of the perfusate. Further, the continuous infusion of a hyposmotic fluid may cause brain lesions and is not approved for human use. In neurocritical patients, the commercial perfusate routinely used is mock cerebrospinal fluid (CSF) with variable concentrations of Na⁺, K⁺, Cl⁻, Ca²⁺, and Mg²⁺.

The aim of our study was to investigate the feasibility of using brain MD as a method to study the dynamic changes in the concentration of ions in patients with an acute brain injury.²¹ We aimed to 1) analyze in an in vitro model whether the recovered microdialysate (using commercially available 100-kDa membranes perfused with mock CSF at 0.3 μL/min) accurately reflects the Na⁺, K⁺, and Cl⁻ concentrations in a medium with a known predefined ionic concentration (matrix) and 2) study the ionic profile of the brain ECF in 2 patients, one with a severe traumatic brain injury and a second with a malignant stroke.

The results of this study showed that the in vitro ionic concentration can be reliably calculated from the dialysate concentrations by using an ordinary least-squares linear regression model. Implementing this method at the bedside of patients with acute brain injuries is feasible and allows clinical monitoring of the ionic concentrations of the brain ECF and the changes in these concentrations over time.

Methods

The present study was conducted in three stages: 1) calibration of the in vitro experimental setting; 2) calculation of the true in vitro concentrations of Na⁺, K⁺, and Cl⁻ by using the conventional method of calculating the RR and by applying a linear regression model; and 3) study of the feasibility of the methodology in 2 patients in whom the probe was placed in different areas of the brain (injured/core, penumbra, or macroscopically normal brain).

Calibration of the in vitro experimental setting

The microdialysis probe

In the in vitro experiments, 9 sterile CMA-71 probes with a 10-mm dialyzing membrane were used (manufacturer reference #8010320; M Dialysis AB, Solna, Sweden). These probes are approved for clinical use in Europe (CE marking approval according to the Medical Device Directive 93/42/EEC). To avoid systematic errors in the manufacturing process, we used catheters from 4 different lots. According to the manufacturer's specifications, this probe has a nominal cutoff of “around 100 kDa.”²² The 60-mm shaft is made of polyurethane and has an outer diameter of 0.9 mm. The dialyzing membrane is 10 mm long, has an outer diameter of 0.6 mm, and is made from polyarylethersulphone. The inlet and outlet tubes are also made from polyurethane and have a 1-mm outer diameter. The catheter contains a gold tip, making it visible on a computed tomography (CT) scan and thus allowing for the determination of the exact position of the probe.

The infusion pump and the perfusate

The in vitro experiments were conducted with a compact, flexible, dual-syringe pump designed for low pulse-free flow rates and suitable for MD (CMA-402 pump; CMA Microdialysis AB, Kista, Sweden). The pump allows for each of the two syringes to be controlled independently and is precalibrated for 1-, 2.5-, and 5-mL syringes and for flow rates between 0.1 and 20 μL/min. The experiments for this study were conducted with a 1-mL syringe connected to the catheter. For all of the experiments, the flow rate was set to infuse commercially available isotonic sterile perfusate that is specially developed for brain MD (perfusion fluid CNS, ref. no.: P000151; M Dialysis AB) at a constant rate of 0.3 μL/min. This artificial solution has a composition similar to human brain interstitial fluid, an osmolality of 305 mOsm/kg, and the following composition: NaCl 147 mmol/L; KCl 2.7 mmol/L; CaCl₂ 1.2 mmol/L; and MgCl₂ 0.85 mmol/L. The total Cl⁻ content for this solution is 153.8 mmol/L. To facilitate the in vitro calibration of the high cut-off membranes, 3% albumin (3 g/dL) was added to the perfusate. The addition of 3% albumin to the perfusate provokes minor changes in the final concentration of ions. The new obtained concentrations were: NaCl 143.5 mmol/L; KCl 2.6 mmol/L; CaCl₂ 1.02 mmol/L; MgCl₂ 0.72 mmol/L; and 144.9 mmol/L as a total content of Cl⁻.

Experimental design and calibration of the system to zero fluid loss

The objective of the laboratory setting was to design an in vitro system that simulates the conditions found in vivo when CMA-71 probes are implanted. The glass tubes—without additives—containing the test solution (BD Vacutainer^®; Becton Dickinson, Franklin Lakes, NJ) were placed on a dry bath (Labnet International, Edison, NJ), and the relative vertical positions of the pump, the tip of the probe inside the tube, and the top of the microvial were controlled, as was the temperature. Controlling the difference in height between the different components of the pump and the probe is crucial for controlling the small changes in hydrostatic pressures inside and outside the probe that can significantly affect fluid recovery. The CMA-71 catheter tip was placed inside the solution through a channel made by a 14G safety IV catheter (Introcan Safety^® 14G, 2.2×50 mm; B. Braun Melsungen AG, Melsungen, Germany) inserted into the center of the rubber closure to establish a channel to introduce the MD probe and prevent fluid evaporation and bacterial contamination (Fig. 1). The other end of the catheter was connected to the CMA-402 pump that infused the perfusion fluid at 0.3 μL/min.

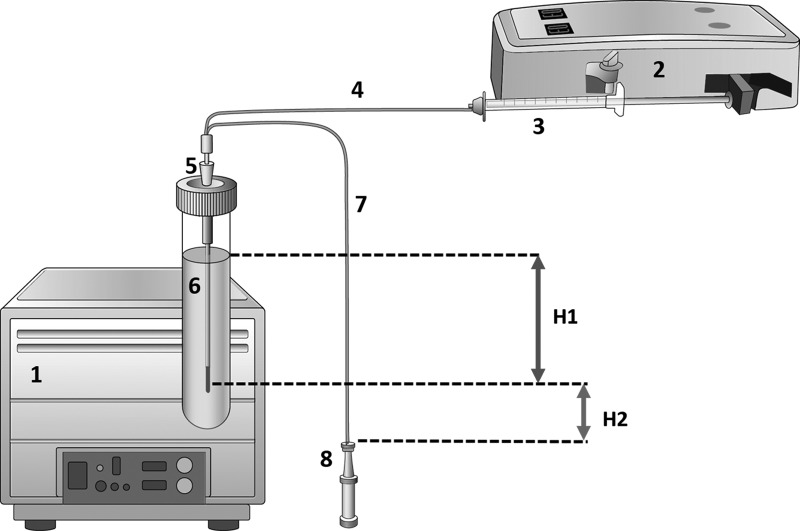
FIG. 1.

Diagram of the general setup for the in vitro experiments. For the sake of clarity, sizes have been altered and are not proportional to the reality. 1) Dry or wet bath, where the tube containing the matrix is placed to control the temperature of the experiment constant. For this particular experiment, a dry bath without agitation was used. 2) CMA 402 dual-syringe pump designed for low pulse-free flow rates. 3) Syringe. 4) Inlet tubing of the CMA-71 probe. 5) 14G safety IV catheter. 6) Matrix solution (for exact composition, see the text). 7) Outlet tubing of the CMA-71 probe. 8) Microvial. H1. Height from the surface of the solution to the mid-point of the dialyzing membrane (10 mm in length); H2. Height from the mid-point of the MD membrane to the top of the microvial. In the real setup and for this particular experiment, the syringe (3) and the microvial tip (8) were in line with the mid-point of the 10-mm MD membrane and therefore H2 was equal to 0 mm.

In each experiment, the first step was to equilibrate the inflow and outflow volumes to make certain that no fluid was lost into the matrix (i.e., to obtain 100% volume recovery) and, consequently, to verify that both hydrostatic and osmotic pressures across the membrane were in equilibrium. To do so, the same isotonic perfusion fluid CNS was used both in the perfusate and in the matrix. In our experiments, the osmotic pressure was equal on both sides of the membrane; thus, according to the Starling equation, the probe's internal hydrostatic pressure and matrix hydrostatic pressure were considered to be in equilibrium when there was no net fluid movement across the dialyzing membrane, and fluid recovery was thus close to 100% (18 μL/h). The hydrostatic pressure inside the probe at the level of the tip is the pressure that the pump generates in the circuit—this was determined to be approximately 1 mm Hg—plus the hydrostatic difference between the pump and the tip of the MD probe (in most experiments, this was set at 0 mmH₂0). The hydrostatic pressure inside the probe at the level of the tip depends on the pressure that the pump generates in the circuit. This was determined in an in vitro experiment in which the pump was connected to a CMA71 probe through a three-way stopcock, and the circuit pressure was continuously monitored for 24 h with a minute-by-minute recording—by a computer and LabChart Software—through the lateral channel by using a conventional solid-state Camino probe. For 1444 readings, the mean circuit pressure was 0.98±0.53 mm Hg. Therefore, for in vitro calculations, we assumed a 1-mm Hg hydrostatic pressure equivalent to 13.6 mmH₂O. The hydrostatic pressure that the matrix exerts on the external side of the MD membrane depends on the fluid density, the gravitational constant, and the vertical height of the matrix column. After various adjustments in the experimental design, it was observed that when the mid-point of the 10-mm membrane was placed 13.6 mm under the matrix surface (H1), a steady state was easily achieved. Thus, the CMA-71 probe was introduced vertically into the tube containing the matrix, with the tip of the dyalizing 18.6 mm below the surface of the solution (Fig. 1). The top of the microvial was aligned with the mid-point of the membrane (H2=0 mm). This setup allowed us to recover approximately 100% (18 μL/h) of the volume, without the need to add any colloid to the perfusate when the matrix and the perfusion fluid were isotonic and did not contain any macromolecules. However, because we used different ionic concentrations in our experiments, it was easier to increase the osmotic pressure by adding albumin to the perfusate to facilitate steady fluid recovery. Different albumin concentrations (2.0–3.5%) were tested, and fluid recoveries close to the expected volumes were achieved when 3% albumin was added.

In vitro determination of relative recovery for the ions of interest

A total of 9 different catheters were used in these experiments. In seven catheters, the experiments were conducted at room temperature (22–23^°C) and in 2 probes at 37^°C. For the sake of simplicity and because the obtained data were not significantly different at both temperatures, most experiments were conducted at room temperature. Different matrix solutions with different ionic concentrations were prepared under sterile conditions and sampled by each catheter. Study matrices were prepared with 1) Milli-Q water, 2) different amount of sodium chloride and potassium chloride salts (Carl Roth, Karlsruhe, Germany), and 3) a constant concentration of 200 mg/L of serum human albumin (Grifols, Barcelona, Spain). This external concentration of albumin was chosen because it is within the reference range for normal human CSF.^23,24 The whole preparation process of the matrices was carried out inside a laminar flow hood to avoid bacterial contamination. The range of ionic concentrations for the different matrices are summarized in Table 1.

Table 1.

Ionic Concentration of MD Perfusates, Reference Range for CSF Ionic Concentrations and Range of In Vitro Tested Concentrations

	Ionic concentration of MD perfusates
	CNS perfusion fluid	CNS perfusion fluid+3% albumin	Ringera	Ringer lactatedb	Normal saline	Control group (lower-upper)	In vitro tested concentrations
Na+ (mmol/L)	147	143.5	145.3	130	154	130–164	115–195
K+ (mmol/L)	2.7	2.6	5.4	5.4	—	2.8–3.6	2.0–7.5
Cl− (mmol/L)	153.8	144.9	155.3	111.8	145	115–144	120–192
Ca2+(mmol/L)	1.2	1.02	4.6	2.7	—	—	—
Mg2+ (mmol/L)	0.85	0.72	—	—	—	—	—
Osmolarity (mOsm/L)	305	286	308.6	273	308	—	—

Lower-upper indicates lower upper thresholds calculated by the robust method described in the National Committee on Clinical Laboratory Standards (NCCLS) and Clinical and Laboratory Standards Institute (CLSI) guidelines C28-A2 and C28-A3 (n=22).

^aComposition from Fresenius Kabi (Bad Homburg, Germany).

^bComposition from B. Braun Melsungen AG (Melsungen, Germany).

MD, microdialysis; CSF, cerebrospinal fluid.

The matrices were placed in 5-mL tubes (BD Vacutainer; Becton Dickinson), and the CMA-71 probes were inserted as shown in Figure 1. Minor adjustments to H2 were made before each experiment to correct for small differences in hydrostatic pressures and obtain a zero-fluid loss and a fluid recovery close to the expected theoretical volume (18 μL/h). In each experiment, the dialysate of the first hour was always discarded. Once a steady state was achieved, each catheter was perfused for a median of 5 days (120 h; min-max, 48–180 h). The microvials were changed every 12 h, and both the container and the matrix were replaced every 24 h to avoid volume loss by evaporation and the consequent variations in hydrostatic pressure and ionic concentration. Every time the microvials were replaced, a small volume of the matrix was sampled to verify that no significant changes had occurred in the solution as a result of evaporation or other uncontrolled factors. The microvials were stored at 4°C in the same conditions as the matrix solution until analysis.

For ion determination, dialysates and matrix samples were analyzed by the AU5400™ analyzer (Diagnostic Systems Group, Melville, NY). This system uses selective ion electrodes with the following detection ranges: 10–400 mmol/L for Na⁺; 2–200 mmol/L for K⁺; and 15–400 mmol/L for Cl⁻. The coefficient of variation for the analyzer in the study period was approximately 1% for all the three ions (0.7% for Na⁺, 1.1% for K⁺, and 0.9% for Cl⁻).

To calculate the true concentration in the matrix, two mathematical models were used: 1) the calculation of RR to correct the concentration obtained in the dialysate. RR was calculated by the equation proposed by Bungay and colleagues^18–20 for the situation when the perfusate contains the solute of interest: RR=(C_md – C_in/C_matrix – C_in)×100, where C_md, C_in, and C_matrix are the analyte concentrations in the microdialysate, inflow perfusate, and the matrix, respectively, and 2) a simple linear regression and the ordinary least squares (OLS) method in which the independent or predictor variable was C_md and the outcome (dependent variable) was C_matrix. The only previous assumption was that both variables were linearly correlated and therefore C_md could be used as a reliable estimator of the true ionic concentration in the medium (C_matrix).

Feasibility study

A prospective study was conducted in 2 patients, one with an severe TBI and the second with a malignant stroke who received ICP and MD monitoring (PR-ATR-286/2013). In summary, brain MD catheters are usually inserted into noninjured brain tissue and/or in regions of interest according to a previously described methodology.²⁵ A CMA-71 brain microdialysis catheter with a 100-kDa cut-off membrane (M Dialysis AB) was used in the 2 patients included in this study, and the position of the probe was confirmed by a control CT scan. Cerebral catheters were perfused with same sterile isotonic CNS fluid at a fixed flow rate of 0.3 μL/min using a CMA-106 pump (M Dialysis AB). The dialysates were collected hourly by the nurse in charge of the patient, using capped microvials—specially designed to collect microvolumetric samples and minimize evaporation—and lactate, pyruvate, glucose, glycerol, and glutamate levels were routinely monitored at the bedside using an Iscus Flex analyzer (M Dialysis AB). After the hourly measurements were completed, the microvials were placed in a rack designed to seal the microvials and prevent evaporation (M Dialysis AB). All racks were stored at −86°C until analysis. In an experimental study we conducted previously, it was established that under these storage conditions, evaporation does not occur and therefore the ionic concentration for Na⁺, K⁺, and Cl⁻ does not change significantly for at least 36 months of storage (unpublished results). Data from the first two microvials were always excluded.

For ion determination, dialysates were analyzed with the same AU5400 analyzer used in the in vitro study. The microvials corresponding to the first 24 h were defrosted on ice. When the Iscus Flex analyzer analyzes metabolites, a volume of 8 μL is used and therefore it is necessary to pool the content of 12 microvials in order to obtain the minimum volume of 85 μL needed to perform the analysis in the AU5400 analyzer. Therefore, two samples for each patient are usually obtained for a 24-h period.

Reference range

For the best approximation to the reference range for extracelullar ionic concentration, we used the CSF concentrations measured with the same analyzer in a cohort of 22 normal volunteers having no neurological or psychiatric history. These also had normal neurological examination results and Mini–Mental State Examination scores of >25. CSF was obtained during spinal anesthesia for urological, general, or vascular surgery after informed consent was obtained from all patients and approval was given by the ethical committee of our center (PRAG-75/2005).

Statistical analysis

Descriptive statistics were obtained for each variable. For continuous variables, the summary statistics used were the mean, median, range, and the standard deviation. Percentages and sample sizes were used to summarize categorical variables. The Shapiro-Wilk's test and inverse probability plot were used to test whether the data followed a normal distribution. To correlate two continuous variables, the most conservative Kendall's tau (when data did not follow a normal distribution) or Pearson's correlation test (for data following a normal distribution) was used. For each ion, scatter plots were built, with [Na⁺]_md, [K⁺]_md, and [Cl⁻]_md in the dialysate as the predictor variables and the true matrix concentrations as the outcome variables. A simple linear regression and the OLS method were used. Adjusted R² values were calculated for all models to test whether linear or nonlinear models adequately explained the relationships between both variables. Statistical analyses were carried out with R software (version 3.0.2; R Foundation for Statistical Computing, Vienna, Austria)²⁶ and the integrated development environment RStudio (v0.98.501; RStudio, Boston, MA).²⁷ The car package was used for regression analysis.²⁸

To calculate the reference interval and the upper and lower thresholds for the ions, we used the distribution-free “robust method” described in the National Committee on Clinical Laboratory Standards (NCCLS) and Clinical and Laboratory Standards Institute (CLSI) guidelines C28-A2 and C28-A3 for estimating percentiles and their 90% confidence intervals (CIs).^29–31 To calculate reference intervals with this method, we used the routine implemented in MedCalc (version 12.2; MedCalc Software, Mariakerke, Belgium).

Results

Relative recovery obtained in the in vitro experiments

The in vitro experiments yielded 95 pairs of samples (matrix-dialysate) for Na⁺ and 94 for K⁺ and Cl⁻ (71 from room temperature experiments and 24 from 37°C experiments). The median RR calculated from Bungay's equation ranged from 103 to 123%. However, the min and max values were very extreme (−212 for Cl⁻ and −400 for Na⁺) because of the fact that Bungay's equation does not take into consideration that C_in can be higher than C_matrix, as was the case in our experiments in which hypertonic and hypotonic matrices were tested. Therefore, we considered this method unreliable for calculating the true concentration of ions in vivo when the MD perfusate used contains ions.

Ionic concentration calculated by the ordinary least squares method

The second approach of using the OLS method to estimate the true ionic concentrations in the matrix from the ionic concentration in the dialysate is summarized in Figures 2, 3, and 4. The goodness of fit for the linear model and the parameter estimates were excellent for all the tested ions. The adjusted R² for the linear models was 0.95 for Na⁺, 0.99 for K⁺, and 0.95 for Cl⁻. In summary, the ionic concentration in vitro could be reliably estimated at any of the two tested temperatures from the ionic concentration in the microdialysate. The best estimate was for K⁺, with a slope of 0.95 (95% CI, 0.93–0.98), an intercept of almost zero, and a R²=0.99.

FIG. 2.

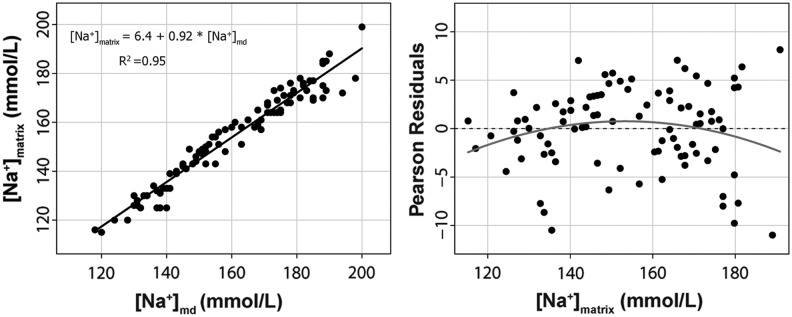
On the left, we show the scatter plot matrix for Na⁺ in the dialysate [Na⁺]_md and the predefined Na⁺ concentration in the matrix [Na⁺]_matrix. The equation to calculate the [Na⁺]_matrix from the assayed concentration in the dialysate is also shown. R²=adjusted r-squared for the model. The right plot shows the Pearson's residuals (expected minus predicted values).

FIG. 3.

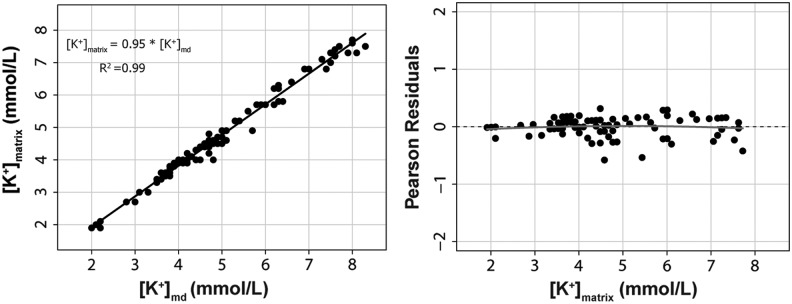
On the left, we represent the scatter plot matrix for K⁺ in the dialysate [K⁺]_md and the predefined K⁺ concentration in the matrix [K⁺]_matrix. The equation to calculate the [K⁺]_matrix from the assayed concentration in the dialysate is also shown. R²=adjusted r-squared for the model. The right plot shows the Pearson's residuals (expected minus predicted values).

FIG. 4.

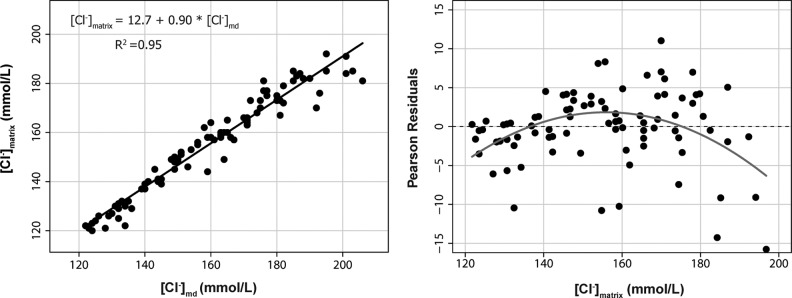
On the left, we represent the scatter plot matrix for Cl⁻ in the dialysate [Cl⁻]_md and the predefined Cl⁻ concentration in the matrix [Cl⁻]_matrix. The equation to calculate the [Cl⁻]_matrix from the assayed concentration in the dialysate is also shown. R²=adjusted r-squared for the model. The right plot shows the Pearson's residuals (expected minus predicted values).

Reference range

This cohort was composed of 22 controls, 7 (32%) men and 15 (68%) women, with a mean age of 65±13 years (min, 41; max, 88). The range of normality for ions in the CSF for this control group is shown in Table 1. The upper threshold using the robust method was 164 mmol/L for Na⁺, 144 mmol/L for Cl⁻, and 3.6 mmol/L for K⁺.

Analysis of ionic profile of the brain extracelullar space in 2 patients

To show the feasibility of the method in the clinical setting, we present the calculated ionic profile of 2 patients in Figures 5 and 6.

FIG. 5.

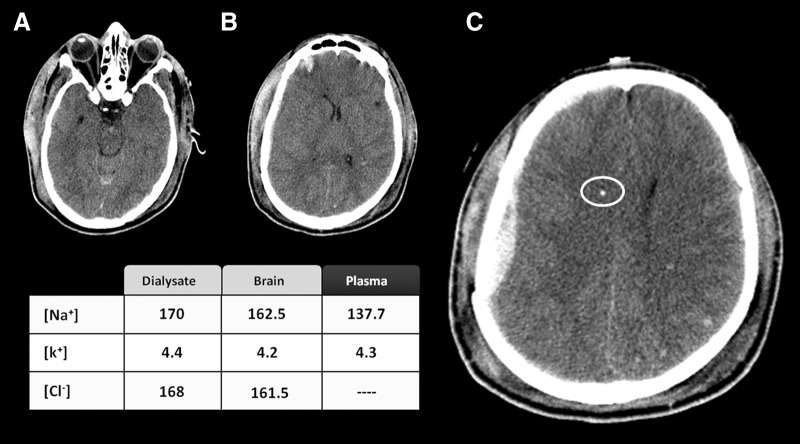
A 24-year-old man was admitted to our hospital after a severe traumatic brain injury with a prehospital Glasgow Coma Score of 6. The computed tomography (CT) scan was classified as a diffuse brain injury type II of the Marshall's classification. In the three CT scan slices shown here (A, B, and C), a small right frontal contusion together with a small subdural hematoma and subarachnoid blood in the interpeduncular cistern are observed. The white circle in (C) indicates the MD probe that was located at a distance of 41 mm from the subdural hematoma. The table summarizes the ionic concentration in the plasma, the dialysate, and the estimated concentration in the brain calculated according the equations described in the text.

FIG. 6.

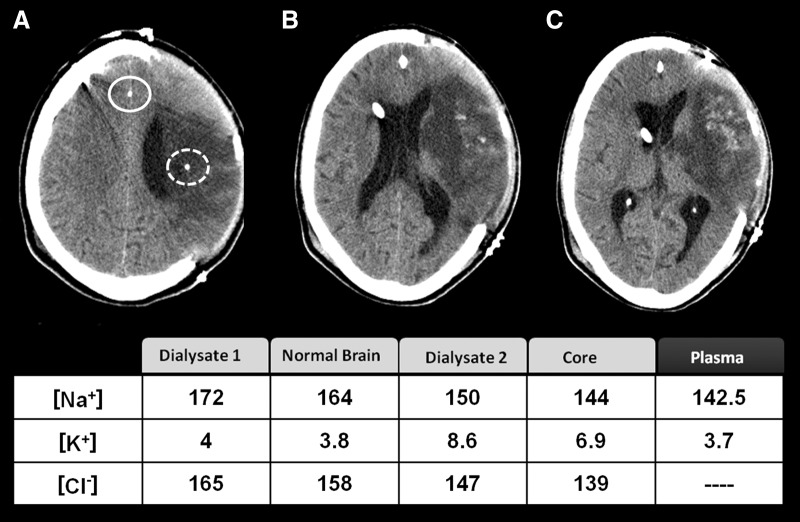
This 52-year-old man was brought to the emergency department following the sudden onset of severe right-sided weakness and difficulty speaking. On admission to our center, the patient showed dense right hemiplegia and expression dysphasia and a score on the National Institutes of Health stroke scale of 22. In the computed tomography scan after decompressive craniectomy was conducted, we observed a massive infarction occupying more than 75% of the territory of the middle cerebral artery with some hemorrhagic component inside the infarction. The continuous and discontinuous white circles indicate the MD probes located in normal brain and in the infarction core, respectively. The table summarizes the ionic concentration in the plasma, the dialysate in normal brain (dialysate 1) and core (dialysate 2), and the estimated concentration in the extracellular fluid according to the equations described in the text. The main finding was that [K⁺]_brain was high in the core.

Patient 1

A 24-year-old man was admitted to our hospital after a fall from a height of 6 m. The first recorded preadmission Glasgow Coma Score was 6. A brain CT scan performed on admission to our center showed a moderate subarachnoid hemorrhage with mild intraventricular hemorrhage and diffuse subcortical petechia, suggesting diffuse axonal injury. A small right subdural hematoma (SDH) was also observed. The patient was transferred to the neurointensive care unit (NICU), and ICP and MD probes were placed and maintained for 114 h. The MD probe was located 41 mm below the nonevacuated acute SDH in what it could be considered an area of structurally normal brain (Fig. 5). The estimated ionic profile 25 h after injury showed a moderate increase in the [Cl⁻]_brain with a normal [Na⁺]_brain and [K⁺]_brain. The plasmatic levels of Na⁺ and K⁺ were both within the normal range.

Patient 2

A 52-year-old right-handed man was brought to the emergency department 90 min after the sudden onset of severe right-sided weakness and difficulty speaking. His past medical history was notable for having been treated for tuberculosis. On admission to our center, the patient presented with dense right hemiplegia and expression dysphasia and a score on the National Institutes of Health stroke scale of 22. A noncontrast head CT showed an ischemic stroke of the left middle cerebral artery (MCA)—of possibly embolic etiology—without mid-line shift. Treatment with tissue plasminogen activator was disregarded because of the infarction size. Given that the diagnosis was of potential malignant infarction, he was admitted to the NICU. On the third day of hospitalization, the patient presented mental confusion and a moderate headache associated with increasing difficulty to arouse. New CT imaging showed a large infarct in the right MCA territory associated with brain swelling and a left-to-right 5-mm mid-line shift. Decompressive hemicraniectomy was conducted 67 h after the stroke. During decompresive surgery, two MD probes were placed, one in the infarction core and the second in the contralateral brain (Fig. 6). Monitoring of brain metabolism (glucose, lactate, and pyruvate) was initiated 6 h after surgery (73 h after stroke onset). The control CT scan performed after surgery showed one MD catheter inside the core and the second in the contralateral hemisphere, close to the mid-line. The ionic profile in the normal brain showed a mild increase in [Cl⁻]_{normal brain} (upper normal threshold, 144 mmol/L) as the only abnormality. The ionic profile in the core showed a significant increase in [K⁺]_core. The obtained values in the dialysate and the calculated concentrations in the brain are shown in Figure 6. The patient presented sudden neurological deterioration 10 days after the stroke. In the CT scan, there was an increase in the hemorrhagic transformation of the left infarction and a significant bulging of the infarcted brain throughout the decompressive area, together with new hypodense lesions in the right hemisphere. The patient died on the tenth day after the stroke.

Discussion

Brain MD is a tool that is still rarely used in the routine management of neurocritical patients. Kitagawa and colleagues showed that only 42 centers worldwide used MD for clinical decision making in the management of patients with TBI, stroke, and aneurysmal subarachnoid hemorrhage in 2012.² However, brain MD is a unique research tool for an in-depth analysis of the complex physiological derangements that occur in acute brain injuries. Brain MD can promote a better understanding of the pathophysiology of ionic disturbances and therefore of brain edema. Ions are the most active osmotic particles of the mammalian brain, and the osmolarity of the intracellular compartment must be in equilibrium with the ECF. Under normal conditions, any disturbance of this equilibrium is rapidly restored to the steady state with the participation of ionic channels, transporters, and ionic pumps.³²

Acute injuries to the brain cause a variable disruption of ionic homeostasis and massive ionic fluxes with subsequent osmotic water movement across the cells. Major contributors to the ionic disturbances of the brain ECF include traumatic depolarization, various types of brain edema (cytotoxic, ionic, and vasogenic), ischemic or nonischemic brain hypoxia, excitotoxicity, cortical spreading depression or seizures, and the direct effects of osmotic drugs used in the management of neurocritical patients. In addition, the ionic profile of the brain ECF is an accurate indicator of the integrity or disturbances in the permeability of the blood–brain barrier.

MD has been extensively used to study the neurochemistry of the brain, but the study of ionic profiles of the brain ECF has been rarely reported in either experimental models or humans. The few clinical studies have concentrated on K^+4–7 because the increase in the [K⁺]_brain is a biomarker of the severity of the brain tissue injury, brain ischemia, and necrotic death.³³ Further, some clinical studies in TBI have shown that an increased [K⁺]_brain is a strong predictor of severe physiological deterioration and of a poor outcome.^6,7

In vitro relative recovery: a requirement to calculate in vivo concentrations

In MD, the perfusate typically does not contain the analyte of interest and operates under nonequilibrium conditions.¹⁰ Under these conditions, the concentration of the solute in the dialysate is only a variable fraction of the true concentration in the ECF.¹⁰ The efficiency in the recovery of any solute is defined by the in vitro RR, the ratio between the concentration in a solution and the concentration in the dialysate. The mathematical model used for this calculation was introduced by Bungay and colleagues in 1990 and is defined—when the perfusate contains the analyte of interest (C_in>0)— by the equation defined in the Methods section of this article.¹⁸ When the solute of interest is not in the perfusate (C_in=0), as occurs in most cases, a simplified equation is used (RR=C_md/C_matrix). Despite the caveats about this mathematical model already described by Bungay and colleagues,³ determining the RR of any analyte is an indispensable requirement to interpret the results in vivo. RR studies are typically conducted by immersing the probes in an inert solution to assess their performance in recovering the target analyte. Once the RR is known, the actual concentration of the analyte in the tissue can be calculated. This theoretical framework has been used both in experimental and clinical studies of the low-molecular-weight metabolites involved in the brain energy metabolism.^{1,10,12,18,20,34}

Methodological problems with ions

The diffusion of ions through the large pores of the high molecular cut-off of the CMA-71 probe should be theoretically fast and therefore their recovery high and only conditioned by the infusion rate and by the potential loss of fluid that can occur with 100-kDa membranes. In brain MD, the probe implanted in the tissue is usually perfused with a fluid that has a variable ionic composition, as shown in Table 1. Normal saline, Ringer, lactated Ringer's, and commercial or custom-made perfusion fluid—with or without colloids (albumine or dextrane)—have been used as perfusates.^6,15,34 Adding colloids to the perfusate facilitates the equilibration of the osmotic pressures in both sides of the probe, thereby avoiding fluid loss into the tissue and making fluid recovery more stable. In our clinical experience with the CMA-71 probes, there is no need to add colloids to maintain a stable volume of dialysate recovery. This steady state can be also achieved in vitro—without colloids—by modifying the hydrostatic pressures inside and outside the probe by changing the heights between the tip's probe, the microvial, and the pump outlet.³⁵

Our study showed that ionic concentrations in vitro—and thus in vivo—cannot be reliably estimated by Bungay's method because this model gives extreme values when C_in>C_matrix. Therefore, this model is less useful when the actual concentrations in the tissue or in the in vitro solution are below the concentrations in the perfusate, as is the case in many of our experiments and in actual patients. Nordenvall and colleagues found a similar problem in a study of rat uterine fluid and used the “inverse relative recovery” to calculate recovery when the perfusate contained a higher ionic concentration than the matrix.⁸ Using this method, these investigators found an RR of 75% for Na⁺ and 96% for K⁺ when using a flow rate of 0.5 μL/min.⁸ However, it is not feasible to apply this method in patients, because the actual ionic concentration is unknown and can be below or above the perfusate's ionic concentration. The alternative of using deionized water as a perfusate is not accepted in humans; if it was, it could modify significantly the ionic concentration of the brain ECF when applied continuously over many hours.

In the in vitro study, the linear regression method was found to be very reliable and robust in estimating the true concentration of the three ions of interest at different temperatures when using the CNS perfusate at a 0.3-μL/min infusion rate and an MD membrane 10 mm long. On average, the slopes showed that the RRs were somewhat above 100% and higher than those reported by other investigators.^6,8 This discrepancy can be explained by the different perfusion speeds: 0.5 μL/min in the study of Nordenvall and colleagues and 2 μL/min in the study of Reinert and colleagues.^6,8 As shown by many studies, infusion speed is inversely related to recovery on any solute in MD.^12,34,36 In order to translate this model to the clinical setting, the basic requirement is that fluid recovery is in a steady state. This fact is not a unique problem for ions, but is a shared problem with the detection of any molecule where the in vitro RR is used to calculate the actual concentrations of the tissue. Ionic analyzers do not take into account changes in dialysate recovery, and therefore significant deviations from the expected recovery can alter the true values. In future clinical studies, the volume of the recovered dialysate should be reported and those microvials that deviate significantly from the expected recovery should be discarded.

We believe that MD used with harmonized clinical settings—perfusate, cathether length, and infusion rate—is an excellent tool for conducting studies of the ionic profile in the brain ECF. This technique opens up an exciting avenue to explore the potential response of the ECF to drugs and different hyperosmolar solutions routinely used in the management of neurocritical patients. It is also possible to study the ionic changes associated with cortical spreading depression or seizures, and this method can be used to investigate the ionic profile associated with different classes of brain edema and how this profile might change with different therapies.^37,38

In our case 2, the core of the infarction showed a high [K⁺]_brain that, if confirmed in more cases, may be an indicator of nonviable tissue. In rat fluid-percussion injury, Katayama and colleagues showed that an increase in the K⁺ dialysate was proportional to the severity of the injury.³⁹ Necrosis behaves as a tissue homogenate and represents a weighted average of the ionic concentration of the intracellular space, the extracellular compartment, and the intravascular components. In addition, necrotic tissue is a powerful magnet for water. As a result, some dilution of the core can occur when the infarction evolves with time. That necrotic tissue attracts water has been shown by Katayama and colleagues in the core of post-traumatic brain contusions^40,41 and might explain the paradoxical normality in [Cl⁻]_brain and [Na⁺]_brain found in the core in our case 2 (Fig. 6). However, additional studies with higher temporal resolution are needed to verify or refute such a hypothesis. An additional issue that necessitates further studies is whether changes in the ionic composition of the perfusate might influence the ionic profile of the brain ECF; normal saline contains no K⁺, and other perfusates contain high Cl⁻ concentrations (normal saline, 148 mmol/L; CNS fluid, 158 mmol/L). Further experimental studies need to be conducted to determine the optimal infusion fluid for monitoring both energy metabolism and ionic concentration.

Limitations of the study and future directions

Our study presents some limitations that merit discussion. It was conducted at only two fixed temperatures and at a constant atmospheric pressure in the matrix. Both temperature and pressure may affect ionic recovery. It is well known that diffusion is temperature dependent, because when temperature increases, the speeds of molecules increase and therefore diffusion occurs more quickly (as defined by the Einstein-Smoluchowski diffusion equation). However, the data at both temperatures did not differ and the differences among individual catheters were negligible. Brain temperature is above 37°C in many patients, and the ICP can be above 25 mm Hg in some patients with acute brain injuries. The effect in recovery of these two variables, if any, should be further analyzed and incorporated in any mathematical model to fine tune the calculation of the true ionic concentration in the brain ECF. We believe that temperature and pressure are not issues in the recovery of small molecules, but additional studies at different temperatures and pressures should be conducted to confirm or refute this hypothesis. In a recently published in vitro study, Galea and colleagues evaluated the efficiency at recovering a 22-kDa protein (interleukin-1 receptor antagonist; ILRa) with CMA71 probes.⁴² They observed an insignificant effect in the RR of ILRa by changing temperature in the 20–37°C range and the pressure of the matrix in the 0–15-mm Hg range.⁴² However, the RR found for this cytokine was very low and showed a wide variability among catheters, an issue already described by others that can be attributed to the limitation of the CMA71 catheter at recovering macromolecules despite their theoretical cutoff.^14,43

The limitation of low spatial resolution—the limited brain tissue sampled by the MD probe—is an intrinsic limitation of the MD technique and cannot be overcome in the study of ionic profiles in vivo. However, placing the probe in the area of interest is a simple solution for studying brain edema. The different ionic profile in the different areas of our case 2 highlights the importance of placing the probes in the areas of interest. The methodology used in this study has a low temporal resolution if applied in vivo (4–12 h) owing to the fact that the assay we used needs a minimum volume of 85 μL for the ionic assay. With standard MD protocols used in neurocritical care (infusion speed of 0.3 μL/min), this requirement necessitates the pooling of at least 8–10 microvials than can be reduced to 4 if dilution of the dialysate is conducted before the assay. With any method of low temporal resolution, the dialysate is only a time-averaged concentration and therefore a snapshot of the average ionic profile. This limitation is not easy to overcome because it depends on both the methodology of MD and the sensitivity of the analytical methods used. Increasing the infusion speed from 0.3 to 0.5–1.0 μL/h will reduce the recovery of the ions and therefore decrease the lower limit of detection for K⁺ (2 mmol/L in our analyzer), which is probably the most relevant cation and a potential surrogate for tissue viability.³³ In addition, the recovery of the energy metabolites used at the bedside (lactate, pyruvate, and glucose) will also be significantly reduced with increasing infusion rate.^{1,2,10,12,20,34} Modifying the range of normality of energy metabolites—depending on the infusion speed—would add extra complexity to a monitoring system that is already quite cumbersome, significantly increasing the workload of nurses and NICU personnel.

For research applications and to explore many issues that are clinically relevant, probably the best analytical method to improve the temporal resolution for ionic determination is inductively coupled plasma mass spectrometry (ICP-MS). This technique is unfortunately unavailable in most hospitals because the equipment is still very expensive. However, this resource is available in many research institutes that conduct environmental, geological, or biomedical research.⁴⁴ ICP-MS offers extremely low detection limits—in the subparts per million (ppm) levels—and needs less than a 20-μL volume.⁴⁴ This is an excellent method that our group is currently exploring. It would allow an improvement in the time resolution to 1 h or less if the perfusion is increased to 0.50 μL/min.

For clinical applications, as far as we know, there are no current alternatives for real-time, online measurements of ions in brain-injured patients. However, a potential option would be to use ion-selective microelectrodes adapted for human use. Ion-selective microelectrodes have a significant lower range of detection, need very small sample volumes, and have a much higher time resolution. However, these electrodes are not as yet available for clinical use. A second alternative is to adapt the outlet of the clinical MD probes to an in-line, solid-state, ion-selective microelectrode that allows real-time assays of the recovered dialysate. The only alternative to improve the time resolution of our method would be to dilute samples before assay with deionized water in order to increase the volume needed by the analyzer. This technique would enable a temporal resolution of approximately 4–6 h. In our opinion, this alternative is feasible and acceptable because the changes observed in ionic profile every 4 h, without altering the monitoring of energy metabolism, is a reasonable trade-off between the accepted indications for clinical use of MD and its added value for conducting clinical research.

Conclusions

Our study shows that, at a standard infusion rate of 0.3 μL/min and with standard commercially available perfusate, the in vitro concentrations of a problem solution can be reliably estimated by using a simple linear regression and the OLS method. In this model, the ionic concentration in the dialysate is used as the predictor to estimate the true concentration in the solution (the outcome variable). The model was excellent for all the ions studies, particularly K⁺. The ionic analyzer used in the present study was a conventional analyzer used in the clinical setting that has the advantage of being easily available and subject to frequent recalibrations and quality-control checks. The use of MD to study the ionic profile of different regions of the injured brain opens up an exciting avenue to explore the complexities of the ionic disturbances and, specifically, the classification of the different types of brain edema.

Acknowledgments

This work has been supported, in part, by the Fondo de Investigación Sanitaria (Instituto de Salud Carlos III) with grants PI10/00302 and FIS PI11/00700, which were cofinanced by the European Regional Development and awarded to M.A. Poca and J. Sahuquillo, respectively. T. Martínez-Valverde and A. Sánchez-Guerrero are the recipients of personal predoctoral grants from the Instituto de Salud Carlos III (grant nos. FI11/00195 and FI12/00074, respectively).

Author Disclosure Statement

No competing financial interests exist.