Ab initio study of the formation and degradation reactions of chlorinated phenols

Abstract

The formation, stability, and reactivity of chlorinated phenoxyl radicials was studied using ab initio methods. All 19 congeners from mono- to penta-chlorinated species were considered. The radical species are formed in combustion reactions via unimolecular scission of the phenoxyl-hydrogen bond or hydrogen atom abstraction by hydrogen atom or hydroxyl radical. The resulting radicals are stable with respect to unimolecular decomposition and reaction with molecular oxygen is relatively slow. Activation energies are similar to those of the phenoxyl radical for both the decomposition pathway and the reaction with molecular oxygen at the more reactive para-position. Calculations were performed with the model chemistries B3LYP/6-31G(d,p), BHandHLYP/6-31G(d,p), BHandHLYP/aug-cc-pVDZ and QCISD(T)/6-31G(d,p)//BHandHLYP/6-31G(d,p) (for selected reactions.) The results suggest the radicals are sufficiently stable and unreactive to be moderately persistent in the atmosphere, especially when associated with some types of particulate matter. An additivity analysis is made to decompose the relative energetics of the congeners into contributions from hydrogen bonding, resonance stabilization, and repulsive interactions. The results of this analysis correlate well with the results of the calculations.

1. Introduction

Chlorinated phenols are toxic chemicals frequently found in hazardous wastes and at Superfund sites. Upon heating or burning they can be converted into even more toxic polychlorinated diben-zo-p-dioxins and dibenzofurans (PCDD/F) by both gas-phase [1] and metal catalyzed pathways [2]. Chlorinated phenoxyl radicals, formed by dissociation or abstraction of the phenolic hydrogen, are resonance stabilized radicals. Phenoxyl radicals are known to be resistant to oxidation [3,4] and chlorinated phenoxyl radicals may even be less reactive. In fact, chlorinated phenoxyl radicals are thought by some to be so stable that they only react with other radicals or themselves, the self-reaction resulting in the formation of PCDD/Fs [5–10]. In addition, it has recently been noticed that substituted phenoxyl radicals were environmentally persistent when associated with copper oxide-containing particles [11].

Monochlorinated phenoxyl radicals are valence isoelectronic with semiquinone radicals which are suspected to be responsible for much of free radical damage induced by inhalation of cigarette smoke. Semiquinone radicals are known to be quite stable [12] and capable of reducing molecular oxygen to superoxide radical anion in a cyclic process [13]. Since monochlorinated phenoxyl radicals are valence isolectronic with semiquinone radicals and probably even more resistant to oxidation due to chlorine substitution, it is possible that chlorinated phenoxyl radicals may be even more toxic than the better studied semiquinone family of radicals.

Previous experimental studies of the thermal degradation behavior of chlorinated phenols have been confined to the mono-, di-, or tri-chlorophenol precursors and their products with an aim for developing a PCDD/F formation mechanism [1,6–9,14–19]. Some of these models have used the O–H bond dissociation energy of phenol as the activation energy for decomposition of chlorinated phenols. Previous computational gas-phase studies of chlorophenols have focused primarily on O–H bond dissociation energies as a function of position of mono- and di-chlorination [20–27]. There are no experimental or computational studies of the stability and reactivity of the 19 congeners of chlorophenol despite the role these species play in the formation of PCCD/F.

The present work is the first study to examine both the stabilities and reactivities of the 19 congeners. Amongst the mono-chlorinated phenols, it is well established that O–H bond dissociation energies are lowered by a para-chloro substituent and are increased by the presence of ortho- and meta-chloro substituents [20,22,23,26,28]. This observation is used as a test of the validity of the present calculations. Earlier ab initio calculations [29] suggest that phenoxyl radical thermally decomposes by proceeding through a rate-determining bicyclic intermediate followed by α-CC bond cleavage to produce CO and a cyclopentadienyl radical. Using this transition state structure as a model, we report the activation energies for concerted elimination of CO to form chlorinated cyclopentadienyl radicals. Chlorinated phenoxyl radicals are significantly resonance stabilized relative to the phenoxyl radical and chlorine substitution may make them even less reactive than phenoxyl radicals, and consequently more persistent, in oxidative environments. To address these issues, bimolecular reactions between 2-, 3-, and 4-monochlorophenoxyl radicals and molecular oxygen were studied.

2. Computational procedures

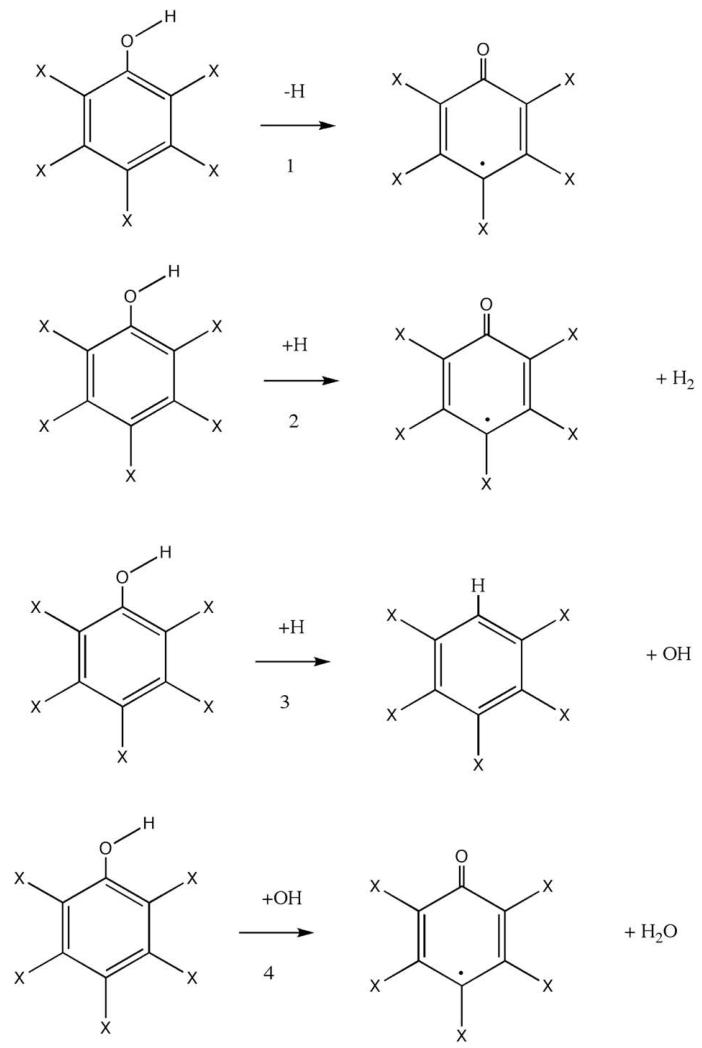
Ab initio calculations were performed using the Gaussian 03 [30] suite of programs. For open-shell systems, restricted methods were used. Despite known deficiencies [31,32], density functional theory (DFT) is a common computational procedure. The best agreement between experimental and calculated values for thermodynamic and kinetic parameters is obtained using computationally expensive correlated methods such as configuration interaction. However, if one is interested in the differences in these parameters between similar compounds, then DFT calculations are accurate [20,22,23,27,33,34]. In terms of absolute values of a thermodynamic parameter, the bond dissociation energy of phenol has been measured experimentally and found to be between 84.0 and 88.8 kcal/mol [8,16,20,22,23,27,33,35–38], in excellent agreement with our calculated value of 89.4 kcal/mol (QClSD(T)/6-31G(d,p)//BHandHLYP/6-31G(d,p)) and in good agreement with our DFT values of ~80–81 kcal/mol [39]. ΔE_rxn for three other routes to the formation of the phenoxyl radical can be estimated from heats of reaction available from experiments [40]. This analysis gives ΔE_rxn = −16.2 kcal/mol for the abstraction of the hydroxyl hydrogen atom by a second hydrogen atom (Fig. 2, Reaction 2), which compares favorably to our previously calculated values of −18.8 kcal/mol (BHandHLYP/aug-cc-pVDZ) and −16.4 kcal/mol (QClSD(T)/6-31G(d,p)//BHandHLYP/6-31G(d,p)). For the displacement of the hydroxyl group by a hydrogen atom (Fig 2, Reaction 3), experiment[40] finds ΔE_rxn = 0.1 kcal/mol and our previous calculations give −8.5 kcal/mol (BHandHLYP/aug-cc-pVDZ) and −6.2 kcal/mol (QClSD(T)/6-31G(d,p)//BHandHLYP/6-31G(d,p).) For the reaction with OH to give water and the phenoxyl radical (Fig 2, Reaction 4), this analysis gives finds ΔE_rxn = −31.2 kcal/mol [40] and our previous calculations give −28 kcal/mol (BHandH-LYP/aug-cc-pVDZ) and −26.5 kcal/mol (QClSD(T)/6-31G(d,p)//BHandHLYP/6-31G(d,p).) This agreement between absolute values of experimental and ab initio calculations is sufficiently accurate for our purposes.

Fig. 2.

Radical forming reactions studied in the present work.

There is less experimental data available for the reactions of radicals relevant to the present work. However, the activation energy has been measured for the decomposition of the phenoxyl radical to CO and cyclopentadienyl radical and found to be ~44 kcal/mol [41]. Ab initio calculations have been performed to analyze this reaction [29]. There are three local maxima along the proposed reaction path and the transition state (with the largest activation energy relative to a nearby local/global minimum) geometry is consistently predicted across a variety of basis sets and ab initio methods [29]. The best estimate from calculation for the activation energy for this reaction is 52.2 kcal/mol (G2M/MP2 model chemistry) in good agreement with the DFT estimate (B3LYP/6-31G* model chemistry) of 56.6 kcal/mol [29]. Our previous calculations found the activation energy to be 61.6 kcal/mol (BHandHLYP/cc-aug-pVDZ model chemistry) [39]. Thus ab initio calculations show similar accuracy for both reaction energies (ΔE_rxn) and activation energies. DFT calculations are therefore somewhat less accurate than higher level ab initio methods for these systems, but still in reasonable agreement with experimentally derived parameters. Most importantly for the present work is that the relative values of ΔE_rxn and activation energies are found to be the same using either DFT or higher level methods [39]. Studies of transition state properties have shown that the BHandHLYP [42] and the MPW1K [32] DFT implementations are reasonably accurate. Based on this information, we used the B3LYP and BHandHLYP DFT methods, and, as a check on the quality of the DFT energies, the QClSD(T)//BHandHLYP model chemistry.

Calculations were performed using the B3LYP/6-31G(d,p) (l), BHandHLYP/6-31G(d,p) (ll), and BHandHLYP/aug-cc-pVDZ (lll) model chemistries. ln some cases, QClSD(T)/6-31G(d,p)//BHandH-LYP/6-31G(d,p) (lV) model chemistry was employed to validate the relative ordering of the DFT results. ln this work, we are interested in the relative ΔE_rxn and E_a for the reactions of a series of similar molecules; therefore, we used different model chemistries to assess the accuracy of our calculations. Full optimizations using CCSD/aug-cc-pVDZ were attempted but proved beyond our computational resources. Stationary points were characterized as either a local minimum structure (no imaginary frequencies) or a transition state (one imaginary frequency) by analytical evaluation of their Hessians. When more than one isomer of a particular species existed, the most stable isomer was used in the calculations. The energies are unscaled and zero-point corrected. All energies except those in Table 5 are given in kcal/mol. Transition states were located by performing relaxed potential energy surface scans followed by implementation of a Synchronous Transit-Guided Quasi-Newton (STQN) method, integrated into the Gaussian suites of programs by Schlegel et al. [43]. Transition states for the radical decomposition and oxidative channels have been lRC confirmed and are similar to those found in our earlier work [39]. ΔE_rxn and E_a were calculated by taking the difference of product or transition state species and reactant species using the zero point corrected energies. The relative values of these parameters were defined as

$$\Delta E_{\mathrm{rxn}}\left(A\text{relative to}B\right)=\Delta E_{\mathrm{rxn}}\left(A\right)-\Delta E_{\mathrm{rxn}}\left(B\right)$$

and

$$E_{\mathrm{a}}\left(A\text{relative to}B\right)=E_{\mathrm{a}}\left(A\right)-E_{\mathrm{a}}\left(B\right).$$

Table 5.

BHandHLYP/aug-cc-pVDZ zero-point corrected absolute energies (in Hartrees) for the monochlorinated phenols and monochlorinated phenoxyl radicals.

Compound	Energy (Hartrees)
o-Chlorophenol	−766.83867
m-Chlorophenol	−766.837384
p-Chlorophenol	−766.836646
o-Chlorophenoxyl radical	−766.208446
m-Chlorphenoxyl radical	−766.209273
p-Chlorophenoxyl radical	−766.211155

3. Results and discussion

3.1. Radical formation

Formation of substituted phenoxyl radicals from their parent phenols is clearly affected by the number and type of the substituents. Previous studies [39,44] found that additional hydroxyl groups at ortho- or para-positions slightly lowered the ΔE_rxn for radical formation. Our study [39] found that the activation energies for elimination of CO from the resulting radicals were increased relative to the phenoxyl radical as a result of the hydroxyl substitution. Reaction of the radicals with molecular oxygen yielded slightly larger values of ΔE_rxn for the substituted species and no obvious trends in the activation energies. The results presented below can therefore be used to contrast chlorine substitution with hydroxyl substitution, as well as comparison amongst the chlorinated congeners.

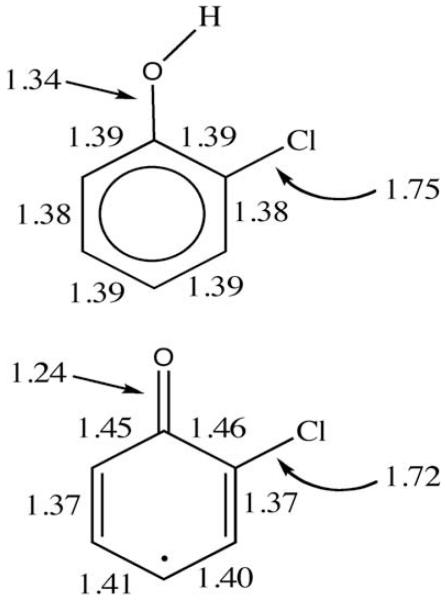
The optimized structures of o-chlorophenol and the o-chlorophenoxyl radical (BHandHLYP/aug-cc-pVDZ) are depicted in Fig. 1, along with the bonding structure and location of the unpaired electron suggested by the bond lengths. The bond lengths are similar for the meta- and para-chloro congeners, and all are similar to phenol and the phenoxyl radical, respectively. The differences between the radical and its parent suggest that there will be substantive differences between parent and radical due to the effect of added chlorine atoms. The bond lengths suggest the resonance structure with the unpaired electron at the 4-position is the most stable. This suggests that the most likely self-reaction product of 2-chlorophenoxyl radicals is a chlorinated 4,4′-diphenyl quinone. In contrast, the structure with the unpaired electron at the 2- or 6-positions can react to give PCDD/F.

Fig. 1.

Geometries of o-chlorophenol and the o-chlorophenoxyl radical. The radical indicates the resonance structure suggested by the bond lengths.

Four different pathways of degradation by decomposition or reaction were investigated. Fig. 2 displays these pathways: (1) unimolecular decomposition via O-H bond scission, (2) abstraction of the hydroxyl hydrogen by reaction with atomic hydrogen, (3) displacement of the hydroxyl group by reaction with atomic hydrogen to produce substituted benzenes, and (4) abstraction of the hydroxyl hydrogen by reaction with OH. The values of ΔE_rxn for these routes are given in Tables 1–4.

Table 1.

ΔE_rxn in kcal/mol for unimolecular decomposition of the chlorophenols producing a hydrogen atom and a chlorinated phenoxyl radical. The values for phenol are also reported for reference. Values relative to phenol are given in parentheses. The model chemistries are B3LYP/6-31G(d,p) (I), BHandHLYP/6-31G(d,p) (II), BHandHLYP/aug-cc-pVDZ (III) and QCISD(T)/6-31G(d,p)//BHandHLYP/6-31G(d,p) (IV).

Compound	I	II	III	IV
Phenol	81.3	80.2	80.5	89.4
2-Chlorophenol	83.1 (+1.8)	82.5 (+2.3)	82.9 (+2.4)	91.1 (+1.7)
3-Chlorophenol	82.4 (+1.1)	81.4 (+1.2)	81.6 (+1.1)	90.6 (+1.2)
4-Chlorophenol	80.7 (−0.6)	80.1 (−0.1)	80.0 (−0.5)	89.0 (−0.4)
2,3-Dichlorophenol	83.8 (+2.5)	83.2 (+3.0)	83.6 (+3.1)
2,4-Dichlorophenol	82.3 (+1.0)	82.1 (+1.9)	82.2 (+1.7)
2,5-Dichlorophenol	83.9 (+2.6)	83.5 (+3.3)	83.8 (+3.3)
2,6-Dichlorophenol	81.9 (+0.6)	81.8 (+1.6)	82.2 (+1.7)
3,4-Dichlorophenol	81.7 (+0.4)	81.2 (+1.0)	80.9 (+0.4)
3,5-Dichlorophenol	83.5 (+2.2)	82.6 (+2.4)	82.7 (+2.2)
2,3,4-Trichlorophenol	82.9 (+1.6)	82.9 (+2.7)	82.9 (+2.4)
2,3,5-Trichlorophenol	84.6 (+3.3)	84.3 (+4.1)	84.5 (+4.0)
2,3,6-Trichlorophenol	82.3 (+1.0)	82.4 (+2.2)	82.7 (+2.2)
2,4,5-Trichlorophenol	83.0 (+1.7)	83.0 (+2.8)	83.0 (+2.5)
2,4,6-Trichlorophenol	81.0 (−0.3)	81.3 (+1.1)	81.3 (+0.8)
3,4,5-Trichlorophenol	82.6 (+1.3)	82.2 (+2.0)	81.9 (+1.4)
2,3,4,5-Tetrachlorophenol		83.9 (+3.7)	83.8 (+3.3)
2,3,5,6-Tetrachlorophenol		82.9 (+2.7)	83.2 (+2.7)
2,3,4,6-Tetrachlorophenol		82.0 (+1.8)	82.0 (+1.5)
Pentachlorophenol		82.6 (+2.4)	82.5 (+2.0)

Table 4.

ΔE_rxn in kcal/mol for bimolecular reaction with OH producing water and chlorinated phenoxyl radical. The values for phenol are also reported for reference. Values relative to phenol are given in parentheses. The model chemistries are B3LYP/6-31G(d,p) (I), BHandHLYP/6-31G(d,p) (II), BHandHLYP/aug-cc-pVDZ (III) and QCISD(T)/6-31G(d,p)// BHandHLYP/6-31G(d,p) (IV).

Compound	I	II	III	IV
Phenol	−30.4	−26.6	−28	−26.5
2-Chlorophenol	−28.6 (+1.8)	−24.4 (+2.2)	−25.6 (+2.4)	−24.9 (+1.6)
3-Chlorophenol	−29.3 (+1.1)	−25.4 (+1.2)	−26.9 (+1.1)	−25.4 (+1.1)
4-Chlorophenol	−31.0 (−0.6)	−26.8 (−0.2)	−28.6 (−0.6)	−27.0 (−0.5)
2,3-Dichlorophenol	−28.0 (+2.4)	−23.6 (+3.0)	−24.9 (+3.1)
2,4-Dichlorophenol	−29.4 (+1.0)	−24.7 (+1.9)	−26.3 (+1.7)
2,5-Dichlorophenol	−27.8 (+2.6)	−23.3 (+3.3)	−24.7 (+3.3)
2,6-Dichlorophenol	−29.9 (+0.5)	−25.1 (+1.5)	−26.3 (+1.7)
3,4-Dichlorophenol	−30.1 (+0.3)	−25.7 (+0.9)	−27.6 (+0.4)
3,5-Dichlorophenol	−28.2 (+2.2)	−24.2 (+2.4)	−25.8 (+2.2)
2,3,4-Trichlorophenol	−28.8 (+1.6)	−23.9 (+2.7)	−25.6 (+2.4)
2,3,5-Trichlorophenol	−27.1 (+3.3)	−22.6 (+4.0)	−24.0 (+4.0)
2,3,6-Trichlorophenol	−29.4 (+1.0)	−24.5 (+2.1)	−25.8 (+2.2)
2,4,5-Trichlorophenol	−28.7 (+1.7)	−23.8 (+2.8)	−25.5 (+2.5)
2,4,6-Trichlorophenol	−30.8 (−0.4)	−25.5 (+1.1)	−27.2 (+0.8)
3,4,5-Trichlorophenol	−29.2 (+1.2)	−24.6 (+2.0)	−26.6 (+1.4)
2,3,4,5-Tetrachlorophenol		−23.0 (+3.6)	−24.7 (+3.3)
2,3,5,6-Tetrachlorophenol		−23.9 (+2.7)	−25.3 (+2.7)
2,3,4,6-Tetrachlorophenol		−24.9 (+1.7)	−26.5 (+1.5)
Pentachlorophenol		−24.3 (+2.3)	−26.0 (+2.0)

With the exception of p-chlorophenol, the BHandHLYP/aug-cc-pVDZ calculated bond dissociation energies (Fig. 2, Reaction 1) of all the substituted phenols are greater than phenol by as much as ~4 kcal/mol (Table 1). Similarly, ΔE_rxn values for hydrogen atom abstraction (Fig. 2, Reaction 2) are greater than the corresponding value for phenol, again by up to ~4 kcal/mol (Table 2).

Table 2.

ΔE_rxn in kcal/mol for bimolecular reaction with a hydrogen atom producing H₂ and a chlorinated phenoxyl radical. The values for phenol are also reported for reference. Values relative to phenol are given in parentheses. The model chemistries are B3LYP/6-31G(d,p) (I), BHandHLYP/6-31G(d,p) (II), BHandHLYP/aug-cc-pVDZ (III) and QCISD(T)/6-31G(d,p)// BHandHLYP/6-31G(d,p) (IV).

Compound	I	II	III	IV
Phenol	−24.0	−23.1	−18.8	−16.4
2-Chlorophenol	−22.2 (+1.8)	−20.8 (+2.3)	−16.4 (+2.4)	−14.7 (+1.7)
3-Chlorophenol	−22.9 (+1.1)	−21.8 (+1.3)	−17.8 (+1.0)	−15.2 (+1.2)
4-Chlorophenol	−24.6 (−0.6)	−23.2 (−0.1)	−19.4 (−0.6)	−16.9 (−0.5)
2,3-Dichlorophenol	−21.5 (+2.5)	−20.0 (+3.1)	−15.7 (+3.1)
2,4-Dichlorophenol	−23.0 (+1.0)	−21.1 (+2.0)	−17.2 (+1.6)
2,5-Dichlorophenol	−21.4 (+2.6)	−19.8 (+3.3)	−15.6 (+3.2)
2,6-Dichlorophenol	−23.4 (+0.6)	−21.5 (+1.6)	−17.2 (+1.6)
3,4-Dichlorophenol	−23.7 (+0.3)	−22.1 (+1.0)	−18.4 (+0.4)
3,5-Dichlorophenol	−21.8 (+2.2)	−20.7 (+2.4)	−16.7 (+2.1)
2,3,4-Trichlorophenol	−22.4 (+1.6)	−20.4 (+2.7)	−16.4 (+2.4)
2,3,5-Trichlorophenol	−20.7 (+3.3)	−19.0 (+4.1)	−14.8 (+4.0)
2,3,6-Trichlorophenol	−23.0 (+1.0)	−20.9 (+2.2)	−16.7 (+2.1)
2,4,5-Trichlorophenol	−22.3 (+1.7)	−20.3 (+2.8)	−16.4 (+2.4)
2,4,6-Trichlorophenol	−24.3 (−0.3)	−22.0 (+1.1)	−18.0 (+0.8)
3,4,5-Trichlorophenol	−22.7 (+1.3)	−21.1 (+2.0)	−17.4 (+1.4)
2,3,4,5-Tetrachlorophenol		−19.4 (+3.7)	−15.5 (+3.3)
2,3,5,6-Tetrachlorophenol		−20.4 (+2.7)	−16.2 (+2.6)
2,3,4,6-Tetrachlorophenol		−21.3 (+2.8)	−17.4 (+1.4)
Pentachlorophenol		−20.7 (+2.4)	−16.8 (+2.0)

The values for dehydroxylation via H-substitution to form chlorinated benzenes (Fig. 2, Reaction 3) do not systematically vary with chlorine substitution, with values ranging from ~2 kcal/mol lower to ~1 kcal/mol greater than phenol (Table 3).

Table 3.

ΔE_rxn in kcal/mol for bimolecular reaction with a hydrogen atom producing OH and chlorobenzene. The values for phenol are also reported for reference. Values relative to phenol are given in parentheses. The model chemistries are B3LYP/6-31G(d,p) (I), BHandHLYP/6-31G(d,p) (II), BHandHLYP/aug-cc-pVDZ (III) and QCISD(T)/6-31G(d,p)//BHandHLYP/6-31G(d,p) (IV).

Compound	I	II	III	IV
Phenol	−2.3	−7.7	−8.5
2-Chlorophenol	−1.5 (+0.8)	−7.0 (+0.7)	−7.8 (+0.7)	−5.2 (+1.0)
3-Chlorophenol	−2.5 (−0.2)	−7.9 (−0.2)	−8.7 (−0.2)	−6.3 (−0.1)
4-Chlorophenol	−2.8 (−0.5)	−8.2 (−0.5)	−9.1 (−0.6)	−6.7 (−0.5)
2,3-Dichlorophenol	−1.5 (+0.8)	−7.0 (+0.7)	−7.8 (+0.7)
2,4-Dichlorophenol	−1.9 (+0.4)	−7.4 (+0.3)	−8.4 (+0.1)
2,5-Dichlorophenol	−1.5 (+0.8)	−7.1 (+0.6)	−7.9 (+0.6)
2,6-Dichlorophenol	−3.5 (−1.2)	−9.0 (−1.3)	−10.1 (−1.6)
3,4-Dichlorophenol	−2.9 (−0.6)	−8.2 (−0.5)	−9.1 (−0.6)
3,5-Dichlorophenol	−2.7 (−0.4)	−8.0 (−0.3)	−8.8 (−0.3)
2,3,4-Trichlorophenol	−1.8 (+0.5)	−7.3 (+0.4)	−8.2 (+0.3)
2,3,5-Trichlorophenol	−1.6 (+0.7)	−7.1 (+0.6)	−7.9 (+0.6)
2,3,6-Trichlorophenol	−3.4 (−1.1)	−9.0 (−1.3)	−10.0 (−1.5)
2,4,5-Trichlorophenol	−2.0 (+0.3)	−7.5 (+0.2)	−8.4 (+0.1)
2,4,6-Trichlorophenol	−3.8 (−1.5)	−9.4 (−1.7)	−10.6 (−2.1)
3,4,5-Trichlorophenol	−3.0 (−0.7)	−8.4 (−0.7)	−9.3 (−0.8)
2,3,4,5-Tetrachlorophenol		−7.4 (+0.3)	−8.3 (+0.2)
2,3,4,6-Tetrachlorophenol		−9.2 (−1.5)	−10.3 (−1.8)
2,3,5,6-Tetrachlorophenol		−9.1 (−1.4)	−10.0 (−1.5)
Pentachlorophenol		−9.4 (−1.7)	−10.5 (−2.0)

Phenoxyl hydrogen abstraction by OH (Fig. 2, Reaction 4) has trends in ΔE_rxn similar to the other chlorophenoxyl radical-producing reactions (Table 4). These results suggest the formation of chlorinated phenoxyl radicals is slightly less energetically favored than the formation of the phenoxyl radical itself.

This contrasts with the effect of hydroxyl substitution in o- and p-semiquinone, which is to decrease the ΔE_rxn for radical formation [39]. Therefore, with the exception of p-chlorophenoxyl radical, we expect radicals to be slightly more difficult to form with chlorine substitution. Relative to phenol, the average bond dissociation energy, ΔE_rxn, (Fig. 2, Reaction 1) via BHandHLYP/aug-cc-pVDZ is +1.0 kcal/mol greater for the mono-substituted phenols, +2.1 kcal/mol greater for the di-substituted phenols, +2.2 kcal/mol greater for the tri-substituted phenols, +2.5 kcal/mol greater for the tetra-substituted phenols, and +2.0 kcal/mol greater for pentachlorophenol. There is thus a modest increase (except for pentachlorophenol) in the bond dissociation energy with increasing chlorination. Abstraction of the hydroxyl hydrogen by H and OH (Fig. 2, Reactions 2 and 4) displays a similar trend. Displacement of hydroxyl by H (Fig. 2, Reaction 3) has the opposite trend; increasing chlorination yields increasingly more negative values for ΔE_rxn.

The absolute energies (in Hartrees) of the mono-chlorinated species using the BHandHLYP/aug-cc-pVDZ model chemistry are given in Table 5. The stability of the mono-chlorinated phenols and phenoxyl radicals can be understood using the concept of electron donation (via resonance) of the hydroxyl and chlorine groups, as well as intramolecular hydrogen bonding. First, the intramolecular hydrogen bond that is formed in o-chlorophenol makes this the most stable of the monochlorophenols. There is EPR evidence from experiment that chlorine acts as an electron donator [28] in p-chlorophenol, presumably via resonance. The hydroxyl group is a strong electron donor (via resonance) [45], while in the radical, the oxygen atom acts as a net electron withdrawing group, again via resonance. Therefore, in the parent compound, having electron donating groups (–OH and –Cl) ortho- or para- with respect to each other is destabilizing, while the opposite is the case in the radical. Thus, p-chlorophenol is less stable than m-chlorophenol and because hydrogen-bonding stabilization outweighs other effects both are less stable than o-chlorophenol. For the radicals, the situation is reversed for the p- and m-chloro-phenoxyl radicals as the m-chlorophenoxyl radical is less stable. ln the o-chlorophenoxyl radical, inductive, electrostatic repulsion, and steric repulsion explain why this is the least stable of the mono-chlorinated radicals.

When these trends are used to make qualitative predictions for the bond dissociation energies, the energetics are consistent with experiment [28] and previous computational works [20,22,23,26]. These same trends were also found in a study of monochlorophenols and dichlorophenols used as precursors to understand chlorinated-dibenzofuran formation under both pyrolytic and oxidative conditions [14]. For the mono-chlorophenols and pyrolytic conditions, p-chlorophenol decomposes most readily while o-chlorophenol is most resistant to decomposition (based on unreacted precursor amounts in identical experiments.)

Displacement of the hydroxyl group by a hydrogen atom to form chlorobenzenes has been previously studied in the gas-phase [46]. lt was reported that this reaction proceeds via an addition/ipso substitution pathway and experimentally the dehydroxylation rate constants for the mono-chlorophenols are similar in magnitude to the analogous reaction for phenol. Specifically, the ratio of the rate constants to that of phenol were 1.08, 0.75, and 0.88 for 2-, 3-, and 4-monochlorophenol, respectively.

3.2. Radical decomposition

The decomposition of the phenoxyl radical to form cyclopentadienyl radical and carbon monoxide has been studied using density functional theory (B3LYP/6-31(d), Fig. 8) [29]. We use these authors’ proposal for the transition state as the starting point for locating transition states for the decomposition of the chlorinated species studied herein. The activation energies and ΔE_rxn for the decomposition via CO elimination of the 19 congeners of the chlorophenoxyl radical are listed in Table 6. In contrast to the parent compounds, the bond lengths in both the transition states and the cyclopentadienyl products exhibit some single and double bond character, as opposed to the aromatic character seen in the parent compounds (Fig 1). Overall, increasing the degree of chlorine substitution results in both lower activation energies and ΔE_rxn, although there are exceptions, e.g. 2,4,6-trichlorophenoxyl radical.

Fig. 8.

Top: Decomposition reaction of the phenoxyl radical to the cyclopentadienyl radical, including the transition state from Ref. [28]. Bottom: A rendering of the transition state for addition of O₂ to 2-chlorophenoxyl radical.

Table 6.

Activation and Reaction energies in kcal/mol for chlorophenoxy radical decomposition to CO and a chlorinated cyclopentadienyl radical. The values for the phenoxyl radical are also reported for reference. Values relative to phenol are given in parentheses. The model chemistries are B3LYP/6-31G(d,p) (I), BHandHLYP/6-31G(d,p) (II), BHandHLYP/aug-cc-pVDZ (III) and QCISD(T)/6-31G(d,p)//BHandHLYP/6-31G(d,p) (IV).

Compound	I		II		III		IV
	E a	Δ E rxn	E a	Δ E rxn	E a	Δ E rxn	E a	Δ E rxn
Phenoxyl	56.4	29.6	62.9	29	61.6	26.4	56.4	22.9
2-Chlorophenoxyl	52.5 (−3.9)	26.4 (−3.2)	60.2 (−2.7)	25.7 (−3.3)	58.8 (−2.8)	22.9 (−3.5)	54.1 (−2.3)	19.5 (−3.4)
3-Chlorophenoxyl	56.5 (+0.1)	26.1 (−3.5)	63.0 (+0.1)	25.9 (−3.1)	62.0 (+0.4)	23.5 (−2.9)	56.3 (−0.1)	18.9 (−4.0)
4-Chlorophenoxyl	57.6 (+1.2)	27.4 (−2.2)	63.6 (+0.7)	26.9 (−2.1)	62.6 (+1.0)	24.6 (−1.8)	57.4 (+1.0)	20.2 (−2.7)
2,3-Dichlorophenoxyl		24.3 (−5.3)	59.0 (−3.9)	23.5 (−5.5)	57.7 (−3.9)	21.2 (−5.2)
2,4-Dichlorophenoxyl		24.7 (−4.9)	61.1 (−1.8)	24.0 (−5.0)	60.0 (−1.6)	21.6 (−4.8)
2,5-Dichlorophenoxyl		23.6 (−6.0)	59.8 (−3.1)	23.1 (−5.9)	58.5 (−3.1)	23.6 (−2.8)
2,6-Dichlorophenoxyl		26.6 −3.0	64.0 (+1.1)	25.4 (−3.6)	62.6 (+1.0)	23.0 (−3.4)
3,4-Dichlorophenoxyl		25.0 (−4.6)	62.0 (−0.9)	24.4 (−4.6)	61.3 (−0.3)	22.6 (−3.8)
3,5-Dichlorophenoxyl		22.8 (−6.8)	62.4 (−0.5)	22.9 (−6.1)	61.5 (−0.1)	20.7 (−5.7)
2,3,4-Trichlorophenoxyl		22.2 (−7.4)	57.9 (−5.0)	21.1 (−7.9)	57.0 (−4.6)	19.2 (−7.2)
2,3,5-Trichlorophenoxyl		20.7 (−8.9)	58.3 (−4.6)	20.4 (−8.6)	57.2 (−4.4)	18.2 (−8.2)
2,3,6-Trichlorophenoxyl		23.9 (−5.7)	62.7 (−0.2)	22.6 (−6.4)	61.5 (−0.1)	20.4 (−6.0)
2,4,5-Trichlorophenoxyl		22.0 (−7.6)	59.1 (−3.8)	21.2 (−7.8)	58.2 (−3.4)	19.2 (−7.2)
2,4,6-Trichlorophenoxyl		24.3 (−5.3)	64.7 (+1.8)	23.2 (−5.8)	63.6 (+2.0)	21.0 (−5.4)
3,4,5-Trichlorophenoxyl		21.3 (−8.3)	59.7 (−3.2)	20.7 (−8.3)	59.2 (−2.4)	19.2 (−7.2)
2,3,4,5-Tetrachlorophenoxyl			55.4 (−7.5)	17.3 (−11.7)	54.7 (−6.9)	15.8 (−10.6)
2,3,5,6-Tetrachlorophenoxyl			60.6 (−2.3)	19.5 (−9.5)	59.5 (−2.1)	17.6 (−8.8)
2,3,4,6-Tetrachlorophenoxyl			60.9 (−2.0)	19.9 (−9.1)	60.0 (−1.6)	18.2 (−8.2)
Pentachlorophenoxyl			57.1 (−5.8)	16.3 (−12.7)	56.5 (−5.1)	15.1 (−11.3)

3.3. Radical reaction with molecular oxygen

The activation energies and ΔE_rxn for reaction of molecular oxygen with various monochlorinated phenoxyl radicals (Fig. 3) are presented in Table 7. Addition of molecular oxygen is slightly favored (based on ΔE_rxn) at the para-position, relative to the ortho-position. This is somewhat surprising for the p-chlorophenoxyl radical. Relative to the phenoxyl radical, reaction at the 4-position in the p- and o-chlorophenoxyl radicals has a greater activation energy, while m-chlorophenoxyl radical has essentially the same the activation energy as the phenoxyl radical.

Fig. 3.

Ortho- and para-addition of molecular oxygen to the para-monosubstituted radical.

Table 7.

Activation and Reaction energies in kcal/mol for bimolecular chlorinated phenoxyl radical-molecular oxygen channels. The values for the phenoxyl radical are also reported for reference. Values relative to phenol are given in parentheses. The model chemistries are B3LYP/6-31G(d,p) (I), BHandHLYP/6-31G(d,p) (II), BHandHLYP/aug-cc-pVDZ (III) and QCISD(T)/6-31G(d,p)//BHandHLYP/6-31G(d,p) (IV).

Compound/addition	I		II		III		IV
	E a	Δ E rxn	E a	Δ E rxn	E a	Δ E rxn	E a	Δ E rxn
Ortho-addition
Phenoxyl	13.7	9.3	23.5	12.3	23.8	12.7	14.6	1.8
2-Chlorophenoxyl (to C-6)	14.9 (+1.2)	11.5 (+2.2)	24.3 (+0.8)	13.6 (+1.3)	24.7 (+0.9)	14.3 (+1.6)	15.5 (+0.9)	3.0 (+1.2)
2-Chlorophenoxyl (to C-2)	15.7 (+2.0)	12.5 (+3.2)	25.8 (+2.3)	14.9 (+2.6)	25.9 (+2.1)	15.2 (+2.5)	15.2 (+0.6)	2.9 (+1.1)
3-Chlorophenoxyl (to C-6)	13.2 (−0.5)	9.0 (−0.3)	23.2 (−0.3)	11.6 (−0.7)	23.3 (−0.5)	11.9 (−0.8)	14.0 (−0.6)	0.7 (−1.1)
3-Chlorophenoxyl (to C–2)	13.7 (0.0)	9.8 (+0.5)	23.8 (+0.3)	13.0 (+0.7)	24.3 (+0.5)	13.8 (+1.1)	15.0 (+0.4)	2.1 (+0.3)
4-Chlorophenoxyl	14.6 (+0.9)	11.3 (+2.0)	24.2 (+0.7)	13.9 (+1.6)	24.5 (+0.8)	14.4 (+1.7)	15.2 (+0.6)	3.4 (+1.6)
Para-addition
Phenoxyl	10.8	6.2	20.7	8.4	20.9	8.5	11.1	−2
2-Chlorophenoxyl	13.8 (+3.0)	7.9 (+1.7)	23.1 (+2.4)	9.8 (+1.4)	22.9 (+2.0)	9.9 (+1.4)	15.8 (+4.7)	−0.5 (+1.5)
3-Chlorophenoxyl	10.7 (−0.1)	7.3 (+1.1)	20.7 (0.0)	9.4 (+1.0)	20.8 (−0.1)	9.6 (+1.1)	10.7 (−0.4)	−1.9 (+0.1)
4-Chlorophenoxyl	14.2 (+3.4)	9.7 (+3.5)	24.6 (+3.9)	12.1 (+3.7)	24.2 (+3.3)	12.1 (+3.6)	14.1 (+3.0)	−0.1 (+1.9)

3.4. Additivity analysis

Given the correlations found for the absolute energies of parent and radical species (vide infra), we investigated whether an additivity analysis can be used to explain the variation in reaction energetics of the various congeners. We began by considering the various factors that contribute to the relative stabilities of parent compounds and resultant radicals. We considered the following aspects of the stability/reactivity (applying to both the parent and resulting radical unless otherwise noted):

• O–Cl repulsion – for both molecular parents and radicals, when an O atom is adjacent to a Cl atom, there is a repulsive interaction, consisting of inductive, electrostatic, and steric effects. We denote this destabilizing repulsion S_O-Cl and for simplicity use the same value for molecular parents and radicals.

• Cl–Cl repulsion – when two Cl atoms are adjacent, there is a destabilizing repulsive interaction, S_Cl–Cl. As with S_O–Cl, we use the same value for both molecular parents and radicals.

• Hydrogen bonding – in a parent compound with a Cl atom adjacent to the OH group there is additional stability when the H atom is directed toward an adjacent Cl atom. We denote this energy EH. This term is only present in the parent compounds.

• Chlorine electron donation – in the parent, molecular compounds, the electron donating (via resonance) character of Cl leads to a destabilization when Cl is ortho- or para- to the –OH group. We denote this energy R_M (molecular parent compound only.) In the radicals, this same effect leads to stabilization when Cl is ortho- or para-relative to the –O group due to the switch from the electron donating –OH group to the electron deficient –O. atom. We denote this energy R_R (radicals only.)

• Delocalization in cyclopentadienyl radicals – in cyclopentadienyl radical, bond lengths suggest the unpaired electron is delocalized over 3 carbon atoms. In the chlorosubstituted cyclopentadienyl radicals, this delocalization occurs in some, but not all of the congeners. lf the delocalization includes a carbon to which a Cl atom is attached, this will lead to a stabilization of the radical. This stabilization energy is denoted by RCl.

• Repulsion between added ³O₂ and Cl and O groups are denoted S_OO2 and S_ClO2, respectively. For simplicity, we have assumed S_ClO2 is the same, whether the Cl and O₂ are geminal or vicinal. A more refined treatment of additivity would allow for a geminal and vicinal value for this quantity.

There are two stable planar isomers of o-chlorphenol; one with the OH bond directed toward the Cl atom and the other with the OH bond directed away from the Cl atom. It is possible to form a hydrogen bond in the former isomer. Our calculations give the difference in energy between these two isomers (and hence the energy of the O–H–Cl hydrogen bond) to be E_H = −3.1 kcal/mol (BHandHLYP/aug-cc-pVDZ.) The energy of p-chlorophenol relative to m-chlorophenol is R_M, which our calculations give as +0.46 (which we round to 0.45) kcal/mol (BHandHLYP/aug-cc-pVDZ.) The energy of m-chlorophenol relative to o-chlorophenol is +0.81 kcal/mol (BHandHLYP/aug-cc-pVDZ) leading to our (rounded) value for S_O–Cl of 1.85 kcal/mol. R_R is determined by the relative energies of the o-chlorophenoxyl and m-chlorophenoxyl radicals and yields R_R= −1.35 kcal/mol. Finally, S_Cl–Cl can be determined by the relative energy of 2,5-dichlorophenol to 2,3-dichlorophenol and yields a rounded value of S_Cl–Cl = 2.55 kcal/mol. For simplicity, we assume no changes in these values for all the chlorinated parent and radical species and ignore the relatively small effect from Cl–Cl resonance effects on the ring. R_Cl is obtained as the difference between 1,2- and 1,3-dichloropentadienyl radicals, which we find to be −0.45 kcal/mol (BHandHLYP/aug-cc-pVDZ). S_OO2 and S_ClO2 are obtained using the differences between the addition of ³O₂ to the 2-, 4-, and 6-positions of the 2-chlorophenoxyl radical and are found to be 4.4 and 0.9 kcal/mol, respectively (BHandHLYP/aug-cc-pVDZ).

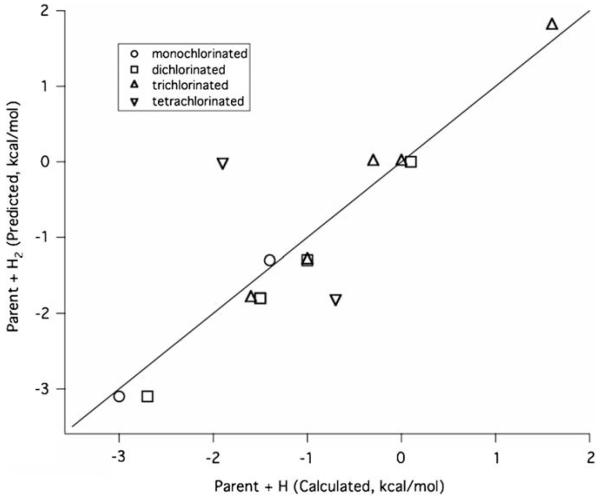
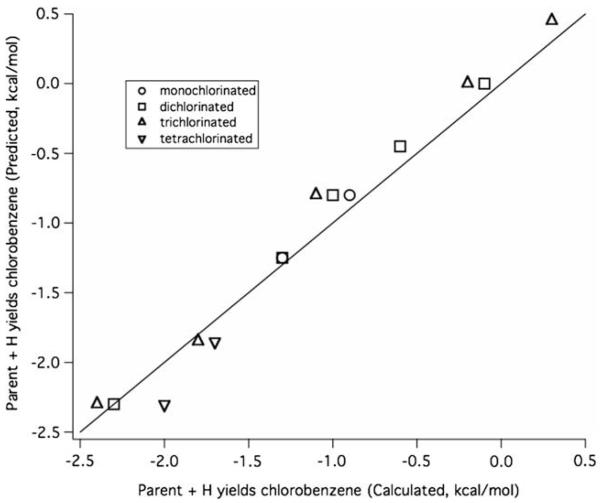
For isomers with the same number of chlorine atoms, these values allow the prediction of the relative values of ΔE_rxn for all the reactions considered in this work. The contributions to the relative energies for the monochlorinated species are given in Table 8. The Appendix shows a calculation using the additivity analysis. Correlation plots of predicted versus calculated values for the ΔE_rxn for the four reaction channels given in Fig. 2. and depicted in Figs. 4–7. Correlation plots for radical consumption channels depicted in Figs. 3 and 8 are given in Figs. 9 and 10. The agreement between calculated and predicted values is excellent and lends credence to the ideas underlying the additivity analysis.

Table 8.

Predictions in kcal/mol for the relative energies of monochlorinated phenols and phenoxyl radicals. See text for definitions of E_H, S_O-Cl, R_M, and R_R.

Species	Calculated	Predicted	E H	S O-CI	R M	R R
o-Chlorophenol	0	0	−3.1	1.85	0.45	0
m-Chlorophenol	0.807	0.8	0	0	0	0
p-Chlorophenol	1.270	1.25	0	0	0.45	0
o-Chlorophenoxy	0	0	0	1.85	0	−1.35
m-Chlorophenoxy	−0.519	−0.5	0	0	0	0
p-Chlorophenoxy	−1.700	−1.85	0	0	0	−1.35

Fig. 4.

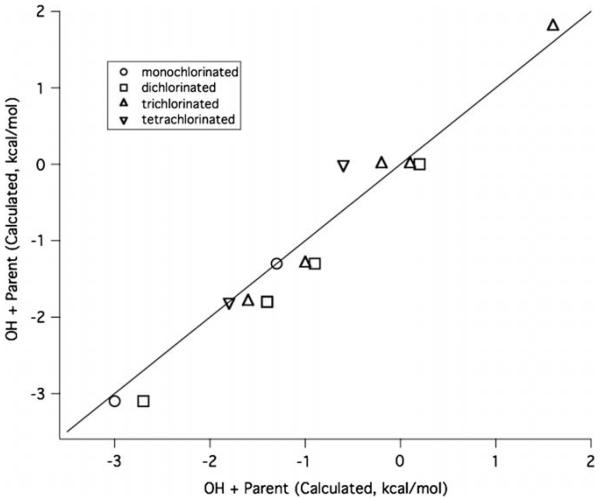
Correlation plot of the predicted versus calculated values for the relative ΔE_rxn for Reaction 1 in Fig. 2. Monochlorinated species are given relative to o-chlorophenol, dichlorinated are relative to 2,3-dichlorophenol, trichlorinated are relative to 2,3,4-trichlorophenol, and tetrachlorinated are relative to 2,3,4,5-tetrachlorophenol.

Fig. 7.

Correlation plot of the predicted versus calculated values for the relative ΔE_rxn for Reaction 4 in Fig. 2. Monochlorinated species are given relative to o-chlorophenol, dichlorinated are relative to 2,3-dichlorophenol, trichlorinated are relative to 2,3,4-trichlorophenol, and tetrachlorinated are relative to 2,3,4,5-tetrachlorophenol.

Fig. 9.

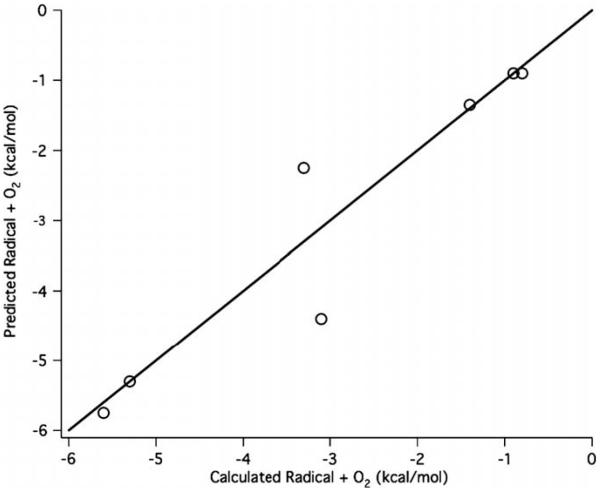
Correlation plot of the predicted versus calculated values for the relative ΔE_rxn for elimination from the chlorinated phenoxyl radicals to form CO and a chlorinated cyclopentadienyl radical. Monochlorinated species are given relative to o-chlorophenoxyl radical, dichlorinated are relative to 2,3-dichlorophenoxyl radical, trichlorinated are relative to 2,3,4-trichlorophenoxyl radical, and tetrachlorinated are relative to 2,3,4,5-tetrachlorophenoxyl radical.

Fig. 10.

Correlation plot of the predicted versus calculated values for the relative ΔE_rxn for the addition of O₂ to the chlorinated cyclopentadienyl radicals. Mono-chlorinated species are given relative to o-chlorophenoxyl radical, dichlorinated are relative to 2,3-dichlorophenoxyl radical, trichlorinated are relative to 2,3,4-trichlorophenoxyl radical, and tetrachlorinated are relative to 2,3,4,5-tetrachlorophenoxyl radical.

While this additivity analysis can in principle be extended to the prediction of activation energies, this requires a careful examination of the transition state geometries, which we determined would require more parameters than would make such a procedure credible. Therefore, we do not present any predictions for activation energies.

4. Conclusions

Chlorine substitution has modest, but measurable impacts on the rate of formation of phenoxyl radicals and the persistence of phenoxyl radicals once they are formed. Relative to phenol, increased chlorination generally increases the ΔE_rxn of radical formation through the phenoxyl radical forming pathways. In contrast, increasing chlorination decreases the ΔE_rxn of formation of chlorobenzenes. Increasing chlorination results in a decrease in the average E_a for decomposition of the radical, viz. greater radical stability. Chlorine substitution slightly increases E_a for reaction with O₂ at the o- and p-positions [11].

A driving force for this study was the discovery that substituted phenoxyl radicals were environmentally persistent when associated with copper oxide-containing particles [11]. While we know that chemisorption of the parent molecular species and electron transfer to the metal on the particle surface are at least partially responsible for this persistence, it is reasonable that these types of radicals may also be persistent in the gas-phase under some conditions.

It is known that ortho- and para-hydroxy substituted phenol (catechol and hydroquinone) form semiquinone radicals that are persistent under some conditions and, most importantly, are reducing agents that initiate formation of biologically damaging reactive oxygen species (ROS) when inhaled. Since the chlorinated phenols are valence isolectronic with catechol and hydroquinone, we were interested in whether chlorinated phenoxyl radicals were as easy to form and were as persistent as semiquinone radicals.

We find that while chlorinated phenoxyl radicals are not as easy to form as semiquinone radicals [39], they are still readily formed compared to most other organic radicals. Once formed, although still quite stable, chlorinated phenoxyl radicals decompose by elimination of CO more readily than semiquinone radicals. This may reduce their concentration in combustion systems and thermal processes. However, once emitted into the atmosphere where the primary route for consumption of radicals is reaction with O₂, our calculations indicate that generally chlorination decreases the rate of reaction with O₂.

In summary, based on our calculations, chlorinated phenoxyl radicals have the potential to be even more environmentally persistent than semiquinone radicals. This suggests that the reduction potentials of chlorinated phenoxyl radicals should also be measured and calculated to determine if they are as powerful and potentially biologically active as semiquinone radicals.

Fig. 5.

Correlation plot of the predicted versus calculated values for the relative ΔE_rxn for Reaction 2 in Fig. 2. Monochlorinated species are given relative to o-chlorophenol, dichlorinated are relative to 2,3-dichlorophenol, trichlorinated are relative to 2,3,4-trichlorophenol, and tetrachlorinated are relative to 2,3,4,5-tetrachlorophenol.

Fig. 6.

Correlation plot of the predicted versus calculated values for the relative ΔE_rxn for Reaction 3 in Fig. 2. Monochlorinated species are given relative to o-chlorophenol, dichlorinated are relative to 2,3-dichlorophenol, trichlorinated are relative to 2,3,4-trichlorophenol, and tetrachlorinated are relative to 2,3,4,5-tetrachlorophenol.

Appendix A

We present the calculation of the relative bond dissociation energies of 2,3-dichlorophenol and 2,4-dichlorophenol as an example of using the additivity analysis. The five energy terms E_H, S_O–Cl, S_Cl–Cl, R_p, and R_R are described in the body of this work and are used here. The relative bond dissociation is given by

$$\Delta E_{\mathrm{rel}}=\Delta E_{2,4}-\Delta E_{2,3}$$

$$\Delta E_{2,4}=E(2,4-\text{dichlorophenoxyl radical})-E(2,4-\text{dichlorophenol})$$

$$\Delta E2,3=E(2,3-\text{dichlorophenoxyl radical})-E(2,3-\text{dichlorophenol})$$

$$E(2,4-\text{dichlorophenoxyl radical})=S_{O-Cl}+2R_R=1.85-2.70=-0.85\mathrm{kcal}∕\mathrm{mol}$$

$$E(2,4-dichlorophenol)=E_H+S_{O-Cl}+2R_M=-3.1+1.85+0.9=-0.35\mathrm{kcal}∕\mathrm{mol}$$

$$E(2,3-\text{dichlorophenoxyl radical})=S_{O-Cl}+S_{Cl-Cl}+R_R=1.85+2.55-1.35=3.05\mathrm{kcal}∕\mathrm{mol}$$

$$E(2,3-\text{dichlorophenol})=E_H+S_{O-Cl}+S_{Cl-Cl}+R_M=-3.1+1.85+2.55+0.45=17.5\mathrm{kcal}∕\mathrm{mol}$$

and therefore,

$$\Delta E_{\mathrm{rel}}=\Delta E_{2,4}-\Delta E_{2,3}=(-.85+.35)-(3.05-1.75)=-1.8\mathrm{kcal}∕\mathrm{mol}$$