Invariance property of wave scattering through disordered media

Significance

The diffusion of particles and waves through disordered media encompasses a large variety of phenomena, from the motion of insects to the scattering of electrons or light in complex environments. One of the core features of diffusive transport is that the mean length of trajectories traversing a system depends only on the size of the system and of its boundary, which are both independent of the microscopic structure of the underlying medium. Here we show, based on insights from wave-scattering theory, that this fundamental invariance property can be significantly extended beyond the diffusive random walk picture. Our result not only provides an interesting link between all the diverse fields in which wave scattering plays a role but also holds promise for a number of practical applications.

Abstract

A fundamental insight in the theory of diffusive random walks is that the mean length of trajectories traversing a finite open system is independent of the details of the diffusion process. Instead, the mean trajectory length depends only on the system's boundary geometry and is thus unaffected by the value of the mean free path. Here we show that this result is rooted on a much deeper level than that of a random walk, which allows us to extend the reach of this universal invariance property beyond the diffusion approximation. Specifically, we demonstrate that an equivalent invariance relation also holds for the scattering of waves in resonant structures as well as in ballistic, chaotic or in Anderson localized systems. Our work unifies a number of specific observations made in quite diverse fields of science ranging from the movement of ants to nuclear scattering theory. Potential experimental realizations using light fields in disordered media are discussed.

In the biological sciences it has been appreciated for some time now that the movement of certain insects (such as ants) on a planar surface can be modeled as a diffusive random walk with a given constant speed v (1–3). Using this connection, Blanco and Fournier (4) proved that the time that these insects spend on average inside a given domain of area A and with an external boundary C is independent of the parameters entering the random walk such as, for example, the transport mean free path (MFP) ${\ell }^{\mathrm{\ast }}$. Specifically, the average time t between the moments when an insect enters the domain and when it first exits it again is given by the simple relation $\langle t\rangle =\pi A/\left(Cv\right)$. One finds that the mean length $\langle l\rangle$ of the corresponding random walk trajectories inside the domain is also constant, $\langle l\rangle =\langle t\rangle \hspace{0.17em}v=\pi A/C$. Similar relations also hold in three dimensions, $\langle t\rangle =4V/\left(\mathrm{\Sigma }v\right)$ and $\langle l\rangle =4V/\mathrm{\Sigma }$, where V is the volume and Σ is the external surface of a given domain. Extensions of this result exist for trajectories beginning inside the domain (5) or for the calculation of averaged residence times inside subdomains (6). As a generalization of the mean-chord-length theorem (7) for straight-line trajectories with an infinite MFP, this fundamental theorem has numerous applications, for instance in the context of food foraging (8) and for the reaction rates in chemistry (9).

The surprising element of this result can be well appreciated when applied to the physical sciences and, in particular, to the transport of light or of other types of waves in scattering media. In that context it is well known that the relevant observable quantities all do depend on ${\ell }^{\mathrm{\ast }}$: In the diffusive regime, the total transmission of a slab of thickness L scales with ${\ell }^{\mathrm{\ast }}/L$ through Ohm’s law, and the characteristic dwell time scales with the so-called Thouless time $L^2/\left(v{\ell }^{\mathrm{\ast }}\right)$ (10). When considering coherent wave effects, ${\ell }^{\mathrm{\ast }}$ also determines the width of the coherent backscattering cone in weak localization (11, 12) and drives the phase-transition from diffusive to Anderson localization (13). An invariant quantity that does not depend on ${\ell }^{\mathrm{\ast }}$ would thus be highly surprising to the community involved in wave scattering through disordered media. Because, in addition, coherent effects such as weak or strong (Anderson) localization clearly fall outside the scope of a diffusive random walk model, one may also expect that an invariance property simply does not exist when wave interference comes into play. As we will demonstrate here explicitly, this expectation is clearly too pessimistic. Instead, we find that an invariant time and length scale can also be defined for waves, even when they scatter nondiffusively, as in the ballistic or in the Anderson localization regime. The key insight that allows us to establish such a very general relation for the mean wave scattering time is its connection to the density of states (DOS), which is the central quantity that stays invariant on a level far beyond the scope of a diffusion approximation.

To describe wave transport in a disordered scattering medium without solving the full wave equation numerically is a challenging task that can be approached from many different angles (10, 14, 15). As the first step, we will consider the radiative transfer equation (RTE), which describes the transport of an averaged radiation field through a disordered medium in the limit $k{\ell }_s\gg 1$, where $k=\omega /c=2\pi /\lambda$ is the wave number and ${\ell }_s$ is the scattering MFP (7, 16). In nonabsorbing media, as considered here, the scattering MFP ${\ell }_s$ is connected to ${\ell }^{\mathrm{\ast }}$ by the anisotropy parameter g, which measures the degree of forward scattering at a scattering event, ${\ell }_s={\ell }^{\mathrm{\ast }}\left(1-g\right)$. In its standard formulation where the RTE does not include wave interference effects it should fully reproduce the predictions by Blanco and Fournier (4) from above. However, one can enhance the scope of the RTE to include specific wave effects such as the dispersion in a medium containing strongly resonant scatterers such as atomic dipoles or Mie spheres (17, 18). In what follows we will consider identical, but randomly placed, resonant and nonabsorbing dipole scatterers described by a polarizability $\alpha \left(\delta \right)=-4\pi /k^3{\left[i+2\delta /\mathrm{\Gamma }\right]}^{-1}$, with $\delta =\omega -{\omega }_0$ the detuning with respect to the resonance frequency ${\omega }_0$, and Γ the linewidth (modeling losses due to scattering only). This specific expression is valid close to the resonance (i.e., $\delta \ll {\omega }_0$) and ensures energy conservation (i.e., the optical theorem is fulfilled). In this case and for a dilute system such that $\mathcal{N}{\lambda }^3\ll 1$, where $\mathcal{N}$ is the density of scatterers, a dispersive form of the RTE can be derived from the Bethe–Salpeter equation (an exact equation for the spatiotemporal autocorrelation function of the electric field) (18):

$$\left[-\frac{i\mathrm{\Omega }}{c}+\mathbf{u}\cdot {\mathbf{\nabla }}_{\mathbf{r}}+{\mu }_e\left(\delta ,\mathrm{\Omega }\right)\right]I\left(\mathbf{u},\mathbf{r},\delta ,\mathrm{\Omega }\right)=\frac{1}{4\pi }{\mu }_s\left(\delta ,\mathrm{\Omega }\right)\times {\displaystyle \int I\left({\mathbf{u}}^{\prime },\mathbf{r},\delta ,\mathrm{\Omega }\right)\mathrm{d}{\mathbf{u}}^{\prime }},$$ [1]

where du′ stands for integration over the solid angle. The specific intensity $I\left(\mathbf{u},\mathbf{r},\delta ,\tau \right)$ (also called spectral radiance) is defined through the Wigner transform of the electric field and describes the radiative flux at position r, along direction u, at frequency δ and at time τ. Eq. 1 is Fourier-transformed with respect to τ (with Ω being the conjugate Fourier variable). The expressions for the extinction and scattering MFP are given by ${\mu }_e\left(\delta ,\mathrm{\Omega }\right)=-i\mathcal{N}k/2\left[\alpha \left(\delta +\mathrm{\Omega }/2\right)-{\alpha }^{\mathrm{\ast }}\left(\delta -\mathrm{\Omega }/2\right)\right]$ and ${\mu }_s\left(\delta ,\mathrm{\Omega }\right)=\mathcal{N}{k}^4/\left(4\pi \right)\alpha \left(\delta +\mathrm{\Omega }/2\right){\alpha }^{\mathrm{\ast }}\left(\delta -\mathrm{\Omega }/2\right)$. The Boltzmann scattering MFP ${\ell }_s\left(\delta \right)={\ell }_0\left[1+4{\delta }^2/{\mathrm{\Gamma }}^2\right]$, with ${\ell }_0={\left[4\pi \mathcal{N}/k^2\right]}^{-1}$ the value at resonance ($\delta =0$), can be changed by varying the detuning δ or the linewidth Γ. Note that the condition $\mathcal{N}{\lambda }^3\ll 1$ is then equivalent to $k{\ell }_s\gg 1$.

On this basis we can evaluate the average time spent by light trajectories inside the medium by calculating the weighted temporal average $\langle t\left(\delta \right)\rangle ={\displaystyle \int \tau {\varphi }_{\mathrm{out}}\left(\delta ,\tau \right)\mathrm{d}\tau }/{\displaystyle \int {\varphi }_{\mathrm{out}}\left(\delta ,\tau \right)\mathrm{d}\tau }$, where the weighting function ${\varphi }_{\mathrm{out}}={\displaystyle {\int }_{\mathrm{\Sigma }}{\displaystyle {\int }_{2\pi }I\left(\mathbf{u},\mathbf{r},\delta ,\tau \right)\mathbf{u}\cdot \mathbf{n}\hspace{0.17em}\mathrm{d}\mathbf{u}\hspace{0.17em}{\mathrm{d}}^2\mathbf{r}}}$ is the outgoing flux at time τ, Σ is the medium boundary, and n the outward normal. In frequency domain, this expression can be cast in the following compact form (Supporting Information):

$$\langle t\left(\delta \right)\rangle ={\frac{-i}{{\varphi }_{\mathrm{out}}\left(\delta ,\mathrm{\Omega }=0\right)}\frac{\partial {\varphi }_{\mathrm{out}}\left(\delta ,\mathrm{\Omega }\right)}{\partial \mathrm{\Omega }}|}_{\mathrm{\Omega }=0},$$ [2]

where we define $t=0$ as the time when the incident flux enters the medium. This expression is also convenient for a numerical computation of $\langle t\left(\delta \right)\rangle$ based on Eq. 1. In the numerical simulation, we consider a 3D slab geometry of length L with on-resonance optical thickness $b_0=L/{\ell }_0$, illuminated by an isotropic and uniform specific intensity on its left interface only (Fig. 1A). This corresponds to a situation where the incident specific intensity does not depend on the point and direction of incidence (Lambert’s cosine law is satisfied). Using a Monte-Carlo scheme (18), we solved Eq. 1 without approximation and obtained the results plotted in Fig. 2. By tuning the linewidth Γ of the scatterers, we can either simulate a nonresonant medium in which the intensity spends most of the time between the scatterers ($\mathrm{\Gamma }{\ell }_0\gg c$) or a resonant medium where the transport time is dominated by intensity trapping inside the scatterers ($\mathrm{\Gamma }{\ell }_0\ll c$).

Fig. 1.

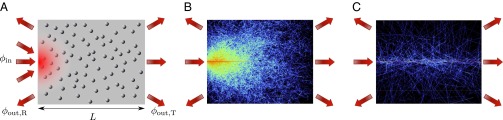
Sketch of the system and light trajectories. (A) Geometry of the 3D slab of length L investigated numerically using the RTE. ${\varphi }_{\mathrm{in}}$ is the incident flux and ${\varphi }_{\mathrm{out},\mathrm{R}}$ and ${\varphi }_{\mathrm{out},\mathrm{T}}$ are the reflected and transmitted fluxes, respectively (${\varphi }_{\mathrm{out}}={\varphi }_{\mathrm{out},\mathrm{R}}+{\varphi }_{\mathrm{out},\mathrm{T}}$). (B and C) Projections of light trajectories inside the system in the case of normal incidence illumination at a specific point on the system boundary (see inward arrow) for two optical thicknesses, (B) $b=10$ and (C) $b=0.59$.

Fig. 2.

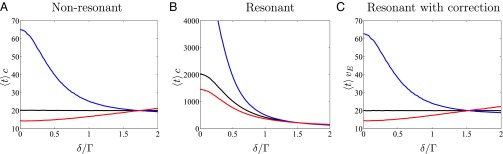
Ensemble-averaged length $\langle l\left(\delta \right)\rangle$ of light trajectories as obtained numerically using the RTE for (A) nonresonant and (B and C) resonant scatterers in a 3D slab of width $L=10$ and optical thickness at resonance $b_0=10$. Black/blue/red lines depict the values for all/transmitted/reflected trajectories, corresponding to the fluxes ${\varphi }_{\mathrm{out}}/{\varphi }_{\mathrm{out},\mathrm{T}}/{\varphi }_{\mathrm{out},\mathrm{R}}$ in Fig. 1. The values for $\langle l\left(\delta \right)\rangle$ were determined through the average time $\langle t\rangle$ multiplied by the speed of light c in A and B and by the energy velocity $v_E$ in C. The renormalization with the energy velocity $v_E$ in the resonant case (C) yields the same universal value $\langle t\rangle v_E=2L$ as obtained by Blanco and Fournier (4) for the nonresonant case $\langle t\rangle c=2L$ (A). For $\delta =0$ and for $\delta =2\mathrm{\Gamma }$, the optical thickness is $b=10$ and $b=0.59$, respectively, such that the above results range from the diffusive to the single-scattering regime.

In the nonresonant case (Fig. 2A), we recover the results by Blanco and Fournier (4) and find an average time $\langle t\left(\delta \right)\rangle$ that is independent of the scattering properties of the medium (i.e., independent of the detuning δ that determines the scattering properties in the present RTE calculation). Moreover, we clearly see that the times associated to the reflected and transmitted parts of the outgoing flux, which can be computed separately, strongly depend on δ, showing that the invariance of the average time $\langle t\left(\delta \right)\rangle$ results from a delicate balance between reflection and transmission (in both their intensities and time delays), as illustrated by light trajectories displayed in Fig. 1 B and C. Also note that by varying the detuning δ from 0 to 2 in Fig. 2A we effectively perform a cross-over from the diffusive to the single scattering regime. In the latter ($\delta \gtrsim 1.5$), the invariance of $\langle t\left(\delta \right)\rangle$ follows directly from the mean-chord-length theorem (7).

In case of a resonant medium (Fig. 2B) the situation is substantially different. The average time $\langle t\left(\delta \right)\rangle$ exhibits a significant dependence on δ, and therefore on the scattering properties of the medium. Because this result clearly falls outside the scope of the invariance relation derived by Blanco and Fournier (4), the question arises whether a new quantity can be defined that remains invariant even in the limit of strongly dispersive scatterers. To address this issue we rewrite the average time $\langle t\left(\delta \right)\rangle$ in Eq. 2 as the ratio of the total energy U stored in the system and the outgoing flux ${\varphi }_{\mathrm{out}}$,

$$\langle t\left(\delta \right)\rangle =\frac{U\left(\delta ,\mathrm{\Omega }=0\right)}{{\varphi }_{\mathrm{out}}\left(\delta ,\mathrm{\Omega }=0\right)}.$$ [3]

As specified in more detail in Supporting Information, this relation measures $\langle t\left(\delta \right)\rangle$ as the time the stored energy U takes to flow out of the medium with flux ${\varphi }_{\mathrm{out}}=-{\varphi }_{\mathrm{in}}$ (in stationary processes without absorption or gain, the incoming and outgoing fluxes are balanced) (19). Expressing ${\varphi }_{\mathrm{out}}$ and U in terms of the specific intensity ${\varphi }_{\mathrm{out}}\left(\delta ,\mathrm{\Omega }\right)={\displaystyle {\int }_{\mathrm{\Sigma }}{\displaystyle {\int }_{2\pi }I\left(\mathbf{u},\mathbf{r},\delta ,\mathrm{\Omega }\right)\mathbf{u}\cdot \mathbf{n}\hspace{0.17em}\mathrm{d}\mathbf{u}\hspace{0.17em}{\mathrm{d}}^2\mathbf{r}}}$ and $U\left(\delta ,\mathrm{\Omega }\right)=v_E^{-1}\left(\delta \right){\displaystyle {\int }_V{\displaystyle {\int }_{4\pi }I\left(\mathbf{u},\mathbf{r},\delta ,\mathrm{\Omega }\right)\mathrm{d}\mathbf{u}\hspace{0.17em}{\mathrm{d}}^3\mathbf{r}}}$, where $v_E\left(\delta \right)$ is the energy (or transport) velocity (17), we obtain

$$\begin{array}{c}\langle t\left(\delta \right)\rangle =\left[\frac{1}{v_E\left(\delta \right)}{\displaystyle \underset{V}{\int }{\displaystyle \underset{4\pi }{\int }I\left(\mathbf{u},\mathbf{r},\delta ,\mathrm{\Omega }=0\right)\mathrm{d}\mathbf{u}\hspace{0.17em}{\mathrm{d}}^3\mathbf{r}}}\right]\\ \times {\left[{\displaystyle \underset{\mathrm{\Sigma }}{\int }{\displaystyle \underset{2\pi }{\int }I\left(\mathbf{u},\mathbf{r},\delta ,\mathrm{\Omega }=0\right)\mathbf{u}\cdot \mathbf{n}\hspace{0.17em}\mathrm{d}\mathbf{u}\hspace{0.17em}{\mathrm{d}}^2\mathbf{r}}}\right]}^{-1}.\end{array}$$ [4]

In this expression V and Σ are the volume and the external boundary of the medium, and n is the outward normal. For a uniform and isotropic illumination on the surface (as assumed here), the specific intensity is uniform, isotropic, and independent on detuning inside the medium (a particular case of such a situation is blackbody radiation) (14). As a result, Eq. 4 can be drastically simplified into $\langle t\left(\delta \right)\rangle =4V/\left[\mathrm{\Sigma }\hspace{0.17em}{v}_E\left(\delta \right)\right]$, which for a slab of thickness L gives $\langle t\left(\delta \right)\rangle =2L/v_E\left(\delta \right)$. This result turns out to be strikingly similar to the invariance relation derived by Blanco and Fournier (4), the only difference being that in resonant media the dispersive form of the energy velocity $v_E\left(\delta \right)$ comes into play. The expression of the energy velocity for resonant scatterers can be determined explicitly (17), and takes the following form (Supporting Information):

$$v_E\left(\delta \right)={\left[\frac{1}{c}+\frac{1}{\mathrm{\Gamma }{\ell }_s\left(\delta \right)}\right]}^{-1}.$$ [5]

The energy velocity allows us to introduce an invariant length scale, $\langle l\rangle =\langle t\left(\delta \right)\rangle v_E=4V/\mathrm{\Sigma }$, which is independent of the scattering properties of the medium for both resonant and nonresonant scattering (in the latter the energy velocity simply reduces to the constant velocity entering the random walk formalism). To prove the correctness of this result, we plot the average length $\langle l\rangle$ in Fig. 2C as obtained by renormalizing the numerical results for $\langle t\left(\delta \right)\rangle$ in Fig. 2B with the analytical expression (Eq. 5) of the transport velocity $v_E$. We find that the resulting curve for $\langle l\left(\delta \right)\rangle =\langle t\left(\delta \right)\rangle v_E$ is, indeed, independent of the detuning δ, with a constant value $\langle l\rangle =2L$. This result is all the more remarkable because the average lengths associated with either the transmitted or the reflected part of the flux display a strong dependence on the scattering properties in the same regime. This again shows that the invariance of the average length $\langle l\rangle$ results from a subtle balance between reflection and transmission.

Whereas the above extension of the RTE allowed us to find a new invariant quantity for the case of scattering in a disordered medium with resonant scatterers, the ansatz of the RTE itself is intrinsically restricted to the limit $k{\ell }_s\gg 1$. The opposite limit, where the wavelength λ is comparable to or even larger than the mean free path ${\ell }_s$, is thus not covered by our foregoing considerations. Because in this strongly scattering limit wave interference can lead to a complete halt of wave diffusion in terms of Anderson localization, the question arises whether localization will lead to a deviation from the above invariance property or not. One could expect such a deviation, for instance on the grounds that localization prevents scattering states to explore the entire scattering volume V of the system. Correspondingly, the volume V and the surface Σ appearing in the invariance relation $\langle t\left(\delta \right)\rangle =4V/\left[\mathrm{\Sigma }{v}_E\left(\delta \right)\right]$ might then have to be rescaled with the localization length ξ.

To explore this question in detail we will now work with the full wave equation in two dimensions which, for stationary light scattering, is given in terms of the Helmholtz equation:

$$\left[\mathrm{\Delta }+n{\left(x,y\right)}^2{k}^2\right]\psi \left(x,y\right)=0.$$ [6]

The linear dispersion $k=\omega /c$ will allow us to use k and ω interchangeably. In the situations we study here, the disorder scattering is induced by the spatial variations of the static refractive index $n\left(x,y\right)$. To evaluate the dwell time of a stationary scattering eigenstate of this equation (with well-defined wave number k) inside a given spatial region one can conveniently use the so-called Wigner–Smith time-delay operator^†:

$$Q\left(\omega \right)=-i\hspace{0.17em}{S}^{-1}\frac{dS}{d\omega },$$ [7]

originally introduced by Wigner in nuclear scattering theory (21) and extended by Smith to multichannel scattering problems (22). Here the ω-dependent scattering matrix S, evaluated at the external boundary C of the considered region, contains all of the complex transmission and reflection amplitudes that connect in- and outgoing waves in a suitable mode basis. To obtain also here the average time associated with wave scattering we take the trace of Q and divide by the number $N\left(\omega \right)$ of incoming scattering channels, $\langle t\left(\omega \right)\rangle =\mathrm{Tr}\left[Q\left(\omega \right)\right]/N\left(\omega \right)$.

To evaluate the average time $\langle t\left(\omega \right)\rangle$ from above, we performed numerical simulations on a 2D scattering region of rectangular shape, attached to perfect semi-infinite waveguides on the left and right (see illustrations in Fig. 3, Lower). Accordingly, the correct number of scattering channels $N\left(\omega \right)$ is given by the total number of flux-carrying modes in both waveguides. Impenetrable and nonoverlapping circular scatterers are randomly placed inside the scattering region and in between them the refractive index is kept constant, $n\left(x,y\right)=1$. The scattering matrix and the corresponding scattering states for this system are calculated by solving the Helmholtz Eq. 6 on a finite-difference grid, using the advanced modular recursive Green’s function method (23, 24). In Fig. 3 we display our numerical results for different degrees of disorder. In Fig. 3A we show the results obtained for an empty scattering region, corresponding to the ballistic transport regime. In Fig. 3B, the case with altogether 13 scatterers is shown, for which already a strong reduction of transmission is observed. The distribution of the transmission eigenvalues $P\left(\tau \right)$ follows here very well the predictions of random matrix theory for the regime of chaotic scattering (Supporting Information). Finally, in Fig. 3C we increased the degree of disorder even more (placing altogether 211 scatterers) so as to enter the regime of Anderson localization. Here the distribution of transmission eigenvalues agrees very well with the predictions for the case when Anderson localization suppresses all but a single transmission eigenchannel (Supporting Information) (25, 26). To make all three cases easily comparable with each other, the different geometries all have the same scattering area A, which for ballistic scattering is the entire rectangular region between the leads, whereas for the other two cases the area occupied by the impenetrable scatterers is not part of A.

Fig. 3.

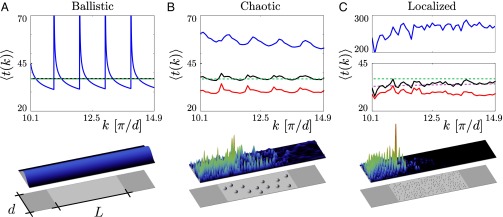
Total average dwell time $\langle t\left(k\right)\rangle$ (black line), transmission delay time (blue line), and reflection delay time (red line) for (A) ballistic scattering through a clean waveguide as well as for (B) chaotic scattering through a disordered waveguide with 13 circular obstacles of radius $r=0.06\hspace{0.17em}d$ and (C) Anderson localized transport through a disordered waveguide with 211 obstacles of $r=0.015\hspace{0.17em}d$ (see Supporting Information for a definition of transmission and reflection delay times). The geometrical parameters were chosen such that all three waveguides have the same width d and the same effective scattering area $A=2.35\hspace{0.17em}{d}^2$. The wavenumber was scanned between $k=10.1\hspace{0.17em}\pi /d$ and $k=14.9\hspace{0.17em}\pi /d$ in all three cases. For the clean waveguide in A the transmission is perfect, and thus the reflection times are strictly zero. The average for the total dwell time (black line) is taken here over the entire wavenumber interval shown and coincides with the estimate of Blanco and Fournier (4), $\langle t\left(k\right)\rangle =\pi A/\left(Cc\right)$ (green dashed line). For the disordered systems in B and C the averages were taken over (B) 250 and (C) 2,500 different random configurations, respectively. Whereas for the chaotic scattering case (B) the results for the average dwell time agree well with the random walk prediction (dashed green line), a systematic deviation is observed for the case of strong disorder (C). Here, very good agreement is found with the estimate for the average dwell time according to the corrected Weyl estimate, Eq. 8 (purple dashed line). (Lower) The intensity of wave functions injected in the lowest-order mode is shown for a specific configuration of scatterers (see gray spheres) embedded in the scattering area (light gray domain in the middle). The flux is incoming from the left and can be transmitted (to the right) or reflected (to the left) through the perfect waveguides attached on both sides (see dark gray areas).

Based on the above identification of the different transport regimes that our model system can be in, we investigate now the corresponding results for the average time $\langle t\left(\omega \right)\rangle$ that we get for each of these limits (Fig. 3). In the ballistic limit (Fig. 3A) we see that the average time, plotted as a function of the incoming wavenumber k, shows pronounced periodic enhancements around the random walk prediction by Blanco and Fournier (4), $\langle t\rangle =\pi A/\left(Cv\right)$. The peaks of these fluctuations can be identified with those positions in $k=k_n=n\hspace{0.17em}\pi /d$, where a new transverse mode opens up in the waveguide of width d. To understand why these mode openings cause an increase in the scattering dwell time we resort to a fundamental connection between the average dwell time $\langle t\rangle$ and the DOS $\rho \left(k\right)$. This relation, $\rho \left(k\right)=N\left(k\right)c\langle t\left(k\right)\rangle /\left(2\pi \right)=c\mathrm{Tr}\left(\text{Q}\right)/\left(2\pi \right)$, was first put forward by Birman, Krein, Lyuboshitz, and Schwinger in the context of quantum electrodynamics and nuclear scattering theory and has meanwhile been used in a variety of different contexts (27–37). Because, in the ballistic regime, each individual incoming mode corresponds to a one-dimensional scattering channel with, correspondingly, an associated square root singularity in the DOS, ${\rho }_n\left(k\right)=\left[L/\left(2\pi \right)\right]k/\sqrt{k^2-k_n^2}$ for $k>k_n$, we can successfully explain the observed oscillations as coming from the successive openings of new waveguide modes. Evaluating the total DOS based on a sum of individual mode contributions, $\rho \left(k\right)={\displaystyle {\sum }_n^N{\rho }_n\left(k\right)}$, and using the above connection to the average time yields results identical to those shown in Fig. 3A. This demonstration also allows us to show that the time, averaged over an interval of k that is larger than the distance between successive mode openings, converges exactly to the prediction by Blanco and Fournier (4). Quite remarkably, we find in this sense that the estimate from the mean-chord-length theorem and, correspondingly, the random walk prediction also holds, on average, for ballistic wave scattering in a system without any disorder.

Moving next to the disordered system in Fig. 3B we see that the presence of the disorder strongly reduces the above mode-induced fluctuations, leaving the frequency-average value of time unchanged. To explain this result, the DOS clearly needs to be estimated differently here than in the ballistic case of uncoupled waveguide modes. Also, because the disorder leads to system- and frequency-specific fluctuations of the DOS, we are looking here for an estimate for the ensemble and frequency-averaged DOS. To obtain this quantity, we invoke a result first put forward by Weyl in 1911 (38), who estimated that the average DOS in the asymptotic limit of $\omega \to \infty$ satisfies the universal law $\rho \left(\omega \right)=A\omega /\left(2\pi c^2\right)$, now called the Weyl law (39). Putting this estimate into the formula relating the average time with the average DOS, we obtain $\langle t\left(\omega \right)\rangle =2\pi \rho \left(\omega \right)/N\left(\omega \right)=A\omega /\left[c^{2}N\left(\omega \right)\right]$. The ω-dependent number of incoming channels is given as an integer-valued step-function $N\left(\omega \right)=\lfloor 2\omega d/\left(c\pi \right)\rfloor$. When smoothing over the steps in this function, that is, $N\left(\omega \right)\approx 2\omega d/\left(c\pi \right)-0.5$, we arrive at the result $\langle t\left(\omega \right)\rangle =2\pi \rho \left(\omega \right)/N\left(\omega \right)\approx \pi A/\left(2dc\right)=\pi A/\left(Cc\right)$. This relation, which is very accurately satisfied by our numerical results, thus confirms the validity of the diffusive random walk prediction by Blanco and Fournier (4) also for disordered wave scattering. Because the above relation for the average dwell time is notably independent of ${\ell }^{\mathrm{\ast }}$, transmission and reflection times for waves, which do strongly depend on ${\ell }^{\mathrm{\ast }}$, need to fully counterbalance each other.

Does this invariance of the average scattering time also persist in the strongly scattering limit, when Anderson localization sets in? Our numerical results shown for this case in Fig. 3C display a small but apparently systematic frequency dependence of the average time $\langle t\left(\omega \right)\rangle$, which increasingly deviates from the result by Blanco and Fournier (4) for decreasing frequencies ω. Because the numerical calculations are very challenging and the frequency derivative appearing in Eq. 7 can reach very large values for highly localized scattering states, we first tested the accuracy of our simulations by evaluating $\langle t\left(\omega \right)\rangle$ also through explicit dwell-time calculations. In analogy to Eq. 3, the expression for the dwell time in the case of the Helmholtz Eq. 6 is given by $t_m={\displaystyle {\int }_A{\psi }_m^{\mathrm{\star }}{n}^2{\psi }_m\hspace{0.17em}{d}^2\mathbf{r}/{\varphi }_{m,\mathrm{in}}}$, where ${\psi }_m$ is the wave function of the m-th scattering channel and ${\varphi }_{m,\mathrm{in}}$ is the corresponding total (stationary) incoming flux. The average dwell time is then given by $\langle t\left(\omega \right)\rangle ={\displaystyle {\sum }_m^N{t}_m\left(\omega \right)/N\left(\omega \right)}$. The results obtained in this way are practically indistinguishable from Fig. 3C. To explain this robust deviation from the result by Blanco and Fournier (4) we thus have a more careful look on the Weyl estimate which, in addition to the leading-order term that we used above, also features a next-order correction proposed by Weyl (39, 40), $\rho \left(\omega \right)=\left[A\omega /c^2+\left(C-B\right)/\left(2c\right)\right]/\left(2\pi \right)$. This correction involves not only the scattering area A but also the internal boundary of the scattering region B, which is notably different from the external boundary C through which waves can scatter in and out. The internal boundary B in the case of our waveguide system under study is given by $B=2L+B_o$, where $B_o$ is given by the total circumference of the scatterers. The open boundary conditions along the external boundary C were approximated with Neumann boundary conditions, which contribute with the opposite sign as the Dirichlet boundary conditions on the surface of the waveguide and of the scatterers. In systems with a small boundary-to-area ratio this next-order correction of the Weyl law is negligible. Because, however, the number of scatterers that we have placed inside the system (from 0 in the ballistic case, to 13 in the chaotic case, to 211 in the localized case) increases this ratio, the additional boundary term in the Weyl law may become important here. To check this explicity, we reevaluate the expression for the average dwell time $\langle t\left(\omega \right)\rangle$ from above when adding this correction, leading us to

$$\langle t\left(\omega \right)\rangle =\frac{1}{c^{2}N\left(\omega \right)}\left[A\hspace{0.17em}\omega +\frac{\left(C-B\right)}{2}c\right].$$ [8]

A comparison of this analytical formula with the numerical results (Fig. 3C) yields excellent agreement and indicates that the observed deviation from the prediction by Blanco and Fournier (4) stems from the comparatively large boundary of the many small scatterers that we placed inside the scattering region. We emphasize at this point that this correction to the Blanco and Fournier estimate only contains the boundary values B and C as additional input and remains entirely independent of any quantities that characterize the scattering process itself, such as ${\ell }^{\mathrm{\ast }}$ or the localization length ξ. This insight is of considerable importance, because it means that Eq. 8 defines a new invariant quantity that is independent of the scattering regime we are in and thus accurately matches our numerical results for the average time in the ballistic, chaotic, and localized limit. This invariant quantity for waves deviates from the prediction by Blanco and Fournier (4) only through an additional term originating in the fact that waves feel the boundary of a scattering region already when being close to it on a scale comparable with the wavelength. We speculate that additional wave corrections to the result by Blanco and Fournier may arise when waves have access to a larger scattering area A than classical particles through the process of tunneling.

In summary, we have derived a universal invariance property for wave transport through disordered media. The invariance of the averaged path length or averaged time spent by a wave in an open finite medium has been established based on scattering theory. In the appropriate limit of diffusive and nonresonant media, the random walk picture is recovered, and the result coincides with the expression of the averaged path length initially established by Blanco and Fournier (4). Our work confers to this invariance property a degree of universality that extends its implications far beyond applications of random walk theory. This extension to waves opens up new possible applications in optics, acoustics, seismology, or radiofrequency technologies, where propagation in complex media is the subject of intense research (41). Indeed, in the context of wave transport through disordered media most spatial or temporal observables scale with ${\ell }^{\mathrm{\ast }}$, and the invariance property derived in this work is particularly counterintuitive and rich in implications. It should find applications in imaging, communications, or light delivery, for instance to generate enhanced light-matter interaction within a certain volume by controlled light deposition, or to design specific structures to enhance light harvesting for solar cells (42, 43). Consider here, for example, that the above invariance property allows us to estimate the time that waves need to transit through a given medium based on a measurement of only the reflected portion of incoming waves and an a priori knowledge of the sample geometry. Particularly intriguing in our eyes is the possibility to get access, through Eq. 8, to the internal surface B of scatterers embedded in a scattering medium through a time-resolved transport experiment. Such an approach could go as far as to measure the fractal dimension of the scatterer surface by linking our results with the Berry–Weyl conjecture (44, 45).

An extension of our findings to media with gain and loss (46, 47) should also be of interest, both from a theoretical and an applied standpoint. Our study should also be very relevant to the field of wave control, which has recently emerged as a powerful paradigm for light manipulation and delivery in complex media (48), showing for instance that suitably shaped wavefronts can deliver light at a specific time and position (49–51). Finally, let us point out that although we only studied here 3D slab and 2D waveguide geometries with uncorrelated disorder, the invariance property, thanks to its connection to the DOS, is very general and should apply to a wide range of geometries and excitation strategies, as well as to nonuniform scattering properties, biological tissues, and correlated disorder, from partially ordered to entirely ordered systems such as Levy glasses or photonic crystals (52, 53). An experimental demonstration of the discussed invariance property should be within reach, in particular in optics, where time-resolved techniques and sensitive detectors are available.