Early inner solar system origin for anomalous sulfur isotopes in differentiated protoplanets

Significance

This investigation focuses on the sulfur isotopic compositions of magmatically differentiated meteorites, the oldest igneous rocks in our solar system. We present evidence of anomalous ³³S depletions in a group of differentiated iron meteorites, along with ³³S enrichments in several other groups. The complementary positive and negative compositions, along with observed covariations in ³⁶S and ³³S, are explained by Lyman-α photolysis of gaseous H₂S in the solar nebula. Confirmation of photochemically predicted ³³S depletions implies that the starting composition of inner solar system sulfur was chondritic, consistent with the Earth, Moon, Mars, and nonmagmatic iron meteorites. Differentiated protoplanets, however, appear to have accreted from materials processed under conditions where sulfur was volatile and UV radiation was present (<∼2 AU).

Abstract

Achondrite meteorites have anomalous enrichments in ³³S, relative to chondrites, which have been attributed to photochemistry in the solar nebula. However, the putative photochemical reactions remain elusive, and predicted accompanying ³³S depletions have not previously been found, which could indicate an erroneous assumption regarding the origins of the ³³S anomalies, or of the bulk solar system S-isotope composition. Here, we report well-resolved anomalous ³³S depletions in IIIF iron meteorites (<−0.02 per mil), and ³³S enrichments in other magmatic iron meteorite groups. The ³³S depletions support the idea that differentiated planetesimals inherited sulfur that was photochemically derived from gases in the early inner solar system (<∼2 AU), and that bulk inner solar system S-isotope composition was chondritic (consistent with IAB iron meteorites, Earth, Moon, and Mars). The range of mass-independent sulfur isotope compositions may reflect spatial or temporal changes influenced by photochemical processes. A tentative correlation between S isotopes and Hf-W core segregation ages suggests that the two systems may be influenced by common factors, such as nebular location and volatile content.

Of all of the extraterrestrial materials found on Earth, iron meteorites have always been the most conspicuous. So-called “magmatic” iron meteorites are likely to be samples from the cores of magmatically differentiated protoplanetary parent bodies (1), whereas “nonmagmatic” iron meteorites are commonly suggested to sample solidified melt pockets that formed via impacts onto nondifferentiated (chondritic) parent bodies (2). Individual members from an iron meteorite group are assumed to derive from a common parent body, based on shared chemical and isotopic characteristics (1–4). Chemical and isotopic differences among the different iron groups provide convincing evidence that different individual parent body planetesimals incorporated genetically distinct precursor materials (1–4).

Recent observations that several achondrite meteorite groups possess small, mass-independent ³³S enrichments relative to chondrites (5) have led to the conclusion that sulfur isotopes were heterogeneously distributed among the materials that accreted to form early solar system planetesimals. This observation, coupled with the ancient ¹⁸²Hf-¹⁸²W ages (within 1–3 My of solar system formation) of magmatic irons (6–8), provides impetus to search for systematic variations in mass-independent sulfur isotope compositions among the iron groups.

Results

We report high-precision δ³⁴S, Δ³³S, and Δ³⁶S data (where Δ³³S = 1000 × {δ³³S – [(δ³⁴S + 1)^0.515 − 1]} and Δ³⁶S = 1000 × {δ³⁶S – [(δ³⁴S + 1)^1.9 − 1]}) for 61 troilite (FeS) nodules extracted from 58 different iron meteorites selected from eight different groups (IAB, IC, IIAB, IIE, IIIAB, IIIF, IVA, and IVB) (Fig. 1, Fig. S1, and Tables S1 and S2). All groups except for IAB and IIE have been classified as magmatic (1, 2). Our data for group IAB includes five chemically (and possibly genetically) distinct subgroups (2). Collectively, all of the iron meteorites examined have overlapping δ³⁴S values consistent with those reported by previous studies (9, 10), ranging from −1.41‰ to +1.29‰ with an average of −0.01 ± 0.81‰ (2σ SD, 2s.d.) (Fig. 1). We have chosen to report uncertainties either as 2σ SEs (2SE) where appropriate (for averages derived from groups with more than eight analyzed members), or as 2s.d. long-term external reproducibility for individual data points and for groups where the number of analyzed samples is small (±0.3‰, ±0.008‰, and ±0.3‰ for δ³⁴S, Δ³³S, and Δ³⁶S, respectively; see SI Text, Fig. S2, and Tables S3 and S4). There is no distinction between magmatic and nonmagmatic irons in δ³⁴S, and most individual groups have average δ³⁴S values within 2s.d. of zero (±0.3‰).

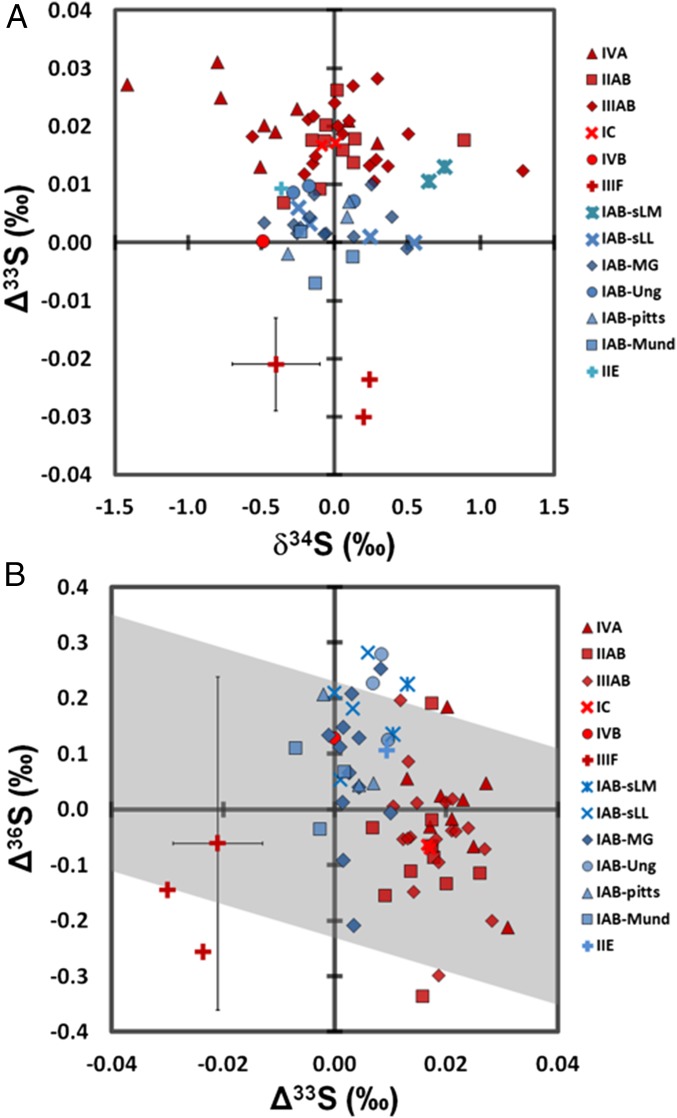
Fig. 1.

Sulfur isotope measurements in iron meteorite troilite. Measurements of (A) Δ³³S vs. δ³⁴S and (B) Δ³⁶S vs. Δ³³S, for acid-volatile sulfur fractions (n = 72) of troilite from 58 iron meteorites belonging to the groups IAB, IC, IIAB, IIE, IIIAB, IIIF, IVA, and IVB. Nonmagmatic and magmatic groups are in blue and red, respectively. Error bars, shown on a single point, represent 2s.d. uncertainties of 0.3‰, 0.008‰, and 0.3‰ for δ³⁴S, Δ³³S, and Δ³⁶S, respectively. Gray band demarcates the fractionation array of H₂S (Δ³⁶S/Δ³³S of ∼−3) by Ly-α photolysis (27). One additional S-isotope measurement on group IIIF (10) is also included.

In contrast to δ³⁴S, the new results show that Δ³³S values are uniform within iron meteorite groups, but that there are resolvable Δ³³S differences between different groups. Values of Δ³³S range from −0.031‰ to +0.031‰ [normalized to troilite from the Canyon Diablo IAB iron meteorite (CDT)], with different iron meteorite groups forming discernible clusters in Δ³³S space (Fig. 1). The nonmagmatic iron meteorites examined show a limited range in Δ³³S compared with magmatic irons: Group IAB (n = 23), including samples from the main group (including CDT), three subgroups, two grouplets, and several ungrouped IAB iron meteorites, has an average Δ³³S of +0.004 ± 0.002‰ (2SE), while Watson, the single meteorite analyzed from nonmagmatic group IIE, has a Δ³³S of +0.010 ± 0.008‰ (2s.d.). Members analyzed from the IAB subgroups do not have resolvable mass-independent sulfur isotopic differences compared with the main group (Fig. 1 and Table S2); this observation is consistent with, but does not require, their derivation from a single parent body (2).

Magmatic irons are characterized by mass-independent S-isotope compositions resolvable from zero (Table S2). Groups IIAB, IIIAB, and IVA have means and 2SE errors, +0.016 ± 0.004‰, +0.018 ± 0.002‰, and +0.022 ± 0.004‰, respectively. Group IC has a mean Δ³³S of +0.017‰, while the only sample analyzed from group IVB has a Δ³³S of 0.000‰; magmatic group IIIF is characterized by an average negative Δ³³S of −0.027‰ [in these cases, the number of analyzed samples is small; uncertainty is comparable to or less than long-term external reproducibility (2s.d. = ±0.008‰)].

Average Δ³⁶S measurements within their uncertainties, like those for δ³⁴S, also overlap for most iron meteorite groups, ranging from −0.34‰ to +0.28‰ (Fig. 1B). However, the nonmagmatic irons appear to have slightly positive Δ³⁶S, while the magmatic irons tend to have more negative values. Two-tailed heteroscedastic t tests were performed between groups to probe the statistical significance of our Δ³⁶S isotope measurements (Table S5). These tests demarcate the probability that two sets of measurements come from the same population, with the output variable (the P value) representing the fractional probability that the two sets are identical. When comparing the Δ³⁶S of magmatic groups IIAB, IIIAB, and IVA to group IAB, P values returned were lower than ∼0.02, indicating a >98% chance that they represent different populations. Although the relationship is poorly defined, there appears to be a negative correlation between Δ³⁶S and Δ³³S [Δ³⁶S/Δ³³S ∼ −7 ± 4 (2s.d.)] that is similar to that calculated from available bulk achondrite analyses (5) [Δ³⁶S/Δ³³S ∼ −6 ± 6 (2s.d.)] (Fig. S3).

Fractionation Mechanisms That Affect Δ³³S.

While a number of mechanisms exist that can fractionate sulfur isotopes, only a few are known to produce the types of variations in Δ³³S and Δ³⁶S seen in our data, and many others can be ruled out. For instance, magmatic processes produce small-magnitude, mass-dependent fractionations because they occur at high temperature and are associated with equilibrium isotope partitioning. Furthermore, kinetic processes that could potentially generate larger fractionations do not provide a simple explanation for the variations of Δ³³S and Δ³⁶S, considering the small range of observed δ³⁴S. Recent studies of magnetic isotope effects (11) have demonstrated that Δ³³S can be modified by processes related to interactions between nuclear and electronic spin of radical intermediates; however, these effects do not produce variations for Δ³⁶S and are not considered to be viable candidates to account for our observations. Another recent study regarding fractionation of gases in imposed low-temperature thermal gradients (of ∼100 °C) has also demonstrated the existence of small anomalous isotope effects capable of modifying Δ³³S (12), but the authors could not resolve an effect for Δ³⁶S. Below, we discuss several mechanisms that have been shown to produce small variations of Δ³³S related to mixing, distillation, and evaporation, and evaluate whether they can explain the iron meteorite data.

Mixing of sulfur pools with different mass-dependent S-isotopic compositions yields small deviations from the mass-dependent array—referred to as mass conservation effects (13). Considering that the largest δ³⁴S variations found in carbonaceous chondrite sulfides are ±8‰ (14), mixing could only generate a Δ³³S of +0.008‰. Given that the range of δ³⁴S found in iron meteorites is significantly smaller, only a very small Δ³³S (+0.001‰) is anticipated as a result of mixing processes, making mixing unlikely as an explanation for the observed variation.

Rayleigh distillation is another type of mass conservation effect that involves the extraction of sulfur from a reactant to produce product and residue with isotopic compositions that lie above the original mass fractionation line (slightly positive Δ³³S). McEwing et al. (15) performed an experiment for which they evaporated troilite at low pressure and high temperature. Measuring δ³⁴S, they determined the fractionation factors associated with the branched reaction for evaporation of troilite to elemental sulfur (1000lnα = −13‰) and to dissociated troilite (1000lnα = −5.4‰). Using their data and assuming canonical mass-dependent fractionation, the Δ³³S variations due to mixing between products and reactants during Rayleigh distillation of troilite to elemental sulfur was calculated to yield a maximum Δ³³S of ∼ +0.009‰ (Fig. S4), decreasing as the reaction’s branching ratio increases toward dissociated troilite. However, the minor sulfur isotopes were not measured, and it is possible that this process deviates slightly from the canonical value; moreover, a recent experimental study (16) has documented anomalous mass laws associated with low-temperature condensation and evaporation of SF₆. The authors (16) attributed this effect to a competition between low-frequency vibrational modes associated with weak chemical interactions between SF₆ clusters in the condensed phase and high-frequency modes associated with the stronger S−F bonds in the clusters themselves and in the free gas-phase SF₆. They diagramed the principle of this competition between effects that enrich the heavy isotope with a shallow slope (e.g., 0.505) and effects that enrich the light isotope with a steeper slope (e.g., 0.515).

To explore whether this may apply to troilite evaporation (which does not have discrete individual S clusters like SF₆), we consider how the contributions from modes that enrich the heavy isotope and those that enrich the light isotope are related to temperature. Inferring a dependence on hν/kT, we project that the contributions from both modes will decrease as temperature increases, reducing the magnitude of the anomalous isotope effect. Direct experiments to evaluate the mass dependence of troilite evaporation are needed to resolve this conclusively, but several other lines of evidence exist to suggest that troilite evaporation does not produce a large anomalous effect, including the following. (i) studies of the isotope effects for sulfur associated with impact gardening of mature lunar soils have been interpreted to indicate that impact devolatilization of sulfur can produce large variations for δ³⁴S, but these processes have canonical mass-dependent fractionations (17). (ii) Data for Δ³³S and Δ³⁶S in the main group of IAB iron meteorites and IAB subgroups (presented here), which are suggested to have been formed by various impacts on a chondritic parent body (2), reveal no resolvable anomalous sulfur isotopic variability. (iii) Isotopic measurements of lunar basalts (this study and ref. 18) exhibit Δ³³S and Δ³⁶S that are not distinguishable from the terrestrial mantle (19), which suggests that the putative Moon-forming giant impact (and subsequent basin-forming impacts) did not fractionate sulfur isotopes in a mass-independent fashion. These three lines of evidence suggest that impact and evaporation processes did not produce the variation seen among the different iron meteorite groups.

Nucleosynthetic and Cosmogenic Production of Rare Sulfur Isotopes.

Cosmic ray effects could also potentially be responsible for the small observed variations in Δ³³S and Δ³⁶S in iron meteorites. In previous studies of spallogenic sulfur production from Fe in the metal phase of iron meteorites, a positive correlation between cosmic ray exposure proxies and both Δ³³S and Δ³⁶S was observed (9, 10) [Δ³⁶S/Δ³³S ∼ +8]. Iron meteorites from many of the groups analyzed in this study (such as the IAB irons) span a large range of cosmic ray exposure ages (20), yet there is no correlation between exposure age proxies (neutron fluence) and the sulfur isotopic composition of troilite. Spallogenic sulfur in the metal phase of iron meteorites is generated from target Fe atoms and found at parts per million concentrations. However, troilite contains a lower concentration of target Fe atoms and a much higher concentration of autochthonous sulfur atoms (10⁴ times higher than observed in the metal phase). Additionally, the slope of the relation obtained for Δ³⁶S/Δ³³S [∼−7 ± 4 (2s.d.)], although poorly constrained, is opposite to that predicted for the spallogenic production of sulfur from Fe [(Δ³⁶S/Δ³³S ∼ +8) (9, 10)]. Instead, the resolvable mass-independent sulfur isotopic differences between magmatic iron groups indicate that different parent bodies likely formed from genetically distinct precursor materials, consistent with evidence from other isotopic systems (1, 3, 4).

Nucleosynthetic anomalies in S would most likely be found through measurements of Δ³⁶S (21) because the nucleosynthetic pathways for ³²S, ³³S, and ³⁴S are related in stellar environments (22, 23). In comparison, ³⁶S, the rarest and therefore the most sensitive of the four stable sulfur isotopes, is created in unique conditions within massive stars before Type II supernova explosion (24). However, recent measurements of presolar SiC by secondary ion mass spectrometry have identified several grains with large ³²S excesses (25). We have modeled the effect of injection of a pure ³²S component into the early solar nebula on the Δ³³S and Δ³⁶S compositions of bulk solar system materials and find that this leads to a unidirectional departure from CDT composition with a Δ³⁶S/Δ³³S slope of −1.9 about the origin (Fig. S4), which does not overlap with the iron meteorite array (∼−7 ± 4). Furthermore, addition of ³²S can only lead to negative Δ³³S values, and leaves the (most abundant) positive Δ³³S signatures unexplained, unless the starting composition of bulk solar system was highly positive (>+0.161‰).

The rare stellar regions that have been suggested to possibly produce positive Δ³³S (excess ³³S) are modeled to produce even greater volumes of excess ³⁶S (24), which have not been documented in presolar grains or at the bulk scale. Additionally, small nucleosynthetic anomalies described for other elements in iron meteorites [such as molybdenum (4)], do not correlate with our sulfur isotope measurements, which would likely be expected if they were attributable to the same mechanism. The injection of sulfur from any nucleosynthetic source would produce a unidirectional departure from CDT, which could only explain our observations if the bulk initial Δ³³S composition of the solar system was nonchondritic, and if the concentration of sulfur in presolar grains was not negligible relative to the total sulfur budgets of early-forming planetesimals.

Fractionation Mechanisms Associated with Gas-Phase Photochemistry.

Photochemically driven isotope fractionation, on the other hand, could have produced anomalous sulfur with both positive and negative Δ³³S and Δ³⁶S variations from a reservoir of bulk chondritic composition. Predictions for sulfur isotope behavior during photochemical reactions, however, rely on a very limited number of experimental studies undertaken at relevant conditions. Photolysis of H₂S by UV radiation with wavelengths longer than ∼220 nm (26) yields a positive Δ³⁶S/Δ³³S array (∼+1.7) which does not match our observations. A series of recent photolysis experiments on H₂S using Lyman-α (Ly-α) radiation, however, provide a possible match to the observed sulfur isotope compositions in iron meteorites, with an array between products and reactants delineating a Δ³⁶S/Δ³³S ratio of ∼−3 (27). Given our uncertainties on Δ³⁶S and the limited spread of our data, this array supports a preaccretionary photochemical origin for the S-isotope signatures seen in troilite from magmatic irons (Fig. 1B). Of the currently known anomalous fractionations, it is Ly-α photolysis of H₂S (27) that is most consistent with the negative correlation between Δ³⁶S and Δ³³S observed in both iron and achondrite meteorites (Fig. S3) and with the conditions present in the inner solar system.

Feasibility of a Photochemical Origin.

Hydrogen sulfide, the most abundant sulfur-bearing gas in the early solar system, is suggested to have resided within the inner ∼2 AU of the young solar nebula (28, 29), and near the surfaces of the disk, because temperatures exceeded ∼700 K, resulting in the evaporation of troilite. Ly-α radiation from the Sun would have been highest during the T-Tauri phase of solar history, which lasts ∼2 My for a star of solar mass (30). A calculation that takes into account the Far-UV photon flux (at 1 AU) for a T-Tauri star of solar mass, and the penetration depth of Ly-α radiation into an evolving protoplanetary disk, presented below, demonstrates that Δ³³S signals of the magnitude observed could be produced, on relevant timescales, in the young protoplanetary disk (see SI Text for details).

To model H₂S photolysis, we use the evolving solar nebula model of Hersant et al. (31) [the same used in Pasek et al. (28)], which has time-dependent midplane temperature and disk surface density, but we assume an isothermal vertical temperature profile, implicitly adding viscous heating (Table 1). The depth of penetration of stellar UV radiation into the solar nebula is determined primarily by dust absorption. The low angle of incidence, and the predominantly forward-scattering nature of the dust, implies strong absorption of stellar UV in the nebular surface region of the disk. By contrast, stellar Ly-α radiation interacts with the H atom layer in the uppermost regions of the nebula, and resonant scattering from H atoms redirects a portion of the Ly-α photons on trajectories more perpendicular to the disk midplane (32). To determine the depth of penetration of Ly-α into the disk at different times in nebular history, we computed the total optical depths from H₂O, H₂S, and dust: the main absorbers of Ly-α radiation (Table S6).

Table 1.

Disk model parameters and time required to photolyze 2% of nebular H₂S for high-mass and low-mass disks with solar and subsolar H₂O abundances

Disk type	T0, K	Σ0, g cm−2	H, AU	nH(0), cm−3	C/O ratio	Zph, AU	tν(Zph), y	nH(Zph)/nH(0)	Noverturns (2% photolysis)	Time required, y
High-mass	1050	5000	0.064	8.6 x 1014	solar	0.288	320	4.0 x 10−5	500	1.6 x 105
(t <50 Ky)	—	—	—	—	∼1.5	0.28	310	7.0 x 10−5	285	8.8 x 104
Low-mass	700	650	0.052	1.4 x 1014	Solar	0.21	200	2.9 x 10−4	70	1.4 x 104
(t <500 Ky)	—	—	—	—	∼1.5	0.202	180	5.3 x 10−4	40	7.2 x 103

T₀, the midplane temperature; Σ₀, the surface density at midplane; H, the scale height; n_H, the number density of H atoms at midplane; Z_ph, the penetration limit (height above midplane) of Ly-α radiation; t_ν(Z_ph), the time required for one overturn at height Z_ph; n_H(Z_ph)/n_H(0), the ratio of H atoms at Z_ph over the midplane value; N_overturns, the number of overturns required.

Assuming solar elemental abundances (33) and a fraction of O atoms trapped in SiO₃ bonds (pyroxene dust) (31), we calculated the Ly-α optical depths for all three absorbers considered here at several values of Z for two end member scenarios, an early high-mass disk (<5 × 10⁴ y) and a late low-mass disk (<5 × 10⁵ y) (Table S6). For the cases with reduced water abundance, [C/O = 1.5], H₂S photolysis will occur slightly deeper in the disk. A more refined calculation (SI Text) for penetration depth takes into account the photolysis timescale for an H₂S molecule at different depths, and yields the depth at which this does not exceed the timescale for turbulent mixing (Table 1), which is in agreement with our coarser estimates.

The depth of penetration for Ly-α photons can be used to estimate the time needed to photolyze a given fraction of the H₂S present in the nebula. The iron meteorites measured here have a maximum Δ³³S of ∼0.03‰ in troilite grains. H₂S photolysis experiments using Ly-α (27) yielded a maximum fractionation of Δ³³S ∼1.5‰ in elemental sulfur, suggesting that only ∼2% of total disk H₂S was photolyzed and trapped in the region of the nebula where magmatic iron meteorite parent body materials were produced. Assuming that turbulent vertical mixing was present due to a magnetorotational instability at 1 AU, the overturn rates are ∼200–300 y (Table 1).

For the two protoplanetary disks of different mass, we calculate the number of overturns necessary to photolyze 2% of total H₂S at 1 AU and find that the timescales for potential production of the anomalous Δ³³S signal are less than 200 Ky (Table 1), consistent with the early accretion and core segregation ages of differentiated protoplanets (1, 6–8).

Additional to the anomalous sulfur produced by H₂S photolysis, other photochemical production mechanisms involving exotic sulfur species [e.g., SiS, HS, AlS, and/or PS (28)] may have also taken place, but photolysis experiments involving these high-temperature sulfide gases have not yet been performed. Despite this fact, we show that photolysis of H₂S is sufficient to explain both the covariation and magnitude of our data on the necessary timescales.

Implications for Accretion of Differentiated Protoplanets.

Trapping photolytic sulfur into a secondary, distinct, chemical phase(s) is required to preserve and transfer an anomalous Δ³³S signal to the precursor materials of magmatic iron parent bodies. However, mechanisms through which these isotope signatures were incorporated into protoplanets remain poorly understood. Due to the higher condensation temperatures of refractory sulfides, such as oldhamite (CaS) [(∼1,200 K) (28)], compared with silicates, their condensation likely occurred within a region optically clear to UV radiation from the young sun. However, the condensation temperature of troilite (∼700 K) is inferior to that of most silicates (28), making it likely that it condensed at higher optical depths. We suggest that the most parsimonious mechanism for incorporation of photolytic sulfur isotope signatures into solid grains is through their incorporation into refractory sulfides such as oldhamite (which can condense in optically thin regions of the solar nebula). The largest positive Δ³³S deviation in achondrites is for oldhamite from the Norton County aubrite (5). Aubrites are thought to come from a highly reduced planetesimal parent body, which is likely to have formed in the innermost regions of the disk (34). Refractory sulfides (such as oldhamite) thus could have acted as early transient carriers of anomalous sulfur into differentiated planetesimal parent bodies in the inner solar system.

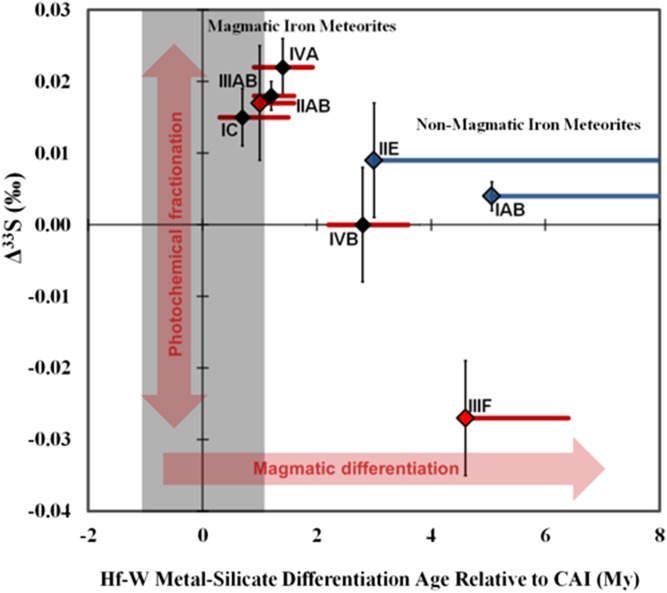
Magmatic iron meteorites progress from positive Δ³³S to negative Δ³³S values, corresponding weakly with published Hf-W core segregation ages (6–8) (Fig. 2). This may be linked to a process associated with the timing or location of the accreting parent bodies. A recent study (6) suggests that the different core segregation ages of magmatic iron parent bodies may be controlled significantly by the volatile content of the accreting materials. An unrelated study has recently suggested that low-volatile materials accreted first in the solar nebula, due to their higher densities (35); if the Hf-W differentiation ages are also related to volatile contents, the relationship between Hf-W age and ∆³³S may represent the gradual removal of an anomalous refractory S component from an inner solar system reservoir. However, the IIIF iron meteorites do not fit the volatile vs. Hf-W age correlation, and ∆³³S values do not appear to correlate with published volatile data in a straightforward fashion, which implies that the correlation between ∆³³S and Hf-W age is not simply a matter of volatile abundance. Other factors, such as the accretion age and nebular location of the different parent bodies, are likely to have also influenced their different core segregation ages and ∆³³S values. Nonmagmatic irons (including IAB subgroups) have ∆³³S indistinguishable from bulk chondrites and Hf-W segregation ages several million years later than most magmatic irons (6–8). Such iron meteorites do not preserve evidence for inheritance of a photochemical sulfur component, and may have accreted in more distal parts of the solar nebula with greater optical densities and at ambient temperatures that precluded the presence of gas-phase H₂S.

Fig. 2.

Δ³³S vs. exposure-corrected Hf-W metal-silicate segregation ages. Average Δ³³S for each group of magmatic (red) (n = 6) and nonmagmatic (blue) (n = 2) iron meteorites plotted against Hf-W ages. Solid black diamonds represent preexposure ε¹⁸²W values (6), hollow diamonds represent maximum calculated cosmogenic exposure corrections on groups IC and IIIF (8), and Sm-based corrections on IAB and IIE (7). Colored lines span the range of maximum corrected values from available data. Error bars represent 2SE for IAB, IVA, IIAB, & IIIAB, and 2s.d. (±0.008‰) for other groups. Gray band represents uncertainty in calcium-aluminum inclusion (CAI) initial.

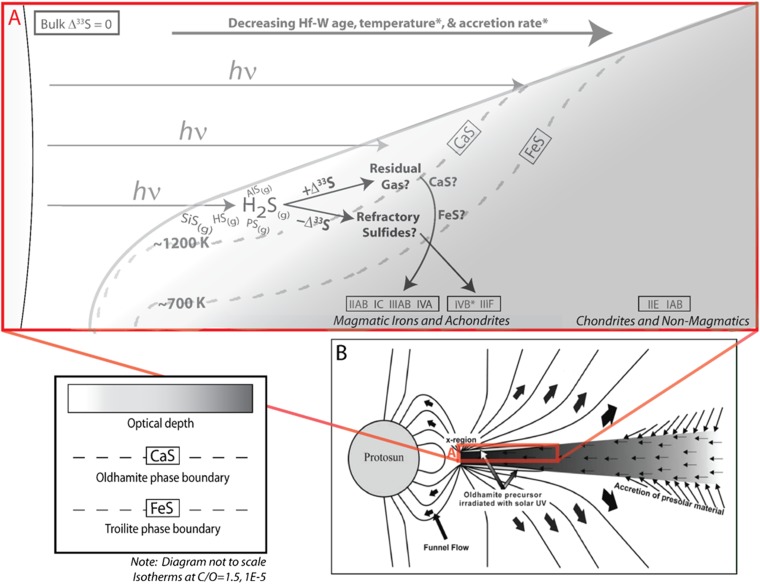
The heliocentric region suggested to have once contained sulfur-bearing gases available for photolysis in the early solar system (28, 29) (<∼2 AU) has also been suggested (through dynamical arguments) as the birthplace of differentiated meteorite parent bodies (36). Combining these constraints with those provided by our sulfur isotope measurements, a working model emerges that links the photolysis of gas-phase sulfur species by Ly-α radiation to the distribution of mass-independent sulfur isotope signatures that were captured by early-forming, inner solar system planetesimals (Fig. 3). The sulfur isotope data suggest that magmatic iron and achondrite parent bodies formed in regions proximal to the Sun, where high temperatures and high photon fluence enabled the creation of anomalous sulfur isotope signatures through gas-phase photolysis. The similar negative Δ³⁶S/Δ³³S arrays for achondrites and iron meteorites is consistent with a shared genetic heritage, and may provide a new system for linking iron groups to their rocky counterparts.

Fig. 3.

(A) Proposed model for sulfur isotope distribution in early solar nebula. In this working model, Hf-W age, temperature, and accretion rate roughly decrease to the right with increasing heliocentric distance. Anomalous Δ³³S is created through the photolysis of sulfur-bearing gases and captured in refractory sulfides that settle down to the midplane, joining other precursors for iron meteorite and achondrite parent bodies. The paucity of H₂S and greater optical depth inhibit the generation of anomalous sulfur signatures at greater heliocentric distances. Isotherm temperatures are from ref. 28. (B) The solar nebula during T-Tauri phase, showing the formation zone of the oldhamite precursor suggested to have carried anomalous sulfur to achondrites . Adapted from ref. 5 with permission from AAAS.

Our new data suggest potential links between the inner solar system and planetesimals with internal heat sources sufficient for early magmatic differentiation. The Δ³³S (and Δ³⁶S) values of the Earth, Moon, and Mars, which are indistinguishable from IAB iron meteorites/bulk chondrites (18, 19, 37, 38), are intermediate between the ³³S-enriched and ³³S-depleted isotopic compositions observed in magmatic irons and achondrites. This implies that the complementary photolytic sulfur isotope signatures captured by these early-formed differentiated protoplanets were either diluted by the later addition of materials with isotopically normal (chondritic/IAB) sulfur or were recombined during the continued accretionary processes that formed the terrestrial planets.

Materials and Methods

Acid volatile sulfur was obtained from crushed troilite nodule samples (∼3–10 mg) allowing the measurement of sulfur isotopic ratios in monosulfide minerals. The samples were heated with degassed 5 N HCl bubbled with flowing N₂ gas; the released H₂S (dominantly from troilite) was then passed through condensers, through an acid trap containing ultrapure water, and captured in a slightly acidic trapping solution containing AgNO₃. The precipitated Ag₂S was thoroughly rinsed with ultrapure water and 1 M NH₄OH solution before drying. This Ag₂S was then reacted with ca. 10 times stoichiometric excess of pure F₂ in Ni fluorination bombs at 250 °C overnight, producing SF₆ gas which was subsequently purified with cryogenic and gas chromatographic techniques. The sulfur isotope abundances were measured using a ThermoFinnigan MAT 253 mass spectrometer monitoring m/z = 127, 128, 129, and 131 $({}^{32}\mathrm{SF}_5^{+},\hspace{0.17em}{}^{33}\mathrm{SF}_5^{+},\hspace{0.17em}{}^{34}\mathrm{SF}_5^{+},\hspace{0.17em}\mathrm{and}\hspace{0.17em}{}^{36}\mathrm{SF}_5^{+})$. All results are reported in per mil (‰) relative to CDT using standard delta notation δⁱS = 1000 × {[(ⁱS/³²S)_sample/(ⁱS/³²S)_CDT] – 1}, where i = 33, 34, 36.