Robust spectrotemporal decomposition by iteratively reweighted least squares

Significance

Classical spectral estimation techniques use sliding windows to enforce temporal smoothness of the spectral estimates of signals with time-varying spectrotemporal representations. This widely applied approach is not well-suited to signals that have low-dimensional, highly structured time–frequency representations. We develop a new Bayesian spectral decomposition framework—spectrotemporal pursuit—to compute spectral estimates that are smooth in time and sparse in frequency. We use a statistical interpretation of sparse recovery to derive efficient algorithms for computing spectrotemporal pursuit spectral estimates. We apply spectrotemporal pursuit to achieve a more precise delineation of the oscillatory structure of human electroencephalogram and neural spiking data under propofol general anesthesia. Spectrotemporal pursuit offers a principled alternative to existing methods for decomposing a signal into a small number of oscillatory components.

Abstract

Classical nonparametric spectral analysis uses sliding windows to capture the dynamic nature of most real-world time series. This universally accepted approach fails to exploit the temporal continuity in the data and is not well-suited for signals with highly structured time–frequency representations. For a time series whose time-varying mean is the superposition of a small number of oscillatory components, we formulate nonparametric batch spectral analysis as a Bayesian estimation problem. We introduce prior distributions on the time–frequency plane that yield maximum a posteriori (MAP) spectral estimates that are continuous in time yet sparse in frequency. Our spectral decomposition procedure, termed spectrotemporal pursuit, can be efficiently computed using an iteratively reweighted least-squares algorithm and scales well with typical data lengths. We show that spectrotemporal pursuit works by applying to the time series a set of data-derived filters. Using a link between Gaussian mixture models, ${\ell }_1$ minimization, and the expectation–maximization algorithm, we prove that spectrotemporal pursuit converges to the global MAP estimate. We illustrate our technique on simulated and real human EEG data as well as on human neural spiking activity recorded during loss of consciousness induced by the anesthetic propofol. For the EEG data, our technique yields significantly denoised spectral estimates that have significantly higher time and frequency resolution than multitaper spectral estimates. For the neural spiking data, we obtain a new spectral representation of neuronal firing rates. Spectrotemporal pursuit offers a robust spectral decomposition framework that is a principled alternative to existing methods for decomposing time series into a small number of smooth oscillatory components.

Across nearly all fields of science and engineering, dynamic behavior in time-series data, due to evolving temporal and/or spatial features, is a ubiquitous phenomenon. Common examples include speech (1), image, and video (2) signals; neural spike trains (3) and EEG (4) measurements; seismic and oceanographic recordings (5); and radar emissions (6). Because the temporal and spatial dynamics in these time series are often complex, nonparametric spectral techniques, rather than parametric, model-based approaches (7), are the methods most widely applied in the analysis of these data. Nonparametric spectral techniques based on Fourier methods (8, 9), wavelets (10, 11), and data-dependent approaches, such as the empirical mode decomposition (EMD) (12, 13), use sliding windows to take account of the dynamic behavior. Although analysis with sliding windows is universally accepted, this approach has several drawbacks.

First, the spectral estimates computed in a given window do not use the estimates computed in adjacent windows, hence the resulting spectral representations do not fully capture the degree of smoothness inherent in the underlying signal. Second, the uncertainty principle (14) imposes stringent limits on the spectral resolution achievable by Fourier-based methods within a window (8, 9). Because the spectral resolution is inversely proportional to the window length, sliding window-based spectral analyses are problematic when the signal dynamics occur at a shorter time-scale than the window length. Third, in many analyses, such as EEG studies (15), speech processing (1), and applications of EMD (13), a common objective is to compute time–frequency representations that are smooth (continuous) in time and sparse in frequency. Current spectral estimation procedures are not specifically tailored to achieve smoothness in time and sparsity in frequency. Finally, batch time-series analyses are also common in many applications (5, 12, 13, 15). Although the batch analyses can use all of the data in the recorded time series to estimate the time–frequency representation at each time point, spectral estimation limited to local windows remains the solution of choice because the computational demands of batch analyses scale poorly with the length of the time series. Using all of the data in batch spectral analyses would enhance both time and frequency resolution.

For a time series whose time-varying mean is the superposition of a small number of smooth oscillatory components, we formulate nonparametric batch spectral analysis as a Bayesian estimation problem. We assume a Gaussian or a point-process observation model for the time series and introduce prior distributions on the time–frequency plane that yield maximum a posteriori (MAP) spectral estimates that are smooth (continuous) in time yet sparse in frequency. Our choice of prior distributions is motivated by EMD (13), and its variants (11, 16), which decompose signals into a small number of oscillatory components. We term our procedure “spectrotemporal pursuit.” To compute the spectrotemporal pursuit spectral estimate, we develop highly efficient, recursive, iteratively reweighted least-squares (IRLS) algorithms in which each iteration is implemented by using fixed interval smoothing algorithms (17, 18). We prove that the spectrotemporal pursuit spectral estimates converge to the global MAP estimates by using an important link between Gaussian mixture models, ${\ell }_1$ minimization, and the expectation–maximization algorithm (19, 20). We show that computation of the spectrotemporal pursuit spectral estimates is equivalent to applying to the time series a bank of data-dependent filters, one for each oscillatory component.

We illustrate spectrotemporal pursuit in simulation studies as well as in analyses of human EEG and neural spiking data (15, 21) recorded during unconsciousness induced by the anesthetic propofol. The spectrotemporal pursuit analysis of the EEG data yields significantly denoised spectral estimates that have higher time and frequency resolution than multitaper spectral estimates. Our analysis of the neural spiking data yields a new spectral description of neural firing rates that can further our understanding of the relationship of spiking activity to local field potentials.

Toy Example

We begin with a toy example to highlight the deficiencies of classical techniques in analyzing time series that exhibit dynamic behavior and the limits they impose on spectral resolution (8, 9). We simulated noisy observations from the linear combination of two amplitude-modulated signals as

$$\begin{array}{l}{y}_t=10{\cos }^8\left(2\pi f_{0}t\right)\sin \left(2\pi f_{1}t\right)\\ \hspace{1em}\hspace{1em}+10\exp \left(4\frac{t-T}{T}\right)\cos \left(2\pi f_{2}t\right)+v_t,\hspace{1em}\text{for}\hspace{0.17em}\hspace{0.17em}0\le t\le T,\end{array}$$ [1]

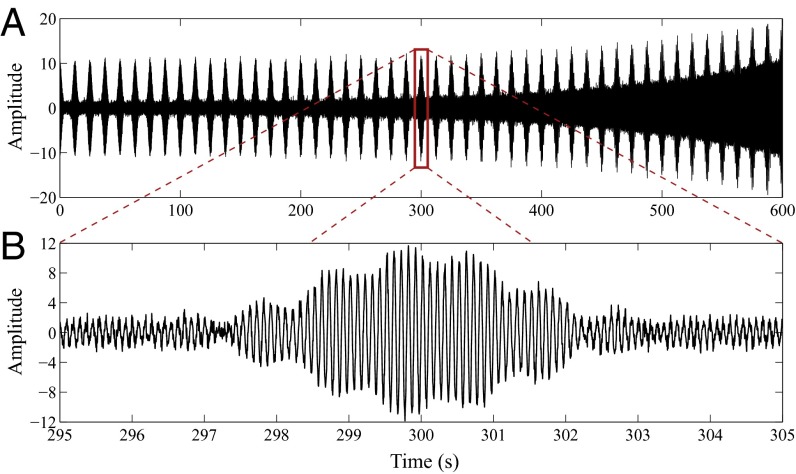
where $f_0=0.04$ Hz, $f_1=10$ Hz, $f_2=11$ Hz, $T=600\hspace{0.17em}\text{s}$, and ${\left(v_t\right)}_{t=1}^T$ is independent, identically distributed, zero-mean Gaussian noise with variance set to achieve a signal-to-noise ratio (SNR) of 5 dB. The simulated data (Fig. 1) consist of a 10-Hz oscillation whose amplitude is modulated by a slow 0.04-Hz oscillation, and an exponentially growing 11-Hz oscillation. The former is motivated by the fact that low-frequency (<1 Hz) phase modulates alpha (8–12 Hz) amplitude during profound unconsciousness, and during the transition into and out of unconsciousness, under propofol-induced general anesthesia (15, 21). We incorporated the latter to demonstrate the desire, in certain applications, to resolve closely spaced amplitude-modulated signals.

Fig. 1.

Linear combination of two amplitude-modulated oscillations at 10- and 11-Hz frequencies, respectively, observed in independent, identically distributed, additive, zero-mean Gaussian noise with variance set to achieve an SNR of 5 dB. (A) The full simulated data according to Eq. 1. (B) Zoomed-in view from $t=295\hspace{0.17em}\text{s}$ to $t=305\hspace{0.17em}\text{s}$.

This toy example poses serious challenges for classical spectral estimation algorithms due to the strong amplitude modulation and dynamic behaviors, observation noise, and identifiability issues (the decomposition is not unique) (11).

In the next section, we develop an analysis paradigm to separate signals such as the 10-and 11-Hz oscillations and recover the time-varying modulating signals. The key to our spectral decomposition framework is the concept of a structured time–frequency representation.

Theory: Robust Spectral Decomposition

The State-Space Model.

Consider a discrete-time signal $y_t,t=\mathrm{1,2},\cdots ,T$ obtained by sampling of an underlying, noise-corrupted, continuous-time signal at a rate $f_s$ (above the Nyquist rate). Given an arbitrary interval of length W, let ${\mathbf{y}}_n≔{\left(y_{\left(n-1\right)W+1},y_{\left(n-1\right)W+2},\cdots ,y_{nW}\right)}^{\prime }$ for $n=\mathrm{1,2},\cdots ,N$ with $N≔\frac{T}{W}$. Without loss of generality, we assume that T is an integer multiple of W and consider the following spectrotemporal representation of ${\mathbf{y}}_n$ as

$${\mathbf{y}}_n={\tilde{\mathbf{F}}}_n{\tilde{\mathbf{x}}}_n+{\mathbf{v}}_n,$$ [2]

where ${\left({\tilde{\mathbf{F}}}_n\right)}_{l,k}≔\exp \left(j2\pi \left(\left(n-1\right)W+l\right)\frac{(k-1)}{K}\right)$ for $l=\mathrm{1,2},\cdots ,W$ and $k=\mathrm{1,2},\cdots ,K$, ${\tilde{\mathbf{x}}}_n≔{\left({\tilde{x}}_{n,1},{\tilde{x}}_{n,2},\cdots ,{\tilde{x}}_{n,K}\right)}^{\prime }\in {\mathrm{ℂ}}^K$, with K being a positive integer, and ${\mathbf{v}}_n$ is independent, identically distributed, additive zero-mean Gaussian noise. Equivalently, we can define the linear observation model of Eq. 2 over a real vector space as follows:

$${\mathbf{y}}_n={\mathbf{F}}_n{\mathbf{x}}_n+{\mathbf{v}}_n,$$ [3]

where ${\left({\mathbf{F}}_n\right)}_{l,k}:=\cos \left(2\pi \left(\left(n-1\right)W+l\right)\frac{(k-1)}{K}\right)$ and ${\left({\mathbf{F}}_n\right)}_{l,k+K/2}:=\sin \left(2\pi \left(\left(n-1\right)W+l\right)\frac{k-1+K/2}{K}\right)$ for $l=\mathrm{1,2},\cdots ,W$ and $k=\mathrm{1,2},\cdots ,\frac{K}{2}$, and ${\mathbf{x}}_n≔{\left(x_{n,1},x_{n,2},\cdots ,x_{n,K}\right)}^{\prime }\in {\mathrm{ℝ}}^K$. We may rewrite Eq. 3 conveniently in vector form as $\mathbf{y}=\mathbf{F}\mathbf{x}+\mathbf{v}$, where F is a $T\times NK$ block-diagonal matrix with ${\mathbf{F}}_n$ on the diagonal blocks:

$$\mathbf{F}≔\left(\begin{array}{cccc}{\mathbf{F}}_1& & & \\ & {\mathbf{F}}_2& & \\ & & \ddots & \\ & & & {\mathbf{F}}_N\end{array}\right),$$ [4]

$\mathbf{y}={\left(y_1,y_2,\cdots ,y_T\right)}^{\prime }\in {\mathrm{ℝ}}^T$, $\mathbf{x}={\left({\mathbf{x}\prime }_1,{\mathbf{x}\prime }_2,\cdots ,{\mathbf{x}\prime }_N\right)}^{\prime }\in {\mathrm{ℝ}}^{NK}$, and $\mathbf{v}={\left({\mathbf{v}\prime }_1,{\mathbf{v}\prime }_2,\cdots ,{\mathbf{v}\prime }_N\right)}^{\prime }\in {\mathrm{ℝ}}^T$. We view x as a time–frequency representation of the time-varying mean of the signal y.

As we show in A Spectrotemporal Pursuit Analysis of Neural Spiking Activity, we can generalize this linear Gaussian forward model to nonlinear spectrotemporal parameterizations of the joint distribution of non-Gaussian data.

Our objective is to compute an estimate $\widehat{\mathbf{x}}$ of x given the data y. The component-wise magnitude-squared of $\widehat{\mathbf{x}}\in {\mathrm{ℝ}}^{NK}$ then gives an estimate of the magnitude spectrum of y. Classical spectral estimation techniques use sliding windows with overlap to implicitly enforce temporal smoothness of the oscillatory components; i.e., adjacent spectral estimates are intended to be close in value. However, rather than being stated explicitly in the form of a model (deterministic or stochastic) for the evolution of the spectral estimates, the temporal smoothness is implicit in the degree of nonoverlap of the respective windows. Moreover, these techniques do not consider sparsity in the frequency domain. In contrast, we take a direct approach that treats ${\left({\mathbf{x}}_n\right)}_{n=1}^N$ as the realization of a sequence of random variables and uses a prior distribution to impose explicitly a stochastic continuity constraint on its elements across time. We impose a model on the components ${\left(x_{n,k}\right)}_{k=1}^K$ for each $n=\mathrm{1,2},\cdots ,N$ to enforce sparsity in the frequency domain. Starting with an initial condition ${\mathbf{x}}_0={(0,\dots ,0)}^{\prime }\in {\mathrm{ℝ}}^K$, we can express the stochastic continuity constraint in the form of the first-order difference equation

$${\mathbf{x}}_n={\mathbf{x}}_{n-1}+{\mathbf{w}}_n,$$ [5]

where $\mathbf{w}={\left({\mathbf{w}}_1\prime ,{\mathbf{w}}_2\prime ,\cdots ,{\mathbf{w}}_N\prime \right)}^{\prime }\in {\mathrm{ℝ}}^{NK}$ is a random vector. To impose stochastic continuity, we assume a joint prior probability density function over ${\mathbf{w}}_1,{\mathbf{w}}_2,\cdots ,{\mathbf{w}}_N$, which in turn imposes a joint probability density function on ${\left({\mathbf{x}}_n\right)}_{n=1}^N$. Motivated by the empirical mode decomposition (13) and its variants (11, 16), we choose prior densities that enforce sparsity in the frequency domain and smoothness in time. In logarithmic form, the priors we propose are

$$\log p_1\left({\mathbf{w}}_1,{\mathbf{w}}_2,\cdots ,{\mathbf{w}}_N\right)=-{\alpha }_1{\displaystyle \sum _{k=1}^K{\left({\displaystyle \sum _{n=1}^N{w}_{n,k}^2}+{\mathit{ϵ}}^2\right)}^{\frac{1}{2}}}+c_1,$$ [6]

and

$$\log p_2\left({\mathbf{w}}_1,{\mathbf{w}}_2,\cdots ,{\mathbf{w}}_N\right)=-{\alpha }_2{\displaystyle \sum _{k=1}^K{\left({\displaystyle \sum _{n=1}^N{\left(w_{n,k}^2+{\mathit{ϵ}}^2\right)}^{\frac{1}{2}}}\right)}^{\frac{1}{2}}}+c_2,$$ [7]

where ${\alpha }_1>0$ and ${\alpha }_2>0$ are constants, ${\text{e}}^{c_1}$ and ${\text{e}}^{c_2}$ are normalization constants, and $\mathit{ϵ}>0$ is a small constant. These priors belong to the Gaussian scale mixture (GSM) family of densities (19, 20). This family of densities has robustness properties in the statistical sense (22). Both $p_1(\cdot )$ and $p_2(\cdot )$ enforce inverse solutions that are spatially sparse and temporally smooth. Indeed, one can interpret Eqs. 6 and 7 as forms of dynamic group-sparse regularization (23). Unlike $p_1(\cdot )$, $p_2(\cdot )$ can capture abrupt changes in the dynamics of the inverse solution. Under each of these priors, the discrete-time stochastic process ${\left({\mathbf{x}}_n\right)}_{n=1}^N$ is a non-Gaussian random process whose increments are statistically dependent.

The Inverse Solution: Spectrotemporal Pursuit.

We formulate the problem of computing a robust spectral decomposition as one of Bayesian estimation in which the posterior density of x given y fully characterizes the space of inverse solutions. The forward model of Eq. 3 specifies the likelihood of the data, that is to say the conditional density of y given x. We assume that the observation noise ${\mathbf{v}}_n$ are samples from independent, identically distributed, zero-mean Gaussian random vectors with covariance ${\sigma }^2\mathbf{I}$. To simplify the notation, we let

$$f_i\left({\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_N\right)≔\log p_i\left({\mathbf{x}}_1-{\mathbf{x}}_0,{\mathbf{x}}_2-{\mathbf{x}}_1,\cdots ,{\mathbf{x}}_N-{\mathbf{x}}_{N-1}\right)$$ [8]

for $i=1$ and 2 in what follows. We compute robust spectral estimates by solving the MAP estimation problem

$$\underset{{\mathbf{x}}_1,\cdots ,{\mathbf{x}}_N}{\text{max}}-{\displaystyle \sum _{n=1}^N\frac{1}{2{\sigma }^2}{\Vert {\mathbf{y}}_n-{\mathbf{F}}_n{\mathbf{x}}_n\Vert }_2^2}+f\left({\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_N\right).$$ [9]

We call the MAP estimation problem of Eq. 9 the spectrotemporal pursuit problem, and its solution the spectrotemporal pursuit estimate. To solve this optimization problem, we can absorb the constant σ in $f(\cdot )$ (specifically in ${\alpha }_1$ in the case of Eq. 6 and ${\alpha }_2$ in the case of Eq. 7). Therefore, henceforth, we assume that $\sigma =1$. In SI Text, we give a continuous-time variational interpretation of spectrotemporal pursuit.

Eq. 9, with $f(\cdot )=f_1(\cdot )$, is a strictly concave optimization problem, which, in principle, can be solved using standard techniques. However, our experience has shown that these techniques do not scale well with N because of the batch nature of the problem. We use the Bayesian formulation of spectrotemporal pursuit—in particular, the relationship between sparsity-promoting priors and the expectation–maximization (EM) algorithm, to develop highly efficient IRLS algorithms that exploit the temporal structure of Eq. 9. Gradient-based algorithms (24, 25) are a popular alternative to IRLS for finding the maximizer of Eq. 9 with $\mathit{ϵ}=0$. One of the advantages of our Bayesian formulation is the ability to characterize the uncertainty of the estimate in the form of confidence bounds. We discuss this in further detail in SI Text, Advantages of IRLS over Gradient-Based Methods.

Link of Spectrotemporal Pursuit to Basis Pursuit Denoising, IRLS Algorithms, and Sparse Recovery.

Spectrotemporal pursuit builds on results in basis pursuit denoising (BPDN) and IRLS algorithms developed to compute sparse decompositions in noise-free systems. Chen et al. (26) demonstrated using the BPDN algorithm that static signals can be decomposed into sparse representations using finite dictionaries obtained by discretizing in the frequency domain. We termed our procedure spectrotemporal pursuit to emphasize the link with BPDN. Daubechies et al. (27) showed under mild conditions that in the absence of noise, IRLS algorithms can recover sparse signals. It is straightforward to see that the IRLS algorithm of Daubechies et al. (27) solves a BPDN-type optimization problem. We recently extended the work of Daubechies et al. (27) to solve the problem of sparse recovery in the presence of noise (20), and broadened the family of IRLS algorithms. The IRLS algorithms we derive in the next section belong to the broader class of IRLS algorithms we introduced (20). The key insight from those results, which we apply here, is that this broad class of IRLS algorithms can be used in the context of Bayesian estimation of state-space models (28) to compute highly structured spatiotemporal decompositions efficiently. In SI Text, we elaborate on these relationships.

An IRLS Algorithm for Spectrotemporal Pursuit.

We show that we can obtain the solution $\widehat{\mathbf{x}}$ to Eq. 9 as the limit of a sequence ${\left({\widehat{\mathbf{x}}}^{\left(\ell \right)}\right)}_{\ell =0}^{\infty }$ whose ${\ell }^{\text{th}}$ element, $\ell =1,\cdots ,\mathrm{\infty }$, is the solution to a Gaussian MAP estimation problem (constrained least-squares program) of the form

$$\underset{{\mathbf{x}}_1,\cdots ,{\mathbf{x}}_N}{\text{max}}-{\displaystyle \sum _{n=1}^N\frac{1}{2{\sigma }^2}{\Vert {\mathbf{y}}_n-{\mathbf{F}}_n{\mathbf{x}}_n\Vert }_2^2}-{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{n=1}^N\frac{{\left(x_{n,k}-x_{n-1,k}\right)}^2}{2{\left({\mathbf{Q}}_n^{\left(\ell \right)}\right)}_{k,k}}}}.$$ [10]

For each ℓ, ${\mathbf{Q}}_n^{\left(\ell \right)}$ is a $K\times K$ diagonal matrix that depends on ${\widehat{\mathbf{x}}}_{n-1}^{\left(\ell -1\right)},{\widehat{\mathbf{x}}}_n^{\left(\ell -1\right)}$ and $f(\cdot )$. For instance, for $f(\cdot )=f_1(\cdot )$,${\mathbf{Q}}_n^{\left(\ell \right)}={\mathbf{Q}}^{\left(\ell \right)}$ does not depend on n and we have

$${\left({\mathbf{Q}}^{\left(\ell \right)}\right)}_{k,k}=\frac{{\left({\displaystyle {\sum }_{n=1}^N{\left({\widehat{x}}_{n,k}^{\left(\ell -1\right)}-{\widehat{x}}_{n-1,k}^{\left(\ell -1\right)}\right)}^2}+{\mathit{ϵ}}^2\right)}^{\frac{1}{2}}}{{\alpha }_1}.$$ [11]

Eq. 10 is a quadratic program with strictly concave objective and block-tridiagonal Hessian. The fixed interval smoother (17) exploits this structure to give an efficient solution to this program via forward–backward substitution. This iterative solution to the spectrotemporal pursuit problem, which we refer to as the spectrotemporal pursuit algorithm, can be implemented using the following steps:

Input: Observations y, initial guess ${\widehat{\mathbf{x}}}^{\left(0\right)}$ of solution, state-noise covariances ${\mathbf{Q}}_n^{\left(0\right)}$, $n=1,\cdots ,N$, initial conditions ${\mathbf{x}}_{0|0}$, ${\mathrm{\Sigma }}_{0|0}$, tolerance $tol\in \left(\mathrm{0,0.01}\right)$, and maximum number of iteration $L_{\text{max}}\in {\mathrm{\mathbb{N}}}^{+}$.

• 0.Initialize iteration number ℓ to 1.
• 1.Filter at time $n=\mathrm{1,2},\cdots ,N$:

• $\begin{array}{l}{\mathbf{x}}_{n|n-1}={\mathbf{x}}_{n-1|n-1}\\ {\mathbf{\Sigma }}_{n|n-1}={\mathbf{\Sigma }}_{n-1|n-1}+{\mathbf{Q}}_n^{\left(\ell \right)}\\ {\mathbf{K}}_n={\mathbf{\Sigma }}_{n|n-1}{\mathbf{F}}_n^H{\left({\mathbf{F}}_n{\mathbf{\Sigma }}_{n|n-1}{\mathbf{F}}_n^H+{\sigma }^2\mathbf{I}\right)}^{-1}\\ {\mathbf{x}}_{n|n}={\mathbf{x}}_{n|n-1}+{\mathbf{K}}_n\left({\mathbf{y}}_n-{\mathbf{F}}_n{\mathbf{x}}_{n|n-1}\right)\\ {\mathbf{\Sigma }}_{n|n}={\mathbf{\Sigma }}_{n|n-1}-{\mathbf{K}}_n{\mathbf{F}}_n{\mathbf{\Sigma }}_{n|n-1}\end{array}$

• 2.Smoother at time $n=N-1,N-2,\cdots ,1$:

• $\begin{array}{l}{\mathbf{B}}_n={\mathbf{\Sigma }}_{n|n}{\mathbf{\Sigma }}_{n+1|n}^{-1}\\ {\mathbf{x}}_{n|N}={\mathbf{x}}_{n|n}+{\mathbf{B}}_n\left({\mathbf{x}}_{n+1|N}-{\mathbf{x}}_{n+1|n}\right)\\ {\mathbf{\Sigma }}_{n|N}={\mathbf{\Sigma }}_{n|n}+{\mathbf{B}}_n\left({\mathbf{\Sigma }}_{n+1|N}-{\mathbf{\Sigma }}_{n+1|n}\right){\mathbf{B}}_n^H\end{array}$

• 3.Let ${\widehat{\mathbf{x}}}_n^{\left(\ell \right)}={\mathbf{x}}_{n|N},n=1,\cdots ,N$ and ${\widehat{\mathbf{x}}}^{\left(\ell \right)}={\left({\widehat{\mathbf{x}}}_1^{{\left(\ell \right)}^{\prime }},\cdots ,{\widehat{\mathbf{x}}}_N^{{\left(\ell \right)}^{\prime }}\right)}^{\prime }$.
• 4.Stop if $\frac{{\Vert {\widehat{\mathbf{x}}}^{\left(\ell \right)}-{\widehat{\mathbf{x}}}^{\left(\ell -1\right)}\Vert }_2}{{\Vert {\widehat{\mathbf{x}}}^{\left(\ell -1\right)}\Vert }_2}<tol$ or $\ell =L_{\text{max}}$, else
• 5.
  Let $\ell =\ell +1$, and update the state covariance ${\mathbf{Q}}_n^{\left(\ell \right)}$. For $f(\cdot )=f_1(\cdot )$, ${\mathbf{Q}}_n^{\left(\ell \right)}={\mathbf{Q}}^{\left(\ell \right)}$ is given by

  $${\left({\mathbf{Q}}^{\left(\ell \right)}\right)}_{k,k}=\frac{{\left({\displaystyle {\sum }_{n=1}^N{\left({\widehat{x}}_{n,k}^{\left(\ell -1\right)}-{\widehat{x}}_{n-1,k}^{\left(\ell -1\right)}\right)}^2}+{\mathit{ϵ}}^2\right)}^{\frac{1}{2}}}{{\alpha }_1}$$
• 6.Go back to 1.

Output: ${\widehat{\mathbf{x}}}^{\left(L\right)}$, where $L\le L_{\text{max}}$ is the number of the last iteration of the algorithm.

For $f(\cdot )=f_1(\cdot )$, starting with ${\widehat{\mathbf{x}}}^{\left(0\right)}$ a guess of the solution, we solve Eq. 10 for $\ell =\mathrm{1,2},\cdots ,L$ with ${\mathbf{Q}}^{\left(\ell \right)}$ iteratively updated using Eq. 11. L is the smallest of $L_{\text{max}}$, a prespecified maximum number of iterations, and the number of iterations when the convergence criterion of step 4 of the spectrotemporal pursuit algorithm is first satisfied. Consistent with previous reports (20), we have found that a small number of IRLS iterations (between 5 and 10) are sufficient in practice. Due to the dynamic nature of our state-space model, the MAP estimation problem Eq. 10 admits an iterative solution given by the fixed interval smoother. As noted previously, ${\mathbf{Q}}^{\left(\ell \right)}$ is independent of n for the penalization function $f_1(\cdot )$.

Solving the IRLS problem in Eq. 10 with ${\left({\mathbf{Q}}^{\left(\ell \right)}\right)}_{k,k}$ in Eq. 11 is an EM algorithm (19, 20) for solving Eq. 9 with $f(\cdot )=f_1(\cdot )$. The EM algorithm minorizes the objective function of Eq. 9 by a local quadratic approximation to the log-prior, which results in the least-squares problem of Eq. 10. The Hessian of the quadratic approximation is a function of ${\mathbf{Q}}^{\left(\ell \right)}$ in Eq. 11. One way to derive Eq. 11 is to invoke the concavity of the function $s^{1/2}$, which implies that the linear approximation around a point $\overline{s}$ satisfies $s^{1/2}\le {\overline{s}}^{1/2}+\frac{1}{2{\overline{s}}^{1/2}}\left(s-\overline{s}\right)$. Applying this result to the log-prior at ${\widehat{\mathbf{x}}}^{\left(\ell -1\right)}$ allows us to readily extract ${\left({\mathbf{Q}}^{\left(\ell \right)}\right)}_{k,k}$ in Eq. 11.

In general, it can be shown that for priors from the GSM family of distributions, the EM algorithm for solving the MAP estimation problem of Eq. 9 results in IRLS solutions (20). The connection to EM theory leads to a class of IRLS algorithms (20) much broader than that considered in the existing literature (27) and a much simpler convergence analysis (20). We establish convergence of the IRLS algorithm of Eq. 10 as a theorem in Appendix: Convergence of the IRLS Algorithm. The convergence does not follow from the analysis of Daubechies et al. (27). The proof requires novel ideas (20) that we adapt to the current setting.

The difficulty in solving the spectrotemporal pursuit problem of Eq. 9 arises from the choice of the prior probability density functions over ${\mathbf{w}}_1,{\mathbf{w}}_2,\cdots ,{\mathbf{w}}_N$ (Eqs. 6 and 7), which, for each $k=1,\cdots ,K$, groups ${\left(w_{n,k}\right)}_{n=1}^N$ across time. At first glance, this grouping suggests a batch solution. However, recognizing the connection with the EM theory for GSMs yields an IRLS solution that can be solved efficiently using the fixed interval smoother, owing to the dynamic structure of the state-space model. A large class of optimization problems can be solved by IRLS (29). In practice, however, the update step of IRLS is challenging. One attractive feature of our formulation is its modularity: each IRLS update step is simple in the sense that it can be solved using any algorithm that can solve a strictly concave quadratic program with block-tridiagonal Hessian.

We can easily specialize the discussion above to $f(\cdot )=f_2(\cdot )$. In particular, if we let

$$\begin{array}{c}{\left({\mathbf{Q}}_n^{\left(\ell \right)}\right)}_{k,k}=\frac{2}{{\alpha }_2}{\left({\left({\widehat{x}}_{n,k}^{\left(\ell -1\right)}-{\widehat{x}}_{n-1,k}^{\left(\ell -1\right)}\right)}^2+{\mathit{ϵ}}^2\right)}^{\frac{1}{2}}\\ \times {\left({\displaystyle \sum _{n^{\prime }=1}^N{\left({\left({\widehat{x}}_{n^{\prime },k}^{\left(\ell -1\right)}-{\widehat{x}}_{n^{\prime }-1,k}^{\left(\ell -1\right)}\right)}^2+{\mathit{ϵ}}^2\right)}^{\frac{1}{2}}}\right)}^{\frac{1}{2}},\end{array}$$ [12]

Eq. 10 becomes an IRLS algorithm for solving the spectrotemporal pursuit problem with $f(\cdot )=f_2(\cdot )$. In this case, we can also prove the convergence of the algorithm. However, because $f_2(\cdot )$ is not concave, we can only guarantee convergence to a stationary point of the objective in Eq. 9 (20). In both cases, the role of ϵ is to avoid division by zero in forming the quadratic approximation of Eq. 10. As in the case of static IRLS (20), we expect the solution to be close, in some sense, to the maximizer of Eq. 9 with $\mathit{ϵ}=0$.

We use the terminology robust spectral estimator and estimate, to refer to spectrotemporal pursuit and its solution, respectively. The former terminology reflects the fact that $f_1(\cdot )$ and $f_2(\cdot )$ correspond to GSM (19) prior distributions on ${\mathbf{x}}_1,{\mathbf{x}}_2-{\mathbf{x}}_1,\cdots ,{\mathbf{x}}_N-{\mathbf{x}}_{N-1}$, which are robust in the statistical sense (19).

Analysis of Spectral Resolution.

Determining the frequency resolution of a given estimator is a central question in spectral estimation. To characterize the resolution for nonparametric spectral estimators, we must study the properties of the so-called “taper” that is applied to the data. For instance, the multitaper spectral estimator uses the discrete prolate spheroidal sequences as tapers, which are known to have very small side lobes in the frequency domain (9). From the recursive form of the fixed interval smoother, it is not evident how the robust estimator fits into the tapering framework of nonparametric spectral estimators. In what follows, we show how the spectral resolution of the robust spectral estimator can be characterized.

Before proceeding with the analysis, let us first consider the linear least-squares estimate of x. Recall the compact form of the forward model $\mathbf{y}=\mathbf{F}\mathbf{x}+\mathbf{v}$, where F is given in Eq. 4. Let us assume for convenience that the window length W is an integer multiple of the number K of discrete frequencies, i.e., $W=rK$ for some integer r, so that ${\mathbf{F}}_n={\mathbf{F}}_1$, for all n. The linear least-squares estimator maps the data y to

$$\widehat{\mathbf{x}}≔\frac{1}{rW}{\mathbf{F}}^H\mathbf{y},$$ [13]

from which we can compute the spectrum as the component-wise magnitude of $\widehat{\mathbf{x}}$ of the data. In other words, the rows of $\left(1/rW\right){\mathbf{F}}^H$ form a bank of filters, which consists of sliding windows of the Fourier basis on the interval $\left[1,W\right]$. The side lobes of these filters determine the spectral resolution. In Appendix: Robust Spectral Decomposition as a Filter Bank, we show that for $f(\cdot )=f_1(\cdot )$, the estimate $\widehat{\mathbf{x}}$ from the robust spectral estimator is given by

$$\underset{\ell \to \infty }{\text{lim}}{\widehat{\mathbf{x}}}^{\left(\ell \right)}=\mathbf{G}{\mathbf{F}}^H\mathbf{y}\text{,}$$ [14]

where G is a weighting matrix and is only a function of the window size W and ${\mathbf{Q}}^{\left(\infty \right)}≔{\lim }_{\ell \to \infty }{\mathbf{Q}}^{\left(\ell \right)}$. The rows of $\mathbf{G}{\mathbf{F}}^H$ form a filter bank whose output is equivalent to that of the robust spectral estimator at windows $n=\mathrm{1,2},\cdots ,N$. As shown in the appendix, the advantages of the weighting matrix G are twofold. First, the weighting shapes the Fourier basis by an effectively exponential taper for higher side-lobe suppression. Second, the choice of ${\mathbf{Q}}^{\left(\infty \right)}$ from the data determines the gain of each filter; i.e., the filters corresponding to the large (small) elements of ${\mathbf{Q}}^{\left(\infty \right)}$ are likely to have a high (low) gain. Therefore, the shaping of the filters is determined by the data itself.

Eq. 14 provides an ex post prescription to analyze the resolution and leakage of the robust spectral estimate; i.e., given W and ${\mathbf{Q}}^{\left(\infty \right)}$, we can form the matrix $\mathbf{G}{\mathbf{F}}^H$, the rows of which are the equivalent bank of filters corresponding to the robust spectral estimator in windows $n=\mathrm{1,2},\cdots ,N$.

Toy Example Revisited

We use the data simulated in the toy example to compare the spectral estimates computed using spectrotemporal pursuit to the spectrogram computed using the multitaper method (8).

Fig. 2 A and B show the spectrogram estimates obtained by the multitaper method with 2-s temporal resolution and the multitaper method with 0.5 Hz frequency resolution, respectively. Fig. 2, Right, shows the zoomed-in view of the estimates in the interval $t=250\hspace{0.17em}\text{s}$ to $t=350\hspace{0.17em}\text{s}$. We used a time bandwidth product of three and five tapers in both cases. The multitaper estimate with 2-s temporal resolution has a theoretical frequency resolution of 3 Hz (9), and as can be seen from Fig. 2A, is unable to resolve the closely spaced signals of 10 and 11 Hz in the frequency domain. However, the temporal details are captured to a certain extent. For the multitaper estimate with 0.5 Hz frequency resolution, the temporal resolution is 12 s and, as can be observed from Fig. 2B, the estimate it produces is smeared along the time axis and does not capture the details of the 0.04-Hz amplitude modulation. However, the two tones of 10 Hz and 11 Hz are well-resolved. For both multitaper instances, a significant amount of the additive noise has leaked into the spectrogram estimates. In other words, the multitaper approach is unable to denoise the estimate. Fig. 2C shows the spectral estimate obtained using spectrotemporal pursuit. Similarly, Fig. 2C, Right, shows the zoomed-in view of the estimate in the interval $t=250\hspace{0.17em}\text{s}$ to $t=350\hspace{0.17em}\text{s}$. Spectrotemporal pursuit gives the sparse, more compact representation that we would hope to recover given the simulated data of Eq. 1. Indeed, we are able to faithfully recover the two tones as well as their temporal modulation. In addition, the spectral estimate from Fig. 2C is significantly denoised relative to that in Fig. 2 A and B. Lastly, as Fig. 2C suggests, spectrotemporal pursuit is able to overcome the fundamental limits imposed by the classical uncertainty principle (14): the spectral estimate of Fig. 2C exhibits high resolution both in time and in frequency; to illustrate this, we examine the two filters that, when applied to the data from the toy example, reproduce the spectrotemporal pursuit spectral estimates at frequencies 10 Hz and 5 Hz, respectively. Fig. 3 shows the equivalent filters corresponding to the spectrotemporal pursuit estimator at frequencies 10 Hz and 5 Hz for $t=300\hspace{0.17em}\text{s}$. The equivalent filter at 10 Hz corresponds to the component $10{\cos }^8\left(2\pi f_{0}t\right)\sin \left(2\pi f_{1}t\right)$ and, as explained in Toy Example, resembles a 10-Hz oscillation that is exponentially decaying in a piece-wise constant fashion. The first side-lobe is ∼10.5 Hz, with a suppression of ∼25 dB. The equivalent filter at 5 Hz, however, corresponds to a frequency that is not part of the signal. Hence, the peak gain is ∼10 dB smaller than that of the 10-Hz filter. As a result, the 5-Hz component of the estimate is negligible.

Fig. 2.

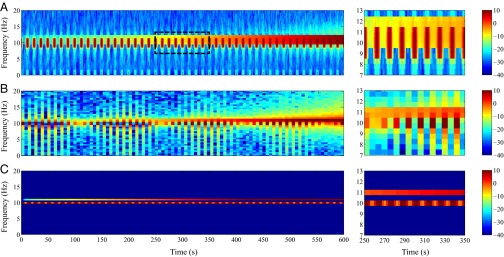
Spectral analysis of the toy example. (A) Multitaper spectrogram with 2-s temporal resolution, (B) multitaper spectrogram with 0.5-Hz frequency resolution, and (C) spectrotemporal pursuit spectral estimator. (Right) Zoomed-in views from $t=250\hspace{0.17em}\text{s}$ to $t=350\hspace{0.17em}\text{s}$. The color scale is in decibels.

Fig. 3.

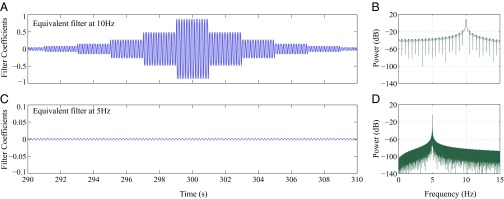
Equivalent filters corresponding to the robust spectral estimate of the toy example. (A) Equivalent filter and (B) its power spectral density (PSD) at $f=10$ Hz and $t=300\hspace{0.17em}\text{s}$. (C) Equivalent filter and (D) its PSD at $f=5$ Hz and $t=300$ s.

This toy example demonstrates the potential of structured time–frequency representations used in the spectrotemporal pursuit framework to go beyond the classical time–frequency resolution limits imposed by the uncertainty principle (14), and capture the dynamics of a signal whose time-varying mean is the sum a small number of oscillatory components.

Applications of Spectrotemporal Pursuit to Neural Signal Processing

A Spectrotemporal Pursuit Analysis of EEG Recordings.

We first illustrate the application of spectrotemporal pursuit by computing the robust spectral decomposition of frontal EEG data recorded from a patient during general anesthesia for a surgical procedure at Massachusetts General Hospital. The recording and analysis of these EEG data are part of an ongoing study that has been approved by the Massachusetts General Hospital Human Research Committee. All data collected were part of routine anesthesia care. General anesthesia is typically induced with propofol and is commonly maintained by administering a propofol infusion. Because data collection interacted in no way with patient management, and because all data were deidentified, informed patient consent was not required. A case is illustrated in Fig. 4. The patient received a bolus i.v. injection of propofol at ∼3.5 min, followed by a propofol infusion at 120 mcg⋅kg⁻¹⋅min⁻¹ that was maintained until minute 27, when the case ended.

Fig. 4.

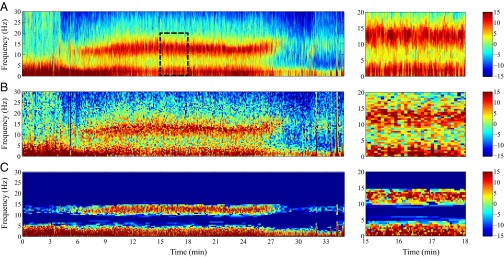
Spectral estimates of real EEG data from a subject undergoing propofol-induced general anesthesia. (A) Multitaper with 2-s temporal resolution, (B) multitaper with 0.5-Hz frequency resolution, and (C) robust spectral estimate. (Right) Respective zoomed-in views from $t=15\hspace{0.17em}\text{min}$ to $t=18\hspace{0.17em}\text{min}$. The color scale is in decibels.

When administered to initiate general anesthesia, propofol produces profound slow (<1 Hz) and delta (1–4 Hz) oscillations (Fig. 4, minute 5) (15, 21). With maintenance of general anesthesia, using propofol we observe an alpha oscillation (8–12 Hz) in addition to the slow and delta oscillations. The presence of the alpha oscillations along with the slow and delta oscillations is a marker of unconsciousness (15, 21). Developing a precise characterization of the dynamic properties of propofol is important for helping to define the neural circuit mechanisms of this anesthetic.

We computed the spectrogram for $T=35$ min of EEG data, sampled at a rate $f_s=250\hspace{0.17em}\text{Hz}$, using the multitaper method with 2-s temporal resolution (Fig. 4A), multitaper method with 0.5 Hz frequency resolution (Fig. 4B), and the magnitude of the spectral estimates from the spectrotemporal pursuit estimator with prior $f_2(\cdot )$ (Fig. 4C). Fig. 4, Right, shows zoomed-in views of the spectrogram from minute 15 to minute 18. For the spectrotemporal pursuit analysis, $W=500$, $N=\mathrm{1,050}$, and we select ${\alpha }_2$ by splitting the data into two sequences consisting of its even and odd times, respectively, and performing a form of twofold cross-validation (30). In other words, we assume that the spectrotemporal pursuit estimate of the spectrum is constant in windows of length 2 s. For each 2-s window of data, ${\mathbf{F}}_n$ is the $500\times 500$ matrix, which is the Fourier basis for the discrete-time interval $\left[\left(n-1\right)W+1,nW\right]$ for $n=\mathrm{1,2},\cdots ,N$. Because the original data are acquired at twice the sampling rate of the even and odd splits, the value of ${\alpha }_2$ used on the original data are half of that obtained by cross-validation because the variance of random walk as in Eq. 5 increases linearly with time.

By setting the choice of tapers or the analysis window, it is possible, with the multitaper method, to achieve either high frequency or high temporal resolution. In contrast, as in the toy example, spectrotemporal pursuit achieves high temporal resolution, high spatial resolution, and performs significant denoising of the spectrogram. As a consequence of the simultaneous enhanced time–frequency resolution in the spectrotemporal pursuit analysis, the slow and delta oscillations are clearly delineated during induction (minute 3.5), whereas during maintenance (minutes 5–27), the oscillations are strongly localized in the slow delta and alpha bands. Furthermore, the denoising induced by spectrotemporal pursuit creates a $\approx 30$-dB difference between these spectral bands and the other frequencies in the spectrum.

The spectrotemporal pursuit analysis offers the possibility of achieving a more precise delineation of the time–frequency properties of the EEG under propofol general anesthesia. We use this method to analyze in detail the dynamics of propofol as well as the other commonly used anesthetics.

A Spectrotemporal Pursuit Analysis of Neural Spiking Activity.

Modulation of neuronal firing rates by brain rhythms has been well documented (21, 31). During propofol-induced general anesthesia, the transition into and out of consciousness is characterized by abrupt changes both in average neuronal firing rates as well as their modulation by a low-frequency ($\approx 0.5$ Hz) oscillation (21). Local field potentials (LFPs) are routinely recorded simultaneously with spike-train data. Typically, the spike-field coherence, a measure of phase synchronization between spike trains and LFPs, is used to quantify the modulation of firing rates by oscillations and its time course. Despite the prevalence of modulation of neuronal firing rates by brain rhythms, there are no principled approaches that use spike-train data alone, without recourse to LFPs, to extract oscillatory dynamics. We adapt our spectrotemporal pursuit framework to point-process data and apply it to neural spiking data acquired from a human subject during the induction of propofol general anesthesia. This study was approved by the Massachusetts General Hospital Human Research Committee. In accordance with the Partners Human Research Committee, informed consent was obtained from all patients.

We assume that the spike train from each of the neurons recorded during the experiment is the realization of a point process (32) in the interval $\left(0,T\right]$. A point process is an ordered sequence of discrete events that occur at random points in continuous time. For a neural spike train, the elements of the sequence give the times in $\left(0,T\right]$ when the membrane potential of a neuron crosses a predetermined threshold—that is, the times when the neuron emits a spike. A point process is fully characterized by its conditional intensity function (CIF) (32). In our notation, the binary time series $y_t\in \left\{\mathrm{0,1}\right\},t=1,\cdots ,T$, represents the discrete-time point-process data. We denote by $0\le {\lambda }_t<\infty ,t=1,\cdots ,T$ the sampled CIF of the point process. Letting ${\mathit{\lambda }}_n≔\left({\lambda }_{\left(n-1\right)W+1},{\lambda }_{\left(n-1\right)W+2},\cdots ,{\lambda }_{nW}\right)\prime$, we begin with a point-process spectrotemporal forward model, which consists of a spectrotemporal parametrization of the CIF as follows:

$$\log {\mathit{\lambda }}_n={\mathbf{F}}_n{\mathbf{x}}_n,$$ [15]

where $\log {\mathit{\lambda }}_n≔{\left(\log {\lambda }_{\left(n-1\right)W+1},\log {\lambda }_{\left(n-1\right)W+2},\cdots ,\log {\lambda }_{nW}\right)}^{\prime }$ for $n=\mathrm{1,2},\cdots ,N$. Eq. 15 is a time–frequency representation of the time-varying CIF of a point process: ${\mathbf{x}}_n,n=\mathrm{1,2},\cdots ,N$ represent the signals modulating each of the oscillations (in ${\mathbf{F}}_n,n=\mathrm{1,2},\cdots ,N$) comprising the CIF.

We estimate ${\left({\mathbf{x}}_n\right)}_{n=1}^N$ by solving the following MAP estimation problem

$$\underset{{\mathbf{x}}_1,\cdots ,{\mathbf{x}}_N}{\text{max}}{\displaystyle \sum _{n=1}^N{\mathbf{y}\prime }_n\log {\mathit{\lambda }}_n}-{\mathbf{1}\prime }_W{\mathit{\lambda }}_n+f_2\left({\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_N\right),$$ [16]

where ${\mathbf{1}}_W$ is the vector of ones in ${\mathrm{ℝ}}^W$, and under a generalized linear model (Eq. 15). The objective function of Eq. 16 trades off the point process log-likelihood (3, 32) with the log-prior in Eq. 7, which enforces sparsity in frequency and smoothness in time. Eq. 16 is a point-process version of spectrotemporal pursuit (Eq. 9). We compute the solution $\widehat{\mathbf{x}}$ to Eq. 16 as the limit of a sequence ${\left({\widehat{\mathbf{x}}}^{\left(\ell \right)}\right)}_{\ell =0}^{\infty }$ whose ${\ell }^{\text{th}}$ element, $\ell =1,\cdots ,\mathrm{\infty }$, is the solution to

$$\underset{{\mathbf{x}}_1,\cdots ,{\mathbf{x}}_N}{\text{max}}{\displaystyle \sum _{n=1}^N{\mathbf{y}}_n\prime {\mathbf{F}}_n{\mathbf{x}}_n}-{\mathbf{1}}_W\prime {\text{e}}^{{\mathbf{F}}_n{\mathbf{x}}_n}-{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{n=1}^N\frac{{\left(x_{n,k}-x_{n-1,k}\right)}^2}{2{\left({\mathbf{Q}}_n^{\left(\ell \right)}\right)}_{k,k}}}},$$ [17]

where ${\mathbf{Q}}_n^{\left(\ell \right)}$ is given in Eq. 12 and ${\text{e}}^{{\mathbf{F}}_n{\mathbf{x}}_n}$ is the ${\mathrm{ℝ}}^W$ vector with entries ${\text{e}}^{{\left({\mathbf{F}}_n{\mathbf{x}}_n\right)}_w},w=\mathrm{1,2},\cdots ,W$. Each iteration can be implemented efficiently using a point-process smoothing algorithm (18). It is not hard to prove that the conclusions of the theorem in Appendix: Convergence of the IRLS Algorithm, regarding convergence, also hold for the sequence generated using this algorithm. However, as stated previously, we can only guarantee convergence to a stationary point of the objective (20) because $f_2(\cdot )$ is not concave.

We used this algorithm to compute a spectral representation of the population rate function of 41 neurons recorded in a patient undergoing intracranial monitoring for surgical treatment of epilepsy (21) using a multichannel microelectrode array implanted in temporal cortex. Recordings were conducted during the administration of propofol for induction of anesthesia. In ref. 21, the authors extensively describe the experimental protocol under which these data were collected and further use the data to elucidate the neurophysiological processes that characterize the transition into loss of consciousness (LOC) during propofol-induced general anesthesia. Fig. 5 depicts the data collected during this experiment as well as the results of our analysis; Fig. 5, Right, show the respective zoomed-in views of Fig. 5, Left, from $t=140\hspace{0.17em}\text{s}$ to $t=152\hspace{0.17em}\text{s}$. Fig. 5 A and B show, respectively, the LFP activity and a raster plot of the neural spiking activity collected during the experiment. The bolus of propofol is administered at ∼ 0 s. As reported in ref. 21, propofol-induced unconsciousness occurs within seconds of the abrupt onset of a slow ($\approx 0.5$ Hz) oscillation in the LFP. Moreover, neuronal spiking is strongly correlated to this slow oscillation, occurring only within a limited slow oscillation-phase window and being silent otherwise.

Fig. 5.

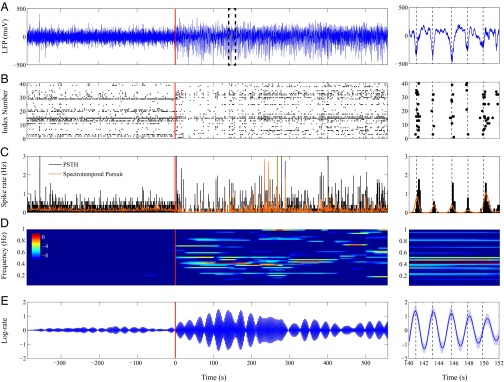
Spectral decomposition of the neural spiking activity from a subject undergoing propofol-induced general anesthesia. (A) LFP activity, (B) raster plot of the spike trains from the 41 units that were simultaneously acquired alongside the LFP activity, (C) PSTH and robust estimate of the firing rate obtained using spectrotemporal pursuit, (D) spectral decomposition of the firing rate in the $\left[0.05,1\right]$-Hz band (color scale in decibels), and (E) $\approx 0.45$-Hz component of log-firing rate (dark blue) with 95% confidence bounds (shaded region). (Right) Respective zoomed-in views from $t=140\hspace{0.17em}\text{s}$ to $t=152\hspace{0.17em}\text{s}$. The transition into LOC is marked by the onset of a strong $\approx 0.45$-Hz oscillation.

We demonstrate modulation of the neural spiking activity by the slow oscillation during the transition into LOC under propofol-induced general anesthesia by analysis of the neural spiking activity alone. Fig. 5C shows the firing rate estimates obtained using the standard peristimulus time histogram (PSTH; black) with a bin size of 125 ms and the spectrotemporal pursuit solution (red), respectively. In each 125-ms bin, the PSTH is the total number of spikes across all units divided by the product of the number of units and the bin size. Consistent with the findings of Lewis et al. (21), the firing rate of the neurons reaches a maximum at the troughs of the slow $\approx 0.5$-Hz oscillation in the LFP. The robust firing rate estimate from spectrotemporal pursuit is much smoother. Fig. 5D shows the novel spectral decomposition of the firing rate of the cortical neurons in the range 0.05 Hz to 1 Hz during propofol-induced general anesthesia. For this analysis, we set $f_s=1$ kHz, $T=\mathrm{1,000}$ s, $W=125$, and $N=\mathrm{8,000}$. In other words, we assume that the spectral decomposition is constant in windows of length 125 ms. For each 125-ms window of data, ${\mathbf{F}}_n$ is a $125\times 50$ matrix obtained using 50 equally spaced values in the range $\left[0.05,1\right]$ Hz. We constructed the observation vector ${\mathbf{y}}_n\in {\mathrm{ℝ}}^{125}$ in each window by summing the spikes from all 41 units in each 1-ms bin. To select ${\alpha }_2$, we split the 41 units randomly into two disjoint sets of 21 and 20 units, respectively, and performed twofold cross-validation on this splitting.

Our analysis reveals that the onset of LOC under propofol-induced general anesthesia in the patient is accompanied by the onset of a strong $\approx 0.45$-Hz oscillation. Fig. 5E shows the contribution of this $\approx 0.45$-Hz oscillation to the log of the population firing rate (Eq. 15). We are able to quantify the extent to which this oscillation modulates the firing rate of cortical neurons at a resolution of 125 ms. Before LOC (before ∼ 0 s), our analysis (Fig. 5E) shows that the slow oscillation does not contribute significantly to the firing rate of cortical neurons. However, during the recovery period, the slow oscillation increases the firing rate of cortical neurons by up to a factor of ∼ 3 above its local mean. Fig. 5E further indicates that the $\approx 0.45$-Hz component of the firing rate estimate from spectrotemporal pursuit is 180 degrees out of phase with the LFP activity. In other words, following LOC, the troughs of the LFP activity coincide with the times at which the contribution of this oscillation to the firing rate of cortical neurons is maximum. We computed the 95% confidence bounds in Fig. 5E, Right, by using the covariance matrices ${\left({\mathbf{\Sigma }}_{n|N}\right)}_{n=1}^N$ from the last iteration of the spectrotemporal pursuit algorithm.

Our analysis demonstrates that spectrotemporal pursuit can help clarify the relationship between neural spiking and LFPs.

Discussion

Robust Spectral Decomposition for Signals with Structured Time–Frequency Representations.

Classical nonparametric spectral estimation methods use sliding windows with overlap to implicitly enforce temporal smoothness of the spectral estimate. This widely adopted approach does not adequately describe signals with highly structured time–frequency representations. We develop a robust nonparametric spectral decomposition paradigm for batch time-series analyses, termed spectrotemporal pursuit, that uses a Bayesian formulation to explicitly enforce smoothness in time and sparsity in frequency of the spectral estimate. Spectrotemporal pursuit yields spectral estimates that are significantly denoised and have significantly higher time and frequency resolution than those obtained using the multitaper method. We illustrated spectrotemporal pursuit on a simulated signal comprising two nearby frequency components with a highly modulated amplitude, as well as on human EEG and on human neural spiking activity both recorded during propofol general anesthesia.

Computation of spectrotemporal pursuit spectral estimates requires solving a high-dimensional optimization problem (Eq. 9 with substitutions from Eqs. 6–8). By using a relation between ${\ell }_1$ minimization, GSM models, and the EM algorithm, we develop computationally efficient IRLS algorithms to compute the spectral decomposition. In the problems we study, these algorithms yield easy-to-implement Kalman (17) and point-process (18) smoothing algorithms. We also sketch a proof of convergence of the algorithms (Appendix) that uses ideas developed in ref. 20. We can readily characterize the achievable spectral resolution of our procedure because the spectrotemporal pursuit solution applies a time-varying, data-dependent filter bank to the observations (Fig. 3).

Spectrotemporal pursuit offers a principled alternative to existing methods, such as EMD, for decomposing a noisy time-series into a small number of oscillatory components (13); in spectrotemporal pursuit, this is easily handled using the regularization parameters ${\alpha }_1$ and ${\alpha }_2$, respectively, in the cases of $f_1(\cdot )$ and $f_2(\cdot )$, which we estimate from the time-series using cross-validation (30).

Alternate Approaches to Compute Spectral Representations of Signals that Exhibit Dynamic Behavior.

For deterministic signal models, notable contributions are those in refs. 33 and 34 for a signal model consisting of a small number of amplitude-modulated oscillations as in refs. 11 and 16. In the context of stochastic signals, the authors in ref. 35 propose an algorithm to estimate the nonparametric, nonstationary spectrum of a Dahlhaus locally stationary process. Lastly, dynamic models with time-varying sparsity have been proposed in several contexts (36, 37). In principle, these latter models can be applied to time-varying parametric spectral estimation using autoregressive models.

In SI Text, we discuss in greater detail the similarities and differences between these works and spectrotemporal pursuit.

Future Work.

In future reports we plan to extend our current formulation of spectrotemporal pursuit to compute smooth in time and sparse in frequency spectral estimates using filter algorithms. This development will be critical for online computation of robust spectral decompositions using our paradigm. We will also extend our formulation to dictionaries other than Fourier representations. The present formulation of spectrotemporal pursuit requires the user to specify the size W of the window over which the spectrum is constant. In our examples, these choices were informed by the time scales that are believed to be physiologically relevant (15, 21). We are currently developing dynamic versions of the matching pursuit algorithm (38), an efficient algorithm for solving sparsity-enforcing optimization problems, which will obviate the need for specifying W.

In conclusion, computing efficient spectral summaries of time series is a common challenge in many fields of science and engineering. Spectrotemporal pursuit offers a new approach to robust spectral analysis of batch time series which should be applicable to a broad range of problems.

Appendix: Convergence of the IRLS Algorithm

The following theorem states the convergence of the IRLS algorithm of Eq. 10.

Theorem. Let ${\widehat{\mathbf{x}}}^{\left(0\right)}\in {\mathrm{ℝ}}^K$ and ${\left({\widehat{\mathbf{x}}}^{\left(\ell \right)}\right)}_{\ell =1}^{\infty }\in {\mathrm{ℝ}}^{NK}$ be the sequence generated by the IRLS algorithm of Eq. 10 with ${\left({\mathbf{Q}}_n^{\left(\ell \right)}\right)}_{k,k}$ as in Eq. 11. Then, (i) ${\left({\widehat{\mathbf{x}}}^{\left(\ell \right)}\right)}_{\ell =0}^{\infty }$ is bounded, (ii) ∃ $\overline{\mathbf{x}}=\underset{\ell \to \infty }{lim}{\widehat{\mathbf{x}}}^{\left(\ell \right)}$, and (iii) ${\left({\widehat{\mathbf{x}}}^{\left(\ell \right)}\right)}_{\ell =0}^{\infty }$ converges to the unique stationary point of the objective of Eq. 9 with $f(\cdot )=f_1(\cdot )$.

The proof follows the same lines as that of theorem 3 in ref. 20. We only give the main ideas here.

Proof 1 (sketch of proof). Let $f(\cdot )=f_1(\cdot )$ in Eq. 9. The concavity of the $\sqrt{\cdot }$ function implies that the objective in Eq. 10 with ${\left({\mathbf{Q}}^{\left(\ell \right)}\right)}_{k,k}$ as in Eq. 11 is a lower bound of that in Eq. 9. Moreover, the difference between these two objectives attains a maximum at ${\widehat{\mathbf{x}}}^{(\ell -1)}$. We can use this to show (20) that Eq. 10 generates a sequence that is nondecreasing when evaluated at the objective of Eq. 9. Along with the fact that the objective of Eq. 9 is strictly concave and coercive (39); this implies that the sequence ${\left({\widehat{\mathbf{x}}}^{\left(\ell \right)}\right)}_{\ell =0}^{\infty }$ lies in a compact set, and hence is bounded. Therefore, there exists a convergent subsequence with limit point $\overline{\mathbf{x}}$. Take any convergent subsequence, each of its elements satisfies the first-order necessary and sufficient optimality conditions for the objective of Eq. 10, which, in the limit, are equivalent to the first-order necessary and sufficient optimality condition for the unique maximizer of Eq. 9.

Appendix: Robust Spectral Decomposition as a Filter Bank

The following proposition characterizes the equivalent filter banks corresponding to the robust spectral estimator:

Proposition. Let $W=rK$ for some integer r, so that ${\mathbf{F}}_n={\mathbf{F}}_1$, for all n and let F be as defined in Eq. 4. Let ${\mathbf{Q}}^{\left(\infty \right)}$ be the element-wise limit point of ${\mathbf{Q}}^{\left(\ell \right)}$. Moreover, suppose that N is large enough so that ${\mathbf{\Sigma }}_{N|N}$ converges to its steady-state value denoted by ${\mathbf{\Sigma }}^{\left(\infty \right)}$ and that each iteration of fixed-interval smoother is initialized using the steady-state value of ${\mathbf{\Sigma }}_{n|n}$ in the previous iteration. Then, the estimate from the robust spectral estimator is given by

$$\underset{\ell \to \infty }{\text{lim}}{\widehat{\mathbf{x}}}^{\left(\ell \right)}=\mathbf{G}{\mathbf{F}}^H\mathbf{y},$$ [18]

where

$$\mathbf{G}≔\left(\begin{array}{ccccc}{\mathbf{\Lambda }}^0\mathbf{\Gamma }& {\mathbf{\Lambda }}^1\mathbf{\Gamma }& {\mathbf{\Lambda }}^2\mathbf{\Gamma }& \cdots & {\mathbf{\Lambda }}^{N-1}\mathbf{\Gamma }\\ {\mathbf{\Lambda }}^1\mathbf{\Gamma }& {\mathbf{\Lambda }}^0\mathbf{\Gamma }& {\mathbf{\Lambda }}^1\mathbf{\Gamma }& \cdots & {\mathbf{\Lambda }}^{N-2}\mathbf{\Gamma }\\ {\mathbf{\Lambda }}^2\mathbf{\Gamma }& {\mathbf{\Lambda }}^1\mathbf{\Gamma }& {\mathbf{\Lambda }}^0\mathbf{\Gamma }& \cdots & {\mathbf{\Lambda }}^{N-3}\mathbf{\Gamma }\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ {\mathbf{\Lambda }}^{N-1}\mathbf{\Gamma }& {\mathbf{\Lambda }}^{N-2}\mathbf{\Gamma }& {\mathbf{\Lambda }}^{N-3}\mathbf{\Gamma }& \cdots & {\mathbf{\Lambda }}^0\mathbf{\Gamma }\end{array}\right),$$ [19]

with

$$\mathbf{\Lambda }≔{\mathbf{\Sigma }}^{\left(\infty \right)}{\left({\mathbf{\Sigma }}^{\left(\infty \right)}+{\mathbf{Q}}^{\left(\infty \right)}\right)}^{-1},$$

and

$$\mathbf{\Gamma }≔\left({\mathbf{\Sigma }}^{\left(\infty \right)}+{\mathbf{Q}}^{\left(\infty \right)}\right)\left[\mathbf{I}-rW{\left({\left({\mathbf{\Sigma }}^{\left(\infty \right)}+{\mathbf{Q}}^{\left(\infty \right)}\right)}^{-1}+rW\mathbf{I}\right)}^{-1}\right].$$

Proof 2 (sketch of proof). Consider the fixed interval smoother at the ${\ell }^{th}$ iteration of the robust spectral estimator. By expanding the estimate ${\widehat{\mathbf{x}}}_{n|N}$ in terms of ${\left({\mathbf{y}}_l\right)}_{l=1}^N$, it is not hard to show that

$$\begin{array}{c}{\widehat{\mathbf{x}}}_{n|N}={\displaystyle \sum _{s=1}^{n-1}\left[{\displaystyle \prod _{m=s}^{n-1}\left(\mathbf{I}-{\mathbf{K}}_m{\mathbf{F}}_m\right)}\right]{\mathbf{K}}_s{\mathbf{y}}_s}\\ +{\mathbf{K}}_n{\mathbf{y}}_n\\ +{\displaystyle \sum _{s=n+1}^N\left[{\displaystyle \prod _{m=n}^s{\mathbf{B}}_m}\right]{\mathbf{K}}_s{\mathbf{y}}_s}\end{array}$$ [20]

with ${\mathbf{B}}_m={\mathbf{\Sigma }}_{m|m}{\mathbf{\Sigma }}_{m+1|m}^{-1}$. Also, we have $\mathbf{I}-{\mathbf{K}}_m{\mathbf{F}}_m={\mathbf{\Sigma }}_{m|m}{\mathbf{\Sigma }}_{m|m-1}^{-1}$. In the steady state, we have ${\mathbf{\Sigma }}_{m|m}={\mathbf{\Sigma }}^{\left(\infty \right)}$ and ${\mathbf{\Sigma }}_{m|m-1}={\mathbf{\Sigma }}^{\left(\infty \right)}+{\mathbf{Q}}^{\left(\infty \right)}$, for all m. Hence, the expression for ${\widehat{\mathbf{x}}}_{n|N}$ simplifies to

$${\widehat{\mathbf{x}}}_{n|N}={\displaystyle \sum _{s=1}^N{\mathbf{\Lambda }}^{\left|s-n\right|}\mathbf{\Gamma }{\mathbf{F}}_s^H{\mathbf{y}}_s},$$ [21]

with Λ and Γ as defined in the statement of the proposition. Expressing the above expression in compact form gives the statement of the proposition.

The proposition states that the spectral estimate at window n is a tapered version of the Fourier transform of the data, where the taper at window s is given by ${\mathbf{\Lambda }}^{\left|s-n\right|}\mathbf{\Gamma }$; this can be viewed as an exponentially decaying taper in the matrix form, because the eigenvalues of Λ are bounded by 1. To illustrate this observation, assume that ${\mathbf{Q}}^{\left(\infty \right)}=q\mathbf{I}$ for some positive constant q. Then, it is not hard to verify that $\mathbf{\Lambda }=\gamma \mathbf{I}$ and $\mathbf{\Gamma }=\eta \mathbf{I}$ for some positive constants $0<\gamma \le 1$ and $\eta >0$. Then, the equivalent sliding taper applied to the data are given by the exponential taper $\eta {\gamma }^{\left|s\right|}$.

The rows of $\mathbf{G}{\mathbf{F}}^H$ form a filter bank whose output is equivalent to that of the robust spectral estimator at windows $n=\mathrm{1,2},\cdots ,N$. As mentioned before, the advantage of the weighting factor G is twofold. First of all, the weighting shapes the Fourier basis by an effectively exponential taper for higher side-lobe suppression. Second, the choice of ${\mathbf{Q}}^{\left(\infty \right)}$ from the data determines the gain of each filter; i.e., the filters corresponding to the large (small) elements of ${\mathbf{Q}}^{\left(\infty \right)}$ are likely to have a high (low) gain. Therefore, the shaping of the filters is determined by the data itself. Note that given ${\mathbf{Q}}^{\left(\infty \right)}$, we can compute ${\mathbf{\Sigma }}^{\left(\infty \right)}$ by numerically solving a Riccati equation, and form the matrix $\mathbf{G}{\mathbf{F}}^H$, the rows of which are the equivalent bank of filters corresponding to the robust spectral estimator at windows $n=\mathrm{1,2},\cdots ,N$.

This characterization of the spectral resolution of the robust spectral estimator, as well as its interpretation as a filter bank, applies to the case of ${\mathbf{Q}}^{\left(\infty \right)}$ independent of n (time); this holds for log-prior $f_1(\cdot )$ and its associated ${\mathbf{Q}}^{\left(\infty \right)}$, which is the element-wise limit of Eq. 11. The element-wise limit of Eq. 12, which corresponds to log-prior $f_2(\cdot )$, is not independent of n. Eq. 2, however, is quite general and adopts a similar form once the appropriate substitutions are made. We restricted our attention to ${\mathbf{Q}}^{\left(\infty \right)}$ independent of n to convey the key ideas.