Enzymatic turnover of macromolecules generates long-lasting protein–water-coupled motions beyond reaction steady state

Significance

The solvent in biological reactions plays an active role in protein function; however, correlating solvation dynamics with specific biological scenarios remains a scientific challenge. Here, we followed time-dependent changes in solvation dynamics using terahertz absorption spectroscopy during proteolysis of collagen substrates by a metalloproteinase. Unexpectedly, we revealed that solvation dynamics do not follow the traditional enzymatic steady-state kinetic theory but generate long-lasting protein–water-coupled motions that last longer than a single catalytic cycle and are substrate-specific. These prolonged solvation dynamics contribute to the net enzyme reactivity impacting substrate binding, positional catalysis, and product release.

Abstract

The main focus of enzymology is on the enzyme rates, substrate structures, and reactivity, whereas the role of solvent dynamics in mediating the biological reaction is often left aside owing to its complex molecular behavior. We used integrated X-ray– and terahertz- based time-resolved spectroscopic tools to study protein–water dynamics during proteolysis of collagen-like substrates by a matrix metalloproteinase. We show equilibration of structural kinetic transitions in the millisecond timescale during degradation of the two model substrates collagen and gelatin, which have different supersecondary structure and flexibility. Unexpectedly, the detected changes in collective enzyme–substrate–water-coupled motions persisted well beyond steady state for both substrates while displaying substrate-specific behaviors. Molecular dynamics simulations further showed that a hydration funnel (i.e., a gradient in retardation of hydrogen bond (HB) dynamics toward the active site) is substrate-dependent, exhibiting a steeper gradient for the more complex enzyme–collagen system. The long-lasting changes in protein–water dynamics reflect a collection of local energetic equilibrium states specifically formed during substrate conversion. Thus, the observed long-lasting water dynamics contribute to the net enzyme reactivity, impacting substrate binding, positional catalysis, and product release.

It has now been a century since the Michaelis–Menten (MM) steady-state theory provided a highly satisfactory description of the kinetic behavior of many enzymes (1, 2). The simplest kinetic mechanism with a single substrate assumes that an enzyme E combines with a substrate S to form an ES complex (known as the Michaelis complex), which undergoes an irreversible reaction to form the product P and the original enzyme. When the steady state is reached, it is assumed that the reaction rate is constant and follows the MM equation: V = k₂[S]([S] + K_m)⁻¹. This theory has been proven to be true for a wide variety of isolated enzymatic reactions in vitro (3) as well as more complicated reaction schemes involving multiple ligands and/or multisubunit enzymes (4). Recently, however, studies of enzyme dynamics together with single-molecule experiments have questioned the generality of existing kinetics steady-state laws for fluctuating enzyme systems (5–7). Steady-state kinetics were shown to depend on conformational transition rates of enzyme–substrate association, catalysis, and product release (6, 8). In addition, the kinetics of simple or isolated reactions can differ from the kinetics of network reactions in a crowded environment as present in the cell (9, 10).

Moreover, within the classical description, the contribution of the solvent in effecting catalysis is almost completely neglected, despite its potential role in mediating enzyme–substrate interactions (11). Importantly, the solvent plays an active role in various protein reactions (12–17), mediates molecular recognition (18–20), or acts as an adhesive to facilitate binding (21). Recently, Lockett et al. (22) observed that the release of water from the binding pocket was responsible for effective molecular recognition rather than the ligand structure, composition, and contact with the binding enzyme. Thus, given the role of solvation dynamics in mediating biological function and the fact that enzymes undergo dynamic conformational fluctuations along the reaction coordinates and evolution of intermediates spanning a wide range of timescales, one might ask if it is still reasonable to assume that all dynamic motions including enzyme, substrate, product, and water equilibrate on the same timescale (i.e., at reaction steady state)?

Recently, we reported the correlation between enzyme structural kinetics and protein–water-coupled motions during the formation of the Michaelis complex between a zinc-dependent protease [membrane type 1 matrix metalloproteinase (MT1-MMP)] and a short (6-mer) peptide substrate (11). Using an integrated spectroscopic approach combining stopped-flow X-ray absorption spectroscopy (XAS) and kinetic terahertz (THz) absorption spectroscopy (KITA), we showed that the protein–water-coupled motions at the enzyme active site were retarded during the formation of the Michaelis complex within the reaction steady state (11). However, in vivo, the substrates of metalloproteinases are often much more complex. For instance, collagen is a substrate of several members of the family of MMPs, and its degradation results in thermal denaturation of its triple-helical region and generation of single α-chain peptides, which form less organized products (for example, gelatin) (23). Recent NMR and crystal structures of inactive MMPs in complex with triple-helical peptides suggested that collagen degradation involves major conformational rearrangements of both enzyme and substrate to facilitate binding and catalysis (24, 25). Therefore, we chose to study the role of solvation dynamics in more complex enzymatic reactions, such as the enzymatic degradation of collagen- and gelatin-like substrates by MT1-MMP, by our established X-ray– and THz-based integrated spectroscopic approach (Fig. 1). Unexpectedly, although enzyme–substrate structural and functional motions (probed by time-resolved XAS, fluorescence, and CD spectroscopies) reached steady state, the protein–water-coupled motions (probed by KITA) equilibrated over much longer timescales, spanning beyond enzyme turnover and steady state, and behaved differently for the two substrates. This newly observed phenomenon indicates that enzymatic processing of complex macromolecules exhibits off steady-state protein–water motions, highlighting the role of solvation dynamics in contributing to the overall reaction reactivity.

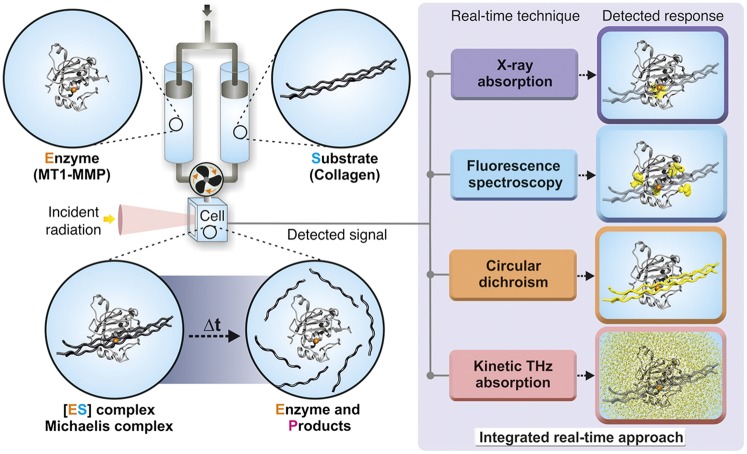
Fig. 1.

Schematic illustration of the experimental setup to measure structural kinetics and solvation dynamics of metalloenzymes. The catalytic domain of human MT1-MMP is shown in the gray cartoon (residues 114–291), and the active site zinc ion is shown in orange. The collagen-like substrate is shown in dark gray. The enzyme and substrate are mixed in a stopped-flow apparatus, and changes in different spectroscopic properties provide information regarding structural dynamic transitions of the enzyme (by fluorescence or XAS), substrate (by CD), or solvent (by KITA).

Results

FRET of Collagen Proteolysis Follows the Classical MM Theory.

We used the collagen model substrate [Gly-Pro-4-hydroxyproline (Hyp)]₅-Gly-Pro-Lys(7-methoxycoumarin-4-yl)-Gly-Pro-Gln-Gly-Cys(4-methoxybenzyl)-Arg-Gly-Gln-Lys(2,4-dinitrophenyl)-Gly-Val-Arg-(Gly-Pro-Hyp)₅-NH₂ as an optimized recognition sequence for MT1-MMP (26, 27). This substrate is biologically active and exhibits self-assembly capability to form triple-helical collagen-like monomers from its single-chain cognate peptide (13.5 kDa). The peptide was also used after heat denaturation for comparison and as a model for a single-stranded gelatin-like substrate (4.5 kDa). In this work, we will refer to the substrates as triple-helical (collagen) and single-stranded (gelatin) substrates. We performed molecular modeling of the substrates followed by docking analyses of the catalytic domain of MT1-MMP with the two substrates (details in Materials and Methods). Our docking results were compared with available NMR structures of structurally homologous MMP–collagen systems (24, 28), showing that the collagen-like substrates exist in either stretched or bended configurations (SI Appendix, Fig. S1). On the contrary, the structure of the gelatin substrate forms a random coil structure, typical of gelatin. Thus, the two substrates exhibit different molecular organizations.

Steady-state analysis ([S] >> [E]) of the degradation of the two substrates was performed using the recombinant MT1-MMP catalytic domain and the FRET substrates as described previously (27). The relationship between the reaction initial velocities and substrate concentrations was found to be hyperbolic and fitted to the MM equation (SI Appendix, Fig. S3). The obtained Michaelis constants (K_M values) for the triple-helical and single-stranded substrates are 6.51 ± 1.10 and 3.76 ± 0.54 µM, respectively. These values indicate that the binding affinity for the triple-helical substrate is twofold lower compared with the single-stranded substrate owing to the bulky structure of the former substrate. Nevertheless, the obtained reaction turnover numbers (k_cat values) for the triple-helical and single-stranded substrates are 3.38 ± 0.25 and 3.00 ± 0.32 s⁻¹, respectively, indicating that the lifetime of a single kinetic cycle is similar for both model substrates: ∼400 ms. The similarity of k_cat values for triple-helical and single-stranded model substrates suggests that, despite their different binding affinities to MT1-MMP, the rate-limiting step of the enzymatic reaction does not depend on substrate affinity and that the enthalpic and entropic contributions are compensated.

Structural Conformational Transitions During Turnover Equilibrate Before Steady State.

To quantify protein and protein–water functional conformational transition within the different kinetic phases of the enzymatic reaction, we developed an experimental scheme correlating several time-resolved spectroscopic techniques. This protocol enables studying of a given enzymatic reaction in solution while quantifying enzyme–substrate–water transitions by different spectroscopic modalities (Fig. 1). To identify specific structural pathways, we measured proteolysis of the model substrates under pre–steady-state conditions using a stopped-flow apparatus. A surplus of substrate (1:20 E:S ratio) was used to avoid enzyme and substrate diffusion processes (11). In this setup, the FRET substrates are mixed with MT1-MMP, and the changes in fluorescence intensities are recorded (Fig. 2A). Our results showed that the reaction can be divided into three phases: (i) kinetic lag phase between 0 and 40 ms, during which no change in fluorescence was detected; (ii) kinetic burst phase between 40 and 400 ms, during which the first catalytic reaction takes place as well as product release; and (iii) steady-state phase. Our analysis showed that triple-helical and single-stranded substrates exhibit similar kinetic lag phases of ∼40 ms, during which the Michaelis complex is formed as shown previously (11). The increase in fluorescence reached steady state after ∼400 ms for both substrates, which is consistent with the obtained lifetimes of a single catalytic cycle derived from the values of k_cat (SI Appendix, Fig. S3). Thus, the enzymatic conversion of the substrate into product reaches steady state within the catalytic turnover (400 ms).

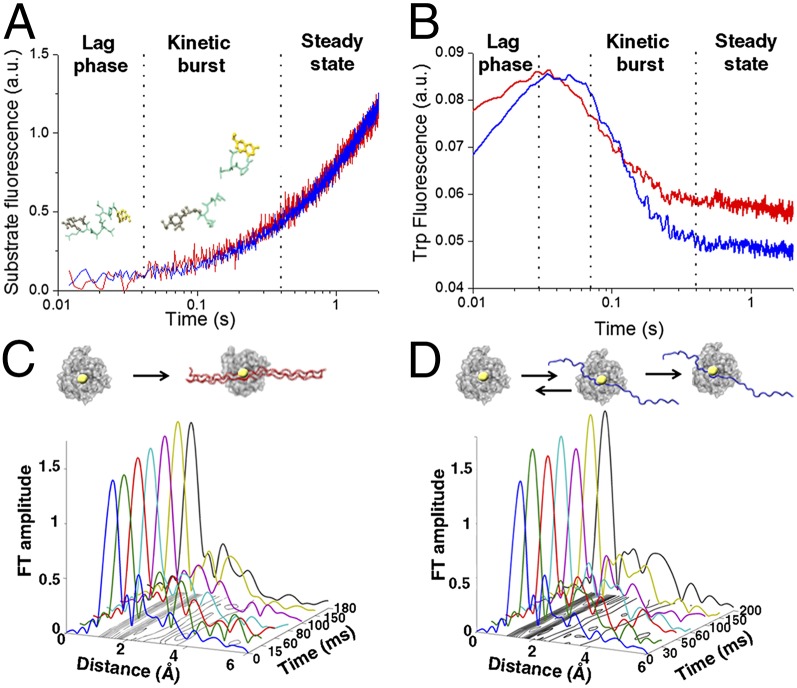
Fig. 2.

Equilibration of enzyme–substrate conformational transitions before steady state. (A) Transient kinetics fluorescence analyses showing the fluorescence emission after mixing MT1-MMP and FRET triple-helical (blue) and single-stranded (red) substrates in a stopped-flow apparatus (λ_excitation = 340 nm; λ_emission > 380 nm). (B) Time-dependent changes in intrinsic Trp and Tyr fluorescence of MT1-MMP measured after mixing MT1-MMP with triple-helical (blue) and single-stranded (red) substrate with λ_excitation = 295 nm and λ_emission = 320 nm. The experiments were conducted under identical conditions to A. (C and D) XAS analysis shows differences in interactions with the zinc ion and the two different model substrates. The X-ray absorption data are presented in the form of Fourier transform (FT) spectra to provide the radial distribution of the atoms within the first and second coordination shells of the catalytic zinc ion in MT1-MMP during hydrolysis of (C) triple-helical or (D) single-stranded substrates. The shape and amplitude of the Fourier transform peaks are directly related to the type and number of amino acid residues in the immediate vicinity of the zinc ion. The increase in the first shell amplitude is correlated with an increase in coordination number. (C) A stable pentacoordinated zinc peptide intermediate is rapidly formed during hydrolysis of the triple-helical substrate. (D) On the contrary, transient binding of the single-stranded substrate is detected before the formation of the stable Michaelis complex.

Time-resolved tryptophan fluorescence (λ_ex = 290 nm) of MT1-MMP during proteolysis was used to study the conformational transitions of the enzyme during this process. MT1-MMP contains four Trp and seven Tyr residues (29), whereas the substrates have neither of these amino acids. Because these residues are abundant across the surface of the enzyme and also, in proximity to the substrate binding site (29), the substrate-specific contributions to the Michaelis complex formation could not be analyzed separately from conformational changes of the enzyme at the same kinetic phase. No change in intrinsic fluorescence was observed either when enzyme or substrate was mixed with buffer or during buffer mixing alone. Thus, the changes reflect specific transitions in the conformation of the enzyme occurring during enzyme–substrate association, catalysis, and product dissociation. Fig. 2B shows that the reaction with the triple-helical substrate induced an increase in fluorescence for 30 ms, which decayed exponentially until ∼400 ms, whereas the fluorescence after the reaction with the single-stranded substrate increased until 70 ms and then exponentially decreased until reaching steady state at ∼400 ms. These results are in line with previously reported analyses, suggesting that conformational changes of MT1-MMP take place during Michaelis complex formation for triple-helical collagen model peptides (24, 25). The net change in tryptophan fluorescence (Fig. 2B) was higher for the single-stranded substrate, indicating a more pronounced conformational rearrangement of the enzyme scaffold required to promote effective Michaelis complex formation while accommodating the substrate.

To quantify correlated secondary structural changes of the triple-helical substrate on hydrolysis, we used time-resolved CD spectroscopy. Changes in molar ellipticity at 205 nm during hydrolysis of the triple-helical substrate could be assigned to two kinetic phases (SI Appendix, Fig. S4): an initial increase in molar ellipticity until 30 ms followed by an exponential decay until ∼400 ms. The duration of the first kinetic phase coincides very well with the duration of the kinetic lag phase of the enzymatic reaction (Fig. 2A) and the changes in the enzyme intrinsic fluorescence (Fig. 2B). This result indicates that rapid unwinding of the triple-helical substrate occurs during the reaction lag phase. This observation supports the two-step mechanism for the hydrolysis of collagen-like substrates, namely unwinding of the triple-helix structure before binding of a single chain to the enzyme active site (30).

Stopped-flow freeze-quenched XAS was used to structurally characterize the binding of the model substrates to the catalytic zinc ion of MT1-MMP. This technique provides time-dependent 3D distance and electronic information on the local structure and the oxidation state of the metal ions’ nearest environment (up to 5 Å) at atomic resolution. The mechanism of substrate hydrolysis involves direct coordination of the substrate to the catalytic zinc ion of MT1-MMP by a specific carbonyl group followed by a nucleophilic attack of a zinc-coordinated water molecule on the carbonyl group (31). Here, recombinant MT1-MMP was rapidly mixed with the peptide substrates, and the reaction mixture was freeze-quenched at selected time points along the reaction coordinates as described previously (11, 31). During the interaction between the enzyme and the triple-helical substrate, we detected a rapid increase in the magnitude of the first coordination shell peak at 1- to 2-Å distance to the catalytic zinc ion (Fig. 2C). This change was attributed to direct coordination of the substrate to the zinc ion to form a stable pentacovalent intermediate complex (SI Appendix, Table S1) (the Michaelis complex), which was shown previously for this enzyme during interaction with a 6-mer single-stranded peptide substrate (11). Thus, hydrolysis of the triple-helical substrate follows an initial rapid formation of a pentacovalent Michaelis complex at the zinc ion during the kinetic lag phase before peptide hydrolysis. Importantly, beyond 15 ms, we obtained a similar coordination number for all time points as well as identical distances between the zinc ion and its coordinating atoms, indicating a strong and stable enzyme–substrate complex.

Using the same protocol, substantial transitions of the zinc coordination number during the interaction with the single-stranded substrate (Fig. 2D) could be detected. Specifically, fluctuations in the first coordination shell peak amplitudes were detected during the kinetic lag and the burst phases (up to 70 ms), which are correlated with the transition from tetra- to pentacovalent zinc peptide intermediates (SI Appendix, Table S2). A stable pentacovalent complex, required for peptide hydrolysis, evolved only after 200 ms. This observation implies that, unlike the triple-helical substrate, the single-stranded substrate undergoes transient-specific and nonspecific binding processes to the enzyme active site before adopting the substrate conformation required for efficient catalysis. These differences propose that degradation of structurally different substrates is accompanied by different structural kinetic events that are required for effective catalysis, but all transitions equilibrate within the enzymatic kinetic burst phase before the system reaches steady state.

Changes in Enzyme–Substrate–Water-Coupled Motions Persist Well Beyond Reaction Steady State.

We next set out to follow the overall changes in protein–water-coupled motions as the reaction proceeds using THz spectroscopy (11, 32). KITA combines a THz time domain spectrometer in the frequency range of 0.3–1 THz and a stopped-flow mixer, allowing a direct detection of the changes in THz transmission during kinetic processes (Fig. 1). KITA measures changes in the collective subpicosecond motion of water networks. The observed signal represents changes in the water–hydrogen bond dynamics occurring during the different reaction kinetic phases. The enzyme was mixed with either the triple-helical substrate or the single-stranded substrate in the stopped-flow apparatus under the same conditions as the fluorescence experiments, and the transmitted amplitude of the THz electric field (E_Mix) at the THz pulse maximum was recorded as a function of time. Mixing of buffer or free enzyme solution was used as a control measurement. SI Appendix, Fig. S5 depicts the KITA(t) signal resulting from degradation of the different substrates. At 250 ms, the absorption of the solution of both enzyme–substrate systems is decreased compared with the buffer. Interestingly, we could observe that the THz absorption reaches transient minima at timescales above catalytic turnover times in both systems. We, thus, set out to record the time-dependent changes in the THz absorption up to 9 s. During this timescale, the triple-helical substrate is thought to be initially degraded successively into two one-half helical chains followed by disassembly processes into separated single chains, whereas the single-stranded substrate is directly degraded into two separated chains (Fig. 3A). According to the derived MM turnover numbers (SI Appendix, Fig. S3), the reaction was expected to be completed within ∼6 s. However, as can be observed in the time-resolved fluorescence studies, the product formation is still ongoing even after 6 s (Fig. 3 B and D). KITA measurements during degradation of the triple-helical substrate along this timescale revealed a 5–10% decrease in the THz absorption compared with buffer (Fig. 3C). Remarkably, we could not observe equilibration to buffer solvation dynamics over this timescale for this substrate. On the contrary, the THz absorption detected during degradation of the single-stranded substrate equilibrated to buffer after 5 s, showing a different solvation dynamic kinetic trajectory (Fig. 3E). Thus, the behavior of the solvent was found to be substrate-specific and correlated with long-lasting structural transitions during product formation.

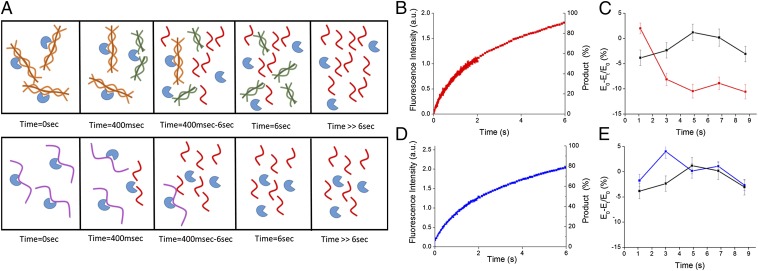
Fig. 3.

Perturbation of the protein–water-coupled motions beyond reaction steady state. (A) Schematic description of the enzymatic reaction and product formation. Time = 0 s, initial enzyme–substrate interaction; Time = 400 ms, end of the first catalytic cycle; Time = 400 ms to 6 s, multiple turnover of the substrates; Time = 6 s, reaction ends according to MM turnover rates (single-chain products are fully formed, whereas triple-helix products require additional disassembly); T >> 6 s, full disassembly of the triple helix to single-chain products. This description is based on prior studies (38). (B and D) Time-resolved fluorescence data for (B) the triple-helical substrate and (D) the single-stranded substrate. Product formation was estimated according to the derived turnover number of the reaction. (C and E) KITA data collected during hydrolysis of (C) triple-helical substrate (red) and (E) single-stranded substrate (blue) and (C and E) data of mixing-only buffer (black). Each data point has been averaged over 20–30 measurements with a time interval of 300 ms.

To examine the contribution of the free substrate to the KITA signal, we measured the THz absorption of substrate solutions at steady state using a p-Germanium THz laser source (33). We found that the THz absorption of both substrate solutions is comparable without any statistically significant differences (SI Appendix, Fig. S6). These results indicate that the fully hydrated substrates exhibit similar hydration dynamics in steady state and thus, are not the main contributors to the detected long-lasting changes in THz absorption. Thus, the detected changes in the KITA signal are a direct result of enzymatic catalysis. Because the single-stranded substrate does not undergo additional product disassembly, we can correlate the initial prolonged changes in hydration dynamics with enzymatic proteolysis, whereas the even longer-lasting effect in case of the triple-helical substrate can additionally be attributed to a more complex process of product disassembly (Fig. 3A).

Formation of the Hydration Funnel Is Substrate-Specific.

To ascribe the changes in protein–water-coupled motions to specific reaction phases, we have conducted molecular dynamics simulations for a total of ∼160 ns that provide a microscopic picture of water dynamics at a specific scenario of the reaction (single shots) (SI Appendix, SI Materials and Methods) (32). We selected starting configurations that are representative of two molecular scenarios as the substrate approaches the catalytic zinc ion and is located at different distances d between the zinc ion and the closest heavy atom of the substrate: (i) the free enzyme (d ≥ 7 Å) and (ii) the enzyme–substrate complex (i.e., the substrate approaching the enzyme active site; 2 Å ≤ d ≤ 6 Å). The hydrogen bond rearrangements in water (breaking and reformation of hydrogen bonds) occurring on the picosecond timescale have been characterized by water–water HB time correlation functions and their hydrogen bond lifetime τ_HB (32). The hydration water dynamics were analyzed in the vicinity of the substrate and the enzyme as well as within the active site.

For the two model substrates, we observed a similar retardation of water motions in the hydration shells of the enzyme and substrates as was observed before for water molecules solvating the enzyme and a small (6-mer) peptide substrate (11) (Fig. 4 and SI Appendix, Fig. S7). Similar hydrogen bond dynamics were found for water molecules solvating both of the substrates and also found by the THz absorption measurements of the free substrates (SI Appendix, Fig. S6). A more pronounced retardation of HB rearrangement dynamics was detected for water molecules at the active site of the enzyme in the unbound scenarios (8 ps for the free MMP–triple helix and 9 ps for the free MMP–single strand). However, when the substrates approached closer to the zinc ion (i.e., in the enzyme–substrate complexes), we observed a substrate-specific additional increase in the water HB lifetime for the water molecules solvating the active site of the enzyme. Specifically, this effect was more pronounced when the enzyme was bound to the triple-helical substrate (>20 ps) rather than the single-stranded substrate (14.5 ps). Thus, the formation of the hydration funnel (i.e., the gradient of retardation in hydrogen bond dynamics) is substrate-specific and differs in magnitude (Fig. 4).

Fig. 4.

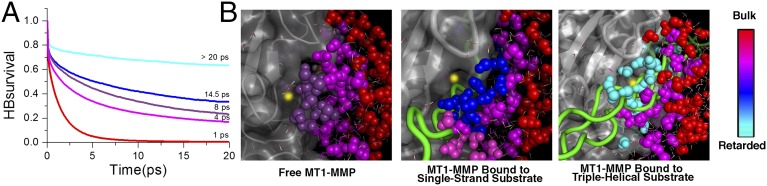
Effect of substrates on the gradients of coupled water motions. (A) Changes in hydration dynamics on Michaelis complex formation. Shown are the averaged hydrogen bond lifetimes τ_HB of bulk water (red line; distance to closest protein atom > 10 Å), water molecules solvating MT1-MMP (magenta line; distance to closest enzyme atom < 3 Å), and water solvating the zinc ion (distance to catalytic zinc ion < 6 Å) in the unbound MMP–triple-helical substrate system (purple line), the MMP–single-stranded substrate system (blue line), and the MMP–triple-helical substrate system (cyan line). (B) A gradient of water motions [from retarded water molecules (cyan) to bulk (red)] is detected in the unbound MT1-MMP when the substrates are at a distance d of ∼7 Å from the zinc ion. When the substrates approach closer to the zinc ion (d ∼ 4.9 Å), an additional decrease in the water HB lifetime at the active site for both substrates is observed. The gradient of water motions depends on the substrate: τ_HB is steeper when the MT1-MMP is bound to the triple-helical substrate (Right) than when it is bound to the single-stranded substrate (Center).

To examine whether product formation affects the hydration funnel, we conducted a molecular dynamics simulation of the complexes formed between the enzyme and the initial products. No significant changes in water dynamics at the water molecules solvating the active site were detected on product formation (SI Appendix, Fig. S8). However, we could detect a difference between the water molecules solvating the active site when bound to collagen vs. gelatin products. In general, we have to state that molecular dynamics simulations are not able to quantitatively rationalize the experimentally observed differences in the THz absorption data for the two investigated systems over a timescale of milliseconds. However, qualitatively, we find clear significant differences for water retardation at the active site. Furthermore, when we analyzed the predicted vibrational density of states, we found that the single-stranded substrate shows an increased amount of lower energies modes as expected for a more flexible structure compared with the triple-helical substrate (34). Most importantly, we observed a correlation between the vibrational mode distribution of the water solvating the catalytic site of the respective enzyme–substrate complex and the low-lying vibrational modes of each substrate (involving a blue shift of the water frequencies compared with bulk water). This correlation indicates a strong coupling between the substrate and the water, which is even more pronounced for the triple-helical substrate. Altogether, these results indicate that the main contribution to the change in THz signal comes from the formation of the different MM complexes between the enzyme and the collagen or gelatin substrates, highlighting the importance of the specific substrate structure for effective binding, which was also shown by our XAS analysis.

Discussion

The current view of the solvent in biological reactions has been revised during the last two decades from a passive medium in which proteins are embedded to an active key player in protein function (35). However, we still do not fully understand the role of water for complex biological processes because of the technical challenges associated with probing real-time changes in water dynamics during reaction. Here, we describe an unprecedented phenomenon, in which the changes in protein–water-coupled motions detected by kinetic THz measurements arising during proteolysis persisted beyond a single catalytic cycle during the interaction between a metalloenzyme and complex collagen-like substrates. On the contrary, the enzyme–substrate structural kinetics detected by stopped-flow XAS were equilibrated at steady state. Because water relaxation, in general, is a fast process, each point in the KITA signal represents a new equilibrium state during the progressive conformational changes exhibited by the complex molecular scenarios shown in Fig. 3A. Thus, each reaction trajectory represents a new set of MM complexes exhibiting different modes of molecular recognition in terms of electrostatic potential and hence, protein–water-coupled motion/dynamics. Thus, changes in hydration dynamics equilibrate along the rugged reaction coordinates after local enzyme and substrate conformational transitions as well as natural/intrinsic water retardation mechanisms as revealed by our integrated analyses. Because the solvation dynamics last beyond the single catalytic cycle, the reactive state of the entire system is prolonged. Therefore, the observed long-lasting water dynamics contribute to the net reactivity, which lasts beyond a single catalytic cycle, keeping the enzymatic reaction live owing to long-lasting protein–water dynamics.

Furthermore, this phenomenon is substrate-specific, having a more pronounced change in the protein–water-coupled motions detected by KITA during degradation of the triple-helix peptide. In addition, the molecular dynamics simulations revealed substrate-specific retardation of the hydrogen bond dynamics of water in the vicinity of the active site and the substrate, giving rise to different hydration funnels. We have previously shown that this water retardation mechanism is critical to the formation of the MM complex (11). Thus, the steeper hydration funnel formed between the enzyme and the triple-helix substrate enables more effective complex formation than with the single-stranded substrate. This mechanism could also explain why, despite the fact that the affinities are lower for the triple-helical substrate than the single-stranded substrate, the binding of the triple-helical substrate to the zinc ion is found to be very effective, as was also detected by the XAS analysis. We should point out that an increase in retardation also lowers the entropic cost of binding. On the contrary, the hydration funnel formed between the single-stranded substrate and the enzyme is shallower. Here, we observe a less-effective molecular recognition process, which was also indicated by the transient binding of the substrate to the zinc ion. Thus, the evolutionary optimized complex molecular architecture of the collagen triple helix is critical for water-mediated effective binding, which might be a very general phenomenon in molecular recognition.

The phenomenon revealed here and the dependence of water dynamics on the complexity of given substrates indicate that the role of solvation dynamics in biology is much more complicated than has been thought initially. Therefore, models of enzymes kinetics as well as the steady-state theory should include solvation dynamics effect beyond reaction steady state as an integral part of the overall reaction coordinates.

Materials and Methods

Expression and Purification of MT1-MMP.

The catalytic domain of human MT1-MMP (residues 114–290) was expressed and purified as described previously (29).

Synthesis of Collagen- and Gelatin-Like Substrates.

The FRET peptide (Gly-Pro-Hyp)₅-Gly-Pro-Lys(7-methoxycoumarin-4-yl)-Gly-Pro-Gln-Gly-Cys(4-methoxybenzyl)-Arg-Gly-Gln-Lys(2,4-dinitrophenyl)-Gly-Val-Arg-(Gly-Pro-Hyp)₅-NH₂ was synthesized as described previously (26). Nonfluorogenic peptide substrates (for XAS experiments) were synthesized by Genscript. The single-chain gelatin-like substrate was generated by heating the triple-helical peptide at 60 °C for 10 min followed by immediate cooling on ice until use.

Steady-State Kinetics.

The MM kinetic parameters of the enzymatic reactions were determined at 25 °C by monitoring the fluorescence intensity on degradation of the fluorogenic peptides. The fluorescence emitted at λ_em = 400 nm was monitored after excitation at λ_ex = 340 nm as described by Lauer-Fields et al. (27). The standard assay mixture contained 50 mM Tris buffer at pH 7.5, 100 mM NaCl, 5 mM CaCl₂, and 0.05% (vol/vol) Brij. K_m and k_cat values were obtained by determining the reaction initial velocities (V_i) at increasing substrate concentrations (by linear fit to less than 10% of the data), plotting [S] against V_i, and fitting the data to the MM equation (V_i = V_max [S] (K_m + [S])^–1.

Transient Fluorescence and Tryptophan Fluorescence Kinetic Studies.

To follow the initial catalytic events during a single catalytic cycle, we used a stopped-flow instrument (SX18; Applied PhotoPhysics). Kinetic assays were conducted at 25 °C in assay buffer without Brij under multiple turnover conditions ([S] >> [E]). The activity of MT1-MMP was initiated by rapid mixing of 1 μM MT1-MMP with 20 μM FRET substrate and monitored after the fluorescence increase at λ_em > 380 nm. Under these conditions, the reaction rate is not diffusion-limited. Changes in tryptophan fluorescence on mixing of enzyme and substrates under identical experimental conditions were followed using λ_ex = 295 nm in a stopped-flow spectrophotometer (Applied PhotoPhysics) with an instrument dead time of 10 ms.

Freeze Quench Sample Preparation.

MT1-MMP was concentrated by ultrafiltration in 20-mL Vivaspin units (10-kDa cutoff; Vivascience AG) to a final concentration of 400 μM. MT1-MMP and nonfluorogenic peptides were mixed at a 1:4 ratio (enzyme:substrate) and freeze-quenched in liquid nitrogen. Freeze quench was carried out in aluminum sample holders (10 × 5 × 0.5 mm³) covered with Mylar tape using the BioKine SFM-300 freeze-quench module (SFM-300; Bio-Logic-Science Instruments SA). Distinct time points for freezing were chosen to be within a single catalytic cycle (0–200 ms). To avoid thermal disorder, which could affect the XAS data, frozen samples were kept in liquid nitrogen at 77 K until the XAS measurements were conducted at the synchrotron.

XAS Data Collection and Analysis.

XAS data collection was done at the National Synchrotron Light Source (Brookhaven National Laboratory, Beamline X3B). The spectra were recorded at the zinc K edge in the fluorescence geometry at low temperature (40 K). The beam energy was defined using a flat silicon monochromator crystal cut in a (111) orientation. The incident beam intensity I₀ was recorded using an ionization chamber. The fluorescence intensity was recorded using a 13-element germanium detector. To calibrate the beam energy, the transmission signal from a zinc foil was measured with a reference ion chamber simultaneously with fluorescence. Several scans (5–13) of each sample were collected and averaged. Data processing and analysis were done as described before (11). The XAS fit parameters were iteratively varied and fixed to examine the stability of each fit. Specifically, the E₀ shifts were varied, whereas the distances and Debye–Waller factors were guessed. Data were fit up to 3.3 Å, including the first, second, and third coordination shells.

THz Data Collection and Analysis.

MT1-MMP activity was initiated by 1:6 (vol/vol) mixing of enzyme and substrate solutions in assay buffer using a 40-μL stopped-flow cell (Unisoku). The final concentrations after mixing were 20 μM MT1-MMP and 400 μM substrate solution, keeping the [E:S] ratio at 1:20. The THz time-domain spectrometer generates terahertz pulses (0.3–1.0 THz) with a repetition rate of 1 GHz. Two sets of kinetic measurements consisting of 20–30 single kinetic measurements were acquired. The obtained time-dependent KITA(t) signal was defined as

$$KITA\left(t\right)=\frac{E_{\text{THz}}\left(0\right)-E_{\text{THz}}\left(t\right)}{E_{\text{THz}}\left(0\right)}.$$

SI Appendix provides a more detailed description.

Molecular Dynamics Simulations.

Molecular dynamics simulations were carried out using the GROMACS package (36). The Chemistry at Harvard Molecular Mechanics CHARMM27 force field (37) was applied for the enzyme and the substrates, and the TIP3P force field was used for water. Equilibration was followed by 20-ns simulations of each system at constant volume and temperature. Ten snapshots were taken every 2 ns from these runs. The snapshots were used as starting points for microcanonical simulations, which were used for data evaluation. These simulations were extended to 100 ps in length. The atomic positions and velocities, saved every 2 fs, were collected for the analyses of water dynamics. A more detailed description is in SI Appendix.