Power transduction of actin filaments ratcheting in vitro against a load

Significance

How the continuous polymerization of actin filaments pushes the cell membrane forward in migrating cells is an intriguing issue that has yet to be fully understood. Molecular mechanisms were proposed, but testing them experimentally is a challenge, due to hardly accessible length scales and to the influence of regulatory proteins constantly changing the mechanical properties of polymerizing filaments. We present an experimental setup designed to minimize the number of parameters influencing filament growth to focus on the mechanism of force generation. We demonstrate that it is consistent with the Brownian ratchet model. Furthermore, we define a criterion for cell migration efficiency and quantify the number of filaments that need to push the membrane to maximize this efficiency.

Abstract

The actin cytoskeleton has the unique capability of producing pushing forces at the leading edge of motile cells without the implication of molecular motors. This phenomenon has been extensively studied theoretically, and molecular models, including the widely known Brownian ratchet, have been proposed. However, supporting experimental work is lacking, due in part to hardly accessible molecular length scales. We designed an experiment to directly probe the mechanism of force generation in a setup where a population of actin filaments grows against a load applied by magnetic microparticles. The filaments, arranged in stiff bundles by fascin, are constrained to point toward the applied load. In this protrusion-like geometry, we are able to directly measure the velocity of filament elongation and its dependence on force. Using numerical simulations, we provide evidence that our experimental data are consistent with a Brownian ratchet-based model. We further demonstrate the existence of a force regime far below stalling where the mechanical power transduced by the ratcheting filaments to the load is maximal. The actin machinery in migrating cells may tune the number of filaments at the leading edge to work in this force regime.

The actin cytoskeleton forms a signal-responsive protein system made of filaments that undergo constant remodeling via directional assembly and disassembly processes. At the leading edge of a migrating cell, protrusive force results from insertional polymerization of actin filament barbed ends against the membrane, pushing it forward (1, 2). A wealth of regulatory proteins adapts the organization of the filaments and their mechanical properties to the movement the cell needs to make. At the single filament level, Hill was the first to propose that the free energy of polymerization could be transduced into mechanical work against the membrane (3). Oster and colleagues transcribed Hill’s conceptual model into a mechanistic one coined Brownian ratchet (4), later refined in the tethered ratchet (5). They showed that a single filament can push against a load because thermal fluctuations of either the load (4) or the filament (5) allow for stochastic insertion of monomers at the polymerizing tip. The amplitude of the fluctuations are force dependent, making the elongation velocity of the filament force dependent as well. The whole force-velocity profile of a single actin filament was never measured experimentally. However, the stalling force of a filament, at which the elongation velocity drops to zero, could be estimated to a few piconewtons (6–8). Comparatively, forces of a few nanonewtons are required to stall the migration of cells (9, 10) or Listeria comet tails (11). This difference of three orders of magnitude points to the need for a large number of cooperating filaments to generate high forces in protrusive structures. Exploring the cooperation within an assembly of filaments polymerizing together against a load remains a hard task for experimentalists. Actin gels (12–14) or brushes (15) have been reconstituted in vitro to measure the amount of force they can generate. In these complex structures, regulatory proteins can cause tethering of the filaments to the load (14), rearrangements under force (16), or variations of filaments number in reaction to force (17). These phenomena shed light on the strong influence of regulatory proteins on force production but impede to draw information on the physical mechanism of force generation.

Here we present an experimental setup that was designed to closely resemble the conceptual view of an array of about 100 independent filaments polymerizing perpendicularly to a load, their tip remaining nontethered to that load. Because the number of parameters affecting the force generation is minimal, we are able to concentrate on the physical interaction of filaments with the load and show that it is compatible with the Brownian ratchet. However, if the Brownian ratchet model is relevant to describe force generation at the single filament level, it gives no information about the collective behavior of the filaments population. This collective aspect of force production is further developed using an analytical model, revealing that filaments cooperation is optimal in a specific regime which ensures maximum transduction of mechanical power to the load.

Experimental Design

We use 3-μm-diameter superparamagnetic beads as a tool to simultaneously manipulate actin filaments, apply forces to them, and measure their reaction to force. The beads are functionalized with a controlled density of gelsolin molecules that act as polymerization primers inducing pointed-end growth of the actin filaments. On applying a magnetic field, a magnetic dipolar attraction force is induced between the beads and holds them organized into chains. Some of the particles in the chain are not coated with primers. These interspersed probe beads provide rigid surfaces against which actin filaments have to push to elongate, thus mimicking a protrusive structure (Fig. 1A). When the magnetic field is turned off, the probe beads freely diffuse out of the magnetic chains. By measuring the magnetic field and the interparticle distance within a pair composed of a probe bead and a primer coated one, the magnetic force opposed to the filaments can be calculated. According to the action-reaction principle, it is equal to the actin growth pressure (Materials and Methods). In the following, we call surface-to-surface distance the gap between actin covered beads and probe beads, averaged over all the pairs in a magnetic chain. Force measurements based on this technique have been successfully used to study electrostatic forces (18), the stiffness of DNA molecules (19), or the elasticity of cross-linked actin gels (20).

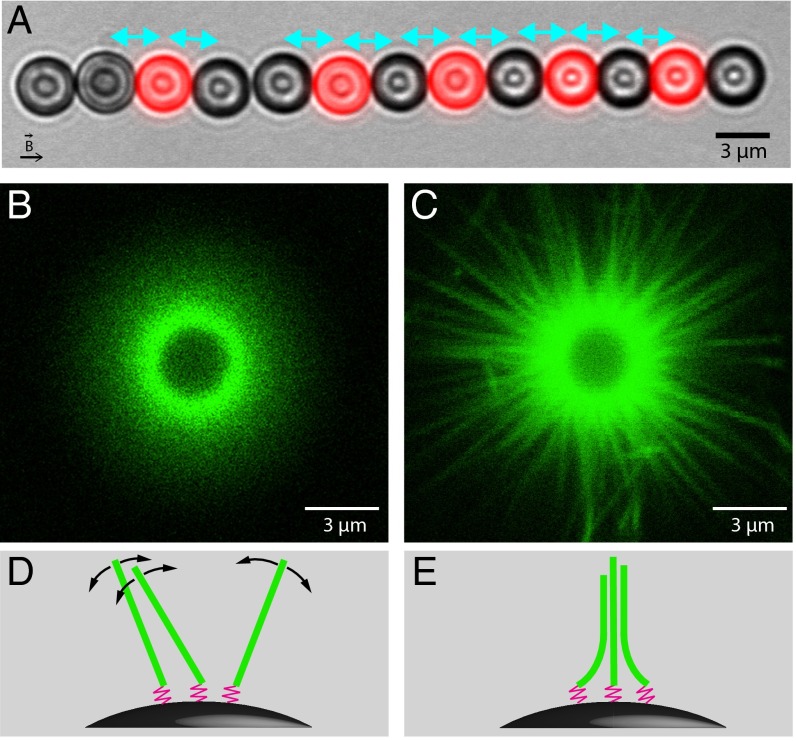
Fig. 1.

(A) Composite optical microscopy image of a typical experiment. Here, actin polymerizes from primer coated beads (black) against fluorescently labeled probe beads (red) under a magnetic force of 4.6 pN (2 μM actin and 2 μM fascin). Cyan arrows indicate the pairs considered for analysis. After 11 min of polymerization, the average surface-to-surface distance is 0.30 μm. (B and C) Differences in the organization of actin filaments caused by fascin. Fluorescent filaments growing on a nonfluorescent bead without magnetic field are observed by confocal microscopy. Images are taken in the equatorial plane of the bead after 3 h of polymerization of (B) 6 μM actin; (C) 6 μM actin and 2 μM fascin. (D and E) Schemes of the organization of the filaments (green) anchored to the surface of magnetic beads by flexible primers (pink) corresponding, respectively, to B and C.

Our experiments are designed to ensure that actin nucleation in bulk is negligible, which is achieved by working close to the actin critical concentration in low salt conditions and by keeping the duration of the experiments within a few tens of minutes. We thus assume that actin polymerization only occurs on the beads. Because the concentration of beads is very low, depletion of the actin monomer pool is negligible, and growth rates remain constant throughout each experiment. The corresponding velocity of free elongation in solution is $v_o=\delta \left(k_{\text{on}}C-k_{\text{off}}\right)=0.42\hspace{0.5em}\text{nm}/\text{s}$, where δ is the size of a monomer, C is the actin monomer concentration, and $k_{\text{on}}C$ (respectively, $k_{\text{off}}$) is the rate of monomer attachment (respectively, detachment) at the tip of a polymerizing filament (Materials and Methods). We check later in this article (Fig. 2) that when filaments are subjected to very small forces, their elongation velocity v tends toward $v_o$.

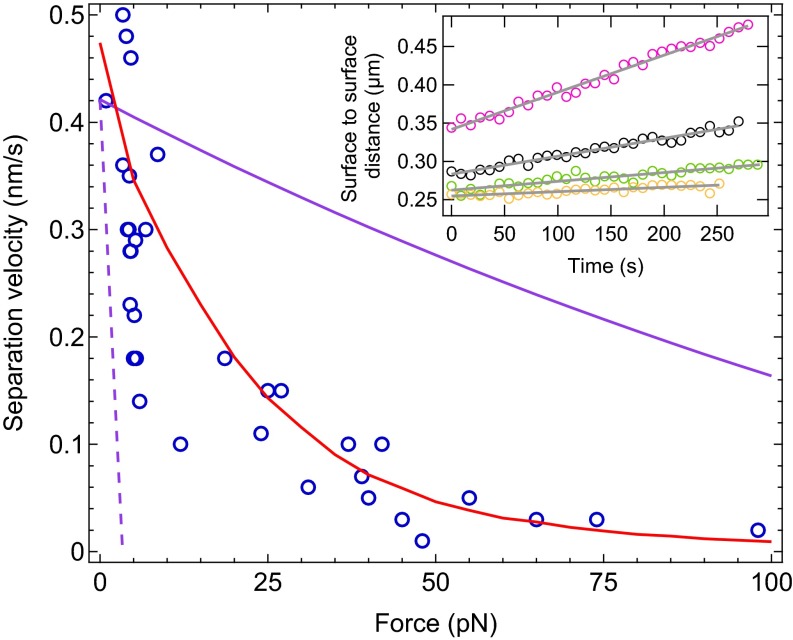
Fig. 2.

Force-velocity profile of the filaments. Each experimental data point (blue circles) corresponds to a single experiment with 2 μM actin and 2 μM fascin. Experimental data can be well reproduced by numerical simulation with $N=130$ filaments (red line). This force-velocity profile is intermediate between perfect mechanical work sharing $v=\delta \left(k_{\text{on}}C{e}^{-\frac{F\delta }{N{k}_{\text{B}}T}}-k_{\text{off}}\right)$ (plain purple line) and no mechanical work sharing $v=\delta \left(k_{\text{on}}C{e}^{-\frac{F\delta }{k_{\text{B}}T}}-k_{\text{off}}\right)$ (broken purple line). (Inset) Reproduction of the experiments performed to obtain four of the data points in the force-velocity profile. A linear fit (gray line) to the time evolution of the surface-to-surface distance is performed while the force is kept constant: pink circles, F = 3.9 pN, v = 0.48 nm/s; black circles, F = 4.5 pN, v = 0.23 nm/s; green circles, F = 24 pN, v = 0.11 nm/s; orange circles, F = 98 pN, v = 0.02 nm/s.

Gelsolin molecules are anchored to the beads via a 3-nm spacer arm (Materials and Methods) acting as a hinge around which filaments can freely pivot (Fig. 1D). In previous work (21), we demonstrated that the loss of rotational freedom of the filaments close to a neighboring bead can generate forces whose origin is entropic. We called this force generation mechanism the entropic model. However, such a soft structure in which filaments can rearrange by rotation is not likely to form in vivo where cytoskeleton filaments are generally cross-linked or bundled.

To make our system more realistic, our assay is here supplemented with fascin, a filament bundling protein present at a high concentration in filopodia. The effect of fascin on the organization of the filaments in our setup is visualized by confocal microscopy with fluorescent actin growing on a nonfluorescent isolated bead. In the absence of fascin (Fig. 1B), single filaments cannot be resolved because of rotational fluctuations around their anchoring point (Fig. 1D and SI Text). However, in the presence of fascin, static bundles are clearly observed (Fig. 1C). This presence of bundles is consistent with an energetic balance (SI Text and Fig. S1) showing that in our geometry, it is favorable for filaments to form bundles with fascin, even though they have to bend slightly for bundling to occur (Fig. 1E). It is thus reasonable to assume that no individual filament coexists with the bundles. Authors have observed that for a molar ratio [fascin]/[actin] > 0.25, which is the case here, the number of filaments in a bundle saturates to 20 (22, 23). Because about 45 bundles are visible in the image of Fig. 1C and assuming that the image depth of field is 1 μm, the total number of filaments per bead $N_{\text{tot}}$ can be estimated to be 16,000.

When the actin bundles polymerize from the surface of magnetic beads in a chain, the surface-to-surface distance is increasing with time. The relationship between the bead separation velocity that we measure and the filament elongation velocity that we seek to study must be clearly established. For that, we need to ensure that no buckling, reorganization, or damage occurs on exposure to force applied with magnetic probe beads. We first submit the bundles to rapid force ramps and find that their mechanical properties are not altered: they only undergo a slight elastic deformation under compression (Figs. S2 and S3 and SI Text). Second, we check the absence of polymerization-induced reorganization under force by applying to the bundles a long sequence of low-high-low forces (Fig. S4 and SI Text). Under high force, bead separation pauses, and the filaments are kept abutting the surface of the probe bead facing them without elongating. When force is subsequently lowered, filaments resume growth with a history-independent velocity.

From these geometrical and mechanical characterization experiments, it can be concluded that bundled actin filaments behave in our setup as an array of stiff rods pointing toward the load applied to them over a large range of forces, without undergoing any reorganization, buckling, or mechanical damage for the duration of the experiments. As a consequence, the measured bead separation velocity directly equals the filament elongation velocity.

Investigation of the Force Generation Mechanism

The dynamics of the filaments growing under load from the surface of magnetic beads can now be characterized. Under constant magnetic force, the surface-to-surface distance grows linearly with time, so that the elongation velocity of the filaments can be easily derived (Fig. 2, Inset). Renewing the experiment with different values of the force allows us to construct the force-velocity profile characterizing the dynamic properties of the filaments (Fig. 2). The obtained profile has a convex shape very similar to the one obtained in the case of the entropic model (21). However, the entropic model applies in a configuration where reorganization and rotation of filaments can take place under force, allowing them to grow at a force-insensitive velocity. In contrast here, the force dependence of the elongation velocity suggests that a ratcheting mechanism is at play.

In the framework of the Brownian ratchet model, the expression of the elongation velocity for a single filament has the form $v=\delta \left(k_{\text{on}}C{e}^{-\frac{F\delta }{k_{\text{B}}T}}-k_{\text{off}}\right)$ (4). The corresponding curve lies well below our experimental force-velocity profile (Fig. 2), indicating that filaments in our setup cooperate to share the mechanical work of moving the load. A simple hypothesis to characterize this cooperation is to assume that the mechanical work is perfectly shared by the N filaments, so that in the above expression of the velocity, F can be replaced by $F/N$. Schaus and Borisy (24) demonstrated that this scenario represents the maximum performance a population of filaments can theoretically attain. In our setup, among the 16,000 filaments on one bead, only a number $N=120$ are actually able to push the neighbor bead (Materials and Methods). Comparing the expression of maximum performance for this value of N with our experimental data clearly shows that mechanical work sharing among the filaments is not optimal (Fig. 2).

No mechanistic model exists to describe the cooperation within an assembly of filaments polymerizing together against a load. To predict the behavior of such an assembly, authors resort to numerical simulations based on the Brownian ratchet at the single filament level (25–27) and on one of different work sharing scenarios (24). Integrating a large range of parameters into the simulations has allowed to improve the understanding of the biochemical functioning of the cytoskeleton (28–30).

To support our experimental findings, we adapted the numerical model developed by van Doorn et al. (25) to our spherical geometry (Materials and Methods and SI Text). The numerical simulations well reproduce the force-velocity measurements (Fig. 2) and also the low-high-low force experimental results of Fig. S4 (Fig. S5). The main assumptions of the model are that (i) bundling has negligible effects on polymerization kinetics (31); (ii) filaments are incompressible; and (iii) filaments have staggered initial length (Fig. S6). The latter hypothesis accounts for the beads surface roughness. If the number of filaments is large enough, it is equivalent to assuming random initial lengths (see SI Text for a detailed discussion of the hypotheses and results of the simulations). The only parameters in the simulations are $k_{\text{on}}$, $k_{\text{off}}$, the bead radius $R_b$, and the number of filaments able to push the neighbor bead N. They are all determined by independent experiments (Materials and Methods) except N. A least-square minimization test yields $N=130$ for an optimal fit of the data. This number is close to the value of $N=120$ derived from the confocal microscopy observations of Fig. 1C.

Altogether, the geometry of the actin filaments population, the dynamic properties of growth under load, and the numerical simulations give a signature of the molecular mechanism of force production that is consistent with the Brownian ratchet. The numerical simulations allow us to predict the level of cooperation among the filaments, which is intermediate between perfect work sharing and no work sharing. Starting from this observation, we now seek to better quantify the performance of a population of filaments by measuring the mechanical power transmitted to the load.

Optimal Regime of Force Transduction

Motile cells can tune the mechanical power transmitted by actin filaments to the membrane either by changing the polymerization kinetic rates (e.g., sequestration of monomers and processive polymerization) or by adjusting the number of filament tips at the leading edge (e.g., branching, capping, and severing) (2). Which combination of these parameters results in optimal motility? One may argue that motility is most efficient when filaments elongate at maximum speed, i.e., when they virtually feel no load. However, this regime is irrelevant because there is no power transduction in this case. Alternatively, the thermodynamic efficiency for N filaments is maximum at the stalling force $F_{\text{stall}}=\frac{N{k}_{\text{B}}T}{\delta }\ln \left(\frac{k_{\text{on}}C}{k_{\text{off}}}\right)$, at which all of the chemical energy of polymerization is transduced into mechanical work (3) but the velocity drops to zero. Thus, cell motility has to operate far from these two limits to both maintain a significant speed and a significant power transduction.

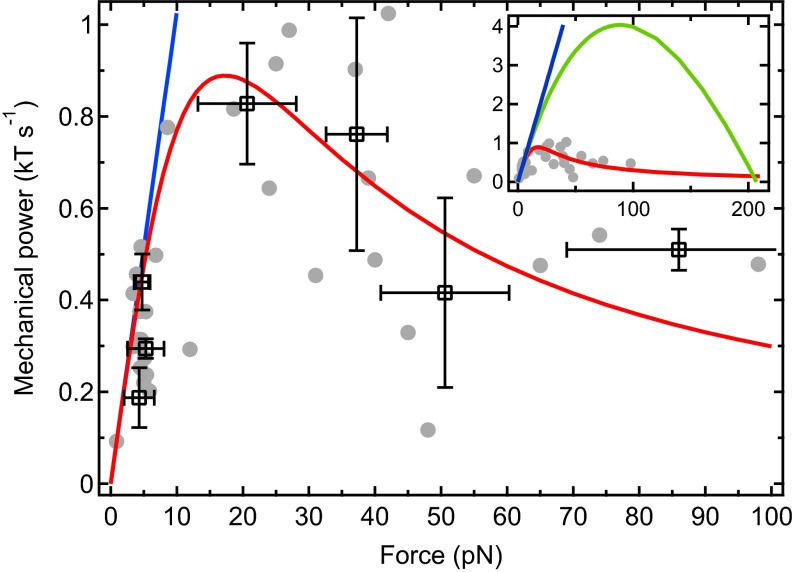
In our experimental setup, the mechanical power P transduced from the filaments to the load can be directly measured. Because the elongation velocity of the filaments equals the bead separation velocity, v, P is simply the product of v by the applied force F (Fig. 3). As anticipated, the data exhibit a maximum in the intermediate force regime. To interpret this maximum, we derive an analytical expression for P within the same framework as in our numerical simulations (Materials and Methods). The important physical ingredients in the derivation are that (i) the mechanical properties of the filaments and their lateral interactions due to bundling are neglected, to focus on the geometrical interaction of the filaments with the wall; and (ii) actin polymerization is assumed to operate at steady state, so that the distribution of filament tip distances to the load is stationary. We find that

$$P\sim \frac{v_o/\delta }{\frac{k_{\text{B}}T}{F\delta }+\frac{F\delta }{N{k}_{\text{B}}T}},$$ [1]

where P is in units of $k_{\text{B}}T$. In the conditions of our experiments with $N=130$, we find good agreement with the experimental data (Fig. 3) but also with the corresponding numerical simulations (Fig. S7). The slope at the origin $P_o=\frac{F{v}_o}{k_{\text{B}}T}$ denotes an ideal regime in which filaments polymerize without feeling the influence of the load. At low forces, P remains close to this ideal regime, indicating that transduced power is limited by the intrinsic growth rate and that essentially one filament bears the load, whereas the others lag behind. However, due to the fast decrease of v in this regime of forces (Fig. 2), P comes to a maximum when a majority of filaments have reached the load (SI Text), at a force that equals

$$F_{P_{\text{max}}}=\sqrt{N}\frac{k_{\text{B}}T}{\delta }.$$ [2]

In the conditions of our experiments, $F_{P_{\text{max}}}=17$ pN. Interestingly, $F_{P_{\text{max}}}$ is independent of the kinetic parameters. Only the velocity reached at $F_{P_{\text{max}}}$ depends on them: we find that $v\left(F_{P_{\text{max}}}\right)=v_o/2$. Moreover, $F_{P_{\text{max}}}$ is only slightly sensitive to the number of filaments compared with the stalling force that is directly proportional to N and thus has a much higher value ($F_{\text{stall}}=210$ pN in our system). The expression of the power transduced to the load in the case of ideal work sharing among the filaments is $P_{\text{id}}=\frac{F\delta }{k_{\text{B}}T}\left(k_{\text{on}}C{e}^{-\frac{F\delta }{N{k}_{\text{B}}T}}-k_{\text{off}}\right)$. The corresponding values of $P_{\text{max}}$ and $F_{P_{\text{max}}}$ are five times higher than the experimental data (Fig. 3, Inset), indicating that filaments in our setup work up to about 20% of their maximum performance (see SI Text for further discussion of this low yield caused by the stochastic nature of monomer insertion against the load).

Fig. 3.

Cluster plot of the mechanical power transmitted by the filaments to the neighboring probe bead (gray disks, data points; open squares, cluster centroids; $n=34$; errors bars, SD). Dataset used is the same as in Fig. 2. A good agreement with the analytical expression of P (red line) is obtained. At low forces, the curve remains very close to the intrinsic growth rate-limited regime $P_o$ (blue line). (Inset) The ideal work sharing model (green line) yields values of $P_{\text{max}}$ and $F_{P_{\text{max}}}$ far above our experimental data.

In our system, N is fixed, and the force can be changed to measure the resulting power transduction. In contrast, in vivo, the number of filament tips at the leading edge of a migrating cell can be adjusted by regulatory proteins, whereas the force F opposing their polymerization is fixed by external parameters, mainly the membrane tension. Assuming that our model can be transposed to actin-based cellular motility despite the different biochemical conditions, Eq. 2 suggests that the actin machinery in a motile cell reacts to the amount of force applied at the leading edge by tuning the number of filament tips so that an efficient power transduction is maintained. This finding adds another piece of evidence to the argument that mechanical feedbacks play an essential role in cell motility (17).

Discussion and Conclusion

In this work, we designed an experimental system of actin filaments growing in a geometry that closely resembles the conceptual view of incompressible filaments polymerizing against a rigid wall. We provided direct evidence that the mechanism by which the wall is pushed forward is a Brownian ratchet at the single filament level.

At the level of the whole population of filaments, we established that transduction of mechanical power by the filaments to the wall is optimal far from the stalling force, when the amplitude of thermal fluctuations is large.

Importantly, we evidenced that the critical parameter for force production by polymerizing filaments is the square root of the number of filaments times the characteristic Brownian ratchet force. This finding brings up two remarks. First, the kinetic parameters and the mechanical properties of the cytoskeleton play only a secondary role in this step of cell migration. Second, the fact that $F_{P_{\text{max}}}$ saturates as $\sqrt{N}$ suggests that such polymerization induced force transduction cannot be scaled up to forces larger than a few tens of piconewtons. This consideration is consistent with the observation that radically different strategies using molecular motors are used by nature to produce larger forces.

The present study characterizes the mechanism of force generation by filaments constrained to polymerize insertionally against a load. We demonstrated in previous work (21) that when this constraint is relaxed and filaments polymerize freely, the mechanism changes. However, in both cases, fluctuations remain the motor of force production and polymerization remains the energy source of this motor. It would thus be interesting to mix populations of fluctuating and nonfluctuating filaments to compare the respective contribution of the two mechanisms to the mechanical power. Alternatively, filaments can be further constrained by transient tethering to the load to polymerize processively, which is the case in the presence of formin in filopodia or N-WASP (neural Wiskott–Aldrich syndrome protein) in lamellipodia. It is likely that the Brownian ratchet-based model presented in this article still holds in this situation, with the only effect of tethering being to alter the amplitude of the fluctuations and thus the kinetic parameters, so that $F_{P_{\text{max}}}$ remains unchanged.

Materials and Methods

Proteins and Buffers.

Actin was purified from rabbit skeletal muscle as previously described (32) and labeled with Alexa488 succinimidyl ester. Ca-ATP-G-actin was converted to Mg-ATP-G-actin before each experiment by incubation in 0.02 mM MgCl₂ and 0.25 mM EGTA. Recombinant human gelsolin was expressed and stored as previously described (21). Before preparation of each new batch of beads, gelsolin was first dialyzed against 10 mM PBS buffer containing 1 mM EGTA and 0.01 wt% NaN₃ and then biotinylated with sulfo-NHS-LC-LC-biotin (EZ-Link Reagent, spacer arm length, 3.05 nm; Thermo Scientific) for 45 min at room temperature at a biotin:actin molar ratio of 15:1. The reaction is almost complete (21), but a second dialysis was performed to eliminate the unreacted biotins. Biotinylated gelsolin was used immediately after preparation. Recombinant human fascin was expressed and purified as previously described (33) and stored at −80 °C in Tris buffer [50 mM Tris (pH 7.5), 150 mM NaCl, 5 mM MgCl₂, and 1 mM DTT]. G-buffer contained 5 mM Tris (pH 7.8), 0.2 mM CaCl₂, 0.2 mM ATP, 1 mM DTT, F-127 0.5 wt%, and NaN₃ 0.01 wt%. Polymerization buffer was made by adding 40 mM KCl and 0.6 mM MgCl₂ to G-buffer.

Actin Kinetics and Thermodynamic Parameters.

Critical concentration $C_{\text{crit}}$ and rate of monomer attachment $k_{\text{on}}$ and detachment $k_{\text{off}}$ at the pointed end in our salt conditions were derived elsewhere (21) from pyrene fluorescence assays (34). Results yielded $C_{\text{crit}}=0.7\hspace{0.5em}\mathrm{\mu }\text{M}$, $k_{\text{on}}=0.12\hspace{0.5em}\mathrm{\mu }{\text{M}}^{-1}\cdot {\text{s}}^{-1}$, and $k_{\text{off}}=k_{\text{on}}{C}_{\text{crit}}=0.084\hspace{0.17em}{\text{s}}^{-1}$. From our working concentration of G-actin, $C=2\hspace{0.5em}\mathrm{\mu }\text{M}$, the elongation velocity of filaments from the pointed end in solution is $v_o=k_{\text{on}}\delta \left(C-C_{\text{crit}}\right)=0.42\text{nm}/\text{s}$.

Sample Preparation.

To prepare probe particles, superparamagnetic beads (Dynabeads M-270 Carboxylic Acid; Dynal Life Technologies) of 2.92 μm in diameter (see below) were coated with Alexa488 fluorophores. Thirty microliters of 0.3 wt% beads was incubated with 0.13 μM Alexa488 hydroxylamine (Molecular Probes, Life Technologies) for 2 h under agitation at 60 °C in 10 mM PBS. Beads were then washed five times in G-buffer and stored at 4 °C in the same buffer. Each batch of gelsolin-coated particles was prepared as previously described (21) from 10 μg streptavidin-covered superparamagnetic beads (Dynabeads M-270 streptavidin; Dynal Life Technologies) of 3.04 μm in diameter (see below) and 1.5 pmol freshly biotinylated gelsolin, stored at 0 °C in G-buffer and used within 24 h. Before each experiment, 0.025 wt% coated beads and 0.01 wt% probe beads were mixed in polymerization buffer with G-actin and fascin. The obtained solution was rapidly transferred to a capillary tube (Vitrocom) sealed at both ends and attached to a microscope slide. Typically, a single experiment lasted 30 min, and no more than 10 experiments were performed with one batch of gelsolin-coated particles.

Force and Distance Measurements.

Our experimental setup, made of an inverted optical microscope equipped with a motorized stage and two magnetic coils, was described elsewhere (21). A homemade particle tracking routine automatically detected the fluorescent probe beads and averaged the interparticle distance between the relevant pairs of particles in real time. Ten minutes after actin polymerization was initiated, a magnetic field of 3 mT ($F\sim 3$ pN) was applied to form the chains of particles. Next, between 1 and 4 min was necessary to find an appropriate chain (i.e., with a large number of interspersed probe beads). Only then was a dynamic measurement started, corresponding to time 0 on the graphs. Interparticle distance was measured every 10 s, allowing for the correction of magnetic field to keep the magnetic force constant. For mechanical measurements, the magnetic field was lowered to 1 mT ($F\sim 0.5$ pN) after formation of the chains and in between the application of force ramps. Each interparticle distance data point was an average over 30 images taken every 100 ms.

Calculation of the Surface-to-Surface Distance.

Our particle tracking routine measured the beads’ centroid-to-centroid distance. Surface-to-surface distance was then derived by subtracting the radius of one gelsolin-coated bead and of one probe bead. Radii were determined by applying a very strong magnetic field to a sample of M-270 streptavidin (respectively, M-270 carboxylic acid) in polymerization buffer. Assuming that particles were in contact, the radius was approximated by half the measured average centroid-to-centroid distance.

Numerical Simulations.

We performed Gillepsie algorithm-based 3D simulations of N filaments growing on a bead, perpendicularly to its surface (25). A force F was applied to them by a probe bead. We made the following assumptions about the filaments: (i) they are rigidly anchored on the surface of the beads; (ii) they are independent, i.e., the rate $k_{\text{on}}$ (respectively, $k_{\text{off}}$) of actin monomer attachment (respectively, detachment) at the tip of a polymerizing filament is not modified by bundling; (iii) they are incompressible; and (iv) they have staggered initial lengths within the size δ of a monomer. The system is rotation-invariant around the axis of the pair of beads. Thus, the relevant parameter is the angle θ filaments form with that axis (Fig. S8). At time $t=0$, the probe bead was positioned as close as possible to the actin covered one without penetrating the filaments. The concentration of G-actin was $C=2\hspace{0.5em}\mathrm{\mu }\text{M}$. In these conditions, the relation $k_{\text{on}}C\ll 2D/{\delta }^2$ (with $D\sim 1\hspace{0.5em}\mathrm{\mu }{\text{m}}^2\cdot {\text{s}}^{-1}$ as the diffusion coefficient of a bead) is satisfied, which means that the movement of the probe bead is limited by the reaction rate of monomers at the polymerizing tip and not by diffusion (4). At each time step, $d\tau$, we randomly chose N times one filament and calculated its distance $L_i$ to the probe bead. If $L_i\ge \delta$, a monomer of size δ could attach to filament i with a probability $k_{\text{on}}Cd\tau$ and detach with a probability $k_{\text{off}}d\tau$, with no effect on the position of the probe bead. If $L_i<\delta$, monomer attachment probability became $k_{\text{on}}C\exp \left[-F\left(\delta -L_i\right)\cos {\theta }_i/k_{\text{B}}T\right]d\tau$, and detachment probability was unchanged. In the case of net elongation of filament i, the probe bead was repelled of a distance $\left(\delta -L_i\right)\cos {\theta }_i$. In the particular case of $L_i=0$ and net shortening, the probe bead was moved as close as possible to the actin covered one without penetrating the filaments. At the end of each time step, the surface-to-surface distance was calculated. This situation corresponds to a partial load-sharing scenario in the classification of ref. 24, characterized in that filaments can push the load a fraction of a monomer forward (Fig. S6).

Analytical Model of Force Transduction by Ratcheting Filaments.

Our model is based on the work by van Doorn et al. (25), who developed a description valid only at the stalling force. We extended it to a larger range of forces by introducing a hypothesis of steady state, which is valid if the force applied to the filaments is well above the characteristic Brownian ratchet force: $F\gg k_{\text{B}}T/\delta$.

We considered a protrusion of N independent parallel filaments rigidly anchored at one end and polymerizing at the other end against a movable load. Each filament has a unique initial length $i\delta /N$, $i\in \left[1\text{;}N\right]$. The load is positioned to abut the tip of the longest filament. Filaments are thus always situated at distances given by multiples of $\delta /N$ from the load, and only one filament can be in contact with it. Only the filaments within a length δ from the load can add length to the protrusion (Fig. S6C), resulting in an average velocity

$$v^{+}={\displaystyle \sum _{n=1}^N{k}_{\text{on}}C{p}_{\text{n}}\frac{\left(N-n\right)\delta }{N}\exp \left[-\frac{\left(N-n\right)\delta }{N}\frac{F}{k_{\text{B}}T}\right]},$$ [3]

where $p_{\text{n}}$ is the probability to find a filament at distance $n\delta /N$ from the load. One needs also to consider the decrease of length of the polymer, due to depolymerization of the longest filament, occurring with an average velocity

$$v^{-}=k_{\text{off}}\frac{\delta }{N}{p}_1+k_{\text{off}}\frac{\delta }{N}{\displaystyle \sum _{n=2}^N\left[n{p}_{\text{n}}{\displaystyle \prod _{j=1}^{n-1}\left(1-p_{\text{j}}\right)}\right]}+k_{\text{off}}\delta {\displaystyle \prod _{j=1}^{N-1}\left(1-p_{\text{j}}\right)}.$$ [4]

So that the velocity of the load is $v=v^{+}-v^{-}$.

To decipher the expression of $p_{\text{n}}$, we considered, at a distance $n\delta /N$ from the load, the flux of subunits going in the direction of the load ${\mathrm{\Phi }}_{\text{n}}^{+}$ and in the opposite direction ${\mathrm{\Phi }}_{\text{n}}^{-}$. Summing the different contributions from all the filaments, we obtained ${\mathrm{\Phi }}_{\text{n}}^{+}=k_{\text{on}}C\hspace{0.17em}{p}_{\text{n}+\text{N}}-p_{\text{n}}\frac{v}{\delta }$ and ${\mathrm{\Phi }}_{\text{n}}^{-}=k_{\text{off}}\hspace{0.17em}{p}_{\text{n}}$. The steady-state hypothesis imposes that ${\mathrm{\Phi }}_{\text{n}}^{+}={\mathrm{\Phi }}_{\text{n}}^{-}$, leading to the following recursion:

$$p_{\text{n}+\text{iN}}={\left(\frac{k_{\text{off}}+v/\delta }{k_{\text{on}}C}\right)}^i{p}_{\text{n}}\hspace{1em}\forall n<N,\hspace{1em}\forall i\in \mathrm{\mathbb{N}}$$ [5]

The condition that a given filament can only be found at distances that are multiples of $\delta /N$ can be expressed as

$${\displaystyle \sum _{i=0}^{\infty }}=p_{\text{n}+\text{iN}}=1\hspace{1em}\forall n<N,$$ [6]

leading to

$$p_{\text{n}+\text{iN}}=\frac{v_o-v}{\delta k_{\text{on}}C}{\left(\frac{k_{\text{off}}+v/\delta }{k_{\text{on}}C}\right)}^i,$$ [7]

with $v_o=\delta \left(k_{\text{on}}C-k_{\text{off}}\right)$ as the elongation velocity of free filaments in solution. $p_{\text{n}+\text{iN}}$ is independent of n so that the average density of filaments is constant within the intervals $\left[i\delta \text{;}\hspace{0.5em}\left(i+1\right)\delta \right]$. The system of equations $\left\{v=v^{+}-v^{-}\text{;}{v}^{+}=f\left[p_{\text{n}}\left(v\right)\right]\text{;}{v}^{-}=f\left[p_{\text{n}}\left(v\right)\right]\right\}$ can be exactly solved. However, to highlight the main physical ingredients of our model, we made the assumption that $v\ll v_o$ so that $v\sim v^{+}$ and arrived at

$$v\sim \frac{v_o}{1+\frac{1}{N}{\left(\frac{F\delta }{k_{\text{B}}T}\right)}^2}.$$ [8]

The force-velocity profile calculated with this expression is very similar to the one obtained by numerical simulations, all parameters being equal (Fig. S7).

The mechanical power transmitted to the load, expressed in units of $k_{\text{B}}T$, is

$$P=\frac{Fv}{k_{\text{B}}T}\sim \frac{v_o/\delta }{\frac{k_{\text{B}}T}{F\delta }+\frac{F\delta }{N{k}_{\text{B}}T}}.$$ [9]

This description was derived in planar geometry. The good agreement with the experimental data (Figs. 2 and 3) shows that, in first approximation, one needs not take into account the sphericity of the beads.

Number of Filaments Involved in Force Generation.

Only a fraction of the filaments on a bead are involved in force generation. They are included in the cone whose apex is the center of a gelsolin-coated bead and the base is defined by the intersection of filament tips growing freely in solution with the neighboring probe bead (see ref. 21 for the derivation of the geometrical calculation). Here with 16,000 filaments per bead, we obtain $N=120$.