Hidden carbon in Earth’s inner core revealed by shear softening in dense Fe₇C₃

Significance

Seismic studies revealed that shear wave (S wave) travels through the inner core at an anomalously low speed, thus challenging the notion of its solidity. Here we show that for the candidate inner core component Fe₇C₃, shear softening associated with a pressure-induced spin-pairing transition leads to exceptionally low S-wave velocity (v_S) in its low-spin and nonmagnetic phase. An Fe₇C₃-dominant inner core would match seismic observations and imply a major carbon reservoir in Earth’s deepest interior.

Abstract

Earth’s inner core is known to consist of crystalline iron alloyed with a small amount of nickel and lighter elements, but the shear wave (S wave) travels through the inner core at about half the speed expected for most iron-rich alloys under relevant pressures. The anomalously low S-wave velocity (v_S) has been attributed to the presence of liquid, hence questioning the solidity of the inner core. Here we report new experimental data up to core pressures on iron carbide Fe₇C₃, a candidate component of the inner core, showing that its sound velocities dropped significantly near the end of a pressure-induced spin-pairing transition, which took place gradually between 10 GPa and 53 GPa. Following the transition, the sound velocities increased with density at an exceptionally low rate. Extrapolating the data to the inner core pressure and accounting for the temperature effect, we found that low-spin Fe₇C₃ can reproduce the observed v_S of the inner core, thus eliminating the need to invoke partial melting or a postulated large temperature effect. The model of a carbon-rich inner core may be consistent with existing constraints on the Earth's carbon budget and would imply that as much as two thirds of the planet's carbon is hidden in its center sphere.

In 1936, Lehmann (1) discovered the inner core, a solid region that produced unexpected arrivals of compressional wave in its shadow zone. Several decades later, the solidity of the inner core was questioned when seismic studies revealed that central sphere of the planet has anomalously low shear wave velocities (S-wave velocities, v_S) (2) and is anisotropic in compressional wave velocity (P-wave velocity, v_P), suggesting the presence of liquid (3). It is now widely accepted that the inner core contains a considerable amount of lighter elements such as sulfur (S), carbon (C), silicon (Si), oxygen (O), and hydrogen (H) (4). Existing data showed that adding carbon to iron (Fe) might partially account for the v_S anomaly and anisotropy (5, 6). Fe₇C₃ has recently emerged as a leading candidate component of the inner core because it is likely the first phase to solidify at core pressures from a liquid containing iron and a small amount of carbon (7). Furthermore, Fe₇C₃ provides a good match for the density of the inner core under relevant conditions (8, 9). Knowledge of the sound velocities of compressed Fe₇C₃ is essential for testing carbon-rich models of the inner core, but relevant data are currently unavailable.

Using the Nuclear Resonant Inelastic X-ray Scattering (NRIXS) technique and the panoramic diamond anvil cells, we have determined the partial phonon density of state (DOS) of ⁵⁷Fe-enriched isotropic aggregate Fe₇C₃ up to 154 GPa and at 300 K (Fig. S1) and then extracted its bulk Debye sound velocity (v_D). Combining the v_D with the existing density (ρ) and isothermal bulk modulus (K_T) data (8), we derived its v_P and v_S (Table S1). A previous experimental investigation revealed two discontinuities in the compressional curve of Fe₇C₃, which were attributed to a magnetic-ordering transition at 5.5–7.5 GPa and a spin-pairing transition near 53 GPa (8). To examine how the magnetic transitions affect the sound velocities and elasticity and to elucidate the nature of the magnetic transitions, we collected Synchrotron Mössbauer Spectroscopy (SMS) data on the same samples during the NRIXS experiments, and performed X-ray Emission Spectroscopy (XES) measurements on polycrystalline Fe₇C₃ up to 94 GPa and at 300 K.

Results and Discussion

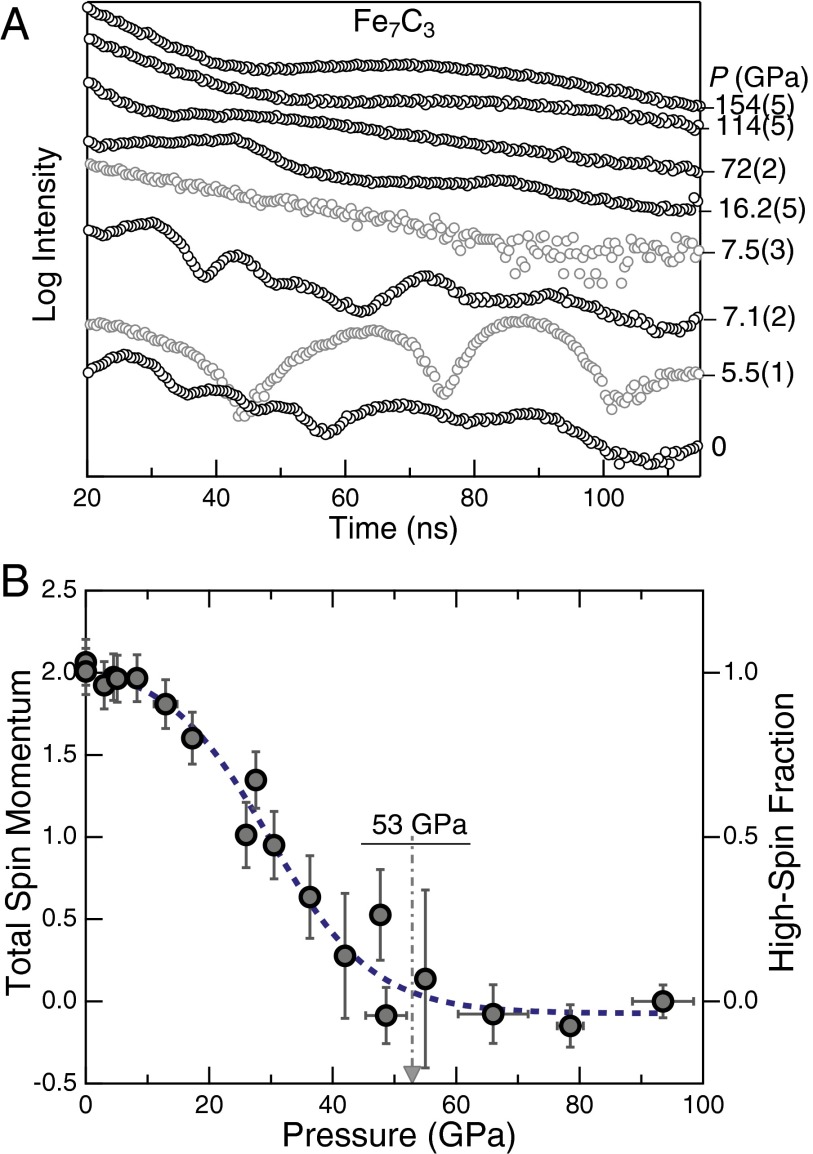
Our sound velocity and magnetic measurements revealed remarkable shear softening in the low-spin Fe₇C₃. At 1 bar the NRIXS results of v_D, v_P, and v_S, and G agree reasonably well with the single existing data point (10) (Fig. 1). The magnetic ordering transition, now placed at 7.1–7.5 GPa on the basis of the SMS data (Fig. 2A), did not show any resolvable effects on the sound velocities. In the XES spectra (Fig. S2), the intensity of the K′_β satellite peak began to drop at 10 GPa. The peak diminished continuously and finally disappeared near 53 GPa, indicating that the total spin momentum of iron approached zero, thus confirming a gradual spin-pairing transition at 10–53 GPa from high-spin to low-spin state (Fig. 2B).

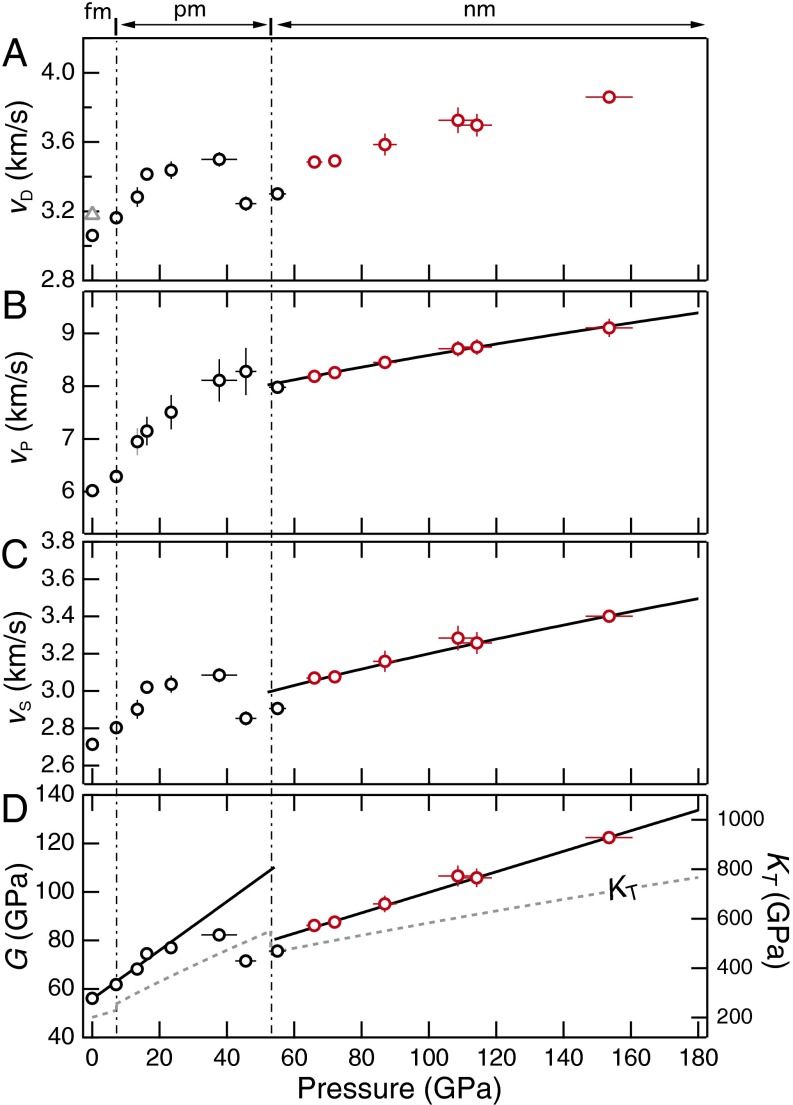
Fig. 1.

Sound velocities and elastic moduli of Fe₇C₃ up to 154 GPa and at 300 K derived from NRIXS measurements. (A) Debye velocity (v_D); (B) compressional-wave velocity (v_P); (C) shear-wave velocity (v_S); and (D) shear modulus (G) and isothermal bulk modulus (K_T). Solid lines are linear fits to the data, which are represented by open circles with error bars. The dot-dashed lines denote abrupt changes in K_T (gray dashed line) (8); fm, ferromagnetic; nm, nonmagnetic (low-spin state); pm, paramagnetic.

Fig. 2.

Pressure-induced magnetic transitions in Fe₇C₃ revealed by XES and SMS measurements. (A) SMS spectra of Fe₇C₃ up to 150 GPa and at 300 K: Black circles (this study), and gray circles (8). Fast oscillation disappears between 7.1 and 7.5 GPa, indicating a magnetic collapse. The spectra at higher pressures were shifted for clarity. (B) Total spin momentum and high-spin fraction of Fe₇C₃ as a function of pressure derived from the XES measurements up to 94 GPa and at 300 K.

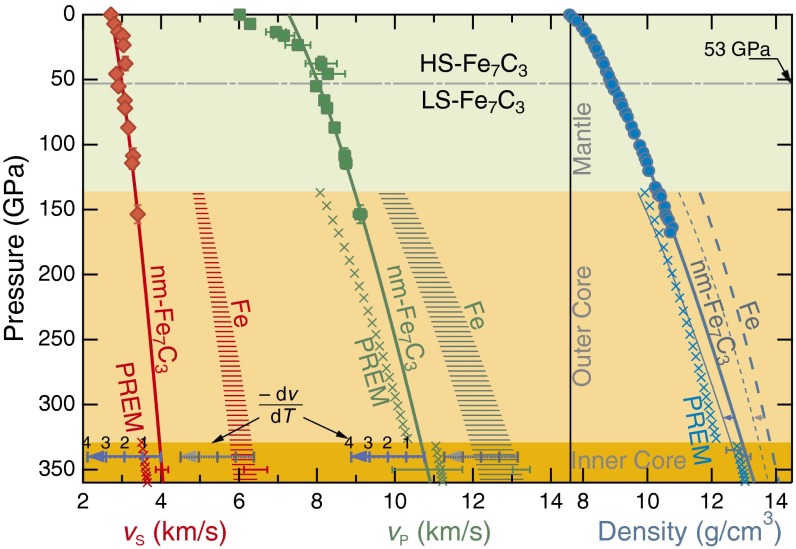
Accompanying the spin transition are pronounced reductions in both the absolute value of the bulk sound velocity v_D and the rate at which it increases with density (Figs. 1 and 3). Because v_D weighs heavily toward v_S (3/v_D³ = 1/v_p³+2/v_S³; hence v_D ≈ 0.84 v_S if v_S ≈ 1/2 v_P), similar reductions in v_S and shear modulus G occurred in this pressure range, indicating shear softening (Fig. 1 C and D). Extrapolating the exceptionally small pressure dependence of the low-spin Fe₇C₃ to the inner core pressure of 330–360 GPa, we obtained a v_S at 300 K that is only ∼14% above the observed values, compared with pure iron which exceeds the observation by more than 65% (Fig. 4).

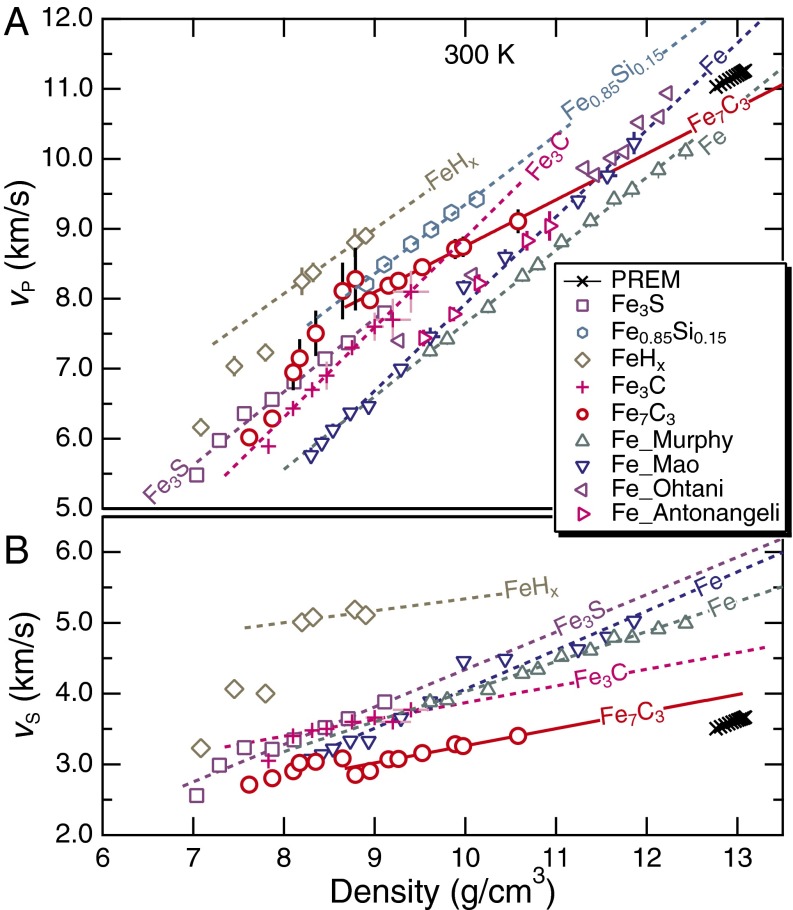
Fig. 3.

Sound velocities (v_P and v_S) of iron and Fe-rich alloys at 300 K from literature and this study. (A) For v_P: brown diamonds, FeH_x (11); purple squares, Fe₃S (12); magenta pluses, Fe₃C (13); light blue hexagons, Fe_0.85Si_0.15 (36); blue down triangles, Fe (23); green upper triangles, Fe (24); magenta left triangles, Fe (37); purple right triangles, Fe (38); red circles, Fe₇C₃ (this study). (B) For v_S: brown diamonds, FeH_x (11); purple squares Fe₃S (12); blue down triangles, Fe (23); green upper triangles, Fe (24); magenta pluses, Fe₃C (13); red circles, Fe₇C₃ (this study). Solid lines represent linear fits to the data of sound velocity versus density, which for Fe₇C₃ at P > 70 GPa give: v_P = 0.66(±0.12)ρ + 2.16(±1.16), v_S = 0.242(±0.045)ρ + 0.843(±0.439). Seismic models for the inner core are represented by preliminary reference Earth model (PREM) (2) (black crosses).

Fig. 4.

Estimated sound velocities (v_P and v_S) and density (ρ) of iron and Fe₇C₃ under inner core conditions. Fe₇C₃ at 300 K: v_P, green squares; v_S, red diamonds; ρ, blue circles (8). The solid curves represent fits to the data and extrapolations on the basis of the third-order Birch–Murnaghan equation-of-state for density and linear relations between velocity and density. The hcp-Fe at 300 K defined by Mao et al. (23) as the upper bound and Murphy et al. (24) as the lower bound: v_P, green shaded area; v_S, red shaded area; ρ, blue long dashed line (39). The thin solid and short dashed curves represent ρ of Fe₇C₃ and hcp-Fe at 5,000 K (8), respectively. The gray and blue ticks represent temperature corrections at 5,000 K for iron and Fe₇C₃, using temperature derivatives (–dv/dT) ranging from 0 to 4 ×10⁻⁴ km⋅s⁻¹⋅K⁻¹. Error bars represent 90% confidence intervals.

The spin-associated shear softening behavior of compressed Fe₇C₃ probably also takes place in other iron alloys, including FeH_x, Fe₃S, and Fe₃C (Fig. 3), although it was not discussed in detail previously (11–13). Mookherjee et al. (10) proposed that aligned spins resist shearing and therefore the shear elastic constant C₄₄ decreases abruptly across a ferromagnetic to nonmagnetic transition in Fe₇C₃. It is not clear if shear softening would apply to the transition to nonmagnetic phase from the paramagnetic phase, where spin was not aligned. Crowhurst et al. (14) explained shear softening in ferropericlase in terms of how stress and strain responded to volume and geometric changes associated with the spin crossover (15). This mechanism, often considered a type of magneto-elastic or spin–phonon coupling, may apply to Fe₇C₃. The structure of Fe₇C₃ can be viewed as carbon atoms occupying the octahedral or six-coordinated interstitial site in the closest-packed iron lattice (10) (Fig. S3). The spin crossover leads to a reduction in the radius of iron atoms (16) and an increase in the C/Fe radius ratio. Fitting carbon atoms into the smaller interstitial sites of low-spin iron lattice may cause structural distortion, as indicated by the flattening of the pressure dependence of the axis ratio a/c at >53 GPa (8). Such distortion may be responsible for the observed shear softening, but the details await further investigations. If the shear softening induced by spin transition is a universal phenomenon for iron-rich alloys, then their effects on the vibrational properties must be considered when extrapolating the high-pressure data to the inner core conditions.

The inner core boundary represents a liquid–solid interface with a temperature near the melting point of its components. Some ab initio calculations (17, 18) suggested that anharmonicity at high temperature would reduce v_S of iron at 330 GPa from ∼6 km/s at 300 K to ∼4 km/s at 5,500 K, thus providing an explanation for the anomalously low v_S. The postulated large effects of high temperature on the v_S of iron-rich alloys, however, have not been observed in experimental studies: Results from face-centered cubic Fe–Ni up to 70 GPa and 1,000 K showed that v_S is barely influenced by temperature (19) and that the v_S of hexagonal close-packed (hcp) iron or Fe₃C is found to decrease with increasing temperature in a nonlinear fashion, enhanced at high temperature but diminished at high pressure (20, 21). Due to the sparse experimental data and often conflicting results on the temperature effects on the v_S of iron-rich alloys, the approach adopted here is to apply a wide range of probable –dv_S/dT based on previous estimates (19, 22) (see Fig. 4).

Considering the experimentally observed temperature effect, our analyses show that at 5,000 K, Fe₇C₃ matches the inner core v_S if –dv_S/dT for Fe₇C₃ is near the lower bound of the experimental constraints on iron at 1.0 × 10⁻⁴ km⋅s⁻¹⋅K⁻¹ (19) (Fig. 4). Moreover, it reproduces the inner core density remarkably well (8). Compared with v_S, the uncertainties in the v_P of iron and Fe₇C₃ are considerably larger (Fig. 4). For instance, the v_P of iron at 330 GPa and 300 K differs by as much as 9% among the recent studies (23, 24). Within the uncertainties, the estimated ranges of v_P of various composition models are all consistent with the inner core observations (Fig. 4). Given the simultaneous matches in all three key parameters, our results suggest that the inner core may consist of Fe₇C₃, rather than the widely assumed model of nearly pure iron. Nickel may be present at ∼5.5% in weight according to geochemical and cosmochemical models (25). Adding nickel, however, only slightly reduces the sound velocities of iron (26, 27). In the absence of data, we assume that nickel has similarly negligible effects on the sound velocities of Fe₇C₃ and therefore will not affect our conclusions.

In the simplified Fe–C binary system, a necessary condition for Fe₇C₃ to form the inner core is that the initial carbon content of the liquid core exceeds that of the eutectic composition. The Earth's carbon budget and the carbon content of the core are poorly constrained (25, 28). Previous studies suggested that the eutectic composition becomes more carbon-poor as pressure increases (e.g., ref. 7). Furthermore, the inner core account for ∼4% of the core’s mass. If all of the core’s carbon concentrates in the inner core, it takes ∼0.3 wt.% of bulk core concentration to make a pure Fe₇C₃ inner core with 8.4 wt.% carbon. The estimated carbon concentration in the core ranges from 0.2 wt.% to 1 wt.% (25, 28, 29). Moreover, as suggested by Wood (30), in the Fe–S–C system, the carbon concentration of the cotectic decreases with increasing sulfur content, reaching 0.34 wt.% carbon at 6.0 wt.% sulfur, and 0.13 wt.% carbon at 10.8 wt.% sulfur. Therefore, Wood (30) proposed that at core pressures, metallic liquids containing several weight percent sulfur may crystallize carbide first even if the carbon content of the liquid is very low (<1%). Given the strong affinity of carbon for iron during core formation (29, 31), it is conceivable that the core contains a sufficient amount of carbon to produce an inner core of Fe₇C₃.

Critical tests of the models require tight constraints on its density and sound velocities at high temperatures and up to 3 Mbar pressures, as well as knowledge of the phase relation of the Fe–C binary system under relevant conditions. Of particular importance is to quantify the effect of temperature on the shear velocity: With the upper bound of −dv_S/dT at 3.7 × 10⁻⁴ km⋅s⁻¹⋅K⁻¹ (22) or for higher estimates of inner core temperatures at 6,000 K or even 7,000 K, the v_S of Fe₇C₃ would be lower than the seismic observations. Furthermore, the anisotropy of the inner core has been a subject of debate and controversies in recent years. Most proposed mechanisms for producing the anisotropy involve the alignment of anisotropic crystals (22). If Fe₇C₃ shows extreme elastic anisotropy similar to Fe₃C (5, 6, 10), then a small degree of alignment would be sufficient to account for the seismic observations. Understanding the elastic anisotropy and rheology of hot and dense Fe₇C₃ would allow further tests of our model.

For an inner core consisting of Fe₇C₃, it is unnecessary to invoke partial melting (3) or the postulated large temperature effect (32, 33) to explain the anomalous seismic properties. A fully frozen Fe₇C₃ inner core would have unique properties and dynamics from one that contains partial melt. Current estimates of carbon in the mantle ranges between 0.8 × 10²⁰ kg and 12.5 × 10²⁰ kg (34). If the inner core is made of Fe₇C₃, its carbon inventory amounts to 60 × 10²⁰ kg, which considerably exceeds the average mantle budget. In this case, the inner core would be the largest carbon reservoir in Earth, accounting for two thirds of its total carbon inventory estimated on the basis of volatility systematics (25). This model challenges the conventional view that the Earth is highly depleted in carbon, and therefore bears on our understanding of Earth's accretion and early differentiation. Carbon in the core may exchange with shallower reservoirs through mantle convection in combination with grain boundary diffusion through the D'' zone (35). Through Earth's history, this process may have played a significant role in the outgassing of CO₂ from the interior and the carbon cycle involving the surface and internal reservoirs.

Methods

Two ⁵⁷Fe₇C₃ samples were synthesized from 94% ⁵⁷Fe-enriched iron powder and graphite using the multianvil apparatuses at the University of Michigan and GeoSoilEnviroCARS of the Advanced Photon Source (APS), Argonne National Laboratory (ANL). For NRIXS and SMS measurements, polycrystalline grains were loaded into panoramic diamond anvil cells (DACs) with beveled diamonds and data were collected at Sector 3-ID-B of the APS at ANL. We used the PHOENIX program package to derive partial phonon DOS and extract Debye sound velocity v_D, as described in detail in Gao et al. (21). Densities and bulk moduli of Fe₇C₃ were calculated from the equation of states in Chen et al. (8) and used as the input parameters to calculate its v_P, v_S, and shear modulus G at a given pressure. For the XES measurements, polycrystalline grains of Fe₇C₃ were loaded into symmetric DACs with beveled diamonds and data were collected at Sector 16-ID-D of APS. The XES spectra were normalized to unity in integrated intensity and aligned along the K_β peak, and the total spin momentum or the high-spin fraction is derived from the K′_β satellite peak intensity of the XES spectra at various pressures. Experimental details are provided in SI Text.