Evolution in changing environments: Modifiers of mutation, recombination, and migration

Significance

Environmental variability is known to promote the evolution of mechanisms that increase phenotypic diversity. The evolution of recombination, mutation, and migration, which endow a population with the needed genetic and phenotypic variability, has been a focus of study in population genetics for more than five decades. Theoretical approaches have focused on conditions for the evolution of recombination, mutation, and migration when environments change periodically and with symmetric selection pressures. Here we extend these models to incorporate random and asymmetric selection. We compare and contrast how fluctuating selection affects the stable rates of these three evolutionary forces and highlight surprising similarities in their evolution under fluctuating selection. This study offers insights into the role of environmental duration, shape, and randomness in predicting the long-term evolutionary advantage of recombination, mutation, and migration.

Abstract

The production and maintenance of genetic and phenotypic diversity under temporally fluctuating selection and the signatures of environmental changes in the patterns of this variation have been important areas of focus in population genetics. On one hand, periods of constant selection pull the genetic makeup of populations toward local fitness optima. On the other, to cope with changes in the selection regime, populations may evolve mechanisms that create a diversity of genotypes. By tuning the rates at which variability is produced—such as the rates of recombination, mutation, or migration—populations may increase their long-term adaptability. Here we use theoretical models to gain insight into how the rates of these three evolutionary forces are shaped by fluctuating selection. We compare and contrast the evolution of recombination, mutation, and migration under similar patterns of environmental change and show that these three sources of phenotypic variation are surprisingly similar in their response to changing selection. We show that the shape, size, variance, and asymmetry of environmental fluctuation have different but predictable effects on evolutionary dynamics.

Under constant selection, a large haploid population is expected to evolve toward a local fitness maximum. However, in natural populations selection may not be constant over time due, for example, to ecological changes, spatial variability, changes in environment, or even shifts in the genetic background (1). Under temporal and spatial heterogeneity in the direction and strength of selection, a population may evolve mechanisms that create and maintain phenotypic diversity, thus increasing the long-term adaptability of the population (2–7). These mechanisms may include changes in the rates at which genetic variability is produced, such as the rates of recombination, mutation, and migration (8).

Understanding how population genetic dynamics are shaped by changing selection has constituted an important component of research in mathematical evolutionary theory over the past five decades. These studies have addressed such issues as the relationship between fluctuations in selection and the dynamics of evolution and how these fluctuations are reflected in the pattern of genotypic frequency variation (9–12).

One important contributor to the pattern of genetic diversity is recombination, which can affect variation by bringing together or breaking apart combinations of alleles. Recombination may accelerate adaptation by expediting the removal of combinations of deleterious alleles from the population, but also slow it down by breaking apart favorable interactions among genes (13–18). The prevalence of recombination in nature has stimulated theoretical efforts to explore the evolution of the recombination rate under a wide variety of modeling assumptions (14–20). Most explanations of the advantage of sex and/or recombination involve either allowing assembly of favored multilocus haplotypes from combinations of epistatically interacting mutations (19–21), or adapting to a changing environment (14, 22, 23).

Charlesworth (14) showed that for a diploid genetic system, when the sign of the linkage disequilibrium varies cyclically in time, increased recombination may be favored if the period of environmental fluctuation is strictly larger than two. This is because, when the selective environment varies between positive and negative epistasis, the linkage disequilibrium is often of the opposite sign to the current epistasis. This lag between epistasis and linkage disequilibrium leads to a mismatch between haplotypes that are most fit and those that are more common, and recombination should be favored because it breaks apart the currently maladapted allele combinations and combines alleles that might constitute a fitter haplotype in the future (14, 17, 22, 23).

Environmental fluctuations can also affect the evolution of the mutation rate. In bacteria, stress can increase the mutation rate by inducing mutagenic mechanisms such as the SOS transcriptional response (24, 25) or contingency loci (26). Theoretical studies have considered both plastic increases in the mutation rate in response to stress (27) and also nonplastic mutation rates that evolve in synchrony with the rate of environmental change. When selection fluctuates periodically and symmetrically between two states with different optimal genotypes, the mutation rate between allelic states should evolve to approximately $1/n$, where n is the number of generations between temporal environmental changes (28, 29). However, numerical simulations showed that the stable mutation rate became zero as the variance in the length of selective cycles increased, or if there were asymmetries in selection pressure between the two environmental states (30).

Variability in selection has also been shown to affect the evolutionarily stable migration rate. When selection is heterogeneous in space but not in time and without variation in the intensity of kin competition (31), migrants cannot displace locally adapted individuals and there is selection against migration (32, 33). This has been shown in population genetic models of selection in multipatch environments with patch-dependent selection of alleles (34–36), and in ecological analyses of the evolution of dispersal (37–43). Migration is suppressed because, in the absence of temporal variation, it limits the ability of populations to adapt to local environmental conditions (44). With temporal variability in selection however, migration can increase the level of local adaptation (45) and higher rates of migration may be favored (46–50).

Here we use the framework of modifier theory to study how environmental fluctuation affects the rates of recombination, mutation, and migration. A modifier approach to study the evolution of genetic systems was first introduced by Nei (51) and Feldman (52) in models for the evolution of recombination. They analyzed the consequences of indirect selection on recombination between genes under viability selection. This approach is based on the assumption that genetic variation exists in the rate of recombination; such genetic variation has been demonstrated using heritability measurements and observed differences between sexes or closely related species (53–55). Recombination and mutation have been shown to be extremely variable across a species’ genome, with areas of low recombination or mutation, as well as hotspots of increased activity (25, 56, 57). The rate of migration and ability to disperse are typically heritable and vary between species and within environments for a single species (58, 59).

We aim to better understand the similarities and differences in the dynamics of these three evolutionarily important forces under similar patterns of environmental change. Elucidating the evolution of recombination, mutation, and migration under fluctuating selection will lead to a more complete understanding of both fundamental evolutionary processes and the pressures that have shaped genomic diversity.

Models of Neutral Modifiers in Changing Environments

Consider an infinite, randomly mating, haploid population and two types of biallelic loci: major loci, which control the phenotype and fitness of this individual, and a modifier locus, which is selectively neutral. The modifier locus is assumed to control the force of interest, which can be the recombination rate between a pair of major loci, the mutation rate between alleles at the major loci, or the migration rate between two demes in a spatially subdivided population. Under what conditions should evolution increase these rates and how do these conditions depend on the pattern of temporal fluctuations in selection?

We address these questions by studying the evolution of the modifier loci and by determining the evolutionarily stable rates as functions of the pattern of fluctuation in selection experienced by the population. As in ref. 52, we frame the problem in terms of the local stability of an equilibrium with one allele fixed at the modifier locus to invasion by another allele introduced at low frequency near this equilibrium. The case where a stable multiallele polymorphism exists at the modifier locus and a new modifier allele arises near this equilibrium (60), and the selection regime fluctuates, will be treated elsewhere.

Evolution of Recombination.

Each individual is defined by three biallelic loci: Two major loci $A/a$ and $B/b$ control the fitness of the individual, whereas a third locus $M/m$ is a modifier locus that controls the recombination rate between the two major loci but is otherwise selectively neutral.

We study the evolution of the modifier locus $M/m$ and determine the stable recombination rate as a function of fluctuation in selection experienced by the population. This entails analysis of the stability of an equilibrium with only M present to invasion by an allele m, introduced near this equilibrium. To that end, we track the frequencies of the eight genotypes MAB, MAb, MaB, Mab, mAB, mAb, maB, and mab. At each generation, the population experiences random mating, recombination, and selection, in that order.

There are three possible recombination rates depending on the genotype at the modifier locus: MM, Mm, and mm produce recombination rates $r_1$, $r_2$ and $r_3$, respectively. With the three loci ordered as above and the modifier locus located on one side of the two major loci, let R be the recombination rate between the modifier locus and the two major loci. We assume no interference between recombination events occurring in the two intervals separating the two major loci and between the modifier locus and the nearest major locus.

Assume two possible types of selection regimes $T_1$ and $T_2$, such that the fitnesses, irrespective of the genotype at the $M/m$ locus, can be represented as follows:

Genotype	AB	Ab	aB	ab
Environment $T_1$	1	$1+s_1$	$1+s_1$	1
Environment $T_2$	$1+s_2$	1	1	$1+s_2$

Thus, if $s_1$, $s_2>0$, the genotypes that are fittest in one environment are less fit in the other. Increased recombination should be favored because, at every environmental change, recombinant offspring are more fit than the nonrecombinant ones (also see refs. 14, 18, 22, and 23).

Evolution of Mutation.

The mutation model recapitulates that of Salathe et al. (30) and Liberman et al. (61), and we include it here for comparison with recombination and migration. A major locus $A/a$ controls the fitness of the individual, whereas a second locus $M/m$ controls the mutation rate between alleles at the major locus but is otherwise selectively neutral. The recombination rate between $A/a$ and $M/m$ is r.

We study the evolution of the modifier locus $M/m$ and determine the stable mutation rate as a function of the pattern of fluctuation in selection. Alelles M and m at the modifier locus produce mutation rates ${\mu }_M$ and ${\mu }_m$, respectively. Assume two types of selection regimes $T_1$ and $T_2$, such that the fitnesses are as follows:

Genotype	A	a
Environment $T_1$	1	$1+s_1$
Environment $T_2$	$1+s_2$	1

If $s_1$, $s_2>0$, then alleles that are fitter in one environment are less fit in the other. At each generation, the population experiences random mating, selection, mutation, and recombination, in that order.

Evolution of Migration.

The population is divided into two demes $E_x$ and $E_y$, with different selection regimes. There are two biallelic loci—a major locus $A/a$ and a modifier locus $M/m$—where the major locus controls the fitness of an individual, whereas the selectively neutral modifier locus controls the migration rate between the two demes. We investigate the evolutionary dynamics of the migration rate between $E_x$ and $E_y$ using an explicit population genetic model to track the frequencies of the four genotypes AM, Am, aM, and am. At each generation, there is recombination between $A/a$ and $M/m$ at rate r, and selection in each deme separately, after which individuals may migrate between the two demes. Again, we frame the question in terms of the local stability of the fixation equilibrium with only M present, producing migration rate ${\nu }_M$, to invasion by allele m, which produces migration rate ${\nu }_m$. We assume ${\nu }_M$ and ${\nu }_m$ to be the same from $E_x$ to $E_y$ as from $E_y$ to $E_x$.

Within each deme, the selection regime varies temporally, with two environmental states, $T_1$ and $T_2$. In $T_1$, the fitnesses are

Deme	$E_x$		$E_y$
Genotype	A	a	A	a
Fitness	$1+s_1$	1	1	$1+s_3$

whereas in $T_2$, they are

Deme	$E_x$		$E_y$
Genotype	A	a	A	a
Fitness	1	$1+s_2$	$1+s_4$	1

Thus, if $s_1$, $s_2$, $s_3$, $s_4>0$, allele A is favored in one temporal state and allele a is favored in the other. This is an important assumption if the fitness regimes $T_1$ and $T_2$ are coordinated between the two demes. Otherwise it is not important which environment is denoted as $T_1$ or $T_2$; all that matters is that environmental change occurs independently in the two demes. If the $s_i$ are all equal, we call the selection symmetric.

Changing Environments: The General Simulation Model.

Initially the population is fixed on allele M at the modifier locus, which determines a rate sampled randomly between 0 and 1 for modifiers of mutation and migration and between 0 and 0.5 for modifiers of recombination, and held constant thereafter. This population evolves for 1,000 generations or until it reaches a stable polymorphic equilibrium at the locus/loci under selection. We then introduce allele m at the modifier locus at a small frequency (10⁻⁴) near this equilibrium. The rate determined by m is the product of the resident rate of M and a number generated from an exponential distribution with mean 1. This allows us to test invading rates that are more often close to the resident rate, as well as those that are far from it. If these invading rates are larger than the biological maxima, then the maxima are used (i.e., 1 for mutation and migration, and 1/2 for recombination). After 5,000 generations, we determine whether the newly introduced allele invaded the population; if the frequency of m is larger than its initial frequency of 10⁻⁴, we call it an invasion. In this case, the new allele had an induced selective advantage over the resident, and it should reach fixation if the population continued to evolve. If allele m invaded, the next invasion trial begins with this invading rate as the resident rate. If there was no invasion, the resident allele determines the same resident rate as in the previous trial. We repeat the invasion steps described above. After at least 500 invasion trials and after the resident rate cannot be invaded in 50 consecutive trials, the final rate in the population is declared to be the evolutionarily stable rate.

With periodic environmental change, the selection regime changes deterministically every n generations, making the environmental period 2n. For random temporal variation, the waiting times between environmental changes have a gamma distribution, which is defined by two parameters: the shape α and the scale β, with mean n = $\alpha \beta$ and variance ψ = $\alpha {\beta }^2$. This allows us to test a wide range of distributions between pure periodicity $\left(\psi =0\right)$ and an exponential waiting time $\left(\psi =1\right)$ by fixing n while varying ψ. If ψ is strictly larger than zero (nonperiodic case), the final stable rate is computed as the average of the stable rates obtained in 10 different simulation runs.

Analytical Results

In the case of mutation rates, Liberman et al. (61) showed that for period 2 and symmetric selection, increased mutation rate is always favored, and the mean fitness at equilibrium is an increasing function of the mutation rate. Also, with period 4, the stable mutation rate is 1/2. Moreover, the critical points of the mean fitness with respect to the mutation rate are those that cannot be invaded. Carja et al. (62) also showed that these results hold with spatial heterogeneity in selection: For period 2 and symmetric selection, a modifier increasing mutation can always invade in the population regardless of the migration rate. Furthermore, for higher environmental periods, analytic computation in Mathematica (Wolfram Mathematica) was used to show that the parameter that controls the evolution is $m_b=\nu +\mu -2\nu \mu$, where ν is the migration rate and μ the mutation rate. In this case, the maximum mean fitness at equilibrium is achieved for mutation rates for which this parameter $m_b$ is on the order of $1/n$, where 2n is the environmental period.

Here, using similar analyses, we study the stable recombination and migration rates as functions of the environmental period, i.e., the length of the period of the fluctuating selection. A general environmental cycle consists of ${\tau }_1+{\tau }_2$ selection steps, the first ${\tau }_1$ of type $T_1$ selection followed by ${\tau }_2$ of type $T_2$ selection. We are able to derive exact analytical conditions for the local stability of fixation in M to invasion by m in the case ${\tau }_1={\tau }_2=1$, i.e., the environment changes every generation under the assumption that all selection coefficients in each of the three models are the same. The mathematical analyses for modification of migration and recombination are in SI Appendix. As noted above, in a temporally constant environment, the reduction principle holds. On the other hand, with fluctuating selection of period 2, a higher rate will invade a population fixed on a given resident rate. The stable rate is 1 for migration and mutation and 1/2 for recombination (the biologically feasible maximum). Note that our results in the haploid case are different from those for a modifier of recombination in a diploid model with period 2 (14).

We were able to obtain analytical solutions only under these very rigid symmetry assumptions and for environmental period of two. For the evolution of the three rates under more general conditions, simulations were used to find the stable rate.

Simulation Results

Periodic Environments.

If the environment changes every generation, we confirm the result found in our mathematical analysis in SI Appendix. If the temporal environment changes deterministically every n generations (i.e., period 2n) in both demes, the uninvadable rates are all decreasing functions of n (Fig. 1). In all our simulations, the stable rates of mutation and migration are quantitatively similar, suggesting that these two forces lead to similar evolutionary dynamics. The stable rates of mutation and migration are on the order of $1/n$, in accord with previous analyses (see refs. 28–30 and 63 for modifiers of mutation). This is also shown in SI Appendix, Fig. S1, which plots the three stable rates as functions of $1/n$ and displays the linear regression fit to our simulated data. Although the slopes corresponding to mutation and migration are very similar, the slope for the recombination rate is about twice these regression coefficients. Fig. 1 presents results for environmental waiting times n with $n\ge 20$, whereas the results for smaller n are shown in SI Appendix, Fig. S2, where important differences in the three stable rates for small environmental periods can be seen. Whereas the stable rate of recombination reaches the allowed maximum, 0.5, for all $n<6$, mutation and migration exhibit different dynamics for small odd and even n. The maximal allowed rate is reached at $n=1$ and $n=3$ for migration; and n equal to 1, 3, 5, and 7 for mutation. This difference between odd and even n in the case of mutation modification was also observed by Liberman et al. (61). SI Appendix, Fig. S3 shows that these results are robust to different values of the symmetric selection coefficient.

Fig. 1.

Evolutionarily stable rates as function of the number of generations before an environmental change n; symmetric selection and periodic environmental change. All selection coefficients are equal to 0.1. Recombination rates between modifier and major loci are 0 (R = 0 for recombination modification and r = 0 for mutation and migration modification). The rate of environmental change, n, equal to half of the environmental period, is on the x axis. The curves represent a fit to the data using a generalized additive model with penalized cubic regression splines.

This uninvadable rate also maximizes mean fitness at equilibrium. We show this in SI Appendix, Fig. S4 for recombination modifiers, and in SI Appendix for migration modifiers; it was also shown by Liberman et al. (61) for the evolution of mutation rates. Although this mean fitness principle holds for migration and mutation modifiers in diploid modifier models, it does not hold for the modification of recombination (64).

As recombination between the modifier locus and the gene(s) under selection increases, the strength of indirect selection on the modifier decreases because the linkage disequilibrium between these genes decreases. SI Appendix, Fig. S5 shows that the stable rates decline with increasing recombination rate between the modifier and the major locus/loci. In earlier studies of neutral modifiers of mutation and recombination, the indirect selection on the modifier locus was of the order of the square of the disequilibrium between the major and the modifier loci (63).

Random Waiting Times.

If the waiting times between temporal changes are random, the $1/n$ rule no longer holds for the evolution of mutation rates (30). Fig. 2 shows the stable rates of recombination, mutation, and migration when the expected time before an environmental change is 10 generations, and this waiting time is sampled from a gamma distribution with variability parameter ψ represented on the x axis. Environmental variability $\psi =0$ is the case of two periodically changing environments with period 10 and recaptures the behavior seen in SI Appendix, Figs. S2 and S3. For small ψ, the three uninvadable rates decrease slightly as symmetric selection intensity increases. As ψ becomes larger, the behavior of the system changes dramatically. We find that the stable rates of recombination and migration can be up to 2 orders of magnitude lower than in the periodic regimes and depend strongly on the selection coefficients. In fact, the decrease in the stable rate is steeper as selection becomes weaker (Fig. 2). SI Appendix, Fig. S6 shows that the results of Fig. 2 are robust to changes in the mean waiting time for environmental change.

Fig. 2.

Evolutionarily stable rates as function of the environmental variability ψ; symmetric selection and random environmental change. All selection coefficients are equal and as presented in the legend. Recombination rate between modifier and major loci is 0.1. Mean waiting time between environmental changes is equal to 10. The variability parameter ψ is presented on the x axis. The curves represent a fit to the data using a generalized additive model with penalized cubic regression splines. The three panels present the results for evolutionarily stable rates of recombination in A, mutation in B, and migration in C.

Asymmetric Selection.

With fitnesses that are more complicated than can be represented by a single parameter (for example, if the selective advantage to allele A of being in environment $T_2$ is greater than the selective advantage to allele a of being in environment $T_1$, in the case of mutation modification), we observe a threshold phenomenon; if the selection coefficients are similar enough, the evolved rates are the same as in symmetric case. However, beyond a certain threshold difference in selection coefficients, there is a sudden drop in the stable rate and nonzero rates can no longer be stable. This threshold determines when nonzero recombination, mutation, and migration rates can be maintained, as shown in Fig. 3, for both periodic and random environmental changes. This was observed previously for mutation modifiers (30) and is qualitatively robust to differences in environmental variability ψ and environmental mean waiting times (SI Appendix, Figs. S7 and S8).

Fig. 3.

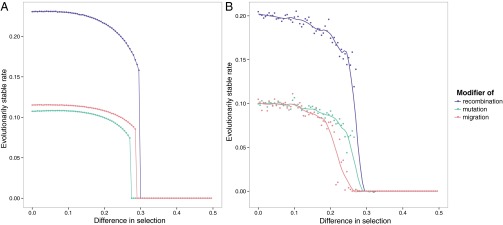
Evolutionarily stable rates as functions of asymmetry in selection. For recombination and mutation, s₂ = 0.5 and the difference in selection s₂ − s₁ is on the x axis. For migration, s₂ = s₄ = 0.5 and s₁ = s₃ with the difference in selection s₂ − s₁ on the x axis. Recombination rates are R = 0.1 for recombination modification and r = 0.1 for mutation and migration modification. (A) Periodic environment, rate 10 (period 20). (B) Mean waiting time between environmental changes is equal to 10 and variability parameter ψ = 0.1. The dots represent averages over 10 runs of the simulation. The curves represent a fit to the data using a generalized additive model with penalized cubic regression splines.

Discussion

We find interesting similarities in the evolutionary dynamics of modifiers of mutation, recombination, and migration. These similarities may stem from the fact that all three forces can enhance a population’s adaptation to a changing environment by increasing the genetic diversity on which selection can act. In a sense, they all allow for anticipation of selection change but they may also create a load. In that context mutation, recombination, and migration can be considered bet-hedging strategies. However, the type of selection acting in the these models is different from what is classically called bet-hedging because we consider an infinite population size with no demography (6).

Our results extend the qualitative messages of previous theoretical work. In constant environments, the reduction principle holds and the rates of mutation, migration, and recombination all evolve toward zero. When environments change periodically through time, these rates can evolve to nonzero values, each decreasing with increasing environmental period. Previous work in the evolution of mutation rates (28, 29) found that with symmetric selection, mutation evolves to be in synchrony with the rate of environmental change: order of $1/n$, where 2n is the environmental period. Here we show that the rate of migration between two demes with different selection pressures also follows this pattern and the stable rates of migration are quantitatively similar to those of mutation. This is because mutation and migration both act to introduce the fitter alleles into the changed environment. We also show that the rate of recombination follows the same qualitative pattern as the rates of mutation and migration.

Previous work has mostly focused on periodic, symmetric environmental changes. The total genetic load differs between randomly changing environments and periodically fluctuating environments and, therefore, evolution under random and periodically fluctuating selection is expected to be different (65). Recombination, mutation and migration are surprisingly similar in their evolutionary response to randomness in waiting time before an environmental change, as measured by ψ; increase in ψ leads to a decrease in all three evolutionary rates. We hypothesize that as ψ increases, the longer stretches of constant selection that favor reduction play a greater role in the dynamics of the system. A decreased role for short environmental durations would explain why the optimal rates of these three forces are small when the environmental fluctuation is random. Moreover, the stable rates increase with selection intensity; when selection is weak, the evolutionary dynamics track environmental shifts slowly and the occasional very long runs of the same environment pose a disadvantage to high recombination, mutation, or migration rates. As selection pressure increases, the system is better able to respond to the more rapid shifts in the environment, which leads to an increase in the three stable rates.

An important limitation of our models is the assumption of infinite population size: In finite populations under a constant environment, drift may be important in shaping the stable rates of the three forces (66–68). A better understanding of the interplay of population size and environmental change in the evolution of recombination, mutation, and migration is needed in both experimental and theoretical settings. Previous work on evolution of dispersal suggested that, with drift, migration will be selected as a way to avoid kin competition (69, 70). Similarly, random genetic drift can affect the evolution of recombination by generating negative disequilibria among selected loci (71) such that beneficial alleles at one locus become associated with deleterious alleles at other loci. Modifiers that increase recombination could help regenerate good combinations of alleles, and will rise in frequency along with these alleles (67, 68, 72). In large populations, it has been proposed that selection on recombination should be inversely proportional to population size (73). However, even with large numbers of individuals, a drift-based advantage to recombination may occur as long as there is spatial structure (71) or selection acts on a large number of loci (73). The interactions between the kinds of fluctuations in fitness studied here and the effects of drift remain to be explored.

A major theoretical challenge is to understand how the different forces discussed here combine to influence the evolution of genetic and phenotypic diversity; in natural populations recombination, mutation, and migration may together counteract the stresses induced by a change in selection. An understanding of the interplay between the types of diversity introduced by the three different forces is needed in theoretical population genetics (50). For example, it has been shown that, with migration among populations, spatial heterogeneity in selection can generate positive or negative linkage disequilibrium and select for recombination even in the absence of genetic drift or temporal heterogeneity (17). This is because natural selection varying across space maintains local differences in gene frequencies, and with migration these differences in frequency can generate patterns of linkage disequilibria within a deme that create a selective pressure for increased recombination. In fact, including migration extends the range of epistasis over which recombination can be favored (17). In our study of mutation modification in two populations connected by migration and undergoing symmetric periodic selection, the parameter that controls the evolution of the system is a nonlinear function of the mutation and migration rates and its stable rate is inversely proportional to the environmental period (62). Mutation and recombination have also been studied together in models for evolution of recombination in constant environments; if the major loci are at an equilibrium between selection against deleterious alleles and mutation toward them, recombination may increase in the population if the linkage disequilibrium is negative (15, 21).

Overall, we find that the three essentially different evolutionary forces are surprisingly similar in how they respond to fluctuating selection, as each of them constitutes a form of genetic bet-hedging and endows a population with the genetic diversity that can accommodate changes in their selective environments. Our models show that knowing the difference in selection between environmental regimes is not sufficient to predict the long-term advantage of these three forces of evolutionary change. Knowledge of the duration, shape, and randomness of the environmental regimes is also essential. Similarly, knowing how the environment fluctuates is of little help without knowing the extent of asymmetry in selection coefficients. Some of these complications have been addressed by Altenberg (35, 50). Future work needs to consider the interactions across multiple dimensions in the parameter space to increase our understanding of how recombination, migration, and mutation contribute to adaptation in fluctuating environments.