Sphericity and symmetry breaking in the formation of Frank–Kasper phases from one component materials

Significance

Understanding how particles fill space has challenged mathematicians, scientists, and technologists since antiquity. This article rationalizes the spontaneous organization of single-component diblock copolymers into multimolecular nanoscale domains that order into a low-symmetry Frank–Kasper (FK) phase with short-range tetrahedral close packing and a giant unit cell that contains 30 particles. This class of crystal structures bridges conventional periodic crystals and low symmetry aperiodic crystals often termed “quasicrystals.” Surprising analogies are thus drawn between the heretofore unexplained formation of FK structures in soft materials, and in certain elemental metals (including manganese and uranium), alloys, and intermetallic compounds, highlighting opportunities to better understand space filling in hard and soft materials by investigation of block polymers with precisely tuned molecular architectures.

Abstract

Frank–Kasper phases are tetrahedrally packed structures occurring in numerous materials, from elements to intermetallics to self-assembled soft materials. They exhibit complex manifolds of Wigner–Seitz cells with many-faceted polyhedra, forming an important bridge between the simple close-packed periodic and quasiperiodic crystals. The recent discovery of the Frank–Kasper σ-phase in diblock and tetrablock polymers stimulated the experiments reported here on a poly(isoprene-b-lactide) diblock copolymer melt. Analysis of small-angle X-ray scattering and mechanical spectroscopy exposes an undiscovered competition between the tendency to form self-assembled particles with spherical symmetry, and the necessity to fill space at uniform density within the framework imposed by the lattice. We thus deduce surprising analogies between the symmetry breaking at the body-centered cubic phase to σ-phase transition in diblock copolymers, mediated by exchange of mass, and the symmetry breaking in certain metals and alloys (such as the elements Mn and U), mediated by exchange of charge. Similar connections are made between the role of sphericity in real space for polymer systems, and the role of sphericity in reciprocal space for metallic systems such as intermetallic compounds and alloys. These findings establish new links between disparate materials classes, provide opportunities to improve the understanding of complex crystallization by building on synergies between hard and soft matter, and, perhaps most significantly, challenge the view that the symmetry breaking required to form reduced symmetry structures (possibly even quasiperiodic crystals) requires particles with multiple predetermined shapes and/or sizes.

The discovery of materials with aperiodic order, often referred to as “quasicrystals,” 30 years ago (1, 2) heralded new and promising vistas for designing materials endowed with unique properties. In the 1950s Frank and Kasper (3, 4) recognized complex tetrahedral atomic- and molecular-packing geometries that bridge the familiar close-packed crystals [e.g., face-centered cubic (FCC), hexagonally close-packed (HCP), and body-centered cubic (BCC) structures] characterized by periodic order, and quasiperiodic crystals (QCs) that extend crystallography beyond the 230 space groups relevant to periodic crystals (5, 6). The scientific literature is replete with examples of Frank–Kasper phases in hard materials, particularly in the area of intermetallics (7–9), but also in a few complex elemental crystals, including manganese (10, 11) and uranium (12). Recently, this class of crystalline order has cropped up in a host of soft materials, including dendrimers (13), surfactant solutions (14), and block polymers (15, 16), often in close proximity to QC phases (17–19). To the best of our knowledge the principles underlying the formation of Frank–Kasper phases across both categories of materials have not been established, presenting enticing challenges to scientist and engineers bent on controllably arranging atoms and molecules for specific materials applications.

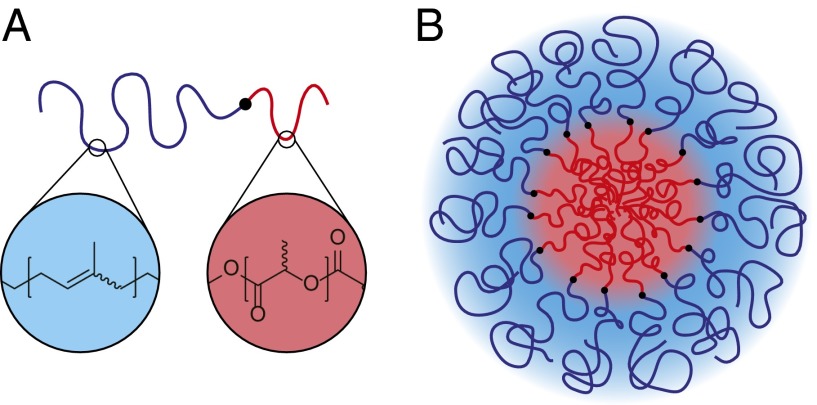
Self-assembly of asymmetric diblock copolymers in excess solvent that selectively interacts with one of the blocks leads to the formation of spherical micelles (20, 21) with a core and corona structure as illustrated in Fig. 1. In the absence of solvent, and under conditions that favor segregation of the two blocks, these soft mesomorphic particles produce ordered structures with a lattice size that scales with the size of the particles, controlled by the overall length (degree of polymerization or molecular weight) of the constituent polymers (22). In this article we offer an analysis and interpretation of experimental data obtained from a short diblock copolymer reported earlier to form a Frank–Kasper σ-phase (23, 24). The compositionally asymmetric poly(isoprene-b-lactide) (PI-PLA; IL) diblock copolymer considered in this work (22% PLA by volume; Fig. 1A) is essentially a single-component system. Here we note that this statement is not rigorously correct because the material is made up of a collection of molecules that span a (relatively narrow) distribution in chain lengths and compositions. We argue that such small deviations from ideality do not interfere with or explain the phenomena reported herein. We find that competition between the preferred spherical particle shape and the need to uniformly fill space (i.e., to avoid thermodynamically costly density variations such as voids) results in a transition from a state with BCC structure ($Im\overline{3}m$ space group symmetry) to a tetragonal Frank–Kasper σ-phase ($P{4}_2\text{/}mnm$ symmetry) upon cooling below the order–disorder transition temperature. This transition is mediated by exchange of mass (diblock copolymer chains), resulting in a redistribution of particle sizes and shapes from the single polyhedron associated with the BCC Wigner–Seitz cells to five discrete cells (30 in total per unit cell; ref. 23), which on average better approximate spherical symmetry.

Fig. 1.

Schematic illustration of (A) the molecular structure of a poly(isoprene-b-lactide) diblock copolymer, and (B) an isolated self-assembled spherical micelle.

Building on this result in soft systems we proceed to draw a number of analogies between the drive toward spherical symmetry in many-body diblock copolymers in real space and long-standing arguments for metals, alloys, and intermetallics regarding the role of sphericity in accommodating the shape of the Fermi surface subject to the constraints imposed by the crystal lattice. In essence we argue that the tendency of alloys and intermetallic compounds to transform to apparently low-symmetry structures, in an attempt to better reconcile the symmetry of the crystal with the spherical reciprocal space symmetry of their (nearly) free electrons, is analogous to the preference for real-space sphericity in the polymeric system studied here. We further highlight analogies between the mechanisms of symmetry breaking in these polymer- and metal-based systems, the former by exchange of mass, the latter by exchange of charge. It is suggested that these analogies provide potentially useful connections between complex crystalline structures in hard and soft matter.

Results and Analysis

The experimental work described in this article focuses on the structure and viscoelastic properties of a poly(isoprene-b-lactide) diblock copolymer denoted IL-15; synthesis and characterization of this compound have been described elsewhere (24). In brief, the overall number-average molecular weight M_n = 3,890 g/mol (dispersity M_w/M_n = 1.12) is divided between PI (2,810 g/mol) and PLA (1,080 g/mol) blocks, which translates into a composition of 22 ± 1% by volume poly(lactide) based on published densities. This asymmetric block copolymer self-assembles into point particles (previously referred to as sphere-forming domains; refs. 23, 24) containing PLA-rich cores surrounded by a corona of PI blocks. Upon cooling, the PLA-rich cores vitrify between 20 and −25 °C; T_g,core ≅ 5 °C using the conventional designation of the glass transition temperature, i.e., half the discontinuity in the heat capacity as determined by differential scanning calorimetry (DSC; Fig. S1). A second glass transition at −66 °C (8 °C wide) is associated with the continuous PI-rich matrix formed by the corona blocks surrounding each core.

Order and Disorder.

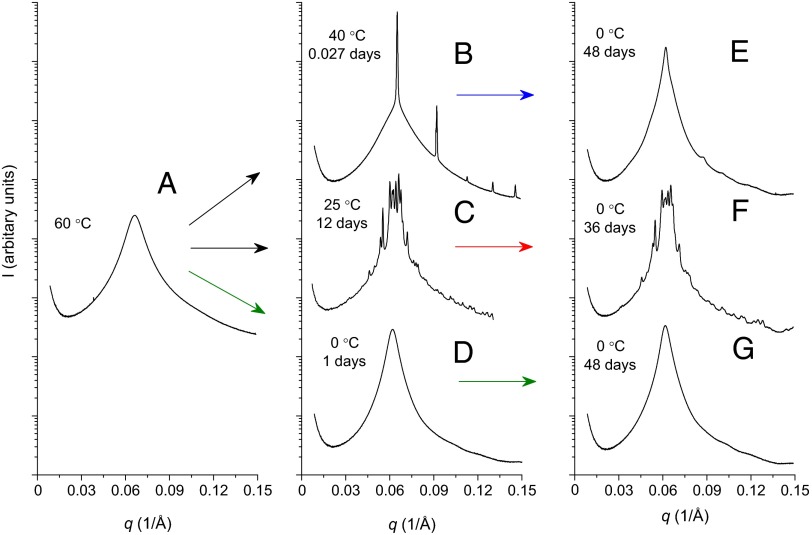
Sample IL-15 exhibits three equilibrium phases: a Frank–Kasper σ-phase ($P{4}_2/mnm$ space group symmetry) at T ≤ 28 °C, a BCC phase ($Im\overline{3}m$ symmetry) for 28 ≤ T ≤ 48 °C, and a disordered state when T > 48 °C. These ordered state symmetries were identified by synchrotron small-angle X-ray scattering (SAXS; Advanced Photon Source, Argonne National Laboratory), following previously reported procedures (23). Order–order and order–disorder transition temperatures, T_σ-BCC ≅ 28 °C and T_ODT = 48 ± 1 °C, respectively, were established using SAXS and linear dynamic mechanical spectroscopy measurements (23). Fig. 2 shows representative SAXS patterns associated with the BCC (40 °C) and σ (25 °C) phases (Fig. 2 B and C) following the evolution of order after rapid cooling (dT/dt > 20 °C/min) from the disordered state (60 °C; Fig. 2A). As described in our earlier report (23), BCC ordering occurs within about 30 min at 40 °C, based on the evolution of the linear dynamic elastic modulus G′. Nearly a day is required at 25 °C to develop the elasticity associated with the σ-phase, and the SAXS pattern continues to evolve higher-order reflections for nearly a month (Fig. 2C), indicative of increasingly greater correlation length.

Fig. 2.

SAXS powder patterns recorded from sample IL-15 following various thermal treatments. Patterns A, D, and G (and nominally E) are associated with a state of disorder. Pattern B derives from a BCC structure, and patterns C and F reflect the quasicrystal approximant Frank–Kasper σ-phase. The arrows indicate rapid (<1 min) temperature changes.

When rapidly cooled from 60 to 0 °C however, ordering is completely suppressed as indicated by the lack of Bragg reflections after aging the material even for 48 d (Fig. 2 A, D, and G). Cooling the fully formed σ-phase from 25 to 0 °C produces imperceptible changes in the scattering pattern (Fig. 2F). However, the BCC phase becomes virtually disordered when quenched from 40 to 0 °C; only vanishingly small vestiges of cubic order persist after 48 d (Fig. 2E).

Ordering Dynamics.

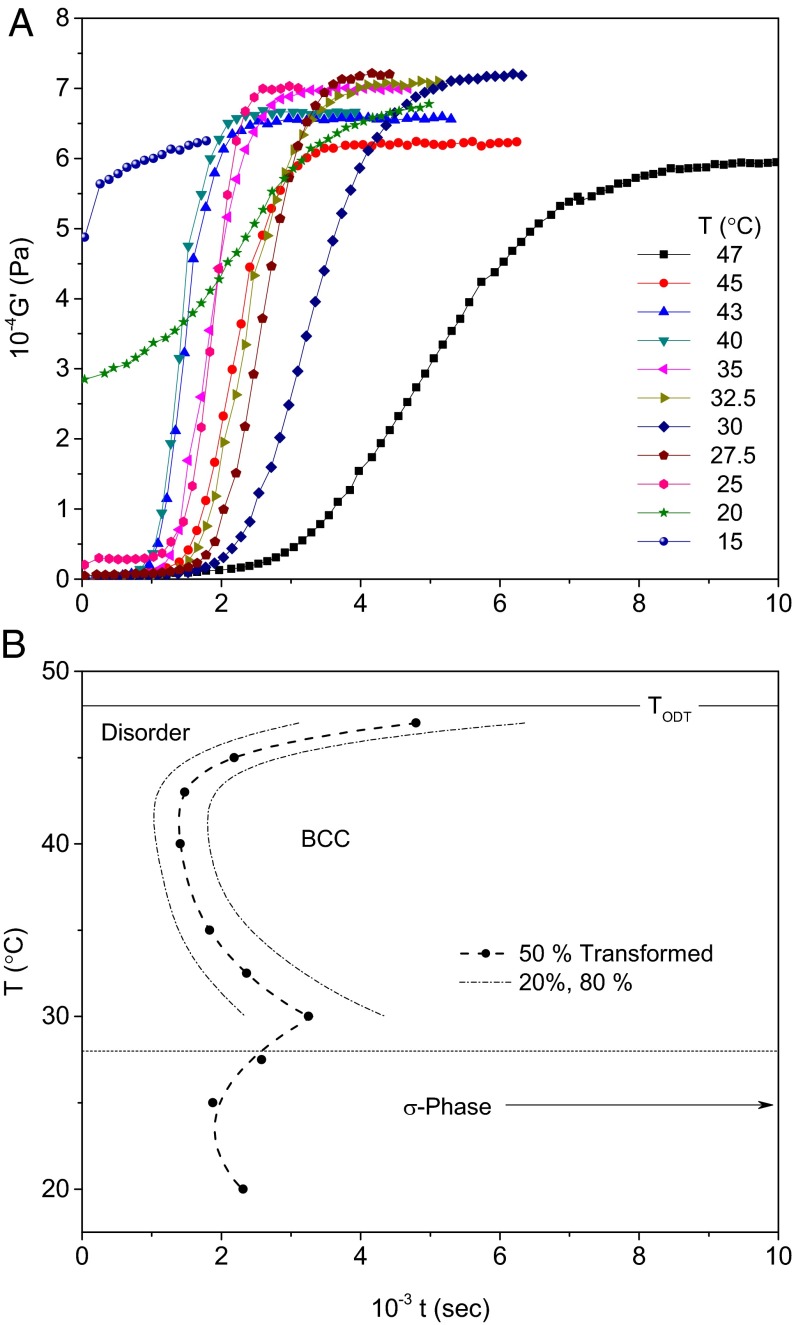
Owing to the facile molecular dynamics of IL-15 (both blocks are well below the entanglement molecular weight) (23), complemented by tractable phase transition kinetics, we were able to quantitatively characterize nucleation and growth of order after quenching from the disordered state. Fig. 3A illustrates the development of the dynamic elastic modulus G′, measured at a frequency of ω = 0.1 rad/s using a parallel plate geometry (25), after rapidly (in ∼30 s) cooling from 60 °C to each target temperature below T_ODT. Between 47 and 20 °C, a characteristic sigmoidal-shaped growth in G′ evidences the development of order. Except for the results obtained at 20 °C, each data set shows an induction period of roughly 15–20 min, followed by the growth of G′ up to an asymptotic level at longer times. These patterns can be modeled based on classical nucleation and growth theory, using X(t) = 1 − exp(−kt⁻ⁿ), where X(t) = (G′ (t) – G′_o)/(G′_∞ − G′_o) represents the fractional change in the elastic modulus, which we equate with the percentage of ordered material. Avrami plots (26) of these results produce n = 3.2 ± 0.2 (Fig. S2A), consistent with the nucleation and growth of order in three dimensions; SAXS experiments confirm BCC symmetry (Fig. 2; refs. 23 and 24). Similar experiments conducted over a period of 24 h after quenching IL-15 to 25 °C lead to n = 2.5 ± 0.2 compatible with ordering with intermediate dimensionality (between 2 and 3), consistent with the formation of the tetragonal Frank–Kasper σ-phase (Fig. S2C). Below about 20 °C, however, the material stiffens almost immediately, obscuring any underlying phase-transition dynamics. Here we note that in all cases the solid state (whether ordered or disordered) represents a relatively soft material (G′ < 10⁴ Pa) owing to the flexible nature of the continuous matrix made up of PI corona blocks.

Fig. 3.

Kinetics of ordering in sample IL-15 following rapid (< 1 min) cooling from 60 °C. (A) Development of elasticity, evidenced by growth in the dynamic elastic modulus G′(ω = 0.1 rad s⁻¹), is associated with the transition from a state of disorder to order. (B) Time-temperature-transformation diagram, which shows the transition from nucleation limited growth of the BCC phase as T → T_ODT to a diffusion limited mode at T << T_ODT. Below about 28 °C the ordering kinetics change, coincident with the growth of the Frank–Kasper σ-phase at long times.

Also shown in Fig. 3B is a time-temperature-transformation diagram identifying the points of 50% growth [i.e., where X(t) = 1/2], and the temporal width of the disorder-to-BCC phase transformation (20–80% completion) as a function of quench depth. The shape of the X(t,T) envelope above 28 °C (i.e., disorder to BCC phase) reflects the consequences of two competing kinetic factors: asymptotically slow nucleation as T → T_ODT and diffusion limitations when T << T_ODT (27). This behavior is abruptly changed below 28 °C, coincident with the phase boundary between the temperatures associated with the equilibrium BCC and Frank–Kasper σ-phases.

Supercooled Disordered State.

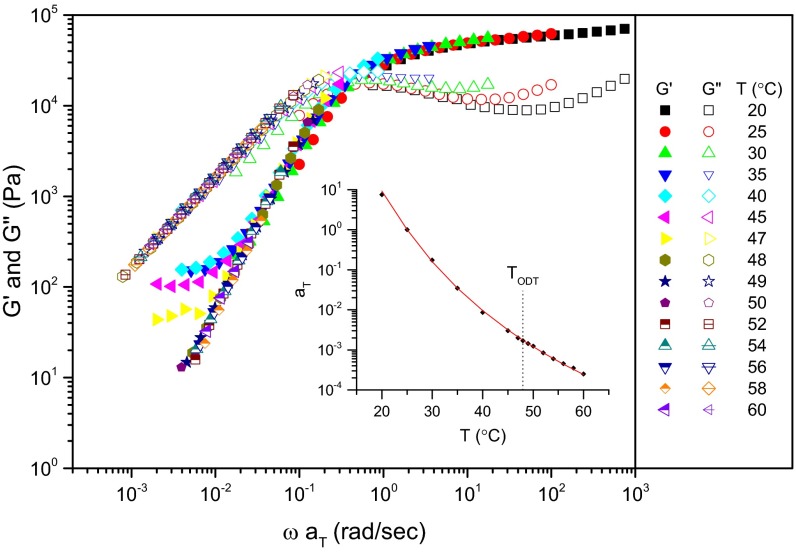
The induction period associated with ordering of IL-15 (Fig. 3) provides a unique opportunity for probing the dynamics of the supercooled disordered state. A viscoelastic spectrum can be obtained over the frequency range 0.1 ≤ ω ≤ 100 rad/s in about 5 min. We have conducted such experiments and determined G′(ω) and the dynamic loss modulus G″(ω) after rapid cooling from 60 °C to various temperatures between 20 and 48 °C, also acquiring equilibrium data between 48 and 60 °C. The results have been shifted along the frequency axis using the time-temperature superposition (TTS) principle (25) and the resulting master plot is shown in Fig. 4 (nonshifted G′ and G″ data are shown in Fig. S3). TTS shift factors were fit to the Williams–Landel–Ferry (WLF) equation (25) and are plotted in Fig. 4, Inset: log(a_T) = −C₁(T − T_ref)/(C₂ + T – T_ref) using a reference temperature T_ref = 25 °C, yielding C₁ = 10.4 and C₂ = 67.3 °C. The frequency dependences of G′(ω) and G″(ω) are consistent with the Maxwell model: For ω << τ⁻¹ the specimen responds as a liquid (G′ ∼ ω² and G″ ∼ ω¹) and for ω >> τ⁻¹ the behavior is characteristic of a soft elastomeric solid (G′ ∼ ω⁰ and G″ ∼ ω⁻¹), where the relaxation time τ is defined by G′(ω) = G″(ω) (25). These results reinforce the notion that the disordered state is a structured fluid above and below T_ODT, consisting of well-formed point particles (micelles) comprised of numerous block copolymer chains. (Because of the low molecular weight of IL-15 the pronounced plateau in G′ cannot be explained by the effects of molecular entanglements). This picture supports conclusions drawn previously by others regarding the non-mean-field structure of asymmetric diblock copolymers in the vicinity of the order–disorder transition (28, 29). We associate τ with the dynamics of the local spatial composition fluctuations in the disordered state. Divergence in τ (i.e., a_T → ∞) in the vicinity of the particle core glass transition temperature (Fig. S1) implicates polymer chain diffusion as the controlling factor in the temperature dependence of the disordered state dynamics, which are much faster than the rate of nucleation of the ordered phases, e.g., at 40 °C, τ ≅ 0.02 seconds whereas the onset of nucleation takes about 10³ s (Fig. 3B).

Fig. 4.

Time–temperature superposed dynamic elastic (G′) and loss (G″) moduli measured as a function of frequency (ω) for the equilibrium (T > T_ODT = 48 ± 1 °C) and supercooled (T < T_ODT) disordered states in sample IL-15. Experiments at T < T_ODT were conducted following rapid cooling (<1 min) from 60 °C. Acquisition of these spectra was completed in less than 10 min. The Inset shows the temperature dependence of the shift factors a_T, which have been fit to the WLF equation with reference temperature T_ref = 25 °C. These results evidence the dynamics of the fluctuating disordered state, which can be represented by the Maxwell model with a single time constant τ⁻¹ = ωa_T defined by the crossover point G′(ω) = G″(ω).

Particle Vitrification.

Quenching to temperatures below 20 °C moves the experimentally accessible viscoelastic window to ω >> τ⁻¹, where G′(ω) and G″(ω) are relatively insensitive to the state of order and disorder. We have used a different strategy in this limit to probe the structure of the material. Rapid changes from 60 °C to temperatures between 0 and 20 °C (< 1 min) were followed by periods of controlled annealing (15 min to 6 h). These aged specimens were then heated at various rates (0.1–5 °C/min) while simultaneously measuring G′ at a fixed frequency (between 0.1 and 1 rad/s). A summary of these experiments is provided in the Supporting Information (Fig. S4 A, B, and C). When quenched to T < 15 °C reheating the specimen produces a distinct response in G′ between 18 and 25 °C due to ordering, regardless of the annealing time; the temperature at which ordering occurs is controlled by the heating rate. When quenched to T > 15 °C the response upon heating depends strongly on the annealing time; long annealing times allow the specimen to order before reheating. These results show conclusively that supercooled disordered IL-15 is “frozen” below 15 ± 1 °C (Fig. 2G). We refer to this as a “glassy” state and note analogies with the behavior of granular materials, foams, emulsions, and colloidal suspensions, which form jammed solids (30). Clearly, the particle glass transition temperature, T_g,p ∼ 15 °C, is correlated with vitrification of the particle cores. Long-range movement of the block copolymer chains is completely arrested when the cores solidify. However, the vitrified material is not a glass in the conventional sense because the particles contain flexible and dynamically active corona blocks that are tethered to the dynamically inactive cores. Nevertheless, this behavior is closely related to the properties of liquids near the glass transition temperature, which we return to in the discussion section.

Discussion

Symmetry Breaking and Mass Exchange in Block Polymers.

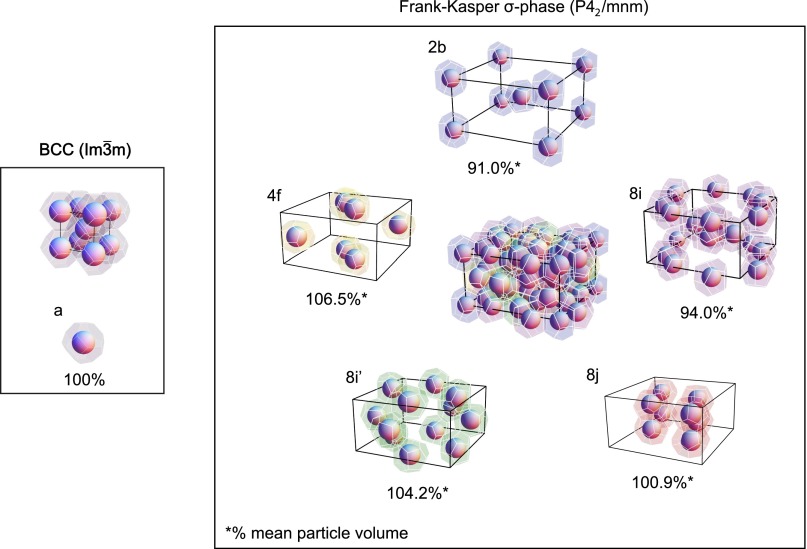
Block polymers order at mesoscopic length scales controlled by the dimensions (e.g., radius of gyration) of the constituent flexible chains (31). Liquidlike packing of chain segments at short length scales (< 1 nm scale) dictates a uniform distribution of monomers, independent of the overall spatial arrangement of the polymer blocks. This constraint mandates that the morphology created by block segregation must partition space at constant density. As a consequence the mesoscopic lattice symmetry imposes unavoidable restrictions on the size and shape of the particles that make up the ordered and disordered morphologies (32–34). We illustrate this feature in Fig. 5 for the BCC and Frank–Kasper σ-phases, which contain 2 and 30 particles per unit cell, respectively. Particle symmetry is captured by the associated Wigner––Seitz cells: one particle size and shape for the cubic structure (each containing ∼193 diblock copolymer chains in our case) and five distinct geometric representations for the tetragonal case (containing between about 176 and 206 chains) (23). Within each unit cell, the polymer blocks are distributed in a manner that balances unfavorable segment–segment interactions and chain stretching.

Fig. 5.

Space-filling representations of the crystal structures for the BCC ($Im\overline{3}m$ space group) and Frank–Kasper σ ($P{4}_2\text{/}mnm$) phases. The faceted polyhedrons represent self-assembled particles that must fill space at uniform density, necessitating distortions in size and shape imposed by the lattice symmetry. The BCC crystal contains one particle per lattice site, each formed from ∼193 block copolymer molecules. The σ-phase has 30 particles per lattice site, split among 5 discrete polyhedral with varying size and shape, at the indicated Wyckoff positions (2b, 4f, 8i, 8i′, 8j, where occupancy is denoted by the integer). The relative volume of each polyhedral is satisfied by varying the number of molecules per particle between approximately 176 and 206.

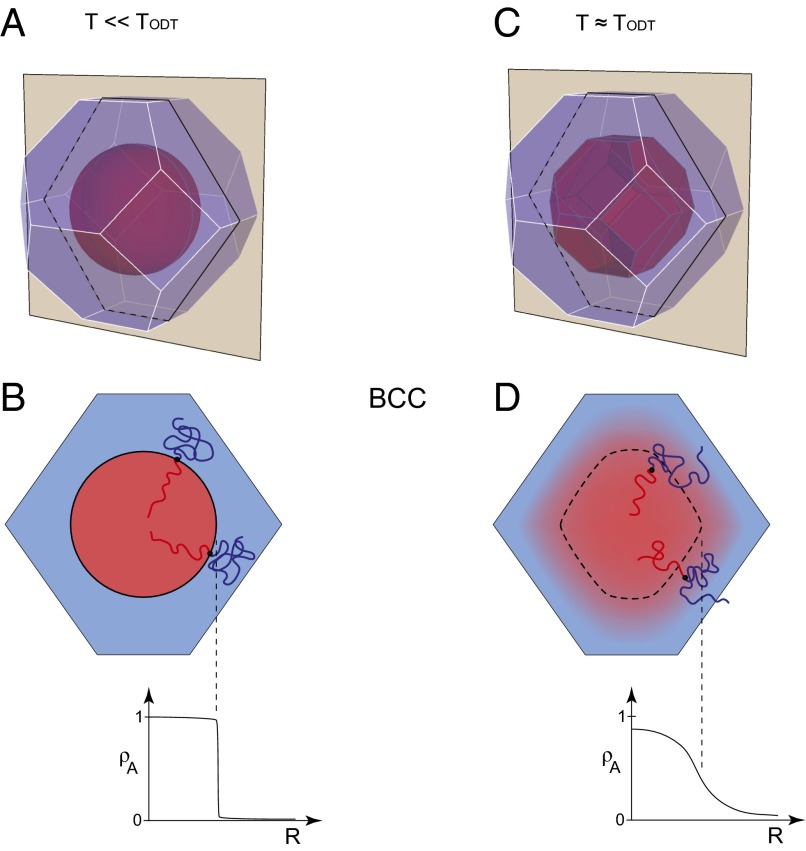
The detailed spatial arrangement of the block segments within a particle is influenced by the temperature as illustrated in Fig. 6. Reducing temperature sharpens the core–corona composition profile and reduces the extent of interpenetration of corona blocks at the Wigner–Seitz cell boundaries. At finite degree of polymerization (N) both interfaces become step functions as T → 0 (Fig. 6B); this is referred to as the strong segregation limit (SSL) (22). Classical mean-field SSL treatments of block copolymer phase behavior provide estimates of the associated interfacial tension γ = (k_BT/a²)(χ/6)^1/2 and composition profile ρ = 1/2[1−tanh (2r/a_I)], where χ ∼ T⁻¹ is the Flory–Huggins segment–segment interaction parameter and a_I = (2/6^1/2)aχ^−1/2 is the characteristic width of the interface; a is the statistical segment length (35). Near T_ODT the composition profile that defines the core–corona interface softens and the corona blocks mingle with neighboring cells as illustrated in Fig. 6D. At a sufficiently high temperature, T >> T_ODT, the micelles evaporate leaving a spatially homogeneous (mean field) distribution of blocks (36). We believe the competition between the tendency to form spherically symmetric interfaces and the restrictions placed on the particle shape by the lattice symmetry drives the transition from BCC to the tetragonal Frank–Kasper σ-phase upon cooling. Grason (33) has expanded on related arguments presented by Ziherl and Kamien (34) that address the formation of the Frank–Kasper A15 phase in block polymers and other soft materials.

Fig. 6.

Illustration of the competition between particle core sphericity and BCC crystal lattice symmetry dictated by the constraint of constant overall density. (A, B) At low temperatures unfavorable interactions between the core and corona blocks produces a sharp composition profile at the core–corona interface and at the Wigner–Seitz cell boundary. (C, D) Increasing the temperature softens the interfacial composition profile and reduces the interfacial tension, accompanied by mingling of corona blocks at the cell boundary. We argue that these real-space depictions can be related to the tradeoff between sphericity of the free-electron-like Fermi surface, when constrained by the Jones zone imposed by lattice symmetry in single component metals such as Mn and U.

Every particle in the BCC structure has eight nearest and six next nearest neighbors, resulting in a Wigner–Seitz cell that is a truncated octahedron with 14 faces. The five discrete types of particles in the σ-phase contain between 12 and 15 neighbors leading to Wigner–Seitz polyhedra that represent a compromise between purely dodecahedral and truncated octahedral arrangements and an average of 13.5 faces (4). On average the Frank–Kasper σ-phase polyhedra are closer to spherical than the BCC case. We have determined the mean isoperimetric quotient (IQ = 36πV²/S³, where V and S are the polyhedral volume and surface area, respectively) (37) for the Frank–Kasper σ-phase to be (IQ)_σ = 0.7624, which exceeds (IQ)_BCC = 0.7534. (See Fig. S5 and Table S1 for a summary of our calculation of IQ). Perfect sphericity is indicated by IQ = 1. Hence, the σ-phase can better accommodate the tendency to minimize distortions away from a spherical particle shape with decreasing temperature; it also just eclipses the mean value for the A15 phase (two types of polyhedra), (IQ)_A15 = 0.7618. [This line of reasoning also explains why BCC packing is favored over FCC, (IQ)_FCC = 0.7405, in the SSL]. We hasten to add that this tradeoff involves yet another competition associated with optimally configuring the blocks within the particle core and corona (33), which presumably favors a single-core diameter.

Within the context of self-consistent mean-field theory (SCFT, N → ∞) the entropic (TΔS) and enthalpic (ΔH = Σγ, where Σ is the total interfacial area within the SSL) contributions to the Gibbs free energy, ΔG = ΔH − TΔS, are governed by the combined parameter χN (22). Reducing temperature leads to an increase in the particle diameter, d ∼ χ^1/6N^2/3, where the reduction in interfacial area exactly compensates for the loss in entropy. However, as T → 0, the Gaussian chain assumption associated with the mean-field theory must fail at some point because the chain cannot be stretched beyond the finite contour length set by N, which places a limit on the magnitude of d. Thus, decreasing N should enhance the drive toward sphericity when the temperature is lowered below T_ODT.

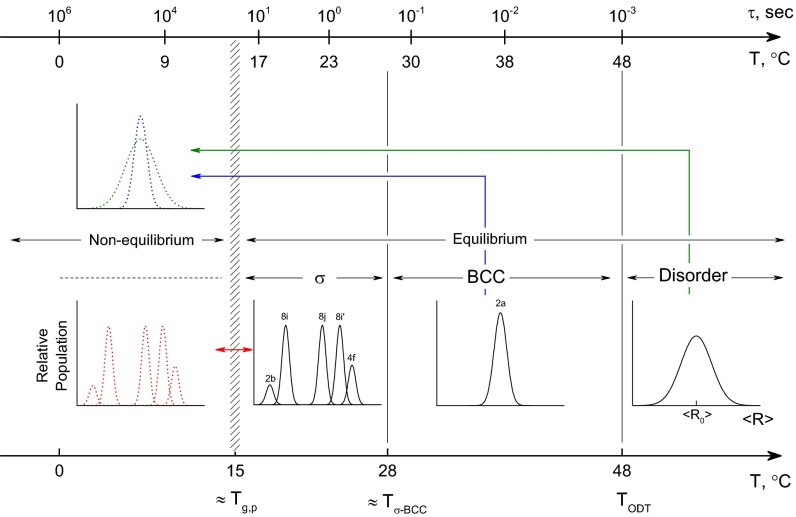
Our observations regarding the distribution in size and shape of the soft particles in the ordered state can be extended to the disordered state. Although we have indisputable diffraction data to justify our assessments of the BCC and Frank–Kasper σ-phases, the detailed structure of the disordered material in the equilibrium (T ≥ T_ODT), supercooled (T ≤ T_ODT) and glassy (T ≤ T_g,p) states can only be inferred from the associated diffuse SAXS patterns shown in Fig. 2. Nevertheless, satisfying the constant density constraint and a state of disorder requires a broad and continuous distribution of particle sizes and shapes at any instant in time. We have illustrated the resulting average distribution of particle sizes <R> taken over all shapes in the disordered state in Fig. 7, along with the corresponding discrete distributions for the BCC and σ-phases. Clearly, growth of the Frank–Kasper sigma phase from the supercooled disordered state requires the transfer of block copolymer chains (mass) between particles. If mass transfer is arrested the system becomes frustrated and cannot break symmetry, which explains the results obtained when IL-15 is rapidly cooled from 60 to 0 °C (Fig. 2 A, D, and G). Vitrification of the PLA-rich particle cores inhibits the exchange of mass, and this suppresses ordering. However, we note that the local composition profile within each particle (Fig. 6 B and D) is established rapidly with respect to the particle relaxation time τ when T > T_g because mass transfer between particles is not required.

Fig. 7.

Symmetry breaking and the exchange of mass in sample IL-15. Transition between the equilibrium BCC and Frank–Kasper σ-phases requires a redistribution of block copolymer molecules from a monomodal population of particles to a distribution of five particle shapes and sizes with a commensurate 15-fold increase in the size of the unit cell. Rapidly cooling the disordered melt below the point of core vitrification (∼15 °C) turns off molecular (mass) exchange leading to a glassy soft solid at T < T_g,p. The arrows between the equilibrium and nonequilibrium states refer to the results shown in Fig. 1. Loss of BCC order upon cooling from 40 to 0 °C (Fig. 1 B and E) suggests a diffusionless transition to a locally structured but globally disordered state before solidification of the core. The upper axis identifies the time constant τ for relaxation of the disordered state as a function of temperature (Fig. 4).

Growth of the σ-phase is preceded by the relatively rapid development of order (Fig. 3); SAXS patterns reported previously (23) include diffraction peaks coincident with BCC symmetry and this early stage of ordering is characterized by the Avrami exponent n = 3.2 ± 0.1 (Fig. S2B). This result suggests that the distributions of particle sizes above and below T_ODT are similar and that the BCC phase nucleates and grows from the supercooled disordered liquid without the net exchange of mass between particles; only the particle shapes change. In this respect, the nucleation and growth of the BCC phase between 28 and 48 °C is exactly analogous to the crystallization of elemental metals from the liquid state, consistent with the behavior shown in Fig. 3B.

We emphasize that growth of the Frank–Kasper σ-phase in IL-15 is not predicated on preparing particles with multiple sizes and shapes (38–40). The system spontaneously selects the optimal arrangement of the (nominally) single components through a competition between chain packing and lattice symmetry. We believe this mechanism is likely to be operative in other forms of soft materials that produce hierarchical structures through the self-assembly of mesoscopic particles.

Transient Structures.

Although this article deals primarily with the formation of equilibrium BCC and Frank–Kasper σ-phases, the consequences of mass transfer (i.e., diffusion) limitations on the phase transition dynamics and the structure of the glassy soft solid warrant a few additional brief remarks. The qualitative change in the ordering kinetics evident in Fig. 3 below about 28 °C is strikingly similar to the phenomena referred to as fast crystal growth in certain glass-forming liquids, where diffusion limitations activate the rapid development of local order through a diffusionless process (41–44). We speculate that the rapid growth in elasticity before the development of the Frank–Kasper phase may reflect the formation of clusters with tetrahedral, or perhaps more symmetrically arranged (e.g., icosahedral) coordination (45), facilitating fast nucleation of BCC order, which ultimately slowly reorganizes into the σ-phase. A related and fascinating observation is disordering of the BCC phase when rapidly cooled from 40 to 0 °C (Fig. 2 B and E). Although we cannot draw completely concrete conclusions regarding this behavior, transitioning to the thermodynamically favored σ-phase likely begins with disordering (melting) of the BCC structure, a diffusionless process that may occur rapidly with respect to the rate of cooling (ca. 20 °C per minute), leading to local clustering as suggested above. Superficially this process resembles a Martensitic transition (46), which may render a state of local order (e.g., icosahedral) but not long-range translational order, perhaps the seeds for the formation of a quasicrystalline state, which is known to lurk at temperatures just below where the Frank–Kasper σ-phase is found in tetrablock terpolymers (19). Quenching the quasicrystal approximant from 25 to 0 °C (Fig. 1 C and F) induces no noticeable structural changes, consistent with this line of reasoning.

Symmetry Breaking and Charge Exchange in Metals.

The essence of the above is that the symmetry breaking required to crystallize such polymer particles in complex tetrahedral structures is achieved via molecular exchange, arising from competition between packing and sphericity. We propose that these two key features, symmetry breaking via chain exchange and competing local and many-body interactions, invoke intriguing analogies with a seemingly different class of one-component solids: the metallic elements. These connections not only elucidate the generality of these concepts, but point to opportunities to further understand complex crystallization using block polymers as model systems.

We first highlight an analogy between symmetry breaking via molecular exchange in block polymers and symmetry breaking via charge exchange in elemental metals. That the majority of the metallic elements adopt close packing is a manifest consequence of nondirectional metallic cohesion involving itinerant electrons. FCC, HCP, and BCC structures thus dominate the metallic region of the periodic table, a trend that breaks down across the metalloids as covalent/ionic tendencies emerge. In the metallic region the detailed trends in the stability of FCC vs. HCP vs. BCC can generally be understood based on one-electron band-structure energies (47, 48). Crystal structure trends of simple alloys can be similarly rationalized, a key concept being that of the Jones zone (49, 50). The idea with the latter is to form a polyhedron in reciprocal space (not necessarily the Brillouin zone) defined by the high structure factor planes, i.e., those where discontinuities in dispersion (energy gaps) occur in a nearly-free-electron model. A given metallic system favors the ground-state crystal structure with a reciprocal lattice such that a free-electron-like Fermi surface defined by the relevant valence electron density is entirely enclosed by the Jones zone, obviating population of higher zones and thus the energy costs associated with the gaps at the zone boundaries. This concept helps rationalize the Hume–Rothery rule for instance, i.e., the observation that many binary alloys undergo phase transformations controlled largely by valence electron count (49, 50). Within a rigid-band virtual crystal picture these transitions occur at compositions where the Fermi surface intersects zone boundaries, triggering transformation to a new structure with a Jones zone enclosing the Fermi surface.

Such simple analyses neglect the fact, however, that there are clear exceptions to simple close packing in the metallic elements, notably for Mn in the transition metals, Pr through Sm in the rare earths, and Pa onward through the transuranics. These elements crystallize in a variety of complex, low-symmetry structures, several of which relate closely to the topologically close-packed Frank–Kasper σ-phase studied in this work. As specific examples to illustrate our proposed connection to block polymers, we first focus on Mn and then U.

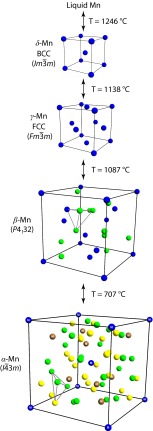
Upon solidification at 1,246 °C Mn crystallizes in a BCC phase (δ-Mn), followed by transformation at 1138 °C to FCC γ-Mn (10, 11). Additional cooling leads to transitions to remarkably complex phases, first β-Mn at 1,087 °C (an A13 structure with space group P4₁32 and 20 atoms per cell) (11), then α-Mn at 707 °C (A12, $I\overline{4}3m$, 58 atoms per cell) (10), both of which have Frank–Kasper-like polytetrahedral structures. These structures and transformations are illustrated in Fig. 8. Central to our argument, the symmetry breaking that must occur upon cooling from the original BCC structure (whose stability is likely strongly influenced by entropic contributions; ref. 51) to these complex lower temperature structures is achieved via spin-dependent charge exchange between originally equivalent Mn sites. This arises from a competition between the drive to strong metallic cohesion on the one hand, and the tendency to maximize spin and obey Hund’s rule on the other (10). The result, in α-Mn, the ground state, is four inequivalent sites with varying coordination, atomic radii, local density-of-states, and magnetic moment (10) as depicted in Fig. 8. Mn can thus be thought of as an intermetallic compound composed of magnetic and nonmagnetic components (10). We contend that such symmetry breaking by spin-dependent charge redistribution is analogous to the symmetry breaking by molecular chain redistribution reported in this work. We emphasize that in both cases a key ingredient in the symmetry lowering is frustration of the natural packing tendency by some local interaction.

Fig. 8.

Illustration (reduced sphere representation) of the unit cells of the sequence of crystalline phases that can occur in Mn. On cooling, this sequence includes δ-Mn (BCC, $Im\overline{3}m$), γ-Mn (FCC, $Fm\overline{3}m$), β-Mn (P4₁32), and α-Mn ($I\overline{4}3m$). Distinct colors in each case represent inequivalent sites, and the label “M” in the case of α-Mn indicates magnetic sites, i.e., those with large moment. Polyhedra are shown in the low-symmetry structures to highlight the local packing arrangement. Note that for α-Mn we label only four inequivalent sites, following Hobbs et al. (10).

To provide another example, similar analogies can be drawn with metallic U, which crystallizes (in its ground-state α-phase) in orthorhombic space group Cmcm (52). This structure is unique among the elements at ambient pressure, as is the existence of a charge density wave (CDW) state below −230 °C, which eventually yields superconductivity (53). Of most relevance to the current work, the complex structure is again thought to arise from competition. In this case the unusually narrow (∼1 eV) 5f bands weaken metallic cohesion to the point that the Peierls-related CDW instability competes (47), symmetry breaking occurring once more via charge redistribution. Upon heating, the ground-state α-phase transforms to the β-phase with P4₂/mnm symmetry (structurally identical to the Frank–Kasper σ-phase), followed by a BCC phase [again, likely stabilized to a significant extent by entropy (51)], and eventually melting at about 1,132 °C (54).

Crystal Symmetry vs. Sphericity.

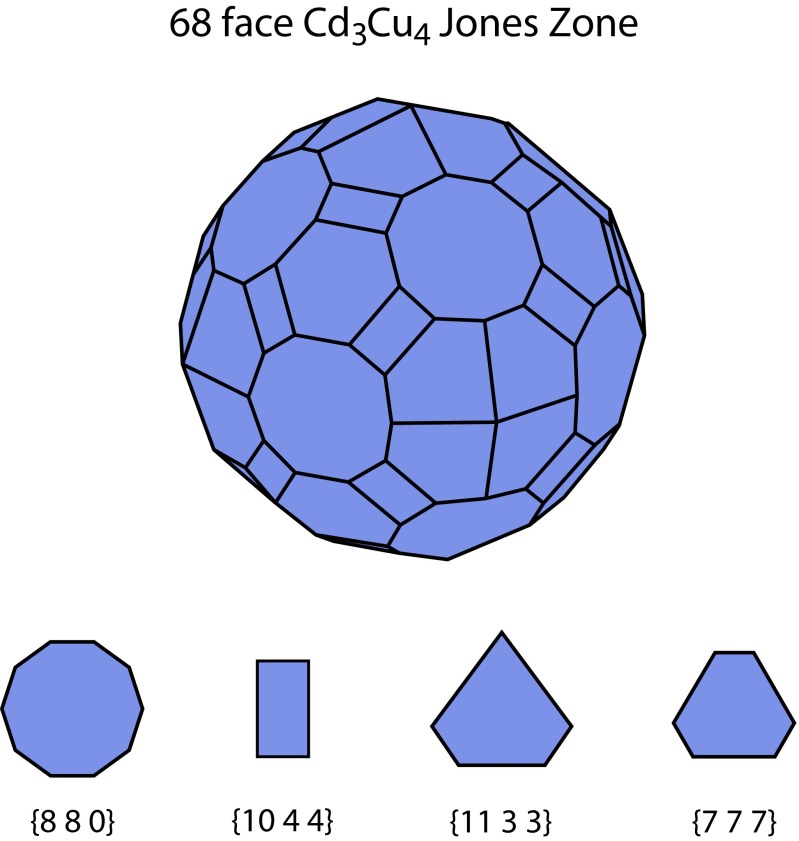
Recent extensions of the Jones zone concept to substantially more complex (often very large unit cell) metallic systems, including binary intermetallic compounds (55), high pressure phases (55, 56), tetrahedrally packed intermetallics (57), and multicomponent quasicrystals (58), offer additional intriguing analogies with our work. Illustrative examples are provided by Lee et al. (57) who demonstrated that the observed stoichiometries of highly complex tetrahedral-cluster-based group 10–12 intermetallic compounds (e.g., in the Cu–Cd system) and related quasicrystal approximants (e.g., Zn₁₁Au₁₅Cd₂₃) can be understood to a surprising extent on the basis of electron count. The essential concept is that the ground-state complex tetrahedral close packing in these materials generates highly structured Jones zones, with as many as 72 facets, conforming to a free-electron-like spherical Fermi surface to a remarkable extent as illustrated in Fig. 9. Lee et al. argue that this drive to sphericity of the Jones zone to optimally reconcile electronic and crystal symmetries leads to pseudosymmetry axes that can be described by 4D point groups, in essence an attempt to exceed the symmetry possible in the 230 three-dimensional space groups of periodic crystals (57).

Fig. 9.

Depiction of the reciprocal space Jones zone in the Cd₃Cu₄ ordered intermetallic alloy, following Lee et al. (57). The family of high-structure factor planes corresponding to each face is shown at the bottom. Note the remarkable sphericity of this 68-face polyhedron.

We propose that the analogies between this situation in reciprocal space in tetrahedrally packed intermetallics and the real-space situation depicted in Figs. 5 and 6 are readily apparent. The role of the originally spherical free-electron Fermi surface in the metallic case can be compared with an isolated spherical block copolymer particle (micelle), for example dispersed in a sea of homopolymer with the same chemistry as the corona blocks. The Jones zone of the reciprocal lattice in the metallic case is analogous to the real space Wigner–Seitz cell in the pure (undiluted) block polymer, as reflected in the core–corona and cell boundary interfaces in Fig. 6D, the shape of which reflect the essential competition between sphericity and crystal symmetry. Most importantly, the symmetry breaking depicted in Fig. 5 can then be viewed as quite analogous to the situation summarized above for tetrahedrally packed intermetallics. The latter adopt ground-state structures that maximize Jones zone sphericity to optimally conform to the electronic symmetry of the free-electron-like Fermi surface (57). In the block copolymer system the symmetry breaking via chain exchange occurs to improve the sphericity of the Wigner–Seitz cells as demonstrated by the improvement in site-averaged isoperimetric quotient. In both cases, the key aspect is competition between crystal symmetry/packing and the preferred local symmetry. It is interesting to note that a necessary consequence of the adoption of a structure with the many-faceted Wigner–Seitz cells shown in Fig. 5 is the existence of a large number of high-structure factor planes, as is self-evident from Fig. 2 C and F. In the intermetallic case the equivalent multifaceted Jones zone (Fig. 9) is the enabling factor in the strong mixing of electronic states that stabilize the observed complex structures (57).

General Comments

The analogies we propose here highlight modest connections between the limits of knowledge of block polymer and intermetallic systems. We anticipate that much additional work can be done, not only to strengthen these points of connection but also to more clearly understand the extent to which the unique features of block polymers can be used to advance the understanding of crystallization in complex, apparently low-symmetry structures. In this context we note that these block polymers not only offer a means to do so in a completely classical system but that they further provide one-component systems with near continuous compositional tunability. In some sense they can thus be viewed as ideal realizations of the virtual crystal approximation and rigid band assumptions used in the application of Jones zone concepts to alloys and intermetallic compounds.

The simplicity and universal nature of the arguments we have presented lead us to ponder why Frank–Kasper phases have not been reported previously in the much studied field of diblock copolymers. Evidence is building to support the notion that a multiblock architecture widens this window (59). An enabling yet complicating feature with block polymers is the exceedingly slow molecular dynamics associated with most synthetic diblock copolymers. Increasing N leads to entanglements and a transition to molecular relaxation by reptation (τ_reptation ∼ N³ in homopolymers) rather than Rouse (τ_Rousse ∼ N²) dynamics (25). The PI-PLA system studied here was designed to overcome such limitations; the relatively large χ parameter leads to ordering at values of N well below the entanglement limit, affording facile dynamics that result in the growth of a polycrystalline material where the individual grains have long-range order. Many other combinations of polymers would be suitable for this purpose and provide independent control of the phase transition kinetics by judiciously positioning order–order and order–disorder transition temperatures relative to particle vitrification through adjustment of N. We predict that increasing the overall chain length of IL-15 by roughly 10% (at constant composition) will elevate the BCC–disorder and σ-phase–BCC transition temperatures by ∼50 °C, possibly exposing additional ordered structures above the particle glass transition temperature, which is essentially independent of N. Mass exchange might also be used in polymer-stabilized inorganic particles through reversible grafting or adsorption, offering a route to hybrid quasiperiodic crystals possibly endowed with tailored photonic band gaps (60).