Corner height influences center of mass kinematics and path trajectory during turning

Abstract

Despite the prevalence of directional changes during every-day gait, relatively little is known about turning compared to straight gait. While the center of mass (COM) movement during straight gait is well characterized, the COM trajectory, and the factors that influence it, are less established for turning. This study investigated the influence of a corner’s height on the COM trajectory as participants walked around the corner. Ten participants (25.3 ± 3.74 years) performed both 90° step and spin turns to the left at self-selected slow, normal, and fast speeds while walking inside a marked path. A pylon was placed on the inside corner of the path. Four different pylon heights were used to correspond to heights of everyday objects: 0 cm (no object), 63 cm (box, crate), 104 cm (desk, table, counter), 167 cm (shelf, cabinet). Obstacle height was found to significantly affect the COM trajectory. Taller obstacles resulted in more distance between the corner and the COM, and between the corner and the COP. Taller obstacles also were associated with greater curvature in the COM trajectory, indicating a smaller turning radius despite the constant 90° corner. Taller obstacles correlated to an increased required coefficient of friction (RCOF) due to the smaller turning radii. Taller obstacles also tended towards greater mediolateral (ML) COM-COP angles, contrary to the initial hypothesis. Additionally, the COM was found to remain outside the base of support (BOS) for the entire first half of stance phase for all conditions indicating a high risk of falls resulting from slips.

Introduction

Human gait has been a widely researched area especially concerning slips, trips, and falls. However, the majority of research has examined straight gait. Turning and non-straight steps make up approximately 35–45% of all steps (Glaister et al., 2007a) yet have received little attention compared to straight gait. An individual’s whole-body center-of-mass (COM) trajectory has been well characterized during straight gait (Gard et al., 2004; Granata and Lockhart, 2008; Lee and Farley, 1998; Lee and Chou, 2006; Lockhart et al., 2003; MacKinnon and Winter, 1993; Orendurff et al., 2004) but is less understood during turning.

Turning is distinctly different than straight walking (Glaister et al., 2008; Hicheur and Berthoz, 2005). Turning requires a much larger required coefficient of friction (RCOF) to prevent slips (Fino and Lockhart, 2014) and has a higher incidence of falls resulting from slips (Yamaguchi et al., 2012a) than straight walking due to the lateral displacement of the COM relative to the base of support (BOS). Larger turning radii affect the orientation of the head and trunk (Sreenivasa et al., 2008), increase the COM displacement outside the BOS (Hollands et al., 2001), and decrease the walking velocity (Dias et al., 2013). Increasing the walking speed has a similar relationship, increasing the COM displacement outside the BOS (Orendurff et al., 2006).

To date, no study has examined how the geometry of an object affects the COM while turning. During turning, individuals lean in towards the apex to compensate for the centripetal force (Courtine and Schieppati, 2003). While the degree to which individuals lean depends on speed (Orendurff et al., 2006) and turning radius (Hollands et al., 2001), the response is unknown if this lean is obstructed by an obstacle. Previous studies have used objects to demark a corner (Grasso et al., 1998) or prevent participants from crossing through a corner (Glaister et al., 2008; Glaister et al., 2007b), but there is currently no knowledge concerning how the object’s shape or size influences the participants’ kinematics. Our earlier analysis reported no effect of obstacle height on RCOF during the push-off phase of gait (Fino and Lockhart, 2014) but did not examine other phases of the turn nor reported COM trajectories. Given that most turns in a crowded environment are to avoid obstacles (Glaister et al., 2007a), it is worth investigating whether the geometry of those obstacles impacts the resulting maneuvers and influences fall risk. While important for researchers wishing to examine turning gait, this knowledge may also be useful in designing pedestrian environments by providing guidelines for the size of barricades, posts, tables, and walls in order to maximize pedestrian flow and reduce the chances of slips and falls.

This study observed the effect of objects’ heights on the COM trajectory at slow, normal, and fast walking speeds during a 90° turn. We hypothesized that taller obstacles would restrict the mediolateral (ML) component of the COM-COP angle, θ_ML. Additionally, taller obstacles were expected to result in wider turns, larger path curvatures, and greater clearance between the obstacle and the COM or COP. The RCOF at weight acceptance was hypothesized to increase with obstacle height and speed. The COM and COP clearance and θ_ML were expected to increase with speed (Fino and Lockhart, 2014; Orendurff et al., 2006) and be greater for step turns compared to spin turns (Taylor et al., 2005).

Methods

Participants

Seven males and three females, 18–45 years of age (mean 25.3 ± 3.74 years), were recruited from Virginia Tech and the surrounding community for the study. Participants were informed of the protocol and gave written informed consent prior to the experiment. Participants were excluded if they had any history of balance disorders, dizziness, musculoskeletal injury within the past year affecting normal gait, any neurological disorders, one or more concussions within the past year, and / or significant visual impairment. The complete protocol was approved by the Institutional Review Board at Virginia Tech.

Experimental Procedure

The full procedure and overheard view of the set-up was reported by Fino and Lockhart (2014). Briefly, participants walked along a 0.75 m wide marked path with a 90° turn. The path was straight for 3.5 m followed by a 90° left turn into a 2.5 m straight segment. The beginning and end of the path were marked with start and stop lines, respectively. A 10 cm diameter pylon was placed on the inside of the 90° corner as the obstacle. Four different pylon heights were used corresponding to heights of everyday objects: 0 cm (no object), 63 cm (box, crate), 104 cm (desk, table, counter), and 167 cm (shelf, cabinet). The floor surface was covered in a Micropore tape (3M, St. Paul, MN 55144-1000, USA) to prevent slipping while turning the corner, especially at fast speeds. Prior testing revealed gait adjustments and slips when performing the task. The tape successfully increased the available friction of the floor allowing the participants’ natural actions to be observed without any adaptations (Fino and Lockhart, 2014). Participants wore their own athletic shoes throughout the experiment.

Three-dimensional kinematics were measured using a six-camera Pro-Reflex motion analysis system (Qualisys Track Manager version 1.6.0.163, Qualisys AB, Gothenburg, Sweden) and 35 infrared-reflective markers placed bilaterally over the first, second, and fifth metatarsal heads, medial and lateral malleolus, calcaneus, medial and lateral femoral condyle, anterior superior iliac spine, trochanter, iliac crest, clavicle (adjacent to the suprasternale), acromioclavicular (AC) joint, lateral humeral condyle, ulnar stylus, third metacarpal head, ear, and top of head. A marker was also placed on top of the corner pylon directly over the inside corner of the path. Two force plates (AMTI # BP6001200100, AMTI Force and Motion, Watertown, MA 02472, USA) (Bertec #K80102, Type 45550-08, Bertec Corporation, OH 43212, USA) were embedded into the walkway at the corner. All data was sampled at 100 Hz.

Participants were instructed to walk normally within the path, to avoid hitting the pylon, and to continue until they reached the stop line. The participants were instructed to walk at one of three speeds: normal (NW), slower than their normal pace (SW), and “as fast as possible without running or jogging” (FW). Warm-up trials were used to adjust the subjects starting position to ensure their turning limb landed on the corner force plate. The participants performed three straight gait trials followed by 24 turning trials for each speed. The turning trials were divided into four blocks, one for each obstacle height. For each obstacle height, participants performed three step turns and three spin turns, where a step turn was defined as a turn away from the stance limb and a spin turn is defined as a turn toward the same side as the stance limb (Taylor et al., 2005). To eliminate order effects, speed, obstacle height, and strategy order was rotated for each participant (Fino and Lockhart, 2014).

Data Analysis

Data from all ten participants were analyzed. Trials in which the participant stepped multiple times on the force plate or only partially stepped on the force plate were excluded from the analysis. A total of 291 of the 720 trials were excluded for this reason (148 slow trials, 84 normal, and 59 fast). The 3-dimensional marker data and the force plate data were filtered using a 5 Hz 2^nd order low-pass Butterworth filter. During the second half of the turning stance phase, several kinematic markers were obstructed from the cameras’ views. Therefore, kinematic data from only the first half of each stance phase was analyzed. All analysis was performed using MATLAB (MATLAB and Statistics Toolbox Release 2013b, The MathWorks, Inc., Natick, Massachusetts, USA).

COM Clearance and COP Distance

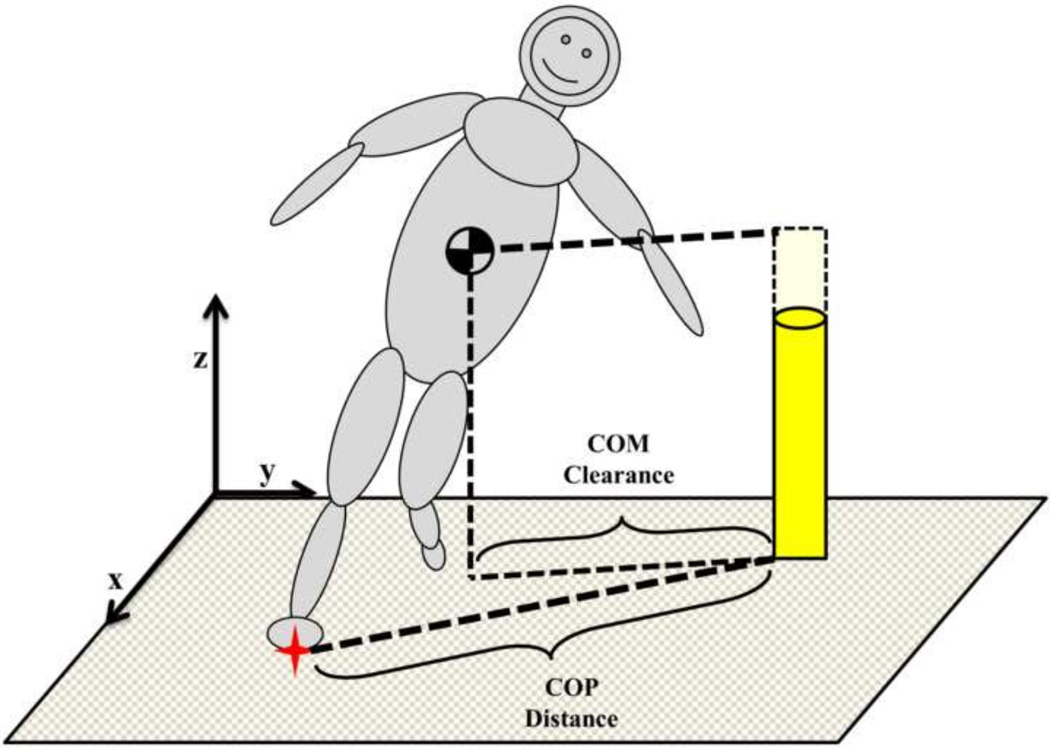
The COM was calculated using individual body segments’ masses and center of mass locations from the reflective markers at the segment endpoints (De Leva, 1996). The COM clearance was calculated as the distance in the horizontal plane from the COM to the corner pylon as shown in Figure 1. Due to the different pylon heights, a vertical projection of the corner pylon was extended upward to the COM height. The ground reactive forces (GRF) were recorded by the force plate and used to calculate the COP according to the force plate manufacturer (Bertec Corporation, OH 43212, USA). The COP distance was calculated as the distance from the COP at weight acceptance to the corner pylon.

Figure 1.

Depiction of COM clearance and COP distance calculations. The COM clearance was the planar distance from the whole-body COM to the pylon (yellow) or pylon projection to the COM horizontal plane. The COP (red star) distance was the horizontal distance from the COP to the base of the pylon.

Required Coefficient of Friction

The RCOF was calculated as

$$RCOF=\frac{F_{\mathit{\text{horizontal}}}}{F_{\mathit{\text{vertical}}}}$$ (1)

where F_vertical is the vertical force F_z and F_horizontal is the resultant sum of F_x and F_y,

$$F_{\mathit{\text{horizontal}}}=\sqrt{F_x^2+F_y^2}.$$ (2)

Maximum RCOF values were extracted from the first half of the stance phase where the stance limb contacted the force plate. The maximum RCOF during the first half of the stance phase corresponded to the RCOF at weight acceptance. Immediately following heel contact and preceding toe-off, large RCOF values have been reported but do not result in slips (Redfern et al., 2001). The large RCOF values are products of extremely small vertical GRFs, which inflate the RCOF values. In practice, however, the opposite limb supports the majority of the body weight. Thus, slipping the foot supporting little body weight does not result in the macroscopic slips associated with slip and fall accidents. To prevent these high RCOF values which do not typically result in slips and falls from distorting the RCOF necessary to prevent a slip, only RCOF values where the vertical force was greater than 50 N were compared (Fino and Lockhart, 2014; Yamaguchi et al., 2012b). Stance time was defined as the time from heel contact to push-off / toe-off (i.e. the vertical force dropped below 50 N as the toe pushed off the ground) during the directional change.

COM-COP Angle

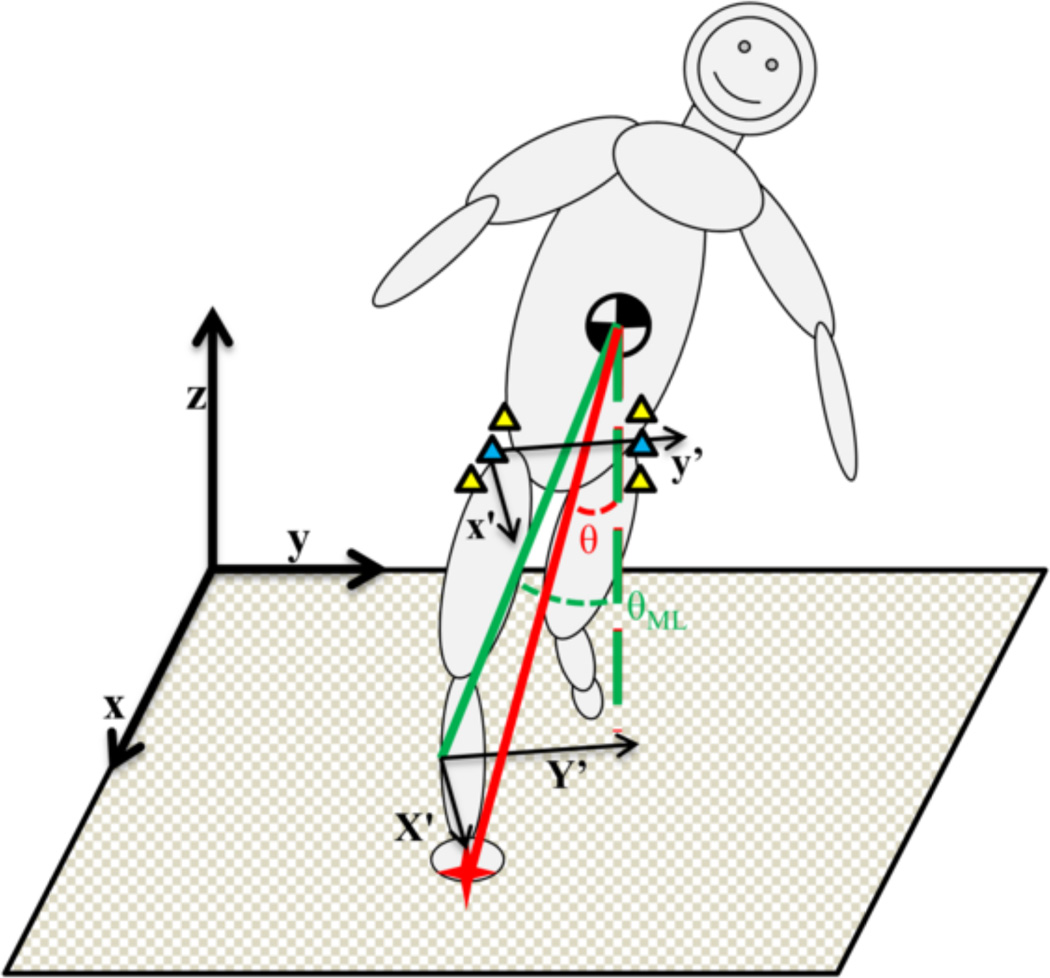
The ML COM-COP angle, θ_ML, was calculated as a component of the total COM-COP angle, θ, between the vertical axis and the line connecting the COM to the COP, (Yamaguchi et al., 2012b)

$$\mathrm{\Theta }={\text{tan}}^{-1}\frac{\sqrt{{(x_{COP}-x_{COM})}^2+{(y_{COP}-y_{COM})}^2}}{z_{COM}}$$ (3)

where x_COP, y_COP are the x and y coordinates of the COP and x_COM, y_COM, and z_COM are the x, y, and z coordinates of the COM. The ML COM-COP angle, θ_ML, shown in Figure 2 was calculated as the ML component of θ using the orientation of the pelvis to construct a body fixed reference frame (Glaister et al., 2007b). The body fixed reference frame was constructed using the mean x, y, and z positions of the right iliac crest and right trochanter markers as the origin (i.e. the pelvis). The reference frame was defined by the projection onto the global x–y plane of the vector from the right pelvis to the left pelvis. θ_ML was calculated at the same time as the RCOF at weight acceptance.

Figure 2.

Diagram of the mediolateral COM-COP angle θ_ML. The ML COM-COP angle was the angle between the vertical and the line connecting the COM to the COP (red star) as seen from the frontal plane of the participant. The frontal plane and participant-fixed coordinate frame was defined by the orientation of the pelvis using the iliac crest and trochanter markers on each side of the body.

COM Curvature

Whereas the turning angle was specified at 90°, the turning radius of the COM may change based on θ_ML and the amount of the outlined path the participants actually utilize. The curvature of the COM trajectory is a more accurate indicator of the true turning radius. The curvature was calculated using a least-squares quadratic fit to the COM trajectory in the horizontal plane. Taking the second derivative of this function with respect to the x axis

$$\frac{d^{2}f(x)}{d{x}^2}=\kappa =\frac{1}{r}$$ (5)

yielded a constant curvature κ equal to the inverse of the radius, $\frac{1}{r}$. The magnitude of the curvature κ was calculated for each COM trajectory.

Approach Speed and Turning Speed

The turning speed was defined as the resultant instantaneous COM velocity at weight acceptance. It was calculated at the same instant as the RCOF at weight acceptance. The approach speed was calculated from the resultant instantaneous COM velocity at weight acceptance one stride before the turn.

Statistical Analysis

Univariate descriptive statistics of the COM clearance, COP distance, RCOF, and θ_ML were calculated at each speed, height, and turning strategy. To determine the relationship between COM clearance, COP radius, RCOF, θ_ML, and curvature to speed, height, and turning strategy, we fit generalized estimating equations (GEE) that account for the within subject correlation among each subject’s trials. We selected the compound symmetry covariance structure as the most appropriate structure for our data after comparing several models using the Akaike information criterion. Model assumptions were validated using the distributions of the residuals for each model. Curvature had a skewed distribution and was thus log transformed in order to satisfy the models’ assumptions. Pairwise contrasts between each obstacle height were performed for each outcome. Trial, two-way and three-way interaction effects were examined using type 3 tests for fixed effects with significant interactions retained in the final model. All hypothesis testing was two-sided using a 0.05 significance level. All analysis was performed in SAS 9.4 (SAS Institute Inc., Cary, NC, USA).

Results

Descriptive Results

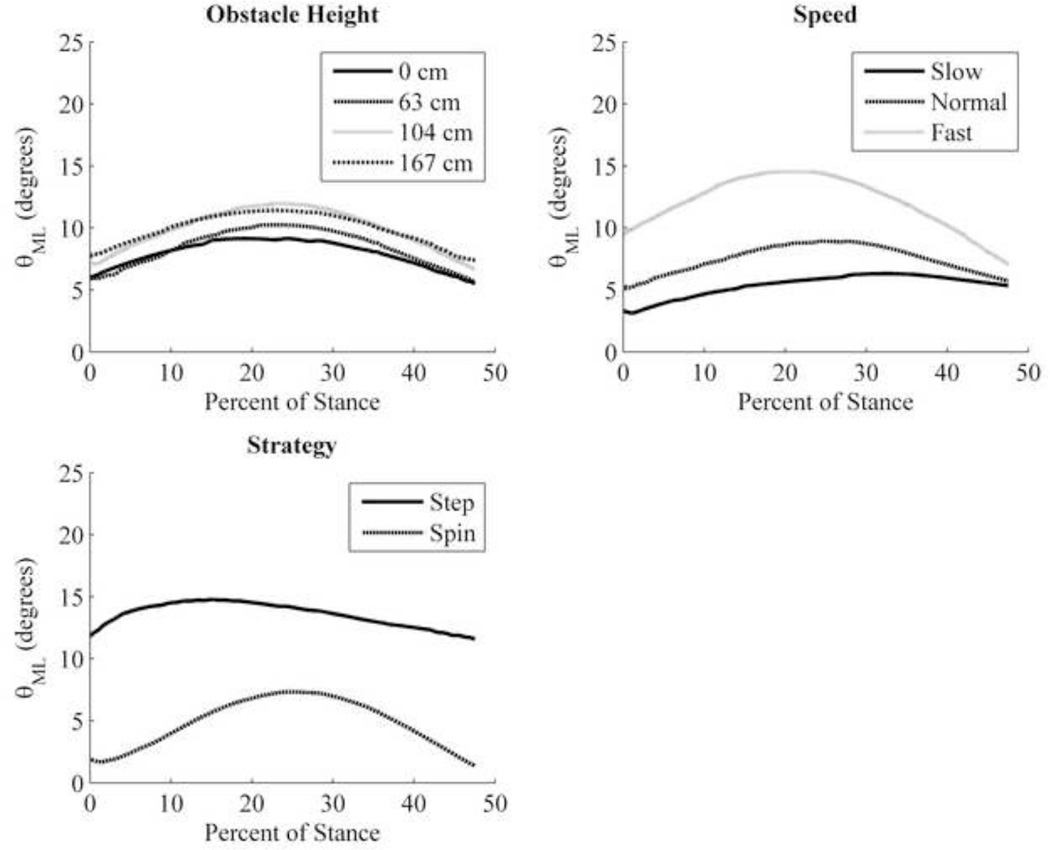
Univariate descriptive statistics are summarized in Table 1. The average height and weight of the participants was 1.78 ± 0.11 meters tall and 79.97 ± 12.39 kg, respectively. Mean approach speeds and turning speeds are summarized in Table 2. On average, weight acceptance occurred at 10% of stance phase. Values for θ_ML are plotted in Figure 3 for the first half of stance phase.

Table 1.

Results from the univariate descriptive statistics: Means and standard deviations for minimum COM clearance, COP distance, RCOF at weight acceptance, and θ_ML by speed, height, and turning strategy. The medians and inter-quartile bounds (Q1, Q3) are presented for curvature.

		COM Clearance (m)		COP Radius (m)		RCOF		ΘML (degrees)		Curvature
	Number of Trials*	Mean	St Dev	Mean	St Dev	Mean	St Dev	Mean	St dev	Mean	[Q1,Q3]
Speed (self-selected)
Slow	92	0.28	0.09	0.45	0.12	0.27	0.07	4.4	6.0	8.7	[4.8, 14.0]
Normal	156	0.25	0.10	0.46	0.14	0.30	0.07	6.8	6.1	6.9	[4.5, 11.1]
Fast	181	0.21	0.10	0.51	0.13	0.41	0.08	12.7	7.0	6.5	[4.0, 10.9]
Height (cm)
0	129	0.15	0.09	0.36	0.13	0.32	0.09	8.1	7.0	4.7	[2.4, 7.3]
63	111	0.23	0.08	0.47	0.11	0.33	0.09	7.6	6.7	5.5	[3.9, 10.3]
104	105	0.30	0.06	0.55	0.10	0.35	0.09	9.3	7.9	8.4	[5.9, 13.2]
167	84	0.33	0.05	0.57	0.09	0.36	0.10	10.4	7.6	10.6	[7.6, 16.1]
Turning Strategy
Step	205	0.25	0.10	0.53	0.13	0.35	0.09	14.6	5.0	9.6	[5.7, 14.6]
Spin	224	0.23	0.10	0.43	0.12	0.33	0.09	3.4	4.4	5.3	[3.5, 8.8]

^*Number of trials analyzed after excluding trials with improper foot placement or multiple steps on the force plate

Table 2.

Average approach speeds for each self-selected speed. Average turning speeds are separated by each variable.

		Approach Speed (m/s)		Turning Speed (m/s)
	Number of Trials	Mean	Std	Mean	Std
Speeds (self-selected)
Slow	92	0.93	0.28	1.10	0.24
Normal	156	1.43	0.36	1.27	0.26
Fast	181	2.03	0.27	1.65	0.25
Height (cm)
0	129	1.48	0.57	1.36	0.33
63	111	1.45	0.54	1.36	0.35
104	105	1.49	0.57	1.41	0.35
167	84	1.45	0.56	1.44	0.33
Turning Strategy
Step	205	1.47	0.54	1.40	0.35
Spin	224	1.46	0.58	1.37	0.33

Figure 3.

Population average plots of θ_ML for the first half of the turning stance for each obstacle height (top-left), speed (top-right), and strategy (bottom-left). Values reported in Tables 1 and 3 reflect means at weight acceptance, which occurred at an average of 10% of stance.

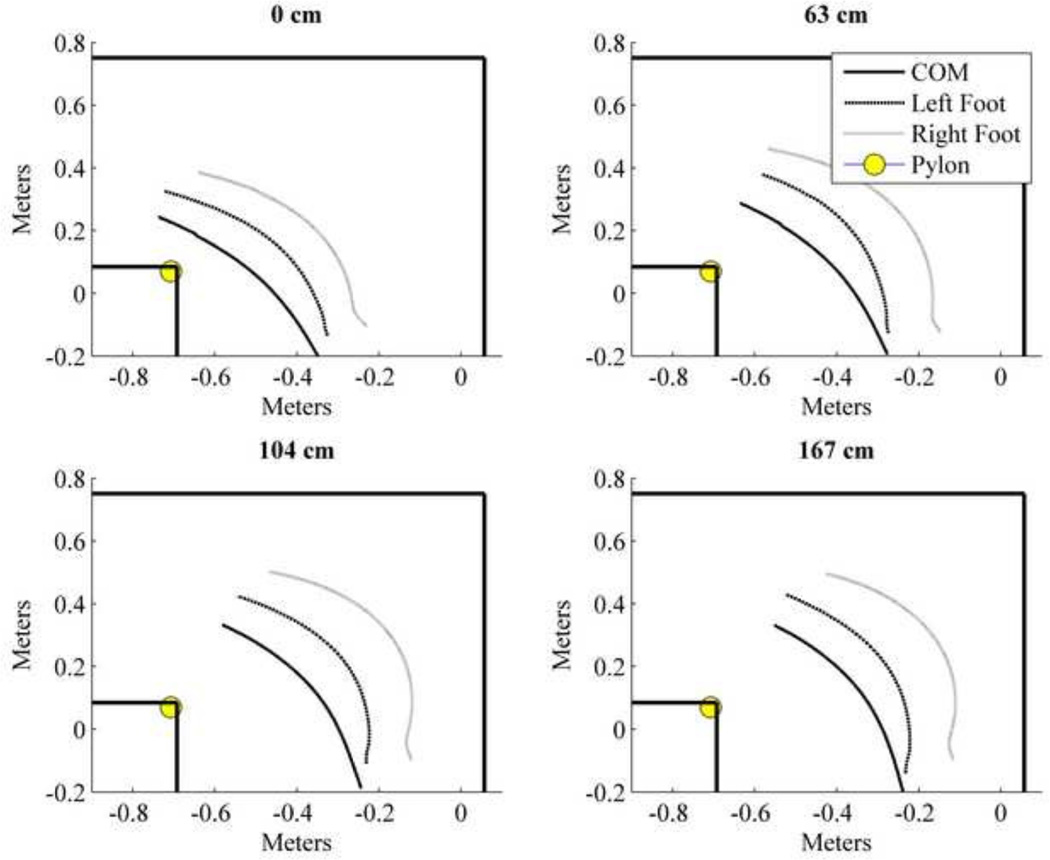
The average trajectories of the COM and the left and right foot COMs are shown in Figures 4–6 for each obstacle height, speed, and strategy. The COM remained outside the BOS during the first half of stance for every condition. The average COM trajectories for each variable are overlaid in Figure 7. All quadratic fits had an R² value greater than 0.9.

Figure 4.

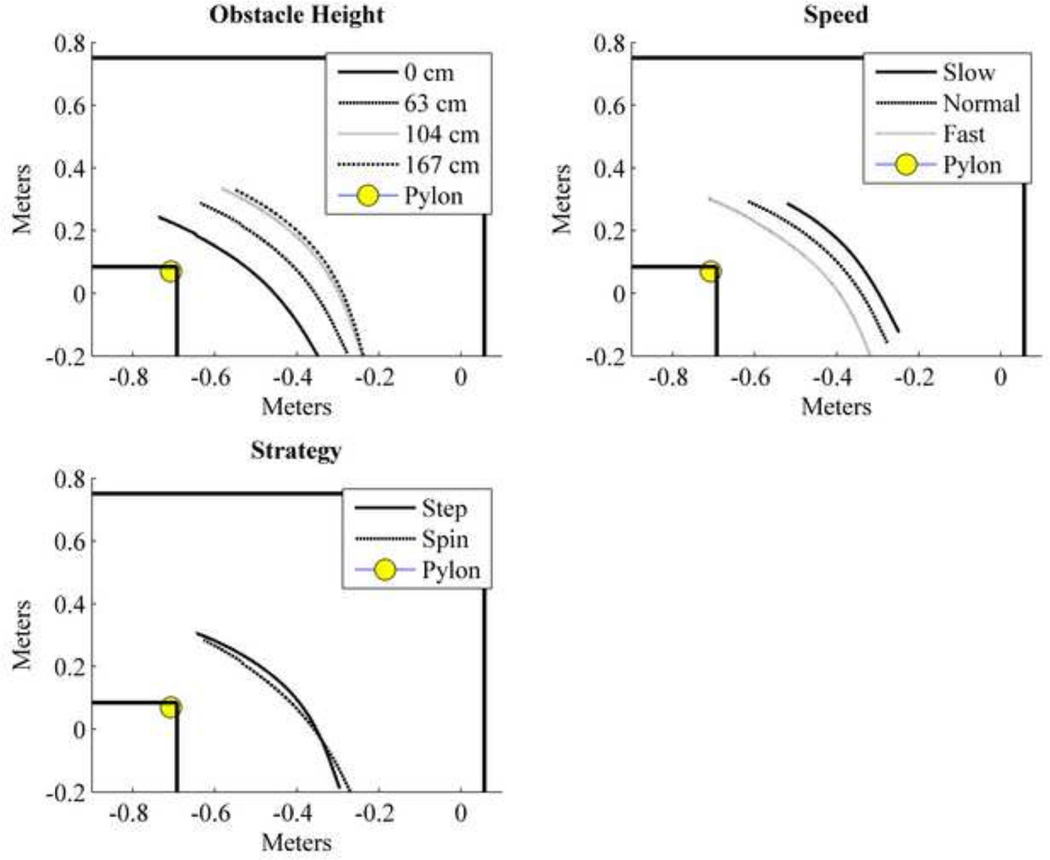
Population average plots for the whole-body (solid line), left foot (dashed line), and right foot (dotted line) COM trajectories over the first half of stance phase for each obstacle height. For all heights, the COM remains outside of the BOS for the entire first half of stance phase. As obstacle height increased, the curvature of the COM trajectory also increased. Left and right foot trajectories show the overall average trajectories which include both step and spin turns.

Figure 6.

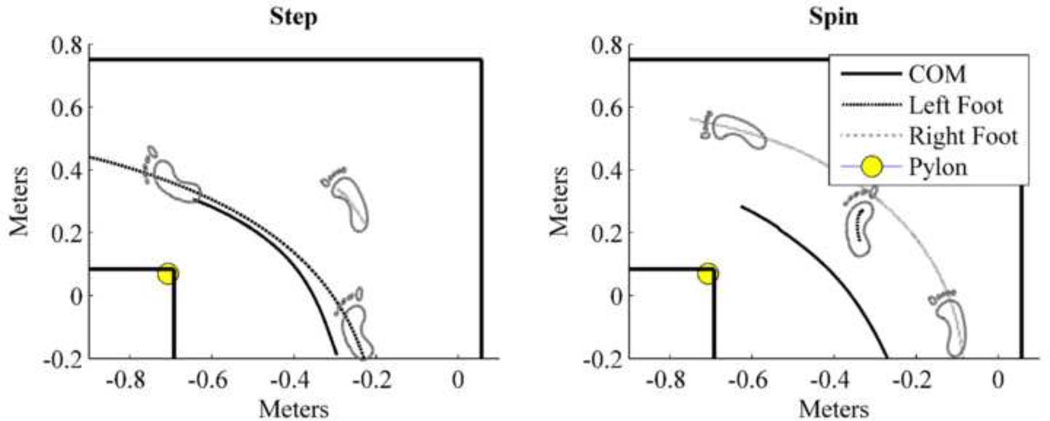
Population average plots for the whole-body (solid line), left foot (dashed line), and right foot (dotted line) COM trajectories over the first half of stance phase for each strategy with representative foot placement. The stance limb for step turns to the left is the right leg, while for spin turns to the left it is the left leg which results in small path lengths for those respective trajectories. For both trajectories, the COM falls outside the BOS for the entire first half of stance. The COM displacement outside the BOS is much higher during spin turns than step turns.

Figure 7.

Population average plots for the COM trajectories separated by variable to show the different trajectories’ average curvatures. Increasing obstacle height resulted in increased curvature. Slower speeds had higher curvature than fast walking speeds. Step turns showed greater curvature than spin turns.

GEE Model Results

From the results of the GEE model presented in Table 3, higher obstacle heights resulted in statistically significant increases in COM clearance, COP distance, RCOF, and curvature. Statistical differences in θ_ML existed between the lowest (0 cm) and tallest (167 cm) obstacle heights. Significant differences were found between all height-wise contrasts for COM clearance, curvature, and COP distance (p<0.0001). Contrasts also showed significantly different RCOF values between heights 104 cm and 167 cm (p=0.0123) with all other contrasts not statistically significant.

Table 3.

Results from GEE models for outcomes: minimum COM clearance, COP distance, RCOF at weight acceptance, and θ_ML by speed, height, and turning strategy. The beta coefficients show the mean differences between each category and the reference. The model intercept (β₀) is also presented as the mean outcome at a normal speed, 0 cm height, and a step turning strategy. The significance level was set at 0.05.

		COM Clearance (m)		COP Radius (m)		RCOF		ΘML (degrees)		Curvature
	Number of Trials	Beta (SE)	P Value	Beta (SE)	P Value	Beta (SE)	P Value	Beta (SE)	P Value	Beta (SE)	P Value
Intercept		0.25 (0.10)	<0.0001	0.40 (0.01)	<0.0001	0.29 (0.01)	<0.0001	12.19 (0.42)	<0.0001	1.77 (0.09)	<0.0001
Speed (self-selected)
Slow	92	0.04 (0.01)	<0.0001*	0.002 (0.01)	0.8264	−0.03 (0.01)	0.0040*	−2.13 (0.45)	<0.0001*	0.42 (0.13)	0.0009*
Normal	156	Ref.		Ref.		Ref.		Ref.		Ref.
Fast	182	−0.05 (0.01)	<0.0001*	0.04 (0.01)	<0.0001*	0.11 (0.01)	<0.0001*	5.78 (0.38)	<0.0001*	−0.23 (0.10)	0.0200*
Height (cm)
0	130	Ref.		Ref.		Ref.		Ref.		Ref.
63	111	0.08 (0.01)	<0.0001†	0.12 (0.01)	<0.0001†	0.02 (0.01)	0.0651	0.15 (0.45)	0.7457	0.35 (0.08)	<0.0001†
104	105	0.16 (0.01)	<0.0001†	0.19 (0.01)	<0.0001†	0.02 (0.01)	0.0123†	0.85 (0.46)	0.0633	0.72 (0.08)	<0.0001†
167	84	0.19 (0.01)	<0.0001†	0.21 (0.01)	<0.0001†	0.03 (0.01)	0.0010†	0.96 (0.49)	0.0488†	0.93 (0.09)	<0.0001†
Turning Strategy
Step	205	Ref.		Ref.		Ref.		Ref.		Ref.
Spin	225	−0.02 (0.01)	0.0141‡	−0.10 (0.01)	<0.0001‡	−0.02 (0.01)	0.0062‡	−11.05 (0.34)	<0.0001‡	−0.57 (0.10)	<0.0001‡
Speed*Strategy Interactions
Slow*Spin		-	-	-	-	-	-	-	-	−0.31 (0.17)	0.0634
Fast*Spin		-	-	-	-	-	-	-	-	0.20 (0.13)	0.1378

^*Significantly different than normal speed

^†Significantly different than 0 cm height (no obstacle)

^‡Significantly different than step turn

COM clearance, RCOF, curvature, and θ_ML at self-selected slow and fast speeds were significantly different compared to normal speeds. Turning strategy significantly affected all outcomes.

There was a significant interaction between speed and turning strategy for curvature (p=0.0072). Spin turns had decreased curvature compared to step turns at slow speeds but increased curvature with respect to step turns at fast speeds. No other significant two or three-way interactions between speed, obstacle height, and turning strategy (p>0.05) and no significant trial effects were found. Measured approach and turning speeds for slow, normal, and fast speeds were significantly different from one another (p<0.0001). No differences were found in turning speed across obstacle height (p=0.79) or turning strategy (p=0.27).

Discussion

This study investigated the impact of a corner obstacle’s height on the kinematics during a turn. We found increased obstacle heights caused participants to give more distance between themselves and the corner. In essence, taller obstacles resulted in wider, sharper turns. Fast speeds, regardless of obstacle height, resulted in less COM clearance and narrower turns compared to normal or slow walking speeds. Similarly, spin turns brought the COM closer to the corner than step turns.

Most prior studies investigating turning used walking paths or destination cues with no obstacle (Akram et al., 2010; Chang and Kram, 2007; Courtine and Schieppati, 2003; Hicheur and Berthoz, 2005; Hicheur et al., 2007; Hicheur et al., 2005; Jindrich et al., 2006; Olivier et al., 2008; Orendurff et al., 2006; Patla et al., 1991 and 1999; Pham et al., 2007; Taylor et al., 2005; Yamaguchi et al., 2012a, b), while other obstacle circumvention studies used 2 m high pylons (Gérin-Lajoie et al., 2006, 2007, and 2008; Vallis and McFadyen, 2003, 2005), 1.53 m tall poles (Glaister et al., 2007b and 2008) or pedestrian barricades (Dias et al., 2013). The present results indicate the height of the corner could be an important factor in the study design. Hicheur et al. (2007) and Pham et al. (2007) showed that when given a target direction, individuals’ planar trajectories tend to follow a stereotyped behavior that minimizes jerk and snap. Fajen and Warren (2003) also provided a dynamical model of steering and route selection based on a two-dimensional, top-down, environment. Fajen and Warren (2003) acknowledged the inability of the system to model obstacles of varying lengths and widths. Our results suggest the height of the obstacle is also an important characteristic, necessitating a three-dimensional model to accurately describe obstacle avoidance. Similarly, the “personal space” characterized by Gérin-Lajoie et al. (2008) would be more accurately defined in three-dimensional vector space rather than two-dimensional.

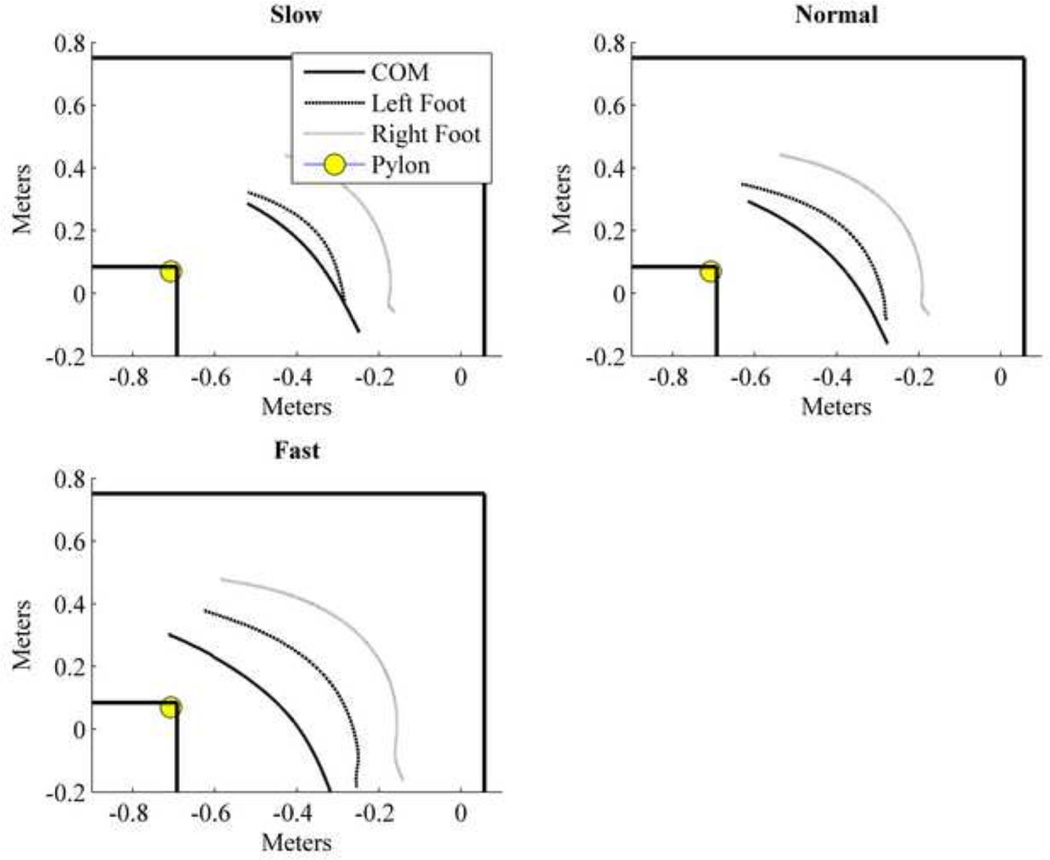
Examining the trajectories of the whole-body COM compared to the left and right foot COMs, we found that the average whole-body COM remains outside the BOS for the entire first half of stance phase regardless of speed, turning strategy, or obstacle height. This contrasts previous results by Taylor et al. (2005) which showed the COM only exited the BOS on spin turns. Taylor et al. (2005) instructed participants to perform quick/abrupt turn in the minimum amount of time, consistent with the theory that turning is an avoidance strategy as characterized by Patla et al. (1991). However, most turns in everyday locomotion occur over several steps (Fajen and Warren, 2003; Glaister et al., 2007a). Accordingly, the subjects in our study were not instructed to make abrupt turns, but instead to turn the corner naturally. The present results regarding speed tend to agree with Orendurff et al. (2006) who reported consistent COM displacement outside the BOS while walking a constant arc at 1.2 m/s and marginal COM displacement at lower speeds of 1.0 m/s. Based on the present trends and the results of Orendurff et al. (2006), it is possible that extremely slow speeds (i.e. 0.6 m/s) may not result in the COM travelling outside the BOS. However, Orendurff et al. (2006) examined turns along a constant radius while transient turns were examined here. Future research should address the motor control strategies and kinematic differences between constant arcs and transient turns.

This new result has large implications for slips and falls. Because the COM remains outside the BOS for the entire first half of stance phase, slips during this weight acceptance phase are more likely to result in falls (Yamaguchi et al., 2012a). Furthermore, the RCOF values found during this weight acceptance phase of turning exceeded the RCOF values for normal walking of μ ≅ 0.20 (Cham and Redfern, 2002; Redfern et al., 2001). This suggests that not only are slips more likely to occur while turning compared to normal walking (Fino and Lockhart, 2014; Yamaguchi et al., 2012b), but slips during the weight acceptance phase of turning may be more likely to result in falls than straight walking slips because COM is displaced outside the BOS. In addition, we found the RCOF at weight acceptance differed between obstacle heights, suggesting the surrounding objects may influence the risk of slipping. While a previous analysis showed no differences between obstacle heights at the time of push-off (Fino and Lockhart, 2014) this difference between obstacle heights may be due to the different path curvatures caused by the obstacle.

When walking around a corner, the centripetal force, F_c, is provided by the frictional force characterized by the individual’s body weight W and the RCOF μ. The centripetal force required to change direction is proportional to the velocity squared, v², and the inverse of the radius, r, also known as the curvature, κ

$$F_c=\mu W=\frac{m{\nu }^2}{r}=m{\nu }^2\kappa .$$ (6)

The RCOF is proportional to the velocity squared and the magnitude of the curvature

$$\mu \propto {\nu }^2\kappa .$$ (7)

As obstacle height increased, it forced the COM further from the corner and increased the curvature. This increased curvature is most likely a cause of the increased RCOF. However, the increased RCOF at weight acceptance for faster speeds, despite a lower curvature, is caused by the proportionality to v², which overcame the decrease in κ. The increased θ_ML also contributed to the increased RCOF values observed during taller obstacle trials (Yamaguchi et al., 2012b). Combined, these results suggest that the radius of the turn, not the angle of the turn as presented by Yamaguchi et al. (2012a), is the critical factor in slip and fall risk during turning. However, if all are performed over the same distance, larger turning angles will necessarily result in a smaller turning radius.

Thus the turning angle will reflect the actual turning radius. The curvature and RCOF results have implications when designing pedestrian environments. For pedestrian walkways and areas, it may be important to consider not only the turning angle of paths (Dias et al., 2013) and the floor space of obstacles but also the height of the barricades, railings, tables, posts, etc. that will impact the pedestrian path. Posts prohibiting vehicular traffic on pedestrian areas should be constructed high enough to be visible and effective, but as low as possible to reduce the effect on pedestrian kinematics reported here. Besides reducing congestion, such design considerations may also be able to reduce the likelihood of slips and falls by maintaining low curvature paths to reduce the RCOF.

Interestingly, across the obstacle heights and turning strategies, an increased COM clearance paired with an increased COP distance. However, as speed increased, the COP radius increased, but the COM clearance decreased. This would indicate greater θ_ML angles at faster speeds consistent with results from Orendurff et al. (2006). This result was observed; faster speeds utilized a greater θ_ML. While we predicted the obstacle height would alter the COM by limiting θ_ML, our results tended towards the opposite. An increase in obstacle height resulted in larger θ_ML values. While only the lowest and highest heights were statistically different in terms of θ_ML, this difference is peculiar as we expected taller obstacles would inhibit the lateral motion of the participants and restrict the degree to which the participants could lean over the obstacle and into the turn. This larger θ_ML for the taller obstacle heights is likely due to an anticipation of the smaller turning radius described above. Participants likely increased θ_ML for taller obstacles because of the increased centripetal force of smaller radii. By leaning into the turn, they reduced the net overturning moment by balancing the moment due to friction with the moment due to their COM displacement. For this study, θ_ML was only calculated at weight acceptance, therefore this result may only be true during the weight acceptance phase of the turn. From Figure 3, it appears that examining the maximum θ_ML may yield different results than when extracting the θ_ML from weight acceptance (~10% stance). Future research should explore this entire result in greater detail.

Overall, these results show obstacle height has a distinct effect on navigational strategies. Future work should investigate whether these effects result in different biomechanical responses such as increased lateral flexion or trunk roll.

This study has three potential limitations. First, the sample size was limited to only 10 people, although the repeated measures increased the total trial sample size to 429 trials. Second, the width of the marked path confined the participants’ trajectory and may have influenced the participants’ movements. This width reduced the variability of the participants’ paths by ensuring the same turning angle (90°) and forced proximity to the corner pylon. Therefore, the results may not represent unrestricted movements around obstacles found in large hallways or open spaces where greater avoidance is possible. Third, the availability of the kinematic marker data from the second half of stance phase was inconsistent. Due to laboratory space requirements, the motion capture cameras were confined to specified locations. This presented difficulties in capturing each kinematic marker once the participants changed directions. Laboratory structures, including the pylon used in the trials, obstructed the views of the cameras causing some but not all kinematic markers to be lost occasionally following the change in direction. Rather than using long spline fits to interpolate these lost data points, we reported only the data which was accurately and consistently captured for each participant. Future analysis should consider the entire stance phase.

Figure 5.

Population average plots for the whole-body (solid line), left foot (dashed line), and right foot (dotted line) COM trajectories over the first half of stance phase for each speed. The COM displacement outside the BOS increases as speed increases, but even at slow speeds the COM travels outside the BOS. Left and right foot trajectories show the overall average trajectories which include both step and spin turns.