Biomechanical implications of intraspecific shape variation in chimpanzee crania: moving towards an integration of geometric morphometrics and finite element analysis

Abstract

In a broad range of evolutionary studies, an understanding of intraspecific variation is needed in order to contextualize and interpret the meaning of variation between species. However, mechanical analyses of primate crania using experimental or modeling methods typically encounter logistical constraints that force them to rely on data gathered from only one or a few individuals. This results in a lack of knowledge concerning the mechanical significance of intraspecific shape variation that limits our ability to infer the significance of interspecific differences. This study uses geometric morphometric methods (GM) and finite element analysis (FEA) to examine the biomechanical implications of shape variation in chimpanzee crania, thereby providing a comparative context in which to interpret shape-related mechanical variation between hominin species. Six finite element models (FEMs) of chimpanzee crania were constructed from CT scans following shape-space Principal Component Analysis (PCA) of a matrix of 709 Procrustes coordinates (digitized onto 21 specimens) to identify the individuals at the extremes of the first three principal components. The FEMs were assigned the material properties of bone and were loaded and constrained to simulate maximal bites on the P³ and M². Resulting strains indicate that intraspecific cranial variation in morphology is associated with quantitatively high levels of variation in strain magnitudes, but qualitatively little variation in the distribution of strain concentrations. Thus, interspecific comparisons should include considerations of the spatial patterning of strains rather than focus only their magnitude.

One objective of evolutionary biomechanics is to attempt to discern if the mechanical consequences of morphological differences may have adaptive significance. This is possible only if mechanical differences are placed in a populational context. In other words, it is difficult to understand the evolutionary significance of interspecific mechanical differences without first understanding intraspecific differences (e.g., Weber et al., 2011). This problem becomes particularly acute when considering the cranial morphology of early hominins. The few well-preserved australopith crania exhibit obvious morphological differences, some of which are inferred to provide mechanical “performance” advantages during feeding by enhancing stress resistance and/or increasing the efficiency of bite force production (e.g., Rak, 1983). In principle, it is possible to analyze the mechanical performance of these hominins and document the differences between them. In doing so, one could demonstrate that a given cranium is stronger or produces greater bite force than another. However, a comparative context is needed in order to evaluate whether or not those differences might be evolutionarily significant. If mechanical variation within a species is high, then one must be cautious in interpreting variation between species, particularly if that variation does not demonstrably exceed that within species. Inversely, if mechanical variation within a species is low, then it is easier to conclude that differences between species may be significant, especially when interspecific variation obviously exceeds intraspecific variation.

This study explores intraspecific variation in cranial shape and associated mechanical performance during simulations of biting in order to provide a context for interpreting shape-related mechanical variation among and between early hominin crania. As a heuristic tool, this study tests the null hypothesis that intraspecific variation in craniofacial shape has no effect on the pattern and magnitude of strains present in the craniofacial skeleton during biting. There is no expectation that this hypothesis will be corroborated; rather, the value of this hypothesis is that its testing provides for a mechanism for evaluating the degree to which measures of biomechanical performance such as stress, strain, strain energy and strain mode vary as a consequence of cranial shape. Measures of performance that exhibit low intraspecific variation despite large intraspecific variation in shape may be particularly useful for providing a basis for comparisons between species. Similarly, performance measures that exhibit high variation within species might be less useful for making interspecific comparisons. We test this hypothesis in the common chimpanzee, Pan troglodytes. Chimpanzees, like all living hominoids, clearly exhibit intraspecific variation in cranial shape, but the mechanical significance of this variation is not well understood. Because P. troglodytes is the extant sister taxon of Homo sapiens, information gleaned from chimpanzees can be used as a guide to interpreting the biomechanical differences among and between extinct hominins and other primates.

Beyond the purely biological objectives described above, this study is part of a broader effort to integrate the methods of morphological and mechanical analyses. During the last two decades, the fields of functional and evolutionary morphology have undergone a revolution that has increased the number and power of methods available for the study of adaptation in living and extinct organisms. In the field of evolutionary morphology, geometric morphometric methods (GM) have transformed the ways in which evolutionary biologists study form (Bookstein, 1991; Slice, 2005; Weber and Bookstein, 2011; Adams et al., 2013). In functional anatomy, finite element analysis (FEA) has become increasingly important for testing hypotheses in human and non-human primate evolutionary biomechanics (Macho et al., 2005; Marinescu et al., 2005; Strait et al., 2005, 2007, 2008, 2009; Kupczik et al., 2007, 2009; Wroe at al., 2007; Wang et al., 2008, 2010a,b; Gröning et al., 2009; Berthaume, 2010; Panagiotopoulou, 2010, 2011a; Benazzi et al., 2011a; 2012; 2013a,b,c ; Chalk et al., 2011; Dumont et al., 2011a, b; Nakashige et al., 2011; O'Higgins et al., 2011; Ross et al., 2011; Wood et al., 2011) and vertebrate biology in general (Guillet at al., 1985; Rayfield et al., 2001; Rayfield, 2004, 2005, 2011; Dumont et al., 2005, 2009; Metzger et al., 2005; Witzel, 2005; McHenry et al., 2006, 2007; Fagan et al., 2007; Bourke et al., 2008; Farke, 2008; Moreno et al., 2008; Pierce et al., 2008, 2009; Snively and Cox, 2008; Wroe et al., 2008; Arbour, 2009; Bell et al., 2009; Jasinoski et al., 2009, 2010; Manning, 2009; Moazen et al., 2009; Slater et al., 2009; Stayton, 2009; Fletcher et al., 2010; Panagiotopoulou, 2011b). The intersection of these two fields and the continuing integration of these two methods promises to provide a powerful toolkit with which researchers can study the mechanics and evolution of anatomical systems.

Finite element analysis is an engineering technique that can be used to examine how objects of complex design respond to loads (Zienkiewicz at al., 2005). In skeletal biomechanics, the method allows researchers to estimate stresses and strains in skeletal materials in a digital (and thus non-invasive) manner. Typically, models are created from computed tomography (CT) scans of skeletal or fossil material using one of several medical imaging and/or computer-aided design (CAD) methods employed to translate greyscale slices into volumetric objects. Depending on size and complexity, the continuum of the object's shape is discretized into volumetric meshes of anywhere from thousands to millions of finite elements (bricks and tetrahedra) that are connected at nodes. Each element is assigned material properties, and forces and constraints are applied to the nodes, resulting in a system of simultaneous algebraic differential equations whose solution gives the displacement at those nodes. Nodal displacements are interpolated over element volumes using known interpolating polynomial functions to obtain element displacement fields which are then differentiated to obtain strains. Material property information relates stresses to strains, enabling stress fields to be constructed, as well as the calculation of strain energy. Patterns of strain can be easily visualized across a structure using color-maps, allowing for a qualitative assessment of the manner in which structures deform during loading. Additionally, strain magnitudes and directions can be measured at specific locations across a structure and compared to values extracted from homologous locations on other models or to strain magnitudes derived from experimental studies.

A constraint on FEA is that the construction of finite element models (FEMs) is time consuming and expensive. Multi-disciplinary research teams and data sharing networks have helped to foster collaboration and drive innovation, but aside from the research and data collection that inform the boundary conditions of FEMs, the modeling of geometry alone can often take weeks to months to complete depending on the complexity of the structure of interest. This poses obvious practical limitations and typically precludes researchers from examining more than one or only a few individuals from any given species. This omission limits the ability to draw conclusions regarding the mechanical and adaptive significance of interspecific shape differences because if variation in shape within species leads to substantial variation in biomechanical performance, our ability to interpret shape differences between species in a mechanical context is considerably restricted (Weber et al., 2011).

Here we describe a conceptually straightforward approach to overcoming this limitation using GM, a collection of statistical methods allowing the quantification and comparison of form and shape in three dimensions (e.g., Bookstein, 1991; Slice, 2005; Weber and Bookstein, 2011; Adams et al., 2013). In short, shape analysis of landmark data is used to select specimens for subsequent finite element modeling that fall along (or near) the extremes of loading for each of the first three principal components axes. This approach ensures that the few FEMs being analyzed still bracket a substantial portion of the range of morphological variation within a species sample. Consequently, it is possible to approach the mechanical consequences of intraspecific variation in a time efficient manner.

MATERIALS AND METHODS

Geometric Morphometrics

As part of a previous study (Benazzi et al., 2011b), 709 cranial landmarks and semilandmarks were digitized from three-dimensional (3D) surfaces derived from the CT scans of 21 adult chimpanzees, including 10 females, 9 males, and 2 individuals of indeterminate sex. These specimens sample at least two chimpanzee subspecies (P. troglodytes schweinfurthii and P. troglodytes verus). The (semi)landmark configurations were converted to shape coordinates by Generalized Procrustes Analysis (GPA) and Principal Components Analysis (PCA) was used to detect the main patterns of shape variation across our chimpanzee sample. Principal components (PCs) 1, 2 and 3 represent more than half (23.4%, 20.8% and 12.6%, respectively) of the shape variation captured by the shape analysis (Figure 1). Multiple regression of the first three PCs on the logarithm of centroid size (LnCS) found no correlation between the first and the third principal component and size (r<0.165, P>0.23), meaning that PC1 and PC3 account for size-independent shape variation. However, PC2 is correlated with size (r= 0.503, P= 0.0117), meaning that PC2 accounts for size-dependent shape variation (static allometry).

Figure 1.

Procrustes shape-space PCA in the space of the first two (A) and second and third (B) eigenvectors computed from the sample of Pan troglodytes. The deformed grand mean configuration in the four directions of the PCs are drawn at the extremity of each axis. The four specimens selected along PC1 and PC2 for FEA are labeled in the PCA plot. Blue dots: males; Orange dots: female; Green dots: specimens excluded from FEA because of poor CT scan quality; Black dot: grand mean.

Specimens lying closest to the extremes of the PC axes show varying combinations of facial prognathism, facial height, zygomatic arch configuration, frontal height and neurocranial length. Because the PCA is based on so many landmarks and semilandmarks, the resulting PCs describe independent axes of morphological variation that preclude simple definition (i.e., there is not simply a “facial prognathism” axis), although PC1 does a good job of discriminating the crania by sex. Positive loadings on PC1 correspond to shape variation related to an orthognathic face (klinorynchy), large and ovoid orbits with a small interorbital distance, posterior displacement of the supraorbital region, a globular neurocranium that is reduced in length, and reduced bimastoid breadth. Negative loadings on PC1 correspond to a prognathic (airorynchy) but vertically short face, sub-rectangular orbits, anterior displacement of the supraorbital region and postorbital sulcus, an anteroposteriorly long neurocranium, wider and larger bimastoid breadth, and laterally displaced zygomatic arches. Positive loadings on PC2 are observed in specimens with a short snout and vertically short face, a reduced zygomatic bone, sub-squared orbits with reduced interorbital distance, a supraorbital region that projects slightly forward, increased neurocranial height, enlargement of the biparietal breadth and concomitant reduction of bimastoid breadth. Negative loadings on PC2 are observed in specimens with prognathic and relatively tall faces, wide and sub-circular orbits, laterally displaced zygomatic bones, increased postorbital constriction, and low and less globular vaults exhibiting reduced breadth at the parietals but increased bimastoid breadth. Positive loadings on PC3 correspond to a prognathic and vertically short face, ovoid orbital shape, large interobital distance, reduced bizygomatic breadth, marked sulcus postorbitalis and a globular neurocranium. Negative loadings on PC3 correspond to klinorynchy and a relatively tall face, large and circular orbits, reduced interorbital distance, large bizygomatic breadth, increased postorbital constriction (reduced minimum frontal breadth), and a low vault and elongated neurocranium.

The specimens with the strongest positive and negative loadings along the first three PCs were selected for FEA, with the caveat that, by chance, the specimens loading at the extreme ends of PC2 were associated with CT scans whose quality was too poor for the purposes of building a model for FEA (segmentation to reconstruct the full suite of internal and external geometry was not feasible, although the scans were sufficient for gathering shape information for GM). Thus, on PC 2, we selected the specimens with the next most extreme loadings on both the positive and negative poles. The specimens identified through this process are designated PC1+, PC1−, PC2+, PC2−, PC3+ and PC3−, respectively. It is important to note that the specimens do not fall exactly on any given axis, and they might be extreme in just one of the PCs and not in others. However, they represent real crania rather than hypothetical ones that have been warped along the trajectory of an axis (e.g., O'Higgins et al 2011). Moreover, we cannot be certain that the first three PCs are the ones that are most functionally significant. It is possible that, for example, the fifth principal component is the one that is the most significant mechanically, or that mechanical significance is distributed evenly over all PCs. Rather, as the first three PCs account for about 57% of the total shape variation, our selection process (namely, selecting specimens at the extremes of the first three PC axes representing the direction of maximum variation through the chimpanzee sample) merely ensures that the specimens selected for FEA represent the main morphological differences found in real chimpanzee crania; they are not being selected because of any a priori functional considerations. However, based on the aspects of cranial shape that vary along the first three PCs (see above), it is not immediately obvious that these PCs would be mechanically insignificant.

Finite Element Model Construction

Cranial CT scans of the six chimpanzee specimens selected through GM were imported in DICOM format to Mimics v 14.0 (Materialise, Ann Arbor, MI USA). Next, the geometry of each specimen was captured using a combination of automatic and manual slice-by-slice segmentation. Separate surfaces were created enclosing volumes for cortical and trabecular bone. Surface files were then imported into Geomagic Studio v 12 (Research Triangle Park, NC, USA) 3D editing software, where model geometry was further edited to reconstruct small gaps in geometry. The models were again surface meshed using the 3Matic module of Mimics. All volumes contained within each model were then imported into the FEA software program Strand 7 (Strand7 Pty Ltd, Sydney, NSW) for the application of boundary conditions and finite element analysis. Final models were composed of 480,000 to 1.5 million 4-noded tetrahedral elements (PC1- : 1,493,102; PC1+: 706,446; PC2- : 1,208, 800; PC2+ : 846,950; PC3- : 482,268; PC3+: 678,716).

Material Properties

To determine the material properties of cortical cranial bone, one fresh frozen chimpanzee and one fresh frozen gorilla cranium were examined using ultrasonic techniques with samples (Figure 2) taken from fifteen different locations across the face and cranial vault (e.g., Schwartz-Dabney and Dechow, 2002, 2003). The gorilla specimen was donated over a decade ago by the Lincoln Park Zoo to the anatomical research collection housed in CFR's laboratory. The chimpanzee cranium was obtained from the tissue collection of the Yerkes Primate Research Center of Emory University (supported by NIH Base Grant RR00165). The deaths of these two individuals were unrelated to the research presented here. The values from the two individuals were averaged to provide an approximation of material properties in African Apes (Table 1). Using the average African Ape values as a guide, spatially heterogeneous isotropic material properties (Table 2) were assigned to each model using a thermal diffusion method in which elastic moduli are smoothly diffused through the skull's cortical bone as heat diffuses through an object (Davis et al., 2011). Trabecular bone was modeled as a volume and assigned material properties accordingly (E = 0.64 GPa, v = 0.28; Ashman et al., 1989).

Figure 2.

Locations from which material properties were collected. Numbers correspond to regions from which material properties have been collected in an ongoing study on hominoid material properties. Numbers missing from this figure correspond to regions from which data were not used in the present study.

Table 1.

Material properties¹ of cranial bone in African apes (average values of one chimpanzee and one gorilla).

Location2	Young's modulus (E)			Shear modulus (G)			Poisson's ratio (v)
	E1	E2	E3	G12	G23	G31	v12_21	v23_32	v13_31
6	9.53	16.12	17.79	3.78	6.30	4.01	0.29	0.34	0.23
7	10.80	9.62	12.63	3.76	4.18	4.57	0.35	0.31	0.28
8	8.65	8.62	10.58	3.04	3.70	3.57	0.41	0.31	0.34
9	9.11	12.23	22.61	4.26	5.77	5.45	0.31	0.35	0.11
10	10.47	15.48	18.43	5.67	5.99	5.98	0.24	0.40	0.22
11	8.38	9.82	12.66	3.57	4.22	4.27	0.32	0.31	0.28
12	11.99	16.65	19.05	5.60	6.85	5.43	0.25	0.30	0.31
13	6.82	9.57	13.98	2.76	4.43	3.28	0.43	0.27	0.34
14	7.23	5.59	16.45	2.32	4.26	4.02	0.51	0.26	0.51
15	8.50	10.98	17.05	3.29	5.56	4.23	0.50	0.19	0.36
16	11.48	14.69	17.81	4.80	6.08	5.94	0.34	0.36	0.14
17	9.50	13.06	18.72	3.77	6.07	4.79	0.44	0.28	0.28
18	9.66	14.34	19.74	3.84	6.73	4.91	0.45	0.26	0.28
20	10.46	14.97	19.45	4.73	8.31	5.80	0.45	0.02	0.37
22	9.04	10.84	19.40	3.32	6.27	4.88	0.50	0.14	0.34

¹E refers to the elastic modulus, G refers to the shear modulus, and v refers to Poisson's ratio. By definition E3 is the axis of maximum stiffness in the plane of the bone. Axis 2 is perpendicular to axis 3 in the plane of the bone, and axis 1 is perpendicular to both 2 and 3. G and v are recorded in planes defined by two axes. The values of v represent averages of two values recorded in each plane.

²Locations as in Fig. 2. Numbered regions that are “missing” from the table correspond to regions from which material properties have been collected in a more extensive sample being collected in an ongoing study.

Table 2.

Material properties thermally diffused through finite element models.

Location1	Young's modulus (E)	Poisson's ratio (v)
6	17.79	0.318
7	12.63	0.318
8	10.58	0.318
9	22.40	0.318
10	18.43	0.318
11	12.66	0.318
12	19.05	0.318
13	13.98	0.318
14	16.45	0.318
15	17.05	0.318
16	17.81	0.318
17	18.72	0.318
18	19.74	0.318
20	18.36	0.318
22	19.40	0.318

¹Locations as in Fig. 2.

Muscle Modeling

The muscles applied to the finite element models in this study were limited to the muscles primarily responsible for closing the jaw during biting: anterior temporalis, superficial and deep masseter and medial pterygoid. The muscle force data were derived from physiological cross sectional area data (PCSA), which were obtained from the dissection of a female chimpanzee (see Table 3, Strait et al., 2009). These data were not scaled by experimental electromyographic (EMG) data because at the time of this FE study, in vivo feeding experiments had not yet been completed for chimpanzees, and thus these data were not available. Because of this, muscle forces were modeled as bilaterally symmetric and at peak (100%) activity level, which approximates maximal static biting. Resulting strain and reaction force magnitudes therefore represent the maximum values that are allowable physiologically, and likely exceed those present in life. However, prior studies (Ross et al., 2005; Strait et al., 2009) demonstrate that the effect of using bilaterally symmetrical forces has a minimal effect on the spatial distribution of strain concentrations, except insofar as strain magnitudes in certain balancing side regions are disproportionately high; strain distributions on the working side are largely unaffected. Fitton et al. (2012) have further demonstrated that strain and deformation patterns are very conservative in the face of variation in muscle force activity.

Table 3.

Muscle forces (N) applied to each model

Specimen	Model volume (mm3)	Anterior temporalis	Superficial masseter	Deep masseter	Medial pterygoid
PC1−	363139	591	608	90	201
1PC1+	285969	504	518	77	171
PC2−	285236	503	518	77	171
PC2+	263980	478	491	73	162
PC3−	394911	648	667	99	220
PC3+	418252	624	642	95	212

¹Specimen used as baseline for scaling purposes

Muscle forces were applied in all models by scaling the PCSA values by the bone volume of each model to the 2/3 power. This procedure ensures that larger models experience larger muscle forces; however the purpose of this approach is not to estimate true muscle forces in each of our models, since it is known that muscle PCSA scales with positive allometry to body mass (Perry and Wall, 2008). Rather, this scaling procedure allows us to eliminate size as a variable affecting strains. Thus, the differences in strain in our models only reflect differences in cranial shape and do not reflect differences in cranial size (Dumont et al., 2009). This allows for an assessment of the effect of shape on structural strength. In order to more closely approximate physiological loading, all of the models were loaded using the tangential plus traction function of BoneLoad, a program that simulates the physiological wrapping of muscle around rigid bony structures and extrapolates muscle forces to vectors (Grosse et al., 2007). Areas of muscle origin were modeled as force plates and focal coordinates were chosen by selecting insertion points for the muscles of mastication on the surface file of a mandible attached to the modeled cranium, using muscle markings as a guide. This had the effect of directing the force vectors for each muscle to run from origin to insertion.

Constraints

Boundary conditions were applied to constrain movement at the articular eminences of the temporomandibular joints(TMJ) and at various bite points. The working (left) side TMJ was constrained in all directions and the balancing (right) side TMJ was constrained in the vertical and anteroposterior directions for all experiments. To constrain the models at the bite points, each model was constrained at the center of the left M² for one simulation (molar biting) and similarly on the left P³ (premolar biting) for another simulation. These minimal constraints have the effect of simulating occlusal and mandibular contacts while preventing the model from experiencing rigid body motion such that when the applied muscle forces exert an inferior pull on the model, reaction forces are generated at each constraint (Dumont et al., 2005; see also Strait et al. 2005). The reaction forces that are generated at the bite point represent the bite force.

Strain metrics

To assess model performance, various types of strain data were collected, each providing different types of information regarding the deformation present in the model. Strains are reported rather than stresses in order to facilitate comparisons with experimental bone strain studies. All of these strains occur at each material point of the models simultaneously. There are two types of strains- normal strains that stretch or compress the material in a given direction and shear strains that distort the material in a given plane. Maximum principal strain is the maximum value of normal strain at a given material point and is tensile (i.e., positive), unless the material is in a state of tri-axial compression. Minimum principal strain is the minimum value of normal strain at the same material point and is compressive (i.e., negative), unless the material is in a state of tri-axial tension. Maximum and minimum principal strains are oriented along principal axes that are orthogonal to each other. Strain mode is the absolute value of the ratio of maximum to minimum principal strain, which describes the degree to which a given material point is primarily in tension, primarily in compression, or primarily in shear (when the principal compressive and tensile strains are equal or nearly so). Maximum shear strain is, as the name implies, the maximum value of shear experienced at a given material point, and is calculated as maximum minus minimum principal strain. Von Mises strain is a measure of distortional strain, meaning non-isometric deformation (i.e., a solid rubber ball thrown into the ocean experiences ever greater compression on all sides as it sinks but remains perfectly spherical, and thus does not experience any von Mises strain). Von Mises strain corresponds to von Mises stress, which is the metric governing the yielding of ductile materials such as bone (Keyak and Rossi, 2000). Thus, it is the strain metric that is arguably most relevant to bone strength. Strain energy density (SED) is the area underneath the stress – strain curve at any given material point and represents the strain energy per unit volume at a material point. Strain energy (SE) is the integral (i.e., volumetric sum) of strain energy density over the volume of the model. Thus, SED provides information about where strain energy is being stored in an object. Maximum principal strain, minimum principal strain, strain mode, maximum shear strain and von Mises strain can be directly calculated from strain measurements (using strain gages or full-field strain measurement techniques) and thus form the basis of in vivo and ex vivo bone strain studies.

Ex vivo validation study

Validation studies are a critical but often overlooked component of FEA. As simplifications and assumptions must necessarily be used in modeling, strain results from FEA should be compared to results of bone strain experiments in order to determine whether or not the FEA is producing realistic results. Because our FEAs are simulating physiological loading conditions, it would be ideal to conduct in vivo validation studies whenever possible. In this regard, we have previously (Strait et al., 2005, 2009; Nakashige et al., 2011; Ross et al., 2011; ) validated two Macaca fascicularis cranial models against in vivo strain data, and are in the process of validating models of Cebus apella and Eulemur fulvus against in vivo data, as well. These studies demonstrate that FEA can produce results that are broadly realistic insofar as strains from FEA fall within the rather expansive envelope of strain data produced by in vivo studies (the variation of in vivo strain data is considerable and should not be unappreciated). The standard of model validity employed by us, therefore, is not one in which a model captures the complete strain regime of a particular individual with an especially high degree of accuracy and precision. Given sufficient time and resources, one might be able to produce a model that met such a standard, but that is not our intention. Rather, our objective is for our models to be suitable to answer basic comparative questions regarding strain patterns in species whose crania differ substantially in shape.

In vivo bone strain analyses have not been performed on P. troglodytes. Thus, we are forced to rely on our published in vivo validation studies on other species to document that realistic cranial FEMs can be built. However, in lieu of in vivo experiments, we have conducted ex vivo bone strain experiments on a fresh frozen chimpanzee cranium. The objective of ex vivo validation is to establish the degree to which assumptions regarding geometry and material properties introduce error into an FEM subjected to simple loading conditions, where error is represented by the difference between experimental and FEA results. There is no doubt that error exists in a model as geometrically and materially complex as a cranium, and in fact all models, as well as all experimental measurements, have error. The key question is whether or not this error is so great that it renders the model incapable of answering the research questions for which it was designed. Thus, after documenting the error in our model, we place it in the context of variation of in vivo bone strain (e.g., Hylander et al., 1991).

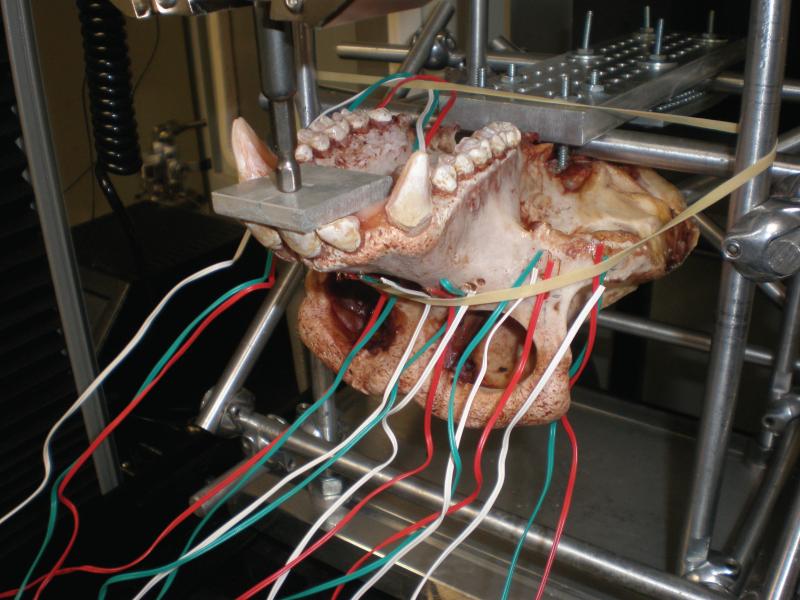
For this validation study, a fresh frozen female chimpanzee (P. troglodytes) head was acquired from the Southwest National Primate Research Center (SNPRC) in San Antonio, Texas (supported by NIHNCRR grant P51 RR013986). The specimen was not subjected to experimentation during life and was 22 years old at death. Although the brain tissue had been removed via transverse sectioning of the neurocranium for a previous study, the muscles of mastication remained intact. The specimen was sent from SNPRC to Arizona State University (ASU) where the masseter and temporalis muscles were removed and measured in order to collect physiological cross sectional area (PCSA) data. Upon completion, the specimen was sent to the Department of Biomedical Sciences at Texas A & M University Baylor College of Dentistry in Dallas, Texas where it was kept frozen until the dissection and strain gage study could commence. The specimen was then refrigerator-thawed and the soft tissue carefully removed. Special care was taken to retain the moisture of the skeletal and soft tissue that would not be directly affected by strain gage attachment.

A testing rig was constructed of steel rods, spherical joints and plates to secure the skull during loading. Four holes were drilled into the neurocranium, anteriorly and laterally to the foramen magnum and 307A carriage bolts (1.85 mm diameter, 14 mm length) with corresponding washers and nuts were used to hold the skull in place on the testing frame (Figure 3). A steel rod was placed between the anterior and posterior bolts to rest between the skull and a metal plate. This rod was then secured to the frame, holding the skull in place upside down and thus allowing for complete access to the dentition, palate and face. For added security, the posterior aspect of the metal plate was also affixed to the frame of the testing rig with four additional 307A bolts, washers and nuts.

Figure 3.

Ex vivo testing rig.

Locations for five strain gauges were chosen on the premaxilla, palate, nasal margin, infraorbital plate, and zygoma. Gages at these locations could be placed on even skeletal surfaces, reducing the likelihood of errors from incomplete bonding (ultimately, however, the strains produced from the infraorbital gage site were aberrant and consequently were discarded). Vishay Micro-Measurements 120WY stacked rosette strain gages were bonded according to Vishay's recommended protocol. Loads were applied using an Instron compressive testing machine fitted with a general tensile grip (CAT # 2716-015) and a flat bit for molar loading, while a metal plate was added to distribute incisor loading across all of the anterior teeth. Loads were applied in Newtons, at intervals, until a maximum of 600N was reached for the molar trials and 300N for the incisor trials. Each load was applied four times in sequence. Variation in strain among the four trials is a coarse measure of the error introduced by the experimental apparatus.

Following the strain experiments, material properties were collected from the specimen, and a FEM was constructed using the methods described above. Some anomalously thick bone in the maxilla exhibited a density gradient in the CT scans, but our model construction methods would not have recognized this gradient when applying material properties. Thus, we modeled this small section as a layer of cortical bone covering trabecular bone. Material properties were assigned to the model using the thermal diffusion method (Davis et al., 2011). The model was constrained at elements of the neurocranium corresponding to the bolt sites and loading was applied to either the M² (600N) or to all incisors (300N).

RESULTS

Ex vivo validation

Table 4 presents the maximum and minimum principal strain values obtained during the ex vivo experimental trials and the FEAs. Those values were then used to calculate maximum shear strain and strain mode that form the basis of our validation (see below). However, one interesting result emerged from examination of the principal strains. Typically, strain gage experiments on bone record a tensile maximum principal strain and a compressive minimum principal strain. However, at the palatal gage site during incisal loading, both principal strains were tensile. This type of deformation might be observed in a membrane that is becoming taut in all directions (i.e., like the skin of a drum). Compressive strains, if they exist, would be perpendicular to the plane of the palate, and would not be detected by a strain gage. FEA did not recover this strain pattern at the gage site. Rather, FEA found a minimum principal strain parallel to the surface of the palate that was compressive. However, FEA finds a region on the palate 2 cm posterior to the gage site in which the compressive minimum principal strain is perpendicular to the plane of the bone. Thus, both FEA and the ex vivo experiments record a distinctive strain pattern in the palate during incisal loading, but strain gradients in the palate are positioned slightly differently in the experiments and model. This implies that refinements to the model might be necessary if the objective of the FEA was to examine palatal strains in detail.

Table 4.

Maximum and minimum principal strain (in microstrain) recorded during molar and incisor loading in four ex vivo experimental trials and FEA, as measured at four gage sites.

	Premaxilla	Dorsal rostrum	Anterior zygomatic	Palate
Max Prin Strain
Molar trial 1	31	147	60	241
Molar trial 2	30	147	63	241
Molar trial 3	36	157	61	232
Molar trial 4	30	150	57	225
Molar FEA	16	238	36	92
Min Prin Strain
Molar trial 1	−21	−122	−95	−231
Molar trial 2	−15	−102	−68	−211
Molar trial 3	−6	−112	−71	−217
Molar trial 4	−10	−120	−67	−215
Molar FEA	−22	−231	−43	−76
Max Prin Strain
Incisor trial 1	35	65	1	112
Incisor trial 2	41	65	2	109
Incisor trial 3	41	70	5	113
Incisor trial 4	36	50	5	104
Incisor FEA	60	114	27	64
Min Prin Strain
Incisor trial 1	−160	−290	−21	43
Incisor trial 2	−151	−275	−12	41
Incisor trial 3	−141	−260	−15	37
Incisor trial 4	−156	−280	−20	31
Incisor FEA	−163	−278	−28	−51

With respect to strain mode, the FEM produced values close to experimental averages (Tables 5, 6) for most of the gage sites. To contextualize the strain mode data, one can heuristically define high tensile gage sites as those in which the magnitude of maximum principal strain is twice that or more of minimum principal strain. In such a case, the logarithm of strain mode (defined as the absolute value of the ratio of maximum to minimum principal strain) would be greater than or equal to 0.301. The opposite would be observed in high compression gage sites, in which the magnitude of maximum principal strain would be half that or less of minimum principal strain, resulting in a log of strain mode that is less than or equal to −0.301. One might further define gage sites experiencing an approximation of shear as those in which the magnitudes of maximum and minimum principal strain are within 50% of each other. Logarithms of strain mode in those areas would vary between -0.176 and 0.176. FEA and ex vivo experiments produced the same basic mode at three of the four gage sites during molar loading. During incisor loading, strain mode is (unsurprisingly) different at the palatal gage site because of the unusual strain pattern detected in the experiments (see above). Experiments and FEA produced similar strain modes at two of the remaining three sites. Notably, the gage sites at which there was poor correspondence in strain mode (the premaxilla during molar loading and the anterior zygomatic during incisor loading) were also the sites at which shear strain magnitudes were very low but ex vivo variability in strain mode was very high. Considering that the four experimental trials in each load case were identical, this indicates a limitation of the experiments to consistently record strain mode in low strain areas. Thus, it is problematic to use such data to evaluate the FEA with respect to such gage sites.

Table 5.

Log of strain mode (the ratio of maximum principal to minimum principal strain) during molar loading in four ex vivo experimental trials and FEA, as measured at four gage sites.

	Premaxilla	Dorsal rostrum	Anterior zygomatic	Palate
Molar trial 1	0.1723	0.0809	−0.1991	0.0184
Molar trial 2	0.2985	0.1592	−0.0334	0.0577
Molar trial 3	0.8002	0.1466	−0.0661	0.0291
Molar trial 4	0.4762	0.0972	−0.0703	0.0197
Ex vivo mean (s.d.)	0.437 (0.272)	0.121 (0.038)	−0.092 (0.073)	0.031 (0.018)
FEA	−0.13	−0.01	−0.08	0.080

Table 6.

Log of strain mode (the ratio of maximum principal to minimum principal strain) during incisor loading in the ex vivo experimental trials and FEA, as measured at four gage sites.

	Premaxilla	Dorsal rostrum	Anterior zygomatic	Palate
Incisor trial 1	−0.6558	−0.6480	−1.2480	0.4210
Incisor trial 2	−0.5687	−0.6247	−0.7637	0.4187
Incisor trial 3	−0.5387	−0.5684	−0.4762	0.4870
Incisor trial 4	−0.6399	−0.7458	−0.5852	0.5342
Ex vivo mean (s.d.)	−0.601 (0.056)	−0.647 (0.074)	−0.768 (0.341)	0.465 (0.056)
FEA	−0.43	−0.39	−0.01	0.1

With respect to maximum shear strain (Tables 7, 8), most FEA values are within 30 – 60 microstrain of the ex vivo averages. Such differences are modest in relation to the variation in shear strain magnitudes recorded in in vivo experiments at most gage sites (e.g., Hylander et al., 1991). Two gage sites during molar loading exhibited higher discrepancies. Strains during FEA were just over 200 microstrain too high on the dorsal rostrum, and nearly 300 microstrain too low on the palate. However, both of these gage sites correctly recorded strains that were higher than those at the premaxilla and anterior zygomatic sites.

Table 7.

Maximum shear strain (in microstrain) during molar loading in the ex vivo experimental trials and FEA, as measured at four gage sites.

	Premaxilla	Dorsal rostrum	Anterior zygomatic	Palate
Molar trial 1	51	269	155	471
Molar trial 2	45	248	130	452
Molar trial 3	41	269	132	448
Molar trial 4	40	269	124	440
Ex vivo mean (s.d.)	44.25 (4.99)	263.75 (10.50)	135.25 (13.60)	452.75 (13.15)
FEA	39	469	79	168

Table 8.

Maximum shear strain (in microstrain) during incisor loading in the ex vivo experimental trials and FEA, as measured at four gage sites.

	Premaxilla	Dorsal rostrum	Anterior zygomatic	Palate
Incisor trial 1	196	356	22	70
Incisor trial 2	191	341	14	67
Incisor trial 3	181	331	20	76
Incisor trial 4	191	331	26	74
Ex vivo mean (s.d.)	189.75 (6.29)	339.75 (11.81)	20.5 (5.0)	71.75 (4.03)
FEA	223	392	55	116

Intraspecific variation in strain

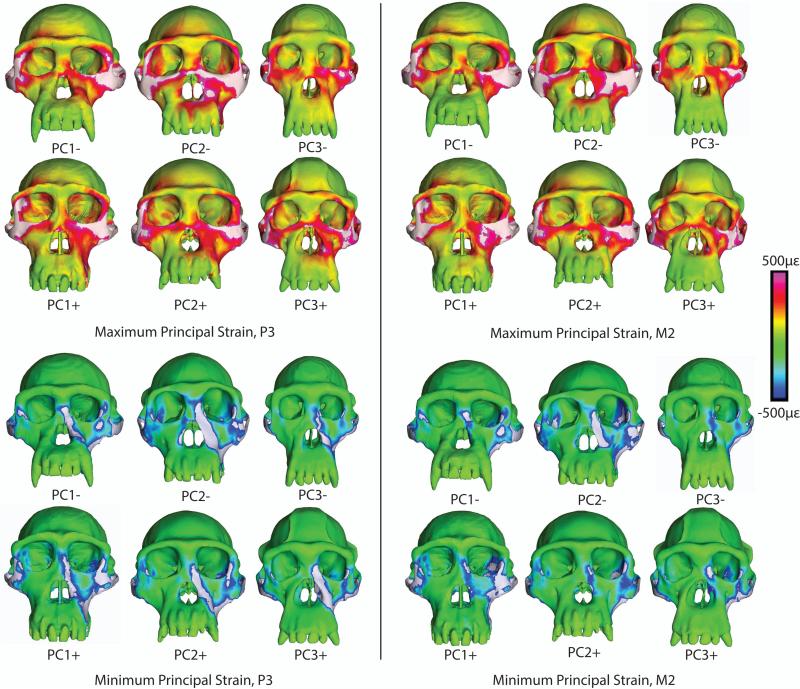
Despite differences in cranial morphology, the chimpanzee FEMs displayed broad similarities in the spatial patterning of high and low strain regions (Figure 4). During premolar loading (Figure 4, left), all models exhibited high concentrations of maximum principal strain in the zygomatic arches, the body of the zygoma (especially on the working [biting] side), the lateral aspect of the postorbital bar above its junction with the zygomatic arch, and the inferior margin of the orbit (especially on the working side). Notable but more moderate concentrations of tensile strain were observed at the superolateral angle of the orbit and along the working side nasal margin. A distinctive pocket of low tensile strain was observed just above the zygomatic root. Strong minimum principal strain concentrations under the same loading conditions are found in the zygomatic arch, the inferior margin of the working side zygomatic root, the working side nasal margin, the inferolateral corner of the orbit, and a discrete spot in the center of the working side zygomatic body. A pocket of weak compressive strain was found in the working side infraorbital plate.

Figure 4.

Color mapping of principal strains in finite element models of the crania of P. troglodytes, during simulated bites on the third premolar and second molar. White indicates areas where strain magnitudes exceed the color scale. Crania are scaled to the same height to visually accentuate differences in shape

During molar loading (Figure 4, right), the distribution of high maximum principal strain concentrations resembles that seen in premolar loading, with the exceptions that strains are generally higher in the working side infraorbital region and usually lower along the working side nasal margin. Strong minimum principal strain concentrations are similar during molar and premolar loading in most areas, except that compressive strains in the working side nasal margin are much lower during molar loading.

Although not shown in color maps, concentrations of moderate to high maximum shear strain, von Mises strain and strain energy density (SED) correspond spatially with regions of strong maximum and/or minimum principal strain. Variation in strain magnitude between models is greatest in the zygomatic arch.

The sampling of quantitative strain and SED data from homologous locations on the different crania (Tables 9, 10) corroborates the observation that changing the bite point has only a modest effect on strain magnitudes and SED in the circumorbital and zygomatic regions, but has a more marked effect on those values in the rostrum (as represented by the nasal margin location) (Figures 5, 6). In other words, bites on the premolars and on the molars influence strains in the circumorbital and zygomatic regions in similar ways, whereas strains in the rostrum during premolar biting are different from those observed during molar biting.

Table 9.

Strain¹ and strain energy density results from simulated premolar bites.

Location2	Specimen	Max Prin (με)	Min Prin (με)	Mode	Max shear (με)	von Mises (με)	SED (J/mm3)
1. Dorsal interorbital	PC1−	201	−79	2.55	280	259	0.29
	PC1+	119	−60	1.98	179	160	0.11
	PC2−	163	−125	1.31	288	249	0.24
	PC2+	124	−48	2.60	172	163	0.11
	PC3−	118	−53	2.22	171	160	0.10
	PC3+	216	−68	3.17	285	271	0.34
2. Working dorsal orbital	PC1−	55	−34	1.59	89	80	0.02
	PC1+	138	−61	2.27	199	189	0.14
	PC2−	53	−88	0.61	141	123	0.06
	PC2+	83	−88	0.95	170	148	0.08
	PC3−	16	−21	0.79	37	32	0.00
	PC3+	73	−92	0.79	165	144	0.07
3. Balancing dorsal orbital	PC1−	197	−86	2.29	283	267	0.28
	PC1+	188	−61	3.10	249	238	0.25
	PC2−	192	−87	2.20	279	264	0.26
	PC2+	187	−95	1.97	282	261	0.25
	PC3−	106	−48	2.23	153	146	0.08
	PC3+	190	−101	1.89	291	268	0.27
4. Working postorbital bar	PC1−	455	−481	0.95	935	810	2.33
	PC1+	432	−305	1.42	737	646	1.53
	PC2−	351	−325	1.08	677	586	1.22
	PC2+	346	−382	0.91	728	631	1.41
	PC3−	150	−168	0.89	318	276	0.27
	PC3+	337	−292	1.15	629	552	1.08
5. Balancing postorbital bar	PC1−	627	−444	1.41	1070	953	3.23
	PC1+	769	−479	1.61	1248	1115	4.56
	PC2−	718	−296	2.43	1013	959	3.64
	PC2+	665	−376	1.77	1041	947	3.30
	PC3−	406	−288	1.41	694	621	1.37
	PC3+	370	−184	2.01	553	504	0.99
6. Working mid-zygoarch	PC1−	1686	−1086	1.55	2772	2475	22.23
	PC1+	1616	−3390	0.48	5006	4791	83.65
	PC2−	1099	−3022	0.36	3903	4120	64.74
	PC2+	1710	−1049	1.63	2759	2495	22.49
	PC3−	337	−524	0.64	861	761	2.15
	PC3+	367	−492	0.75	859	757	2.04
7. Balancing mid-zygo arch	PC1−	1994	−676	2.95	2670	2583	27.96
	PC1+	1275	−2683	0.48	3958	3549	53.64
	PC2−	955	−2448	0.39	3403	3268	42.16
	PC2+	1912	−1227	1.56	3139	2793	28.54
	PC3−	417	−375	1.11	792	686	1.71
	PC3+	534	−179	2.99	713	699	2.00
8. Working zygo root	PC1−	391	−514	0.76	905	788	2.26
	PC1+	370	−827	0.45	1198	1080	5.07
	PC2−	359	−979	0.37	1339	1202	7.50
	PC2+	316	−835	0.38	1152	1137	4.92
	PC3−	537	−785	0.68	1323	1174	4.96
	PC3+	245	−721	0.34	966	868	4.17
9. Balancing zygo root	PC1−	314	−378	0.83	691	601	1.29
	PC1+	154	−539	0.29	693	644	2.23
	PC2−	240	−608	0.39	848	749	3.03
	PC2+	232	−275	0.84	506	440	0.69
	PC3−	347	−302	1.15	649	566	1.13
	PC3+	101	−287	0.35	387	350	0.64
10. Working infraorbital	PC1−	452	−425	1.06	877	760	2.04
	PC1+	530	−404	1.31	934	811	2.44
	PC2−	385	−211	1.82	596	560	1.12
	PC2+	572	−423	1.35	994	877	2.74
	PC3−	452	−310	1.46	762	671	1.65
	PC3+	575	−479	1.20	1054	916	2.99
11. Balancing infraorbital	PC1−	334	−276	1.21	610	531	1.01
	PC1+	199	−146	1.36	346	304	0.33
	PC2−	374	−193	1.94	530	566	1.02
	PC2+	361	−262	1.38	623	553	1.09
	PC3−	414	−202	2.05	615	574	1.24
	PC3+	477	−351	1.36	828	722	1.92
12. Working nasal margin	PC1−	356	−525	0.66	871	775	2.18
	PC1+	216	−463	0.47	679	625	1.54
	PC2−	351	−891	0.39	1183	1243	5.60
	PC2+	207	−484	0.43	691	639	1.68
	PC3−	311	−701	0.44	1012	934	3.52
	PC3+	284	−812	0.35	1096	1086	4.62

¹Max Prin = maximum principal strain. Min Prin = minimum principal strain. Mode = the absolute value of Max Prin / Min Prin. Max Shear = maximum shear strain. Von Mises = von Mises strain. SED = strain energy density.

²Locations numbered as in Fig. 5.

Table 10.

Strain¹ and strain energy density results from simulated molar bites.

Location2	Specimen	Max Prin (με)	Min Prin (με)	Mode	Max shear (με)	von Mises (με)	SED (J/mm3)
1. Dorsal interorbital	PC1−	194	−76	2.57	270	250	0.27
	PC1+	114	−58	1.96	171	154	0.10
	PC2−	138	−96	1.46	235	204	0.16
	PC2+	132	−49	2.70	181	174	0.12
	PC3−	108	−45	2.39	153	145	0.08
	PC3+	198	−64	3.10	262	250	0.28
2. Working dorsal orbital	PC1−	33	−26	1.26	60	52	0.01
	PC1+	81	−37	2.18	118	111	0.05
	PC2−	47	−91	0.51	138	120	0.07
	PC2+	26	−48	0.53	74	68	0.02
	PC3−	5	−22	0.23	27	26	0.00
	PC3+	46	−78	0.59	124	110	0.05
3. Balancing dorsal orbital	PC1−	195	−88	2.23	283	267	0.27
	PC1+	207	−67	3.08	274	262	0.31
	PC2−	209	−87	2.40	296	282	0.31
	PC2+	189	−91	2.08	279	260	0.26
	PC3−	110	−46	2.40	156	140	0.09
	PC3+	199	−111	1.80	310	284	0.30
4. Working postorbital bar	PC1−	365	−431	0.85	796	692	1.70
	PC1+	278	−229	1.21	507	440	0.70
	PC2−	223	−290	0.77	513	450	0.72
	PC2+	229	−298	0.77	527	460	0.76
	PC3−	93	−150	0.62	243	216	0.17
	PC3+	273	−264	1.03	537	468	0.78
5. Balancing postorbital bar	PC1−	624	−437	1.43	1061	947	3.19
	PC1+	817	−492	1.66	1309	1175	5.08
	PC2−	750	−296	2.54	1045	997	3.96
	PC2+	652	−363	1.79	1015	926	3.16
	PC3−	413	−283	1.46	696	626	1.39
	PC3+	367	−169	2.17	536	492	0.97
6. Working mid-zygoarch	PC1−	1629	−1029	1.58	2658	2379	20.59
	PC1+	1622	−3416	0.47	5039	4832	84.99
	PC2−	1113	−2996	0.37	4109	3879	63.70
	PC2+	1615	−995	1.62	2610	2364	20.12
	PC3−	334	−522	0.64	856	757	2.14
	PC3+	293	−445	0.66	737	662	1.57
7. Balancing mid-zygo arch	PC1−	1955	−668	2.93	2623	2528	26.91
	PC1+	1275	−2675	0.48	3950	3542	53.31
	PC2−	953	−2443	0.39	3396	3261	41.98
	PC2+	1869	−1203	1.55	3073	2733	27.32
	PC3−	405	−364	1.11	769	666	1.61
	PC3+	515	−172	3.00	686	672	1.86
8. Working zygo root	PC1−	388	−523	0.74	910	795	2.30
	PC1+	414	−1061	0.39	1475	1340	8.41
	PC2−	380	−831	0.6	1211	1803	5.20
	PC2+	365	−933	0.39	1298	1266	6.13
	PC3−	570	−888	0.64	1459	1303	6.16
	PC3+	350	−928	0.38	1278	1143	6.79
9. Balancing zygo root	PC1−	319	−398	0.80	716	625	1.39
	PC1+	141	−503	0.28	644	598	1.95
	PC2−	236	−607	0.39	843	747	2.99
	PC2+	227	−288	0.79	514	448	0.72
	PC3−	351	−308	1.14	659	575	1.17
	PC3+	108	−306	0.35	415	375	0.73
10. Working infraorbital	PC1−	441	−374	1.18	816	708	1.79
	PC1+	552	−398	1.39	950	823	2.66
	PC2−	467	−227	2.06	694	660	1.59
	PC2+	551	−376	1.47	926	830	2.45
	PC3−	438	−280	1.57	718	632	1.51
	PC3+	578	−498	1.16	1076	935	3.11
11. Balancing infraorbital	PC1−	324	−267	1.21	591	515	0.94
	PC1+	191	−135	1.42	325	287	0.30
	PC2−	360	−169	2.14	529	502	0.94
	PC2+	352	−245	1.43	597	531	1.01
	PC3−	403	−182	2.21	585	552	1.16
	PC3+	448	−307	1.46	754	660	1.63
12. Working nasal margin	PC1−	202	−191	1.06	393	340	0.41
	PC1+	141	−119	1.19	260	225	0.19
	PC2−	224	−457	0.49	681	625	1.51
	PC2+	111	−133	0.84	244	211	0.17
	PC3−	193	−269	0.72	462	408	0.60
	PC3+	149	−197	0.75	346	302	0.33

¹Max Prin = maximum principal strain. Min Prin = minimum principal strain. Mode = the absolute value of Max Prin / Min Prin. Max Shear = maximum shear strain. Von Mises = von Mises strain. SED = strain energy density.

²Locations numbered as in Fig. 5.

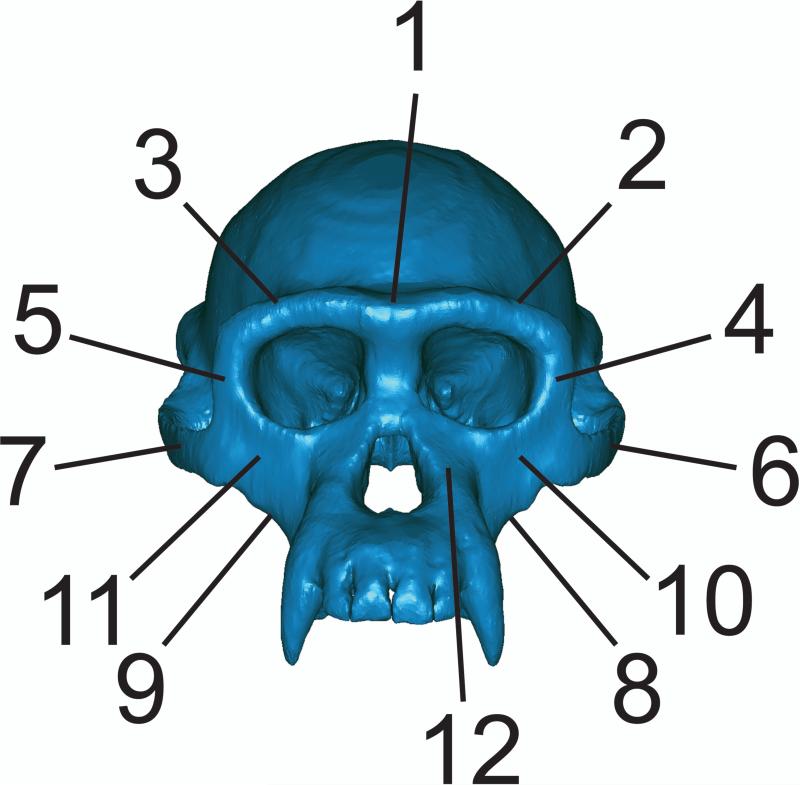
Figure 5.

Key to regions where strains were sampled in finite element models. 1 = Dorsal interorbital. 2 = Working side dorsal orbital. 3 = Balancing side dorsal orbital. 4 = Working side postorbital bar. 5 = Balancing side postorbital bar. 6 = Working side zygomatic arch. 7 = Balancing side zygomatic arch. 8 = Working side zygomatic root. 9 = Balancing side zygomatic root. 10 = Working side infraorbital. 11 = Balancing side infraorbital. 12 = Working side nasal margin.

Figure 6.

Box plots of strains at specified locations across all models. Maximum principal strain during (A) P³ and (B) M² loading. Minimum principal strain during (C) P³ and (D) M² loading. Maximum shear strain during (E) P³ and (F) M² loading. Von Mises strain during (G) P3 and (H) M² loading. Strain energy density (SED) during (I) P³ and (J) M² loading. See Figure 5 for a key to the sampling locations.

On balance, the spatial distribution of high strain concentrations is conservative in the face of marked intraspecific morphological variation (Figure 4). This implies that the differences between individuals are principally in magnitude rather than distribution. Indeed, strain magnitudes and SED sampled from locations across each cranium exhibit high levels of variation as revealed by coefficients of variation (CVs) (Table 11); although the values of the CVs reported here may be artificially inflated due to the procedure used to sample specimens, the statistic is nonetheless a useful, simple metric for detecting patterns of variability. These are highest in the zygomatic arches and working side dorsal orbital region, and lowest in the working side infraorbital region, with CVs of strain ranging in all regions from between about 10 to about 80. Coefficients of variation for SED are higher than those for strain magnitude, but this is not unexpected given that SED is equivalent to the area under the stress-strain curve at a particular material point, and thus is expected to scale as a square rather than linearly. The similarity of strain distributions is more easily visualized by normalizing the scales of the color maps relative to the average magnitude of strains from selected nodes across the cranium (Figures 5, 7); the maximum value on the scale of each cranium is equal to the average magnitude observed at 10 locations (all of those in Tables 9 and 10 except the zygomatic arches, whose high magnitude yet highly variable strain values would unduly influence the results). By resetting the scale against which colors are plotted, a map is produced that represents “relative strain.” These images effectively depict the distribution of relatively high and relatively low strain areas across the cranium without reference to an absolute strain scale. These relative strain maps confirm that the distribution of principal strain concentrations across the cranium in P. troglodytes is largely consistent despite differences in cranial shape.

Table 11.

Coefficients of variation for strain¹ and strain energy density results from simulated premolar and molar bites.

Location2	Bite	Max Prin	Min Prin	Mode	Max shear	von Mises	SED
1. Dorsal interorbital	Premolar	27.8	39.0	27.4	26.4	25.9	53.1
	Molar	26.7	29.2	24.5	23.6	23.6	51.6
2. Working dorsal orbital	Premolar	58.2	47.9	54.7	44.9	46.6	79.7
	Molar	64.1	56.2	81.6	48.0	47.1	82.0
3. Balancing dorsal orbital	Premolar	19.7	25.9	18.9	20.5	19.8	32.5
	Molar	20.2	27.4	18.5	20.9	20.1	32.8
4. Working postorbital bar	Premolar	31.1	35.4	18.8	30.1	30.0	51.2
	Molar	36.8	33.5	24.2	33.7	33.2	61.5
5. Balancing postorbital bar	Premolar	28.0	31.9	22.2	27.7	27.6	48.5
	Molar	29.8	34.2	23.6	29.6	29.9	52.4
6. Working mid-zygo arch	Premolar	57.0	80.2	61.0	61.1	65.0	102.8
	Molar	58.2	82.8	63.0	64.3	67.0	106.7
7. Balancing mid-zygo arch	Premolar	56.9	84.6	73.3	56.3	55.8	81.0
	Molar	56.8	85.4	73.3	57.0	56.6	81.9
8. Working zygo root	Premolar	26.2	19.9	35.9	15.7	16.5	35.1
	Molar	19.6	21.1	29.9	16.2	25.6	34.8
9. Balancing zygo root	Premolar	40.2	35.7	54.2	25.6	25.7	62.8
	Molar	41.4	32.1	54.2	23.8	23.6	58.0
10. Working infraorbital	Premolar	15.5	26.0	19.1	19.3	17.4	32.4
	Molar	12.4	24.4	22.4	17.1	15.3	29.8
11. Balancing infraorbital	Premolar	25.9	30.6	22.7	26.4	24.9	46.3
	Molar	25.3	30.2	25.6	224.79.5	36.0	43.0
12. Working nasal margin	Premolar	22.5	28.6	11.2	26.5	28.5	52.7
	Molar	25.3	54.6	29.9	40.5	43.4	94.0

¹Max Prin = maximum principal strain. Min Prin = minimum principal strain. Mode = the absolute value of Max Prin / Min Prin. Max Shear = maximum shear strain. Von Mises = von Mises strain. SED = strain energy density.

²Locations numbered as in Fig. 5.

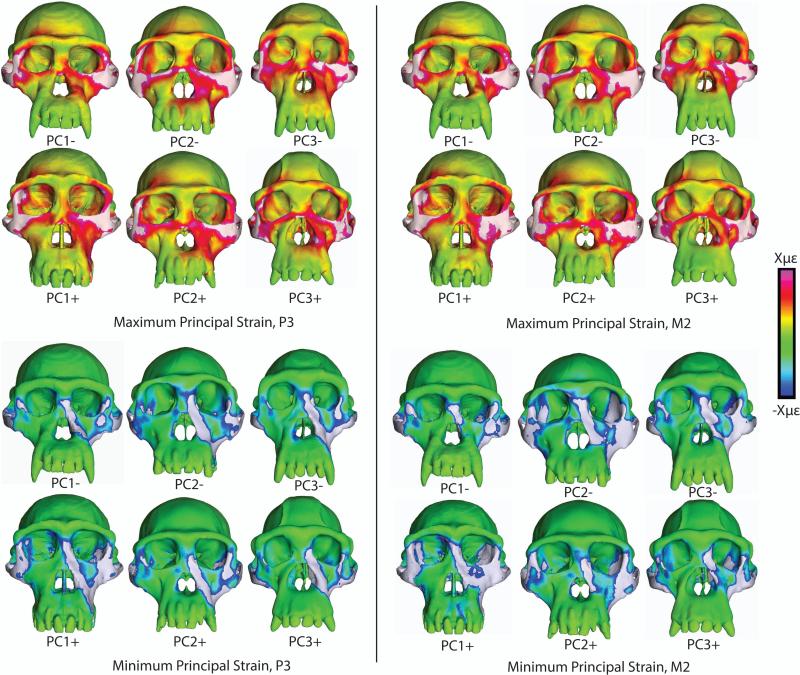
Figure 7.

Visualization of normalized scale color maps to depict the relative principal strains in finite element models of chimpanzee crania during simulated bites on the third premolar and second molar. Color scale corresponds to the average of strain values collected from ten locations on each model for each bite point. The scale ranges from –X to X, where X differs in each image as follows: Premolar bite, maximum principal strain: PC1- : 502; PC1+ : 486; PC2- : 556; PC2+ : 477; PC3-: 370; PC3+ : 473. Premolar bite, minimum principal strain: PC1- : 441; PC1+ : 371; PC2- : 484; PC2+ : 405; PC3- : 336; PC3+ : 239. Molar bite, maximum principal strain: PC1- : 446; PC1+ : 446; PC2- : 516; PC2+: 420; PC3- : 311; PC3+ : 423. Molar bite, minimum principal strain: PC1- : 354; PC1+ : 288; PC2- : 325; PC2+ : 301; PC3- : 239; PC3+ : 317. White indicates areas where strain magnitudes exceed the color scale.

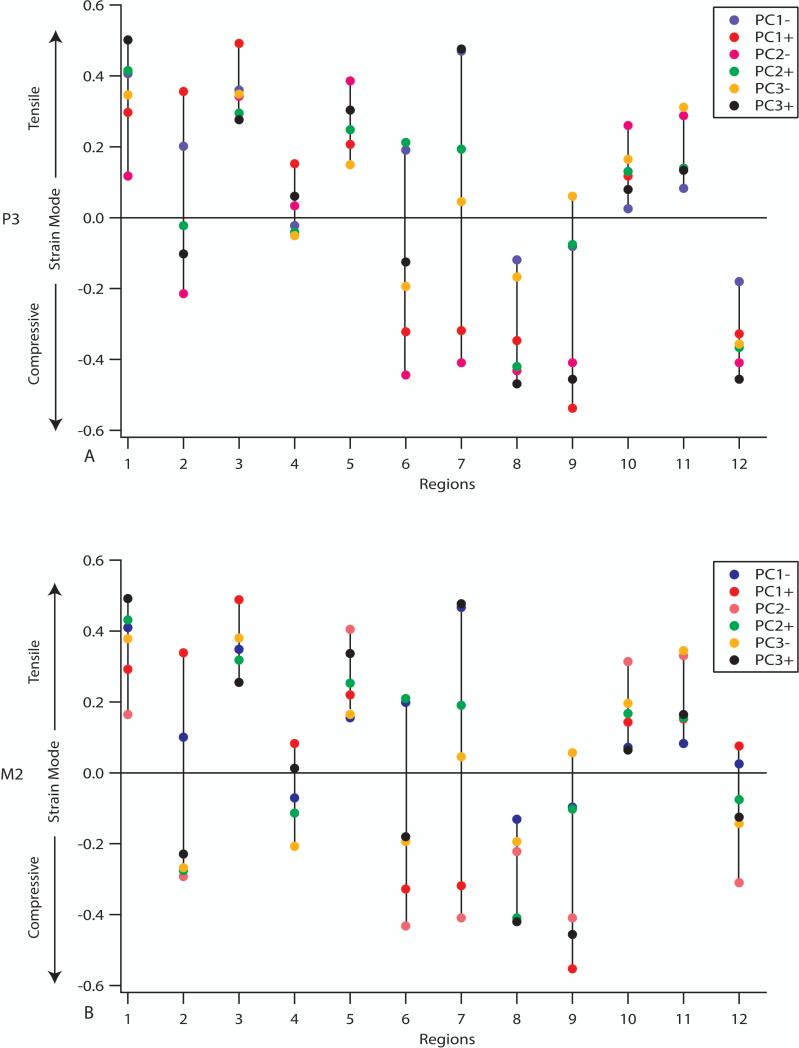
A consideration of strain mode (the ratio of maximum to minimum principal strains) reveals that the nature of strains (i.e., primarily tensile, primarily compressive, primarily shear [when principal compressive and tensile strains are similar]) can vary in complicated ways in crania of different shape (Figure 8). During premolar loading, five regions consistently exhibit stronger tensile than compressive strains (dorsal interorbital, balancing side dorsal orbital, balancing side postorbital bar, and the working and balancing side infraorbital regions). Two regions consistently exhibit stronger compressive than tensile strains (working side zygomatic root, working side nasal margin). Five regions do not consistently display a dominance of either maximum or minimum principal strain (working side dorsal orbital, working side postorbital bar, working and balancing side zygomatic arch, and the balancing side zygomatic root regions), indicating that strain gradients in these areas are steep and may be distributed differently in crania of alternate shape. For these regions, strains taken from a single point do not do justice to the complexity of the overall strain pattern. The working side postorbital bar gage site consistently experiences strain modes indicative of shear, but strains in the bar as a whole are extremely complex as one moves from medial to lateral across the structure. Molar loading essentially reveals the same patterning in strain mode, except with respect to the working side nasal margin. This region no longer consistently experiences strong compression, but is variable with respect to the dominance of tension and compression in a way that is consistent with an approximation of shear. This further corroborates the observation that bite point position has only a subtle effect on strains in the circumorbital region, but a stronger effect on strains in the rostrum.

Figure 8.

Distribution of strain mode (log of ratio of maximum to minimum principal strain) by region for A) premolar biting and B) molar biting. Negative values are compressive dominant and positive values are tensile dominant.

DISCUSSION

Validation

The validation study reveals that the FEA incorporates error. Is this error so great as to raise doubts about whether strain patterns in the chimpanzee sample can be meaningfully interpreted? In this context, it is important to consider the variability present in the in vivo experimental bone strain data set. In experiments in which a single individual is repeatedly fed foods of the same “type” (i.e., apple with skin), it is not uncommon for the standard deviation of maximum shear strain to exceed one quarter to one third of the mean (Hylander et al., 1991). Considering that most of the dispersion around the mean should fall within two standard deviations in either direction, this indicates that in many experiments in which food material properties, skeletal geometry and bone material properties are invariant, the experimental variability is nonetheless substantial and roughly comparable to the error in the FEA. When one further considers that variation in strain between individuals may further be as great as a factor of 2 or 3, it becomes evident that the error in our FEMs does not preclude the possibility that they can produce broadly realistic simulations of feeding mechanics, as has been demonstrated in our in vivo validation studies (Strait et al., 2005, 2009; Nakashige et al., 2011; Ross et al., 2011). Examinations of Tables 1 and 2 reveal that our assumptions about material properties incorporate error that, on their own, could explain part or much of the discrepancy in strain values observed between FEA and ex vivo experiments, and yet our assumptions in this regard are more accurate than those typically employed in FEA of vertebrate crania. Moreover, our FEM necessarily incorporates morphological simplifications that undoubtedly contribute to the error.

In addition, discrepancies between strain gage experiments and a single FEM do not necessarily mean that comparisons between multiple FEMs are invalid. Consider that the six chimpanzee FEMs exhibit considerable variation in strain magnitude but overall similarity in strain distribution. Error in each FEM introduces “noise” into the results, but does not invalidate these similarities.

In summary, the ex vivo validation study demonstrates that FEMs of primate (and, arguably, vertebrate) crania are suitable for drawing conclusions about broad patterns of stress and strain (especially when comparing crania of substantially different shapes), but should be interpreted cautiously if the objective is to quantitatively characterize in detail the stress and strain states of a particular area of a specific individual.

Integrating FEA and GM

Important steps have been taken in recent years to integrate GM and FEA (e.g., O'Higgins et al., 2011), but important challenges remain (Weber et al., 2011). To date, GM has been used to reconstruct the morphology of damaged or distorted fossil specimen for use in FEA (Benazzi et al., 2011b; O'Higgins et al., 2011), to warp crania, mandibles or other skeletal elements into different shapes that are subsequently the basis of FEA (e.g., Pierce et al., 2008; Stayton, 2009; Gröning et al., 2011a; Panagiotopoulou, 2011c; Parr et al., 2012), and to describe the displacements present in FEMs under a variety of loading regimes (Ross et al., 2005; Gröning et al., 2011b; Fitton et al., 2012). Important work has also been done developing the statistical basis for comparing strains in different models (Bookstein, 2013). Here we have employed a simple approach to address one of the central criticisms of many applications of FEA in evolutionary biomechanics, namely, that evolutionary inferences must be based on assessments of variation that are lacking in analyses of only one or two randomly chosen specimens. Our approach does not use GM to warp crania into new shapes that fall along statistically independent axes of variation; rather, it is based on FEA of actual rather than theoretical specimens. Thus, there is no danger that the warping process will introduce unrealistic yet undetected morphology that may bias mechanical results (see sensitivity analysis in O'Higgins et al. [2011]). Indeed, the strength of our approach is that it is widely applicable, time efficient (in the sense that relatively few, rather than many models need to be built), and relies on a minimum of untested assumptions about the validity of analyzing warped structures mechanically. Warping, of course, provides the conceptual advantage of allowing the examination of the mechanical correlates of independent aspects of shape, but it does so at the expense of analyzing shapes that are not necessarily biologically “real.”

Evaluation of null hypothesis

It would be ideal to have a statistical test that would allow one to objectively and quantitatively test the null hypothesis that intraspecific morphological variation has no effect on the pattern and magnitude of strains present in the craniofacial skeleton during biting. Unfortunately, such a test does not yet exist, and even if it did, the current sample of chimpanzees would very likely be an unsuitable subject for it. Despite the fact that each FEM contains hundreds of thousands of nodes, each of which provides information about multiple measures of stress, strain and displacements, these data do not represent millions of independent variables. Rather, FEA is a deterministic process such that, once input parameters are provided, the solution of the entire model is fixed. It is incorrect to ask whether or not the strains in any two FEMs, in isolation, are statistically significantly different from each other, because in fact they are simply and obviously different (see discussion in Strait et al., 2005). However, in principle it should be possible to document the manner in which the two models differ from each other and then contextualize those differences by asking whether or not they are likely to be observed in a random sample of individuals from a natural population. This is not yet possible. First, the chimpanzees examined here were not randomly selected. Rather they were chosen specifically because they are morphologically different from each other. At best, they provide coarse information about the range of mechanical variation expected in chimpanzees; they do not otherwise provide insight into “natural” mechanical variation in the species. More broadly, there is not yet available a statistical tool that would efficiently allow a quantitative assessment of strain patterns within and between species that takes advantage of the huge amount of information provided by FEA while simultaneously accounting for the three dimensional spatial information that varies across the FEMs. It is vitally important that such tools be developed, and Bookstein's (2013) treatment of the mathematics underlying GM and FEA appears to point the way forward. Practical obstacles to the implementation of his methodology remain to be overcome, but these are the challenges that must be faced in order to achieve true integration of shape and mechanical analyses. Concerted effort by a community of like-minded researchers will be needed to tackle this problem.

In the interim, the present study is an incremental step towards the achievement of these goals. As noted, the approach employed here provides some information about the quantitative and qualitative range of mechanical variation expected within a species. This provides a rough framework in which to contextualize mechanical differences between, for example, individuals of different species. It is not as yet possible to objectively falsify the null hypothesis, but it appears at least subjectively that the hypothesis applies more strongly to certain measures of strain compared to others.

Results indicate that strain magnitudes can vary considerably within species simply as a function of shape variation. This variability is most pronounced in the zygomatic arch but is impressively high in most regions of the face with the exception of the working side infraorbital region (Table 11). This finding cautions against placing too much importance on even seemingly large differences in strain magnitudes when comparing crania from different species. Certainly, strain magnitude is important because strains may play a role in regulating bone remodeling (Rubin and Lanyon, 1984, 1985; Beaupre et al., 1990; Carter, 1990; Goodship, 1992; Currey, 2002; 2003). Moreover, strain is a consequence of stress, which in turn is related to bone failure due to fatigue or high loads. Strain is also a variable that can be directly measured experimentally. Yet, although one can certainly interpret strain data to infer that a given cranial shape is stronger or weaker than another, one must exercise caution when inferring that a given cranial shape has evolved to be stronger than another in the absence of evidence showing that variation in strain magnitudes between species exceeds that within species. Note that this does not necessarily mean that strain magnitudes are uninformative when interspecific differences do not obviously exceed intraspecific differences. Rather, they might be informative, but an interpretation of those strains in an evolutionary context might require a more nuanced explanation than simply characterizing crania as being strong or weak.

One way to interpret strain magnitudes would be to focus on the distribution of high strain regions across the cranium. In this study, the distribution of strain magnitudes emerged as a variable with qualitatively low levels of intraspecific variation across the range of morphological variation encompassed by our sample. In other words, despite manifest variation in morphology, the underlying geometry of the specimens is such that the same regions in different specimens experience high vs. low strains. The absolute magnitudes of those high and low strains may vary between specimens, but the spatial distributions of these areas remains constant. This suggests that morphological variation within this species does not disrupt the fundamental structural architecture; i.e., the crania of all members of the species function in mechanically similar ways. If this interpretation is correct, and this pattern also characterizes other species, it suggests that when individuals of different species exhibit obvious differences in strain distribution, then those patterns may be attributable to interspecific rather than intraspecific morphological variation. Precisely which aspects of shape variation produce the largest variation in mechanical performance in any particular case (species, system) is therefore important to elucidate. We hypothesize that notable differences in strain distribution may reflect differences in evolutionary history and, perhaps, adaptation. This hypothesis can be tested by examining intraspecific patterns of strain distribution within multiple species and predicts that intraspecific variation in strain distribution may often be smaller than interspecific variation.

These findings have implications for interpretations of mechanical differences between and among fossil hominin species. Although it is worthwhile to document whether specimens exhibit generally high or generally low strains under controlled loading regimes, such comparisons should also document whether the specimens exhibit strain distributions that are similar or different. Key research questions include: Are australopith crania stronger than those of extant non-human apes? Are they stronger than those of early Homo? Are the crania of certain australopiths stronger than those of other australopiths? To what extent do strain distributions in australopiths differ from those seen in extant non-human apes? To what extent do strain distributions in australopiths differ from each other? Does each species have a distinctive pattern, or do some species share a common pattern? Do distributions differ between putative australopith grades (i.e., robust vs. gracile australopiths)? Do early hominin species exhibiting marked variation in craniofacial form (e.g., Australopithecus africanus) exhibit a common strain distribution? Are the strain distributions in the putatively distinct species Homo habilis sensu stricto and H. rudolfensis similar or different? Does facial reduction in Homo correspond to weaker crania and distinct strain distributions? What specific aspects of cranial shape underlie the differences in strength and/or strain distribution seen in exant hominoids and fossil hominins? We suggest that addressing these questions may provide valuable insights into the feeding mechanics, behavior, adaptation and evolution of extinct hominins.

CONCLUSION

A full integration of GM and FEA remains an unfulfilled goal, but the study presented here takes steps in that direction. Most critically, it develops a straightforward framework for evaluating the mechanical correlates of intraspecific morphological variation. This information will be vital for efforts to understanding the evolution of mechanically significant forms. As the sister taxon of humans, mechanical variation in chimpanzees is expected to play a major role in establishing the framework for interpreting mechanical differences among and between fossil hominins. It is hypothesized here that intraspecific variation in shape does not disrupt underlying species-level aspects of geometry that are mechanically conservative. If true, it points towards a research program focusing on the pattern by which strains are distributed across the cranium in non-human primates and fossil hominins.