Abstract
Lithiation of 1,4-difluorobenzene with lithium diisopropylamide (LDA) in THF at −78 °C joins the ranks of a growing number of metalations that occur under conditions in which the rates of aggregate exchanges are comparable to the rates of metalation. As such, a substantial number of barriers vie for rate limitation. Rate studies reveal that rate-limiting steps and even the choice of reaction coordinate depend on subtle variations in concentration. Deuteration shifts the rate-limiting step and markedly alters the concentration dependencies and overall rate law. This narrative is less about ortholithiation per se and more about rate limitation and the dynamics of LDA aggregate exchange.
Introduction
A survey of more than 500 total syntheses shows that lithium diisopropylamide (LDA) is the most frequently used reagent in organic synthesis.1,2 It is this prominence that piqued our interest in structural and mechanistic studies of LDA—studies that have now spanned more than 25 years.3 For several practical reasons, we focused mechanistic studies on reactions that could be monitored at temperatures ranging from −55 to +25°. Despite a large number of mechanistic variations arising from dozens of substrate–solvent combinations, the aggregate equilibrations were rapid on the time scales of the rate-limiting substrate lithiation.
The opposite limiting behavior has been the focus of Reich and co-workers using rapid-injection NMR spectroscopy. LDA-mediated enolizations of reactive ketones that are observable on short time scales below −135 °C4 are rapid on the time scales of aggregate exchanges.5
There is necessarily a window of substrate reactivity—a critical temperature range—in which readily observed lithiations and LDA aggregate exchanges occur at comparable rates. In this regime, the chemistry would certainly become complex. In an irony that will be lost on few organic chemists, this twilight zone for LDA/tetrahydrofuran (THF)-mediated lithiations is centered at −78 °C:6,7any LDA/THF-mediated lithiation that proceeds at observable rates at −78oC is occurring under nonlimiting conditions in which aggregation events and reactions with substrate vie to be rate limiting. Under such nonlimiting conditions, the rules governing reactivity change markedly: aggregates are no longer in full equilibrium; the rate-limiting step shifts unpredictably with subtle changes in reaction conditions; catalysis by traces of extraneous lithium salts (especially lithium chloride) and autocatalysis by the developing product become acute; and substituting deuterium for protium can change the rate, mechanism, and rate law. In short, LDA/THF-mediated lithiations observed at −78 °C are complex even by the standards of organolithium chemistry.
 |
1 |
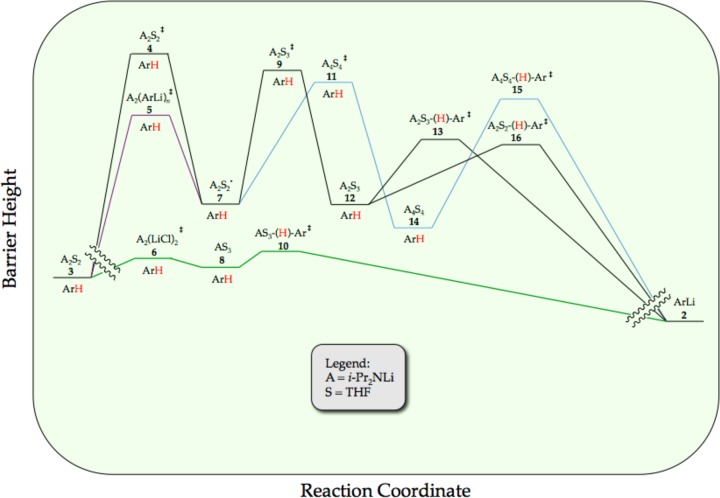
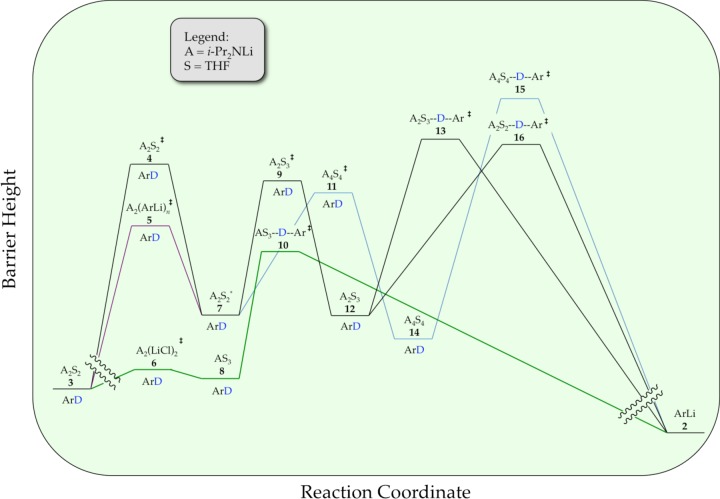
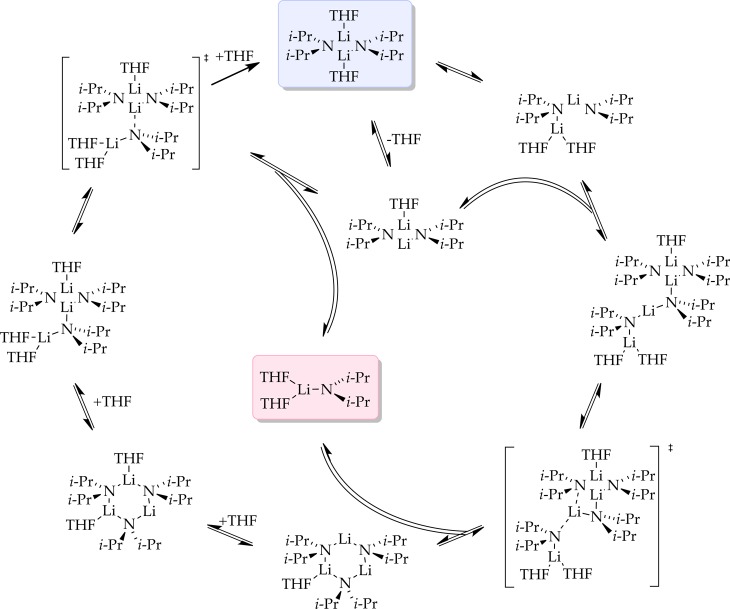
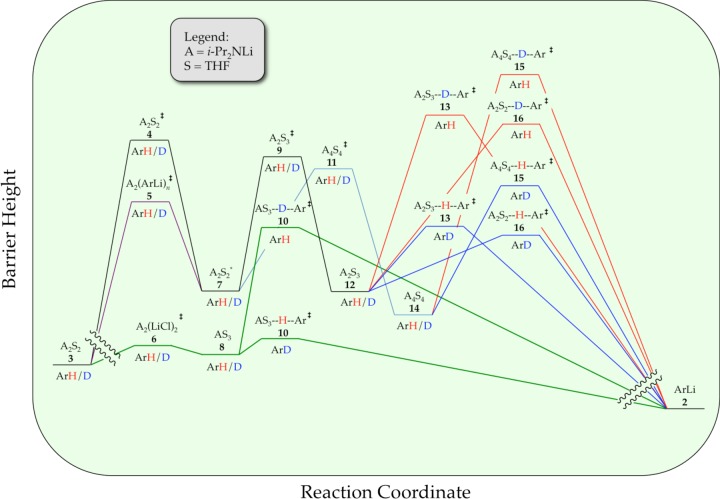
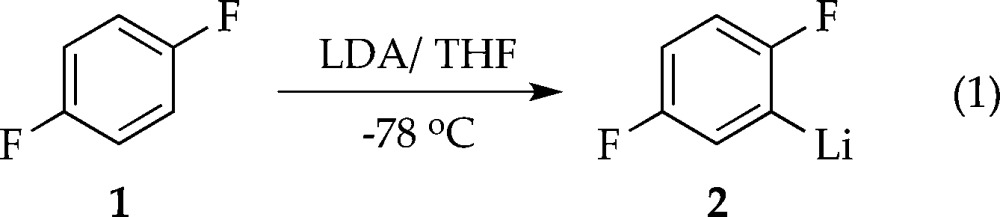
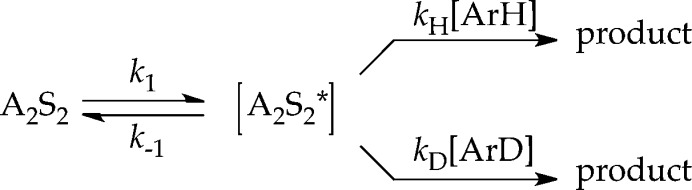
We describe herein mechanistic studies of the LDA/THF-mediated lithiation of 1,4-difluorobenzene (1) (eq 1).8 Spoiler alert: here is what we find. Lithiation of arene 1 by dimeric LDA occurs through the cascading deaggregation illustrated by the reaction coordinate diagram in Scheme 1. Note that Scheme 1 connotes qualitative relative barrier heights but lacks the implicit balancing to be called a free energy diagram. It is also a living, breathing diagram that changes consequentially with concentrations and, as we describe, isotopic substitution. In the absence of catalysis, rate-limiting deaggregation occurs via disolvated dimer transition state 4. Autocatalysis9,10 by the resulting aryllithium via mixed-aggregate-based transition structure 5 circumvents 4, revealing LDA-tetramer-based transition state 11 lurking over the thermochemical horizon.11 Perdeuteration of 1, by virtue of the often large and highly variable isotope effects for LDA-mediated ortholithiations,11 drops the zero-point energy (ZPE) of the barrier corresponding to 4 to reveal two competing dimer-based proton transfers (13 and 16) as the highest remaining barriers. Lithium chloride—the most efficient deaggregation catalyst reported to date—circumvents barriers corresponding to the aforementioned transition states altogether via mixed-aggregate-based transition state 6 delineated previously,6 affording trisolvated-monomer-based transition structure 10 for proton transfer.
Scheme 1.
These conclusions emanate from a series of spectroscopic, kinetic, and computational studies of the reaction cascade involved in the lithiation of 1 and its perdeuterated analogue. The mechanistic changes accompanying subtle changes in conditions are legion, but we have not peered beyond rate-limiting steps with such clarity as described below. The discussion is written for the nonspecialist wishing to skip the detailed Results.
Results
To simplify the results and discussion, we introduce the following shorthand used in Scheme 1: A = an LDA subunit, S = THF, ArH = arene 1, ArD = tetradeuterated arene 1-d4, and ArLi refers to aryllithiums 2 or 2-d3. By example, A2S2 corresponds to disolvated LDA dimer 3. We will denote general structures and their more specific counterparts (ArLi 2 and 2a, for example) interchangeably depending on the context. ArH and ArD are mechanistically so different that they demanded fully independent rate studies; they are presented in separate sections within the following subsections: uncatalyzed, autocatalyzed, and LiCl-catalyzed lithiations. The key to understanding the results is that changes in conditions—essentially any changes—shift the rate-limiting steps and consequentially alter the mathematical form of the accompanying rate law. We begin with some foundational structural studies.
Reaction Profile
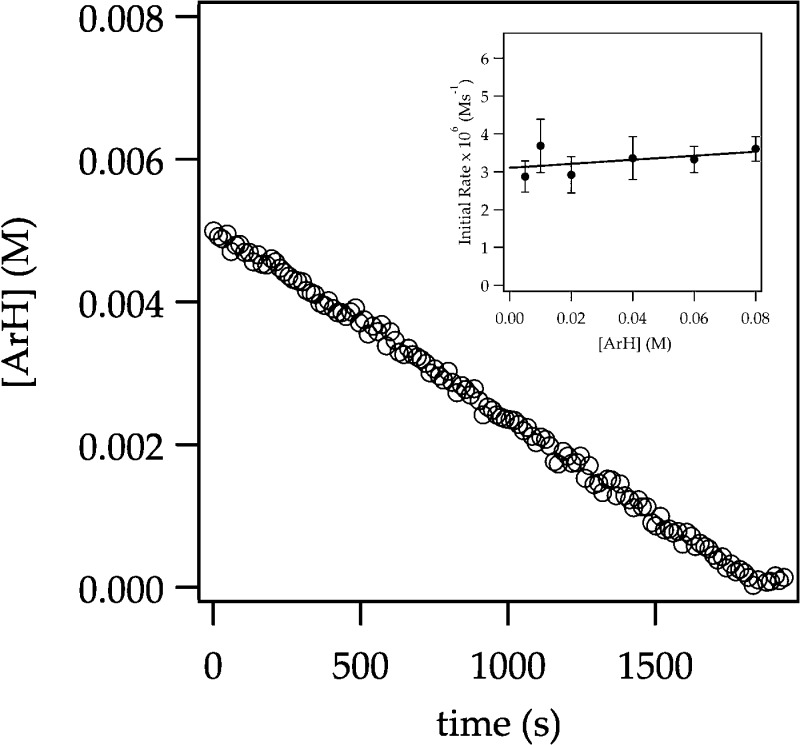
Metalation of relatively high concentrations of ArH by LDA specifically at low THF concentrations promotes mixed aggregation. 19F NMR spectroscopy shows the time dependence of a number of species: a downwardly curving decay of ArH, a nearly linear formation of ArLi, and sigmoidal growth of an LDA–ArLi mixed aggregate (Figure 1). The mixed aggregate is much less relevant than one might think, and the other decays are much more complex than most could imagine. The curves represent a best-fit numerical integration to a model described herein. We begin with the relatively simple task of characterizing the observable species.
Figure 1.
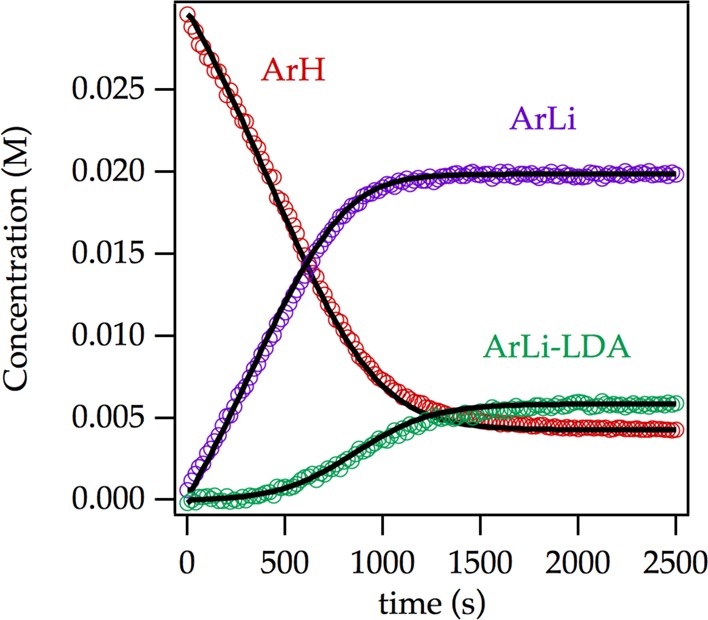
Time-dependent concentrations measured by 19F NMR spectroscopy using 0.10 M LDA and 0.030 M ArH in 3.05 M THF/hexanes at −65 °C. The curves represent a best-fit numerical integration to the emergent model (vide infra).
Solution Structures
Previous studies of [6Li,15N]LDA using 6Li and 15N NMR
spectroscopies have revealed exclusively disolvated dimer 3.12 Aryllithium 2 is shown
to be trisolvated monomer 2a. Trisolvated mixed dimer 17 is observed at low levels and only at high LDA and low THF concentrations.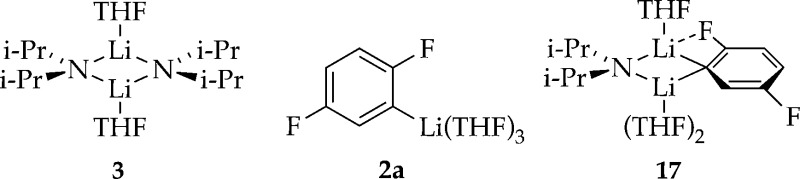
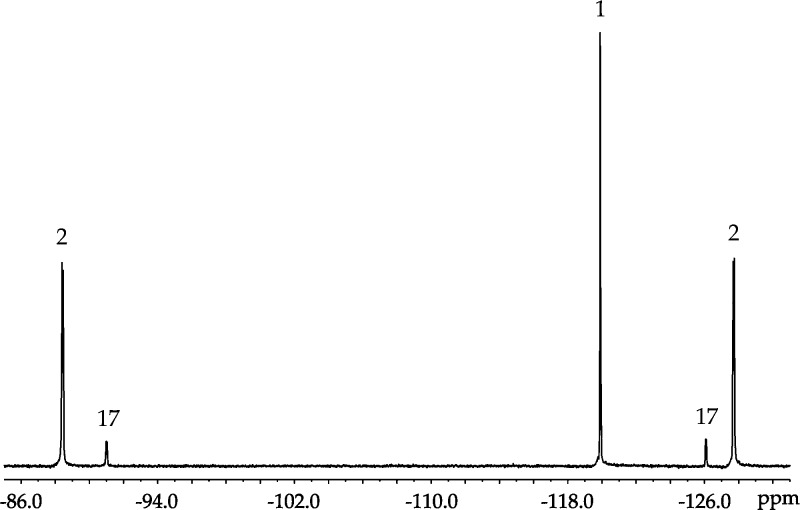
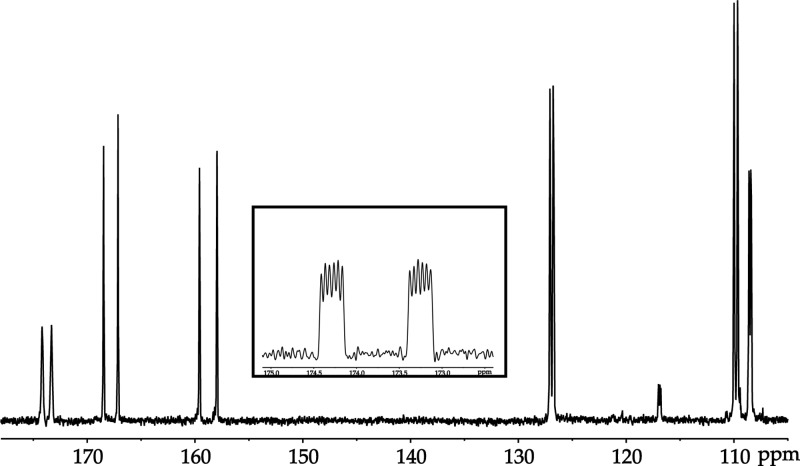
19F NMR spectroscopy of a sample prepared from 2:1 LDA/ArH in 3.5 M THF reveals a pair of doublets owing to five-bond 19F–19F coupling with additional 1H–19F coupling discernible using window functions,6 consistent with 2a (Figure 2). The 19F–19F coupling was confirmed with single-frequency 19F decoupling.13 A 13C NMR spectrum shows the carbanionic carbon resonance of 2a as a triplet (JLi–C = 6.0 Hz) further split by a large (130 Hz) two-bond 19F–13C coupling and a small (18.6 Hz) three-bond 19F–13C coupling (Figure 3; inset).14 The large two-bond coupling has been noted previously for ortholithiated fluoroarenes.15
Figure 2.
19F NMR spectrum of LDA (0.10 M) with ArH (0.050 M) and diisopropylamine (0.050 M) in 3.5 M THF/hexanes at −78 °C. 1: δ −119.90 (s). 2: δ −127.71 (d, 5JF–F = 31.6 Hz), −88.43 (d, 5JF–F = 31.6 Hz). 17: δ −126.09 (d, 5JF–F = 31.0 Hz), −91.01 (d, 5JF–F = 31.0 Hz). Excess amine was added to establish the balanced equilibrium.
Figure 3.
13C{1H} NMR spectrum of ArLi generated from ArH (0.30 M) with [6Li]LDA (0.40 M) in 12.2 M THF-d8 at −105 °C: δ 173.75 (ddt, 2JC–F = 130.2 Hz, 3JC–F = 18.6 Hz, 1JC–Li = 6.0 Hz), 167.81 (d, 1JC–F = 201.7 Hz), 158.77 (d, 1JC–F = 244.7 Hz), 126.90 (dd, 2JC–F = 44.8 Hz, 3JC–F = 8.8 Hz), 109.82 (dd, 2JC–F = 49.3 Hz, 3JC–F = 3.7 Hz), 108.50 (dd, 2JC–F = 25.5 Hz, 3JC–F = 7.2 Hz).
We determined the solvation number of 2a using three independent methods:
(1) We relied on the recently completed assignment of bis-trifluoromethylated aryllithium 18 as a trisolvated monomer.16 Monitoring the equilibrium in eq 2 versus THF concentration shows no dependence (±10%) over a 10-fold THF concentration range, confirming 2a as a trisolvate.
 |
2 |
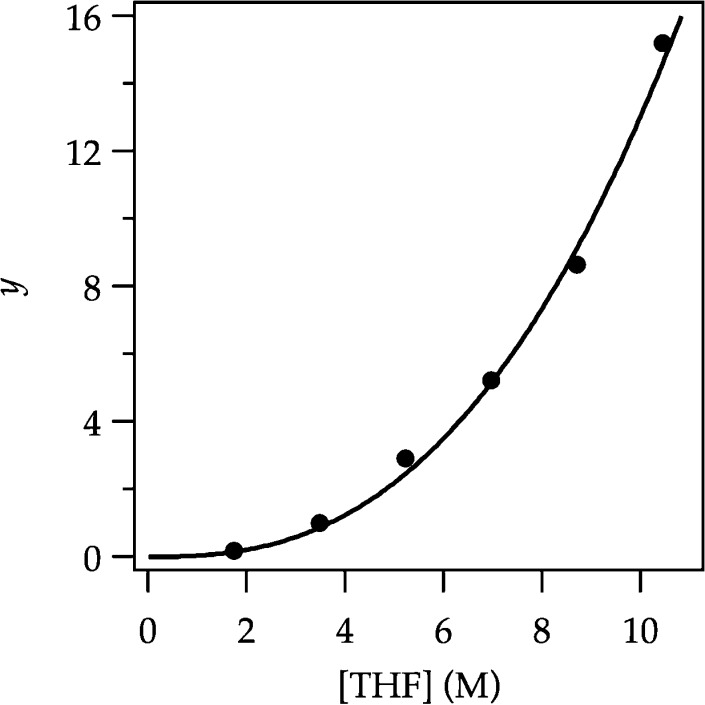
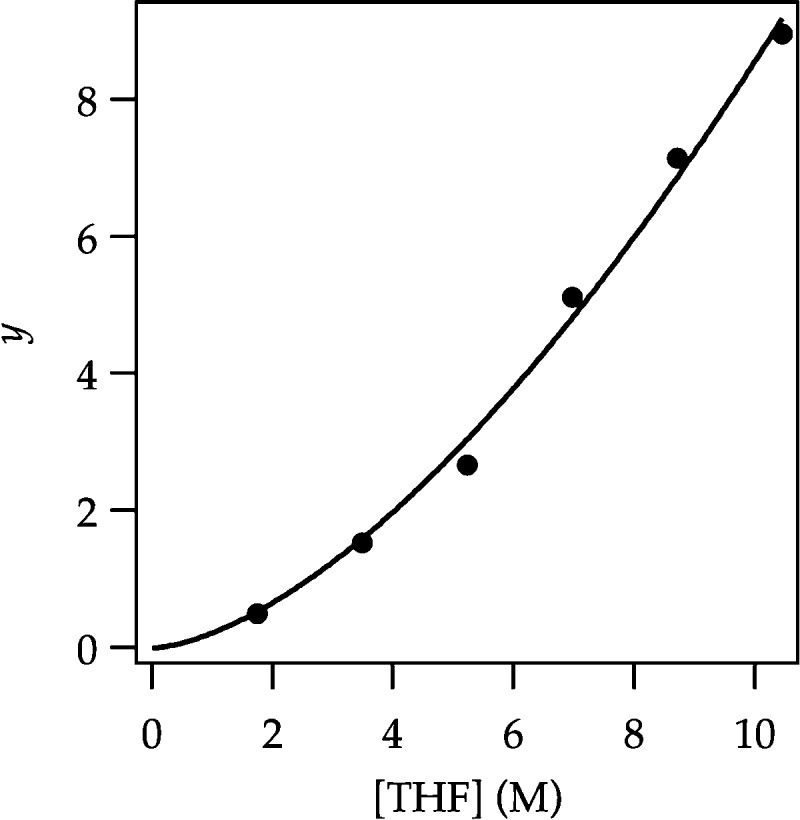
(2) Lithiation using excess i-Pr2NH and variable THF concentrations (eq 3), conditions in which ArLi and ArH coexist at equilibrium, establishes the solvation number according to eq 4 (Figure 4). Monitoring the concentrations of ArH and ArLi with 19F NMR spectroscopy and back calculating the concentrations of i-Pr2NH and LDA affords the solvation number of 3.6 ± 0.2.
 |
3 |
| 4 |
Figure 4.
Plot of y from eq 4 versus [THF] in hexanes cosolvent for the ortholithiation of ArH (0.050 M) with LDA (0.10 M) in the presence of added diisopropylamine (0.050 M) measured by 19F NMR spectroscopy at −78 °C. The curve depicts an unweighted least-squares fit to y = a[THF]n. [a = (0.03 ± 0.01) × 10–2, n = 2.6 ± 0.2].
(3) Density functional theory (DFT) computations at the B3LYP/6-31G(d) level17 with single-point calculations at the MP2 level of theory of the serial solvation revealed that trisolvate 2a is 7.3 kcal more stable than the corresponding disolvate (eq 5); no minimum was found for the tetrasolvate.18 Hereafter, we draw ArLi 2 as trisolvate 2a.
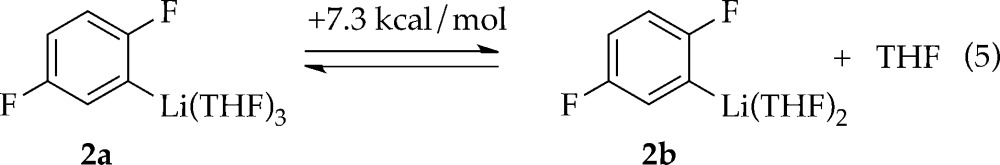 |
5 |
In the presence of excess [6Li,15N]LDA12 and low THF concentration, 19F NMR spectroscopy shows the two doublets of 2a along with two additional broad doublets corresponding to mixed dimer 17 that resolve into more complex multiplets owing to 1H–19F coupling with application of window functions.6 Computations showed a 6.3 kcal/mol greater stability of trisolvated dimer 17b than disolvate 17a (eq 6). (The computations show a distinct F–Li interaction in 17a,b). Monitoring the mixed dimer equilibrium versus THF concentration (eq 7 and Figure 5) and fitting according to eq 8 implicates trisolvated mixed dimer 17 (solvation number of 2.4 ± 0.1). The distinction is not germane to the rate and mechanistic studies.
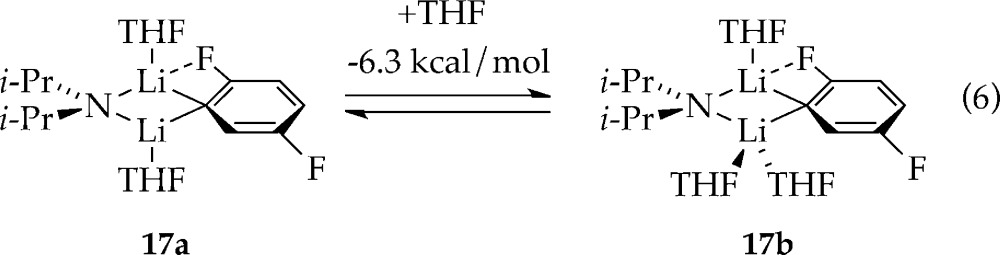 |
6 |
 |
7 |
| 8 |
Figure 5.
Plot of y (eq 8) versus [THF] in hexanes cosolvent for the ortholithiation of ArH (0.050 M) with LDA (0.10 M) in the presence of diisopropylamine (0.050 M) measured with 19F NMR spectroscopy at −78 °C. The curve depicts an unweighted least-squares fit to y = a[THF]3–n. [a = 0.21 ± 0.05, n = 1.4 ± 0.1].
Rate Studies: General Protocols
Lithiation of ArH using analytically pure (recrystallized) LDA6d was monitored using in situ IR spectroscopy19 by following the disappearance of a strong arene stretch at 1510 cm–1. The precise protocols were situation dependent, however. Reactions that were carried out at low ArH concentrations (0.0050 M ArH) and that were also clearly first order in ArH were followed to >5 half-lives, and the pseudo-first-order rate constants (kobsd) were determined with standard nonlinear fits.3 Under non-pseudo-first-order conditions in situations in which rate-limiting deaggregation dominates or under conditions in which autocatalysis caused deviation from a first-order decay, the initial rates20 were determined by following the reaction to 5% conversion and extracting the rate at t = 0 from a polynomial fit as described.6 Reaction orders in THF and LDA were determined by plotting either kobsd or initial rate versus the respective concentrations.21
Uncatalyzed Lithiation of ArH: Rate-Limiting Deaggregation
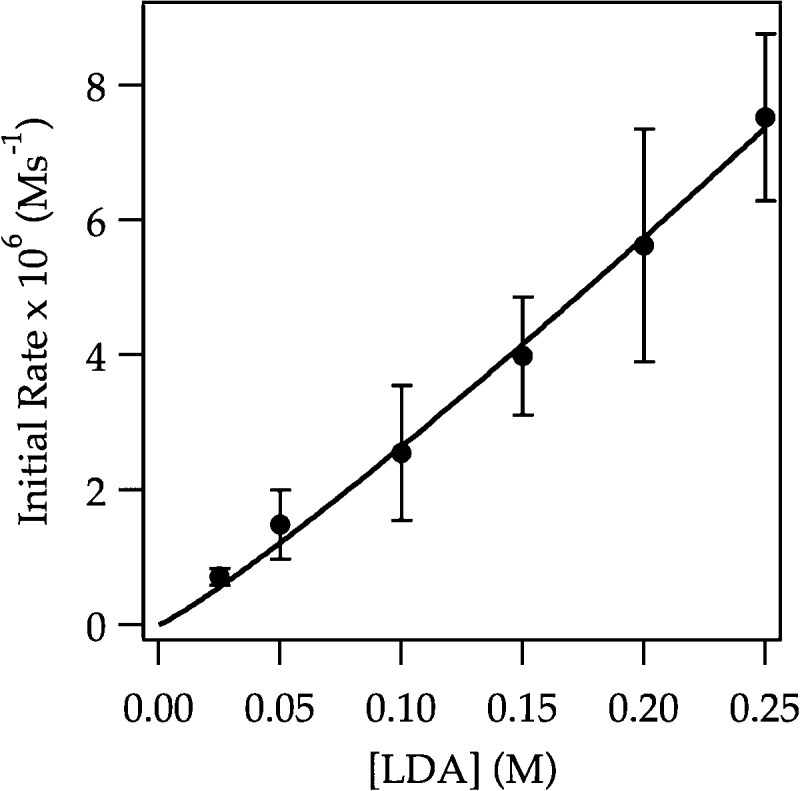
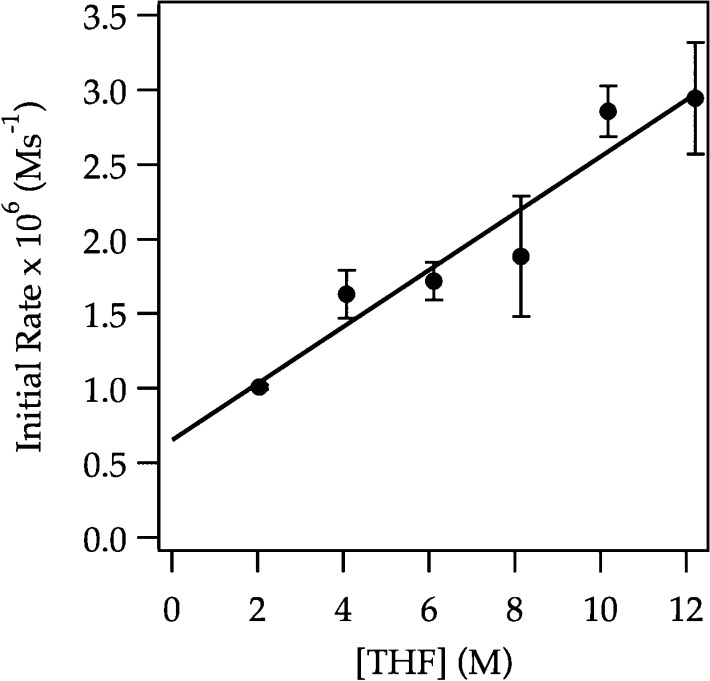
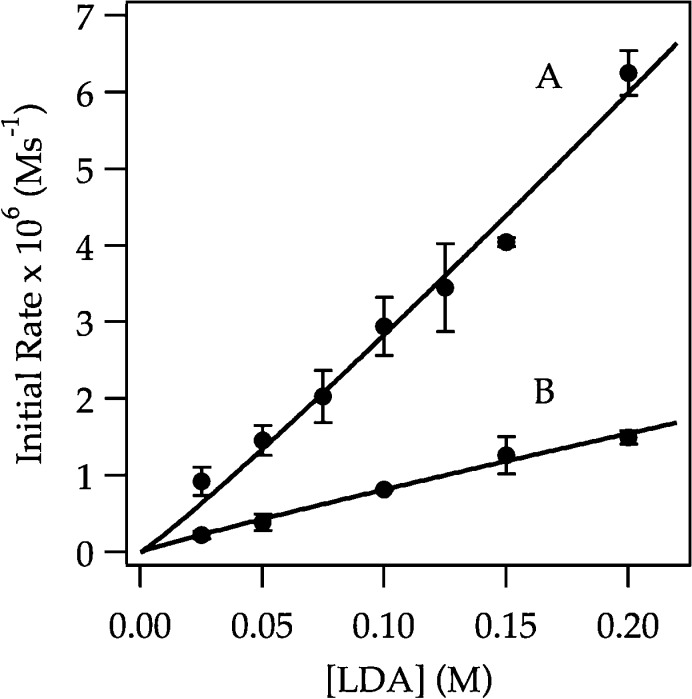
Rate studies reveal a rate law described by eq 9 that is consistent with rate-limiting deaggregation of dimer 4 (eq 10).22 Lithiation of ArH at low concentrations (0.0050 M) shows a linearity (Figure 6) that suggests either zeroth order in arene or an inherently upwardly curving decay being straightened by autocatalysis;6 a plot of initial rate versus ArH concentration shows a clear ArH concentration independence consistent with a zeroth order in ArH (Figure 6 inset). The initial rates are also zeroth-order in THF (Figure 7); the cosolvent dependence illustrates a standard control experiment confirming that the downward slope derives from small medium effects.3 An approximate first-order (1.12 ± 0.06 order) dependence on LDA concentration (Figure 8) is consistent with a dimer-based transition structure.23 The slight upward curvature signifying an elevated LDA order foreshadows mechanistic complexity. Isotopic labeling studies confirm post-rate-limiting proton transfer, but the complexity demands that we describe perdeuterated arene in its own section. The overall idealized24 rate law (eq 9) is consistent with a dominant disolvated-dimer-based rate-limiting deaggregation (eq 10) as noted in previous studies.6
| 9 |
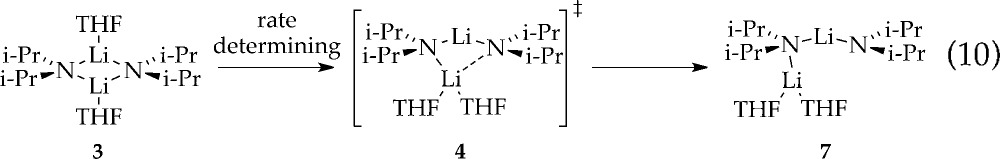 |
10 |
Figure 6.
Representative plot showing linear decay for the ortholithiation of ArH (0.0050 M) with LDA (0.10 M) in 12.2 M THF monitored using IR spectroscopy at −78 °C. Inset shows a plot of initial rate versus [ArH] (initial arene concentration) for the ortholithiation of ArH with LDA (0.10 M) in THF (12.2 M) measured with IR spectroscopy at −78 °C. The curve depicts an unweighted least-squares fit to y = a[ArH] ± b. [a = (5 ± 5) × 10–6, b = (3.1 ± 0.2) × 10–6].
Figure 7.
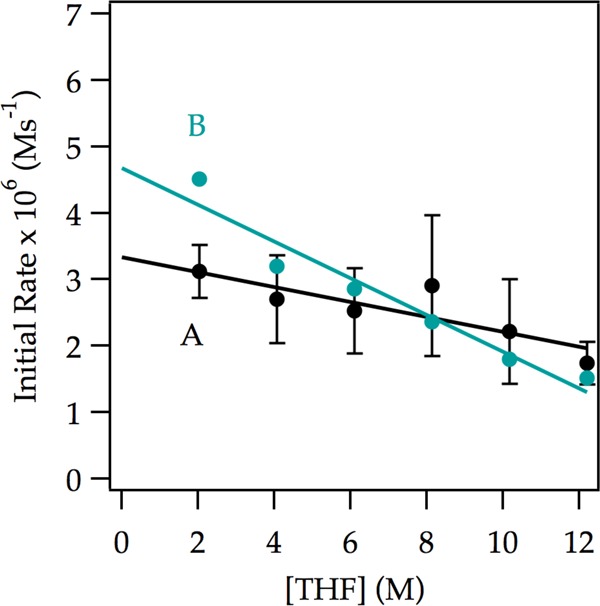
Plot of initial rate versus [THF] in Et2O (curve A) and in hexanes (curve B) cosolvent for the ortholithiation of ArH (0.050 M) by LDA (0.10 M) at −78 °C. The data were measured with IR spectroscopy. The curves depict unweighted least-squares fits to y = a[THF] ± b. Curve A: a = (−1.1 ± 0.3) × 10–7, b = (3.3 ± 0.3) × 10–6. Curve B: a = (−2.8 ± 0.3) × 10–7, b = (4.7 ± 0.3) × 10–6. The greater slope using hexanes as cosolvent compared with that using Et2O as cosolvent illustrates the influence of long-range medium effects.
Figure 8.
Plot of initial rate versus [LDA] in THF (12.2 M) for the ortholithiation of ArH (0.0050 M) measured with IR spectroscopy at −78 °C. The curve depicts an unweighted least-squares fit to y = a[LDA]n. [a = (3.5 ± 0.3) × 10–5, n = 1.12 ± 0.06].
Autocatalyzed Lithiation of ArH: Rate-Limiting Aggregation
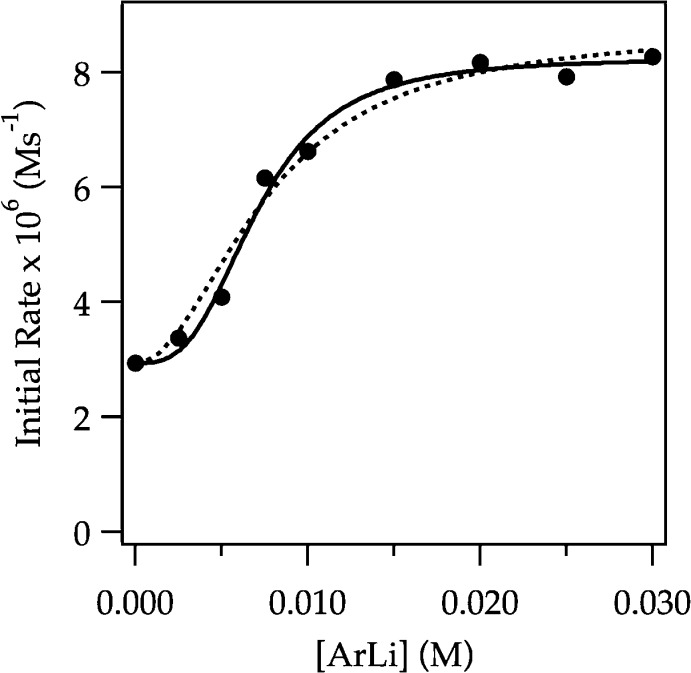
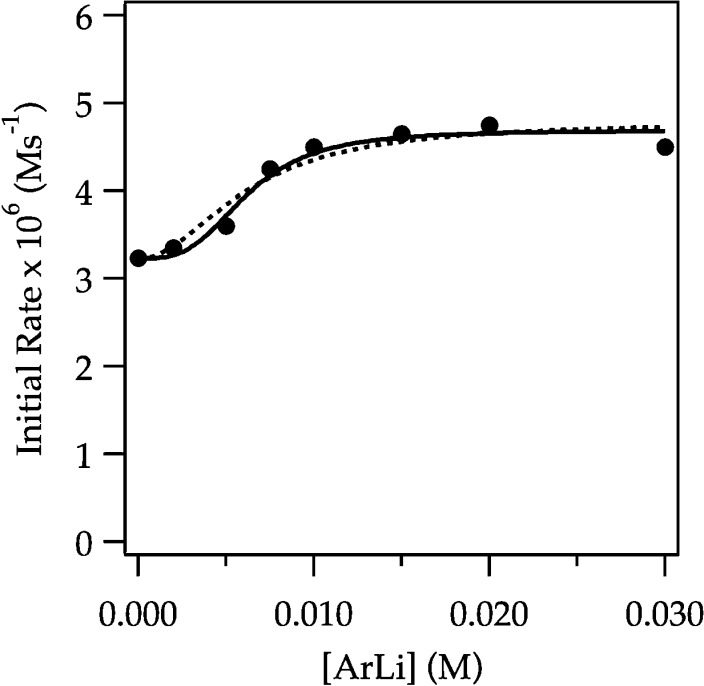
We suspected that the subtle upward curvature in Figure 6 is masked by downward curvature arising from autocatalysis.6 Lithiations using larger concentrations of ArH—conditions allowing aryllithium 2 to build to appreciable concentrations—reveal the anticipated albeit subtle downward curvature (Figure 9). To tease out the underlying mechanistic changes, we carried out the lithiations under pseudo-first-order conditions with varying concentrations of ArLi. Figure 10 shows the rates versus ArLi concentration and reveals a sigmoid consistent with higher-order saturation kinetics but only a small (3-fold) overall increase in rate. Fitting the data to eq 11 afforded a 3.0 ± 0.4 order in ArLi.25 Previous studies are fully consistent with such higher-order catalysis but showed only second-order ArLi dependencies. The analogous second-order curve is included to show the similarity. We suspect that the disagreement is not about the mechanism per se but rather due to the sensitivity of such determinations.
| 11 |
Figure 9.
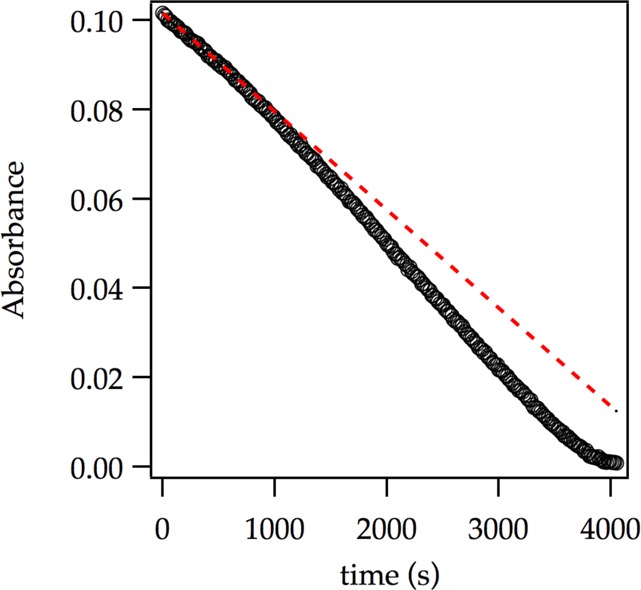
Representative plot showing sigmoidal decay for the ortholithiation of ArH (0.020 M) with LDA (0.10 M) in 12.2 M THF monitored with IR spectroscopy at −78 °C. The red dotted line depicts the time-dependent linear decay extrapolated from the initial rate in the absence of autocatalysis.
Figure 10.
Plot of initial rate versus [ArLi] for the ortholithiation of ArH (0.0050 M) by 0.10 M LDA in 12.2 M THF monitored with IR spectroscopy at −78 °C. The curve depicts an unweighted least-squares fit to eq 11. Solid curve: a = 2 ± 4, b = (3 ± 8) × 106, c = 2.94 × 10–6, n = 3.0 ± 0.5. Dotted curve: n is set at 2; a = (9 ± 2) × 10–2), b = (1.7 ± 0.3) × 104, c = 2.94 × 10–6.
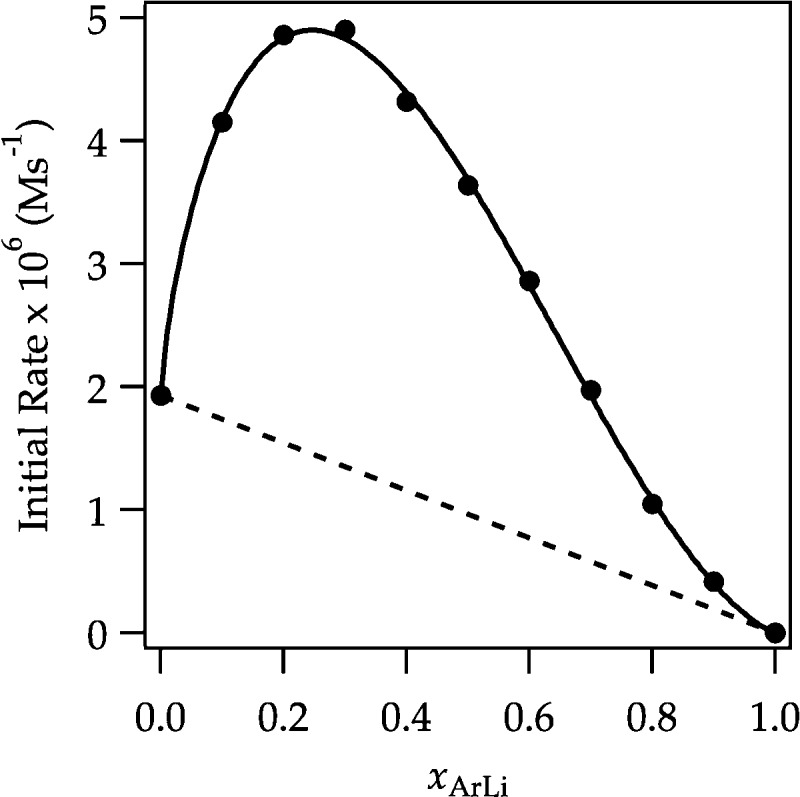
For an alternative view of the autocatalysis, we applied the method of continuous variations (a Job plot).6,26 Initial rates were monitored versus the mole fraction of ArLi while keeping the total normality of ArLi and LDA constant (Figure 11). The curve corresponds to a nonlinear least-squares fit to the generalized expression in eq 12. Equation 12 is an approximation because it corresponds to a fit of a statistical Job plot.27 Moreover, in contrast to normal Job plots in which the curvature and position of the maximum provide insight into relative stoichiometries (via parameters m and n in eq 12), the shifting rate-limiting step precludes such a simple interpretation. Had ArLi been a highly efficient catalyst, for example, the maximum would have been pressed against the left-hand y axis irrespective of stoichiometry. Figure 11 does, however, offer a visually retrievable, qualitative view of the catalysis.
| 12 |
Figure 11.
Plot of initial rates versus mole fraction of ArLi (XArLi) for the serial injection of 0.010 M aliquots of ArH to 0.10 M LDA in 12.2 M THF monitored with IR spectroscopy at −78 °C. The dotted curve depicts the theoretical initial rates in the absence of autocatalysis. The solid curve depicts an unweighted least-squares fit to eq 12. [k = (1.67 ± 0.09) × 10–5, k′ = (1.93 ± 0.05) × 10–6, n = 0.75 ± 0.3, m = 1.87 ± 0.05].
ArLi catalysis offers a remarkable mechanistic probe that requires some explaining. Although the saturation has the superficial appearance of Michaelis–Menten kinetics in which an intermediate becomes the dominant observable form,28 no such form exists. Instead, saturation corresponds to a shift in the rate-limiting step as described by eqs 13 and 14.6 Saturation occurs when rate-limiting deaggregation favored at zero or low ArLi concentration —k–1 + kArLi[ArLi] ≪ k2— shifts to a new rate-limiting step at high ArLi concentration —k–1 + kArLi[ArLi] ≫ k2—. As the evidence shows, the new rate-limiting step still does not involve proton transfer.
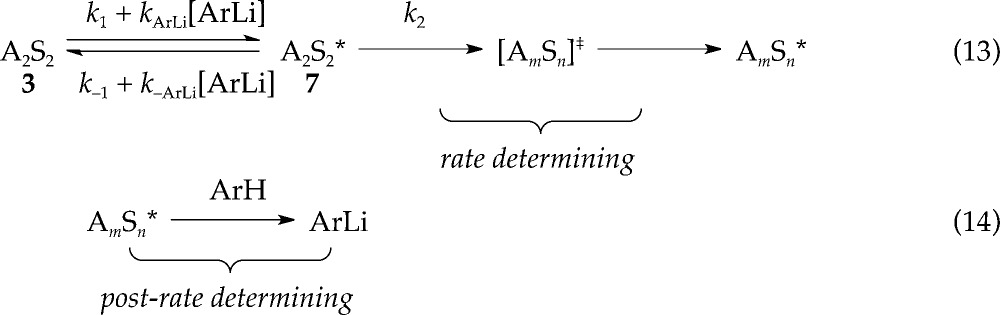 |
13 |
To ascertain the nature of the new rate-limiting step, we simply added sufficient ArLi at the outset of the reaction (0.020 M ArLi) to establish full saturation (plateau in Figure 10) and determine a rate law. A zeroth-order in substrate, zeroth order in THF, and second order in LDA (Figure 12) affords the idealized rate law in eq 15 and implicates a tetrasolvated tetramer-based LDA aggregation as the rate-limiting step (eq 16). We had detected kinetic evidence of LDA tetramers previously6 but without such clarity. The roles of ArLi catalysis and mixed tetramer intermediates remain shrouded in mystery despite considerable experimental and computational probing.6 Nonetheless, catalyzing the aggregate exchange of dimer 3 has revealed a rate-limiting tetramer pathway (labeled 11 in Scheme 1) lurking just beyond the first barrier. In theory, we could bring the proton transfer into view by slowing the trapping step in eq 14 through deuteration. In practice, it is not that simple.
| 15 |
 |
16 |
Figure 12.
Plot of initial rate versus [LDA] in THF (12.2 M) for the ortholithiation of ArH (0.0050 M) in the presence of 0.020 M ArLi monitored with IR spectroscopy at −78 °C. The curve depicts an unweighted least-squares fit to y = a[LDA]n. [a = (7 ± 1) × 10–4, n = 1.80 ± 0.09].
LiCl-Catalyzed Lithiation of ArH
Previous studies have shown marked catalysis by traces of LiCl attributed in all instances to catalyzed deaggregations and monomer-based lithiations.6 LiCl (0.0010 M) accelerates the lithiation of ArH by LDA/THF so much that rates can not be monitored at −78 °C with technology available to us. Notably, at full saturation using ArLi as a catalyst (Figure 10), added LiCl causes a further rate spike (Figure 13), confirming that ArLi and LiCl catalyze distinctly different processes.29 Lithiation of less reactive ArD under LiCl catalysis proves more revealing.
Figure 13.
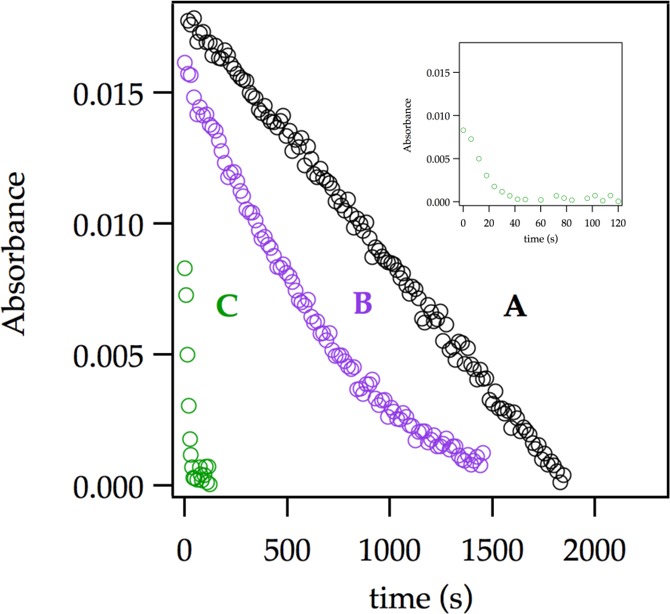
Representative plot showing the absorbance of ArH versus time for the ortholithiation of ArH (0.0050 M) with LDA (0.10 M) in THF (12.2 M) at −78 °C (curve A). Curve B shows the decay under the same conditions as in A but with 0.020 M ArLi. After the lithiation was complete, 0.0010 M LiCl was added and a second aliquot was injected into this mixture (curve C; see inset for expansion). Reactions were monitored with IR spectroscopy.
Uncatalyzed Lithiation of ArD: Rate-Limiting Deaggregation
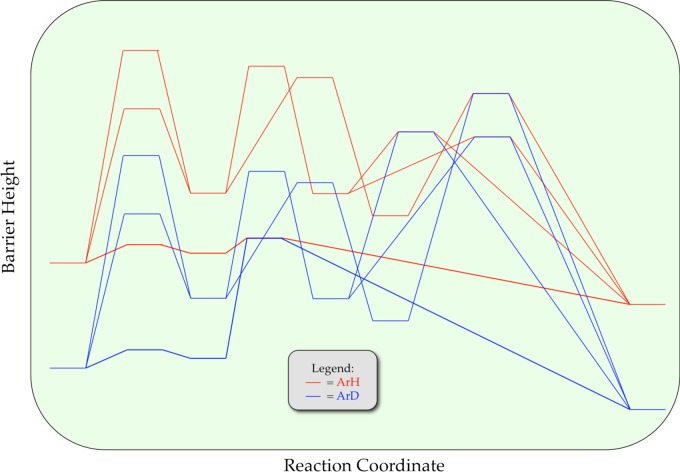
As noted in the Introduction, lithiations of ArH and perdeuterated arene 1-d4 (ArD) are markedly different. We offer the reaction coordinate diagram in Scheme 2 showing qualitative (relative) barrier heights for lithiation of ArD to aid the discussion. Of course, the ArH and ArD barriers in Schemes 1 and 2 can be placed on the same diagram to fully display the influence of isotopic substitution, but the cost is a considerable increase in complexity; we will do so in the Discussion. As a reminder to the reader, the diagram is a static snapshot of a much more fluid picture in which the relative barriers vary markedly with changes in the concentrations of LDA, THF, and ArD.
Scheme 2.
LDA-mediated lithiation of ArD at low concentration (0.0025 M ArD) affords a decay showing an upward curvature that is neither zeroth nor first order. The intermolecular kinetic isotope effect (KIE)—the isotope effect obtained from independently measured initial rates for ArH and ArD—is near unity (kH/kD = 1.5). The complementary competitive isotope effect, obtained by monitoring the relative rates within a single reaction vessel6 reveals biphasic kinetics (Figure 14) from which kH/kD = 40 was determined from the initial rates. The biphasic kinetics and large isotope effects are highly characteristic of a dominantly post-rate-limiting lithiation in which the less reactive ArD does not react until ArH is consumed.6 The fits in Figure 14 derive from a numerical integration using the simplified model in Scheme 3.6
Figure 14.
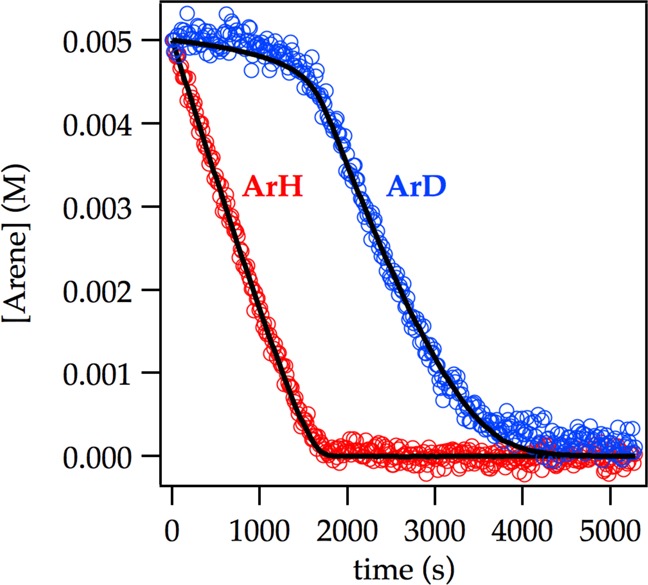
Competitive ortholithiation of ArH (0.0050 M) and ArD (0.0050 M) with LDA (0.10 M) in THF (12.2 M) at −78 °C. The curves result from a best-fit numerical integration to the highly simplified model in Scheme 3 and afford kH/kD = 30 (Supporting Information). By contrast, measuring the initial slopes directly affords kH/kD = 40.
Scheme 3.
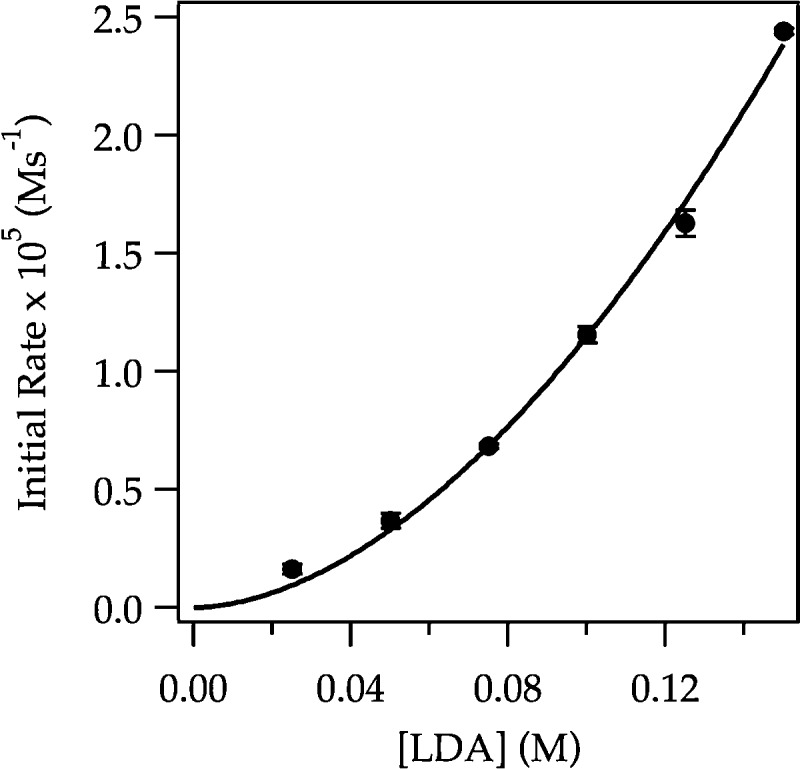
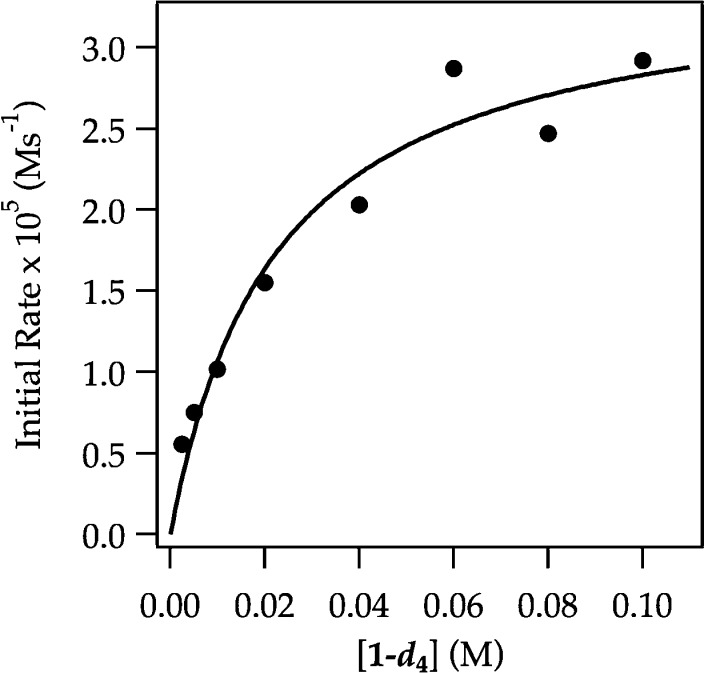
Detailed rate studies reveal the origins of these odd behaviors and present a new view of the ortholithiation. In contrast to ArH in which the lithiation occurs in a post-rate-limiting step, rate limitation for ArD depends on concentration (Figure 15). The rate studies are consistent with the rate law described by eq 17 and mechanisms described by eqs 18–20. The evidence is presented in the limits of high and low ArD concentration as follows.
| 17 |
| 18 |
| 19 |
| 20 |
High ArD concentration limit:
| 21 |
| 22 |
Low ArD concentration limit:
| 23 |
| 24 |
| 25 |
Figure 15.
Plot of initial rate versus [ArD] for the ortholithiation of ArD with LDA (0.10 M) in THF (12.2 M) monitored with IR spectroscopy at −78 °C. The curve depicts an unweighted least-squares fit to a first-order saturation function: −d[ArH]/dt = (a[ArD])/(1 ± b[ArD]). [a = (1.5 ± 0.3) × 10–3, b = (3.5 ± 0.8) × 102].
(1) At high ArD concentration trapping of a fleeting (dimeric) intermediate A2S2* is efficient (k–1 < k2[ArD] and k–1 < k3[ArD][S] in eqs 17–20), rendering the reaction zeroth order in ArD (eqs 21 and 22). The initial rates show a first-order dependence on LDA concentration and a zeroth-order dependence on THF concentration. The rate law in eq 17 reduces to the much simpler rate law in eq 21, which corresponds to the rate-limiting dimer fragmentation (via 4) described by eq 10.
(2) At low ArD concentration the trapping is inefficient (k–1 > k2[ArD] and k–1 > k3[ArD][S] in eqs 17–20). A linear dependence on THF concentration with a significant nonzero intercept (Figure 16) and first-order LDA dependencies at both low and high THF concentrations (Figure 17) reduce the rate law to that in eq 23. The data are consistent with an A2S2–A2S2* dimer-based pre-equilibrium and an emergent superposition of rate-limiting di- and trisolvated-dimer-based lithiations (eqs 24 and 25). The failure to observe the saturation kinetics for ArH stemmed from the high reactivity and consequent efficient trapping at both low and high concentrations, which may have obscured the trisolvated-dimer-based mechanism made visible by ArD. Evidence exists, however, that the high isotopic sensitivity diverts proton and deuterium transfers through distinctly different pathways (vide infra).
Figure 16.
Plot of initial rate versus [THF] in Et2O for the ortholithiation of ArD (0.0020 M) by LDA (0.10 M) monitored with IR spectroscopy at −78 °C. The curve depicts an unweighted least-squares fit to y = a[THF] ± b. [a = (1.9 ± 0.3) × 10–7, b = (7 ± 2) × 10–7].
Figure 17.
Plot of initial rate versus [LDA] in 12.2 M THF (curve A: 12.2 M, curve B: 2.03 M) for the ortholithiation of ArD (0.0020 M) monitored with IR spectroscopy at −78 °C. Curve A depicts an unweighted least-squares fit to y = a[LDA]n. [a = (3.4 ± 5) × 10–5, n = 1.08 ± 0.08]. Curve B depicts an unweighted least-squares fit to y = a[LDA]n. [a = (6.8 ± 0.9) × 10–6, n = 0.92 ± 0.07].
With stoichiometries of the rate-limiting transition structures in hand, we examined di- and trisolvated-dimer-based metalations computationally (eq 26).30 The energy difference is negligible.
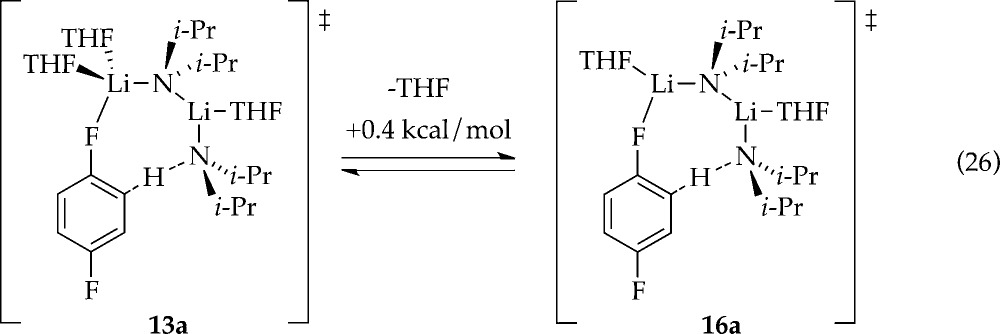 |
26 |
Autocatalyzed Lithiation of ArD: Dimer-Based Lithiation
Recall that metalations autocatalyzed by ArLi (Scheme 1) bypass the rate-limiting conversion of starting LDA dimer 3 to putative open dimer A2S2* 4, revealing rate-limiting [A4S4]⧧ transition structure 11 and a kinetically invisible post-rate-limiting metalation of ArH. Guided by previous studies implicating analogous tetramer-based pathways, we surmised that suppressing the rate of metalation using ArD would bring either a tetramer- or a monomer-based metalation into view.31,32As stated, this idea contains embedded flaws; the story is considerably more nuanced.
Monitoring the initial rates for the metalation of ArD versus ArLi concentration (perdeuterated aryllithium 2-d3 to be more precise) showed saturation kinetics (Figure 18) analogous to that for ArH (Figure 10) with an attenuated acceleration but the same high-order dependence on ArLi concentration. (One could be excused for not detecting this saturation behavior.)
Figure 18.
Plot of initial rate versus [ArLi] (specifically, 2-d3) for the ortholithiation of ArD (0.0020 M) by 0.10 M LDA in 12.2 M THF monitored with IR spectroscopy at −78 °C. The curve depicts an unweighted least-squares fit to −d[ArH]/dt = (a[ArD]n)/(1 ± b[ArD]n) ± c.33 Solid curve: [a = (6 ± 2), b = (4 ± 1) × 106, c = 2.94 × 10–6, n = 3]. Dotted curve: [a = (4 ± 1) × 10–2), b = (2.5 ± 0.9) × 104, c = 3.23 × 10–6, n = 2].
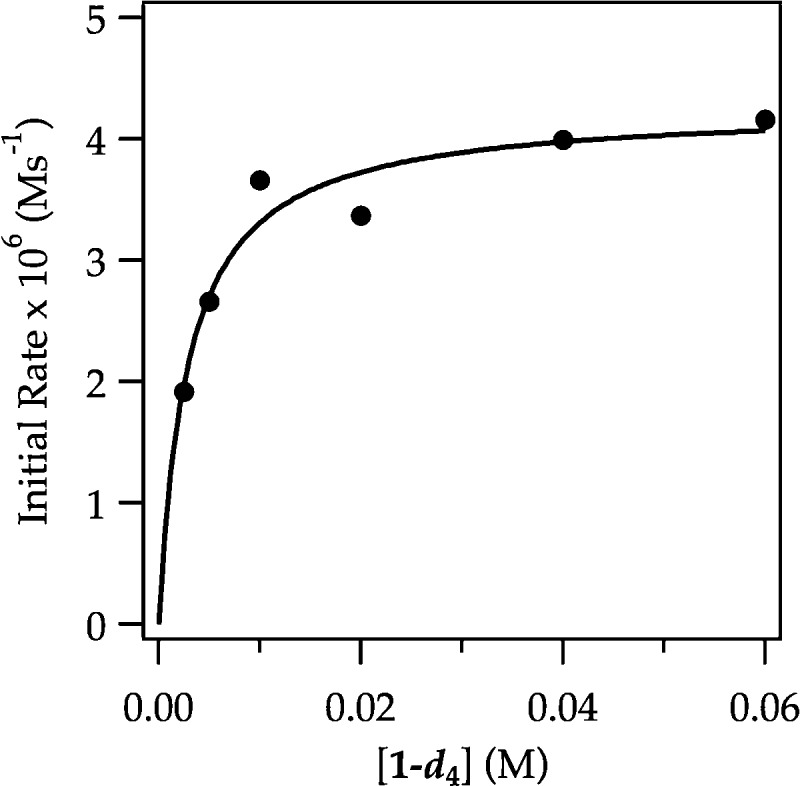
As already described, the mechanism in the limit of low (zero) ArLi concentration is via A2S2-based transition structure 4 using ArH. Ascertaining the concentration dependencies at saturation (0.020 M ArLi) gives unexpected results. A plot of rates versus ArD reveals saturation kinetics, indicating an ArD concentration dependence at low ArD and ArD concentration independence at high ArD (Figure 19). To be clear, this plot depicts saturation in substrate superimposed on saturation in ArLi. We treat the two limiting behaviors observed in the ArD saturation kinetics separately.
Figure 19.
Plot of initial rate versus [ArD] for the ortholithiation of ArD in the presence of 0.020 M ArLi (2-d3) with LDA (0.10 M) in 12.2 M THF monitored with IR spectroscopy at −78 °C. The curve depicts an unweighted least-squares fit to a first-order saturation function: −d[ArD]/dt = (a[ArD])/(1 ± b[ArD]). [a = (1.6 ± 0.3) × 10–3, b = 40 ± 10].
(1) In the limit of low ArD with added ArLi, the dependence on ArD concentration attests to ArD participation in the rate-limiting step. The decays of ArD also show curvatures consistent with significant contributions from a first-order dependence as expected for at least a partially rate-limiting metalation. Plots of initial rates versus LDA and THF show nearly linear dependencies (with a small nonzero intercept with THF), implicating a transition structure of stoichiometry [A2S3(ArD)]⧧. Because the proton transfer for ArH under ArLi-catalyzed conditions was not kinetically visible, we could not measure the intermolecular isotope effect. An ArH/ArD competition shows biphasic behavior (Figure 20) consistent with the trapping of a common intermediate in a post-rate-limiting step and a substantial KIE (kH/kD = 12). This is consistent with the partial mechanism in Scheme 3 in which ArH is scavenging A2S2* (directly or via tetramer 14, Scheme 1), largely precluding deuterium transfer.
Figure 20.
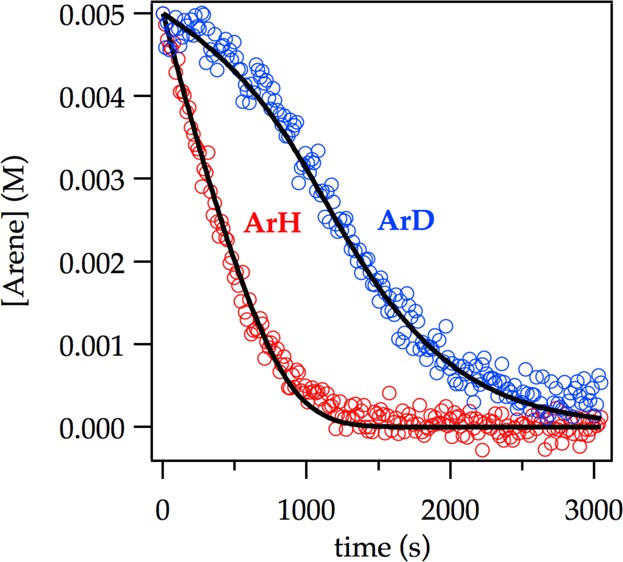
Competitive ortholithiation of ArH (0.0050 M) and ArD (0.0050 M) with LDA (0.10 M) in the presence of 0.020 M ArLi in 12.2 M THF at −78 °C. The curves result from a best-fit numerical integration to the highly simplified model in Scheme 3 and afford kH/kD = 6.3. Fitting the initial rates of both decays (linearly) directly affords kH/kD = 12.
(2) In the limit of high ArD with added ArLi, the decays of ArD are decidedly linear (zeroth order), and orders in LDA and THF are both unity. The rate-limiting transition state is of stoichiometry [A2S3]⧧9 (Scheme 2).
The most unexpected aspect of the rate studies using ArLi as the catalyst is that the metalation of ArH proceeds via a rate-limiting A4S4-tetramer-based aggregation event, whereas ArD diverts to A2S2- and A2S3-dimer-based mechanisms. Although one could infer the intermediacy of tetramer en route from one dimer to another, we believe there is a more rational explanation (vide infra).
LiCl-Catalyzed Lithiation of ArD: Monomer-Based Lithiation
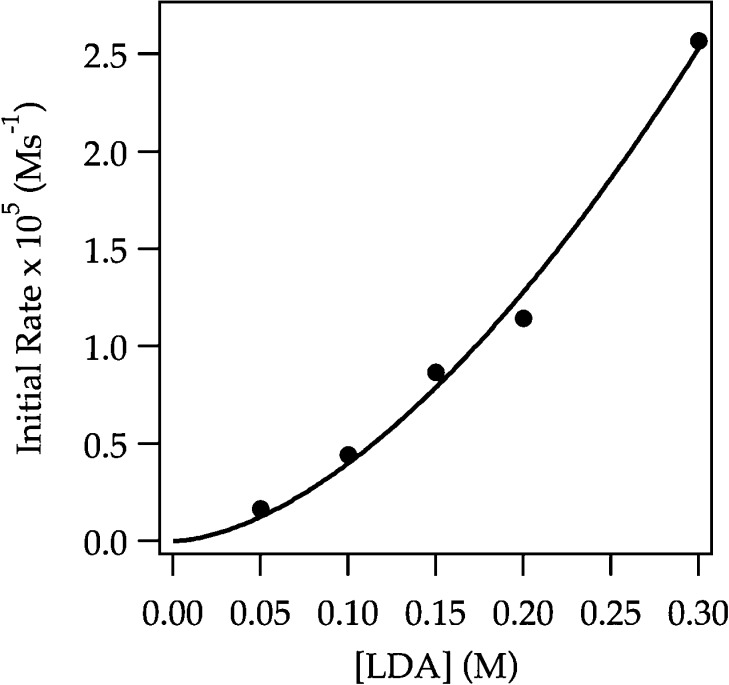
In previous studies of LDA/THF-mediated lithiations at −78 °C, the dramatic effects of LiCl on rates were traced to monomer-based lithiations without exception.6 Metalations of ArH were too fast to test this thesis, but ArD metalations proved highly tractable. Monitoring the ArD metalation versus LiCl shows a second-order dependence that saturates at very low (>0.0010 M) LiCl concentrations, as expected from previous studies (Figure 21).6 The threefold acceleration is small owing to a very large isotope effect (kH/kD > 50). The lithiations of ArD at full saturation (0.0015 M LiCl) follow a clean exponential decay consistent with rate-limiting ortholithiation. A half-order LDA dependence and second-order THF dependence (Figure 22) are consistent with the rate law in eq 27 and the generic trisolvated-monomer-based mechanism described by eqs 28 and 29.
| 27 |
| 28 |
| 29 |
| 30 |
Computational studies probing the relative efficacies of the open and closed trisolvated-monomer-based transition structures support the closed form presumably owing to a strong Li–F interaction (eq 31).
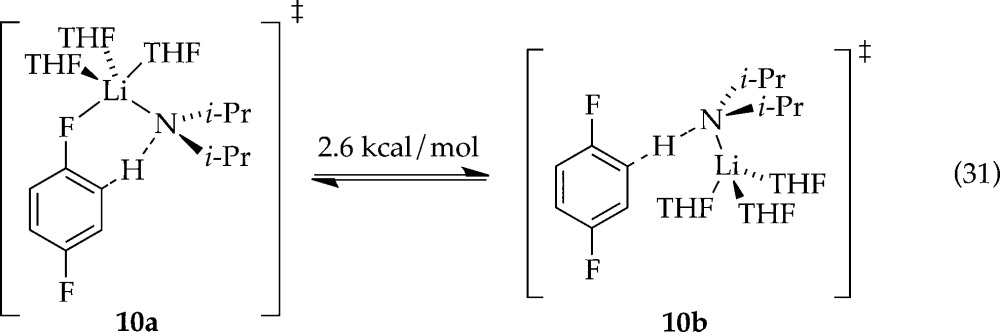 |
31 |
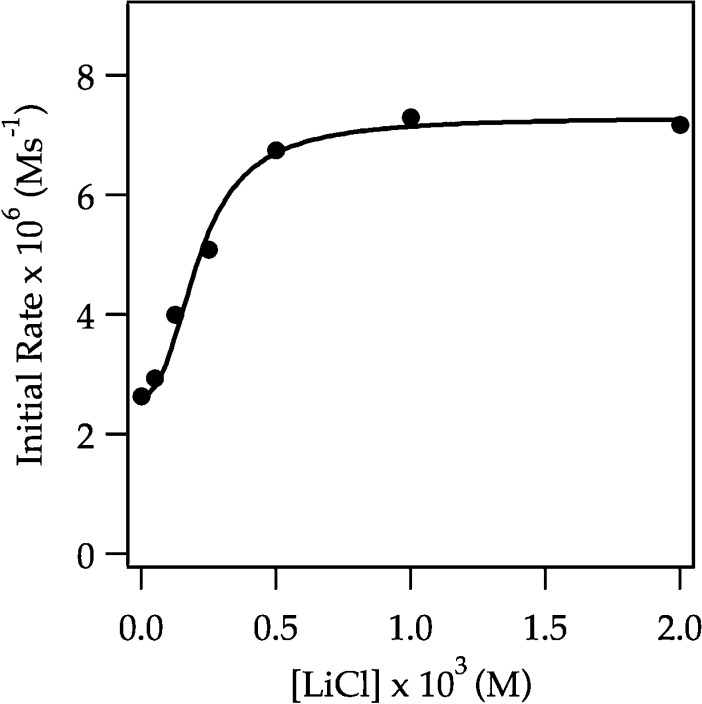
Figure 21.
Plot of initial rate versus [LiCl] for the ortholithiation of ArD (0.0020 M) by 0.10 M LDA in 12.2 M THF monitored with IR spectroscopy at −78 °C. The curve depicts an unweighted least-squares fit to eq 30.33 [ArD] = 0.0020 M, [A2S2] = 0.050 M, c = 2.63 × 10–6. [k1 = (5 ± 1) × 102, k–1 = (6 ± 2) × 107, k2 = 4.06, n = 2.0].
Figure 22.
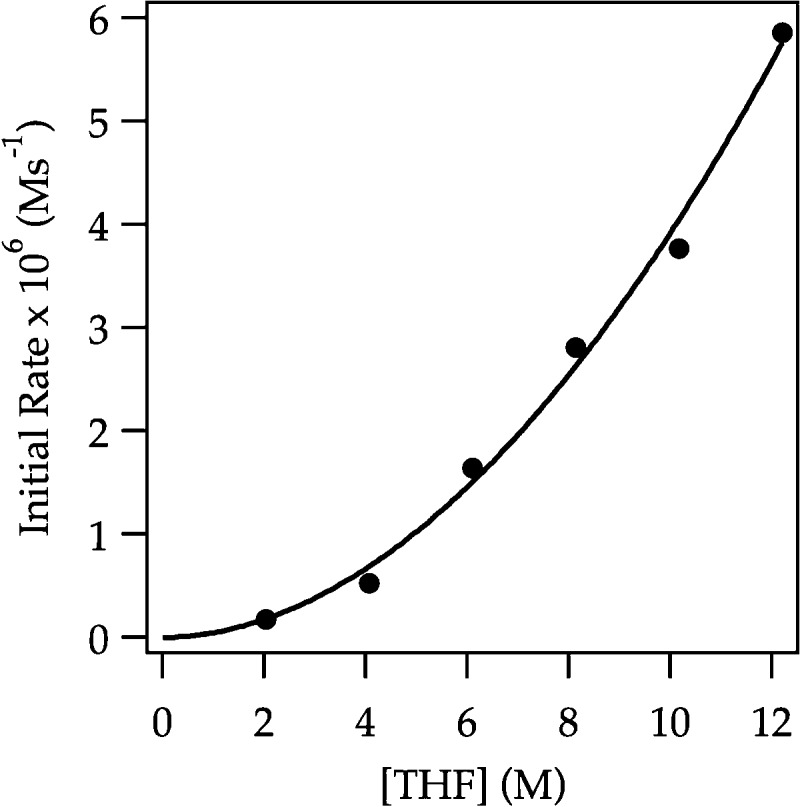
Plot of initial rate versus [THF] in Et2O for the ortholithiation of ArD (0.0020 M) by LDA (0.10 M) in the presence of 1.5 mol % LiCl (1.5 mM) monitored with IR spectroscopy at −78 °C. The curve depicts an unweighted least-squares fit to y = a[THF]n. [a = (5 ± 1) × 10–8, n = 1.9 ± 0.1].
Exchange Studies of LDA
The rate studies of various metalations have suggested that several LDA aggregation events may be detectable using NMR spectroscopy: (a) LDA subunit exchange should be observable on laboratory time scales at low temperatures, and (b) the subunit exchange might occur via a dissociative dimer-derived deaggregation or a tetramer-based associative mechanism. We examined these suppositions using two distinctly different probes of LDA subunit exchange. Let us first consider the two mechanisms:
Dissociative subunit exchange:
| 32 |
Associative subunit exchange:
| 33 |
To facilitate the discussion, we use A2 and B2 as shorthand for [6Li]LDA and [6Li,15N]LDA, respectively. The two mechanisms are highly simplified but easily distinguished nonetheless. In the dissociative mechanism (eq 32), the rate-limiting step for subunit exchange is necessarily dimer-based, affording an overall first-order dependence; once a dimer dissociates it is committed to exchange albeit statistically weighted based on the probability of reaggregating in a mixed isotopic form. Although this statistical factor within unequal populations of A2 and B2 can be accounted for,34 it is more expedient to eliminate it by maintaining equal relative proportions of A2 and B2. The associative mechanism in eq 33, by contrast, necessarily involves a tetramer-based rate-limiting step and would manifest an overall second-order dependence. We examined the concentration dependencies using two complementary experiments.
Experiment 1: Low-Temperature Exchange
We examined the time-dependent conversion of [6Li]LDA and [6Li,15N]LDA to the mono-15N-labeled isotopologue (eq 34) at fixed 1:1 stoichiometry. The exchange was easily followed using 6Li NMR spectroscopy on laboratory time scales at −60 °C (Figure 23). This is satisfyingly consistent with the rate-limiting aggregation events detected in the ortholithiation rate studies. The extended time scales of the exchange when compared with the metalations stems from the second-order conditions. A plot of initial rate versus total LDA concentration in equimolar [6Li]LDA and [6Li,15N]LDA mixtures (Figure 24) shows an upward curvature and an order of 1.7 consistent with a composite first- and second-order dependencies expected for competing dimer- and tetramer-based exchange. The rates are also independent of the THF concentration, implicating A2S2- and A4S4-based transition structures.
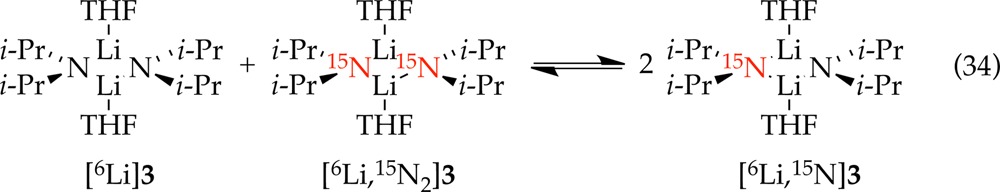 |
34 |
Figure 23.
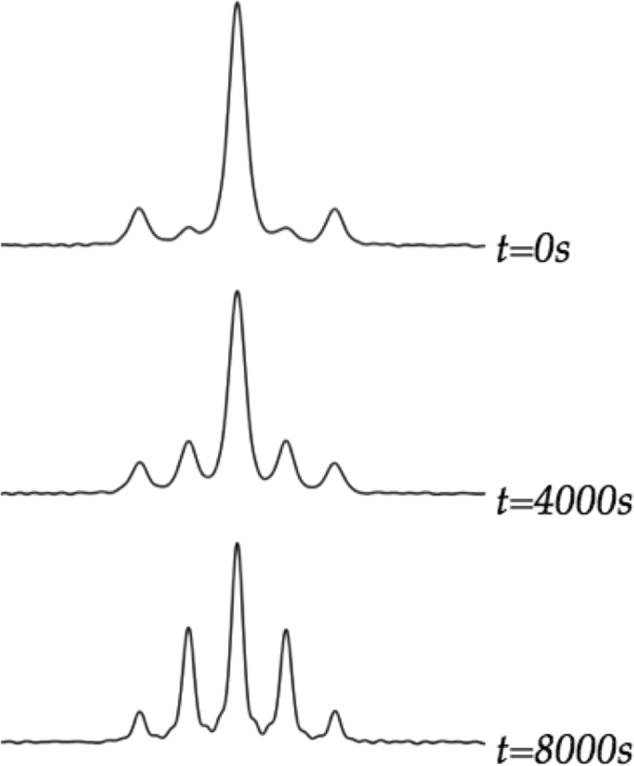
6Li NMR spectra showing the 6Li nuclear exchange of [6Li]LDA (0.10 M) and doubly 15N-labeled [6Li,15N]LDA (0.10 M) in 12.2 M THF at −60 °C (eq 34).
Figure 24.
Plot of initial rate for the loss of [6Li,15N]LDA in 1:1 mixtures of [6Li]LDA and [6Li,15N]LDA versus total [LDA] titer at −60 °C in 12.2 M THF. The curve depicts an unweighted least-squares fit to y = a[LDA]n. [a = (1.9 ± 0.3) × 10–4, n = 1.7 ± 0.1].
Experiment 2
We examined LDA subunit exchange by monitoring the temperature-dependent coalescence of the 6Li triplet of [6Li,15N]LDA. Lineshape analysis was carried out using WinDNMR software developed by Reich.35 The 6Li nuclear exchange rate was simulated by inspection. If exchange of monomer subunits occurs by a unimolecular process the resulting rate constant, kexch, would be independent of the LDA concentration. By contrast, an overall bimolecular exchange mechanism would manifest a linear dependence of kexch on LDA concentration. In the event, kexch shows a distinct linear dependence and a substantial non-zero y-intercept (eq 35) for all THF concentrations (Figure 25), implicating competing unimolecular and bimolecular pathways (eq 36). Moreover, the 12–fold range of THF concentrations shows minor slope and intercept variations at both low and high [6Li,15N]LDA consistent with zeroth-order THF dependencies as expected for A2S2- and A4S4-based rate-limiting transition structures.
 |
35 |
Figure 25.
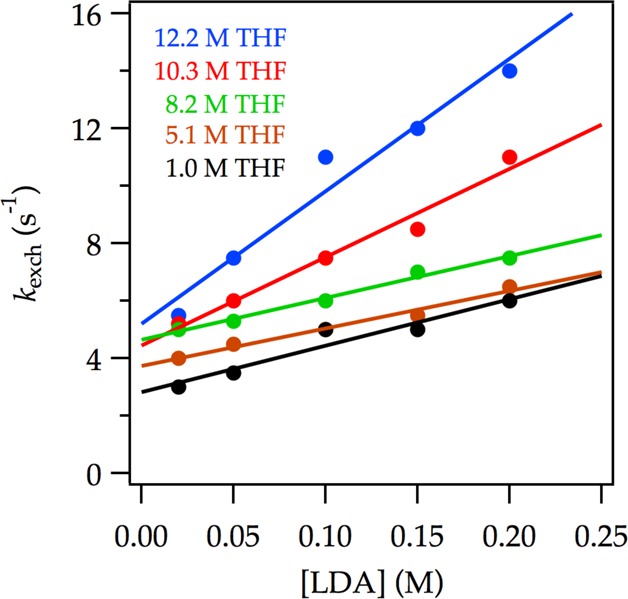
Plot of 6Li nuclear exchange rate at 35 °C versus [LDA] at varying [6Li,15N]LDA and THF concentrations with hexanes as cosolvent. The curve depicts an unweighted least-squares fit to linear functions.
Tetramer Formation: DFT Computations
We had previously examined in considerable detail the dimer-based deaggregation of LDA to monomer.7 We turned to DFT computations to examine how A4S4 tetramers might be formed and how they might be involved in a metalation. This computational problem is extremely difficult (in our hands); we offer the artist’s rendition of a reaction coordinate in Scheme 4. The intermediates and transition structures drawn are viable by computational standards. They provide energies, but we do not take them seriously. The role of bridging THFs36,37 as transitional substructures in critical deaggregation steps were detected in dimer-based deaggregation,7 whereas the higher aggregates appear to be too congested for such THF bridging. The computed solvation numbers come up short by one (A4S3 rather than A4S4 observed kinetically). The most fundamental flaw and the origin of the highest energies (26 kcal/mol maximum) is that two high energy forms—monosolvated cyclic dimer and disolvated open dimer—condense to form tetramers. This scenario seems unlikely, but it was the best we could do.38
Scheme 4.
Discussion
Ongoing studies of LDA-mediated metalations under nonequilibrium conditions are, in essence, a study of LDA deaggregation and rate limitation. Paradoxical behaviors abound under these conditions in which aggregation exchanges and reactions with substrates battle to determine the rate-limiting step. Studies of the ortholithiation of 1,4-difluorobenzene (1) and its perdeuterated analogue (1-d4) reveal the reaction coordinate illustrated in Schemes 1 and 2. For readers who bypassed the Results, we reiterate a shorthand introduced to simplify the presentation: (1) the various LDA-based fragments are reduced to AmSn notations in which A and S connote the LDA subunits and coordinated THF ligands, respectively; (2) arene 1 and its perdeuterated analogue 1-d4 are represented as ArH and ArD, respectively; (3) aryllithium 2, perdeuterated aryllithium 2-d3, and structurally most accurate trisolvated monomer 2a are collectively denoted as simply ArLi.
A staggering number of kinetically detectable minima and maxima cluster in an energetically very narrow window—a reaction coordinate approximating a metaphorical washboard. The resulting complexity is breathtaking. Changing concentrations of ArH, LDA, and THF alter the relative dominance of the barriers, resulting in wild swings in concentration dependencies and rate laws. Swapping ArD for ArH—a simple experiment in most settings—completely transforms the rate laws and observed mechanisms. Autocatalysis by ArLi accelerates the metalation and shifts the rate-limiting steps, markedly changing the rate laws. Adding traces of LiCl similarly accelerates the reaction but does so via catalysis on an altogether different portion of the reaction coordinate. Saturation kinetics—simultaneously superimposed saturation kinetics—are legion owing to the relentlessly shifting rate-limiting steps.
In short, the rules governing rates and mechanisms under conditions in which aggregates are in full equilibrium falter badly for nonequilibrium conditions. Within this chaotic picture, however, are several critically important common denominators: (1) the complexity stems from coincident barriers to reaction with substrate and barriers corresponding to LDA aggregation and solvation steps, and (2) the conditions under which this coincidence occurs—LDA/THF/–78 °C—is the same for any substrate that reacts measurably. Although the different substrates6 probe a single process—the deaggregation of LDA dimer 3—each substrate provides a different perspective and different mechanistic insights.
We begin the analysis with an overview of the mechanism in the context of the reaction coordinate diagram depicted in Scheme 1. To reiterate, Scheme 1 was constructed from rate studies under many conditions. It represents a snapshot of a living, breathing reaction coordinate in which the relative barrier heights depend on many parameters. Because the equilibria are implicitly rather than explicitly balanced to minimize clutter—fragments of LDA and solvent molecules are inserted only where needed—we avoid labeling the y axis as “energy”. We could balance all equilibria but at considerable pedagogic cost.
Summary
We opened the results with a reaction profile (Figure 1) showing the formation of ArLi and an LDA-ArLi mixed aggregate characterized as 2a and 17, respectively. Mixed aggregate 17 is only observable under highly specialized circumstances—low THF and high LDA concentrations—and is of little to no importance to our mechanistic thinking. Odd curvatures, however, are a consequence of a zeroth-order dependence in substrate overlaid with low levels of autocatalysis. The model used to generate the curves in Figure 1 stems from the rate studies.39 We hasten to add that the quality of the fit is satisfying and consistent with the conclusions but should not be construed as confirmation.
The metalation of ArH by LDA dimer 3 (A2S2) proceeds via the [A2S2]⧧ rate-limiting transition structure 4 to give fleeting A2S2*-dimer-based intermediate 7. A chemically tangible, computationally viable depiction of this dimer to open dimer conversion is shown in eq 10.6,7 Ensuing autocatalysis accelerates the overall reaction via A2(ArLi)n transition structure 5 (n = 2 or 3). Although the acceleration is moderate, it circumvents the [A2S2]⧧ barrier, revealing a well-defined tetramer-based [A4S4]⧧ barrier previously lurking over the horizon that does not formally include ArH in the transition structure. (We should clarify this statement by noting that we define “transition structure” as the purely molecular depiction and the “transition state” as the energetically complete analog that includes all the necessary fragments including those not yet actively participating.40) The structures affiliated with A2(ArLi)n and [A4S4]⧧ higher aggregates have been discussed previously in the context of A2(ArLi)2 ladder structures.6 (If we are forced to accept an A2(ArLi)3 mixed-pentamer-based transition structure, we have no ideas worthy of sharing.) The role of A4S4 tetramers that we detected in the metalation rate studies was confirmed by NMR spectroscopic studies of LDA showing significant tetramer-based subunit exchange. We provided a calculated reaction coordinate for a tetramer-based deaggregation of LDA, dimer-to-tetramer-to-monomer, in Scheme 4. Although somewhat whimsical, the minima and maxima are legitimate by computational benchmarks.
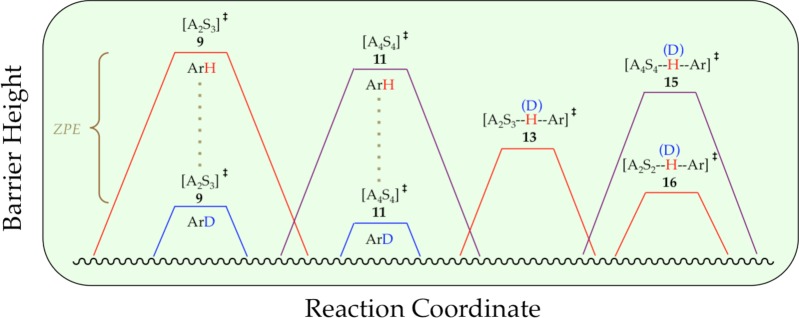
We exploited large KIEs to detect or infer the existence of additional components of the reaction coordinate in Scheme 1. A higher [A2S3]⧧ barrier 9 is inferred from direct detection of [A2S2(ArH)]⧧and [A2S3(ArH)]⧧ transition structures 13 and 16, which correspond to the ortholithiations (proton/deuterium transfers) as shown in Scheme 5. We include the computationally viable A2S2*–[A2S3]⧧–A2S3* (7–9–12) transformation implicit in Scheme 1.
Scheme 5.
The tetramer-based metalation of 15 could be inferred from the kinetically detectable [A4S4]⧧ aggregation event, yet [A4S4(ArH)]⧧-based lithiation was not kinetically visible and could be questioned in light of the previously6 noted tetramer-based deaggregation to monomers.
All reactions of LDA under nonequilibrium conditions studied to date have been accelerated by LiCl at ppm levels owing to the catalysis of dimer–monomer exchange.6 Adding LiCl causes metalations of ArH to be immeasurably fast. The efficacy of LiCl relative to ArLi, in conjunction with saturation kinetics for both showing different rates at saturation, confirms that ArLi and LiCl catalyze different steps. Indeed, in contrast to the ArLi-catalyzed dimer–dimer equilibration, LiCl diverts the ortholithiation of the less reactive ArD form through [AS3(ArD)]⧧-based transition structure 10. Open- and closed-monomer-based transition structures (eq 31) are computationally viable.
Direct Detection of Slow LDA Subunit Exchange
We have described NMR spectroscopic studies of the exchange of [6Li]LDA and [6Li,15N]LDA. The most important finding is that LDA subunits exchange slowly on laboratory time scales at −78 °C consistent with the ortholithiation results. Direct rate studies of the subunit exchanges as well as complementary LDA coalescence studies implicated both dissociative (dimer-based) and associative (tetramer-based) exchange mechanisms, a satisfying result given that both are prominent in the lithiation rate studies. Extensive computational studies of the dissociative pathways had been published.7 Scheme 4 provides insight into the tetramer-based events, although the computational studies were difficult as noted above. Overall, evidence that LDA associates to tetramer en route to monomers is both convincing and provocative.
What Dictates Rate Limitation?
This work calls out for a discussion of the basic principles underlying rate limitation.41 Imagine the simplified scenario illustrated in Scheme 6 in which an A2S2 partial deaggregation is followed by an A4S4 tetramer and subsequent post-rate-limiting lithiation of ArH. We have chosen this particular sequence owing to its pedagogic value rather than its central importance. (The tetramer-based metalation was a minor contributor at best.) We further imposed the restriction that the relative barrier heights are similar and follow the order [A2S2]⧧ > [A4S4]⧧ > [A4S4(ArH)]⧧, which is consistent with a subset of the experimental results. We now present some concepts using a series of questions and answers.
Scheme 6.
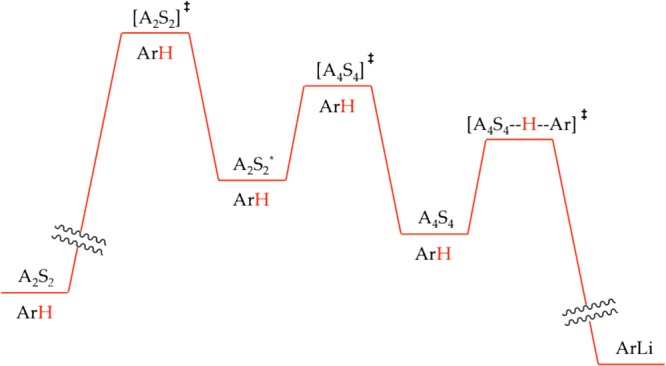
(1) How does the [A4S4]⧧ barrier influence the reaction rate and rate law? Conventional wisdom suggests that [A2S2]⧧ is the rate-limiting barrier, and [A4S4]⧧ is irrelevant, but that is not altogether correct. The existence of seemingly post-rate-limiting intermediate A2S2* imposes a barrier-weighted statistical factor on the rate. Once formed, A2S2* has <100% probability of proceeding to product. In the limit that [A2S2]⧧ and [A4S4]⧧ present barriers of equal height, that probability reduces to 50%. The rate law would also reflect barrier-weighted contributions from [A2S2]⧧ and [A4S4]⧧, including reaction orders that would be intermediate values rather than tidy integers. As the rate-limiting step shifts, so does the rate law.
(2) How do you peer beyond a rate-limiting step? There are isotopic labeling studies to probe post-rate-limiting steps through competition experiments (see part 6 for example).30,42 More direct approaches either lower the obstructing barrier or elevate the subsequent barrier. Let us explore these latter strategies further. Recall that the energy diagrams are not static, but rather shift with changing concentrations of all participating species.
(3) How does substrate concentration influence reaction rates and mechanism? At high ArH concentration, the barrier height for metalation is low as drawn in Scheme 6, and the metalation is post-rate-limiting. At lower concentrations, however, all minima and maxima drop relative to the [A4S4--H--Ar]⧧ barrier, rendering the metalation rate limiting. Using eq 37 as an alternative perspective, post-rate-limiting metalation occurs when k–1 ≪ k2[ArH], and the intermediate denoted generically as AmSn is efficiently converted to ArLi with high fidelity. At low ArH concentrations, however, the trapping becomes inefficient, k–1 ≫ k2[ArH], and AmSn is in a fully established equilibrium with A2S2. A plot of rate versus [ArH] over a wide concentration range would display saturation kinetics. Although the rate-limiting metalations of ArH were too fast to observe, we noted saturation behavior under several circumstances with ArD (Figures 15 and 19). Deuteration, however, introduces enormous complexities (see part 6).
| 37 |
(4) How would changing the concentration of LDA influence the rates? Elevated LDA concentration would promote the higher-order step by lowering the [A4S4]⧧ height relative to that of [A2S2]⧧, with the ironic effect of eliminating residual contributions of the tetramer-based step from the rate law. Viewed from the alternative perspective in eq 38, elevated LDA concentration imposes k2[A2S2] ≫ k–1 and renders the step corresponding to k1 rate-limiting. By contrast, lowering the LDA concentration would raise [A4S4]⧧, causing [A4S4]⧧ to come into parity and eventually dominate [A2S2]⧧. Varying LDA concentration over the full range would afford a rate law that reflects the shifting rate-limiting step by showing a shift from second-order LDA dependence at low LDA concentrations to a first-order dependence at elevated concentrations. Although we detected dimer- and tetramer-based metalations in the experiments above, the concentration range is too narrow to observe such a shift.43 As a final note, the relative heights of the [A4S4]⧧ and [A4S4(ArH)]⧧ barriers do not change with LDA concentration. Consequently, changing the LDA concentration cannot bring the tetramer-based metalation into view.
| 38 |
(5) What are the consequences of catalyzing the dimer-to-dimer conversion, circumventing [A2S2]⧧ in Scheme 6? This is precisely the effect of autocatalysis by ArLi. The short answer is that the rate-limiting step is shifted to transition structure [A4S4]⧧. To understand the role of catalysis let us consider the alternative perspective in eq 39. When [A2S2]⧧ is rate-limiting, catalysis of the forward step accelerates the formation of A2S2* and the overall reaction. At elevated catalyst loading, catalysis of the back reaction makes k–cat[cat] ≫ k2[A2S2] with a consequent shift of the rate-limiting step to [A4S4]⧧. The kinetics would show saturation in catalyst (as in Figures 10 and 18) and an accompanying shift from first to second order in LDA. Here is the curious part: catalysis of the forward step is the source of acceleration whereas catalysis of the back reaction shifts the rate-limiting step.
| 39 |
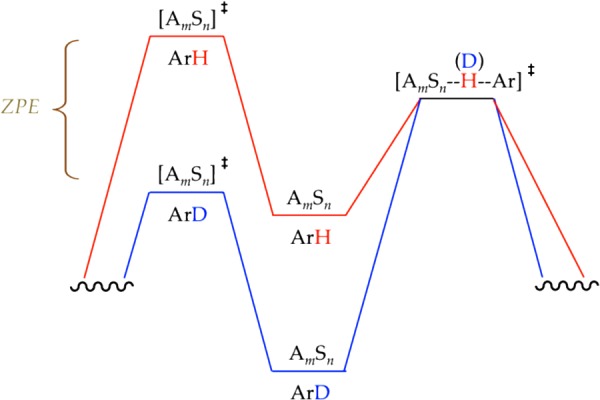
(6) How does isotopic substitution shift the rate-limiting step? Recall that the isotope effects are quite large, and the relative barrier heights for the different transition states cluster in a narrow energetic range. Scheme 7 shows barriers for the highly simplified and generic reaction coordinate with barriers for ArD superimposed on those for ArH. Of course, the core principle is that the rate depression through deuteration stems from a lower zero point energy (ZPE) in the ground state that is eliminated at the transition state. (Although tunneling in the transition structure is certainly possible—even probable—it does not change the model.44) When applied to sequential barriers in Scheme 7, ZPE also stabilizes the preceding transition state that includes both the [AmSn]⧧ and ArD components owing to net stabilization of ArD with the consequent shift to rate-limiting metalation, [AmSn--H(D)--Ar]⧧. Thus, the passive role of the arene ZPE in the nonmetalation-based aggregation step shifts the rate-limiting step.
Scheme 7.
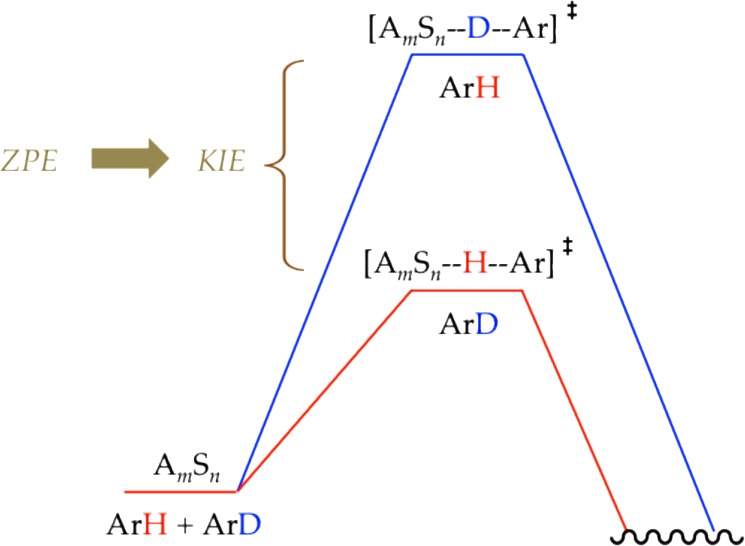
(7) What are the origins of the competitive isotope effects and biphasic kinetics? Measurement of kinetic isotopes through competition of deuterated and protonated substrates necessarily leads to biphasic kinetics (Figures 14 and 20) if the metalation step is post rate limiting. We are unaware of other clean examples of such biphasic kinetics. A highly simplified model in Scheme 3 adequately fit the data using numerical integration. Biphasic kinetics ostensibly stem from efficient trapping by the more reactive protio form (ArH) first and by the deuterio form (ArD) only after the ArH is consumed, but this outcome is misleading as written. Imagine the competition of ArH and ArD represented in the idealized reaction coordinate diagram in Scheme 8. Note that ArH and ArD are both included in a single thermochemical depiction of the ground state. To a first approximation, the C–H and C–D stretches are lost in the transition state. The competitive isotope effect—preferential proton versus deuterium transfer—stems from the lower ZPE of ArD in the transition state. By using an ArH–ArD mixture not only in the vessel but also in the thermochemical diagram, we have arithmetically shifted the isotopic contribution of ZPE to the transition state. We return to this concept below.
Scheme 8.
(8) How does isotopic labeling divert a reaction through an entirely different reaction coordinate? Using catalyzed conditions we observed a tetramer-based [A4S4]⧧ rate-limiting step. Anticipating that deuteration would suppress the metalation rate and bring a tetramer-based metalation ([A4Sn(ArD)]⧧) into view—an assertion that should feel charged with intellectual risk at this point—we were surprised to detect [A2S2(ArD)]⧧ and [A2S3(ArD)]⧧ (dimer-based) metalations. Let us strip away the inordinate complexities of Schemes 1 and 2 by gazing at just the relative barrier heights (Scheme 9). In short, the relative energies of [A2S2]⧧ and [A4S4]⧧ aggregation events do not correlate with the relative energies of the [A2S2(ArD)]⧧, [A2S3(ArD)]⧧, and [A4Sn(ArD)]⧧ metalations. In fact, there is no reason whatsoever to expect such a correlation of the two fundamentally different processes such as aggregation and metalation. This is easy to say in retrospect. By shifting the rate-limiting step, fleeting intermediates A2S2*, A2S3, and A4S4 are all formed at equilibrium with starting LDA dimer A2S2, causing the choice of pathway to derive exclusively from the relative facilities of the proton transfers.
Scheme 9.
(9) Can the reaction coordinate diagrams corresponding to reaction of ArH (Scheme 1) and ArD (Scheme 2) be presented as a single, self-consistent, coherent reaction coordinate diagram? In short, they sure better be superimposable, and indeed such a depiction is self-consistent (Scheme 10). As to whether the picture is coherent, we have our doubts, and adding labels to Scheme 10 would likely not help.
Scheme 10.
A unified depiction, however, is not impossible. The problem with superimposing Schemes 1 and 2 to create Scheme 10 is that there are six distinct minima and five maxima in which contributions from ZPE create different energies corresponding to ArH (red) and ArD (blue)—12 minima and 14 maxima in total. Taking a cue from the discussion of the competitive isotopic studies (part 7) and from shifting the ZPEs to only four transition states, we offer a fully labeled variant as Scheme 11 with no further comment except to marvel at the finished product.
Scheme 11.
Conclusions
Metalations of many substrates, including 1,4-difluorobenzene, using LDA/THF at −78 °C exhibit remarkable rate behaviors owing to the coincidence of barrier heights for aggregation events and metalations. Complexity aside, there are real consequences. Trace impurities such as LiCl can accelerate metalations moderately or massively (up to 100-fold), depending on the substrate. Commercial LDA and LDA generated in situ are very different—a difference that can be eliminated by adding traces of Et3NHCl as a LiCl precursor to commercial LDA.6,45 But the consequences are more subtle than that. Given the hypersensitivity of the choice of substrate to the ensuing mechanism, nonequilibrating aggregates cause erratic regio- and stereoselectivities. Autocatalysis by products (such as aryllithium 2) alter the mechanisms. Such feedback loops cause regioselectivities to vary with percent conversion and with the number of equivalents of LDA used.6,46
The metalation of arene 1 has provided the best view to date of how rate-limiting aggregation and solvation events involved in LDA deaggregation can dictate rates and mechanisms. We found, for example, that lithium salts can catalyze different steps involved in the deaggregation. Aryllithium 2 catalyzes LDA closed-to-open dimer conversion, whereas LiCl catalyzes dimer-to-monomer conversion. LDA-tetramer-based chemistry keeps surfacing and continues to challenge us.
This work offered a plethora of examples of saturation kinetics arising from shifting rate-limiting steps, often superimposing saturation behaviors. The plotline that emerged in many ways is more about understanding rate limitation and how to probe specific steps along a reaction coordinate than about organolithium chemistry per se.
We also have made some noteworthy observations that received scant attention. The Job plots used to study autocatalysis represent exceedingly rare examples of Job plots used to study reaction kinetics.26 There are a multitude of opportunities being overlooked by the chemistry community. Although measured competitive KIEs reveal highly characteristic biphasic kinetics, we must confess to being unaware of others exploiting such diagnostic behavior. Overall, the methodological developments required to study this remarkably complex organometallic problem are as poignant as the chemistry itself.
Experimental Section
Reagents and Solvents
THF, Et2O, and hexanes were distilled from blue or purple solutions containing sodium benzophenone ketyl. The hexanes contained 1% tetraglyme to dissolve the ketyl. Et3N·HCl was recrystallized from THF/2-propanol.45 Literature procedures47 were modified to prepare LDA as a LiCl- and ligand-free solid.6d Solutions of LDA were titrated using a literature method.48
IR Spectroscopic analyses
IR spectra were recorded using an in situ IR spectrometer fitted with a 30-bounce, silicon-tipped probe. The spectra were acquired in 16 scans at a gain of 1 and a resolution of 4 cm–1. A representative reaction was carried out as follows: The IR probe was inserted through a nylon adapter and O-ring seal into an oven-dried, cylindrical flask fitted with a magnetic stir bar and a T-joint. The T-joint was capped by a septum for injections and a nitrogen line. After evacuation under full vacuum, heating, and flushing with nitrogen, the flask was charged with LDA (108 mg, 1.01 mmol) in THF and cooled in a dry ice–acetone bath prepared with fresh acetone. LiCl was added via a THF stock solution prepared from Et3N·HCl and LDA. After recording a background spectrum, we added arene 1 (0.76 mmol) with stirring. For the most rapid reactions, IR spectra were recorded every 3 s with monitoring of the absorbance at 1510 cm–1 over the course of the reaction.
NMR Spectroscopic Analyses
All NMR samples were prepared using stock solutions and sealed under partial vacuum. Standard 6Li, 13C, 15N, and 19F NMR spectra were recorded on a 500 MHz spectrometer at 73.57, 125.79, 50.66, and 470.35 MHz, respectively. The 6Li, 13C, and 15N resonances are referenced to 0.30 M [6Li]LiCl/MeOH at −90 °C (0.0 ppm), the CH2O resonance of THF at −90 °C (67.57 ppm), and neat Me2NEt at −90 °C (25.7 ppm), respectively.
2,3,5,6-Tetradeutero-1,4-difluorobenzene (1-d4, ArD)
A 10.6 M solution of n-BuLi in hexanes (4.8 mL, 50.1 mmol) was added via syringe pump to a solution of 1,4-difluorobenzene (1, ArH, 5.0 mL, 48.6 mmol) in 150 mL of dry THF at −78 °C under argon over 20 min. The solution was stirred for an additional 25 min. MeOD (2.05 mL, 50.1 mmol) was added via syringe pump over 20 min. The mixture was allowed to stir for 30 min. Without any intervening workups sequential additions of 1.1 equiv of n-BuLi and 1.1 equiv of MeOD were repeated five additional times. A final aliquot of MeOD (10 mL, 5.0 equiv) was added to quench the reaction fully. After the mixture was allowed to warm to room temperature, the pH was adjusted to 1.0 with 4.0 M aq HCl to dissolve all lithium salts. Organic and aqueous layers were separated, and the organic layer was extracted with additional cold 0.020 M HCl to remove excess THF. Extraction was stopped when the total organic volume was approximately 10 mL. The organic layer was dried over Na2SO4 and distilled. The product was collected as a colorless liquid (1.75 g, 15.3 mmol) via distillation at 88 °C in 31.5% yield: 13C NMR δ 158.8 (dqn, 2JC–F = 243.0 Hz, 2JC–D = 1.7 Hz), 116.10 (tdd, 2JC–D = 25.2 Hz, 2JC–F = 19.4 Hz, 2JC–F = 13.2 Hz); LRMS 118.1 m/z shows 98% 1-d4.
Numeric Integrations
The time-dependent concentration plots obtained using IR spectroscopy were fit to mechanistic models expressed by a set of differential equations. The curve-fitting operation minimizes χ-square in searching for the coefficient values (rate constants). The Levenberg–Marquardt algorithm49 was used for the χ-square minimization and is a form of nonlinear, least-squares fitting. The fitting procedure implements numeric integration based on the backward differentiation formula50 to solve the differential equations, yielding functions describing concentration versus time.
Acknowledgments
We thank the National Institutes of Health (GM39764) and the National Science Foundation (CHE 0650880) for direct support of this work.
Supporting Information Available
NMR, rate and computational data, and a complete list of authors for ref (17). This material is available free of charge via the Internet at http://pubs.acs.org.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Reich H. J.Survey of Natural Product Syntheses; http://www.chem.wisc.edu/areas/reich/syntheses/syntheses.htm.
- a Eames J.Product Subclass 6: Lithium Amides. In Science of Synthesis; Snieckus V., Ed.; Thieme; New York, 2006; Vol. 8a, p 173. [Google Scholar]; b Clayden J.Organolithiums: Selectivity for Synthesis; Pergamon: New York, 2002. [Google Scholar]
- Collum D. B.; McNeil A. J.; Ramírez A. Angew. Chem., Int. Ed. 2007, 46, 3002. [DOI] [PubMed] [Google Scholar]
- Reich H. J. J. Org. Chem. 2012, 77, 5471. [DOI] [PubMed] [Google Scholar]
- a McGarrity J. F.; Ogle C. A. J. Am. Chem. Soc. 1985, 107, 1810. [Google Scholar]; b Jones A. C.; Sanders A. W.; Bevan M. J.; Reich H. J. J. Am. Chem. Soc. 2007, 129, 3492. [DOI] [PubMed] [Google Scholar]; c Jones A. C.; Sanders A. W.; Sikorski W. H.; Jansen K. L.; Reich H. J. J. Am. Chem. Soc. 2008, 130, 6060. [DOI] [PubMed] [Google Scholar]
- a Singh K. J.; Hoepker A. C.; Collum D. B. J. Am. Chem. Soc. 2008, 130, 18008. [DOI] [PMC free article] [PubMed] [Google Scholar]; b Gupta L.; Hoepker A. C.; Singh K. J.; Collum D. B. J. Org. Chem. 2009, 74, 2231. [DOI] [PMC free article] [PubMed] [Google Scholar]; c Ma Y.; Hoepker A. C.; Gupta L.; Faggin M. F.; Collum D. B. J. Am. Chem. Soc. 2010, 132, 15610. [DOI] [PMC free article] [PubMed] [Google Scholar]; d Hoepker A. C.; Gupta L.; Ma Y.; Faggin M. F.; Collum D. B. J. Am. Chem. Soc. 2011, 133, 7135. [DOI] [PMC free article] [PubMed] [Google Scholar]; e Gupta L.; Hoepker A. C.; Ma Y.; Viciu M. S.; Faggin M. F.; Collum D. B. J. Org. Chem. 2013, 78, 4214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoepker A. C.; Collum D. B. J. Org. Chem. 2011, 76, 7985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- a Scott J. P.; Brewer S. E.; Davies A. J.; Brands K. M. J. Synlett 2004, 1646. [Google Scholar]; b Buker H. H.; Nibbering N. M. M.; Espinosa D.; Mongin F.; Schlosser M. Tetrahedron Lett. 1997, 38, 8519. [Google Scholar]; c For gas-phase additivity effects of fluorine substituents, see:Hyla-Kryspin I.; Grimme S.; Buker H. H.; Nibbering N. M. M.; Cottet F.; Schlosser M. Chem.—Eur. J. 2005, 11, 1251. [DOI] [PubMed] [Google Scholar]
- a Besson C.; Finney E. E.; Finke R. G. J. Am. Chem. Soc. 2005, 127, 8179. [DOI] [PubMed] [Google Scholar]; b Besson C.; Finney E. E.; Finke R. G. Chem. Mater. 2005, 17, 4925. [DOI] [PubMed] [Google Scholar]; c Huang K. T.; Keszler A.; Patel N.; Patel R. P.; Gladwin M. T.; Kim-Shapiro D. B.; Hogg N. J. Biol. Chem. 2005, 280, 31126. [DOI] [PubMed] [Google Scholar]; d Huang Z.; Shiva S.; Kim-Shapiro D. B.; Patel R. P.; Ringwood L. A.; Irby C. E.; Huang K. T.; Ho C.; Hogg N.; Schechter A. N.; Gladwin M. T. J. Clin. Invest. 2005, 115, 2099. [DOI] [PMC free article] [PubMed] [Google Scholar]; e Tanj S.; Ohno A.; Sato I.; Soai K. Org. Lett. 2001, 3, 287. [DOI] [PubMed] [Google Scholar]; f Barrios-Landeros F.; Carrow B. P.; Hartwig J. F. J. Am. Chem. Soc. 2008, 130, 5842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- a Depue J. S.; Collum D. B. J. Am. Chem. Soc. 1988, 110, 5524. [Google Scholar]; b Nudelman N. S.; Velurtas S.; Grela M. A. J. Phys. Org. Chem. 2003, 16, 669. [Google Scholar]; c Alberts A. H.; Wynberg H. J. Am. Chem. Soc. 1989, 111, 7265. [Google Scholar]; d Alberts A. H.; Wynberg H. J. Chem. Soc., Chem. Commun. 1990, 453. [Google Scholar]
- a Seebach D. In Proceedings of the Robert A. Welch Foundation Conferences on Chemistry and Biochemistry; Wiley: New York, 1984; p 93. [Google Scholar]; b Seebach D. Angew. Chem., Int. Ed. Engl. 1988, 27, 1624. [Google Scholar]; c Tchoubar B.; Loupy A.. Salt Effects in Organic and Organometallic Chemistry; VCH: New York, 1992; Chapters 4, 5, and 7. [Google Scholar]; d Caubère P. Chem. Rev. 1993, 93, 2317. [Google Scholar]
- a Collum D. B. Acc. Chem. Res. 1993, 26, 227. [Google Scholar]
- a Gakh Y. G.; Gakh A. A.; Gronenborn A. M. Magn. Reson. Chem. 2000, 38, 551. [Google Scholar]; b McGill C. A.; Nordon A.; Littlejohn D. J. Process Anal. Chem. 2001, 6, 36. [DOI] [PubMed] [Google Scholar]; c Espinet P.; Albeniz A. C.; Casares J. A.; Martinez-Ilarduya J. M. Coor. Chem. Rev. 2008, 252, 2180. [Google Scholar]
- Günther H. J. Braz. Chem. 1999, 10, 241–262. [Google Scholar]
- a Riggs J. C.; Ramírez A.; Cremeens M. E.; Bashore C. G.; Candler J.; Wirtz M. C.; Coe J. W.; Collum D. B. J. Am. Chem. Soc. 2008, 130, 3406. [DOI] [PubMed] [Google Scholar]; b Ramírez A.; Candler J.; Bashore C. G.; Wirtz M. C.; Coe J. W.; Collum D. B. J. Am. Chem. Soc. 2004, 126, 14700. [DOI] [PubMed] [Google Scholar]; c Menzel K.; Fisher E. L.; DiMichele L.; Frantz D. E.; Nelson T. D.; Kress M. H. J. Org. Chem. 2006, 71, 2188. [DOI] [PubMed] [Google Scholar]; d 2JC–F values have been correlated with π-bond orders and total electronic charge at the 13C atom:Doddrell D.; Barfield M.; Adcock W.; Aurangzeb M.; Jordan D. J. Chem. Soc., Perkin Trans. 2 1976, 402. [Google Scholar]
- Liang J.; Collum D. B. Unpublished results.
- Frisch M. J.; et al. GaussianVersion 3.09; revision A.1; Gaussian, Inc.: Wallingford, CT, 2009. [Google Scholar]
- The computations use the Gaussian standard state of 1.0 atm. If the THF concentration is corrected to neat THF (approximately 12 M), each solvation step benefits from approximately 2.0 kcal/mol of additional stabilization at −78 °C (195 K):Pratt L. M.; Merry S.; Nguyen S. C.; Quan P.; Thanh B. T. Tetrahedron 2006, 62, 10821. [Google Scholar]
- Rein A. J.; Donahue S. M.; Pavlosky M. A. Curr. Opin. Drug Discovery Dev. 2000, 3, 734. [PubMed] [Google Scholar]
- Casado J.; Lopez-Quintela M. A.; Lorenzo-Barral F. M. J. Chem. Educ. 1986, 63, 450. [Google Scholar]
- The concentration of LDA, although expressed in units of molarity, refers to the concentration of the monomer unit (normality).
- Open dimers were first proposed for the isomerization of oxiranes to allylic alcohols by mixed metal bases. See:Mordini A.; Rayana E. B.; Margot C.; Schlosser M. Tetrahedron 1990, 46, 2401. [Google Scholar]; For a bibliography of lithium amide open dimers, see:Ramírez A.; Sun X.; Collum D. B. J. Am. Chem. Soc. 2006, 128, 10326.and references cited therein. [DOI] [PubMed] [Google Scholar]
- The rate law provides the stoichiometry of the transition structure relative to that of the reactants:Edwards J. O.; Greene E. F.; Ross J. J. Chem. Educ. 1968, 45, 381. [Google Scholar]
- We define the idealized rate law as that obtained by rounding the observed reaction orders to the nearest rational order.
- Equations 11 and 30 are approximations, good ones, but approximations nonetheless. The non-zero intercept is conveniently addressed with an added constant. We have derived the rigorous and decidedly more complex counterparts (Supporting Information). They require additional fitting parameters yet offer no additional significant difference nor added insights in comparison to the simple versions.
- Renny J. S.; Tomasevich L. L.; Tallmadge E. H.; Collum D. B. Angew. Chem., Int. Ed. 2013, 52, 11998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The mathematical function described by eq 12 includes no provision for the build up of intermediate mixed aggregate, which is an imperfect approximation under such stoichiometric conditions. The shifting rate-limiting step adds additional imprecisions to the model.
- Frey P. A.; Hegeman A. D.. Enzymatic Reaction Mechanisms; Oxford University Press: New York, 2007; Chapter 2. [Google Scholar]
- ArLi- and LiCl-catalyzed metalations of 2-fluoropyridines showed saturation kinetics that afforded saturation plateaus at very close but not identical rates. We suspect, in retrospect, that the ArLi and LiCl may have been operating on two different parts of the reaction coordinate in that case as well.
- Selected examples of fully characterized through-space Li–F interactions:; a Armstrong D. R.; Khandelwal A. H.; Kerr L. C.; Peasey S.; Raithby P. R.; Shields G. P.; Snaith R.; Wright D. S. Chem. Commun. 1998, 1011. [Google Scholar]; b Plenio H.; Diodone R. J. Am. Chem. Soc. 1996, 118, 356. [Google Scholar]; c Henderson K. W.; Dorigo A. E.; Liu Q.-Y.; Williard P. G. J. Am. Chem. Soc. 1997, 119, 11855. [Google Scholar]; d Kessar S. V.; Singh P.; Singh K. N.; Bharatam P. V.; Sharma A. K.; Lata S.; Kaur A. Angew. Chem., Int. Ed. 2008, 47, 4703. [DOI] [PubMed] [Google Scholar]; e Lee W.-Y.; Liang L.-C. Inorg. Chem. 2008, 47, 3298. [DOI] [PubMed] [Google Scholar]; f Stalke D.; Klingebiel U.; Sheldrick G. M. Chem. Ber. 1988, 121, 1457. [Google Scholar]; g Sini G.; Tessier A.; Pytkowicz J.; Brigaud T. Chem.—Eur. J. 2008, 14, 3363.and references cited therein. [DOI] [PubMed] [Google Scholar]
- Cyclic tetramers of lithium 2,2,6,6-tetramethylpiperidide were shown to react by dissociation to dimers:Wiedemann S. H.; Ramírez A.; Collum D. B. J. Am. Chem. Soc. 2003, 125, 15893. [DOI] [PubMed] [Google Scholar]
- Lithium amide tetramers:; a Cyclic:Lucht B. L.; Collum D. B. J. Am. Chem. Soc. 1994, 116, 7949. [Google Scholar]; b Ladders:Armstrong D. R.; Barr D.; Clegg W.; Mulvey R. E.; Reed D.; Snaith R.; Wade K. J. Chem. Soc., Chem. Commun. 1986, 869. [Google Scholar]; c Ladders:Gardiner M. G.; Raston C. L. Inorg. Chem. 1996, 35, 4047. [DOI] [PubMed] [Google Scholar]; d Ladders:Vestergren M.; Eriksson J.; Hilmersson G.; Hakansson M. J. Organomet. Chem. 2003, 682, 172. [Google Scholar]; e Ladders:Boche G.; Langlotz I.; Marsch M.; Harms K.; Nudelman N. E. S. Angew. Chem. 1992, 104, 1239. [Google Scholar]; f Cubic:Gardiner M. G.; Raston C. L. Inorg. Chem. 1995, 34, 4206. [Google Scholar]
- The equation as written using adjustable parameter c is an approximation. The more rigorous analogue described in the Supporting Information fits the data but provides no net changes in the conclusion despite the marked increase in complexity.
- Holding the concentration of A2 constant and varying B2, for example, will afford a saturation behavior displaying a first-order dependence on B2 in the limit of low B2 and zeroth order dependence in the limit of a large excess of B2. (A derivation is provided in the Supporting Information.) This behavior originates purely from the statistical probabilities of reaggregation.
- Reich H. J.http://www.chem.wisc.edu/areas/reich/plt/windnmr.htm.
- We have asserted that
bridging THF ligands
may play an important role in deaggregations. Studies of direct dimer-based
dissociation supported this notion:
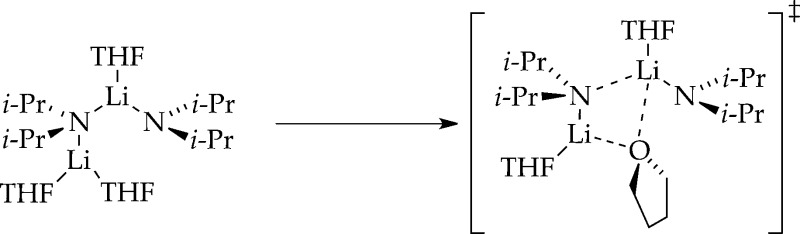 Computations akin to those shown in Scheme 4 using Me2NLi as a less demanding model uncovered
possible transition structures with bridging THF ligands. Analogous
attempts using the more hindered i-Pr2NLi fragment, however, provided no support.
Computations akin to those shown in Scheme 4 using Me2NLi as a less demanding model uncovered
possible transition structures with bridging THF ligands. Analogous
attempts using the more hindered i-Pr2NLi fragment, however, provided no support. - Representative examples of structurally characterized bridging THF ligands:; a Pratt L. M.; Merry A.; Nguyen S. C.; Quanb P.; Thanh B. T. Tetrahedron 2006, 62, 10821. [Google Scholar]; b Clegg W.; Liddle S. T.; Mulvey R. E.; Robertson A. Chem. Commun. 1999, 511. [Google Scholar]; c Boche G.; Boie C.; Bosold F.; Harms K.; Marsch M. Angew. Chem., Int. Ed. 1994, 33, 115. [Google Scholar]; d Daniele S.; Drost C.; Gehrhus B.; Hawkins S. M.; Hitchcock P. B.; Lappert M. F.; Merle P. G.; Bott S. G. J. Chem. Soc., Dalton Trans. 2001, 3179. [Google Scholar]; e Chivers T.; Fedorchuk C.; Parvez M. Inorg. Chem. 2004, 43, 2643. [DOI] [PubMed] [Google Scholar]; f Briand G. G.; Chivers T.; Parvez M. J. Chem. Soc., Dalton Trans. 2002, 3785. [Google Scholar]
- We also computationally examined the possible intermediacy of four-rung LDA ladders as key intermediates, possibly dissociating to a monomer and trimer. For Lithium amide ladders showing open-dimer-like subunits, see:Armstrong D. R.; Barr D.; Clegg W.; Hodgson S. M.; Mulvey R. E.; Reed D.; Snaith R.; Wright D. S. J. Am. Chem. Soc. 1989, 111, 4719.Although minima were found, we obtained no evidence that ladders were on, rather than tangential to, the reaction coordinate en route to monomers. [Google Scholar]
- The model used to numerically integrate the
curves in Figure 1 is as follows (with appropriate
color coding):
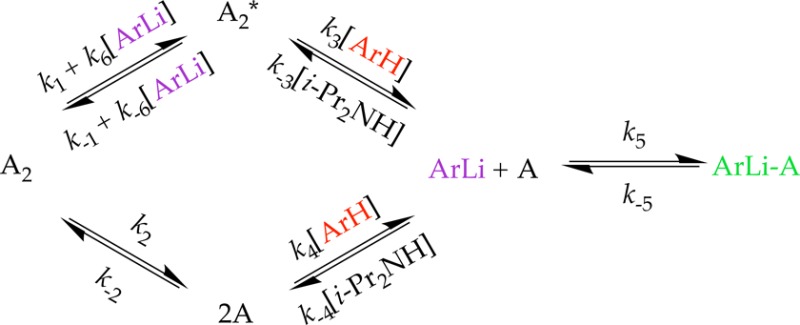 The role of A2 (3) A2* (7), A (8), and ArLi–A
(17) and their interconversions are founded in the structural
and rate studies. The model is underdetermined (such as the magnitudes
of k2 and k–2), but not profoundly so.
The role of A2 (3) A2* (7), A (8), and ArLi–A
(17) and their interconversions are founded in the structural
and rate studies. The model is underdetermined (such as the magnitudes
of k2 and k–2), but not profoundly so. - We infer that “reactant” and “transition structure” (often awkwardly referred to as a “transition state structure”) have structural connotations whereas “ground state” and “transition state” have energetic connotations:Bauer S. H.; Wilcox C. F. Jr. J. Chem. Educ. 1995, 72, 13–16. [Google Scholar]
- a Stegelmann C.; Andreasen A.; Campbell C. T. J. Am. Chem. Soc. 2009, 131, 8077. [DOI] [PubMed] [Google Scholar]; b Maniscalco S. J.; Tally J. F.; Fisher H. F. Arch. Biochem. Biophys. 2004, 425, 165. [DOI] [PubMed] [Google Scholar]
- a Carpenter B. K.Determination of Organic Reaction Mechanisms; Wiley: New York, 1984. [Google Scholar]; b Whisler M. C.; MacNeil S.; Snieckus V.; Beak P. Angew. Chem., Int. Ed. 2004, 43, 2206. [DOI] [PubMed] [Google Scholar]
- We are unaware of a clean example of an upwardly curving second-order dependence giving way to a linear first-order dependence.
- We have kept a distance from any debate about the role of tunneling despite routinely observed isotope effects that exceed 40. The use of reaction coordinate diagrams with affiliated zero point energies argue for bringing tunnelling into the discussion. One could, for example, invoke a normal isotope effect that is magnified by contributions in the transition structure owing to the reluctance of deuteria to tunnel. Apportioning the ArH–ArD energy gap in this way, however, does not change the qualitative model presented.
- Snaith and co-workers underscored the merits of R3NHX salts as precursors to anhydrous LiX salts. See:Barr D.; Snaith R.; Wright D. S.; Mulvey R. E.; Wade K. J. Am. Chem. Soc. 1987, 109, 7891. [Google Scholar]
- Galiano-Roth A. S.; Kim Y.-J.; Gilchrist J. H.; Harrison A. T.; Fuller D. J.; Collum D. B. J. Am. Chem. Soc. 1991, 113, 5053. [Google Scholar]
- a Marck W.; Huisgen R. Chem. Ber. 1960, 93, 608. [Google Scholar]; b Gaudemar-Bardone F.; Gaudemar M. Synthesis 1979, 463. [Google Scholar]; c Reetz M. T.; Maier W. F. Liebigs Ann. Chem. 1980, 1471. [Google Scholar]; d Williard P. G.; Carpenter G. B. J. Am. Chem. Soc. 1986, 108, 462. [DOI] [PubMed] [Google Scholar]; f Williard P. G.; Salvino J. M. J. Org. Chem. 1993, 58, 1. [Google Scholar]; e Morrison R. C.; Hall R. W.; Rathman T. L. Stable Lithium Diisopropylamide and Method of Preparation. U.S. Patent 4,595,779, June 17, 1986.
- Kofron W. G.; Baclawski L. M. J. Org. Chem. 1976, 41, 1879. [Google Scholar]
- For an explanation of Levenberg–Marquardt nonlinear least-squares optimization, see:Press W. H.; Flannery B. P.; Teukolsky S. A.; Vetterling V. T.. Numerical Recipes in C; Cambridge University Press: London, 1988; Chapter 14.4. [Google Scholar]
- Brown P. N.; Byrne G. D.; Hindmarsh A. C. SIAM J. Sci. Stat. Comp. 1989, 10, 1038. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.