Segmentation and quantification of blood vessels for OCT-based micro-angiograms using hybrid shape/intensity compounding

Abstract

Optical coherence tomography (OCT) based microangiography is capable of visualizing 3D functional blood vessel networks within microcirculatory tissue beds in vivo. To provide the quantitative information of vasculature from the microangiograms such as vessel diameter and morphology, it is necessary to develop efficient vessel segmentation algorithms. In this paper, we propose to develop a hybrid Hessian/intensity based method to segment and quantify shape and diameter of the blood vessels innervating capillary beds that are imaged by functional OCT in vivo. The proposed method utilizes the multi-scale Hessian filters to segment tubular structures such as blood vessels, but compounded by the intensity-based segmentation method to mitigate the limitations of Hessian filter's sensitivity to the selection of scale parameters. Such compounding segmentation scheme takes the advantage of morphological nature of Hessian filters while correcting for the scale parameter selection by intensity-based segmentation. The proposed algorithm is tested on a wound healing model and its performance of segmentation vessels is quantified by a publicly available manual segmentation dataset. We believe that this method will play an important role in the quantification of micro-angiograms for microcirculation research in ophthalmology and diagnosing retinal eye diseases involved with microcirculation.

Introduction

Optical coherence tomography (OCT) is a non-contact imaging technique based on light backscattering properties of the tissue structures [Huang et al.,1991; Tomlins and Wang, 2005; Fercher et al., 2003]. Similar to ultrasound Doppler modes, OCT hemodynamic information can be acquired in addition to structure information. Compared to ultrasound imaging, OCT resolution is higher (<10 μm) while the penetration and imaging depth is limited (< 2mm) which diversifies their applications. In order to quantify and measure geometrical and physical parameters of blood vessels from the acquired OCT angiograms, a segmentation algorithm has to be developed. Segmentation algorithm returns a binary map of the location of blood vessels in contrast to non-blood vessel surrounding background tissue.

Since the primary clinical application of OCT has been in the field of ophthalmology, numerous methods have been reported in the literature to segment blood vessels from OCT intensity and angiogram images. Some techniques in the literature utilize structural and cross-section information of the OCT B-scan upon which the blood vessels are located. Goldenberg et al. [Goldenberg et al., 2013] proposed a method to measure the diameters of large retinal blood vessels using OCT structural cross-sections. Since they combined OCT with the infrared images, it is possible to identify each of the large arteries and veins on the OCT raster scans in which the vessel lumen appears as reduced scattering high-contrast vessel-like shape in the infrared image. Similarly, Pilch et al. (2012) and Srivastava et al. (2013) have proposed a model-based technique that utilizes machine learning algorithm to train for the circular shape of blood vessels when OCT data is correlated with infrared camera image. Since choroidal vessels appear darker than their surrounding tissue on OCT cross-sectional structures, similar approaches have been proposed to segment choroidal vasculature from en-face OCT structural images [Duan et al., 2013; Sohrab et al., 2012].

Utilizing the dynamic OCT speckle signals induced by moving blood cells within patent vessels, optical microangiography (OMAG) is developed to obtain 3-D blood perfusion maps in microcirculatory tissue beds in vivo using frequency-analyses of dynamic OCT signals [Wang et al., 2007; Wang and Hurst, 2007]. There exist numerous techniques for OMAG processing from OCT signals such as complex value differentiation [Subhash et al., 2011], intensity value differentiation [Huang et al., 2014], correlation mapping OCT (cmOCT) [Jonathan et al., 2011], correlation masking [Choi et al., 2014], split spectrum amplitude decorrelation [Jia et al., 2012], cross-sectional filters [Reif et al., 2014] and eigen-regression filters [Yousefi et al., 2011]. After obtaining the OMAG blood flow perfusion map, a simple adaptive threshold intensity-based algorithm can be developed to segment blood vessels from their surrounding tissues. However, the limitations of intensity-based techniques are their sensitivity to the selection of a threshold parameter and lack of sensitivity to the shape and morphology of the vessels.

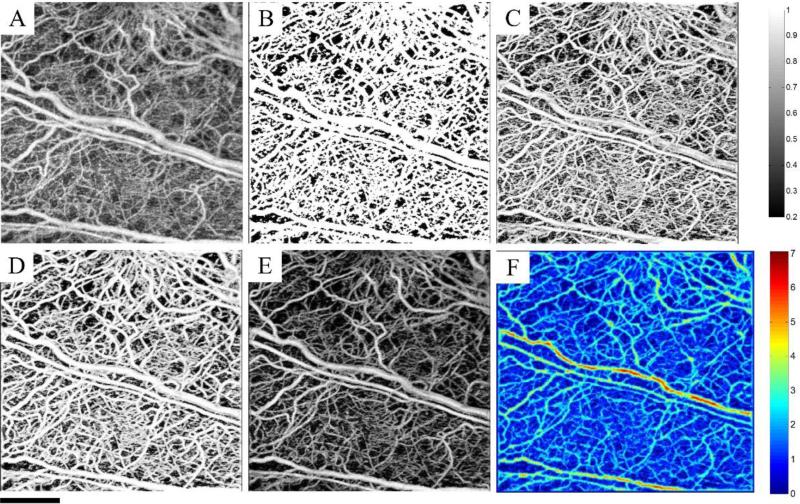
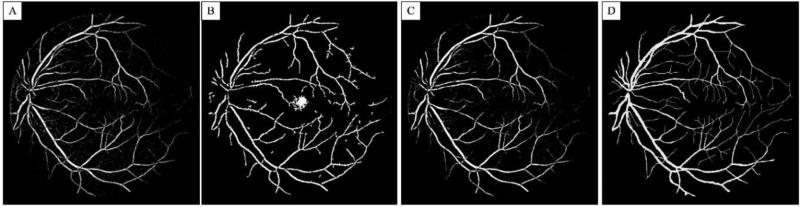
Besides adaptive thresholding on OCT angiograms, other techniques based on Hessian filters have also been proposed in the animal studies [Zhang et al., 2014; Lee et al., 2014; Poole et al., 2014; Kowalski et al., 2014]. Although widely used in the segmentation of tubular structures, multi-scale Hessian filters tend to blur the vasculature map. Typically, the multi-scale Hessian filters require a known range of scales to maximize the vesselness function, over that range to find the maximum scale. However, if the upper limit of the scales is chosen large enough to account for measuring the large vessels, smaller vessels appear blurred. Fig. 1 shows segmentation results on mouse ear pinna vasculature using multi-scale Hessian filters where the sensitivity of the method to the maximum scale can be clearly observed. Figs. 1(A-C) show the vessel map after segmentation using maximum scales of 2, 5 and 10, respectively, and Figs. 1(D-F) show the vessel radius estimated using distance transform of the inverted binary image after segmentation [Gonzalez and Woods, 2008]. It can be observed that the estimated vessel radius is very sensitive to the pre-selected value of the maximum scale. The distance transform results are the minimum number of pixels in between each foreground pixel to the boundary of the object (vessel). The distance transform of a blood vessel should have maxima on the vessel centerline. The exact vessel diameter/radius can be measured after correcting for the beam broadening and calibrating the spatial size of each voxel. The calibration would be the same for each system when the object is given at a specific depth of focus, therefore can be performed before imaging. In order to minimize the sensitivity of the segmentation technique to the maximum scale parameter of Hessian filters, another segmentation technique based on intensity value can be utilized in parallel to the Hessian technique and the final segmentation can be achieved by compounding these results.

Fig. 1.

Sensitivity of the Hessian-based filters to the maximum scale. (A-C) Hessian-based segmented vessels using the maximum scales of 2, 5 and 10, respectively. (D-F) Corresponding vessel radius using distance transform on the binary image.

One of the artifacts observed in all OCT angiography techniques is the elongated vessels or tail artifact for which the vessel cross-section does not appear circular but line-like shape. The reason behind this artifact is that red blood cells are highly scattering while the received signal below the vessels is weaker. Therefore rapidly fluctuating speckle signals below the vessels causes the shadow-like artifacts in the angiogram data [Choi et al., 2013]. Due to this limitation, most of the vessel extraction algorithms to segment 3D blood vessels [Kirbas and Quek, 2004] will fail to segment OCT angiograms.

In this paper, we propose an alternative approach towards segmentation of blood vessels from OMAG data. Our proposed technique combines shape-based segmentation technique based on Hessian vesselness filters and intensity-based segmentation to overcome limitations of both cases. In order to overcome the shadowing artifacts in OCT angiograms, we propose resampling the 3D dataset in depth direction and applying the segmentation method at each depth. Finally, the segmented results are stacked together to form 3D angiogram. The segmented binary maps can be utilized to further quantify morphological and structural information of microcirculatory network in vivo. After segmentation, the vessel diameter and centerline can be quantified. Utilizing this non-invasive and label-free technique in retinal OCT angiography [An et al, 2010, An et al, 2011] can be beneficial in analyzing retinal vessel morphology and structures for routine monitoring and diagnoses of various eye diseases such as diabetic retinopathy and age-related macular degeneration. This segmentation technique is not limited to retina vasculature and can be utilized for quantification of blood vessels in other applications such as dermatology and small animal imaging.

Methods

After acquiring and processing OCT/OMAG cross-section images, a 3D matrix is formed. Usually blood vessels in the OCT angiograms do not appear as perfect tubular structures and some tail artifact is often observed underneath relatively large vessels. Therefore utilizing a 3D-based Hessian approach directly to the 3D OCT angiogram can cause errors. In order to overcome these limitations we can re-arrange and re-sample the volumetric data set along the depth direction such that each frame corresponds to the microcirculation map at one specific depth, called orthoslice, or enface image. In other words, the volumetric data is re-arranged from Z-X-Y coordinates into X-Y-Z coordinates. For each depth-specific orthoslice, segmentation algorithm is performed and the segmented images are stacked into a new 3D dataset. Finally, the segmented volumetric data is re-arranged from X-Y-Z back to Z-X-Y coordinates so that it is equivalent to the input data set. The segmentation procedure is utilized by compounding two independent segmentation schemes, one based on the shape of blood vessels and the other on the intensity values of foreground/background. Multi-scale Hessian filters and morphological binary segmentation techniques were utilized and compounded in our shape-based and intensity-based methods.

Morphological Image Segmentation (Intensity-based)

First, image pre-processing (Gaussian smoothing filters) and histogram equalization is performed on the original image. Then, foreground and background objects are detected where foreground accounts for the desired objects (vessels) that are interested in segmenting. Foreground markers, i.e. the connected regions of pixels inside of each foreground object, and background markers can be detected using opening-by-reconstruction and closing-by-reconstruction morphological techniques that clean up the original image [Vincent, 1993]. This cleaning up operation creates flat maxima inside each object in the foreground image. Then, the foreground object (binary) and markers can be detected by performing adaptive thresholding and local maxima detection on the cleaned image, respectively. The background image can also be calculated by inverting the foreground binary image. Since original images are sometimes noisy and non-uniform, some un-necessary local minima are produced, leading to an over-segmentation. Over-segmentation means that instead of one large area representing one object in the image, a number of smaller areas with each one covering a fractional portion of the object in the image are produced. In order to minimize the effect of noise and inhomogeneity, a pre-processing step should be utilized such as histogram equalization [Yousefi et al., 2013].

Multi-scale Hessian vesselness function

The local behavior of the 2^nd order gradient image (Hessian matrix) is utilized to identify the boundaries of tubular blood vessels and contrasting them from background and other scattering tissues [Frangi et al., 1998]. The multi-scale nature of the method allows for the identification of the vessels in different sizes. Based on linear space theory, the 2^nd order derivative of a discrete matrix (digital image) can be estimated by convolving (filtering) the original image with the 2^nd derivative of a Gaussian kernel. The advantage of this convolution is that the derivative operation reduces to linear filtering that simplifies the implementation on hardware and real-time systems.

The second order derivative can be expressed as

$$\delta x^{T}H{\left(I\right)}_s\delta x=\left(\frac{\partial }{\partial x}\right)\left(\frac{\partial }{\partial x}\right)I(x,s)=s^{2\gamma }I(x,s)\ast \frac{{\partial }^2}{\partial x^2}G(x,s)$$ (1)

where I(x,s) is the original image at scale s and location x, H(·)_s, is the gradient vector of the image at scale s, γ, is the derivative normalization parameter and $G(x,s)=\frac{1}{\sqrt{2\pi s^2}}{e}^{-\frac{{\Vert x\Vert }^2}{2s^2}}$. By analyzing the eigenvalues and eigenvectors of the Hessian matrix, the principal direction of the local structure can be extracted which is the direction of the smallest curvature (along the vessel). By definition, the eigenvalues and vectors of the Hessian matrix are given by solving the equations H_ses,i = λ_s,i e_s,i where λ_{s, i} is the i-th eigenvalue at scale corresponding to normalized eigenvector e_s,i and ($\mid {\lambda }_3\mid \le \mid {\lambda }_2\mid \le \mid {\lambda }_1\mid$) for a three-dimensional structure. For an ideal tubular structure ${\lambda }_3\mid \approx 0$, $\mid {\lambda }_3\mid \ll \mid {\lambda }_2\mid$ and ${\lambda }_2\approx {\lambda }_1$.

Based on the second order ellipsoid, two geometric ratios are defined

$$R_A=\frac{\mid {\lambda }_2\mid }{\mid {\lambda }_3\mid }\text{and}{R}_B=\frac{\mid {\lambda }_1\mid }{\sqrt{{\lambda }_2{\lambda }_3}}$$ (2)

The first ratio (R_B) accounts for the deviation from a blob-like structure but cannot distinguish between a line-like and a plate-like pattern. The second ratio refers to the largest cross-sectional area of the ellipsoid that can distinguish between plate-like and line-like structures since it is zero in the latter case. In order to distinguish background noise where no structure is present, Frobenius matrix norm is utilized. This measure is derived from eigenvalues of Hessian matrix by

$$R_C={\mid \mid H\mid \mid }_F=\sqrt{\sum _{j\le D}{\lambda }_j^2}$$ (3)

where D is the dimension of the image. It will be low in the background where no structure is present and the eigenvalues are small for the lack of contrast. In regions with high contrast compared to the background, the norm will become larger since at least one of the eigenvalues will be large.

The vesselness function at scale is defined as

$$v_0\left(s\right)=\{\begin{array}{cc}0\hfill & if{\lambda }_2<0or{\lambda }_3<0\hfill \\ \left(1-e^{-\frac{R_A^2}{2{\alpha }^2}}\right)\hfill & \ast e^{-\frac{R_B^2}{2{\beta }^2}}\ast (1-e^{-\frac{R_C^2}{2{\theta }^2}})\hfill \end{array}\phantom{\}}$$ (4)

where α, β and Φ are thresholds which control the sensitivity of the line filter to the measures R_A, R_B and R_C. The idea behind this expression is to map the features into probability-like estimates of vesselness according to different criteria. The vesselness measure is analyzed at different scales. The response of the line filter will be maximum at a scale that approximately matches the vessel size.

$$V_0\left(\gamma \right)=\arg ma{x}_s\left\{v_0(s,\gamma )\right\},s_{min}<s<s_{max}$$ (5)

where s_min and s_max are lower and upper bounds in the range of scales (vessel sizes).

By utilizing matrix properties of eigenvalues, the computational complexity of this approach is reduced to simple 2-D filtering with already-known Gaussian derivative kernels at multiple scales. Since all of the operations are performed on matrices, the computation can be parallelized on the processing unit and real-time segmentation can be performed on the structure images.

Hybrid shape/intensity compounding technique

By combining the shape-based (Hessian filters) and intensity-based (morphological segmentation) techniques, it is feasible to achieve a segmentation technique that is both sensitive to the shape and intensity of the objects. In doing so, the shape-based and intensity-based techniques are compounded using a weighted average scheme where the weighting coefficients are chosen by the user to obtain the best performance. The weighted average of two images can be expressed by a linear combination of the images given by

$$I_{out}=\alpha \times I_1+(1-\alpha )\times I_2$$ (6)

where I₁ and I₂ are input images, α is scalar value between [0,1] and I_out is the output image produced by the linear combination of input images. The combination of shape-based and intensity-based techniques allows for the efficient segmentation of blood vessels where the algorithm is sensitive to both shape and intensity of the vessels. Also, Hessian vesselness function does not treat all pixels within the vessels the same and the vessel centerlines always have higher vesselness function. The intensity-based technique corrects for the blurring artifact and unwanted vessel boundary enlargement in the Hessian treatment due to inaccurate choice of maximum scale value. Fig. 2 shows the performance of the morphological segmentation technique, Hessian vesselness filtering and their combination on a 3D data set whose maximum intensity projection map is shown in Fig. 2(A). Fig. 2(B) shows the segmentation results using morphological segmentation. Morphological segmentation is only sensitive to the intensity values and does not take into account the shape of the vessel. These limitations can produce false positive segmentation in the image. Also, the vessel boundaries are not clearly defined and all pixels within a vessel are treated equally. Fig. 2(C) shows the segmentation results by using Hessian vesselness filters and Fig. 2(D) shows the results achieved by combining both methods, i.e. compounding. By visual comparison, it can be observed that the segmented blood perfusion map in Fig. 2(D) is less sensitive to intensity variations and the choice of maximum scales, leading to preserved vessel shapes. The binary map can be overlaid on the original image to suppress the background and increase the contrast. The high-contrast background suppressed image is shown in Fig. 2(E) and the estimate of the vessel radius using distance transform is shown in Fig. 2(G).

Fig. 2.

Combined Hessian vesselness (shape-based) and intensity-based segmentation techniques. (A) MIP of the original image. (B) MIP of the segmented image using the intensity-based morphological segmentation technique. (C) MIP of the segmented image using Hessian vesselness filters (D) MIP of the combined techniques (E) Overlaid the segmented binary image on top of the original image to suppress the background. (F) MIP of the estimated vessel radius using distance transform on the binary segmented vessels.

Experimental animal model and system setup

To assess the utility of the proposed hybrid segmentation method to quantify the blood vessels, we used a functional OCT system (see below) to obtain a series of vascular networks over time within microcirculatory tissue beds in vivo in a wound healing model in mouse pinna. The proposed method is then used to monitor changes in the vasculature and the vessel diameter [Jung et al., 2013; Yousefi et al., 2014]. Non-invasive in vivo OMAG images were acquired from the pinna of a healthy ~6 weeks old male hairless mouse (Crl:SKH1-Hrhr) weighting approximately 25g. During the experiment, the mouse was anesthetized using 2% isoflurance (0.2 L/min O2, 0.8 L/min air). The ear was kept flat on a microscope glass using a removable double-sided tape. The experimental protocol was in compliance with the Federal guidelines for care and handling of small rodents and approved by the Institution Animal Care and Use Committee (IACUC) of the University of Washington, Seattle.

To generate the OMAG images of microcirculatory tissue beds in vivo, we utilized a high speed spectral domain OCT (SD-OCT) system, which was reported in [Yousefi et al., 2014]. Briefly, the system used a light source with the center wavelength of 1310 nm and bandwidth of 65 nm, providing an axial resolution of ~12 μm in air. In the sample arm, a microscopy objective lens with 18-mm focal length was used to achieve ~5.8 μm lateral resolution. The imaging speed of the system was 47,000 lines per second, achieved by a 14-bit, 1024-pixels InGaAs linescan camera (SUI, Goodrich Corp). The system had a measured signal to noise ratio of 105 dB with a light power on the sample at ~3 mW. The imaging field of view was ~ 2.2x2.2 mm² on the sample.

The scanning protocol was based on three-dimensional ultrahigh-sensitive optical micro-angiography (UHS-OMAG) technique that requires acquisition of multiple B-scans at the same spatial location and then shifting the slow-scanning mirror to the adjacent cross-section [Wang et al., 2010; Wang and Hurst, 2007]. Each B-scan consisted of 400 A-lines covering a range of ~ 2.2 mm on the sample. The C-scan consisted of 400 scan locations with B-scan repetition of 8 frames per location for flow imaging and quantification. The total size of the dataset was 1.28x10⁶ A-lines. In order to cover a large field of view, multiple overlapping 3-D scans were acquired and the sample was translated using a mechanical stage. This allowed imaging a large area on the mouse ear pinna.

The acquired data was transferred to a personal computer (PC) and processed off-line using an m-file code developed on Matlab^© (The Mathworks Inc.). The processing consisted of removing interference signal from reference arm, dispersion correction, resampling each A-line from non-linear wavelength space to the linear K-space and applying fast Fourier transform (FFT) [Wang and Ma, 2006]. The FFT amplitude of the repeated B-scans at the same spatial location was averaged temporally to generate structure cross-section images. The procedures to map blood flow perfusion and lymphatic vessels are explained below.

A 1 mm biopsy punch was performed on the mouse ear pinna and the injured area was monitored on a weekly basis. After OMAG processing using the method of eigendecomposition [Yousefi et al., 2011], the 3D perfusion maps were resampled along the depth direction and each depth en-face image was segmented using the proposed hybrid method. The resampling step takes the 3D data matrix and rearranges the coordinates from Z-X-Y to X-Y-Z where Z is the depth coordinate, X and Y are spatial coordinates. Although up-sampling and interpolation followed by smoothing filtering can also be performed to improve the image quality, we found that the segmentation does not depend on filtering. After resampling, each frame is in the X-Y coordinates arranged along the depth (depth enface). The proposed segmentation is performed on each enface frame. For each frame, the distance transform and binary maps were calculated. Also, to enhance the microvasculature contrast and improve the visualization of microcirculations, the original image was masked with the binary image map to generate high-contrast high-resolution microcirculation maps within the tissue beds. Finally, the segmented 3D data set is rearranged from X-Y-Z coordinates back to original Z-X-Y coordinates to be identical to the input OCT/OMAG data set.

Experimental results and discussions

Angiogenesis assessment in wound healing model

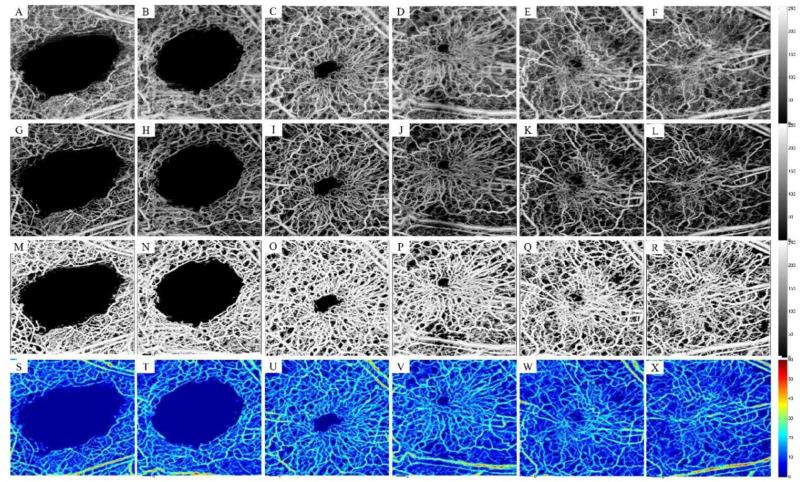
We have previously shown how OMAG can be utilized to monitor wound healing process and its various phases from a qualitative point of view [Yousefi et al., 2014]. In the following sections, we utilize the proposed segmentation method to quantify the healing process and angiogenesis. Figures 3(A-F) show the maximum intensity projection of 3D OMAG, showing the microcirculation responses during the healing process after inducing the 1 mm biopsy punch. Fig. 3(A) was captured ~10 seconds after the injury. At this moment, the blood has coagulated on the damaged blood vessels and microcirculation has been rewired from collateral vessels to support the downstream injured tissue. Figs. 3(B-F) were captured on weeks 1, 3, 4, 9 and 18 after inducing the biopsy punch. Figs. 3(G-L) show the high-contrast masked microcirculation map after segmenting the blood vessels and removing the background. It can be clearly observed that the contrast of the masked image is much higher than the original data and individual capillaries can be visually resolved. The segmented binary images are shown in Figs. 3(M-R). The vessel diameters were estimated using the distance transform and their value was calibrated using the system parameters and the maximum distance projections of the corresponding angiogenesis maps are shown in Figs. 3(S-X).

Fig. 3.

Segmentation of the wound healing model using the combined scheme. (A) Remaining microcirculation in the wound area a few seconds after inducing the punch (B-F) Angiogenesis and natural healing process on week 1, 3, 4, 9 and 18. (G-L) Corresponding high-contrast microcirculation after masking the segmented binary mask on the original data. (M-R) Binary segmented microcirculation using the combined segmentation technique. (S-X) Maximum distance transform projection map corrected for beam broadening and voxel size corresponding to the first row. Field of view is 2x2 mm².

Immediately after punch in our wound healing model, injured capillaries and blood vessels coagulate and prevent tissue from bleeding. After one week, neovasculature within granulation tissue can be clearly observed that takes the form of a “pile of woven wool”. At the second week, wound contraction has already started pulling the neovasculature within the granulation tissue together and the “pile of wool” starts to open up. As the wound healing process continues towards the center of the wound, more granulation tissue is formed at the wound edges followed by neovascularization and angiogenesis. At maturation phase (around week-18), some new vessels have grown larger while others have disappeared due to apoptosis.

We quantified the diameter of newly formed vessels in the wound area as well as vessel area density in the region of interest. The region of interest was defined as a circular shape around the wound location. We manually located the center of the circle to be roughly at the center of the wound. The radius of the circle was selected large enough to cover the wound and was kept fixed in between all samples. The vessel diameter values were calculated by finding the vessel centerline using binary skeletonizing algorithm [Gonzalez and Woods, 2002] and the values of the distance transform on the skeleton map were used as an estimate of the vessel diameter. Fig. 4(A) shows the overlaid vasculature captured at the 3^rd week after the injury and its skeletonized map is shown in Fig. 4(B). The skeleton map is an estimate of the centerline location of blood vessels. Fig. 4(C) shows the distance transform corresponding to the binary image of Fig. 4(A) and the corresponding distance transform on the vessel centerlines are shown in Fig. 4(D). The vessel diameter estimates are given in auxiliary units and the exact value can be found after correcting for system parameters and beam broadening for each voxel. For our purpose, the relative values of the estimated vessel diameter over the time should be valid. The diameter of the new vessels in the wound area can be quantified by forming the histogram distribution of Fig. 4(A).

Fig. 4.

Segmented blood vessels on 3^rd week. (B) Skeletonized vessel map. (C) Distance transform in the ROI. (D) Distance transform on the skeleton map of (B). Field of view is 2x2 mm².

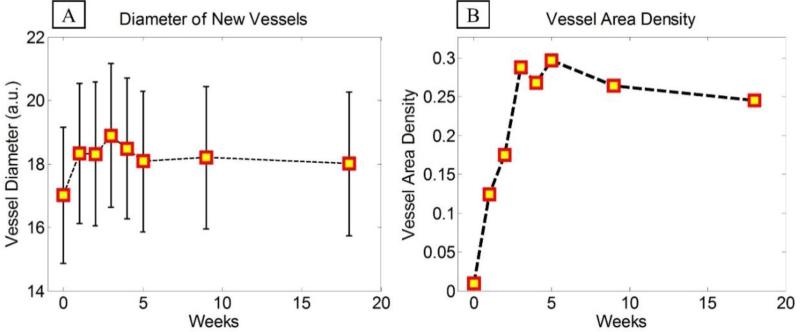
Similar procedure was performed on all other images and the distribution of vessel diameter was estimated for each experiment. It can be observed in Fig. 5(A) that during the healing process, vessel diameters increase for a couple of weeks until the wound area closes (3^rd week) and then decreases and stabilizes as the tissue matures and wound heals. Fig. 5(B) shows the changes in the vessel area density in the wound area during the healing process. The vessel area density was estimated by finding the ratio of the vessel area (nonzero maps on the binary image) divided by the total imaging area within the region of interest around the initial wound injury. Similar to the diameter changes, first the vessel area density monotonically increased until the wound area was fully closed. Then, the area density reduced due to tissue maturation and recess of some vessels within the granulation tissue.

Fig. 5.

(A) Diameter of new vessels in the wound area shown in the form of mean ± standard deviation (B) Average vessel area density in the wound area during the healing process.

Test on fundus camera images

Besides visual and qualitative validation of segmentation results, segmentation algorithms can be quantitatively assessed by comparing the results with gold standard methods of segmentation. Since no gold standard technique exists in digital segmentation, one way is to compare the results with those from manual segmentation done by trained experts. Although manual segmentation from one expert can be erroneous, combination of manual segmentations done by multiple users can reduce the error and therefore can be utilized as the gold standard. To the best of our knowledge, there is no standard OCT microangiography database. Therefore, we tested our algorithm on the Utrecht University's digital retinal images for vessel extraction (DRIVE) database [Staal et al., 2004; Niemeijer et al., 2004]. The DRIVE database consists of 40 fundus camera retina images, which are frequently used by many researchers to test the segmentation algorithms to extract blood vessel information. The photographs in the DRIVE database were obtained from a diabetic retinopathy screening program in The Netherlands. Briefly, the screening population consisted of 400 diabetic subjects between 25-90 years of age. 40 photographs have been randomly selected, of which 33 do not show any sign of diabetic retinopathy while 7 show signs of mild early diabetic retinopathy. The images were acquired using a Canon CR5 non- mydriatic 3CCD camera with a 45 degree field of view (FOV). Each image was captured using 8 bits per color plane at 768 by 584 pixels. The FOV of each image is circular with a diameter of approximately 540 pixels. For this database, the images have been cropped around the FOV. For each image, a mask image is provided that delineates the FOV. For the set of 40 images, manual segmentations are available that can be used as the gold standard. All human observers who manually segmented the vasculature were instructed and trained by an experienced ophthalmologist. They were asked to mark all pixels for the vessels if they felt at least 70% certain. All of the images contained in the database were actually used for making clinical diagnoses.

We should note that our segmentation technique is originally developed for OCT microangiography but we can generalize the algorithm to other modalities such as retinal fundus images. Since the main characteristic of retinal vessels in fundus camera is their contrast from surrounding tissue background and their low intensity due to light absorption, our segmentation technique is sensitive to the preprocessing stage that converts the fundus image to an image similar to those generated by optical microangiography.

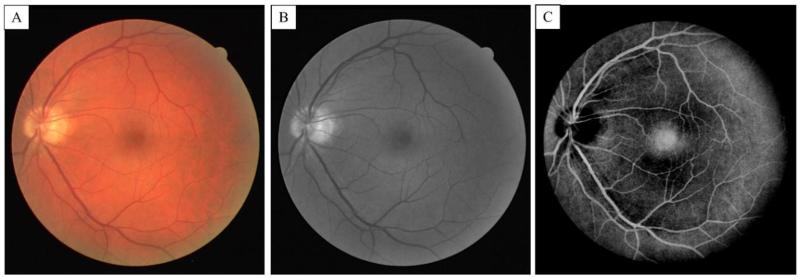
In our pre-processing algorithm, the green channel of the fundus images was utilized and a 3*3 Gaussian smoothing filter followed by adaptive histogram equalization was performed to generate a uniform distribution of pixels. Because of absorption properties of red blood cells and retina tissue, the green channel of color fundus images usually generates the highest contrast between blood vessels and background [Hoover et al., 2000]. Finally the image was inverted to make blood vessels appear brighter than the adjacent tissue. Figs. 6(A-B) show the color and the corresponding green channel of a retinal fundus image from the DRIVE dataset, respectively. The corresponding contrast-enhanced inverted image after intensity inversion and masking is shown in Fig. 6(C). It can be observed that the retinal vessels have been enhanced while other features in the image such as the low-intensity foveal region also appear bright. In this case, we expect that sensitivity of our segmentation technique may drop while specificity should be acceptable.

Fig. 6.

(A) Fundus color image of retina from the DRIVE data set (B) The green channel of the color image. (C) Contras-enhanced and inverted fundus image from the green channel after the pre-processing filtering.

Figure 7 shows segmentation results on the enhanced image shown in Fig. 6(C). Figs. 7(A-C) show segmentation results using Hessian vesselness filters, intensity-based filter and the proposed hybrid methods, respectively. The manual segmentation (gold standard) is also shown in Fig. 7(D) for comparison. It can be observed that intensity-based technique has some errors around the low-intensity fovea region as well as small and low-contrast vessels. On the other hand, Hessian vesselness filters show better results at fovea and smaller vessels while they have error near the optic nerve head where the intensity variations are high. Also, the Hessian segmentation shows some errors near vessel branching edges. The proposed hybrid method takes these limitations into account and minimizes the error generated by both algorithms.

Fig. 7.

Segmentation results. (A) Hessian filter. (B) Intensity segmentation. (C) Combined Hessian and intensity filter. (D) Manual segmentation.

We tested our algorithm on all 40 images in the DRIVE dataset and measured sensitivity, specificity and accuracy of our algorithm with respect to the manual segmentations. Table 1 summarizes the results that indicate true and false segmentation rates given the manual segmentation results. The following parameters are defined as following. The sensitivity or true positive rate is defined as the rate of pixels that were segmented by both manual and automatic segmentation techniques (true positive) divided by total number pixels segmented by the gold standard. Higher sensitivity indicates how similar the manual and automatic techniques are in terms of segmenting the blood vessels. The specificity or true negative rate is defined as the rate of pixels that were correctly not segmented by both techniques (true negative) divided by the total number of non-vessel pixels. Finally, the accuracy is defined as the rate of pixels correctly segmented and not segmented by the algorithm (true positive + true negative) divided by the total number of pixels in the image.

Table 1.

Segmentation results using the proposed segmentation technique.

	Manual Segmentation 1	Manual Segmentation 2
Sensitivity	0.77 ± 0.05	0.79 ± 0.04
Specificity	0.95 ± 0.02	0.95 ± 0.01
Accuracy	0.93 ± 0.02	0.94 ± 0.01

We can see from Table 1 that the sensitivity of our proposed method is relatively low, as we predicted. This is mainly due to the assumptions we made on the fundus images regarding the intensity of retinal vessels. On the other hand, some small vessels that were represented by only one pixel in the manual segmentation images were not detected because of their relatively low contrast against background and morphological opening operations performed on the images. However, the specificity and accuracy of our proposed method are relatively high which indicates that most of the large and high contrast vessels were accurately segmented.

Although our technique is not meant for vessel segmentation of fundus camera images, we compared our results with a few techniques in the literature that worked on the same data set to get a better sense on how existing methods perform on the DRIVE dataset. The first column in Table 2 indicates the method used for retinal vessel segmentation from DRIVE fundus camera image database and the second column indicates the accuracy results of its corresponding technique. We borrowed these results for comparison from the Image Sciences Institute's website.

Table 2.

Comparison between the performance accuracy of several techniques in the literature.

Method	Accuracy
Staal et al., (2004)	0.944
Niemeijer et al., (2004)	0.941
Zana et al., (2001)	0.937
Jiang et al., (2003)	0.921
Martínez-Pérez et al., (1999)	0.918
Chaudhuri et al., (1989)	0.877
Al-Diri et al., (2009)	0.925
Hybrid Hessian [This study]	0.933

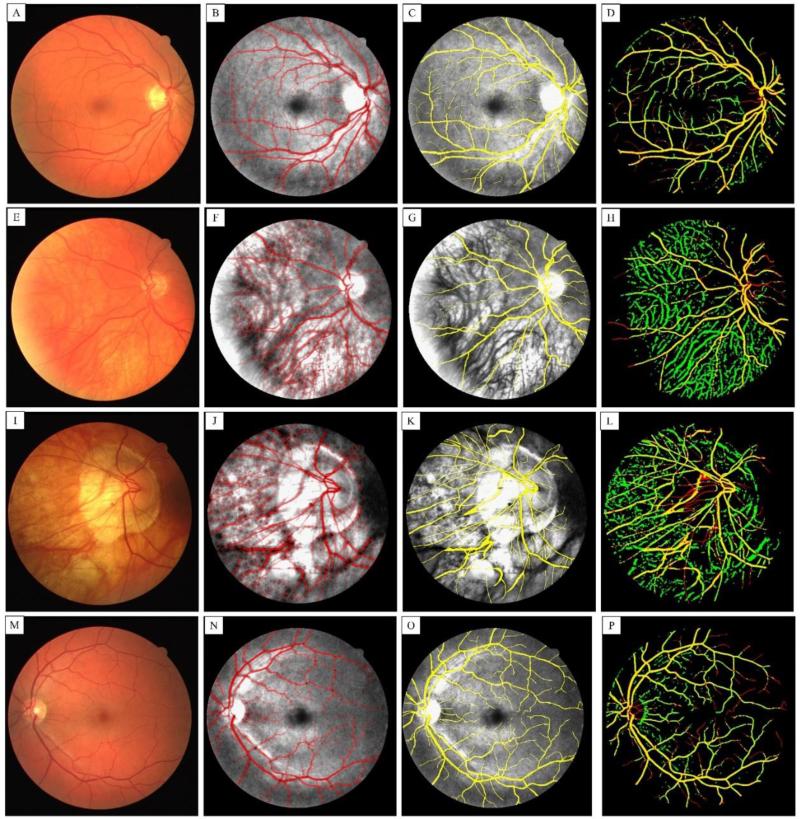
Figure 8 shows the performance of our segmentation technique compared with manual segmentation (gold standard) and possible cases that our technique can fail. The first column shows fundus camera images (Figs. 8 (A), (E), (I) and (M)). The second column shows the segmentation results using our combined technique overlaid on top of the equalized green channel where red color indicates segmented vessel and gray areas show non-segmented background (Figs. 8 (B), (F), (J) and (N)). The third column shows the result of manual segmentation (gold standard) coded with yellow color overlaid on the green channel of fundus image (Figs. 8 (C), (G), (K) and (O)). The last column shows the corresponding segmentation comparison where the yellow color indicates true positive, red color indicates true negative and green value indicates false positive segmentation results (Figs. 8 (D), (H), (L) and (P)). For the cases that retinal layer was very thin (second and third rows), the choroidal vasculature would also be segmented into the image, giving increased the rate of false positives. It can be observed that our segmentation technique performed very well on main and large retinal vessels. However, our technique deviated from the manual segmentation results on small vessels with a very low contrast on the actual images. When retinal layer was thin due to macular degeneration, choroidal vasculature were more obvious in the green channel and they were segmented by our algorithm. However, the users who performed the manual segmentation could avoid doing so by having a prior knowledge about those vessels. Other cases that manual and automatic segmentation techniques did not match were at the location of the optic disk head where the intensity was a much higher than normal due to nerve loss. In addition, low contrast appearance of vessels in the disk head caused failure in segmenting these vessels during our pre-processing step.

Fig. 8.

First column (A, E, I and M) shows fundus camera of four different retina images from the DRIVE dataset. The second column (B, F, J and N) shows the corresponding segmentation results using our combined technique overlaid on top of the equalized green channel where red color shows segmented vessel and gray areas show non-segmented background. The third column (C, G, K and O) shows the result of manual segmentation (gold standard) coded with yellow color overlaid on the green channel of fundus image. The last column (D, H, L and P) shows the corresponding segmentation comparison where the yellow color indicates true positive, red color indicates true negative and green value indicates false positive segmentation results. For the cases that retina layer was thinned (second and third row), the choroid vasculature have also been segmented into the image.

In general, the segmentation results are highly correlated with the vessel appearance resulted from our pre-processing step. However, if the vessels are clearly contrasted from their surrounding tissue, our proposed technique can be utilized to efficiently segment those vessels. Since the DRIVE is a standard dataset and manual segmentation results are available as gold standard, we performed our method on that dataset to challenge the efficiency and compare the results with the existing techniques.

Conclusions

In this paper, we have proposed a modified Hessian-based vesselness model to segment blood vessels within the tissue beds. Since the estimated vessel diameter and other geometrical parameters highly depend on the maximum scale parameter in the Hessian vesselness model, we have proposed a correction segmentation technique. The efficiency of our algorithm was tested on angiogenesis in a wound healing model to provide an ability to quantify the healing process after a biopsy punch. To quantify the accuracy of the proposed segmentation technique, standard dataset with manual segmentation results from a publicly available retina fundus images were selected. The segmentation algorithm was compared with the manual segmentation provided by the experts and achieved a reasonably good results compared to the results of other techniques reported on the datasets. Our segmentation technique is not limited to OCT angiography and can be applied to other imaging techniques with similar vasculature pattern such as contrast-enhanced multi-photon microscopy, 3D Doppler ultrasound and photo-acoustic angiography.

Highlights.

• Automatic segmentation of OCT-based angiograms for blood vessel quantification.

• Resampling along the depth to minimize tail artifacts presented in OCT.

• Compounding Hessian vesselness filters with intensity-based techniques.

• Useful in quantitative assessment of tissue microvessels and capillaries.