Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2016 May 1.
Published in final edited form as: J Magn Reson Imaging. 2014 Jun 23;41(5):1447–1453. doi: 10.1002/jmri.24675

Fast Susceptibility-Weighted Imaging (SWI) with 3D Short-Axis Propeller (SAP)-EPI

Samantha J Holdsworth 1, Kristen W Yeom 2, Michael E Moseley 1, S Skare 3
PMCID: PMC4275419  NIHMSID: NIHMS601447  PMID: 24956237

Abstract

Purpose

Susceptibility-Weighted Imaging (SWI) in neuroimaging can be challenging due to long scan times of 3D Gradient Recalled Echo (GRE), while faster techniques such as 3D interleaved EPI (iEPI) are prone to motion artifacts. Here we outline and implement a 3D Short-Axis Propeller Echo-Planar Imaging (SAP-EPI) trajectory as a faster, motion-correctable approach for SWI.

Methods

Experiments were conducted on a 3T MRI system. 3D SAP-EPI, 3D iEPI, and 3D GRE SWI scans were acquired on two volunteers. Controlled motion experiments were conducted to test the motion-correction capability of 3D SAP-EPI. 3D SAP-EPI SWI data were acquired on two pediatric patients as a potential alternative to 2D GRE used clinically.

Results

3D GRE images had a better target resolution (0.47 × 0.94 × 2mm, scan time = 5min), iEPI and SAP-EPI images (resolution = 0.94 × 0.94 × 2mm) were acquired in a faster scan time (1:52min) with twice the brain coverage. SAP-EPI showed motion-correction capability and some immunity to undersampling from rejected data.

Conclusion

While 3D SAP-EPI suffers from some geometric distortion, its short scan time and motion-correction capability suggest that SAP-EPI may be a useful alternative to GRE and iEPI for use in SWI, particularly in uncooperative patients.

Keywords: Susceptibility-Weighted Imaging, SWI, Short-Axis Propeller EPI, SAP-EPI, motion correction

Introduction

Susceptibility-weighted imaging (SWI) has been utilized for evaluating intracranial blood products, mineralization, thromboses, venous structures, vessels and other sources of susceptibility effects [1–2]. A SWI image is typically obtained by acquiring a high-resolution, flow-compensated, 3D Gradient Recalled Echo (GRE) (T2*-weighted) image, and then by combining the phase and magnitude images.

SWI has proven useful in a variety of clinical settings, including in the evaluation of arterial venous malformations, occult venous disease, multiple sclerosis, trauma, tumors, and functional brain imaging [3–9]. However, its clinical implementation for neuroimaging can be challenging due to the long scan time of the 3D GRE sequence (ranging from 5 to 10 minutes at 3T).

A 3D GRE-EPI trajectory is a faster alternative to 3D GRE. However, EPI is prone to off-resonance artifacts such as signal drop-out, image blurring, and geometric distortion even when coupled with parallel imaging. Interleaved (‘multi-shot’) EPI (iEPI) approaches can help to reduce distortion artifacts (at the expense of scan time), however – like standard GRE – even small head motion can cause phase errors that typically result in ghosting artifacts and unreliable phase maps. Navigator-based phase correction can help mitigate image ghosting; however, residual non-equidistant sampling in k-space may require excessive oversampling or averaging [10].

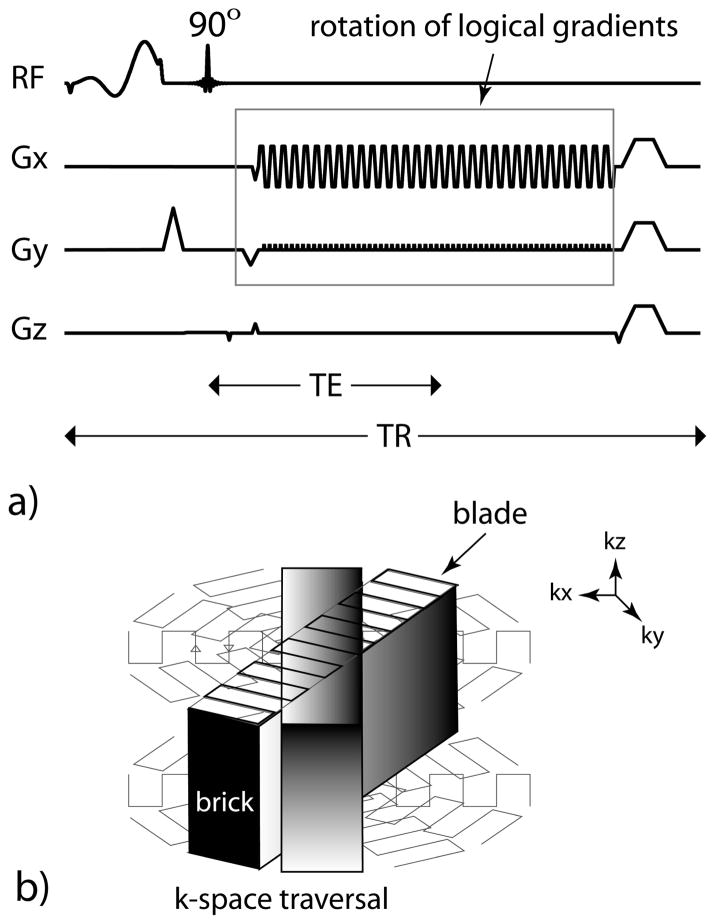
Here, we extend the short-axis readout propeller (SAP)-EPI trajectory [11] (Fig. 1) to 3D, and explore it as an alternative approach to 3D GRE and 3D GRE-EPI sequences used for SWI processing. In SAP-EPI, overlapping ‘propeller blades’ are acquired to produce the combined k-space data that supports the desired target resolution. SAP-EPI reduces distortions compared with EPI by shortening the trajectory along the width of the blade. Ignoring slew rate limitations, a SAP-EPI scan offers a distortion reduction of Nx/Nfreq over a conventional EPI scan, where Nx is the target acquisition size and Nfreq the width of the SAP-EPI blade in the frequency encoding direction. Further distortion reduction can be achieved in SAP-EPI via parallel imaging methods such as generalized autocalibrating partially parallel acquisitions (GRAPPA) [12–13].

Figure 1.

Figure 1

Open in a new tab

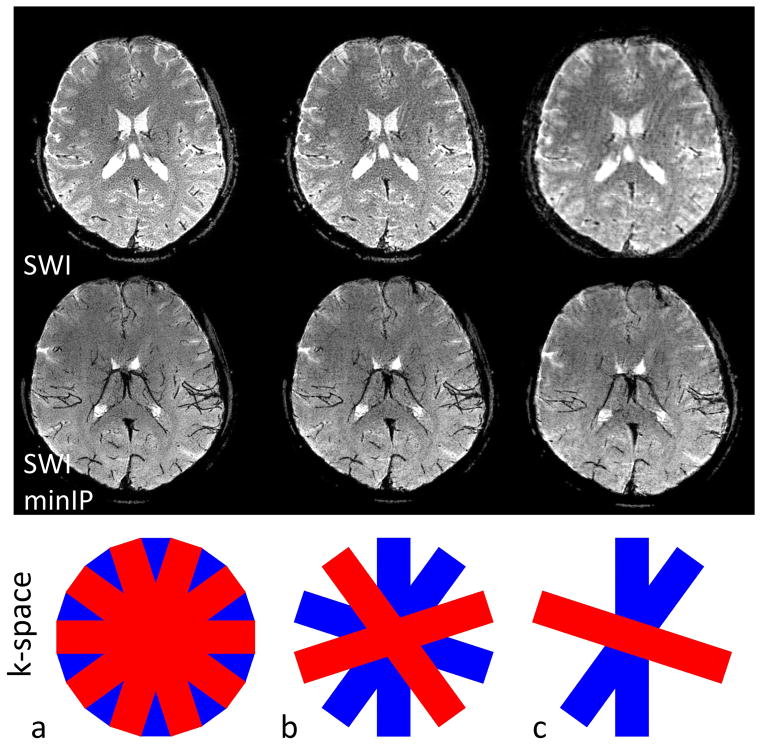
3D SAP-EPI SWI (a) pulse timing diagram and (b) k-space traversal. One blade is acquired for every z-partition – resulting in one ‘brick’, which is then rotated.

SAP-EPI also has robust motion-correction properties. In SAP-EPI, each blade is acquired at the full image FOV, and thus there is greater data consistency within each blade compared to Cartesian or iEPI where motion can induce harmful gaps in k-space – resulting in image ghosting. This improved data consistency in SAP-EPI makes the risk of ‘intra-blade’ motion and image ghosting small. To achieve a 3D volume, a set of SAP-EPI blades are phase encoded in the slice direction to form a ‘brick’ acquired with full brain coverage in a few seconds – making the risk of ‘intra-brick’ motion not entirely non-negligible. However, due to the acquisition of several rotated, overlapping bricks (to fill the desired resolution in 3D) that heavily sample the center of k-space, one may be able to ‘throw out’ a select number of motion-corrupted bricks without sacrificing appreciable image quality. To include a safety margin, scan time can be traded for increased robustness against motion by increasing the number of overlapping bricks.

Nevertheless, the greatest risk of motion occurs between bricks – that is, ‘inter-brick’ motion. Since each brick represents a (low-resolution) full FOV 3D image, it is possible to correct for motion between bricks using a standard 3D rigid-body realignment procedure. Here, gaps in k-space can also occur following the correction of rotational motion of individual bricks. However, these gaps tend to only occur in the periphery of the final assembled k-space – the effect of which is more benign than those that would propagate throughout a 3D iEPI or Cartesian encoding scheme.

The objective of this study was to present human 3D SAP-EPI SWI images, to implement and outline a parallel-imaging enhanced 3D SAP-EPI reconstruction procedure, and to demonstrate initial motion-corrected 3D SAP-EPI SWI human data from controlled rigid-body motion experiments.

Methods

Pulse sequence

The 3D SAP-EPI pulse sequence timing diagram and k-space trajectory are shown in Figure 1. For each repetition (TR), an imaging echo is formed. During each echo formation, a SAP-EPI sampling trajectory acquired with a GRAPPA acceleration factor, R, is played out to acquire a specific segment or blade of k-space (Fig. 1b). In our current implementation, each brick can be described as being acquired with a single-shot technique with R averages (NEX), whereby the averages are different interleaves – to enable Nyquist-ghost correction and GRAPPA-weights [12–13] estimation and application. Here, the interleaves are separated in the same way as traditional interleaved EPI; however, in this case each interleaf is reconstructed using parallel imaging and acts as a single fully sampled k-space [14]. A slice-encoding gradient is then played out to form a stack of blades (or brick) for a given blade angle. Overlapping bricks are then acquired by rotating the logical x-y gradients. Here, the brick also acts as a navigator since it samples the central portion of k-space. With enough bricks chosen for a given target resolution, a full 3D k-space is formed after gridding.

Image reconstruction

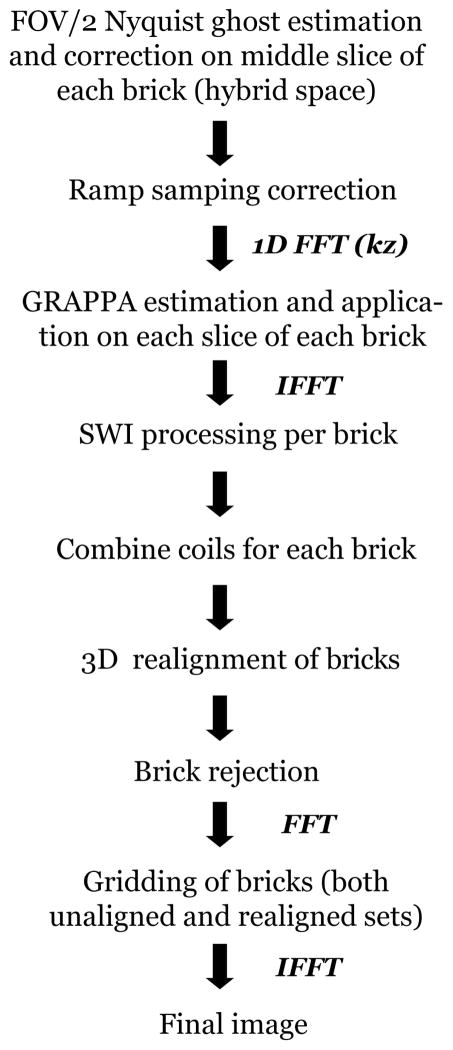
Figure 2 outlines the reconstruction procedure. All image reconstruction was performed using compiled and threaded MATLAB code (version 7.8.0; Mathworks, Natick, MA, USA). All of the processing steps described below used MATLAB code developed in-house.

Figure 2.

Figure 2

Open in a new tab

3D SAP-EPI reconstruction pipeline.

Nyquist-ghost correction of each fully-sampled brick (made up of R interleaves in the phase encoding direction) was performed using an image entropy-based, iterative calibration scheme [15]. The Nyquist-ghost calibration parameters were first estimated on the middle slice in hybrid-space, and these parameters were used to correct for each brick. Ramp sampling correction was then performed to correct for the non-uniformally sampled k-space points of each blade. After performing a 1D FFT along kz, GRAPPA weights were estimated on each brick, with an R = number of interleaves (NEX) = 4. The GRAPPA weights derived from a given brick were subsequently applied on each interleave of the same brick, yielding R brick instances (NEX). The reason behind this split-up process was to allow for some small amount of motion correction between the interleaves.

SWI-processing was performed on each coil image on a per-brick basis by generating a phase mask of each brick using a 2D Hanning window [1–2]. The phase mask was multiplied by the magnitude brick-image five times to produce individual SWI-processed bricks. The coils for each brick were then combined using the sum-of-squares. Motion correction between bricks was optionally performed in 3D using a sum-of-squares metric [16], using a reference (uncorrupted) brick with the highest signal intensity. Finally, the bricks were gridded to produce the final full-resolution image.

Volunteer and patient studies

With institutional review board (IRB) approval, all experiments were conducted on two healthy adult volunteers and two pediatric patients using a 3T whole-body GE MR750 Discovery (GE Healthcare, Milwaukee, WI) and an eight-channel head coil. Informed consent was obtained from the volunteers, and informed parental consent and assent were obtained for the pediatric patients.

3D SAP-EPI, 3D GRE, and 3D iEPI scans were acquired on 31 year old and 28 year old male volunteers. For the volunteer studies, the following scan parameters were used for the SAP-EPI and iEPI sequence: matrix size = 256 × 256, TR/TE/FA = 55ms/20ms/20º, FOV = 24 × 24 × 12.8 cm3, 64 z-partitions, slice-thickness = 2 mm. The SAP-EPI sequence used 8 blades of width 64, R = NEX = 4, leading to a brick frame rate of 3.5 s, a target resolution of 0.94 × 0.94 × 2 mm, and a scan time of 1:52 min. The EPI sequence used 32 interleaves for an equivalent resolution and scan time. A high resolution flow-compensated GRE sequence was acquired for comparison (matrix size = 512 × 256, rectangular FOV = 0.75, TR/TE/FA = 37ms/20ms/20º, z-partitions = 32, slice-thickness = 2 mm, corresponding to a target resolution of 0.47 × 0.94 × 2 mm and a scan time of 5 min). Note that, since we strived to keep the echo time of all sequences fixed for comparison (TE = 20ms), the 3D SAP-EPI and iEPI sequences were acquired with the minimum in-plane resolution required to achieve this echo time – as such, the 3D SAP-EPI and iEPI sequences achieved half the in-plane resolution (0.94 mm) of the 3D GRE sequence (0.46 mm). A side-by-side comparison was performed by a board-certified neuroradiologist with a certificate of added qualification (7 years-experience) to assess the primary diagnostic qualitative differences between the datasets.

To test the initial performance of 3D SAP-EPI clinically, 3D SAP-EPI SWI images were also acquired on 10 year old and 17 year old pediatric patients at the end of the existing clinical protocol, which included a routine 2D T2*-weighted GRE sequence (TE = 15 ms, TR=650 ms, flip angle=20º, slice thickness = 5 mm, 1 mm gap, FOV = 18–24 cm, rectangular FOV = 0.75, matrix = 384×168, BW=15 kHz, with flow compensation enabled, scan time = 1:50 minutes). 3D SAP-EPI data were acquired with the same parameters as used for the volunteer, except that an R = NEX = 3 was used, corresponding to a scan time of 1:24 min. A neuroradiologist compared the 3D SAP-EPI and 2D GRE images for difference in diagnostic quality when assessing for hemorrhagic lesions, if present, and overall quality of vascular delineation.

Controlled motion experiments

On the first volunteer, a second 3D SAP-EPI dataset was acquired (with identical imaging parameters) after the volunteer was asked to perform a through-plane head rotation of ~10º. Brick data were mixed, such that every second brick was chosen from the rotated dataset. Each brick was 3D motion corrected (in the image domain) against the first brick prior to gridding (in k-space). The second volunteer was asked to move their head up to ~30º five times (in both a through- and in-plane direction) throughout the duration of the 3D SAP-EPI scan. A neuroradiologist assessed the datasets on subjective image quality.

Results

Figure 3 shows a side-by-side comparison between the SWI-processed images acquired with 3D iEPI, 3D SAP-EPI, and 3D GRE. The target in-plane resolution was highest for the 3D GRE scan (resolution = 0.47 × 0.94 × 2 mm, scan time = 5minutes), however the 3D iEPI and 3D SAP-EPI scans were acquired with twice the brain coverage and in less than half the scan time (resolution = 0.94 × 0.94 × 2mm, scan time = 1:52min).

Figure 3.

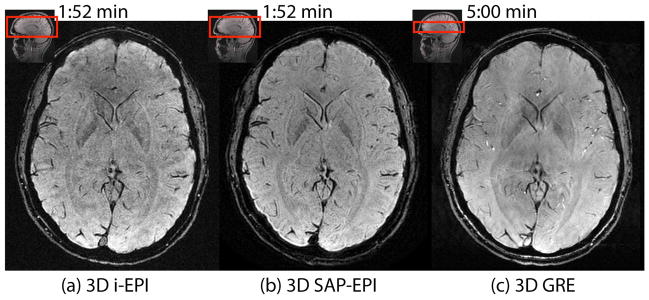
Figure 3

Open in a new tab

SWI-processed (a) 3D interleaved EPI (32 shots), (b) 3D SAP-EPI (R = NEX = 4, 8 blades), and (c) reference 3D GRE images. Note that the 3D GRE image was scanned with half the coverage of i-EPI and SAP-EPI and with a longer scan time –however it was acquired with half the voxel size of these sequences in the frequency encoding direction.

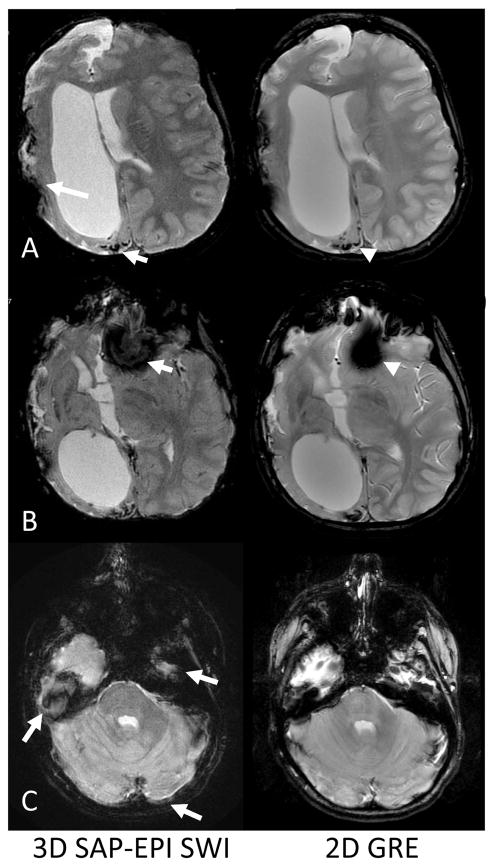
Figure 4 shows 3D SAP-EPI data acquired on a 10 year old pediatric patient with moya moya disease, with the routine 2D GRE sequence as a reference. Multiple foci of hemosiderin associated with prior cerebral ischemic injury along the right posterior parieto-occipital region are well-delineated by the 3D SAP-EPI image (Fig. 4a). While the target through-plane resolution is higher for 3D SAP-EPI, artifacts are prominent in areas of susceptibility, especially along the right fronto-temporal regions of surgical changes and at the skull base regions, including anterior and middle cranial fossae (Fig. 4b-c).

Figure 4.

Figure 4

Open in a new tab

Comparison of 2D GRE and 3D SAP-EPI SWI. A. A 10-year old boy presenting after right extracranial-intracranial (EC-IC) bypass surgery for moya moya disease showed extensive old right cerebral ischemic injury. Abnormal hemosiderin deposition at site of prior cortical ischemic injury is well-delineated by the SAP-EPI (short arrow) and comparable to standard 2D GRE used for routine MRI (arrowhead). Note artifacts arising from right EC-IC surgical changes (long arrow). B. Inferiorly, note increased signal drop-out near the anterior cranial fossa (arrow) compared to 2D GRE (arrowhead).

C. More inferiorly, blurring artifacts characteristic of SAP-EPI are shown in the middle cranial fossa, in the posterior brain, and posteriorly along the petrous bone (arrows).

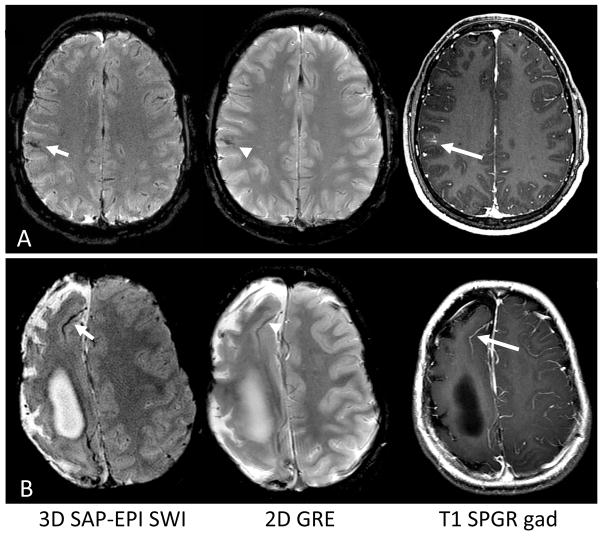
Figure 5a shows data acquired on the 17 year old patient whereby 3D SAP-EPI SWI improved conspicuity of a developmental venous anomaly compared with 2D GRE, as confirmed by the T1 contrast-enhanced image. Figure 5b shows additional images of the 10 year old patient from Figure 4 but at a higher axial plane. Here, deoxyhemoglobin associated a leptomeningeal collateral characteristic of moya moya disease is more conspicuous on 3D SAP-EPI SWI compared to 2D GRE.

Figure 5.

Figure 5

Open in a new tab

Improved delineation of vascular structures by SWI-processing of SAP-EPI. A. A developmental venous anomaly is seen in a 17-year old boy. This anomalous congenital venous structure is more clearly identified as a dark, curvilinear structure on the SWI-processed image (short arrow) as compared to 2D GRE (arrowhead) and confirmed by contrast-enhanced T1 SPGR image (long arrow). B. Right frontal leptomeningeal collateral vessel is more clearly delineated by SWI (short arrow) compared to 2D GRE (arrowhead) and confirmed by T1 contrast-enhanced image (long arrow) in a 10-year boy with old right cerebral brain ischemic injury from underlying moya moya disease.

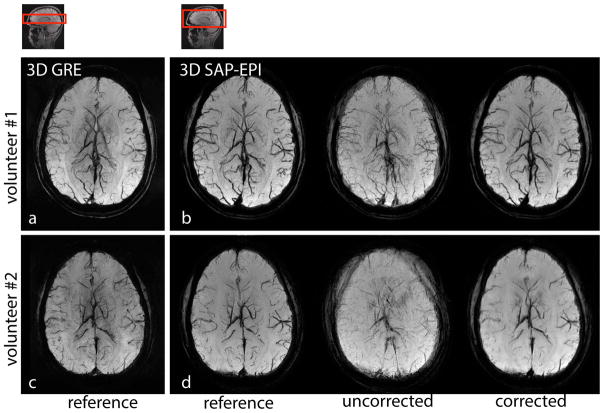
Figure 6 depicts motion corrected 3D SAP-EPI SWI minimum intensity projection (minIP) datasets alongside reference (motionless) SAP-EPI and GRE datasets. Fig. 6b shows the motion-corrected ‘mixed-blade’ dataset whereby two separate unaligned datasets are retrospectively mixed and subsequently motion corrected. Fig. 6d shows a more extreme case of motion – whereby the volunteer was asked to rotate their head in various through- and in-plane directions five times during the scan, resulting in considerable blurring in the uncorrected image. The motion-corrected SAP-EPI images agree well with the reference SAP-EPI images, with the exception of some residual image blurring in the motion-corrected datasets. Note that all realigned blades were incorporated in the final reconstruction. Note also that small vessels are overall more easily depicted in the reference GRE images.

Figure 6.

Figure 6

Open in a new tab

(a) and (c) 3D GRE, (b) and (d) 3D SAP-EPI SWI minIP images of two volunteers showing the reference (motionless), motion-corrupted, and 3D motion corrected images. Volunteer #1 moved their head once during the scan (in-plane motion), and volunteer #2 moved their head through-out the scan (both in- and through-plane motion).

Figure 7 represents the stability of the final SAP-EPI image quality when bricks are rejected in the event that one or more bricks are corrupted (that is, intra-brick motion). Fig. 7a is the fully sampled SWI and SWI minIP images complete with 10 bricks, and Fig. 7b is a subset of this (5 bricks or 50% of the original number of bricks) –showing considerable immunity to undersampling. Fig. 7c shows only 3 (less uniformly-distributed) bricks remaining (30% of the original number of bricks) – showing that while the final gridded images contain undersampling artifacts and become blurred from loss of resolution, the larger vascular architecture remains mostly intact.

Figure 7.

Figure 7

Open in a new tab

3D SAP-EPI SWI and SWI minIP images acquired on a volunteer, showing (a) the fully sampled (10 brick) dataset (b) a dataset reconstructed with only half the number of acquired bricks, and (c) the same dataset reconstructed with only three bricks.

Discussion

Perhaps one of the greatest hindrances to the adoption of SWI in the clinics is the long scan time associated with standard 3D GRE used for SWI processing. On subjective evaluation from a neuroradiologist, the resolution, SNR, and geometric fidelity were highest for the GRE scans, and – in some cases – found that small vessels were more easily depicted in the GRE image. However, iEPI and SAP-EPI implemented in this work have a considerably reduced scan time and a better extent of brain coverage than GRE (64 partitions in 1:52 min for iEPI and SAP-EPI, versus 32 partitions in 5 min for GRE). Parallel imaging can be used to reduce the scan time of GRE by up to a factor of ~3 (8-channel head coil) – although this can result in a significant SNR penalty.

A shortcoming of GRE and multi-shot EPI methods is that even small motion can induce gaps throughout k-space – causing ghosting artifacts and phase errors that can affect the final SWI-processed image. SAP-EPI may be a suitable alternative to these techniques, as it helps to alleviate some of these problems. Coupled with parallel imaging, SAP-EPI permits the acquisition of a consistent motion-free blade with reduced distortion compared with EPI, and in a reduced overall scan time compared with GRE. In addition, any motion that does occur between blades can be corrected for via 3D rigid-body correction. In the event that intra-brick motion occurs (within the brick frame rate, in this case, of 3.5 s), several bricks could be thrown out with the use of an automated bad-volume scheme such as k-space entropy [17] or a GRAPPA fit error metric [18]. Rejecting 50% of the bricks of a fully sampled dataset – representing a considerable amount of motion in the clinical context – did not appear to sacrifice appreciable image quality according to a neuroradiologist, while rejecting 70% of the bricks resulted in undersampling and blurring artifacts. Note that 3D prospective-based motion correction methods that allow one to reacquire blades and/or bricks may be an alternative strategy to simply ‘throwing away’ bricks retrospectively [19–24].

A limitation of this study is that, due to scan time constraints at our pediatric hospital, we did not acquire 3D GRE scans on patients with which to compare the performance of 3D SAP-EPI. Furthermore, since we strived to keep the echo time fixed between all 3D SWI sequences (TE = 20ms) – which limited the target resolution one could achieve with 3D SAP-EPI and iEPI, the resolution of 3D GRE (0.47 × 0.94 × 2 mm) and 3D SAP-EPI/iEPI (0.94 × 0.94 × 2 mm) was not identical – making this study incompatible with a fair SNR assessment between the methods.

In addition, the performance of the motion correction capability of the 3D SAP-EPI trajectory was not systematically tested in the clinical arena. A further shortcoming of this study was the use of multiple interleaves (NEX) in the 3D SAP-EPI acquisition, which slows down the acquisition of a brick. Further work will employ the use the continuous GRAPPA sampling kernel [25], which will avoid the need for the acquisition of multiple interleaves and result in a three- to four-fold reduction in scan time for the parameters used here.

Conclusion

Here we have presented SWI images acquired with an efficient propeller-based EPI readout method called 3D SAP-EPI, which has an inherent ability to allow motion correction. While 3D SAP-EPI still suffers from some geometric distortion, its significantly shorter scan time than GRE and motion-correction capability suggest that 3D SAP-EPI may be a useful alternative to GRE for use in susceptibility-weighted imaging, particularly in uncooperative patients.

Acknowledgments

Grant support and other assistance: NIH 2RO1 NS047607-06, the Center of Advanced MR Technology at Stanford (P41 EB015891), Lucas Foundation.

References

  • 1.Haacke EM, Up Y, Cheng YC, et al. Susceptibility weighted imaging (SWI) Magn Reson Med. 2004;52:612–618. doi: 10.1002/mrm.20198. [DOI] [PubMed] [Google Scholar]
  • 2.Reichenbach JR, Venkatesan R, Schillinger DJ, et al. Small vessels in the human brain: MR venography with deoxyhemoglobin as an intrinsic contrast agent. Radiology. 1997;2004:272–277. doi: 10.1148/radiology.204.1.9205259. [DOI] [PubMed] [Google Scholar]
  • 3.Mittal S, Wu Z, Neelavalli J, et al. Susceptibility-weighted imaging: technical aspects and clinical applications, part 2. AJNR Am J Neuroradiol. 2009;30:232–52. doi: 10.3174/ajnr.A1461. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Tong KA, Ashwal S, Obenaus A, et al. Susceptibility-weighted MR imaging: a review of clinical applications in children. AJNR Am J Neuroradiol. 2008;29:9–17. doi: 10.3174/ajnr.A0786. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Zhu WZ, Qi JP, Zhan CJ, et al. Magnetic resonance susceptibility weighted imaging in detecting intracranial calcification and hemorrhage. Chin Med J (Engl) 2008;121:2021–25. [PubMed] [Google Scholar]
  • 6.Haacke EM, Mittal S, Wu Z, et al. Susceptibility-weighted imaging: technical aspects and clinical applications, part 1. AJNR Am J Neuroradiol. 2009;30:19–30. doi: 10.3174/ajnr.A1400. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Niwa T, Aida N, Takahara T, et al. Imaging and clinical characteristics of children with multiple foci of microsusceptibility changes in the brain on susceptibility-weighted MRI. Pediatr Radiol. 2010;40:1657–62. doi: 10.1007/s00247-010-1665-z. [DOI] [PubMed] [Google Scholar]
  • 8.Ong BC, Stuckey SL. Susceptibility weighted imaging: a pictorial review. J Med Imaging Radiat Oncol. 2010;54:435–49. doi: 10.1111/j.1754-9485.2010.02208.x. [DOI] [PubMed] [Google Scholar]
  • 9.Robinson RJ, Bhuta S. Susceptibility-weighted imaging of the brain: current utility and potential applications. J Neuroimaging. 2011;21:e189–204. doi: 10.1111/j.1552-6569.2010.00516.x. [DOI] [PubMed] [Google Scholar]
  • 10.Atkinson D, Porter DA, Hill DL, Calamante F, Connelly A. Sampling and [10] reconstruction effects due to motion in diffusion-weighted interleaved echo planar imaging. Magn Reson Med. 2000;44:101–109. doi: 10.1002/1522-2594(200007)44:1<101::aid-mrm15>3.0.co;2-s. [DOI] [PubMed] [Google Scholar]
  • 11.Skare S, Newbould RD, Clayton DB, Bammer R. Propeller EPI in the other direction. Magn Reson Med. 2006;55:1298–1307. doi: 10.1002/mrm.20890. [DOI] [PubMed] [Google Scholar]
  • 12.Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA) Magn Reson Med. 2002;47:1202–1210. doi: 10.1002/mrm.10171. [DOI] [PubMed] [Google Scholar]
  • 13.Qu P, Shen GX, Wang C, Wu B, Yuan J. Tailored utilization of acquired k-space points for GRAPPA reconstruction. J Magn Reson. 2005;174:60–67. doi: 10.1016/j.jmr.2005.01.015. [DOI] [PubMed] [Google Scholar]
  • 14.Holdsworth SJ, Aksoy M, Newbould R, Yeom K, Van AT, Barnes PD, Bammer R, Skare S. Diffusion tensor imaging (DTI) with retrospective motion correction for large-scale pediatric imaging. Journal for Magnetic Resonance Imaging. 2012;36(4):961–71. doi: 10.1002/jmri.23710. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Skare S, Clayton DB, Newbould RD, Moseley ME, Bammer R. A fast and robust minimum entropy based ghost correction. Proceedings of the 14th Annual Meeting of the ISMRM; Seattle. 2006. p. Abstract 2349. [Google Scholar]
  • 16.Friston KJ, Ashburner J, Frith CD, Poline J-B, Heather JD, Frackowiak RSJ. Spatial registration and normalization of images Hum. Brain Map. 1995;2:165–189. [Google Scholar]
  • 17.Holdsworth SJ, Skare S, Bammer R. On the application of phase correction and use of k-space entropy in partial Fourier diffusion-weighted EPI. 17th Annual Meeting of the ISMRM; Hawaii. 2009. p. 4617. [Google Scholar]
  • 18.Skare S. Motion Correction of a new T1-w Propeller Sequence (SE-prop). 20th Annual Meeting of the ISMRM; Melbourne, Australia. 2012. p. 5543. [Google Scholar]
  • 19.White N, Roddey C, Shankaranarayanan A, Han E, Rettmann D, Santos J, Kuperman J, Dale A. PROMO: Real-time prospective motion correction in MRI using image-based tracking. Magn Reson Med. 2010;63:91–105. doi: 10.1002/mrm.22176. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Anderson AG, III, Velikina J, Block W, Wieben O, Samsonov A. Adaptive retrospective correction of motion artifacts in cranial MRI with multicoil three-dimensional radial acquisitions. Magn Reson Med. 2013;69:1094–103. doi: 10.1002/mrm.24348. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Ward Ha, Riederer SJ, Grimm RC, Ehman RL, Felmlee JP, Jack CR. Prospective multiaxial motion correction for fMRI. Magn Reson Med. 2000;43:459–69. doi: 10.1002/(sici)1522-2594(200003)43:3<459::aid-mrm19>3.0.co;2-1. [DOI] [PubMed] [Google Scholar]
  • 22.Welch EB, Manduca A, Grimm RC, Ward HA, Jack CR. Spherical navigator echoes for full 3D rigid body motion measurement in MRI. Magn Reson Med. 2002;47:32–41. doi: 10.1002/mrm.10012. [DOI] [PubMed] [Google Scholar]
  • 23.Thesen S, Heid O, Mueller E, Schad LR. Prospective acquisition correction for head motion with image-based tracking for real-time fMRI. Magn Reson Med. 2000;44:457–65. doi: 10.1002/1522-2594(200009)44:3<457::aid-mrm17>3.0.co;2-r. [DOI] [PubMed] [Google Scholar]
  • 24.Zaitsev M, Dold C, Sakas G, Hennig J, Speck O. Magnetic resonance imaging of freely moving objects: prospective real-time motion correction using an external optical motion tracking system. Neuroimage. 2006;31:1038–50. doi: 10.1016/j.neuroimage.2006.01.039. [DOI] [PubMed] [Google Scholar]
  • 25.Skare S, Newbould RD, Nordell A, Holdsworth SJ, Bammer R. An auto-calibrated angularly continuous 2D GRAPPA kernel for propeller trajectories. Magnetic Resonance in Medicine. 2008;60(6):1457–1465. doi: 10.1002/mrm.21788. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES